基于氢储能的热电联供型微电网优化调度方法

李奇; 邹雪俐; 蒲雨辰; 陈维荣; 赵淑丹

doi:10.3969/j.issn.0258-2724.20210348

基于氢储能的热电联供型微电网优化调度方法

doi: 10.3969/j.issn.0258-2724.20210348

1.
西南交通大学电气工程学院，四川成都611756
2.
国网山西省电力公司临汾供电公司，山西临汾041000

基金项目: 国家自然科学基金（51977181）；霍英东教育基金会高等院校青年教师基金（171104）

详细信息

作者简介:
李奇（1984—），男，教授，博士，博士生导师，研究方向为轨道交通新能源技术、综合能源系统运行与控制等，E-mail：liqi0800@163.com

通讯作者:
陈维荣（1965—），男，教授，博士，博士生导师，研究方向为轨道交通新能源技术，电力系统及其自动化，燃料电池技术及应用，E-mail：wrchen@swjtu.cn

中图分类号: TM911.4
计量
- 文章访问数: 892
- HTML全文浏览量: 393
- PDF下载量: 125
- 被引次数: 4
出版历程
- 收稿日期: 2021-04-29
- 修回日期: 2021-09-05
- 网络出版日期: 2022-11-29
- 刊出日期: 2021-10-28

Optimal Schedule of Combined Heat-Power Microgrid Based on Hydrogen Energy Storage

1.
School of Electrical Engineering, Southwest Jiaotong University, Chengdu 611756, China
2.
Linfen Power Supply Company, State Grid Shanxi Electric Power Company, Linfen 041000, China

摘要

摘要:
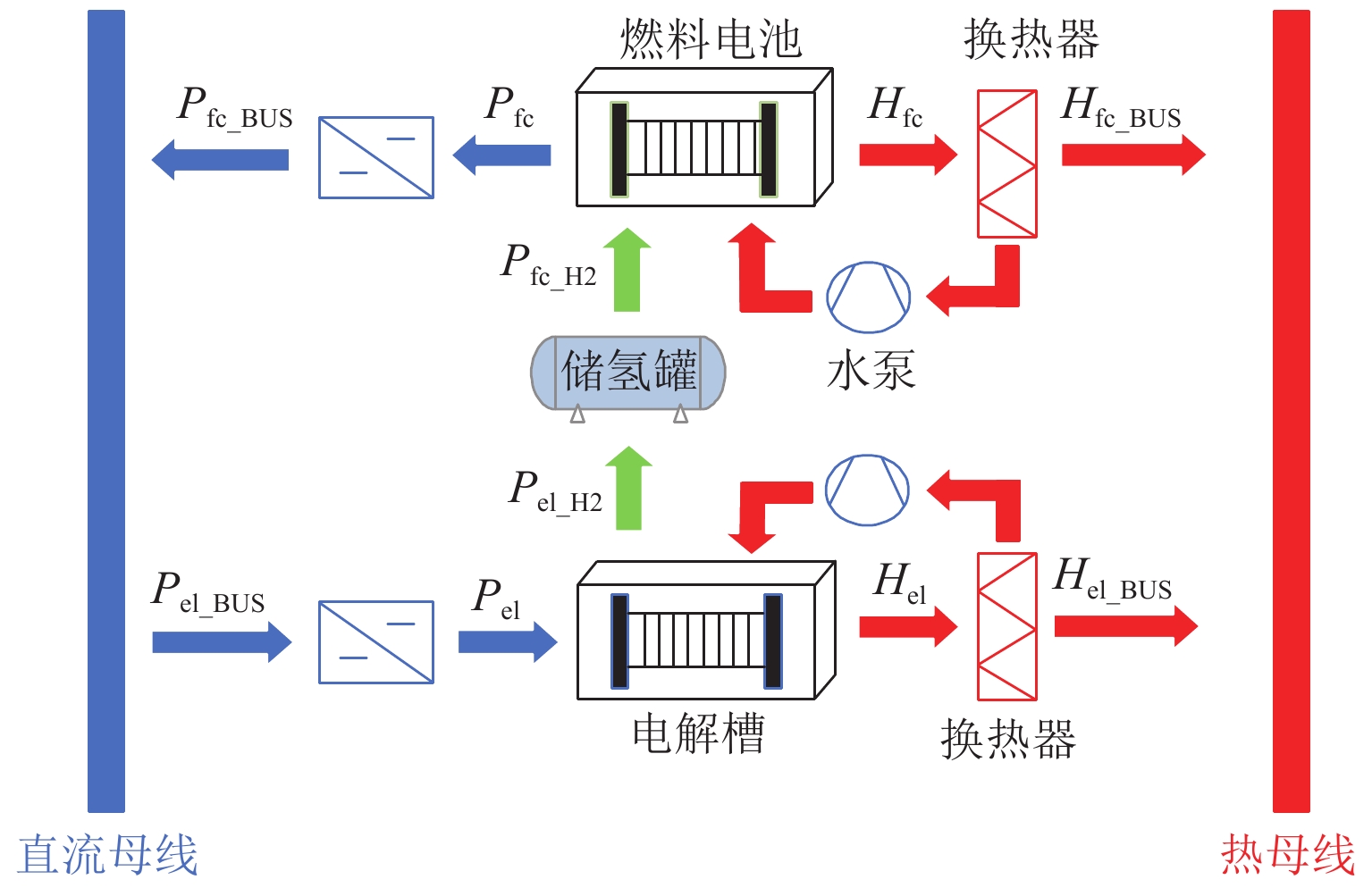
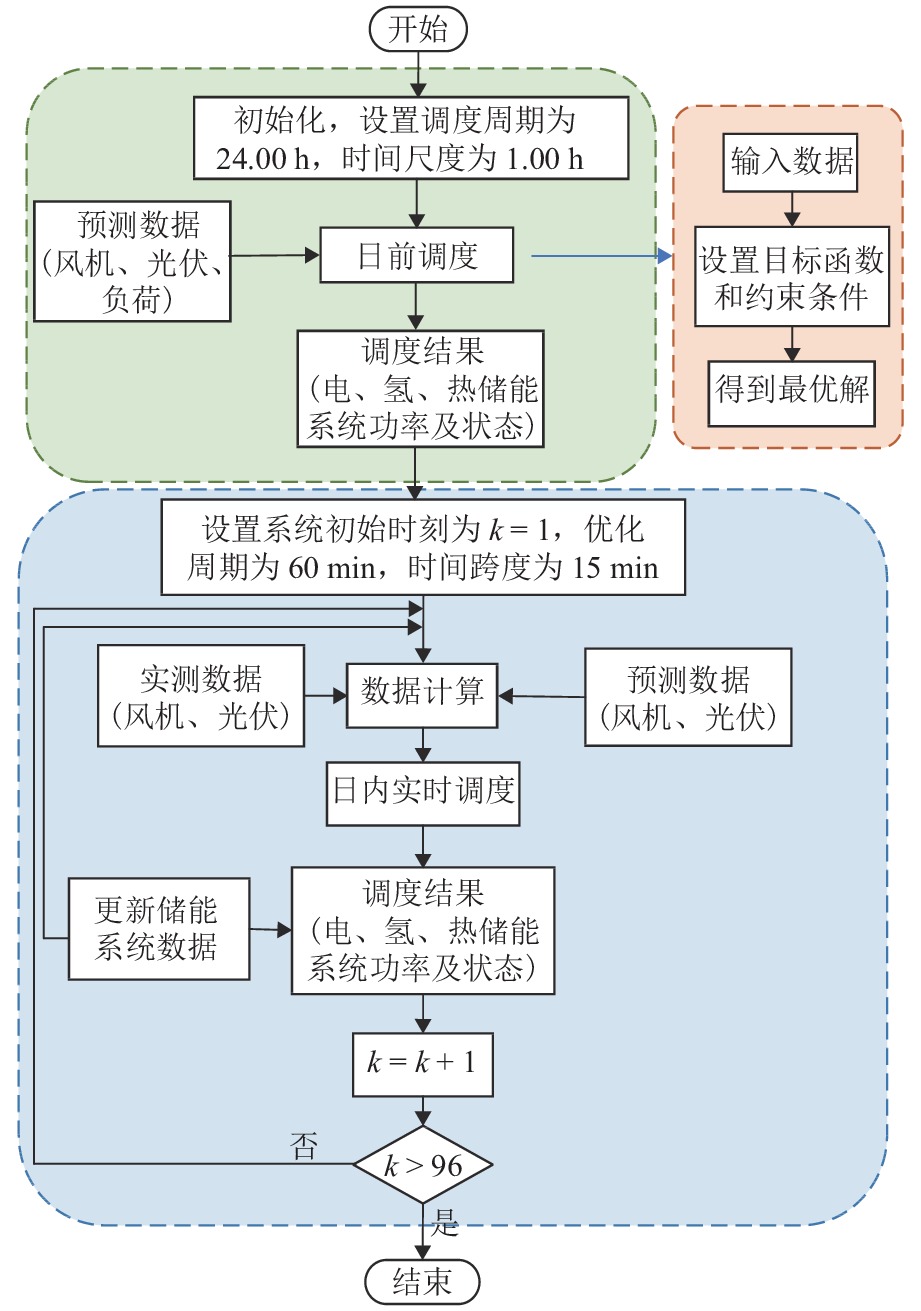
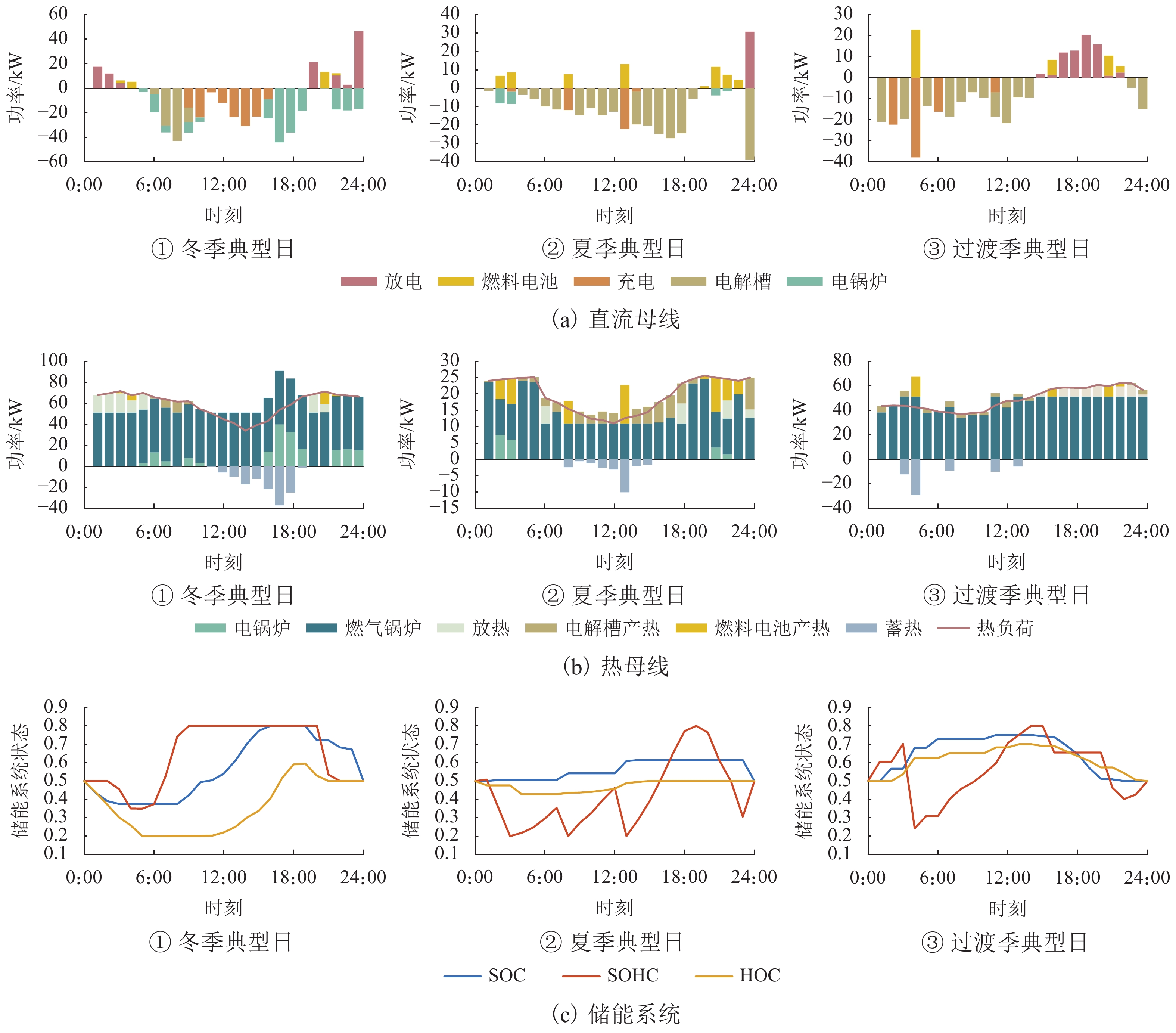
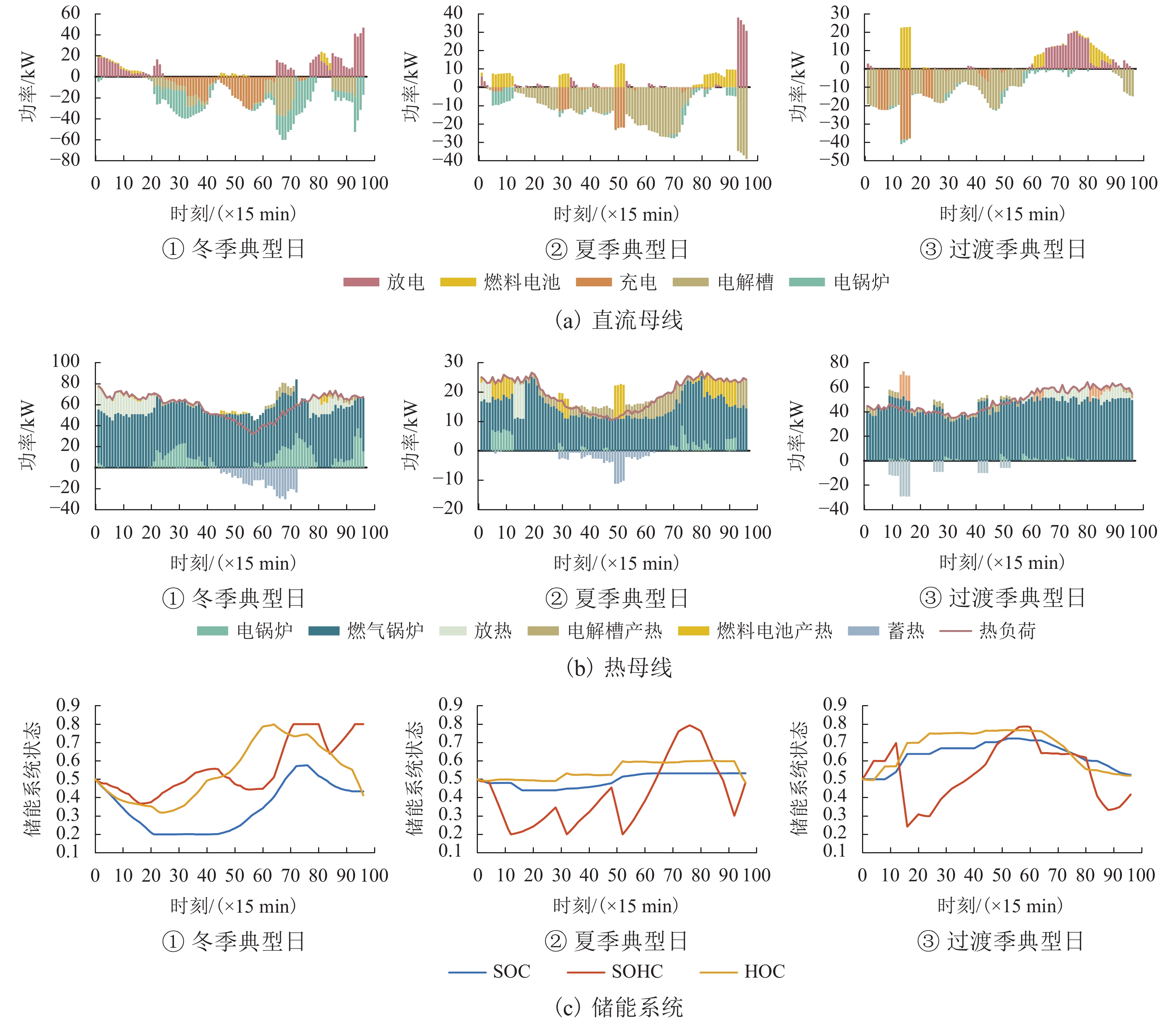
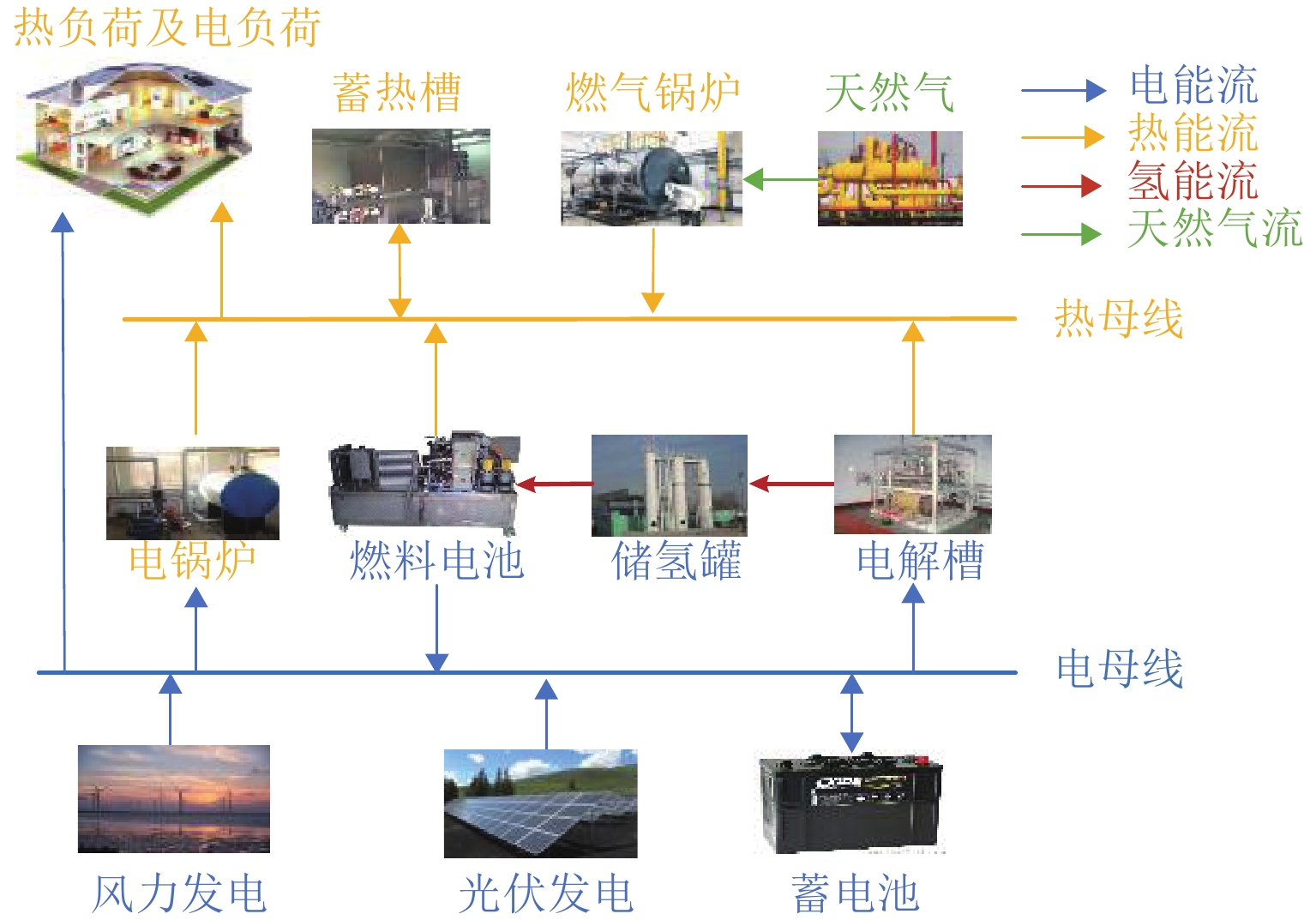
针对质子交换膜燃料电池和电解槽的热电联供特性，为避免氢能系统的热能浪费并进一步提高氢能系统的效率，搭建了一种考虑氢能系统的热电联供型光伏/风机/燃料电池/蓄电池/电锅炉/燃气锅炉微电网系统，提出一种包括日前调度与实时优化的两阶段优化调度方法. 所建系统考虑了电氢转换时的余热回收，将氢能系统作为热电氢耦合设备，实现了电、热、氢能的协调利用与相互转换，有效提高了能量利用率. 在第一阶段调度中，根据日前的风光发电出力及负荷需求预测，以微电网整体运行成本最小为目标，采用混合整数线性规划方法实现日前最优全局调度；在第二阶段调度中，根据超短期预测结果，使用模型预测控制嵌入混合整数二次规划算法，减小预测误差带来的经济性影响. 最后，通过冬、夏及过渡季典型日算例可知，本文所提出的两阶段调度方法在3种季节典型日的总成本较日前全局最优调度分别降低了3.24%、0.76%、1.66%；通过在不同场景下对本文所提方法进行仿真验证，相较于不考虑能量耦合的基础场景，考虑热电耦合系统和热电氢耦合系统时，优化调度的总成本和污染气体治理成本分别降低了15.58%、24.93%. 结果表明：本文所提方法具有一定的实时性及通用性，能够满足微网内热电负荷需求，实现稳定独立运行，改善系统的运行经济性与环保性.
- 氢能 /
- 热电联供型微电网 /
- 优化调度
Abstract:
According to the cogeneration characteristics of proton exchange membrane fuel cell and electrolyzer, in order to avoid the waste of heat energy in the hydrogen energy system and further improve the system efficiency, a combined heat–power microgrid system for photovoltaic, wind turbines, fuel cells, batteries, electric boilers, and gas boilers is built by incorporating hydrogen energy system, and a two-stage optimal dispathing method is proposed, including day-ahead scheduling and real-time optimization. The proposed system takes into account the waste heat recovery during the electricity-to-hydrogen conversion, and uses the hydrogen energy system as a thermal-electricity-hydrogen coupling equipment to realize the coordinated utilization and mutual conversion of electricity, heat, and hydrogen energy, and effectively improves the energy utilization rate. In the first stage of scheduling, according to the forecast of the wind-solar power system output and load demand in the day before, the mixed integer linear programming method is used to achieve the day-ahead optimal global schedule with the goal of minimizing the total operation cost of the microgrid. In the second stage of scheduling, based on the results of ultra-short-term predictions, the mixed integer quadratic programming algorithm is embedded in the model predictive control to lessen the economic influence from the prediction errors. Finally, through calculation examples of typical days in winter, summer and transitional seasons, compared with the day-ahead global optimal scheduling, the total cost of the two-stage scheduling method is reduced by 3.24%, 0.76% and 1.66%, respectively, in three types of seasonal days. Through the proposed method are simulated and verified in different scenarios, compared with the basic scenario without energy coupling, in the cases of involving the thermoelectric hydrogen coupling system and thermoelectric coupling system, the total cost and cost of pollution gas treatment with optimal scheduling are reduced by 15.58% and 24.93% respectively. The results show that the proposed method has a real-time and universal quality, which can meet the thermal and electrical load demand in the microgrid, realize stable and independent operation, and improve the system economy and environmental protection.
- hydrogen energy /
- combined heat-power microgrid /
- optimal scheduling

HTML全文

在科学技术和工程技术快速进步和发展的大环境下，人类致力于开发地表以下更深层的地下空间. 以往常常使用的针对地表浅层的工程类比法在深层次开挖活动中使用就不那么准确. 经过100多年的研究，国内外形成了多种地应力场模拟的方法.

朱光仪等^[1-2]充分考虑岩体自重与构造应力的影响，采用三维建模结合回归分析的方法对计算区域实测地应力进行了反演. 郭运华等^[3]在综合分析各种方法优劣的基础上，选择了多元回归分析法对岩体实测地应力进行反演分析. 李金锁等^[4]通过原位地应力测量，确定了隧道区域的地应力状态，采用三维有限元方法确定了工程区的地应力分布. 白世伟等^[5]利用不断调整侧压力系数的方法对隧道围岩地应力进行研究，表面区域的地形地貌条件以及隧道埋深都会对隧道轴线各点的地应力产生影响. 赵跃堂等^[6]结合动力松弛算法和系统阻尼算法分析了大型地下结构初始地应力状态的可行性. 夏彬伟等^[7]结合渝沙高速公路共和隧道地应力量测资料，获得每一组侧压系数下的测试段地应力，利用横观各向同性弹塑性本构模型计算得到隧道轴线方向的初始地应力大小和方向. 田勇等^[8]利用多约束优化方法，通过目标区块边界荷载反演，进行了应力场的反演模拟. 刘宁等^[9]采用非连续数值分析方法建立三维模型，利用褶皱构造和断裂构造在现今构造挤压作用下的响应方式揭示了沿线地应力存在的分区现象. 由此可见，地应力反演分析是地下工程中较为重要的环节，为设计锚固支护提供了前提条件.

本文根据对某隧道进行现场地应力测试，通过有限元模拟反演了现场围岩地应力分布规律，为岩爆和大变形预测提供依据，同时为施工隧工提供一定的指导作用.

1. 区域地质环境

1.1 地形地貌

某隧道为越岭隧道，隧址区山高坡陡，属高山、极高山构造剥蚀地貌，地表高程2 715～4 225 m，外营力以冰水侵蚀作用、冻融作用为主，同时伴有生物风化等作用，为典型高原地貌. 受构造及岩性控制明显，其主体山脉走向与构造线延展方向基本一致，呈北北西展布，岭脊呈S形弯延起伏，河谷多呈V形谷. 隧址地貌如图1所示.

图 1 隧道地貌

Figure 1. Tunnel topography map

下载: 全尺寸图片幻灯片

1.2 地层岩性

隧址区地表零星分布第四系，下伏基岩主要为侵入岩和变质岩. 变质岩主要为三叠系砂板岩，侵入岩主要为花岗闪长岩、二长花岗岩等，深大断裂附近挤压强烈变质形成糜棱岩.

1.3 地质构造

隧区在一级构造上所在区域地处扬子陆块与松潘—甘孜造山带衔接处西侧，东邻龙门山构造带，如图2所示. 区内褶皱、断裂比较发育，印支、喜山运动使盖层发生褶皱，并奠定了现今的构造轮廓，形成以北西向为主的构造线. 在二级构造上处于鲜水河构造带内，隧区主要构造形迹走向为NW向.

图 2 研究区大地构造

Figure 2. Tectonic map of the study area

下载: 全尺寸图片幻灯片

地质构造背景极为复杂，断裂发育，主要发育有鲜水河断裂分支雅拉河断裂带、色拉哈—康定断裂带、三道桥等3条区域性深大断裂以及F4-4、F10-1 、F10-2等一系列次级断裂构造，见图3 （隧道全长17730 m）. 图中，DZ开头的都为测孔编号

图 3 隧道纵剖面及地应力测孔

Figure 3. Tunnel profile and borehole map for in-situ stress measurement

下载: 全尺寸图片幻灯片

1.4 区域地应力特征

区域应力主要来自青藏高原物质的向南东方向逃逸所产生的挤压应力，主要受鲜水河断裂带左行走滑作用控制. 隧址区现今主应力方向为NW-NWW向，主应力方向与隧址区主体构造小角度相交，隧道大致走向为NE向SW行进，区域地应力和隧道轴线呈大角度相交. 整个测区属于应力集中区域，高地应力将是深埋长大隧道面临的主要工程地质问题，硬岩可能发生岩爆，软岩和断层带可能发生大变形.

2. 现场地应力测试结果及分析

水压致裂法地应力测量是目前国际上能较好地直接进行深孔地应力测量的先进方法. 该方法无需知道岩石的力学参数就可获得地层中现今地应力的多种参量，并具有操作简便、可在任意深度进行连续或重复测试、测量速度快、测值稳定可靠等优点. 缺点是只宜用铅垂孔进行测量，且必须假定铅垂方向为一个主应力方向，不适合于地形变化大的浅部. 本项研究结合该方法优点，采用数值模拟来弥补其缺点，即两种方法相互补充、对照和印证，从而提高了研究结果的可信度.

地应力测试的目的是测量地层原位地应力的大小和方向. 通过原地应力测量，确定隧道围岩的现今地壳应力状态，即原地应力的大小和方向，小型水压致裂法地应力测量是一种能够可靠而有效测量地壳深部应力的方法. 水压致裂原地应力测量是以弹性力学为基础，通过小体积、高压的流体注入，小型压裂测试在测试层位产生一条张性裂缝并将破裂扩展到远离井筒影响范围的原始地层中.

在工程区采用钻孔水压致裂法进行了深孔地应力测试，并假定：1）测试孔是竖直的，即岩层中的竖向主应力平行于孔轴；2）测试孔在测试段内为圆形且测试孔相对地层是无限小的，这个假定确保了弹性力学解的实用性；3）岩层中的孔隙压力为净水压力；4）岩石的渗透率较低，即在小型压裂过程中，测试孔内的流体压力不会在短时间内影响岩石的孔隙压力. 根据水压致裂法测试结果得到DZ-04号测孔地应力分布如图4与表1所示. 图中：H为埋深. 表1中：P₀为自重压力；P_b为破裂压力；P_r为重张压力；P_s为瞬时关闭压力；以上压力值为地表监测仪器显示量值与水柱压力相加所得；T为岩石抗拉强度.

图 4 DZ-04号测孔地应力沿深度分布规律

Figure 4. Distribution law of ground stress along depth in dZ-04 measuring hole

下载: 全尺寸图片幻灯片

通过DZ-04号测孔应力测量结果可以分析得出：主应力值随地层深度增加而增加，在380～685 m测试深度范围内，竖向应力为9.88～17.81 MPa，最大水平主应力为10.99～20.28 MPa，最小水平主应力为8.94～15.98 MPa. 侧压系数为1.111～1.138，表明地应力以水平应力占主导，方向为N49°～N57°，和区域地应力一致.

通过拟合计算可得：最大和最小主应力的线性拟合系数分别为0.990 2和0.995 4，显示主应力随深度变化趋势的线性度较好，说明了本次水压致裂测量结果的可靠性和代表性.

表 1 DZ-04号测孔水压致裂地应力测量结果

Table 1. Measurement results of ground stress caused by water pressure in borehole DZ-04

测段序号	测段中心深度/m	压裂参数/MPa					应力值/MPa			破裂方向/（°）
测段序号	测段中心深度/m	P₀	P_b	P_r	P_s	T	σ_H	σ_h	σ_v	破裂方向/（°）
1	685.0～685.7	15.98	26.20	20.95	19.21	5.25	20.28	15.98	17.81	N53W
2	624.0～624.7	14.78	24.26	19.76	18.13	4.50	18.46	14.78	16.22	N58W
3	504.0～504.7	11.69	18.00	14.50	13.29	3.50	15.63	11.69	13.10	N65W
4	440.0～440.7	9.88	15.43	12.01	11.49	3.42	13.32	9.88	11.44
5	380.0～380.7	8.94	13.50	12.11	10.34	1.39	10.99	8.94	9.88

下载: 导出CSV

| 显示表格

根据相同的方法，对其余各孔地应力分布进行线性拟合，所得结果如表2所示.

表 2 不同钻孔地应力拟合结果

Table 2. In-situ stress fitting results of different boreholes

孔号	拟合公式	最大值/ MPa	最小值/ MPa
DZ-01	σ_H=0.031 2H−8.027 0 σ_h=0.010 9H + 0.328 0	14.24	11.19
DZ-01-1	σ_H=0.022 8H−1.417 0 σ_h=0.009 1H + 3.226 0	17.88	10.84
DZ-01-2	σ_H=0.023 3H−0.188 4 σ_h=0.014 1H + 1.029 9	11.44	7.91
DZ-02	σ_H=0.042 6H−6.773 9 σ_h=0.031 9H−4.133 3	36.91	28.53
DZ-03-1	σ_H=0.038 9H−2.014 1 σ_h=0.025 4H + 1.037 8	41.69	29.84
DZ-04	σ_H=0.033 9H−0.106 7 σ_h=0.027 3H−0.073 8	27.85	22.12
DZ-04-2	σ_H=0.040 2H−2.167 2 σ_h=0.027 2H + 0.383 1	27.86	20.39
DZ07	σ_H=0.018 4H + 3.284 6 σ_h=0.013 4H + 1.547 3	18.65	13.49

下载: 导出CSV

| 显示表格

3. 某隧道地应力场模拟

采用边界荷载法，施加合适的边界条件，对水压致裂法测量得到的原地应力结果进行拟合，开展隧道地应力反演，获得地应力计算结果.

3.1 模型建立

通过综合勘察绘制隧道纵断面，使用ANSYS软件建立隧道纵断面的二维模型，模型包含隧道长为17 730 m，模型厚度为1 000 m. 模型中包含隧道沿线的各个地层及断层，共有12个组和164万个网格单元，如图5所示.

通过对隧道区域地质构造及地应力测试结果进行分析，其构造应力主要来源于NW向，因而模型的边界设置为：底边界和两个侧边界采用位移边界条件，两个侧边界采用应力边界，如图6所示. 图中：W为竖向应力；F为不同方向的水平应力.

图 5 模型计算示意

Figure 5. Model calculation diagram

下载: 全尺寸图片幻灯片

地应力反演计算时岩体采用弹性本构模型，计算参数如表1所示. 根据不同钻孔水压致裂测得的地应力结果可以看出：隧址区的最大水平主应力在深度方向的递增梯度约为0.385 MPa/km，最小水平主应力在深度方向的递增梯度约为0.257 MPa/km. 根据隧道钻孔取样试验结果，结合《工程地质手册》（第五版）相关经验值，取隧道主要围岩物理力学参数如表3、4所示.

图 6 边界条件示意

Figure 6. Schematic diagram of boundary conditions

下载: 全尺寸图片幻灯片

表 3 隧道围岩物理力学参数

Table 3. Physical and mechanical parameters of tunnel surrounding rock

地层	围岩级别	弹性模量/GPa	泊松比	体积模量/GPa	剪切模量/GPa	密度/ （kg•m⁻³）
板岩	Ⅳ	20	0.32	18.52	13.20	2 630
板岩	Ⅴ	6	0.35	6.67	4.05	2 600
花岗岩	Ⅲ	50	0.25	33.33	31.25	2 750
	Ⅳ	20	0.30	16.67	13.00	2 650
	Ⅴ	6	0.35	6.67	4.05	2 600
糜棱岩	Ⅳ	22	0.30	18.33	14.30	2 650
糜棱岩	Ⅴ	8	0.35	8.89	5.40	2 620

下载: 导出CSV

| 显示表格

表 4 隧道断层破碎带力学参数

Table 4. Mechanical parameters of tunnel fault fracture zone

断层	弹性模量/ GPa	泊松比	体积模量/ GPa	剪切模量/ GPa	密度/ （kg•m⁻³）
F1	9.0	0.24	5.77	3.63	2 250
F2	8.5	0.25	5.67	3.40	2 250
F4	8.1	0.25	5.40	3.24	2 250
F5	8.2	0.25	5.47	3.28	2 250
F6	7.9	0.26	5.49	3.13	2 250
F7	7.5	0.26	5.21	2.98	2 250

下载: 导出CSV

| 显示表格

3.2 模型验证

为验证数值反演结果的有效性，将计算结果与钻孔实测地应力进行比较，限于篇幅，仅将DZ-04与DZ-07号钻孔与数值模拟结果进行对比，如表5、6所示.

通过对比可得：数值模拟计算的结果与地应力测量结果大致相当，拟合度均接近于1，表明数值计算的拟合精度较高，其计算结果真实可信.

表 5 DZ-04应力计算结果与实测应力值对比

Table 5. Comparison between calculated and measured results of dZ-04 horizontal principal stress

测段序号	深度/m	$\sigma_{\rm{H}}$			$\sigma_{\rm{h}}$			$\sigma_{\rm{v}}$
测段序号	深度/m	实测/MPa	计算/MPa	拟合度/%	实测/MPa	计算/MPa	拟合度/%	实测/MPa	计算/MPa	拟合度/%
1	835.7	27.85	30.8	111	22.12	21.87	99	21.71	23.45	108
2	705.7	24.23	27.56	114	20.45	19.45	95	18.33	20.22	110
3	635.7	21.27	22.35	105	16.74	17.36	104	16.51	14.53	88
4	540.7	18.80	18.56	99	14.58	15.98	110	14.04	12.56	89
5	455.7	14.78	14.32	97	12.23	13.65	112	11.83	9.76	83

下载: 导出CSV

| 显示表格

表 6 DZ-07应力计算结果与实测应力值对比

Table 6. Comparison between calculated and measured results of dZ-07 maximum horizontal principal stress

测段序号	深度/m	$\sigma_{\rm{H}}$			$\sigma_{\rm{h}}$			$\sigma_{\rm{v}}$
测段序号	深度/m	实测/MPa	计算/MPa	拟合度/%	实测/MPa	计算/MPa	拟合度/%	实测/MPa	计算/MPa	拟合度/%
1	294.5	8.91	8.45	95	5.85	6.21	106	7.80	8.32	107
2	382.5	10.39	11.20	108	7.13	8.02	112	10.14	11.23	111
3	546.6	13.03	12.67	97	9.07	10.08	111	14.48	15.64	108
4	659.5	15.06	14.76	98	10.80	11.78	109	17.48	18.56	106
5	758.5	17.75	16.87	95	12.69	13.65	108	20.10	21.47	107
6	835.0	18.65	19.19	103	13.49	15.04	111	22.13	24.51	111

下载: 导出CSV

| 显示表格

3.3 结果分析

3.3.1 最大主应力

根据隧道数值模拟结果，提取模型最大主应力云图与最大主应力折线图如图7所示.

从云图及折线图可以看出，隧道沿线最大地应力随埋深、岩性、断裂构造的变化而有所变化，将其分段描述如下：

1） CK260 + 150～CK263 + 960最大主应力值为3.80～17.48 MPa，无断层的位置最大主应力为6.86～22.48 MPa，在断层F1、F2发育位置，最大主应力值则急剧减小，最小值在F1（CK261）位置，为3.80 MPa.

图 7 隧道最大主应力云图及数值折线图

Figure 7. Cloud diagram and numerical broken-line diagram of maximum principal stress of tunnel

下载: 全尺寸图片幻灯片

2） CK263 + 960～CK265 + 892最大主应力值为9.47～26.62 MPa，在断层F4位置（CK263 + 960），最大主应力值则急剧减小，为9.47 MPa.

3）由于隧道在里程段CK265 + 892～CK272 + 488埋深最大，且其岩性为花岗闪长岩和二长花岗岩，重度较大，其最大主应力值在整个隧道轴线中是最大的，为22.94～32.14 MPa.

4）由于 CK272 + 488～CK277 + 880地形变化，隧道埋深逐渐减小，最大主应力值缓慢变小，其值为1.49～21.40 MPa，同样存在断层位置减小，断层两端增大的规律.

5）由于在CK263 + 942处地形变化大，所以地应力也急剧增加. 在该里程段中存在5个岩性分界面，分别位于CK263 + 960、 CK265 + 892、 CK266 + 717、 CK267 + 726、CK275 + 954，在这些位置最大主应力值均有所增加.

隧道各里程段最大主应力值如表7所示：

综合最大主应力云图、折线图以及表7可以看出：最大主应力值主要受到埋深、岩石重度以及构造应力的影响，在构造应力一定的条件下，埋深越大，岩石重度越大，则最大主应力的值越大. 而在断层位置，由于岩石破裂使应力得到释放，所以最大主应力值比同深度的完整岩体较低；在岩性分界面以及断裂附近的上盘，则会发生应力集中，出现应力增高的现象.

表 7 隧道各里程段最大主应力值

Table 7. Maximum principal stress in each mileage section of tunnel

地层或断层编号	里程段	最大主应力值/MPa
D1	CK260 + 150～CK261 + 000	6.86～9.02
F1	CK261 + 000～CK261 + 200	3.80～7.97
D1	CK261 + 200～CK262 + 154	8.75～13.57
F2	CK262 + 154～CK262 + 405	4.53～14.33
D1	CK262 + 405～CK263 + 960	13.60～17.48
F4	CK263 + 960～CK264 + 412	9.47～27.13
D2	CK264 + 412～CK265 + 892	21.32～26.62
D3	CK265 + 892～CK266 + 717	25.80～30.15
D4	CK266 + 717～CK267 + 726	25.80～30.15
D3	CK267 + 726～CK267 + 873	25.80～30.15
D3	CK267 + 873～CK268 + 652	30.01～32.14
D3	CK268 + 652～CK272 + 488	22.94～29.83
F5	CK272 + 488～CK272 + 639	10.58～18.84
D3	CK272 + 639～CK275 + 648	13.63～21.40
F6	CK275 + 648～CK275 + 954	8.86～14.36
D5	CK275 + 954～CK277 + 880	1.49～12.81

下载: 导出CSV

| 显示表格

3.3.2 中间主应力

根据隧道数值模拟结果，提取模型中间主应力云图如图8所示.

由图8可知：隧道中间主应力值在0～30.21 MPa，与最大主应力有相似的规律，随埋深变化明显，在断层部位有所下降，而在断层的两端围岩中则发生了应力集中，隧道轴线沿线中间主应力值约在0～13.00 MPa.

图 8 隧道中间主应力云图

Figure 8. Cloud diagram of principal stress in the middle of tunnel

下载: 全尺寸图片幻灯片

3.3.3 最小主应力

模型最小主应力云图如图9所示. 由图9可知：隧道最小主应力值在0～29.84 MPa，与最大主应力有相似的规律，随埋深变化明显，在断层部位有所下降，而在断层的两端围岩中则发生了应力集中，隧道轴线沿线最小主应力值在0～6.00 MPa.

图 9 隧道最小主应力云图

Figure 9. Cloud diagram of minimum principal stress of tunnel

下载: 全尺寸图片幻灯片

综上所述：隧道沿线最大主应力值主要受埋深的影响，隧道埋深越大，其围岩最大主应力越大；断裂与完整岩体交汇处最大主应力差值较大，岩性分界面处则存在应力集中，隧道开挖会扰乱这些位置的应力状况，形成应力释放条件，产生岩爆.

4. 结　论

1）本文结合水压致裂法获取8个测孔实测地应力进行了地应力反演计算，获得洞轴线各个里程段落任一点地应力值，并获取其分布规律，为岩爆和大变形合理预测、针对性设计以及综合防控奠定了基础.

2）隧道纵断面水平最大主应力为32.14 MPa，最小主应力为29.84 MPa，侧压力系数为1.363～1.438，最大水平主应力在深度方向的递增梯度约为0.385 MPa/km，最小水平主应力在深度方向的递增梯度约为0.257 MPa/km. 实测围岩地应力方向为NW—NWW向，和区域地应力方向基本一致，围岩地应力水平高，具备发生岩爆和大变形的条件.

3）地应力在断层部位得到了一定程度的释放，地应力较小，断层两侧的完整岩体应力存在一定程度的集中，应力值较高. 在断层段设计和施工时应充分考虑应力的释放和局部集中因素.

4）由于岩石物理力学试验参数偏少且离散性较大，地应力反演模型参数取值不够准确，地应力计算结果可能会存在一定误差.

致谢：感谢中铁二院院控科研项目基金（KYY2019004）对本论文的支持.

图 1 热电氢联供型微电网系统结构

Figure 1. Structure of combined heat-power-hydrogen microgrid system

下载: 全尺寸图片幻灯片

图 2 氢储能系统原理

Figure 2. Schematic of hydrogen energy storage system

下载: 全尺寸图片幻灯片

图 3 两阶段优化调度求解流程

Figure 3. Solution flow of two-stage optimal scheduling

下载: 全尺寸图片幻灯片

图 4 LSTM预测流程

Figure 4. Flow chart of LSTM forecast

下载: 全尺寸图片幻灯片

图 5 灰色预测流程

Figure 5. Flow chart of grey forecast

下载: 全尺寸图片幻灯片

图 6 日前优化结果

Figure 6. Day-ahead optimization results

下载: 全尺寸图片幻灯片

图 7 日内优化结果

Figure 7. Real-time optimization results

下载: 全尺寸图片幻灯片

表 1 日前优化成本和日内优化成本

Table 1. Day-ahead and real-time optimized cost 元

成本项目	冬季典型日		夏季典型日		过渡季典型日
成本项目	调度成本	优化成本	调度成本	优化成本	调度成本	优化成本
运维	436.78	435.00	226.02	221.54	317.08	312.65
燃料	623.59	597.28	162.67	164.51	504.94	496.62
污染气体治理	169.67	157.87	44.21	43.58	136.82	133.69
总成本	1230.04	1190.15	432.90	429.63	958.85	942.96

下载: 导出CSV

表 2 微电网各能量占比

Table 2. Energy proportion in microgrid %

季节	电能	热能	总能量利用率
冬季	71.97	28.03	89.43
夏季	76.13	23.87	91.16
过渡季	63.87	36.13	93.13

下载: 导出CSV

表 3 不同场景下的调度成本

Table 3. Scheduling cost in different scenarios 元

场景	运维成本	燃料成本	污染气体治理成本	总成本
1	235.58	214.81	58.53	508.92
2	198.76	200.47	56.14	455.37
3	229.61	160.33	44.83	434.37
4	221.54	164.51	43.58	429.63

下载: 导出CSV

表 4 优化调度的计算时间

Table 4. Calculation time for optimal scheduling s

计算时间	冬季典型日	夏季典型日	过渡季典型日
调度	5.59	6.37	6.15
优化	87.76	85.56	86.92
总时间	93.36	91.93	93.08

下载: 导出CSV

表 5 不同权重系数下的优化成本

Table 5. Optimal cost under different weight coefficients

季节	组编号	λ₁	λ₂	λ₃	λ₄	λ₅	λ₆	λ₇	运维成本/元	燃料成本/元	污染气体治理成本/元	总成本/元
冬季	1	0.3	0.5	0.1	0.21	0.2	0.3	0.1	435.00	597.28	157.87	1190.15
	2	0.2	0.2	0.2	0.2	0.2	0.2	0.2	438.33	602.02	158.66	1199.00
	3	0.4	0.3	0.2	0.1	0.3	0.2	0.3	439.09	595.60	157.64	1192.33
	4	0.5	0.4	0.3	0.2	0.4	0.5	0.2	438.73	597.92	158.09	1194.74
	5	0.3	0.3	0.1	0.21	0.2	0.2	0.2	438.94	597.63	157.96	1194.53
夏季	1	0.3	0.5	0.1	0.21	0.2	0.3	0.1	221.54	164.51	43.58	429.63
	2	0.2	0.2	0.2	0.2	0.2	0.2	0.2	222.67	165.18	44.28	432.12
	3	0.4	0.3	0.2	0.1	0.3	0.2	0.3	222.31	165.36	44.25	431.92
	4	0.5	0.4	0.3	0.2	0.4	0.5	0.2	222.43	165.26	44.24	431.94
	5	0.3	0.3	0.1	0.21	0.2	0.2	0.2	222.77	164.99	44.45	432.21
过渡季	1	0.3	0.5	0.1	0.21	0.2	0.3	0.1	312.65	496.62	133.69	942.96
	2	0.2	0.2	0.2	0.2	0.2	0.2	0.2	314.01	496.54	134.21	944.76
	3	0.4	0.3	0.2	0.1	0.3	0.2	0.3	313.56	496.02	134.02	943.59
	4	0.5	0.4	0.3	0.2	0.4	0.5	0.2	313.69	496.16	134.07	943.91
	5	0.3	0.3	0.1	0.21	0.2	0.2	0.2	313.58	496.77	134.22	944.57

下载: 导出CSV

参考文献(27)

[1]	ZHU D F, YANG B, LIU Q, et al. Energy trading in microgrids for synergies among electricity, hydrogen and heat networks[J]. Applied Energy, 2020, 272: 115225. doi: 10.1016/j.apenergy.2020.115225
[2]	李奇,蒲雨辰,韩莹,等. 电-氢孤岛直流微电网的分层能量管理[J]. 西南交通大学学报,2020,55(5): 912-919. LI Qi, PU Yuchen, HAN Ying, et al. Hierarchical energy management of electricity-hydrogen island DC microgrid[J]. Journal of Southwest Jiaotong University, 2020, 55(5): 912-919.
[3]	李奇,赵淑丹,蒲雨辰,等. 考虑电氢耦合的混合储能微电网容量配置优化[J]. 电工技术学报,2021,36(3): 486-495. LIQi, ZHAO Shudan, PU Yuchen, et al. Capacity optimization of hybrid energy storage microgrid considering electricity-hydrogen coupling[J]. Transactions of China Electrotechnical Society, 2021, 36(3): 486-495.
[4]	NADERIPOUR A, ABDUL-MALEK Z, NOWDEH S A, et al. Optimal allocation for combined heat and power system with respect to maximum allowable capacity for reduced losses and improved voltage profile and reliability of microgrids considering loading condition[J]. Energy, 2020, 196: 117124.1-117124.13.
[5]	王丹,黄德裕,胡庆娥,等. 基于电-热联合市场出清的综合需求响应建模及策略[J]. 电力系统自动化,2020,44(12): 13-21. doi: 10.7500/AEPS20191220007 WANG Dan, HUANG Deyu, HU Qing ’e, et al. Modeling and strategy of integrated demand response based on joint electricity-heat clearing market[J]. Automation of Electric Power Systems, 2020, 44(12): 13-21. doi: 10.7500/AEPS20191220007
[6]	杨冬锋,姜超,蔡国伟,等. 考虑电热耦合的交直流微电网多目标优化配置[J]. 电力系统自动化,2020,44(8): 124-132. YANG Dongfeng, JIANG Chao, CAI Guowei, et al. Multi-objective optimization configuration of AC/DC microgrid considering electro-thermal coupling[J]. Automation of Electric Power Systems, 2020, 44(8): 124-132.
[7]	BORNAPOUR M, HOOSHMAND R A, KHODABAKHSHIAN A, et al. Optimal stochastic coordinated scheduling of proton exchange membrane fuel cell-combined heat and power, wind and photovoltaic units in micro grids considering hydrogen storage[J]. Applied Energy, 2017, 202: 308-322. doi: 10.1016/j.apenergy.2017.05.133
[8]	王丹,智云强,贾宏杰,等. 基于多能源站协调的区域电力-热力系统日前经济调度[J]. 电力系统自动化,2018,42(13): 59-67. doi: 10.7500/AEPS20171129003 WANG Dan, ZHI Yunqiang, JIA Hongjie, et al. Day-ahead economic dispatch strategy of regional electricity-heating integrated energy system based on multiple energy stations[J]. Automation of Electric Power Systems, 2018, 42(13): 59-67. doi: 10.7500/AEPS20171129003
[9]	靳小龙,穆云飞,贾宏杰,等. 集成智能楼宇的微网系统多时间尺度模型预测调度方法[J]. 电力系统自动化,2019,43(16): 25-33. doi: 10.7500/AEPS20180629016 JIN Xiaolong, MU Yunfei, JIA Hongjie, et al. Model predictive control based multiple-time-scheduling method for microgrid system with smart buildings integrated[J]. Automation of Electric Power Systems, 2019, 43(16): 25-33. doi: 10.7500/AEPS20180629016
[10]	JIN X L, WU J Z, MU Y F, et al. Hierarchical microgrid energy management in an office building[J]. Applied Energy, 2017, 208: 480-494. doi: 10.1016/j.apenergy.2017.10.002
[11]	AGHAEI J, ALIZADEH M I. Multi-objective self-scheduling of CHP (combined heat and power)-based microgrids considering demand response programs and ESSs (energy storage systems)[J]. Energy, 2013, 55: 1044-1054. doi: 10.1016/j.energy.2013.04.048
[12]	GUO X G, BAO Z J, LAI H J, et al. Model predictive control considering scenario optimisation for microgrid dispatching with wind power and electric vehicle[J]. The Journal of Engineering, 2017, 2017(13): 2539-2543. doi: 10.1049/joe.2017.0785
[13]	YANG H M, PAN H, LUO F J, et al. Operational planning of electric vehicles for balancing wind power and load fluctuations in a microgrid[J]. IEEE Transactions on Sustainable Energy, 2017, 8(2): 592-604. doi: 10.1109/TSTE.2016.2613941
[14]	吴鸣,骆钊,季宇,等. 基于模型预测控制的冷热电联供型微网动态优化调度[J]. 中国电机工程学报,2017,37(24): 7174-7184. WU Ming, LUO Zhao, JI Yu, et al. Model predictive control based dynamic optimal scheduling for cooling, heating and power microgrid[J]. Proceedings of the CSEE, 2017, 37(24): 7174-7184.
[15]	GU W, WANG Z H, WU Z, et al. An online optimal dispatch schedule for CCHP microgrids based on model predictive control[J]. 2017 IEEE Power & Energy Society General Meeting, 2017, 8(5): 2332-2342.
[16]	陈维荣,于瑾,李奇,等. 电-氢多能互补型微电网的VSG平衡电流控制方法[J]. 西南交通大学学报,2019,54(6): 1323-1331. doi: 10.3969/j.issn.0258-2724.20180860 CHEN Weirong, YU Jin, LI Qi, et al. Balanced current control method for virtual synchronous generator in electro-hydrogen multi-energy complementary microgrid[J]. Journal of Southwest Jiaotong University, 2019, 54(6): 1323-1331. doi: 10.3969/j.issn.0258-2724.20180860
[17]	孔令国,蔡国伟,李龙飞,等. 风光氢综合能源系统在线能量调控策略与实验平台搭建[J]. 电工技术学报,2018,33(14): 3371-3384. doi: 10.19595/j.cnki.1000-6753.tces.170597 KONG Lingguo, CAI Guowei, LI Longfei, et al. Online energy control strategy and experimental platform of integrated energy system of wind, photovoltaic and hydrogen[J]. Transactions of China Electrotechnical Society, 2018, 33(14): 3371-3384. doi: 10.19595/j.cnki.1000-6753.tces.170597
[18]	蒲雨辰,李奇,陈维荣,等. 计及最小使用成本及储能状态平衡的电-氢混合储能孤岛直流微电网能量管理[J]. 电网技术,2019,43(3): 918-927. doi: 10.13335/j.1000-3673.pst.2018.1528 PU Yuchen, LI Qi, CHEN Weirong, et al. Energy management for islanded DC microgrid with hybrid electric-hydrogen energy storage system based on minimum utilization cost and energy storage state balance[J]. Power System Technology, 2019, 43(3): 918-927. doi: 10.13335/j.1000-3673.pst.2018.1528
[19]	LI J R, LIN J, SONG Y H, et al. Operation optimization of power to hydrogen and heat (P2HH) in ADN coordinated with the district heating network[J]. IEEE Transactions on Sustainable Energy, 2019, 10(4): 1672-1683. doi: 10.1109/TSTE.2018.2868827
[20]	PASHAEI-DIDANI H, NOJAVAN S, NOUROLLAHI R, et al. Optimal economic-emission performance of fuel cell/CHP/storage based microgrid[J]. International Journal of Hydrogen Energy, 2019, 44(13): 6896-6908. doi: 10.1016/j.ijhydene.2019.01.201
[21]	随权,马啸,魏繁荣,等. 计及燃料电池热-电综合利用的能源网日前调度优化策略[J]. 中国电机工程学报,2019,39(6): 1603-1613, 1857. SUI Quan, MA Xiao, WEI Fanrong, et al. Day-ahead dispatching optimization strategy for energy network considering fuel cell thermal-electric comprehensive utilization[J]. Proceedings of the CSEE, 2019, 39(6): 1603-1613, 1857.
[22]	HU Q, LIN J, ZENG Q, et al. Optimal control of a hydrogen microgrid based on an experiment validated P2HH model[J]. IET Renewable Power Generation, 2020, 14(3): 364-371. doi: 10.1049/iet-rpg.2019.0544
[23]	丁明,王波,赵波,等. 独立风光柴储微网系统容量优化配置[J]. 电网技术,2013,37(3): 575-581. doi: 10.13335/j.1000-3673.pst.2013.03.002 DING Ming, WANG Bo, ZHAO Bo, et al. Configuration optimization of capacity of standalone PV-wind-diesel-battery hybrid microgrid[J]. Power System Technology, 2013, 37(3): 575-581. doi: 10.13335/j.1000-3673.pst.2013.03.002
[24]	熊焰,吴杰康,王强,等. 风光气储互补发电的冷热电联供优化协调模型及求解方法[J]. 中国电机工程学报,2015,35(14): 3616-3625. XIONG Yan, WU Jiekang, WANG Qiang, et al. An optimization coordination model and solution for combined cooling, heating and electric power systems with complimentary generation of wind, PV, gas and energy storage[J]. Proceedings of the CSEE, 2015, 35(14): 3616-3625.
[25]	LI Q, CHEN W R, LIU Z X, et al. Development of energy management system based on a power sharing strategy for a fuel cell-battery-supercapacitor hybrid tramway[J]. Journal of Power Sources, 2015, 279: 267-280. doi: 10.1016/j.jpowsour.2014.12.042
[26]	ERGEN T, KOZAT S S. Online training of LSTM networks in distributed systems for variable length data sequences[J]. IEEE Transactions on Neural Networks and Learning Systems, 2018, 29(10): 5159-5165. doi: 10.1109/TNNLS.2017.2770179
[27]	MA H W, ZHANG D Q. A grey forecasting model for coal production and consumption[C]//2009 IEEE International Conference on Grey Systems and Intelligent Services (GSIS 2009). Nanjing: IEEE, 2009: 512-516.

施引文献

期刊类型引用(3)

1.	杨猛，王云飞，赵家斌，周敬，王永景，李永乐. 考虑气动力跨向振幅依存性和相关性的桥梁涡振响应分析. 西南交通大学学报. 2025(01): 45-52 . 本站查看
2.	李永乐，朱金，万田保，李涵，秦顺全. 大跨度钢-混结合梁悬索桥涡激振动控制指标体系研究. 桥梁建设. 2024(02): 22-30 . 百度学术
3.	向活跃，王一少，蔡佩宏，李永乐. 竖向涡激振动对大跨度城市轨道专用桥行车性能的影响研究. 振动与冲击. 2024(24): 251-258 . 百度学术

其他类型引用(1)

附加材料(1)

- 2023年第1期李奇附加材料
  .docx
  
  下载

访问统计

点击查看大图

图(7) / 表(5)

计量

文章访问数: 892
HTML全文浏览量: 393
PDF下载量: 125
被引次数: 4

1. 区域地质环境
1.1 地形地貌
1.2 地层岩性
1.3 地质构造
1.4 区域地应力特征
2. 现场地应力测试结果及分析
3. 某隧道地应力场模拟
3.1 模型建立
3.2 模型验证
3.3 结果分析
4. 结　论

基于氢储能的热电联供型微电网优化调度方法

doi: 10.3969/j.issn.0258-2724.20210348

作者简介: 李奇（1984—），男，教授，博士，博士生导师，研究方向为轨道交通新能源技术、综合能源系统运行与控制等，E-mail：liqi0800@163.com

通讯作者: 陈维荣（1965—），男，教授，博士，博士生导师，研究方向为轨道交通新能源技术，电力系统及其自动化，燃料电池技术及应用，E-mail：wrchen@swjtu.cn

计量

出版历程