低屈服点波形钢板剪力墙减震耗能性能数值分析

卫星; 周林君; 李刚

doi:10.3969/j.issn.0258-2724.20210305

低屈服点波形钢板剪力墙减震耗能性能数值分析

doi: 10.3969/j.issn.0258-2724.20210305

西南交通大学土木工程学院，四川成都610031

基金项目: 四川省科技创新人才项目（2020JDRC0009）

详细信息

作者简介:
卫星（1976—），男，教授，博士，研究方向为钢结构桥梁行为，E-mail： we_star@swjtu.cn

中图分类号: TU398.2；TU352.1
计量
- 文章访问数: 380
- HTML全文浏览量: 123
- PDF下载量: 32
- 被引次数: 4
出版历程
- 收稿日期: 2021-04-20
- 修回日期: 2021-07-17
- 网络出版日期: 2023-02-13
- 刊出日期: 2021-08-05

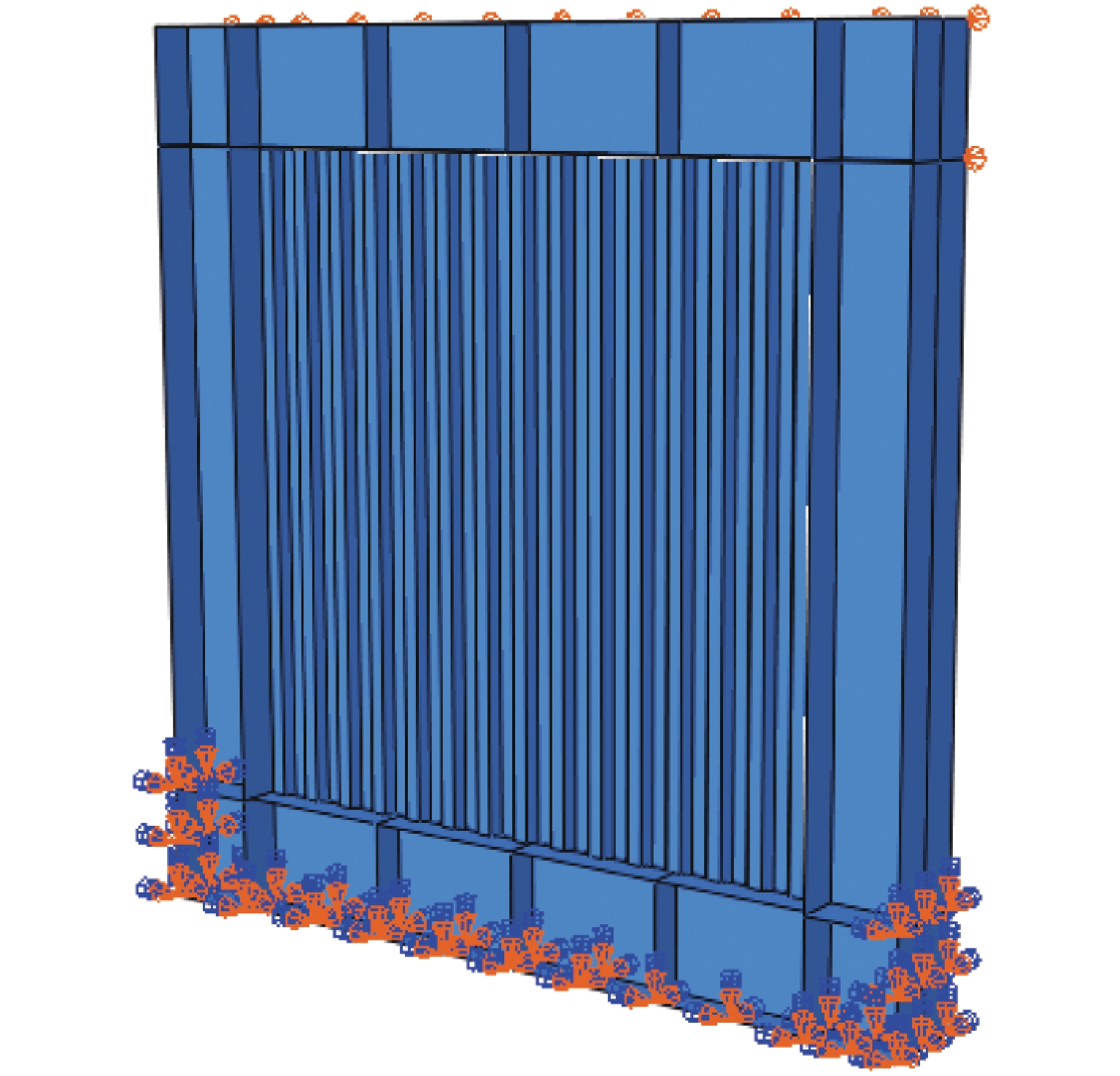
Numerical Analysis of Seismic Energy Dissipation Performance of Corrugated Steel Plate Shear Wall with Low Yield Point

School of Civil Engineering, Southwest Jiaotong University, Chengdu 610031, China

摘要

摘要:
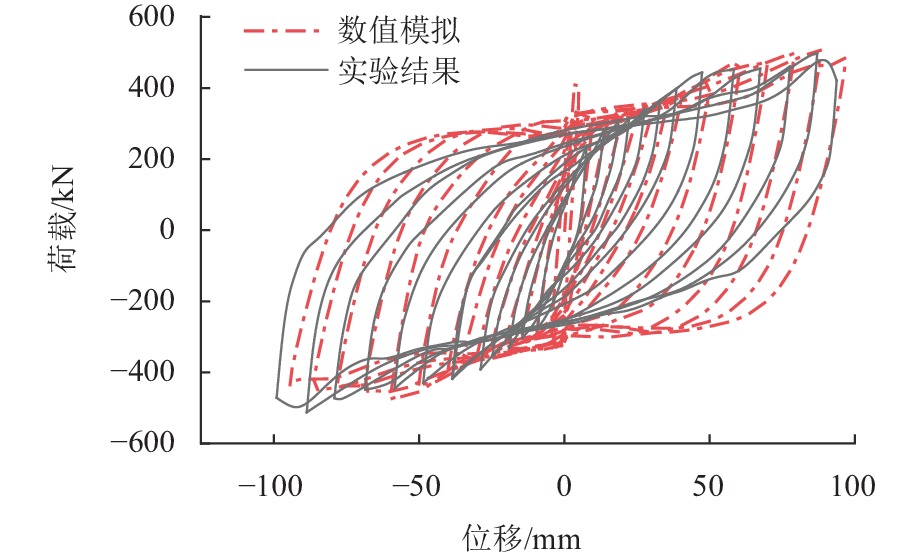
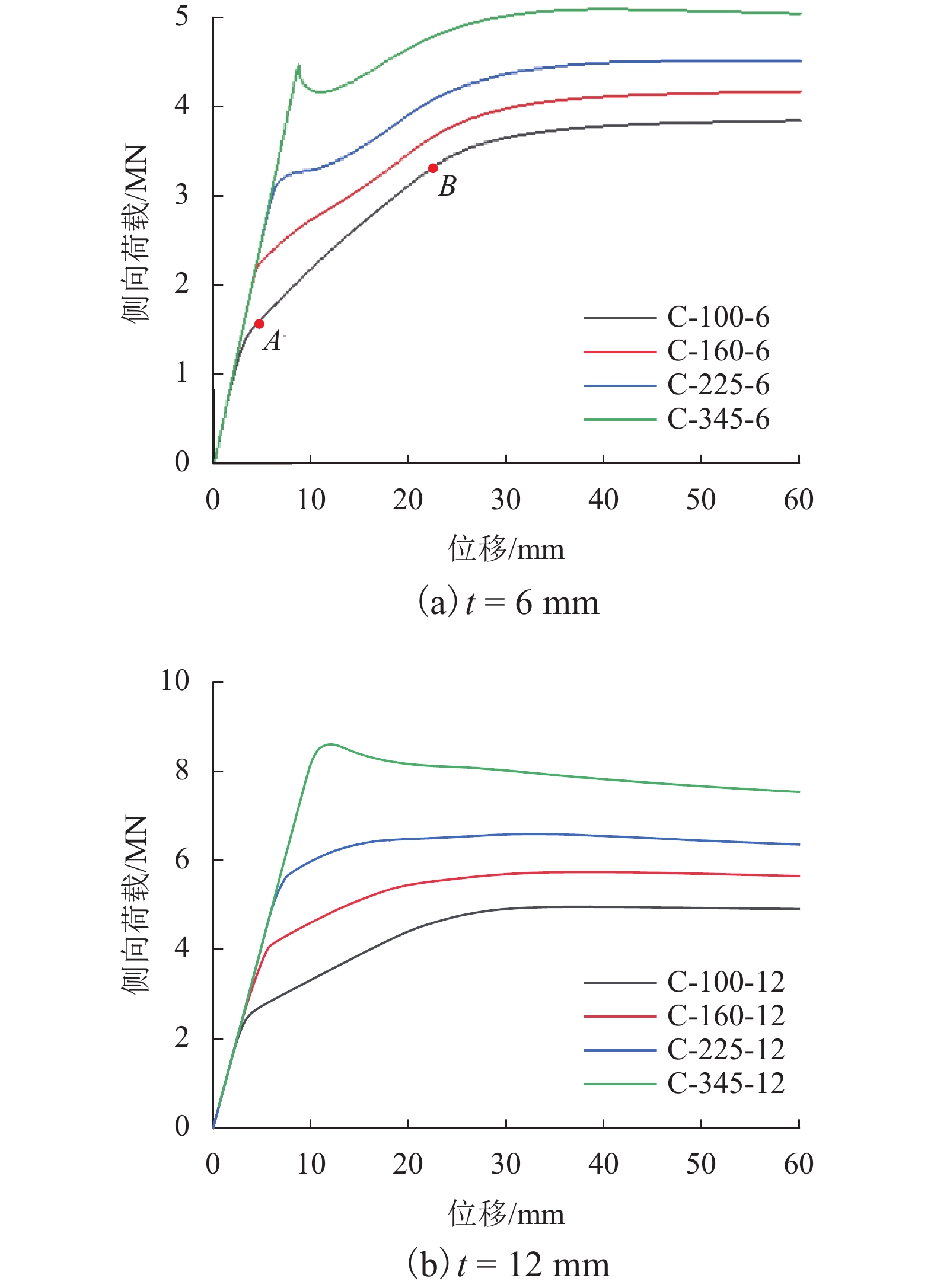
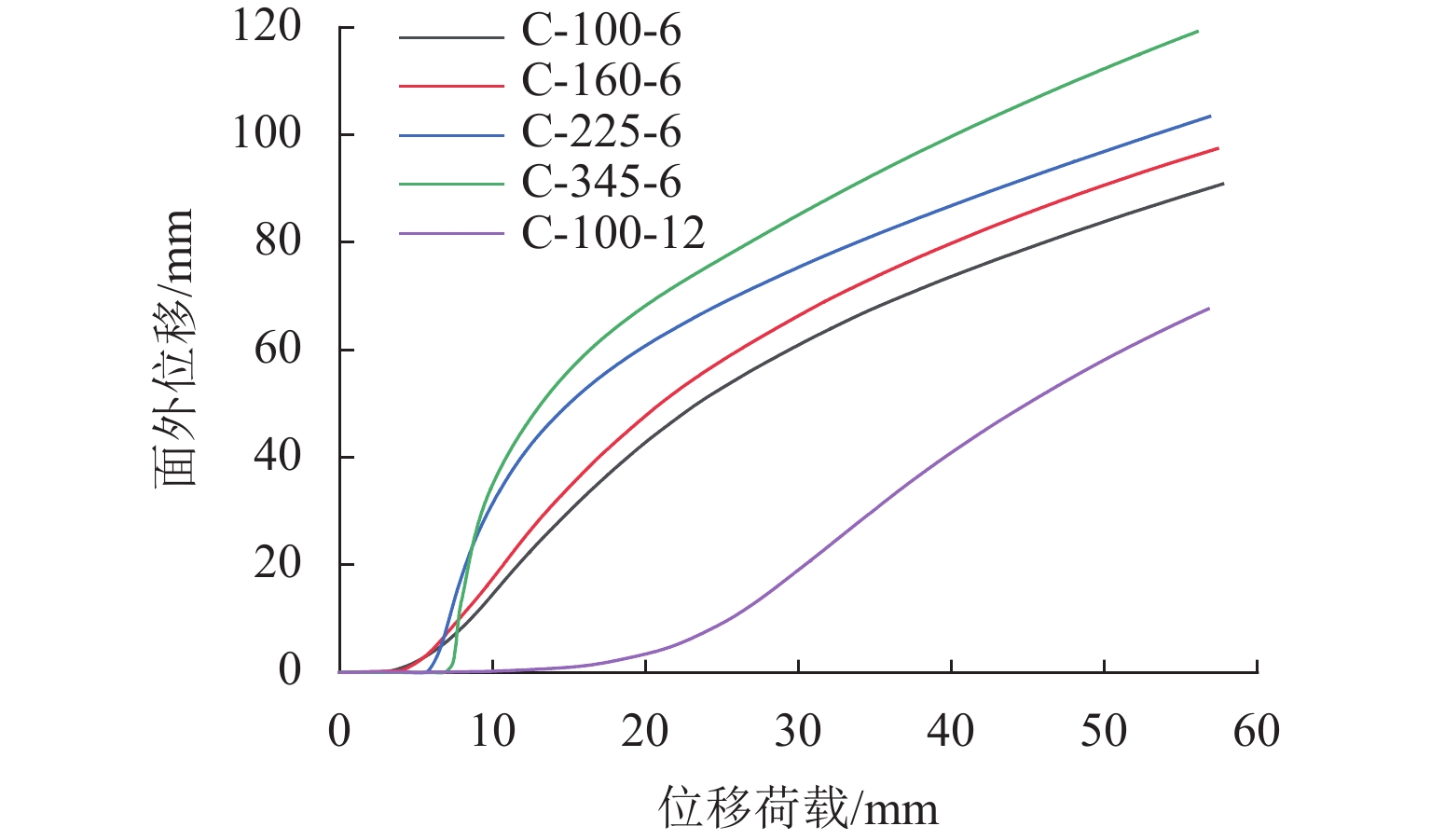
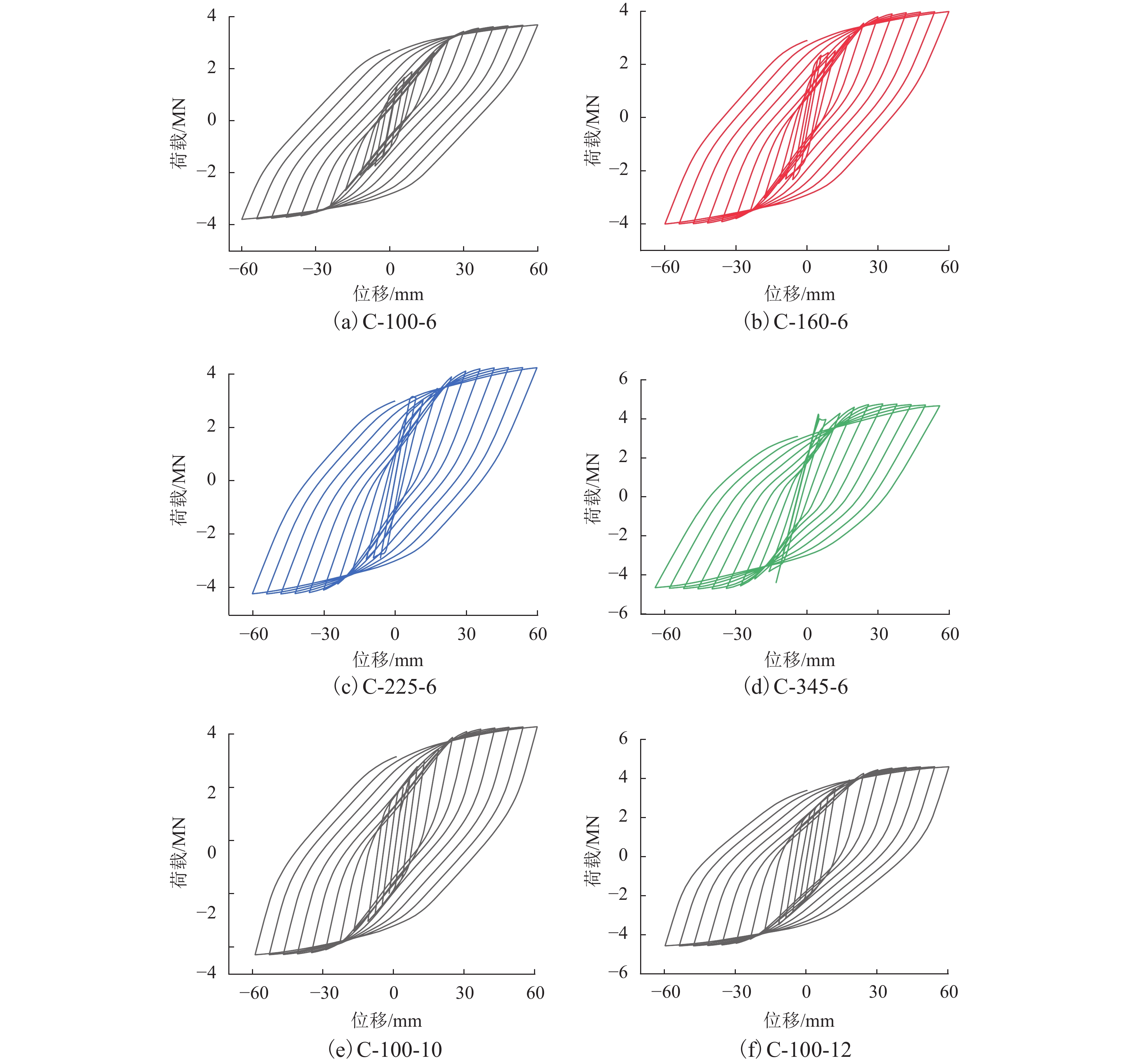
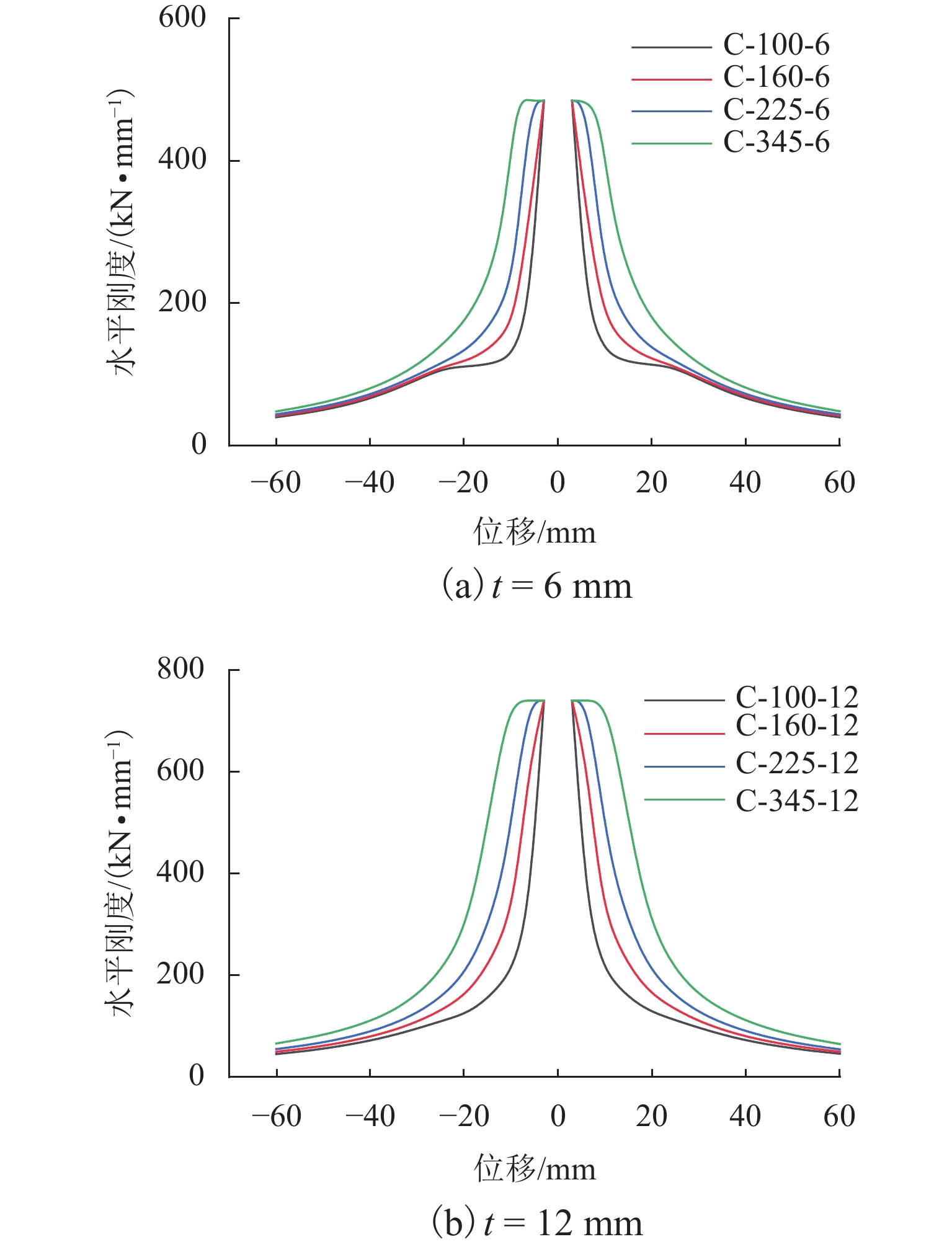
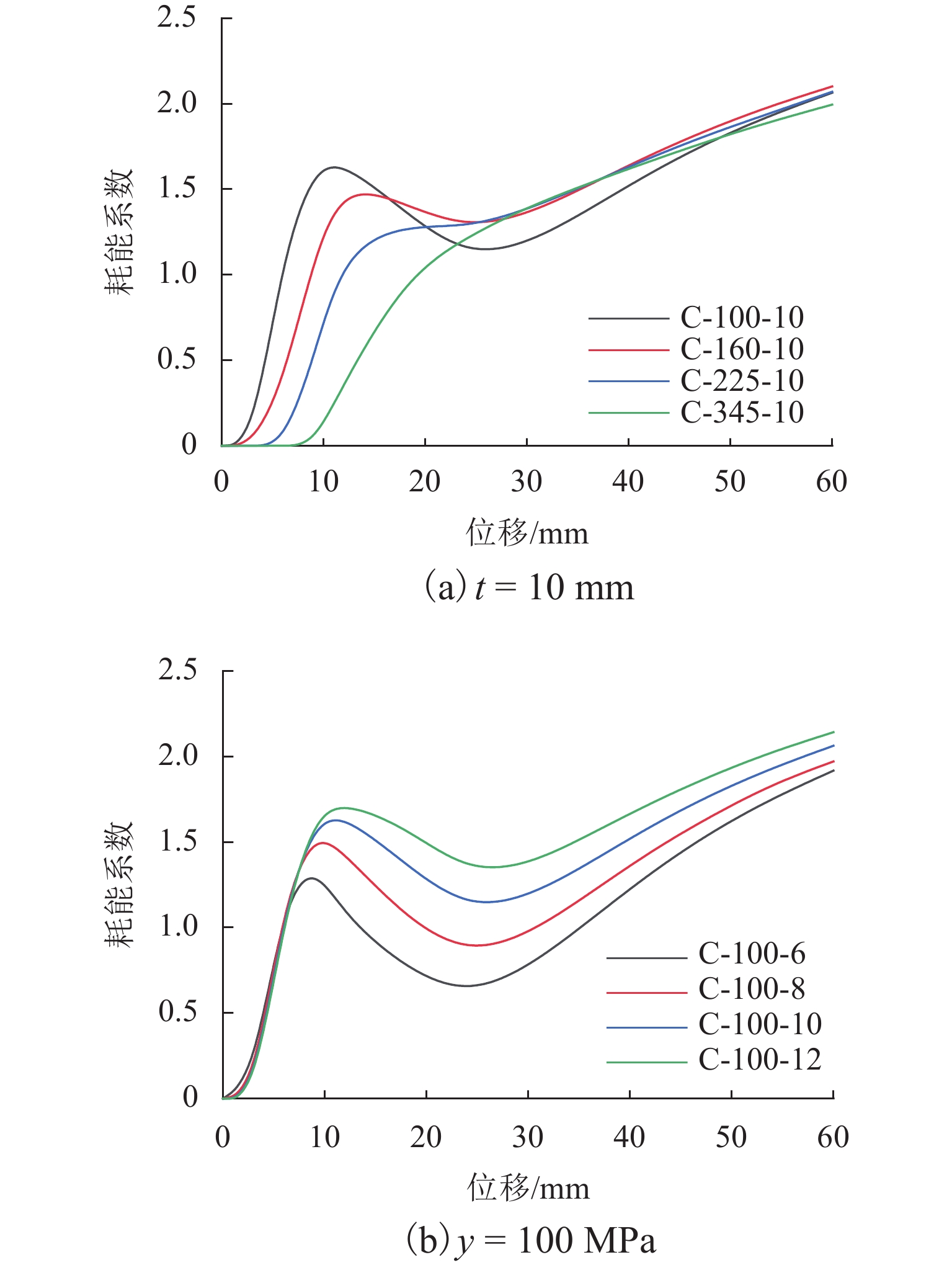
为了研究低屈服点波形钢板剪力墙（corrugated steel plate shear wall，CSPSW）新型抗侧向荷载系统减震耗能性能，利用有限元软件ABAQUS，对16个CSPSW有限元模型进行横向单调和循环荷载作用下的减震耗能性能数值分析，并以波形钢板屈服强度和板厚为关键参数，综合分析其对结构抗侧性能、滞回性能、刚度退化、延性和能量耗散等性能的影响规律. 研究结果表明：低屈服点CSPSW与普通钢板剪力墙初始刚度相同，但抗侧性能弱于后者；与普通屈服强度CSPSW相比，低屈服点CSPSW滞回曲线更饱满，耗能性能更好，且延性更好；随着波形钢板屈服强度降低，低屈服点CSPSW延性和耗能性能均提高，结构水平刚度退化加快；随着波形钢板厚度增大，低屈服点CSPSW初始刚度和结构耗能性能均提高，承载能力变化较小.
- 低屈服点钢 /
- 波形钢板剪力墙 /
- 有限元分析 /
- 减震耗能
Abstract:
In order to study the seismic performance of low-yield-point corrugated steel plate shear walls (CSPSWs), a new type of lateral-resistant load system, the finite element software ABAQUS was used to numerically analyze the seismic energy dissipation behavior of 16 CSPSWs under lateral monotonic and cyclic loads. The yield strength and thickness of the infill CSPSWs were selected as the key parameters in the parametric study of the new wall system to assess their impact on the lateral resistance performance, hysteresis performance, stiffness degradation, ductility, and energy dissipation. The results show that the low-yield-point CSPSWs possess the same initial stiffness as that of the ordinary steel plate shear wall, but has a weaker lateral resistance than the latter. Compared with the ordinary-yield-strength CSPSWs, the low-yield-point CSPSWs is capable of developing a fuller hysteresis curve. The energy dissipation and ductility of the new wall system are also better than those of the ordinary-yield-strength CSPSWs. As the yield strength of the CSPSWs decreases, the ductility and energy dissipation of the low-yield-point CSPSWs increase, and the degradation of structural horizontal stiffness accelerates. As the thickness of the low-yield-point stress CSPSWs increases, the initial rigidity and structural energy dissipation increase, while the load-bearing capacity changes less.
- low yield point steel /
- corrugated steel plate shear walls /
- finite element analysis /
- aseimic consumed energy behavior

HTML全文

随着我国西部大开发的不断开展，高海拔隧道建设越来越多，规划建设的某高原铁路沿线海拔多高于3 km，桥隧比在80%以上，拥有数座长度超过20 km的铁路隧道. 为克服高海拔隧道施工低压低氧的困难，保障施工人员工作效率及生理健康，供氧是最直接的改善措施之一. 众多学者对高海拔供氧进行了相关研究，郭春等^[1-2]研究了高海拔供氧标准，得到了不同劳动强度和不同海拔高度下人体最低需氧量；孙志涛^[3]对高海拔施工缺氧进行了分级，得到了高海拔隧道施工氧含量的控制标准；王明年等^[4-5]对高海拔施工供氧技术进行了总结，得到高海拔供氧技术，包含个人携氧供氧、弥散式供氧、综合供氧、氧吧车供氧和室内鼻息式供氧，在不同隧道施工工序下应组合供氧方法和供氧系统，以适应不同劳动强度下施工人员的供氧需求和心理需求；谢文强^[6]对高海拔隧道施工供氧标准进行了研究，得到了不同海拔高度人体所需最小耗氧量和通气量；严涛等^[7]对高海拔供氧参数进行研究，建议海拔高度在3 000 m以上施工进行供氧. 目前高海拔隧道施工供氧方面的研究，主要集中在供氧标准及供氧方式两部分，研究手段基本以理论分析与公式推导为主，缺少现场的实际测试.

在数据拟合方面，BP （back propagation）神经网络目前在多维变量拟合应用中较多，由于BP神经网络自身存在收敛慢、波动大的缺陷^[8-10]，大量学者基于BP神经网络做了较多优化，并进行了应用. Wang 等^[11]通过MEC-BP神经网络对箱梁施工扰度进行了拟合预测，得到MEC-BP神经网络拟合预测结果优于BP神经网络结构；李步遥等^[12]基于MEC-BP神经网络对基坑水平位移进行了反演分析，得到MEC-BP神经网络收敛速度快于GA-BP神经网络^[8]，且结果优于GA-BP （genetic algorithms back propagation）神经网络和BP神经网络；王春晓等^[13]基于MEC-BP神经网络对群桩轴力进行预测，得到MEC-BP神经网络预测精度及准确度明显高于BP神经网络.

本文通过高海拔隧道供氧实验，对高海拔隧道施工人员进行现场测试，并运用MEC-BP神经网络对现场测试数据进行拟合，研究高海拔人员劳动功率和氧浓度对劳动强度的影响规律，其中劳动强度通过平均能量代谢率表示.

1. MEC-BP神经网络模型简介

1.1 BP神经网络

BP神经网络算法^[11]是一种基于输出误差逆向传播的多层前馈神经网络算法，对于三层前馈神经网络，其基本结构由输入层、隐含层、输出层构成，根据神经网络层建立的输入输出函数Q以及误差函数E 分别为

$Q = \psi \left( \sum\limits_{j = 1}^m {{w_{jk}}{y_i} - \theta _k} \right) = \psi \left( \sum\limits_{j = 1}^m {{w_{jk}}\varphi \left( \sum\limits_{i = 1}^n {{w_{ik}}{x_i}} - \theta _j \right)} - \theta _k \right),$

(1)

$E = \frac{1}{{2S}}\sum\limits_{t = 1}^S {{{({T_t} - {O_t})}^2}},$

(2)

式中： $\psi ({\text{•}})$ 和 $\varphi ({\text{•}})$ 分别为输出层和隐含层的传递函数； $w_{jk}$ 、 $w _{ik}$ 分别为第k个输出层下的第j个隐含层和第i个输入层的连接权重； $\theta _j$ 、 $\theta _k$ 分别为第j个隐含层和第k个输出层的阈值；S为样本数量； $O$ _t为第t个样本预测输出值； $x_i$ 和 $y_i$ 分别为隐含层输入和输出值； $T_t$ 为实验测试值.

由于BP神经网络算法存在收敛慢和局部最小值的缺陷，接下来引入思维进化算法（MEC）对BP神经网络进行优化.

1.2 MEC算法

MEC算法^[11]是一种基于遗传算法改进的优化算法，运用MEC算法对BP神经网络的权值和阈值进行最优搜索，能提高BP神经网络的收敛速度和精度. 其基本步骤如下：

步骤1　种群初始化. 先将总体随机分成a个个体(m₁，m_2，…，m_a)，通过式（3）对各个体进行打分，并根据分数将个体分为w个优等子种群（每个优等种群包含b个个体）和r个临时子种群（每个临时种群包含h个个体）两大类，这两个种群分别用M_supi和M_temi表达，如式（4）所示.

$S = \frac{1}{{1 + E}} ,$

(3)

$\left\{ \begin{gathered} {M_{\sup i}} = \{ {m_1},{m_2}, \cdots, {m_b}\},\quad i = 1,2, \cdots, w , \\ {M_{{\rm{tem}}i}} = \{ {m_1},{m_2}, \cdots, {m_h}\} ,\quad i = 1,2, \cdots, r . \end{gathered} \right.$

(4)

步骤2　种群内竞争. 选出在每个子种群中得分最高的个体，按照正态分布将得分重新排序并再次进行得分计算，当最高得分者保持不变时，该最高得分者所在子种群即视为成熟，最高得分即代表该子种群得分.

步骤3　种群间竞争. 如果临时子种群（S_temi）得分高于成熟的优等子种群（S_supi），那么成熟的优等种群将会被该临时种群替代. 相反，如果临时种群得分较低，那么该临时种群将会解散，再重新生成新的临时种群，步骤2将产生新的临时种群.

1.3 MEC-BP神经网络拟合预测模型

MEC-BP神经网络拟合预测模型框架如图1所示. 图中：i_max、E_max分别为最大迭代次数和最大误差.

图 1 MEC-BP神经网络框架

Figure 1. MEC-BP neural network framework

下载: 全尺寸图片幻灯片

其基本流程为根据所选数据结构确定BP神经网络结构，通过MEC方法优化获得BP神经网络权值和阈值，进而得到优化的BP神经网络，通过优化的BP神经网络对给予的测试数据进行验证和预测.

2. 高海拔隧道供氧实验

高海拔供氧实验在西藏拉萨达孜区的圭嘎拉隧道进行，实验地点海拔高度约为4 200 m，实验测试对象为现场6名隧道技术施工人员，年龄在20岁～30岁，现场测试及仪器如图2所示.

图 2 现场测试及实验仪器

Figure 2. Field test and experimental instrument diagram

下载: 全尺寸图片幻灯片

实验通过调节供氧端制氧含量来设置供氧浓度，根据相关资料研究的氧浓度安全上限和实验的安全性^{[6, 14]}，供氧浓度设置为20.9%、25.0%和29.0%，通过调节骑行台设置50、75、100 W的骑行功率. 实验中，每位测试人员需在不同的氧浓度和骑行功率下骑行10 min，最后记录肺通量和相关生理参数. 根据相关肺通量和平均能量代谢率关系式^[15-16]，将标准化后的肺通量数值按照式（4）计算平均能量代谢率，现场测试及计算数据如表1所示.

表 1 现场测试及计算数据

Table 1. Field test and calculation data

测试人员编号	氧浓度/%	功率/W	肺通量/(L·min⁻¹)	A/m²	测试环境温度/K	标准肺通气量/ (L·min⁻¹)	平均能量代谢率/ (kJ·(min·m²)⁻¹)
1 号	20.9	50	10.52	1.86	298.15	5.78	0.57
	25.0	50	7.88	1.86	286.15	4.51	0.50
	29.0	50	7.29	1.86	284.15	4.20	0.48
	20.9	75	20.03	1.86	296.15	11.08	0.96
	25.0	75	17.07	1.86	288.15	9.71	0.69
	29.0	75	17.02	1.86	290.15	9.61	0.67
	20.9	100	32.75	1.86	298.15	18.00	2.21
	25.0	100	27.88	1.86	292.15	15.64	1.80
	29.0	100	27.94	1.86	292.15	15.67	1.80
2 号	20.9	50	9.75	1.80	299.15	5.34	0.56
	25.0	50	7.52	1.80	292.15	4.22	0.49
	29.0	50	6.73	1.80	284.15	3.88	0.47
	20.9	75	20.45	1.80	298.15	11.24	1.06
	25.0	75	18.12	1.80	298.15	9.96	0.81
	29.0	75	16.41	1.80	284.15	9.46	0.71
	20.9	100	27.54	1.80	298.15	15.13	1.80
	25.0	100	23.89	1.80	290.15	13.49	1.50
	29.0	100	22.87	1.80	289.15	12.96	1.39
3 号	20.9	50	8.64	1.72	298.15	4.75	0.53
	25.0	50	7.39	1.72	291.15	4.16	0.50
	29.0	50	6.91	1.72	283.15	4.00	0.49
	20.9	75	23.56	1.72	297.15	12.99	1.52
	25.0	75	20.45	1.72	298.15	11.24	1.17
	29.0	75	19.31	1.72	285.15	11.10	1.14
	20.9	100	29.44	1.72	298.15	16.18	2.14
	25.0	100	26.56	1.72	289.15	15.05	1.92
	29.0	100	25.44	1.72	285.15	14.62	1.84
4 号	20.9	50	10.74	1.85	298.15	5.90	0.59
	25.0	50	7.86	1.85	291.15	4.42	0.49
	29.0	50	6.66	1.85	282.15	3.87	0.46
	20.9	75	18.64	1.85	295.15	10.35	0.83
	25.0	75	16.24	1.85	292.15	9.11	0.59
	29.0	75	13.52	1.85	284.15	7.80	0.53
	20.9	100	25.79	1.85	298.15	14.17	1.55
	25.0	100	22.17	1.85	300.15	12.10	1.17
	29.0	100	21.25	1.85	283.15	12.30	1.20
5 号	20.9	50	10.22	1.99	298.15	5.62	0.54
	25.0	50	8.54	1.99	292.15	4.79	0.49
	29.0	50	7.47	1.99	282.15	4.34	0.47
	20.9	75	19.39	1.99	298.15	10.66	0.74
	25.0	75	18.72	1.99	292.15	10.50	0.71
	29.0	75	18.35	1.99	283.15	10.62	0.73
	20.9	100	28.27	1.99	298.15	15.54	1.60
	25.0	100	25.88	1.99	299.15	14.17	1.37
	29.0	100	24.33	1.99	285.15	13.98	1.33
6 号	20.9	50	9.99	1.85	298.15	5.49	0.56
	25.0	50	7.35	1.85	291.15	4.14	0.48
	29.0	50	6.19	1.85	282.15	3.59	0.45
	20.9	75	19.31	1.85	298.15	10.61	0.88
	25.0	75	19.17	1.85	294.15	10.68	0.89
	29.0	75	18.84	1.85	292.15	10.57	0.87
	20.9	100	27.5	1.85	300.15	15.01	1.70
	25.0	100	26.09	1.85	299.15	14.29	1.57
	29.0	100	25.13	1.85	289.15	14.24	1.56

下载: 导出CSV

| 显示表格

$V_{\rm{E}} = \frac{{V_1P_1T}}{{PT_1}} ,$

(5)

$\left\{ \begin{gathered} \lg \; M = 0.094 \; 5\frac{V_{\rm{E}}}{A} - 0.533\;94, \quad V_{\rm{E}} \in (3.0,7.3), \\ M = \dfrac{{{{10}^{0.094\;5\tfrac{{V_{\rm{E}}}}{A} - 0.533\;94}} + 13.26 - {{10}^{1.164\;8 - 0.012\;58\tfrac{{V_{\rm{E}}}}{A}}}}}{2}, \\ \lg (13.26 - M) = 1.164\;8 - 0.012\;58\frac{{V_{\rm{E}}}}{A},\quad V_{\rm{E}} \geqslant 8.0, \\ \quad V_{\rm{E}} \in [7.3,8.0) , \\ \end{gathered} \right.$

(6)

式中： $V_{\rm{E}}$ 为标准状态肺通气量（L/min）； $V_{1}$ 为相应海拔高度下肺通气量（L/min）；P为标准大气压（101.325 kPa）；P₁为相应海拔高度下大气压（实测取60.8 kPa）；T为标准状态温度（273.15 K）；T₁为相应海拔高度下温度（K）；M为平均能量代谢率（kJ/（min•m²））；A为体表面积（m²），如式（7）.

$A = 0.006 \;1H + 0.012\; 4W - 0.009\; 9 \text{，}$

(7)

式中：H为身高（cm）；W为体重（kg）.

从测试数据中看出，高海拔施工人员平均能量代谢率较低，且在100 W时最大平均能量代谢率为2.21 kJ/（min•m²）；高海拔施工人员平均能量代谢率随着功率增加而增加，在相同骑行功率下，平均能量代谢率随着氧浓度增加有减小趋势，且在100 W骑行功率减小较为明显.

3. MEC-BP神经网络算法拟合结果

根据数据特征，输入神经元选2个（功率、氧浓度），隐藏神经元个数取为10个，输出神经元为1个（平均新陈代谢率），种群规模大小取为100，训练数据取前5个人的45个数据，测试数据取最后1个人的9个数据. 神经网络结构如图3所示. 运用MATLAB R2016a对测试数据进行拟合，MEC-BP迭代次数及拟合优度如图4所示. 图5和图6分别给出了GA-BP和BP神经网络拟合优度及均方误差. 根据式（2）计算出MEC-BP、GA-BP、BP神经网络测试值与预测值均方误差分别为0.0139、0.0130、0.0255. 从拟合优度可以看出，MEC-BP神经网络优化算法相对较好，且均方误差较小，在计算过程中收敛速度快，在第4迭代步时验证集拟合均方根误差达到最小值0.054，在短时间内通过训练能达到较高拟合度，且训练、验证和测试的拟合优度较为平稳.

图 3 BP神经网络结构

Figure 3. Structure diagram of BP neural network

下载: 全尺寸图片幻灯片

图 4 MEC-BP迭代收敛及拟合优度

Figure 4. MEC-BP iterative convergence and goodness of fit

下载: 全尺寸图片幻灯片

图 5 GA-BP拟合优度

Figure 5. GA-BP goodness of fit

下载: 全尺寸图片幻灯片

图 6 BP拟合优度

Figure 6. BP goodness of fit

下载: 全尺寸图片幻灯片

从图7可以看出：在骑行功率为50 W时，平均能量代谢率随氧浓度变化不明显；在骑行功率为75 W时，平均能量代谢率随着氧浓度增加而减小，减小梯度小于100 W时变化曲率；在功率100 W时，当氧浓度小于25%时，平均能量代谢率随着氧浓度增加逐渐减小，当氧浓度大于25%时，平均能量代谢率随着氧浓度增加趋于平稳.

图 7 MEC-BP拟合平均能量代谢率变化

Figure 7. MEC-BP fitting average energy metabolic rate change chart

下载: 全尺寸图片幻灯片

4. 结　论

通过在高海拔进行高原供氧实验，运用MEC-BP神经网络优化算法对高海拔供氧测试数据进行了拟合，得到如下结论：

1）通过MEC-BP神经网络拟合的测试数据可以看出，拟合曲线变化规律与现场测试数据变化规律基本一致，验证了MEC-BP神经网络拟合的有效性.

2）通过不同算法对比分析了高原供氧数据拟合结果的准确性，MEC-BP神经网络在测试、验证和训练的拟合优度上相对稳定且精度较高，均方误差较小，拟合效果较好，可为多维数据拟合提供参考.

3）通过高海拔现场测试和MEC-BP神经网络拟合数据得到，50 W和75 W骑行功率下平均能量代谢率随氧浓度变化较小，100 W骑行功率下平均能量代谢率随氧浓度变化较大；25%供氧浓度可以作为4 200 m高海拔较高劳动强度的供氧浓度参考值.

致谢：成都哲学社会科学规划项目（2019CS107）；成都市科技项目（2019-YFYF-00121-SN）.

图 1 波形钢板细部尺寸

Figure 1. Details of corrugated steel plate

下载: 全尺寸图片幻灯片

图 2 低屈服点CSPSW尺寸

Figure 2. Model size of low-yield-point CSPSW

下载: 全尺寸图片幻灯片

图 3 低屈服点CSPSW有限元模

Figure 3. Finite element model of low-yield-point CSPSWs

下载: 全尺寸图片幻灯片

图 4 加载制度

Figure 4. Cyclic loading protocol

下载: 全尺寸图片幻灯片

图 5 数值分析和试验破坏形式对比

Figure 5. Deflected shape numerical and experimental results

下载: 全尺寸图片幻灯片

图 6 滞回曲线数值分析和试验结果比较

Figure 6. Comparison of numerical and experimental hysteresis curvers

下载: 全尺寸图片幻灯片

图 7 荷载-位移曲线

Figure 7. Load-displacement curves

下载: 全尺寸图片幻灯片

图 8 平面外变形对比

Figure 8. Out-of-plane deformation comparison

下载: 全尺寸图片幻灯片

图 9 CSPSW模型在屈服位移处Mises应力云图

Figure 9. Mises stess diagram of CSPSW models at the yield displacement

下载: 全尺寸图片幻灯片

图 10 CSPSW模型在最大加载位移处Mises应力云图

Figure 10. Mises stess diagram of CSPSW models at the maximum loading displacement

下载: 全尺寸图片幻灯片

图 11 不同屈服强度和板厚波形板的CSPSW滞回曲线

Figure 11. Hysteresis curves of CSPSW models with corrugated plate of different yield strength and thickness

下载: 全尺寸图片幻灯片

图 12 刚度退化曲线

Figure 12. Stiffness degradation curves

下载: 全尺寸图片幻灯片

图 13 模型能量耗散曲线

Figure 13. Energy dissipation curves

下载: 全尺寸图片幻灯片

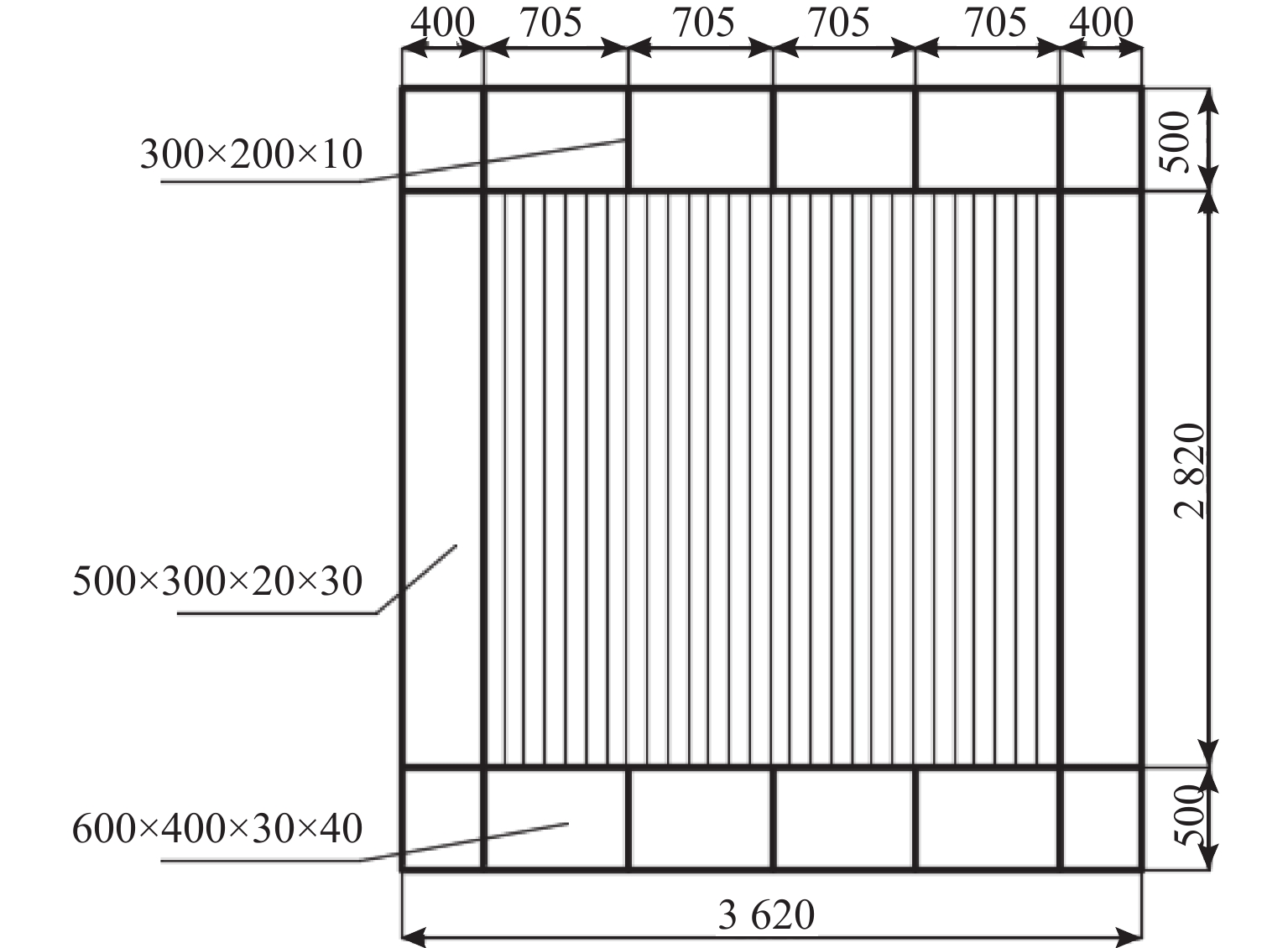
表 1 低屈服点CSPSW模型特征描述

Table 1. Characteristic description of low-yield-point CSPSW models

y/MPa	t/mm
100	6、8、10、12
160
225
345

下载: 导出CSV

表 2 特征位移和延性系数

Table 2. Characteristic displacement and ductility factor

模型编号	屈服位移/mm	极限位移/mm	μ
C-100-6	3.00	60.00	20.00
C-160-6	4.00	60.00	15.00
C-225-6	5.98	60.00	10.04
C-345-6	7.47	60.00	8.03
C-100-8	3.00	60.00	20.00
C-160-8	4.00	60.00	15.00
C-225-8	5.87	60.00	10.21
C-345-8	8.75	60.00	6.86
C-100-10	3.00	60.00	20.00
C-160-10	4.94	60.00	12.13
C-225-10	6.94	60.00	8.64
C-345-10	9.66	60.00	6.21
C-100-12	3.00	60.00	20.00
C-160-12	4.94	60.00	12.13
C-225-12	6.96	60.00	8.61
C-345-12	9.93	34.35	3.46

下载: 导出CSV

参考文献(17)

[1]	黄育琪. 低屈服点钢板剪力墙力学性能研究[D]. 西安: 西安建筑科技大学, 2013.
[2]	赵秋红,李楠,孙军浩. 波纹钢板剪力墙结构的抗侧性能分析[J]. 天津大学学报(自然科学与工程技术版),2016,49(增1): 152-160. ZHAO Qiuhong, LI Nan, SUN Junhao. Analysis on lateral performance of sinusoidally corrugated steel plate shear walls[J]. Journal of Tianjin University (Science and Technology), 2016, 49(S1): 152-160.
[3]	谭平,魏瑶,李洋,等. 波纹钢板剪力墙抗震性能试验研究[J]. 土木工程学报,2018,51(5): 8-15. doi: 10.15951/j.tmgcxb.2018.05.002 TAN Ping, WEI Yao, LI Yang, et al. Experimental investigation on performance of corrugated steel plate shear wall[J]. China Civil Engineering Journal, 2018, 51(5): 8-15. doi: 10.15951/j.tmgcxb.2018.05.002
[4]	EMAMI F, MOFID M, VAFAI A. Experimental study on cyclic behavior of trapezoidally corrugated steel shear walls[J]. Engineering Structures, 2013, 48: 750-762. doi: 10.1016/j.engstruct.2012.11.028
[5]	李志安,王伟,吴泽锋,等. 波形钢板剪力墙滞回性能有限元分析[J]. 施工技术,2018,47(15): 8-12. LI Zhian, WANG Wei, WU Zefeng. Finite element analysis of hysteretic behavior of corrugated steel plate shear wall[J]. Construction Technology, 2018, 47(15): 8-12.
[6]	孙军浩. 波纹钢板剪力墙的抗侧及抗震性能研究[D]. 天津: 天津大学, 2016.
[7]	KALALI H, GHAZIJAHANI T G, HAJSADEGHI M, et al. Numerical study on steel shear walls with sinusoidal corrugated plates[J]. Latin American Journal of Solids and Structures, 2016, 13(15): 2802-2814. doi: 10.1590/1679-78252837
[8]	赵秋红,邱静,李楠,等. 梯形波纹钢板剪力墙抗震性能试验研究[J]. 建筑结构学报,2018,39(增2): 112-120. ZHAO Qiuhong, QIU Jing, LI Nan, et al. Experimental study on seismic performance of trapezoidally corrugated steel plate shear walls[J]. Journal of Building Structures, 2018, 39(S2): 112-120.
[9]	郑宏,杨瑞鹏,王玮,等. 往复加载下十字加劲波纹钢板剪力墙的滞回性能分析[J]. 结构工程师,2021,37(1): 15-23. ZHENG Hong, YANG Ruipeng, WANG Wei, et al. Hysteresis performance analysis of shear wall with cross-stiffening corrugated steel plate under cyclic loading[J]. Structural Engineers, 2021, 37(1): 15-23.
[10]	施刚,王珣,高阳,等. 国产低屈服点钢材循环加载试验研究[J]. 工程力学,2018,35(8): 30-38. doi: 10.6052/j.issn.1000-4750.2017.08.0617 SHI Gang, WANG Xun, GAO Yang, et al. Experimental study on domestic low yield point steels under cyclic loading[J]. Engineering Mechanics, 2018, 35(8): 30-38. doi: 10.6052/j.issn.1000-4750.2017.08.0617
[11]	中国工程建设标准化协会. 波纹腹板钢结构技术规程: CECS 291—2011[S]. 北京: 中国计划出版社, 2011.
[12]	Canadian Standards Association (CSA). Limit states design of steel structures: CAN/CSA S16[S]. Ontario: [s.n.], 1994.
[13]	Canadian Standards Association (CSA). Limit states design of steel structures: CAN/CSA S16-01[S]. Ontario: [s.n.], 2001.
[14]	中国工程建设标准化协会. 波纹腹板钢结构技术规程CECS291—2001[S]. 北京: 中国计划出版社, 2012.
[15]	中华人民共和国铁道部. 建筑抗震设计规范: GB 50011—2010[S]. 北京: 中国建筑工业出版社, 2010.
[16]	SABOURI-GHOMI S, VENTURA C E, KHARRAZI M H. Shear analysis and design of ductile steel plate walls[J]. Journal of Structural Engineering, 2005, 131(6): 878-889. doi: 10.1061/(ASCE)0733-9445(2005)131:6(878)
[17]	顾强. 钢结构滞回性能及抗震设计[M]. 北京: 中国建筑工业出版社, 2009: 431-432.