Traffic Data Imputation Based on Graph Regularization and Schatten-p Norm Minimization
-
摘要:
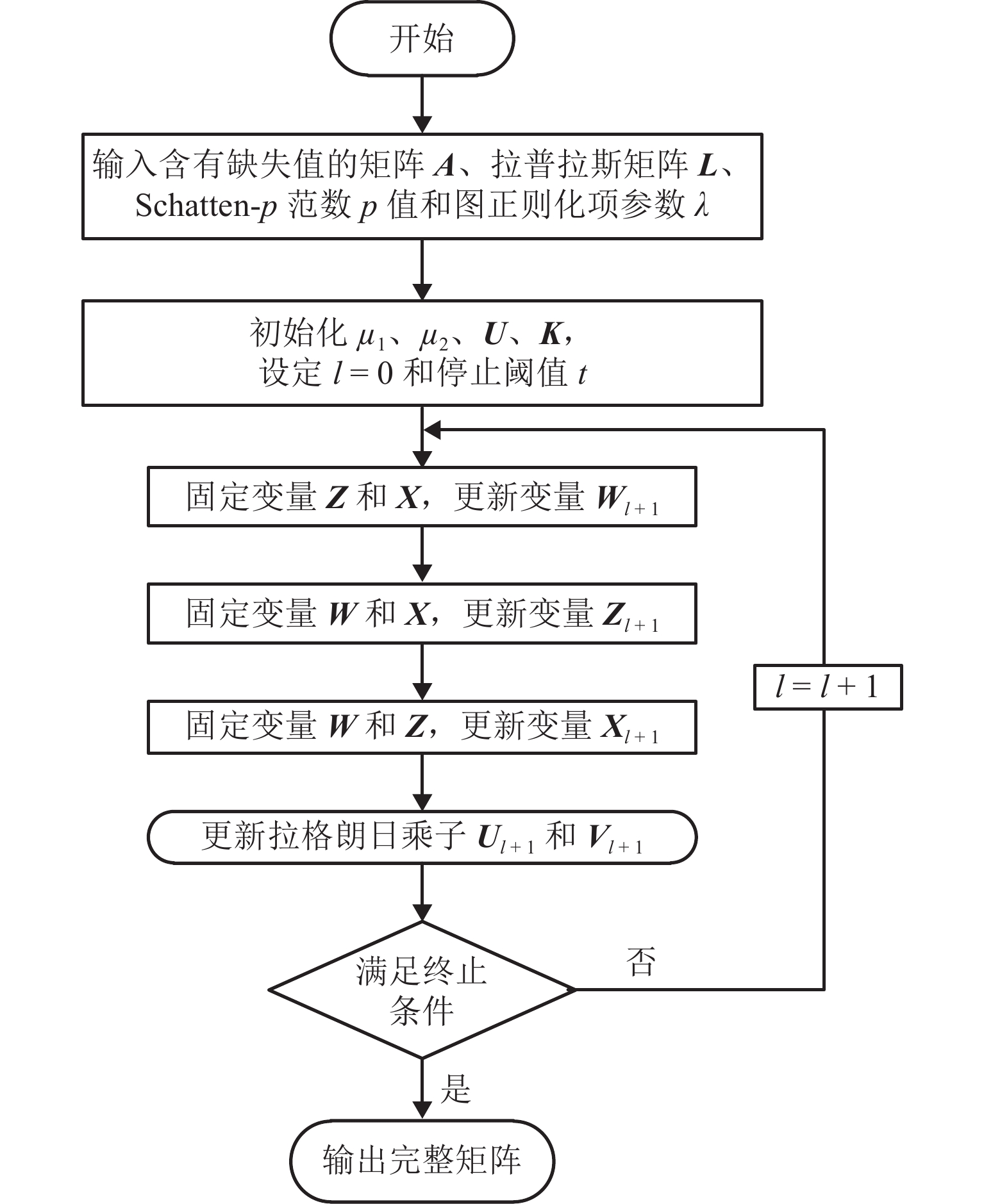
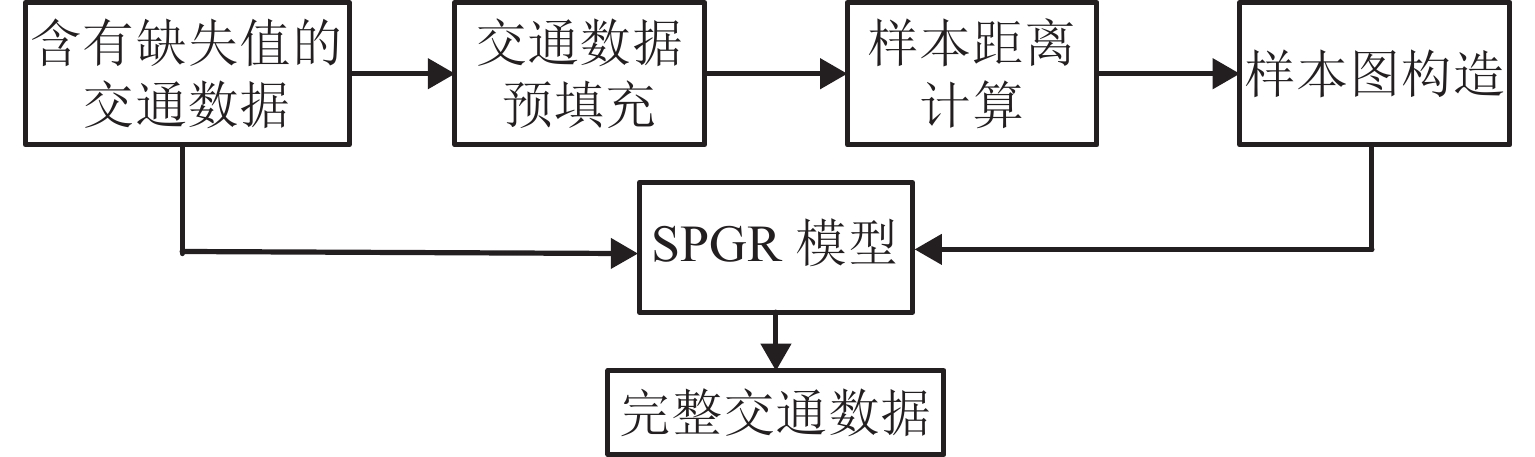
为充分利用交通数据低秩特性与局部近邻关系，准确恢复交通数据采集系统中的缺失数据，首先，应用基于核范数的低秩矩阵补全模型对交通数据矩阵进行预插补，以获得缺失值的初始估计，基于此，构建表征数据局部近邻结构的图模型；然后，提出融合图正则化和Schatten-
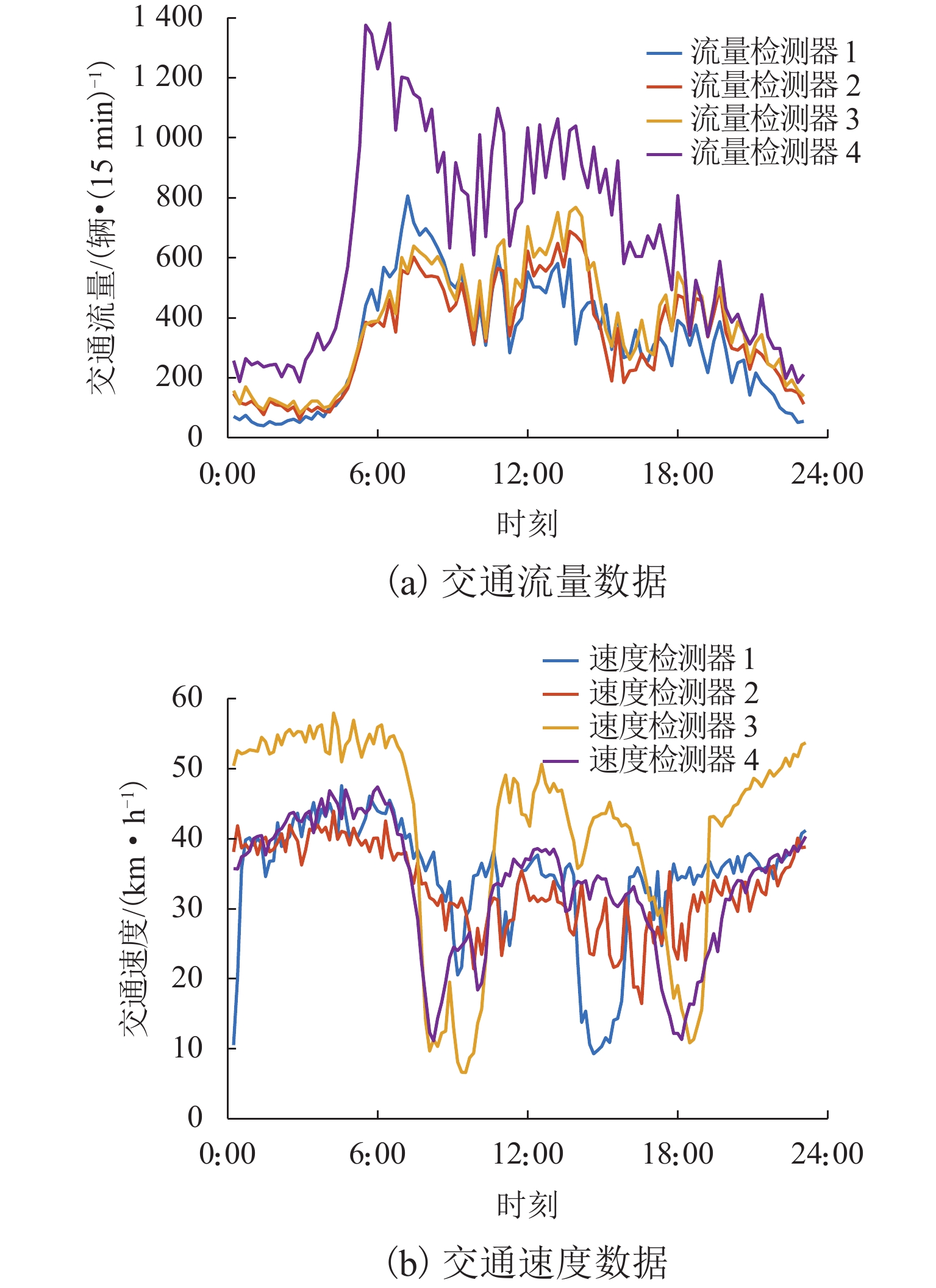
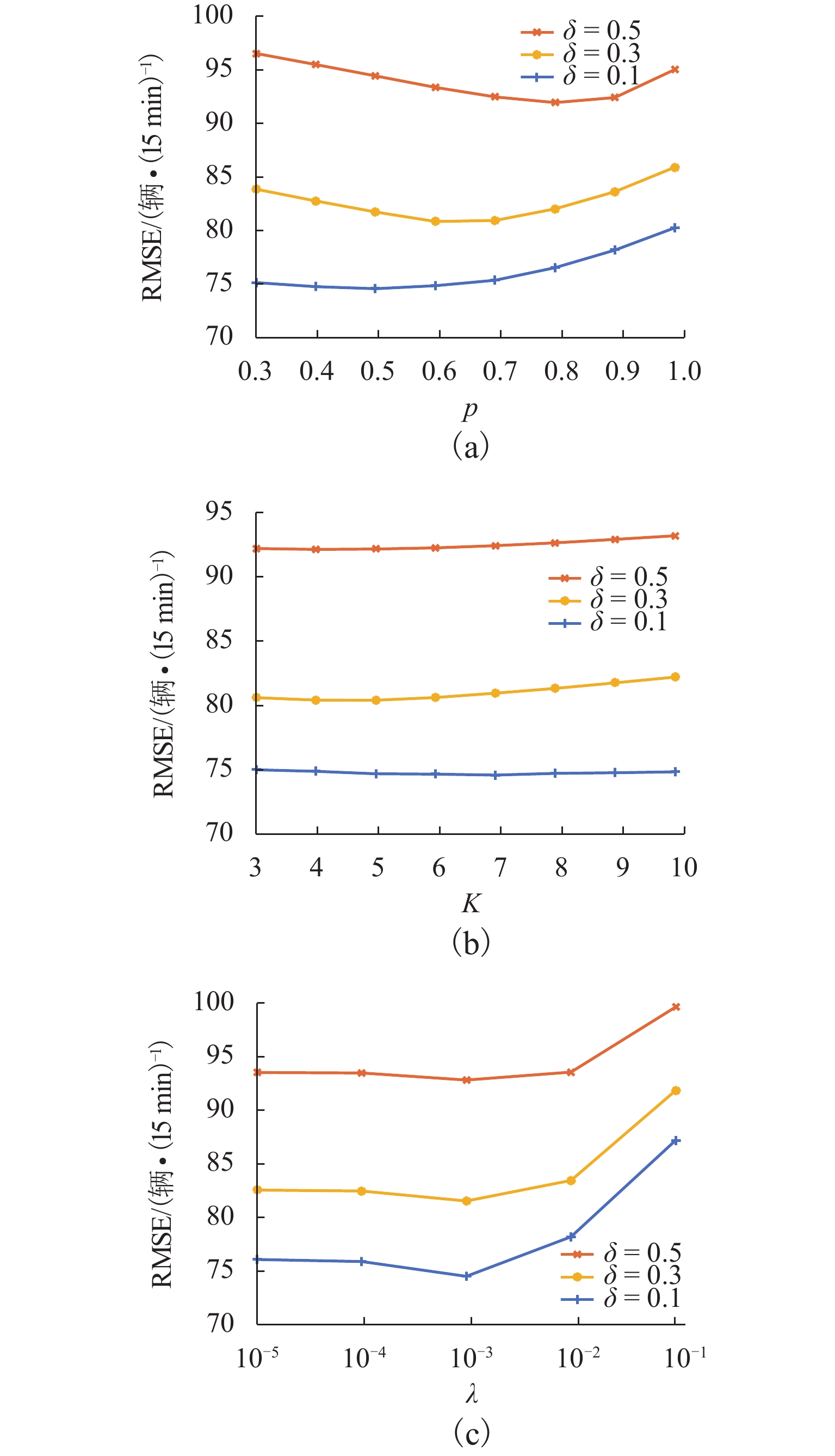
p 范数最小化的交通数据缺失值恢复模型；进一步，提出基于交替方向乘子框架的优化算法，求解缺失值恢复的最优化问题，得到最终的数据恢复结果；最后，用实际的高速公路交通流量和速度数据比较多种方法的恢复误差，同时给出所提方法的参数敏感性分析. 实验结果表明：在完全随机缺失、随机缺失和混合缺失模式下，缺失率为10% ~ 50%时，相比于局部最小二乘、概率主成分分析和低秩矩阵补全等方法，基于图正则化和Schatten-p 范数最小化的算法恢复误差降低了3.02% ~ 28.49%.-
关键词:
- 智能交通 /
- 数据恢复 /
- Schatten-p范数 /
- 交通数据 /
- 图正则化
Abstract:To make full use of the low-rank characteristics and local neighbor relationship of the traffic data, and accurately recover the missing data in traffic data acquisition system, firstly, the traffic data matrix is pre-interpolated by the low-rank matrix completion model based on kernel norm to obtain the initial estimate of the missing data. Based on this, a graph model that characterizes the local neighbor structure of the data is constructed. Then, a missing value imputation model combining graph regularization and Schatten-
p norm minimization is proposed. Furthermore, an optimization algorithm based on alternating direction multiplier framework is proposed to solve the optimization of missing value imputation, so as to obtain the final imputation result. Finally, the real expressway traffic volume and speed data are used to compare the imputation errors of several methods, and the parameter sensitivity of the proposed method is analyzed. The experimental results show that compared with local least squares, probabilistic principal component analysis and low-rank matrix completion, the proposed method reduces the error of traffic data imputation by 3.02%−28.49% when the missing rate is 10%−50% in missing completely at random mode, missing at random mode and mixed missing mode.-
Key words:
- intelligent transportation /
- data imputation /
- Schatten-p norm /
- traffic data /
- graph regularization
-
图 3 同一天中不同传感器交通流和交通速度的变化情况
Figure 3. Changes in traffic flow and speed from different sensors over the same day
图 5 SPGR模型在交通流量数据上的RMSE随参数
$ p $ 、$ K $ 、$ \lambda $ 的变化Figure 5. RMSEs of SPGR model on traffic flow data varied with the parameters of
$ p、K、\lambda $ 表 1 MCAR模式下不同算法的恢复误差
Table 1. Imputation error of different algorithms in MCAR mode
算法 δ 交通流量 交通速度 RMSE/（辆·
（15 min）−1）MAPE/% RMSE/
（km·h−1）MAPE/% LRMC 0.1 80.63 13.29 2.53 5.76 0.2 83.80 13.75 2.64 6.07 0.3 86.58 14.29 2.65 6.40 0.4 90.94 14.86 2.79 6.83 0.5 95.91 15.74 2.99 7.37 PPCA 0.1 79.06 13.00 2.41 5.82 0.2 82.98 13.80 2.53 6.08 0.3 85.47 14.67 2.72 6.27 0.4 89.69 15.55 2.81 6.85 0.5 95.83 17.11 2.98 6.95 LLS 0.1 76.62 13.26 3.15 7.40 0.2 82.26 14.21 3.28 7.74 0.3 89.94 15.81 3.43 8.13 0.4 99.01 17.61 3.67 8.82 0.5 113.01 19.92 4.06 9.76 SP 0.1 75.77 12.73 2.39 5.65 0.2 78.36 13.18 2.50 5.95 0.3 82.43 13.73 2.63 6.31 0.4 88.06 14.51 2.78 6.74 0.5 93.66 15.56 2.98 7.29 SPGR 0.1 74.56 12.67 2.38 5.64 0.2 76.96 13.17 2.50 5.95 0.3 80.93 13.59 2.63 6.30 0.4 86.24 14.38 2.76 6.70 0.5 92.40 15.44 2.95 7.19 
下载: 导出CSV
表 2 MAR模式下不同算法的恢复误差
Table 2. Imputation error of different algorithms in MAR mode
算法 δ 交通流量 交通速度 RMSE/（辆·
（15 min）−1）MAPE/% RMSE/
（km·h−1）MAPE/% LRMC 0.1 98.31 14.62 3.38 8.42 0.2 100.92 15.14 3.45 8.68 0.3 103.11 15.72 3.48 8.77 0.4 106.22 16.30 3.55 8.98 0.5 109.81 17.03 3.63 9.15 PPCA 0.1 90.14 13.71 3.60 8.48 0.2 95.13 14.70 3.75 8.83 0.3 97.45 15.49 3.77 8.87 0.4 101.55 18.49 3.80 8.93 0.5 105.51 17.72 3.85 9.02 LLS 0.1 84.31 13.40 3.75 8.89 0.2 91.89 14.70 3.86 9.30 0.3 100.10 16.38 3.91 9.40 0.4 112.55 16.44 4.11 10.02 0.5 130.83 21.11 4.51 10.69 SP 0.1 88.08 13.64 3.26 8.17 0.2 90.99 14.09 3.37 8.42 0.3 94.50 14.96 3.43 8.60 0.4 99.86 15.83 3.53 8.86 0.5 105.22 16.77 3.60 9.00 SPGR 0.1 86.31 13.51 3.22 7.97 0.2 89.01 13.93 3.31 8.23 0.3 92.76 14.79 3.36 8.35 0.4 97.51 15.63 3.48 8.64 0.5 101.82 16.62 3.56 8.81
下载: 导出CSV
表 3 MIXED模式下不同算法的恢复误差
Table 3. Imputation error of different algorithms in MIXED mode
算法 δ 交通流量 交通速度 RMSE/（辆·
（15 min）−1）MAPE/% RMSE/
（km·h−1）MAPE/% LRMC 0.1 89.57 13.56 2.97 7.10 0.2 92.73 14.31 2.99 7.28 0.3 95.18 14.70 3.10 7.59 0.4 99.00 15.61 3.19 7.86 0.5 103.12 16.24 2.99 8.24 PPCA 0.1 84.40 12.95 3.13 7.24 0.2 89.37 14.08 3.10 7.33 0.3 91.37 14.76 3.18 7.57 0.4 95.26 16.10 3.24 7.73 0.5 100.80 17.33 2.98 7.91 LLS 0.1 79.48 13.11 3.65 8.05 0.2 86.60 14.34 3.54 8.39 0.3 93.75 15.77 3.66 8.74 0.4 104.31 17.83 3.82 9.20 0.5 118.90 20.15 4.06 10.09 SP 0.1 82.10 12.85 2.92 6.95 0.2 85.54 13.62 3.02 7.10 0.3 88.72 14.34 3.10 7.49 0.4 94.10 15.35 3.18 7.79 0.5 99.60 16.18 3.31 8.15 SPGR 0.1 80.51 12.74 2.86 6.81 0.2 83.82 13.49 2.89 7.03 0.3 86.62 14.18 3.02 7.36 0.4 92.01 15.21 3.10 7.62 0.5 97.81 16.04 3.24 7.98
下载: 导出CSV
表 4 在交通流量数据上不同初始化方法对SPGR恢复误差的影响
Table 4. Effect of different initialization methods on SPGR imputation error on traffic flow data
辆/15 min 数据模式 KNN LLS LRMC MCAR 81.21 80.99 80.93 MAR 93.68 93.14 92.76 MIXED 87.74 87.48 86.62
下载: 导出CSV
-
[1] 陈程. 基于稀疏表示的交通数据缺失值恢复方法研究[D]. 镇江: 江苏大学, 2020. [2] HENRICKSON K, ZOU Y J, WANG Y H. Flexible and robust method for missing loop detector data imputation[J]. Transportation Research Record: Journal of the Transportation Research Board, 2015, 2527(1): 29-36. doi: 10.3141/2527-04 [3] 孙玲,刘浩,牛树云. 考虑时空相关性的固定检测缺失数据重构算法[J]. 交通运输工程学报,2010,10(5): 121-126. doi: 10.3969/j.issn.1671-1637.2010.05.021SUN Ling, LIU Hao, NIU Shuyun. Reconstructive method of missing data for location-specific detector considering spatio-temporal relationship[J]. Journal of Traffic and Transportation Engineering, 2010, 10(5): 121-126. doi: 10.3969/j.issn.1671-1637.2010.05.021 [4] CHEN Y Y, LV Y S, WANG F Y. Traffic flow imputation using parallel data and generative adversarial networks[J]. IEEE Transactions on Intelligent Transportation Systems, 2020, 21(4): 1624-1630. doi: 10.1109/TITS.2019.2910295 [5] RODRIGUES F, HENRICKSON K, PEREIRA F C. Multi-output Gaussian processes for crowdsourced traffic data imputation[J]. IEEE Transactions on Intelligent Transportation Systems, 2019, 20(2): 594-603. doi: 10.1109/TITS.2018.2817879 [6] 李林超,曲栩,张健,等. 基于特征级融合的高速公路异质交通流数据修复方法[J]. 东南大学学报(自然科学版),2018,48(5): 972-978. doi: 10.3969/j.issn.1001-0505.2018.05.029LI Linchao, QU Xu, ZHANG Jian, et al. Missing value imputation method for heterogeneous traffic flow data based on feature fusion[J]. Journal of Southeast University (Natural Science Edition), 2018, 48(5): 972-978. doi: 10.3969/j.issn.1001-0505.2018.05.029 [7] LI Q, TAN H C, WU Y K, et al. Traffic flow prediction with missing data imputed by tensor completion methods[J]. IEEE Access, 2020, 8: 63188-63201. doi: 10.1109/ACCESS.2020.2984588 [8] CHEN X Y, HE Z C, CHEN Y X, et al. Missing traffic data imputation and pattern discovery with a Bayesian augmented tensor factorization model[J]. Transportation Research Part C: Emerging Technologies, 2019, 104: 66-77. doi: 10.1016/j.trc.2019.03.003 [9] CHEN X B, CAI Y F, YE Q L, et al. Graph regularized local self-representation for missing value imputation with applications to on-road traffic sensor data[J]. Neurocomputing, 2018, 303: 47-59. doi: 10.1016/j.neucom.2018.04.029 [10] BOYD S, PARIKH N, CHU E, et al. Distributed optimization and statistical learning via the alternating direction method of multipliers[J]. Foundations and Trends, 2011, 3(1): 1-122. [11] NIE F P, WANG H, HUANG H, et al. Joint Schatten p-norm and ℓ p-norm robust matrix completion for missing value recovery[J]. Knowledge and Information Systems, 2015, 42(3): 525-544. doi: 10.1007/s10115-013-0713-z [12] BARTELS R H, STEWART G W. Solution of the matrix equation AX + XB = C[J]. Communications of the ACM, 1972, 15(9): 820-826. doi: 10.1145/361573.361582 [13] LI L C, ZHANG J, WANG Y G, et al. Missing value imputation for traffic-related time series data based on a multi-view learning method[J]. IEEE Transactions on Intelligent Transportation Systems, 2019, 20(8): 2933-2943. doi: 10.1109/TITS.2018.2869768 [14] ZHANG Y, LIU Y C. Data imputation using least squares support vector machines in urban arterial streets[J]. IEEE Signal Processing Letters, 2009, 16(5): 414-417. doi: 10.1109/LSP.2009.2016451 -
下载:
点击查看大图
计量
- 文章访问数: 284
- HTML全文浏览量: 92
- PDF下载量: 32
- 被引次数: 0