基于动态罚函数的铁路车流分配与径路优化模型

薛锋; 刘泳博; 户佐安; 陈逸飞

doi:10.3969/j.issn.0258-2724.20210226

基于动态罚函数的铁路车流分配与径路优化模型

doi: 10.3969/j.issn.0258-2724.20210226

薛锋^{1, 2, 3,},
刘泳博^2,,
户佐安^{1, 2, 3, ,},
陈逸飞²

1.
西南交通大学交通运输与物流学院，四川成都 611756
2.
西南交通大学唐山研究生院，河北唐山 063000
3.
西南交通大学综合交通大数据应用技术国家工程实验室，四川成都 611756

基金项目: 国家自然科学基金（61203175）；四川省自然科学基金（2022NSFSC0471）；四川省科技计划（2021YJ0067，2021YJ0077）

详细信息

作者简介:
薛锋（1981— ），男，副教授，博士，研究方向为运输组织理论与系统优化，E-mail：xuefeng.7@163.com

通讯作者:
户佐安（1979— ），男，副教授，博士，研究方向为运输组织理论与系统优化，E-mail：huzuoan@swjtu.edu.cn

中图分类号: U292.3
计量
- 文章访问数: 351
- HTML全文浏览量: 1484
- PDF下载量: 87
- 被引次数: 0
出版历程
- 收稿日期: 2021-03-29
- 修回日期: 2021-12-13
- 网络出版日期: 2022-08-02
- 刊出日期: 2021-12-16

Railcar Traffic Distribution and Route Optimization Model Based on Dynamic Penalty Function

XUE Feng^{1, 2, 3
,},
LIU Yongbo^2
,,
HU Zuoan^{1, 2, 3
, ,},
CHEN Yifei²

1.
School of Transportation and Logistics, Southwest Jiaotong University, Chengdu 611756, China
2.
Graduate School of Tangshan, Southwest Jiaotong University, Tangshan 063000, China
3.
National Engineering Laboratory of Integrated Transportation Big Data Application Technology, Southwest Jiaotong University, Chengdu 611756, China

摘要

摘要:
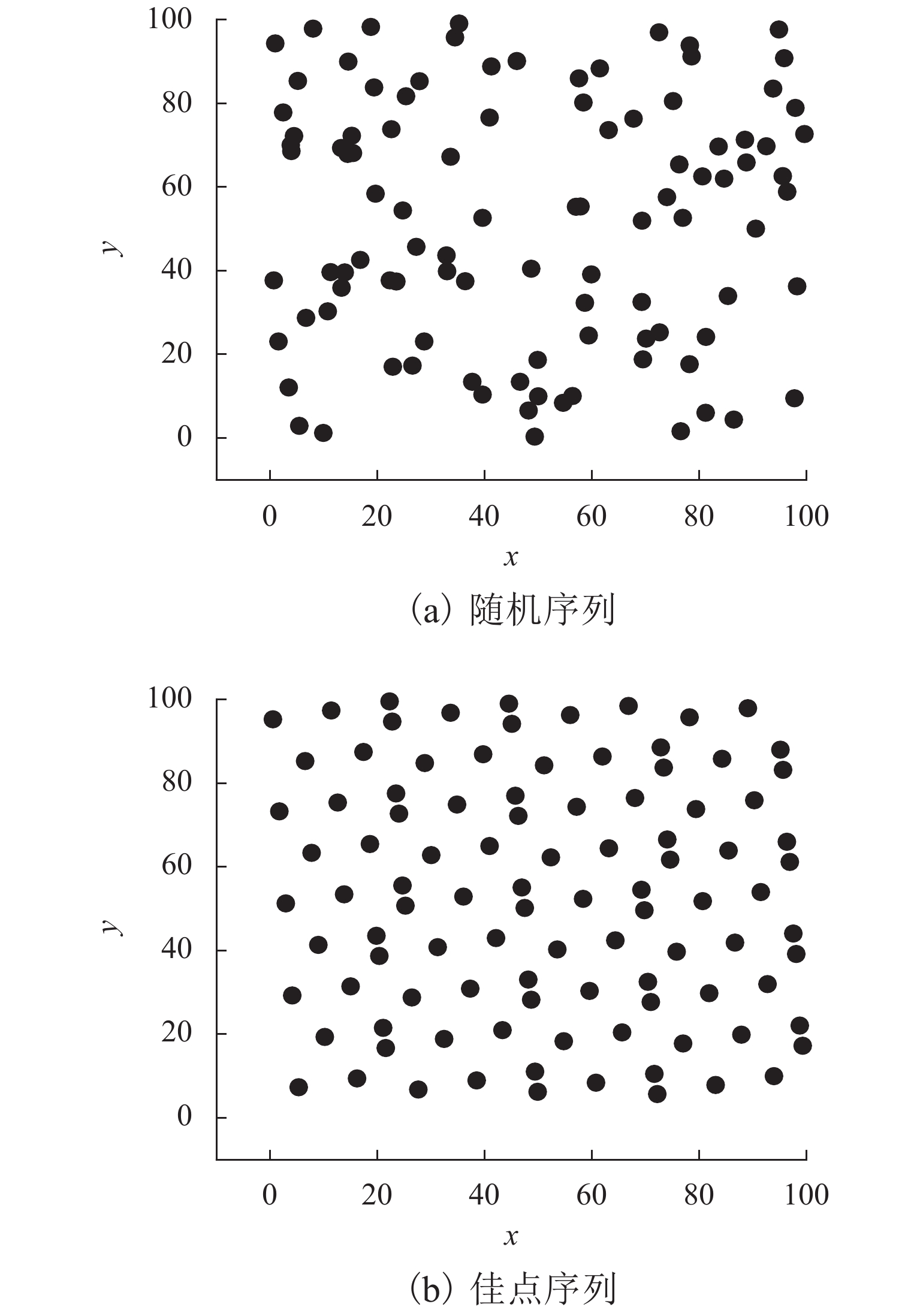
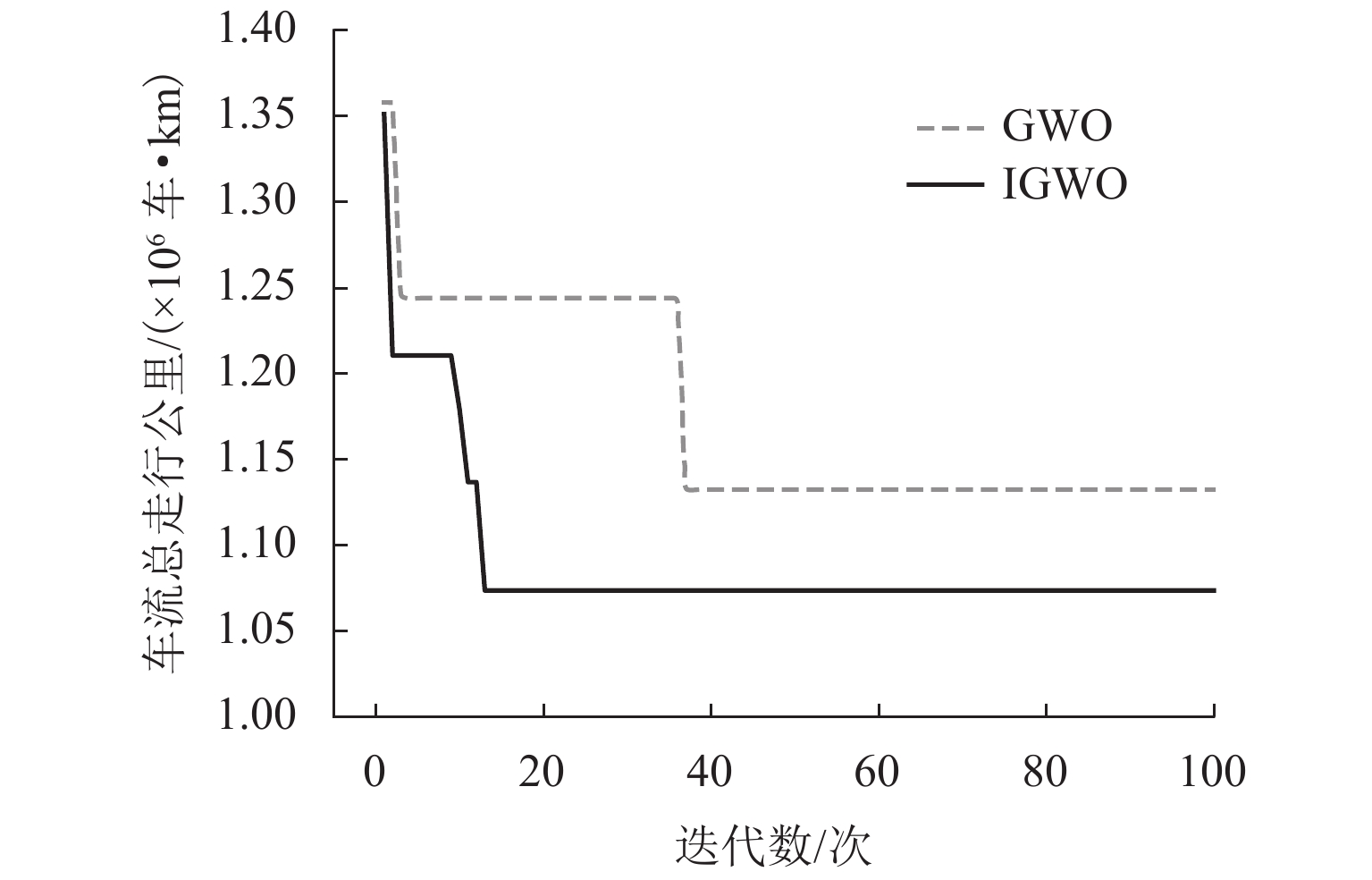
为解决铁路车流分配与径路优化模型中的难约束问题，避免群智能算法在应对该问题时难以求解的不足，提出了一种基于惩罚函数的约束优化方法. 首先，在车流分配及径路优化基本模型的基础上设置虚拟弧，在目标函数中增加惩罚项的方式松弛掉模型中的弧段能力约束，同时对惩罚项中的惩罚力度和惩罚因子设计动态更新的策略；然后，将改进灰狼算法（improved grey wolf algorithm，IGWO）应用于车流分配与径路优化模型的求解；最后，结合某一地区的路网数据，对改进前、后的模型和算法进行对比分析. 算例结果表明：与改进前的模型相比，引入惩罚项之后，IGWO可以在限定的范围内找到满足弧段能力约束的可行解；与灰狼算法（gray wolf algorithm，GWO）相比，IGWO计算所得的配流方案使OD （origin-destination）货流的平均绕行率和货物总走行公里数分别下降了2.6%和5.2%.
- 铁路运输 /
- 车流分配 /
- 径路优化 /
- 惩罚函数 /
- 约束优化 /
- 改进灰狼算法
Abstract:
In order to solve the constraint difficulty in the railway traffic distribution and route optimization model, and the inadequacy of swarm intelligence algorithm, a constraint optimization method based on penalty function is proposed. First, a virtual arc is set on the basis of the basic model of traffic distribution and route optimization, and the arc segment capability constraints in the model are relaxed by adding a penalty term to the objective function. Meanwhile, a dynamic update strategy is designed for the penalty intensity and penalty factor of the penalty term. Then, the improved grey wolf algorithm (IGWO) is applied to the solution of traffic distribution and route optimization models. Finally, combined with the road network data in a certain area, the models and algorithms before and after improvement are compared and analyzed. The results of case study show that, compared with the model before improvement, after introducing the penalty term, IGWO can find feasible solutions that satisfy the arc capacity constraints within a limited range; compared with the grey wolf algorithm (GWO), the distribution scheme calculated by IGWO reduces the average detour rate of the OD (origin-destination) cargo flow and the total cargo kilometers by 2.6% and 5.2%, respectively.
- railway transportation /
- railway traffic assignment /
- route optimization /
- penalty function /
- constraint optimization /
- improved grey wolf algorithm

HTML全文

图 1 简化路网

Figure 1. Simplified railway network

下载: 全尺寸图片幻灯片

图 2 两种方式下初始种群的分布

Figure 2. Distribution of initial population in two modes

下载: 全尺寸图片幻灯片

图 3 编码操作

Figure 3. Encoding operation

下载: 全尺寸图片幻灯片

图 4 IGWO在求解模型Q的流程

Figure 4. Flowchart of IGWO solving model Q

下载: 全尺寸图片幻灯片

图 5 某区域简化路网

Figure 5. Simplified railway network of a certain area

下载: 全尺寸图片幻灯片

图 6 GWO和IGWO的求解示意

Figure 6. Solution illustration of GWO and IGWO

下载: 全尺寸图片幻灯片

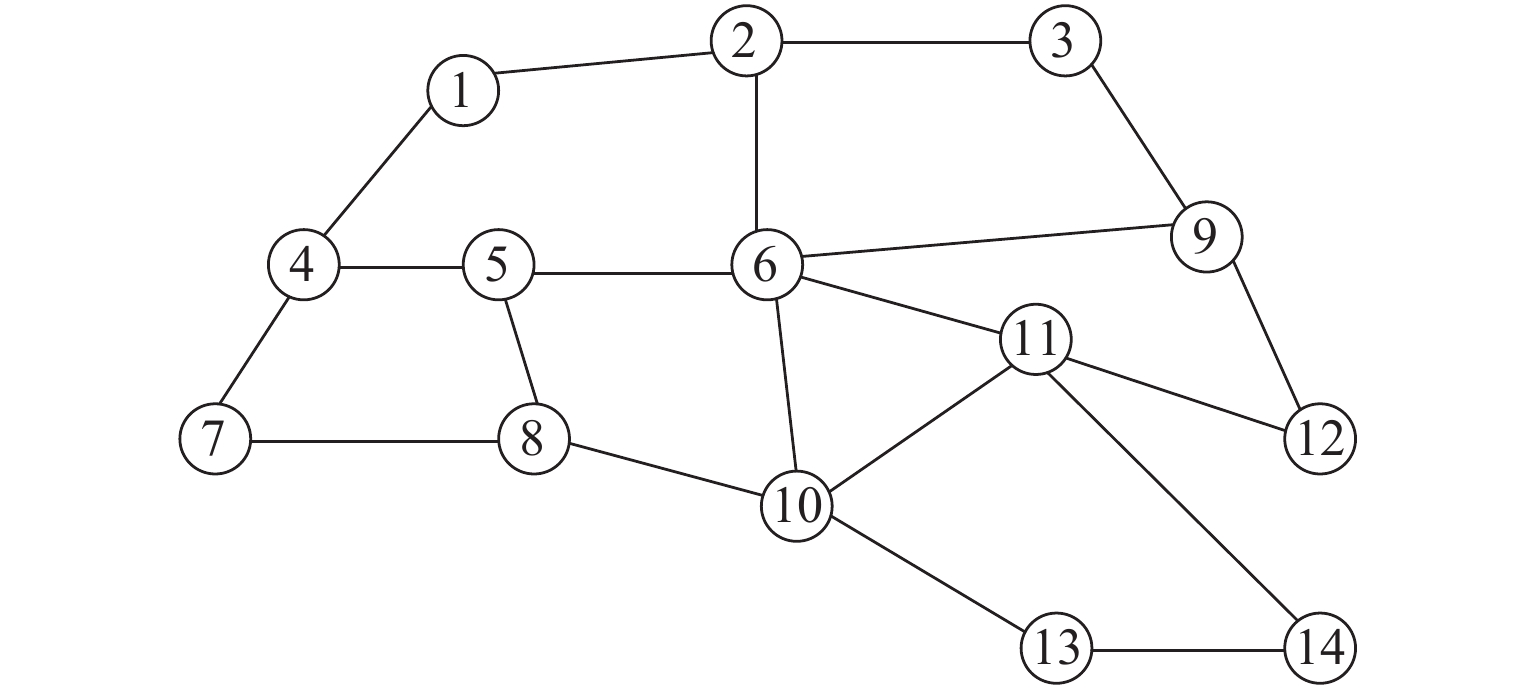
表 1 路网相关参数

Table 1. Railway network parameters

弧段	里程/km	线路容量/ ( × 10⁴车)	弧段	里程/km	线路容量/ ( × 10⁴车)
(1,2)	210	300	(6,10)	246	300
(1,4)	265	300	(6,11)	280	300
(2,3)	232	300	(9,12)	503	300
(2,6)	123	300	(10,11)	130	300
(3,9)	480	380	(10,13)	115	300
(4,5)	109	300	(11,12)	336	300
(4,7)	190	300	(11,14)	218	300
(5,6)	172	300	(13,14)	158	300
(5,8)	149	380	(7,8)	117	380
(6,9)	368	380	(8,10)	220	400

下载: 导出CSV

表 2 年车流OD量

Table 2. Annual OD volume of cargo flow

发站	到站	年 OD 量/ （× 10⁴车）	发站	到站	年 OD 量/ （ × 10⁴车）
3	7	55	3	11	52
7	9	35	10	3	40
7	14	50	2	12	50
12	7	45	4	9	45
8	9	64	11	4	46
8	12	52	5	13	70
1	8	60	5	12	68
1	14	40	14	5	62
12	1	50	3	13	50
3	8	65	10	1	45

下载: 导出CSV

表 3 车流径路的优化方案

Table 3. Optimization scheme of cargo flow route

发站	到站	优化后的车流径路
3	7	3→2→1→4→5→8→7
7	9	7→8→5→6→2→3→9
7	14	7→8→10→13→14
12	7	12→11→6→2→1→4→7
8	9	8→5→4→1→2→6→9
8	12	8→5→6→9→12
1	8	1→4→7→8
1	14	1→4→5→8→10→13→14
12	1	12→9→3→2→1
3	8	3→9→6→10→8
3	11	3→9→6→10→11
10	3	10→6→2→3
2	12	2→6→11→12
4	9	4→7→8→10→6→9
11	4	11→14→13→10→8→7→4
5	13	5→8→10→11→14→13
5	12	5→8→10→13→14→11→12
14	5	14→11→6→5
3	13	3→9→6→11→10→13
10	1	10→6→2→1

下载: 导出CSV

表 4 区间通过流量统计

Table 4. Interval traffic statistics

弧段	区间车流量/（ × 10⁴车）	线路利用率/%
(1,2)	256	86.33
(1,4)	264	88.00
(2,3)	180	60.00
(2,6)	279	93.00
(3,9)	252	66.32
(4,5)	119	39.67
(4,7)	236	78.67
(5,6)	149	49.67
(5,8)	344	90.53
(6,9)	328	86.31
(6,10)	247	82.33
(6,11)	207	69.00
(9,12)	102	34.00
(10,11)	172	57.33
(0,13)	254	84.67
(11,12)	163	54.33
(11,14)	246	82.00
(13,14)	274	91.33
(7,8)	331	87.11
(8,10)	384	96.00

下载: 导出CSV

表 5 改进前后模型的车流总走行公里

Table 5. Cargo flow kilometers before and after improving model

模型	算法	车流总走行数/ （车 • km）
模型 P	GWO	无法在限定范围内找到可行解
模型 P	IGWO	无法在限定范围内找到可行解
模型 Q	GWO	1132405
模型 Q	IGWO	1073973

下载: 导出CSV

表 6 两种算法的质量指标

Table 6. Quality metrics for two algorithms

算法	平均绕行率	选择最短路径的 OD 数/个	车流总走行数/ （车 • km）
GWO	1.55	3	1132405
IGWO	1.51	6	1073973

下载: 导出CSV

参考文献(19)

[1]	纪丽君,林柏梁,乔国会,等. 基于多商品流模型的铁路网车流分配和径路优化模型[J]. 中国铁道科学,2011,32(3): 107-110. JI Lijun, LIN Boliang, QIAO Guohui, et al. Car flow assignment and routing optimization model of railway network based on multi-commodity flow model[J]. China Railway Science, 2011, 32(3): 107-110.
[2]	温旭红,林柏梁,王龙,等. 基于多商品网络流理论的铁路车流分配及径路优化模型[J]. 北京交通大学学报,2013,37(3): 117-121. doi: 10.3969/j.issn.1673-0291.2013.03.022 WEN Xuhong, LIN Boliang, WANG Long, et al. Optimization model for railway car flow assignment and routing plan based on multi-commodity network flow theory[J]. Journal of Beijing Jiaotong University, 2013, 37(3): 117-121. doi: 10.3969/j.issn.1673-0291.2013.03.022
[3]	温旭红,林柏梁,陈雷. 基于树形结构的铁路车流径路优化模型[J]. 铁道学报,2016,38(4): 1-6. doi: 10.3969/j.issn.1001-8360.2016.04.001 WEN Xuhong, LIN Boliang, CHEN Lei. Optimization model of railway vehicle flow routing based on tree form[J]. Journal of the China Railway Society, 2016, 38(4): 1-6. doi: 10.3969/j.issn.1001-8360.2016.04.001
[4]	严余松,户佐安,李宵寅. 基于车流量波动的列车编组计划与车流径路综合优化[J]. 交通运输系统工程与信息,2017,17(4): 124-131. doi: 10.16097/j.cnki.1009-6744.2017.04.019 YAN Yusong, HU Zuoan, LI Xiaoyin. Comprehensive optimization of train formation plan and wagon-flow path based on fluctuating wagon-flow[J]. Journal of Transportation Systems Engineering and Information Technology, 2017, 17(4): 124-131. doi: 10.16097/j.cnki.1009-6744.2017.04.019
[5]	王文宪,柏伟,邓鹏. 考虑换重条件的重载直达车流组织研究[J]. 交通运输工程与信息学报,2013,11(1): 68-73. doi: 10.3969/j.issn.1672-4747.2013.01.013 WANG Wenxian, BAI Wei, DENG Peng. Study on optimized organization scheme for through heavy haul trains based on changing-for-weight[J]. Journal of Transportation Engineering and Information, 2013, 11(1): 68-73. doi: 10.3969/j.issn.1672-4747.2013.01.013
[6]	UPADHYAY A, BOLIA N. Combined empty and loaded train scheduling for dedicated freight railway corridors[J]. Computers & Industrial Engineering, 2014, 76: 23-31.
[7]	BORNDÖRFER R, KLUG T, SCHLECHTE T, et al. The freight train routing problem for congested railway networks with mixed traffic[J]. Transportation Science, 2016, 50(2): 408-423. doi: 10.1287/trsc.2015.0656
[8]	YAGHINI M, MOMENI M, SARMADI M. An improved local branching approach for train formation planning[J]. Applied Mathematical Modelling, 2013, 37(4): 2300-2307. doi: 10.1016/j.apm.2012.05.016
[9]	KHALED A A, JIN M Z, CLARKE D B, et al. Train design and routing optimization for evaluating criticality of freight railroad infrastructures[J]. Transportation Research Part B:Methodological, 2015, 71: 71-84. doi: 10.1016/j.trb.2014.10.002
[10]	温旭红. 铁路车流分配优化模型与拉格朗日松弛算法求解研究[D]. 北京: 北京交通大学, 2016.
[11]	MIRJALILI S, MIRJALILI S M, LEWIS A. Grey wolf optimizer[J]. Advances in Engineering Software, 2014, 69: 46-61. doi: 10.1016/j.advengsoft.2013.12.007
[12]	FARIS H, ALJARAH I, AL-BETAR M A, et al. Grey wolf optimizer:a review of recent variants and applications[J]. Neural Computing and Applications, 2018, 30(2): 413-435. doi: 10.1007/s00521-017-3272-5
[13]	ZHU E D, CRAINIC T G, GENDREAU M. Scheduled service network design for freight rail transportation[J]. Operations Research, 2014, 62(2): 383-400. doi: 10.1287/opre.2013.1254
[14]	黄戈文,蔡延光,戚远航,等. 自适应遗传灰狼优化算法求解带容量约束的车辆路径问题[J]. 电子学报,2019,47(12): 2602-2610. HUANG Gewen, CAI Yanguang, QI Yuanhang, et al. Adaptive genetic grey wolf optimizer algorithm for capacitated vehicle routing problem[J]. Acta Electronica Sinica, 2019, 47(12): 2602-2610.
[15]	WANG C Y, MA C, ZHOU J C. A new class of exact penalty functions and penalty algorithms[J]. Journal of Global Optimization, 2014, 58(1): 51-73. doi: 10.1007/s10898-013-0111-9
[16]	甘敏,彭辉. 一种新的自适应惩罚函数算法求解约束优化问题[J]. 信息与控制,2009,38(1): 24-28. doi: 10.3969/j.issn.1002-0411.2009.01.004 GAN Min, PENG Hui. A new adaptive penalty function based algorithm for solving constrained optimization problems[J]. Information and Control, 2009, 38(1): 24-28. doi: 10.3969/j.issn.1002-0411.2009.01.004
[17]	吴亮红,王耀南,周少武,等. 采用非固定多段映射罚函数的非线性约束优化差分进化算法[J]. 系统工程理论与实践,2007,27(3): 128-133,160. doi: 10.3321/j.issn:1000-6788.2007.03.019 WU Lianghong, WANG Yaonan, ZHOU Shaowu, et al. Differential evolution for nonlinear constrained optimization using non-stationary multi-stage assignment penalty function[J]. Systems Engineering—Theory & Practice, 2007, 27(3): 128-133,160. doi: 10.3321/j.issn:1000-6788.2007.03.019
[18]	肖赤心,蔡自兴,王勇,等. 一种基于佳点集原理的约束优化进化算法[J]. 控制与决策,2009,24(2): 249-253,258. doi: 10.3321/j.issn:1001-0920.2009.02.018 XIAO Chixin, CAI Zixing, WANG Yong, et al. Constrained optimization evolutionary algorithm based on good lattice points principle[J]. Control and Decision, 2009, 24(2): 249-253,258. doi: 10.3321/j.issn:1001-0920.2009.02.018
[19]	张文胜,郝孜奇,朱冀军,等. 基于改进灰狼算法优化BP神经网络的短时交通流预测模型[J]. 交通运输系统工程与信息,2020,20(2): 196-203. doi: 10.16097/j.cnki.1009-6744.2020.02.029 ZHANG Wensheng, HAO Ziqi, ZHU Jijun, et al. BP neural network model for short-time traffic flow forecasting based on transformed grey wolf optimizer algorithm[J]. Journal of Transportation Systems Engineering and Information Technology, 2020, 20(2): 196-203. doi: 10.16097/j.cnki.1009-6744.2020.02.029