Fault Diagnosis Method Based on Deep Active Learning For MVB Network
-
摘要:
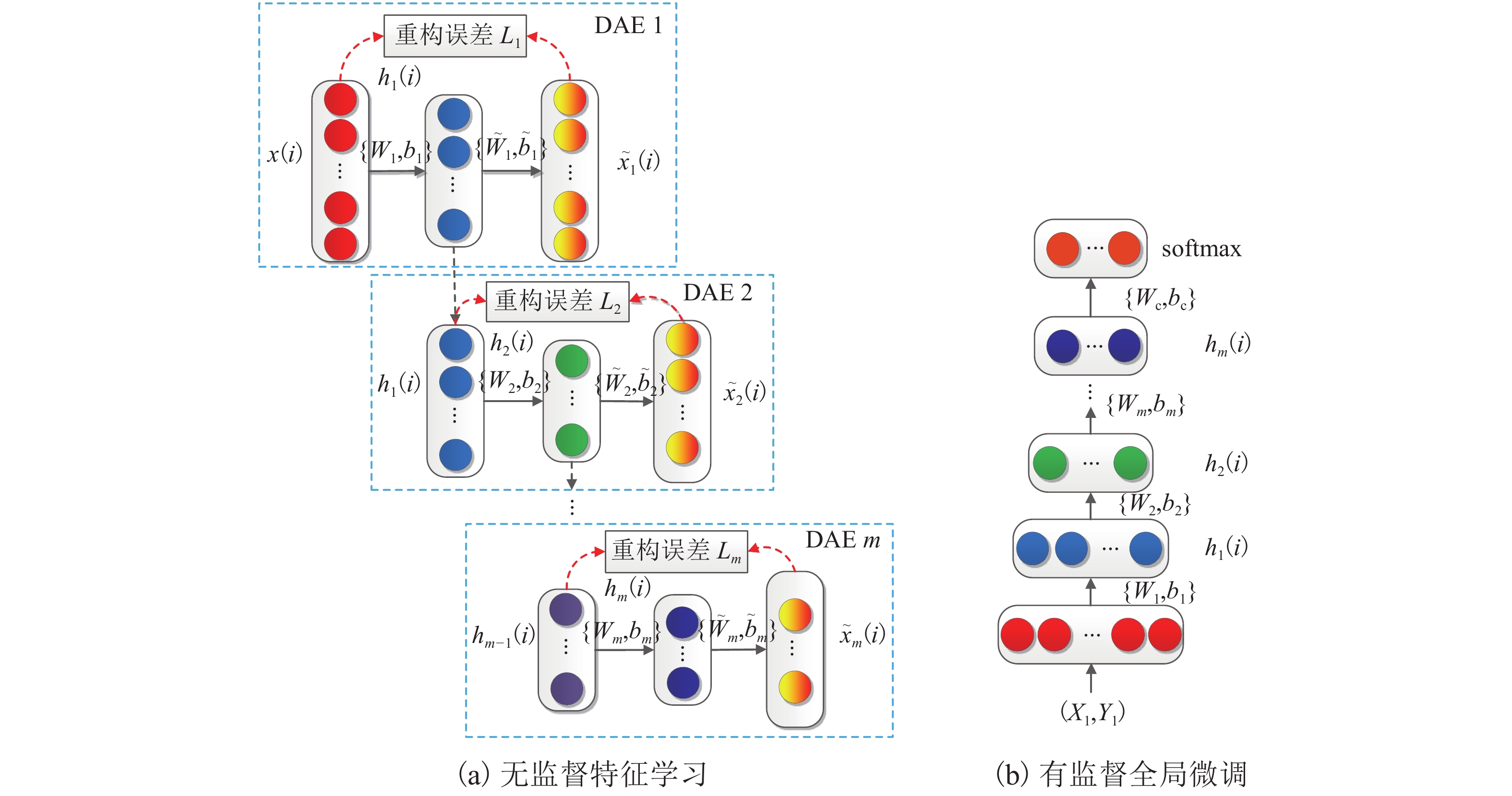
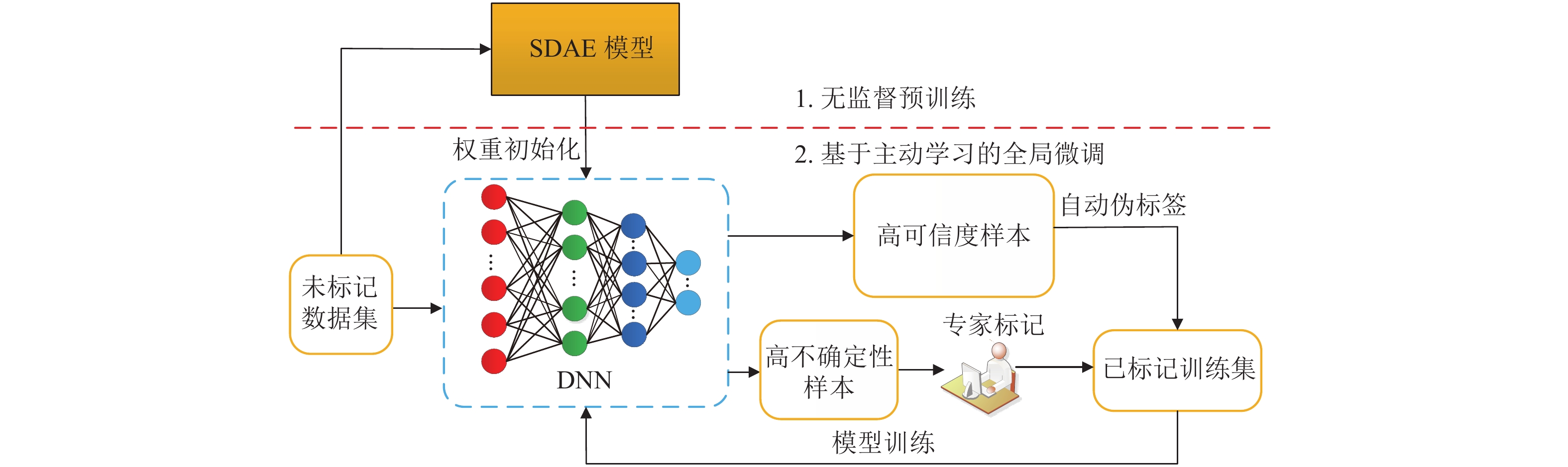
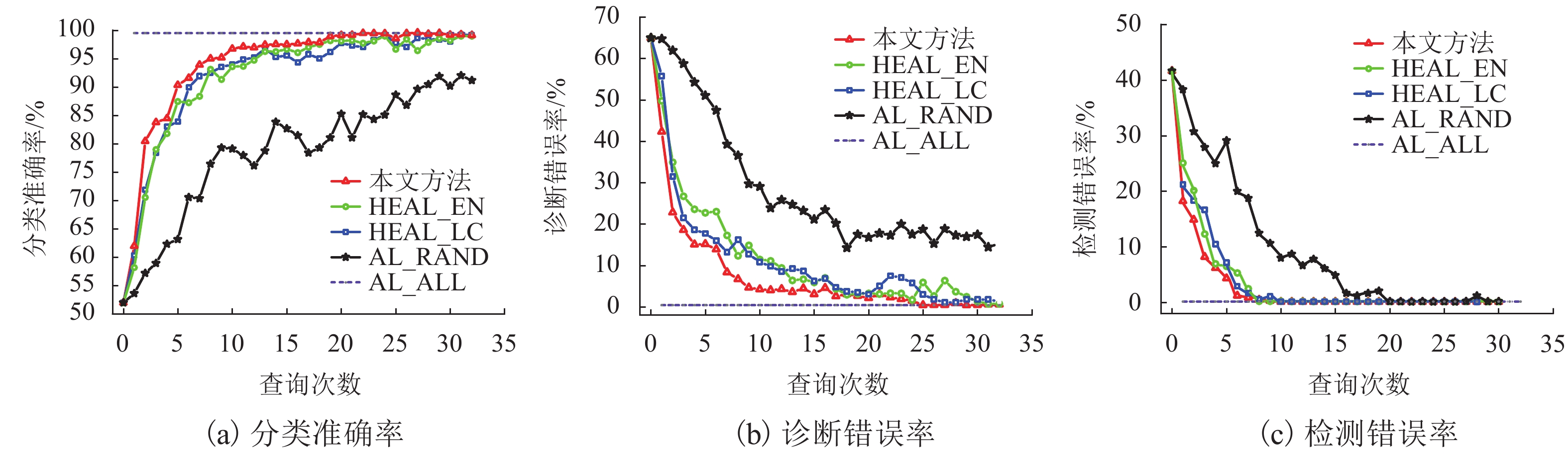
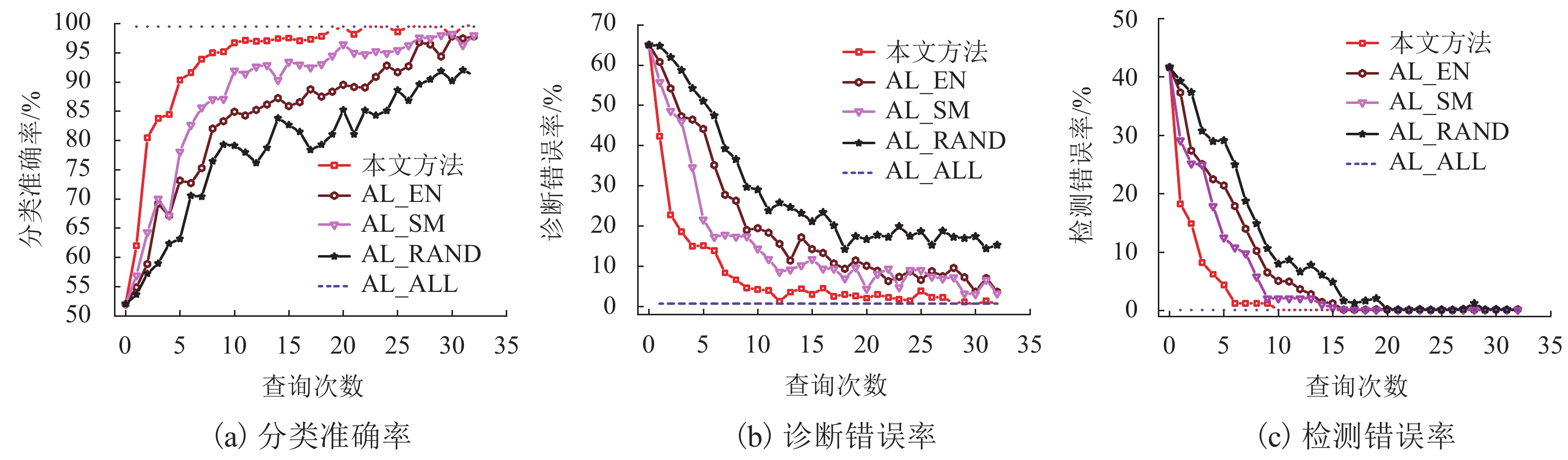
多功能车辆总线MVB （multiple vehicle bus）用于传输重要的列车运行控制指令和监视信息，准确地诊断MVB网络故障是列车智能运维的基础，为此，提出一种将主动学习和深度神经网络相结合的MVB网络故障诊断方法. 该方法采用堆叠去噪自编码器自动提取MVB信号物理波形特征，并将该特征用于训练深度神经网络来实现MVB网络故障模式分类；基于不确定性和可信度的高效主动学习方法，可解决实际应用中标记样本不足和人工标记成本高昂的问题，使用少量标记训练样本就能得到高性能的深度神经网络模型. 实验结果表明：为达到90%以上分类准确率，所提方法只需要600个标记训练样本，小于随机采样方法所需标记训练样本数的2 800个；在相同标记训练样本数下，所提方法在3种性能指标下均优于传统方法.
Abstract:Multiple vehicle bus (MVB) is employed to transmit important train operation control instructions and monitoring information, and accurate diagnosis of the fault types of MVB network is the basis of the intelligent operation and maintenance system. To this end, a fault diagnosis method for MVB network is proposed, which combines the active learning and deep neural networks. It adopts the stacked denoising autoencoder to automatically extract physical features from the electrical MVB signals; then the features are used to train a deep neural network classifier for identifying MVB fault classes. An efficient active learning method based on uncertainty and credibility can solve the problems of insufficient labeled samples and high costs of manual labeling in practical application. It can build a competitive classifier with a small number of labeled training samples. Experiment results demonstrate that to achieve a high accuracy above 90%, the proposed method requires 600 labeled training samples, which is less than 2800 labeled training samples required by random sampling method. With the same number of labeled samples, the proposed method can achieve the better performance as to three different metrics than traditional methods.
-
图 5 不确定性和可信度相结合的主动学习方法的对比实验结果
Figure 5. Comparison results of active learning methods based on uncertainty and credibility
图 6 与基于不确定性的主动学习方法的对比实验结果
Figure 6. Comparison results with different active learning methods based on uncertainty estimation
图 7 查询过程中带标签训练样本的类别分布
Figure 7. Class distributions of labeled training samples in query process
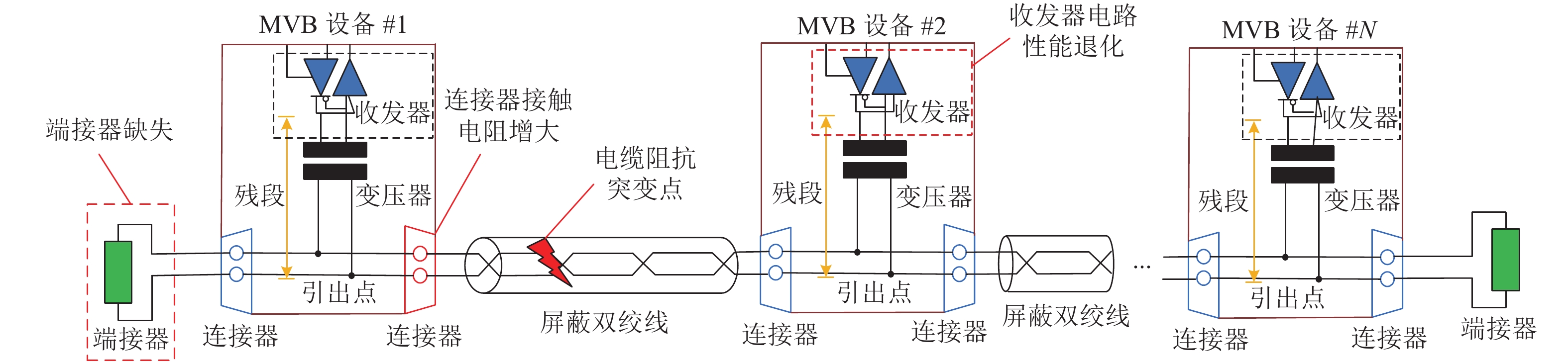
表 1 MVB网络常见故障
Table 1. Typical faults of MVB network
故障名称 故障描述 断路故障 MVB电缆或连接器断开，部分设备离线 短路故障 MVB两根电缆或连接器针脚之间短接，导致MVB网络通信中断 终端电阻缺失 因人为或外力因素造成终端电阻缺失，出现严重的阻抗不匹配，造成信号严重畸变 收发器电路故障 因元器件老化等原因造成在此设备处阻抗突变，从而造成信号畸变 连接器
老化连接器老化导致接触电阻增大，造成传输阻抗不匹配，信号物理波形质量下降 电缆性能退化 因安装不当、老化等原因，造成电缆传输特性阻抗发生变化，造成信号物理波形质量下降，导致MVB网络通信性能退化 
下载: 导出CSV
表 2 不同已标记训练样本数下的分类准确率
Table 2. Classification accuracy under different numbers of labeled samples
%
下载: 导出CSV
-
[1] LUEDICKE D, LEHNER A. Train communication networks and prospects[J]. IEEE Communications Magazine, 2019, 57(9): 39-43. doi: 10.1109/MCOM.001.1800957 [2] 李召召,王立德,岳川,等. 基于MKLSVM的MVB端接故障诊断[J]. 北京交通大学学报,2019,43(2): 100-106. doi: 10.11860/j.issn.1673-0291.20180128LI Zhaozhao, WANG Lide, YUE Chuan, et al. Terminating fault diagnosis of MVB based on MKLSVM[J]. Journal of Beijing Jiaotong University, 2019, 43(2): 100-106. doi: 10.11860/j.issn.1673-0291.20180128 [3] LI Z Z, WANG L D, YANG Y Y. Fault diagnosis of the train communication network based on weighted support vector machine[J]. IEEJ Transactions on Electrical and Electronic Engineering, 2020, 15(7): 1077-1088. doi: 10.1002/tee.23153 [4] KIRANYAZ S, INCE T, ABDELJABER O, et al. 1-D convolutional neural networks for signal processing applications[C]//IEEE International Conference on Acoustics, Speech and Signal Processing. New York: IEEE, 2019: 8360-8364. [5] WANG Y L, PAN Z F, YUAN X F, et al. A novel deep learning based fault diagnosis approach for chemical process with extended deep belief network[J]. ISA Transactions, 2020, 96: 457-467. doi: 10.1016/j.isatra.2019.07.001 [6] LU C, WANG Z Y, QIN W L, et al. Fault diagnosis of rotary machinery components using a stacked denoising autoencoder-based health state identification[J]. Signal Process, 2017, 130: 377-388. doi: 10.1016/j.sigpro.2016.07.028 [7] DE BRUIN T, VERBERT K, BABUSKA R. Railway track circuit fault diagnosis using recurrent neural networks[J]. IEEE Transactions on Neural Networks and Learning Systems, 2017, 28(3): 523-533. doi: 10.1109/TNNLS.2016.2551940 [8] CAO X Y, YAO J, XU Z B, et al. Hyperspectral image classification with convolutional neural network and active learning[J]. IEEE Transactions on Geoscience and Remote Sensing, 2020, 58(7): 4604-4616. doi: 10.1109/TGRS.2020.2964627 [9] BI H X, XU F, WEI Z Q, et al. An active deep learning approach for minimally supervised PolSAR image classification[J]. IEEE Transactions on Geoscience and Remote Sensing, 2019, 57(11): 9378-9395. doi: 10.1109/TGRS.2019.2926434 [10] ZHANG A M, LI B H, WANG W H, et al. MII:a novel text classification model combining deep active learning with BERT[J]. CMC-Comput. Mat. Contin, 2020, 63(3): 1499-1514. [11] ZHAO Xiukuan, LI Min, XU Jinwu, et al. An effective procedure exploiting unlabeled data to build monitoring system[J]. Expert Systems with Applications, 2011, 38(8): 10199-10204. doi: 10.1016/j.eswa.2011.02.078 [12] PENG Peng, ZHANG Wenjia, ZHANG Yi, et al. Cost sensitive active learning using bidirectional gated recurrent neural networks for imbalanced fault diagnosis[J]. Neurocomputing, 2020, 407: 232-245. doi: 10.1016/j.neucom.2020.04.075 [13] KUMAR P, GUPTA A. Active learning query strategies for classification, regression, and clustering: a survey[J]. Journal of Computer Science and Technology, 2020, 35(4): 913-945. doi: 10.1007/s11390-020-9487-4 [14] RAHHAL M M Al, BAZI Y, ALHICHRI H, et al. Deep learning approach for active classification of electrocardiogram signals[J]. Information Science, 2016, 345: 340-354. doi: 10.1016/j.ins.2016.01.082 [15] JIANG P, HU Z X, LIU J, et al. Fault diagnosis based on chemical sensor data with an active deep neural network[J]. Sensors, 2016, 16(10): 1695 [16] SHIM J, KANG S, CHO S. Active learning of convolutional neural network for cost-effective wafer map pattern classification[J]. IEEE Transactions on Semiconductor Manufacturing, 2020, 33(2): 258-266. doi: 10.1109/TSM.2020.2974867 [17] 朱琴跃,谢维达,谭喜堂. MVB协议一致性测试研究与实现[J]. 铁道学报,2007,29(4): 115-120. doi: 10.3321/j.issn:1001-8360.2007.04.024ZHU Qinyue, XIE Weida, TAN Xitang. Research on MVB protocol conformance testing[J]. Journal of the China Railway Society, 2007, 29(4): 115-120. doi: 10.3321/j.issn:1001-8360.2007.04.024 [18] CHEN M, ZHU K, WANG R, et al Dusit. active learning-based fault diagnosis in self-organizing cellular networks[J]. IEEE Communications Letters, 2020, 24(8): 1734-1737. doi: 10.1109/LCOMM.2020.2991449 -
下载:
点击查看大图
计量
- 文章访问数: 292
- HTML全文浏览量: 230
- PDF下载量: 49
- 被引次数: 0