Directed Graph Based Risk Analysis of Fire Spread in Buildings in Chinese Traditional Villages
-
摘要:
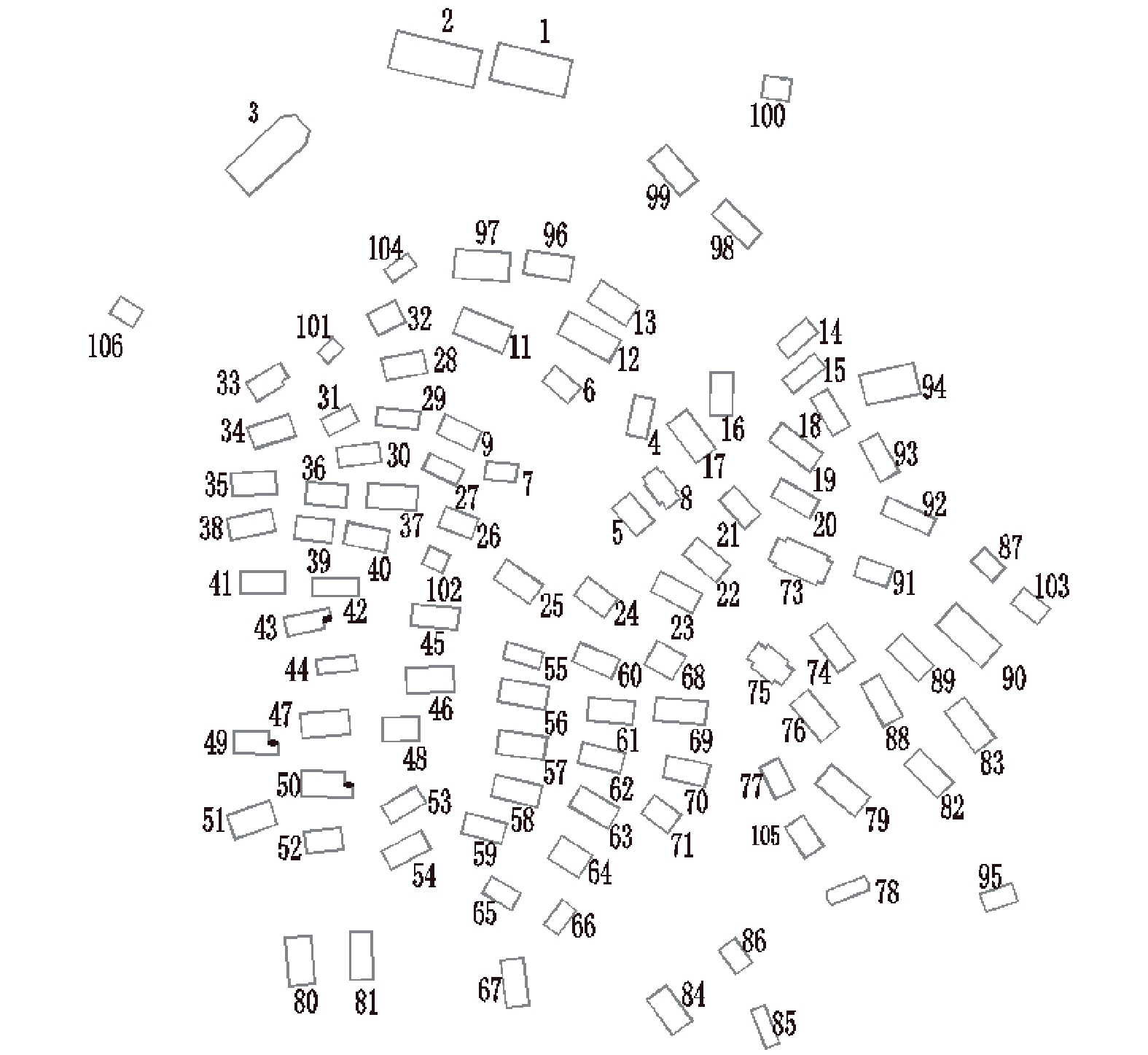
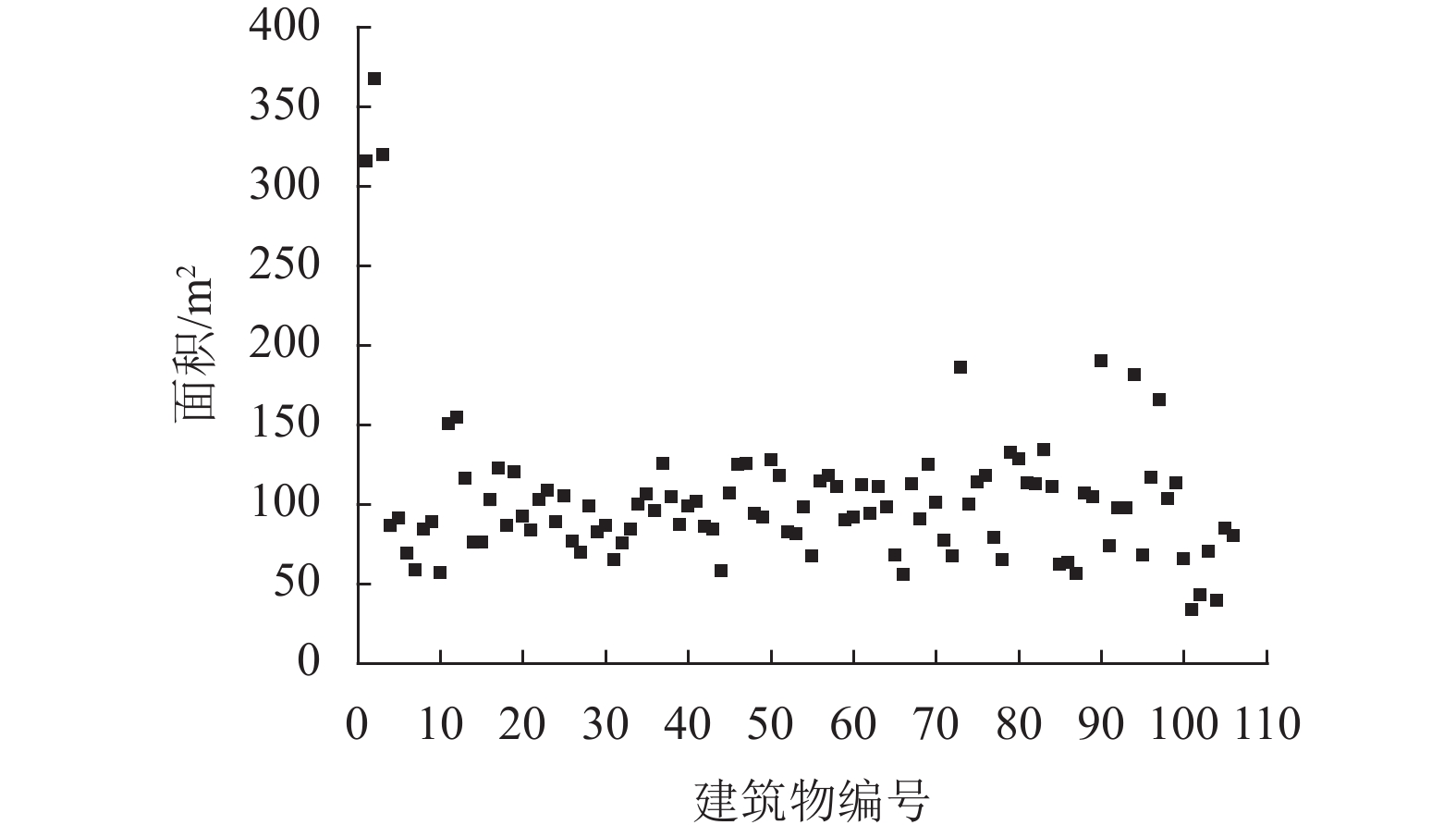
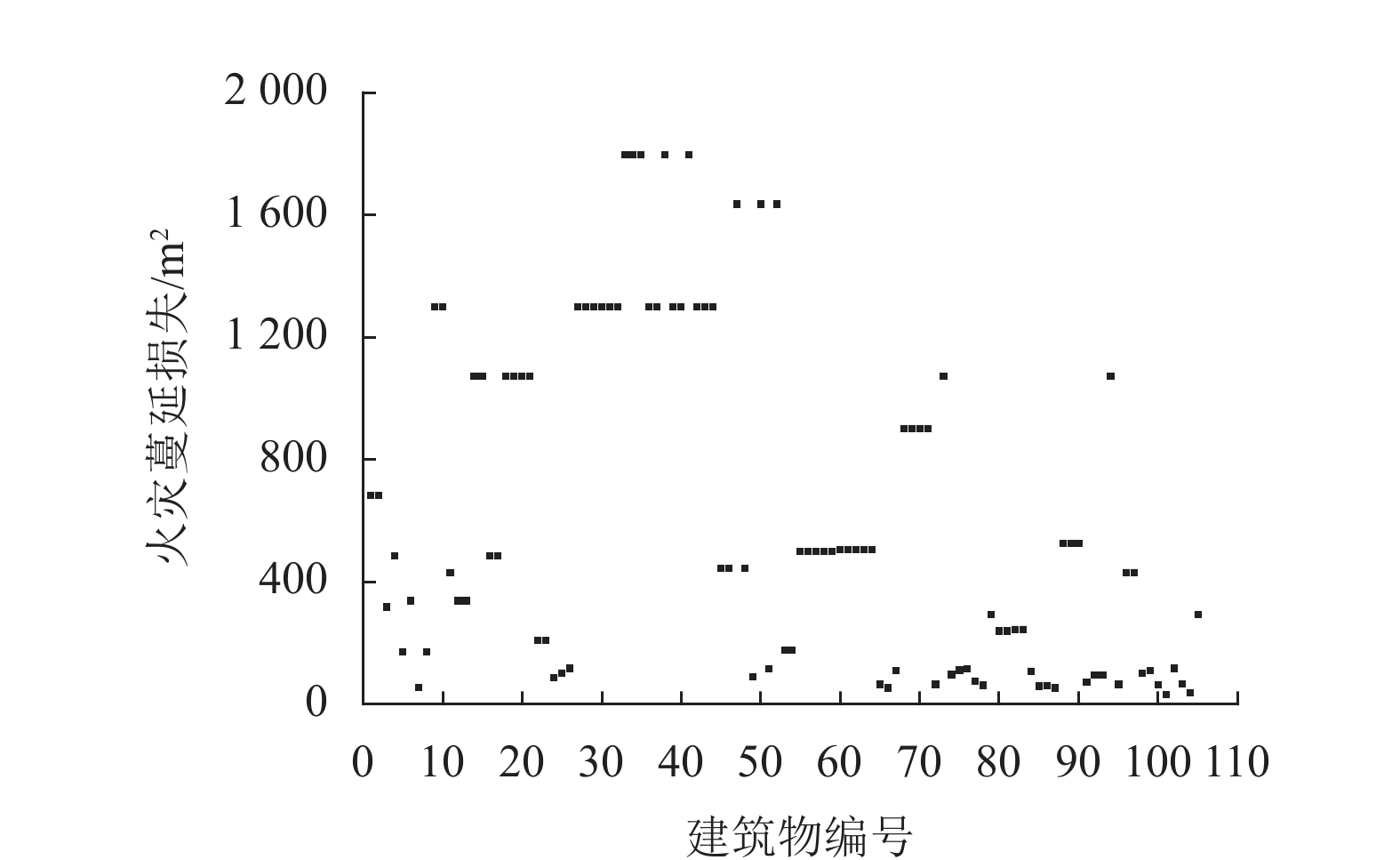
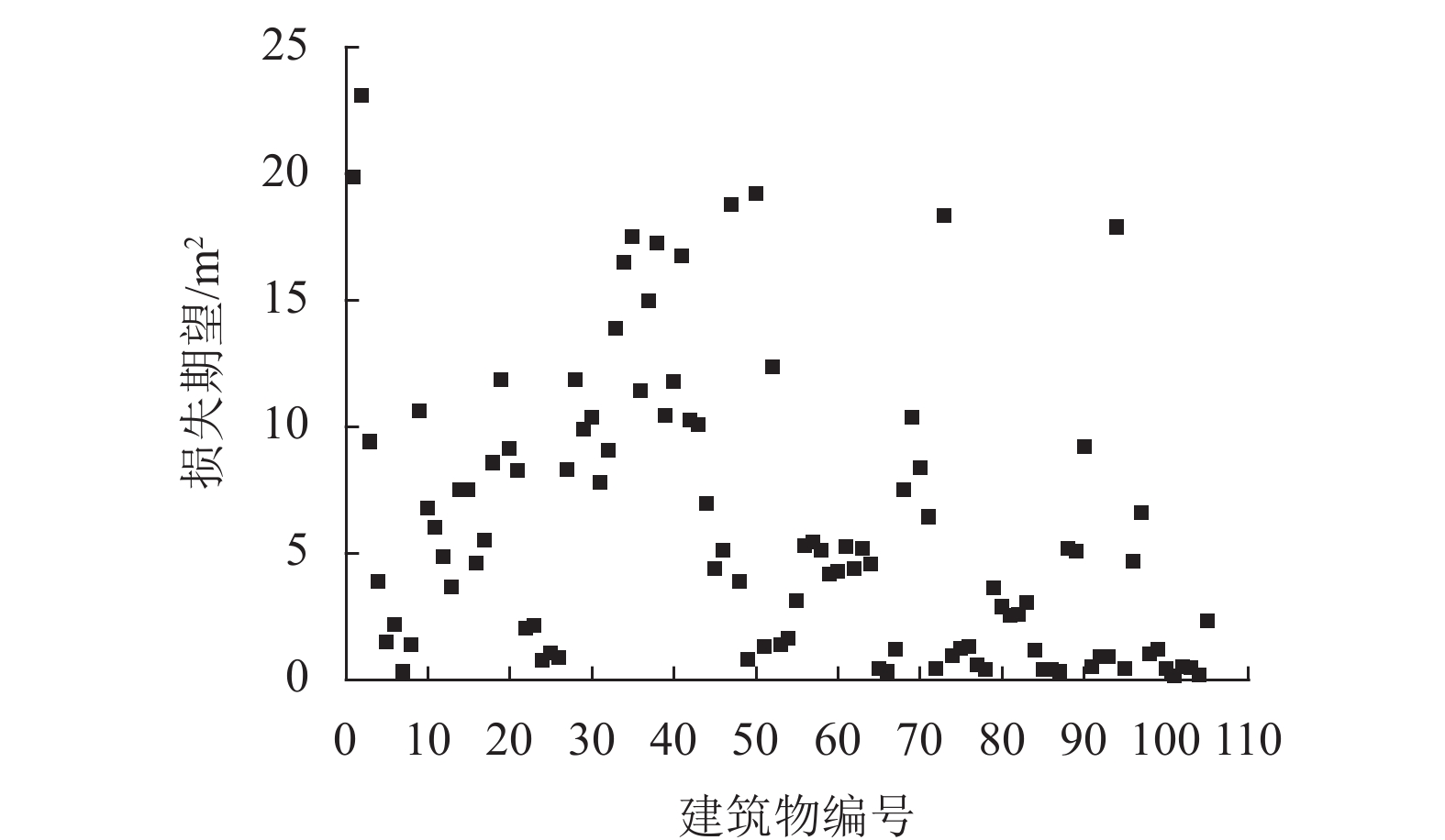
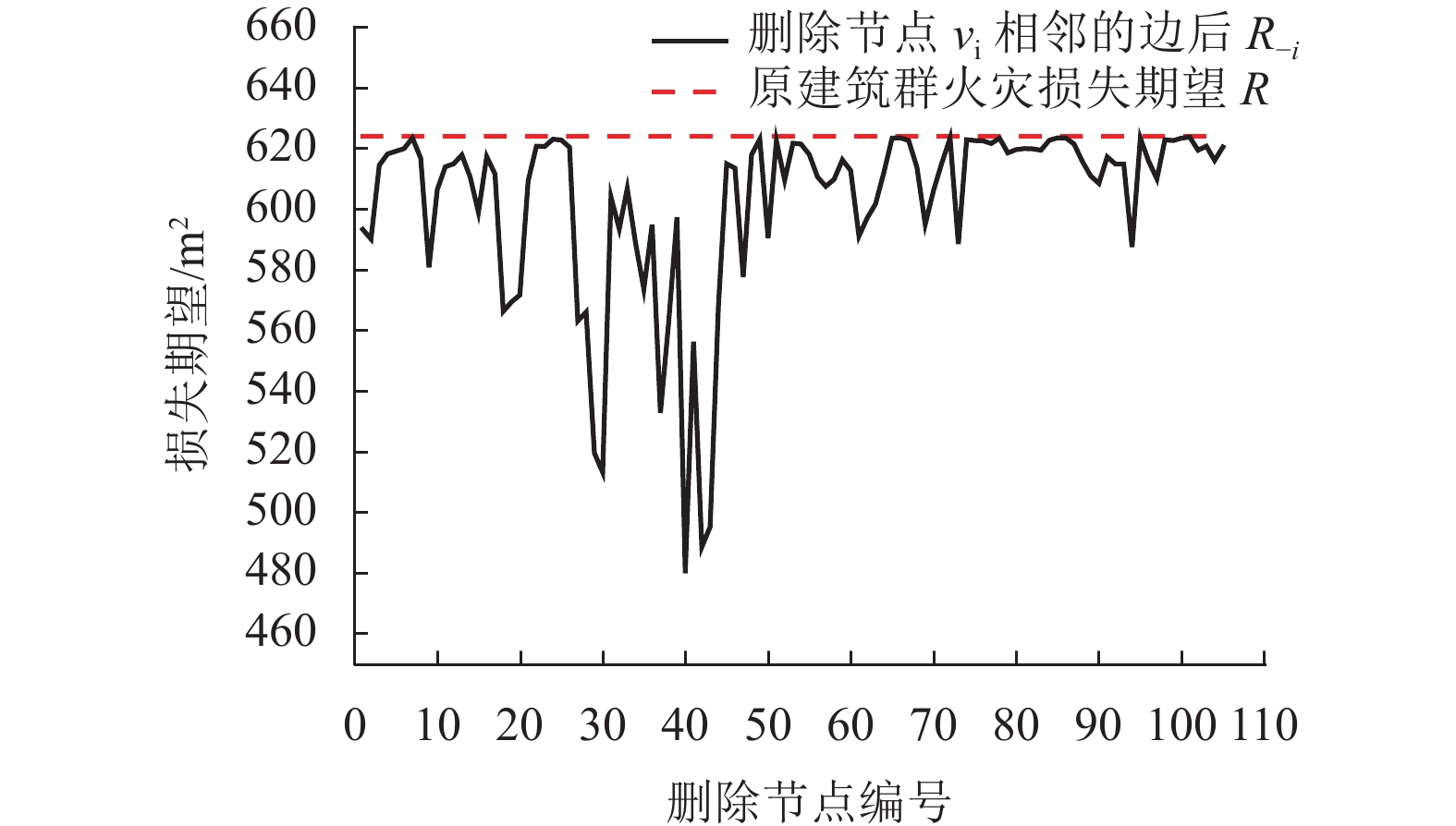
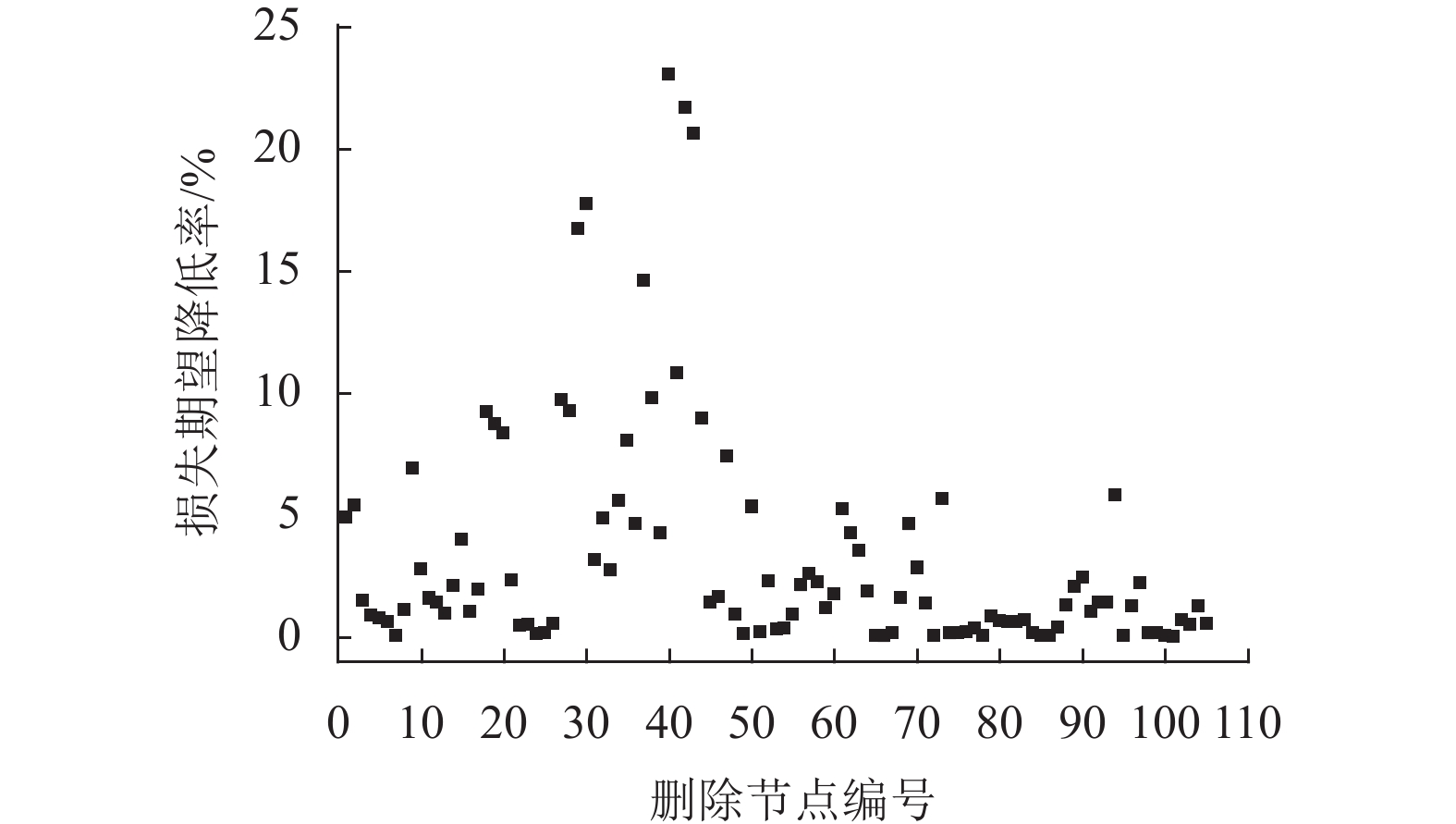
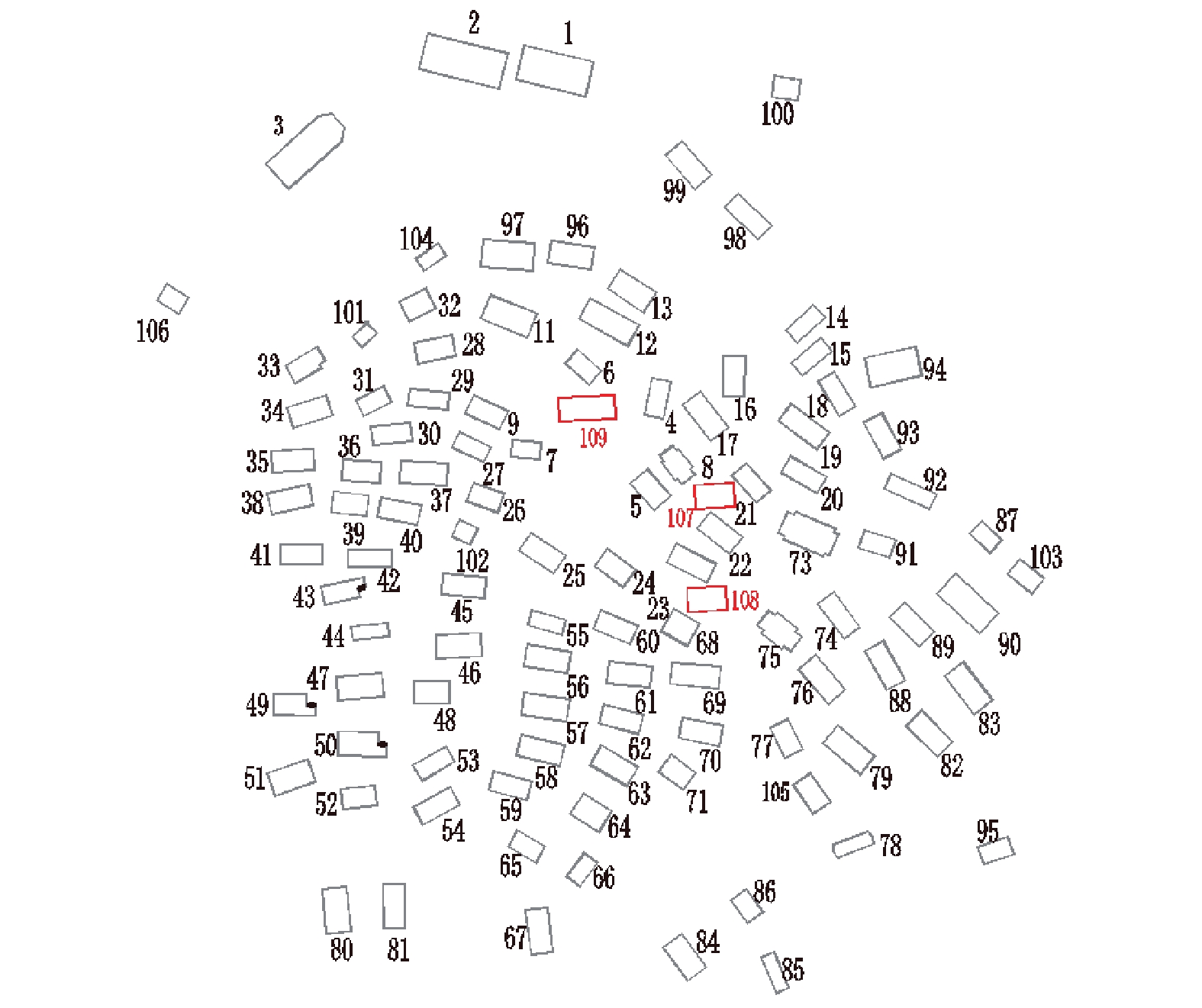
在传统村落开发保护过程中，建筑消防改造及建筑布局改变等会导致火灾风险发生变化. 火灾蔓延模拟工作量大、成本高及基础资料获取困难. 为克服这些难点，首先，将单体建筑视为有向图的节点、建筑间的火灾蔓延关系视为节点间的边，通过火灾蔓延模拟判断节点周边局部蔓延路径，并建立有向图的邻接矩阵，利用有向图遍历算法确定特定火灾场景下的蔓延范围，给出考虑多场景建筑群火灾蔓延的损失期望；然后，通过增删节点或边修正有向图邻接矩阵，反映建筑改造、增建或树木对建筑群火灾蔓延关系的变化，重新应用节点遍历算法确定变化后的建筑群火灾蔓延风险；最后，以某一传统村落为例验证方法的有效性. 研究结果表明：本文方法可快速计算动态变化的建筑群火灾蔓延风险，减少火灾蔓延再模拟的工作量；在火灾蔓延防控上，对危险性较高的6个节点进行消防加强改造，可使建筑群火灾蔓延的最大损失及损失期望分别降低61.9%、52.1%；在建筑规划或管理上，应避免新增建筑、树木等可燃物位于建筑密集区域或连通多个建筑密集区域的“桥节点”处.
Abstract:In the development and protection of traditional villages, building renovation and layout change for fire prevention may cause the changes in fire risk. Fire spread simulation is marked by large workloads, high costs and difficulty in acquiring basic data. To cope with these, first, the single building is regarded as the node of the directed graph, and the fire spread relationship between buildings as the edge between nodes. The local spread path around the node is judged through the fire spread simulation, the adjacency matrix of the directed graph is established, the spread range under a specific fire scene is determined by the traversing directed graph algorithm, and the loss expectation for the multiple fire spread scenarios is presented. The adjacency matrix of the directed graph is modified by adding and deleting nodes or edges to reflect the changes of building renovation and addition and trees on the fire spread relationships, and the traversing algorithm of nodes is reused to determine the fire spread risk of the buildings. Finally, a traditional village is used as an example to verify the proposed method. The results show that the proposed method can quickly calculate the fire spread risk of the dynamically changing village buildings and reduces the workload of fire spread re-simulation. In terms of fire spread prevention and control, the maximum loss and loss expectation of fire spread between buildings can be respectively reduced by 61.9% and 52.1% through improving fire preventions of 6 highly-risky nodes. For building planning or management, it is necessary to avoid the case of new buildings, trees and other combustible materials locating in densely built areas or link-nodes connecting multiple densely built areas.
-
行驶舒适性与路面的平整程度、车辆状态、运行速度等方面密切相关，被广泛认为是路面服务性能评价的重要参考指标. 路面的不平整激励是引起汽车振动并导致舒适性下降的核心因素，道路表面横向、 纵向、水平向的各种波长及幅值的复杂变形组合构成了路面的不平度[1]. 作为激励源，不平度的连续变化会引起车辆的随机振动，局部突变则会引起车辆的瞬态振动，二者共同作用，通过车身悬架系统传递至人体，最终引起其心理和生理上的舒适性感受变化.
国际上用于评估行驶舒适性的指标众多，例如舒适度指数（ride number，RN）、国际平整度指数（international roughness index，IRI）、行驶质量指数（riding quality index，RQI）以及加权加速度均方根（weighed root-mean-square acceleration，WRMSA）等. 利用这些评价指标，现有文献研究集中在宏观层面的路段行驶质量和人车振动特性进行分析[2-4]，但对于路面局部变形（如桥头差异沉降、坑槽、窨井沉陷）导致的冲击振动问题却鲜有涉及.
已有研究表明路面局部变形引起的冲击振动对行驶舒适性具有显著影响[5-6]，但尚未明确其中的定量关系，部分文献也提出过路面中桥头差异沉降及窨井沉陷等局部变形的控制阈值[7-9]，但是缺乏有效的理论支撑. 另有文献提出以较短长度作为行驶质量评价单元能够更加准确地描述路面的服务性能[10]，但是较短的单元长度可能会造成路面波长截断现象[2]，导致评价结果失真. 由于路面局部变形随机存在于路面中，且其导致的振动具有瞬时性特点，因此，难以通过现场试验获取变形激励与振动感受之间的定量关系.
鉴于此，本文从理论上研究局部变形对舒适性的影响. 首先，建立典型路面局部变形简化模型作为振动激励源，基于两自由度车辆强迫振动模型，从理论上推导出振动模型中簧上质量位移和加速度时间历程函数，再根据ISO 2631-1[11]中的频率加权系数分布特点设计频率加权滤波器对竖向加速度进行滤波，求解不同工况下的均方根加速度，评估人体的振动感受，最后提出不同类型局部变形的评价标准，以期为路面精细化养护管理提供依据.
1. 路面局部变形纵断面形式假定
文献[2, 12]对上海城市道路进行详细调研发现，引起道路纵断面高程局部异常波动的不平整因素主要是窨井变形、桥头差异沉降、路面修补等，各类因素的统计结果如图1所示.
由图1可知，窨井损坏和修补（包括路面开挖回填）是最主要的变形形式，其次是桥头差异沉降. 但是，实际路面中路面修补一般面积较大，且对行车影响十分有限；路面开挖则一般为临时性养护管理；另外，由于轮胎存在包络特性，伸缩缝问题也不具显著影响. 为进一步研究变形的影响，本文根据其余常见局部变形的形态特征，将其分为3类：
1） 错台型，描述同一断面的高程突变，如桥头差异沉降；
2） 双断面型，描述路面规则的凹凸变形，行进中的轮胎会在极短时间内经过变形区域的两端，如窨井沉陷或拱起；
3） 曲面型，描述路面较均匀的凸起，如路面拥包等.
建立激励模型需首先假定各类局部变形的函数形式，由于路面局部变形处纵断面高程一般具有突变特性，传统简谐函数难以描述其断面特点，因此对3类变形进行简化（如图2所示），以高差
$ \Delta g $ 作为变形衡量指标，纵断面高程y(t)如式（1）～（3）所示.1） 错台型
y(t)={0,t=0,Δg,0<t⩽l/v, (1) 式中：l 为变形部分长度； t 为时间； v 为车速.
2） 双断面型
y(t)={0,t=0,Δg,0<t⩽d/v,0,t>d/v, (2) 式中：
$ d $ 为凹凸部分直径或长度.3） 曲面型
y(t)={0,t=0,−4Δgvl2(vt2−lt),0<t⩽l/v,0,t>l/v. (3) 2. 人体竖向位移及竖向加速度推导
振动舒适性评价一般以加速度为基础指标，已有研究中加速度多为现场实测值，不同车辆之间难以对比. 本文通过两自由度车辆强迫振动模型的求解，从理论上推导人体的竖向位移和加速度响应.
2.1 两自由度车辆强迫振动模型
为统一各国的平整度度量标准，世界银行曾在巴西进行了大量平整度试验（international road roughness experiment），试验中首次构想出两自由度1/4理想车模型[13]，由于理想车的运动方程恒定，固定车辆参数后，相当于利用同一辆车在任意地方行驶，因此，其测试方法具有很好的移植性. 1/4车模型如图3所示，图中：
$ {m_{\text{s}}} $ 为簧上质量，$ {m_{\text{t}}} $ 为簧下质量，$ {K_{\text{s}}} $ 为悬架刚度系数，$ {K_{\text{t}}} $ 为轮胎刚度系数，$ {C_{\text{s}}} $ 为悬架阻尼系数，$ {Z_{\text{s}}} $ 和$ {Z_{\text{t}}} $ 分别为簧上质量和簧下质量的绝对位移.运动方程为
ms∙∙Zs+Cs(∙Zs−∙Zt)+Ks(Zs−Zt)=0， (4) mt∙∙Zt+Cs(∙Zt−∙Zs)+Ks(Zt−Zs)+Kt(Zt−y)=0. (5) 将式（4）、（5）等式左右两侧同时除以ms，得
∙∙Zs+c(∙Zs−∙Zt)+k2(Zs−Zt)=0， (6) u∙∙Zt+c(∙Zt−∙Zs)+k2(Zt−Zs)+k1(Zt−y)=0， (7) 式中：系数
$c = {C_{\text{s}}}/{m_{\text{s}}} = 6.00\;{{\rm{s}}^{ - 1}}；$ 系数$u = {m_{\text{t}}}/{m_{\text{s}}} = 0.15$ ；系数$ {k_1} = {K_{\text{t}}}/{m_{\text{s}}} = 653\;{{\rm{s}}^{ - 2}}；$ 系数$ {k_2} = {K_{\text{s}}}/{m_{\text{s}}} = 63.3\;{{\rm{s}}^{ - 2}} $ .2.2 任意路面变形激励下人体竖向位移的时域函数
路面局部变形对两自由度车辆振动系统的激励不具有简谐特性和周期特性，在这种激振作用下，系统通常仅有瞬态振动，故为求得加速度的时域函数，可以采用卷积积分法[14]求解簧上质量的加速度响应，具体过程如下：
1） 求解1/4车振动系统对于单位脉冲激励
$ \delta \left( t \right) $ 的响应函数；2） 利用卷积积分法求解路面局部变形激励作用下的系统响应.
簧上质量的竖向位移可近似认为是人体的竖向位移. 由于运动方程存在耦合，故需要对方程进行解耦，运动方程如式（8）所示.
M∙∙Z+C∙Z+KZ=Y， (8) 式中：M、C、K、Z、Y分别为质量矩阵、阻尼矩阵、刚度矩阵、位移矩阵、输入矩阵，
M=[ms00mt],C=[Cs−Cs−CsCs],K=[Ks−Ks−KsKs+Kt],Z=[ZsZt]T,Y=[0Kty]T. 运动方程中阻尼矩阵无法通过实模态变换实现对角化，因此采用复模态变换求解[15]. 首先，令式（8）
$ {\boldsymbol{Y}} =\bf{ 0} $ 得到自由振动方程，设特解为$ {\boldsymbol{\mu }}{{\rm{e}}^{{\boldsymbol{\lambda }}t}} $ ，$ {\boldsymbol{\mu }} $ 、λ分别为特征向量和特征值，可求解振动系统的特征方程为|λ2M+λC+K|=0. (9) 二自由度系统存在4个特征值，且为2对共轭复数. 将1/4车模型参数代入特征方程可得4个特征值分别为
{λ1=−20.4+64.4i,λ2=−2.6+7.3i,λ3=−20.4−64.4i,λ4=−2.6−7.3i. (10) 代入自由振动方程，对应的特征向量构成复模态矩阵
${\boldsymbol{\mu }} = \left[ {μ1μ2μ3μ4} \right]$ ，其中：{μ1=[μ11μ12]T=[1−4.2+10.5i]T,μ2=[μ21μ22]T=[10.074+0.054i]T,μ3=[μ31μ32]T=[1−4.2−10.5i]T,μ4=[μ41μ42]T=[10.074−0.054i]T, (11) 由于上述复模态矩阵无法直接变换，因此这里引入状态变量
$ {\boldsymbol{x}} $ 对方程解耦[15]，补充恒等式${\boldsymbol{M}}\mathop {\boldsymbol{Z}}\limits^ \bullet - {\boldsymbol{M}}\mathop {\boldsymbol{Z}}\limits^ \bullet = {\bf{0}}$ ，将运动方程转换为状态方程：˜M∙x+˜Kx=˜Y， (12) 式中：
x=[∙ZZ]T;˜M=[0MMC]； ˜K=[−M00K];˜Y=[0Y]T. 特征向量构成复模态矩阵：
V=[λ1μ1μ1λ2μ2μ2λ3μ3μ3λ4μ4μ4]. (13) $ {\boldsymbol{V}} $ 具有关于${\boldsymbol{\widetilde{M}}}$ 和$\mathop {\boldsymbol{\widetilde{K}}}\limits$ 的加权正交性，满足λi˜MVi+˜KVi=0,i=1,2,3,4, (14) 式中：
$ {{\boldsymbol{V}}_i} $ 为矩阵V的第i个列向量.代入
$\mathop {\boldsymbol{\widetilde{M}}}\limits$ 、$\mathop {\boldsymbol{\widetilde{K}}}\limits$ ，并作复模态变换$ {\boldsymbol{x}} = {\boldsymbol{Vp}} $ ，其中p为模态变换响应列阵，代入式（12）可对振动方程解耦：diag(m1,m2,m3,m4)∙p+diag(−λ1m1,−λ2m2,−λ3m3,−λ4m4)p=VT˜Y， (15) 式中：
${m_i} = {{\boldsymbol{V}}_i}^{\rm{T}}\mathop {\boldsymbol{\widetilde{M}}}\limits {{\boldsymbol{V}}_i}$ 将式（10）、（11）代入式（15），求得
{m1=(1730−1774i)ms,m2=ms14i,m3=(1730+1774i)ms,m4=−ms14i. (16) 当初始输入为单位脉冲信号，式（15）化简为
∙pi−λipi=μi2miδ(t). (17) 式中：
$ {p_i} $ 为响应列阵中第i个值.式(17)等式两边取跨零积分，得
∫0+ε0−ε(∙pi−λipi)dt=μi2mi∫0+ε0−εδ(t)dt， (18) 式中：
$ \varepsilon $ 为极小量.得到系统的单位脉冲激励响应为
hi(t)=μi2mieλit. (19) 利用卷积积分方法，可求得在任意激励
${K_{\text{t}}}y(t)$ 下的响应为pi=∫t0h(t−τ)Kty(τ)dτ=Ktμi2mi∫t0eλi(t−τ)y(τ)dτ, (20) 代入
$ {\boldsymbol{x}} = {\boldsymbol{Vp}} $ 得到[∙ZZ]=[λ1μ1μ1λ2μ2μ2λ3μ3μ3λ4μ4μ4]×[p1p2p3p4]T. (21) 可得
Z=[4∑i=1μi1pi4∑i=1μi2pi]=[4∑i=1Ktμi1μi2mi∫t0eλi(t−τ)y(τ)dτ4∑i=1Ktμi22mi∫t0eλi(t−τ)y(τ)dτ]， (22) $ {Z_{\text{s}}} $ 即为$ y\left( t \right) $ 激励下的人体竖向位移.2.3 局部变形激励下的人体竖向加速度
由式（22）可知：人体竖向位移的变化振动与系统的参数及路面激励相关，1/4车模型参数固定后，位移则是路面激励的函数. 对位移求二阶导数可以得到加速度函数[16]，下面分别推导3类典型局部变形激励下的加速度响应.
2.3.1 错台型
车辆在经过错台型变形会经历两个阶段，以桥头跳车为例，第一阶段为驶上但是未离开桥面，第二阶段为驶离桥面. 车辆经过两处错台，引起两次跳车. 但是，实际桥梁具有一定长度，汽车经过第一处错台导致的加速度响应会在短时间内衰减为0，而此时车辆仍未驶下桥面，故每次错台视作为一处变形. 考虑驶上错台的加速度时间历程，即
$0 \leqslant t \leqslant l/ v$ ，联立式（1）、（22）求解得Zs={0,t=0,KtΔg4∑i=1μi2λimi(eλit−1),0<t⩽l/v, (23) 对其求二阶导数，得到竖向加速度为
as={0,t=0,KtΔg4∑i=1λiμi2mieλit,0<t⩽l/v. (24) 2.3.2 双断面型
双断面型变形的长度一般较小，例如窨井的直径一般仅为0.5 m左右，导致车辆驶过瞬间会连续经过变形两端，且间隔时间极短，两次振动响应会发生叠加，所以车轮驶上驶下变形的两次冲击都需要考虑在内，加速度响应为分段函数，联立式（2）、（22）求解，结果如式（25）所示.
{Z_{\text{s}}} = \left\{ {\begin{array}{*{20}{l}}
\begin{gathered}
0,\;\;\;t = 0, \hfill \\
{K_{\text{t}}}\Delta g \displaystyle \sum\limits_{i = 1}^4 {\dfrac{{{\mu _{i2}}}}{{{\lambda _i}{m_i}}}\left( {{{\rm{e}}^{{\lambda _i}t}} - 1} \right),\;\;\;0 \lt t \lt d/v,} \hfill \\
\end{gathered} \\
{{K_{\text{t}}}\Delta g \displaystyle \sum\limits_{i = 1}^4 {\dfrac{{{\mu _{i2}}}}{{{\lambda _i}{m_i}}}\left( {{{\rm{e}}^{{\lambda _i}t}} - {{\rm{e}}^{{\lambda _i}\left( {t - d/v} \right)}}} \right),\;\;\;t \geqslant d/v.} }
\end{array}} \right.(25) 对式（25）求二阶导，得到竖向加速度为
{a_{\text{s}}} = \left\{ {\begin{array}{*{20}{l}}
\begin{gathered}
\;0,\;\;\;t = 0, \hfill \\
{K_{\text{t}}}\Delta g \displaystyle \sum\limits_{i = 1}^4 {\dfrac{{{\lambda _i}{\mu _{i2}}}}{{{m_i}}}{{\rm{e}}^{{\lambda _i}t}},\;\;\;0 \lt t \lt d/v,} \hfill \\
\end{gathered} \\
{{K_{\text{t}}}\Delta g \displaystyle \sum\limits_{i = 1}^4 {\dfrac{{{\lambda _i}{\mu _{i2}}}}{{{m_i}}}\left( {{{\rm{e}}^{{\lambda _i}t}} - {{\rm{e}}^{{\lambda _i}\left( {t - d/v} \right)}}} \right),\;\;\;t \geqslant d/v.} }
\end{array}} \right.(26) 2.3.3 曲面型
此类变形断面为平滑曲线，在变形长度较大时，振动响应会减弱. 联立式（3）、（22）求解，结果如式（27）所示. 同理可得竖向加速度结果如式（28）所示.
Zs={0,t=0,4∑i=14ΔgvKtμi2λi3mil2(vλi2t2−2veλit+λileλit−λi2lt+2vλit−λil+2v),0<t<l/v,4∑i=14ΔgvKtμi2λi3mil2eλi(t−l/v)(λileλil/v−2veλil/v+λil+2v),t⩾l/v. (27) as={0,t=0,4∑i=14ΔgvKtμi2λimil2((λil−2v)eλit+2v),0<t<l/v,4∑i=14ΔgvKtμi2λimil2eλi(t−l/v)(λileλil/v+λil−2veλil/v+2v),t⩾l/v. (28) 3. 基于频率加权的振动舒适性评价
局部变形激励导致的人车振动为瞬时冲击，不具周期性特征，ISO 2631-1[11]推荐采用运行均方根法来评价这种路面偶然激励导致的振动感受，其形式为
aw(t0)=√1τ0∫t0t0−τ0a2w(t)dt， (29) 式中：
$ {t_0} $ 为瞬时激励发生时刻；$ {\tau _0} $ 为持续时间；$ {a_{\rm{w}}}\left( t \right) $ 为瞬时频率加权加速度.欲求
$ {a_{\rm{w}}}\left( t \right) $ ，需要对竖向加速度的时域值进行频率加权滤波. 由第2节可知，竖向加速度时域值与行车速度、变形长度、变形高差相关，因本文主要研究不同类型局部变形引起的人体振动，故先统一车速和变形长度两个变量. 根据现行城市道路规范[17]，道路设计速度为20～60 km/h，本文车速取40 km/h；实际路面中双断面型变形多表现为窨井的凸起或沉陷损坏，窨井的直径一般为0.6～0.7 m[2]，本文取0.6 m.3.1 频率加权滤波器设计
人体对不同频率的振动敏感程度不同，一般认为0.5～80.0 Hz是振动舒适性评价的考虑范围，竖向振动频率加权函数[18]为
Wk(f)={0.5,0.5<f⩽2.0,f/4,2.0<f⩽4.0,1.0,4.0<f⩽12.5,12.5/f,12.5<f⩽80.0, (30) 式中：f 为竖向振动频率.
$ {W_{\text{k}}} $ 在低频段和高频段均呈现抑制性，而在中间频段则具有较好的通过性，所以可以设计带通滤波器进行频率加权滤波. 因运行均方根计算对加速度相位要求不高，故采用IIR （infinite impulse response）数字滤波器设计，并借助MATLAB信号处理工具箱完成. 巴特沃斯滤波器原型具有通带内最大平坦和随频率升高而单调递减特性，与标准中的$ {W_{\text{k}}} $ 具有较高契合度，因此本文采用巴特沃斯带通滤波器.数字滤波器通过间接法设计，步骤如下：
步骤1 确定数字滤波器技术指标；
步骤2 将数字滤波器技术指标转换为模拟低通滤波器技术指标；
步骤3 设计模拟低通滤波器（滤波器原型）；
步骤4 通过频率转换，将模拟低通滤波器转变为模拟带通等滤波器；
步骤5 模拟滤波器数字化.
由MATLAB中buttord函数先确定滤波器阶数，再由buttap函数设计出滤波器原型，并借助lp2bp函数实现模拟低通至模拟带通的转换，最后由bilinear函数完成数字化.
根据
$ {W_{\text{k}}} $ 渐近线形式，频率加权函数在4.0～12.5 Hz，权重保持为1，考虑巴特沃斯滤波器的过渡特性，试算后取通带范围为2.5～18.0 Hz，通过上述过程可最终设计出频率加权函数滤波器，本文同时设计了一个对比滤波器，两者的区别在于阻带最小衰减量不同. 设计滤波器的幅频特性与ISO 2631-1[11]中的频率加权函数对比如图4所示.图4可见，设计滤波器在高频段具有一定误差，但在25.0 Hz以下人体最敏感的低频段吻合度高，且在80.0 Hz之后迅速衰减为0，而对比滤波器则与之相反. 考虑到路面局部变形的激振频率主要为低频振动（如图5），高频段的权重实际意义不大，即保证通带频率范围的特性更为关键，因此，本文设计的带通滤波器适用性更高.
3.2 3类局部变形激励作用下振动舒适性评价
因局部变形高差与时间变化无关，可视为固定系数，因此，将代表性车速和变形长度代入式（24）、（26）和式（28）可得竖向加速度的时域函数，通过带通滤波器后可得到瞬时频率加权加速度，频率记权前后的加速度变化情况如图6所示.
根据运行均方根的定义，通过数值积分方法计算得到3类局部变形作用下的均方根加速度，如式（31）～（33）所示. 其中，加速度持续时间取为1 s[11].
图 6 滤波前后的竖向加速度对比Figure 6. Vertical acceleration comparison before and after filtering1） 错台型
aw=KtΔg[∫10(4∑i=1λiμi2mieλit)2dt]0.5=42.04Δg. (31) 2） 双断面型
aw=KtΔg×[∫lv0(4∑i=1λiμi2mieλit)2dt+∫1lv(4∑i=1λiμi2mi(eλit−eλi(t−lv)))2dt]0.5=72.07Δg. (32) 3） 曲面型
aw=4ΔgvKtl(A+B)0.5=61.28Δg， (33) 式中：
A=∫lv0(4∑i=1μi2λimi((λil−2v)eλit+2v))2dt；B=∫1lv(4∑i=1μi2λimieλi(t−l/v)(λileλil/v+λil−2veλil/v+2v))2dt. 变形高差与均方根加速度之间的理论关系如图7所示. 结合ISO 2631-1[11]给出的舒适度评价标准，本文计算出的局部变形评价标准如表1所示. 当错台型、双断面型及曲面型局部变形分别达到 4.76、2.78、3.26 cm时，行驶质量均达到极不舒适.
综合上述分析，3类局部变形激励作用时的均方根加速度均和变形高差呈正比关系；在典型行驶车速40 km/h和变形长度0.6 m情况下，同样的变形高差作用，双断面型对人体舒适性影响最强烈，曲面型次之，错台型影响相对最小. 值得注意的是，实际路面中，曲面型变形多表现为路面拥包等损坏，长度不一. 当式（33）中局部变形长度l较大时，均方根加速度aw 的比例系数会减小，如图8所示. 本文所取的0.6 m变形长度几乎为曲面型变形的最不利长度，当长度约为0.3 ～ 1.5 m，同等高差时曲面型影响大于错台型，路面养护管理中应当重点考虑该长度范围.
图 7 均方根加速度与局部变形高差的关系Figure 7. Relationship between root-mean-square acceleration and height difference of local deformation表 1 局部变形高差评价标准Table 1. Evaluation criteria for height difference of local deformation均方根加速度/
(m • s−2)振动感受 △g 范围/cm 错台型 双断面型 曲面型 < 0.315 没有不
舒适< 0.75 < 0.45 < 0.51 0.315～0.630 有些不
舒适0.75～
1.500.45～
0.870.51～
1.030.500～1.000 比较不
舒适1.19～
2.380.69～
1.390.82～
1.630.800～1.600 不舒适 1.90～
3.811.11～
2.221.31～
2.611.250～2.500 很不舒适 2.97～ 5.95 1.73～ 3.47 2.04～ 4.08 > 2.000 极不舒适 > 4.76 > 2.78 > 3.26 
图 8 变形长度与比例系数的关系Figure 8. Relationship between length of deformation and evaluation coefficient4. 结 论
1） 对路面中常见的局部变形形式进行分析总结，建立了错台型、双断面型和曲面型3类典型局部变形的纵断面模型.
2） 求解两自由度汽车强迫振动模型，推导出任意路面变形激励作用时人体竖向位移的时域变化函数；根据3类局部变形的纵断面特征从理论上得出人体竖向加速度的时域解，并对函数式中变形长度和行驶车速两个参数作出合理假定.
3） 依据ISO 2631-1评价标准中竖向加速度的频率加权系数分布，设计了频率加权函数数字带通滤波器；对3类局部变形激励下的竖向加速度信号进行滤波，得到瞬时频率加权加速度并求解出均方根加速度；最后根据标准中舒适度划分方法确定了基于舒适性的3类局部变形评价标准. 结果表明：3类局部变形激励作用下，均方根加速度均与局部变形高差呈正比关系，同等变形程度下，双断面型变形的行驶不适度最高.
4） 路面养护管理中，可结合高精度检测设备及时获取路面严重错台型及双断面型局部变形的位置，做好养护和修复工作，提高路面服务性能和寿命.
5） 文中研究结果适用于城市道路沥青路面，城市道路水泥路面可以参考；对于公路路面中的类似问题，需要做进一步的研究.
-
图 7 删除节点vi后建筑群火灾蔓延损失期望
Figure 7. Loss expectation of fire spread in buildings after deleting node vi
图 8 删除节点vi的相连边后建筑群火灾蔓延损失期望降低率
Figure 8. Reduction rate in loss expectation of fire spread in buildings after deleting edges connecting node vi
图 10 增加节点后建筑群火灾场景蔓延情况
Figure 10. Scenario of fire spread in buildings after adding nodes
表 1 改造不同节点数量后建筑群火灾蔓延风险
Table 1. Fire spread risk for different numbers of nodes involved in fire preventions
改造
节点/个改造节点编号 有向图
边/条L(i)max/m2 R /m2 ΔR−i /% 1 40 121 1074 481 22.9 2 40，18 113 973 424 32.1 3 40，18，30 107 902 368 41.0 4 40，18，30，61 102 724 337 46.0 5 40，18，30，61，38 96 684 316 49.4 6 40，18，30，61，38，20 92 684 299 52.1 
下载: 导出CSV
表 2 增加不同节点数量后建筑群火灾蔓延风险
Table 2. Fire spread risk of buildings for adding different numbers of nodes
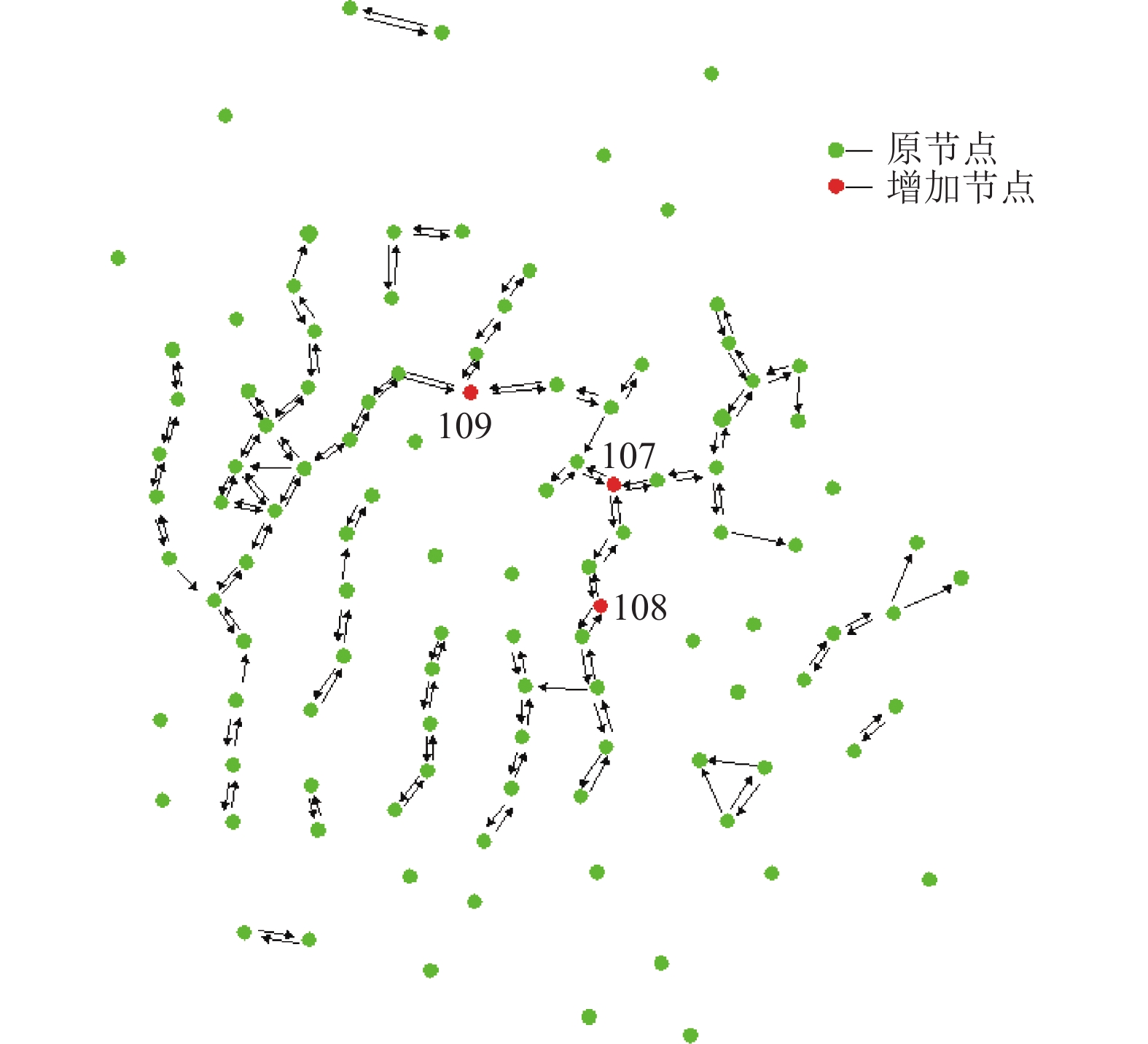
增加节点/个 增加节
点编号有向图边数
/条L max(i)/m2 R/m2 ΔR + i /% 1 107 135 1 873 752 20.5 2 107，108 139 2 875 960 53.8 3 107，108，109 145 5 311 1 829 193.1
下载: 导出CSV
-
[1] 冯骥才. 传统村落的困境与出路——兼谈传统村落是另一类文化遗产[J]. 民间文化论坛,2013(1): 7-12. [2] 高楠,邬超,白凯,等. 中国传统村落空间分异及影响因素[J]. 陕西师范大学学报(自然科学版),2020,48(4): 97-107.GAO Nan, WU Chao, BAI Kai, et al. Spatial differentiation and influencing factors of Chinese traditional villages[J]. Journal of Shaanxi Normal University (Natural Science Edition), 2020, 48(4): 97-107. [3] 《中国火灾大典》编辑委员会. 中国火灾大典[M]. 上海: 上海科学技术出版社, 1997. [4] International Organization for Standardization. Fire safety engineering—guidance on fire risk assessment: ISO/PDTS 16732 —2005[S]. Geneva: ISO Office, 2005 [5] 范维澄, 孙金华, 陆守香, 等. 火灾风险评估方法学[M]. 北京: 科学出版社, 2004 [6] 保野健治郎,高井広行,难波义郎. ロジスティック曲線による建物火災の延焼速度式に関する基礎的研究[J]. 日本建筑学会论文报告集,1982(311): 137-144.YASUNO K, TAKAI H, NAMBA Y. A basic study on fire spread formula of houses used by logistic curve[J]. Transactions of the Architectural Institute of Japan, 1982(311): 137-144. [7] 黄维章,张锁春,雷光耀,等. 城市火灾蔓延的数学模型和计算机模拟[J]. 计算物理,1993,10(1): 9-19.HUANG Weizhang, ZHANG Suochun, LEI Guangyao, et al. A mathematical model of an urban fire-spread and computer simulation[J]. Chinese Journal of Computation Physics, 1993, 10(1): 9-19. [8] NISHINO T, TANAKA T, HOKUGO A. An evaluation method for the urban post-earthquake fire risk considering multiple scenarios of fire spread and evacuation[J]. Fire Safety Journal, 2012, 54: 167-180. doi: 10.1016/j.firesaf.2012.06.002 [9] OHGAI A, GOHNAI Y, WATANABE K. Cellular automata modeling of fire spread in built-up areas—a tool to aid community-based planning for disaster mitigation[J]. Computers,Environment and Urban Systems, 2007, 31(4): 441-460. doi: 10.1016/j.compenvurbsys.2006.10.001 [10] 孟晓静,杨立中,李健. 基于元胞自动机的城市区域火蔓延概率模型探讨[J]. 中国安全科学学报,2008,18(2): 28-33,176. doi: 10.3969/j.issn.1003-3033.2008.02.005MENG Xiaojing, YANG Lizhong, LI Jian. Probability model of urban district fire spread based on cellular automata[J]. China Safety Science Journal (CSSJ), 2008, 18(2): 28-33,176. doi: 10.3969/j.issn.1003-3033.2008.02.005 [11] 柳春光,王碧君,潘建伟. 基于元胞自动机的城市地震次生火灾蔓延模型[J]. 自然灾害学报,2010,19(1): 152-157.LIU Chunguang, WANG Bijun, PAN Jianwei. Urban post-earthquake fire spread model based on cellular automata[J]. Journal of Natural Disasters, 2010, 19(1): 152-157. [12] HIMOTO K, TANAKA T. Development and validation of a physics-based urban fire spread model[J]. Fire Safety Journal, 2008, 43(7): 477-494. doi: 10.1016/j.firesaf.2007.12.008 [13] ZHAO S J, XIONG L Y, REN A Z. A spatial–temporal stochastic simulation of fire outbreaks following earthquake based on GIS[J]. Journal of Fire Sciences, 2006, 24(4): 313-339. doi: 10.1177/0734904106060786 [14] 赵思健,任爱珠,熊利亚. 城市地震次生火灾研究综述[J]. 自然灾害学报,2006,15(2): 57-67. doi: 10.3969/j.issn.1004-4574.2006.02.010ZHAO Sijian, REN Aizhu, XIONG Liya. Review of studies on urban post-earthquake fires[J]. Journal of Natural Disasters, 2006, 15(2): 57-67. doi: 10.3969/j.issn.1004-4574.2006.02.010 [15] 张健,宋志刚,李全旺,等. 木结构建筑群火灾蔓延危险建筑的识别及防火改造效果评价[J]. 工程力学,2020,37(4): 60-69.ZHANG Jian, SONG Zhigang, LI Quanwang, et al. Identification and fire protection evaluation of critical buildings to prevent fire spread in densely built wood building areas[J]. Engineering Mechanics, 2020, 37(4): 60-69. [16] HIMOTO K, TANAKA T. A physically-based model for urban fire spread[J]. Fire Safety Science, 2003, 7: 129-140. doi: 10.3801/IAFSS.FSS.7-129 [17] 卓新建, 苏永美. 图论及其应用[M]. 北京: 北京邮电大学出版社, 2018. [18] 郭世泽, 陆哲明. 复杂网络基础理论[M]. 北京: 科学出版社, 2012. [19] Technical Committee on Exposure Fire Protection. Standard for doors and other opening protective: NFPA80A[S]. Quincy, Massachusetts: National Fire Protection Association, 2017. [20] 中华人民共和国住房和城乡建设部, 中华人民共和国国家质量监督检验检疫总局. 自动喷水灭火系统设计规范: GB 50084—2017[S]. 北京: 中国计划出版社, 2017. 期刊类型引用(3)
1. 周宝宏，李辉. 高速公路沥青路面施工工程抗变形能力模拟分析. 建筑机械. 2024(05): 181-185 . 
百度学术2. 查旭东，眭子凡，张浚轩，许海信. 道路窨井盖-井周路面的病害处治与智慧检测监管综述. 中国公路学报. 2024(12): 357-380 . 百度学术3. 崔阳文，张明，傅耀宇，余永光，皮大伟. 应用ISO 2631-1与ISO 2631-5评估某军用越野汽车振动水平. 南京理工大学学报. 2022(03): 344-351 . 百度学术其他类型引用(1)
-
下载:
下载:
百度学术
点击查看大图
计量
- 文章访问数: 285
- HTML全文浏览量: 190
- PDF下载量: 9
- 被引次数: 4