Rail Friction Self-Excited Vibration in Braking Section of High-Speed Railway
-
摘要:
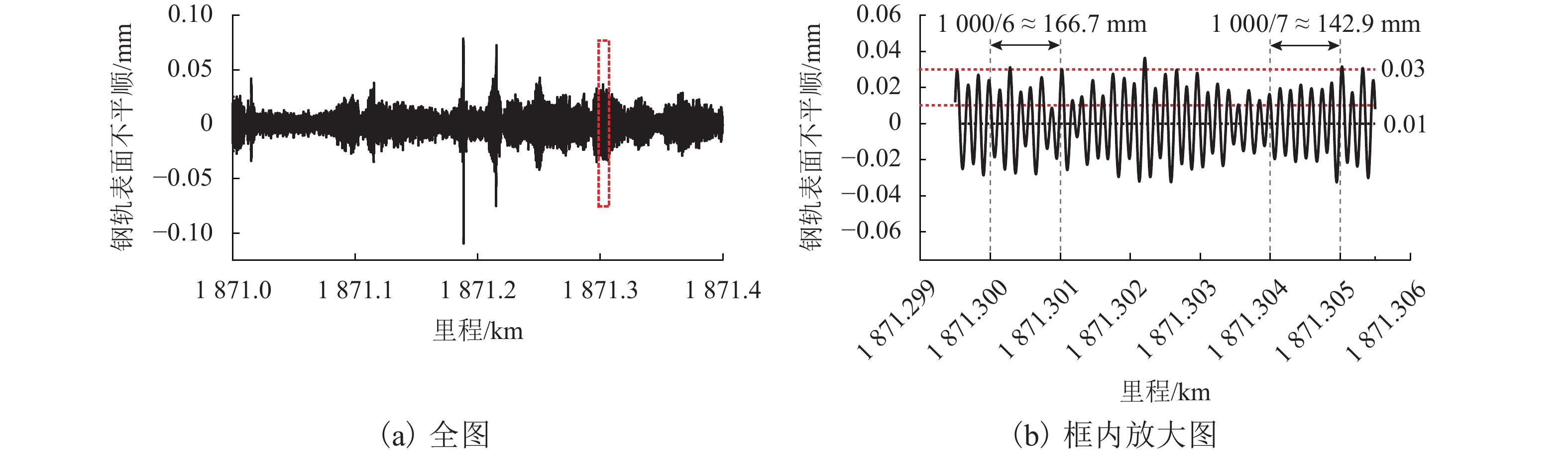
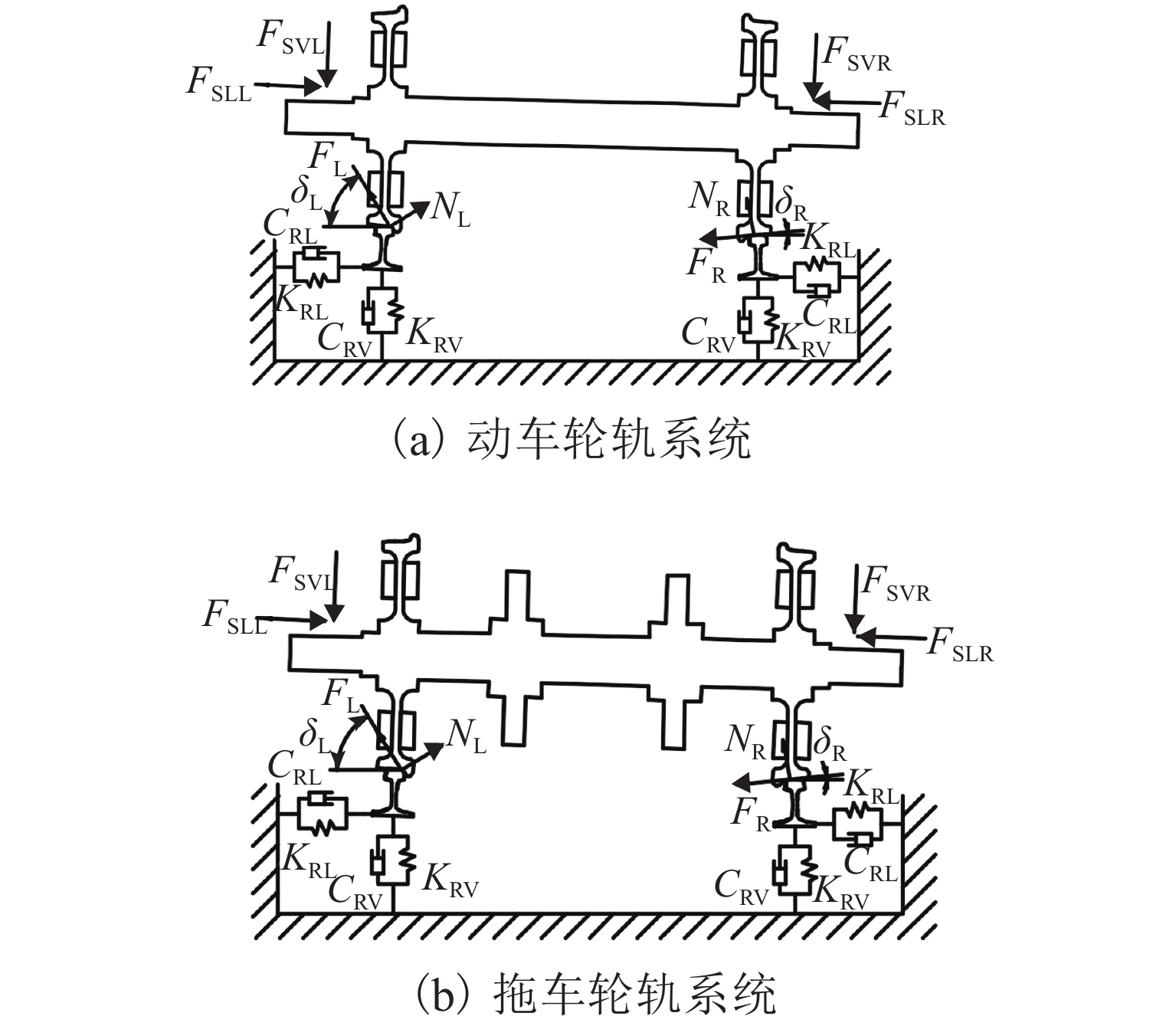
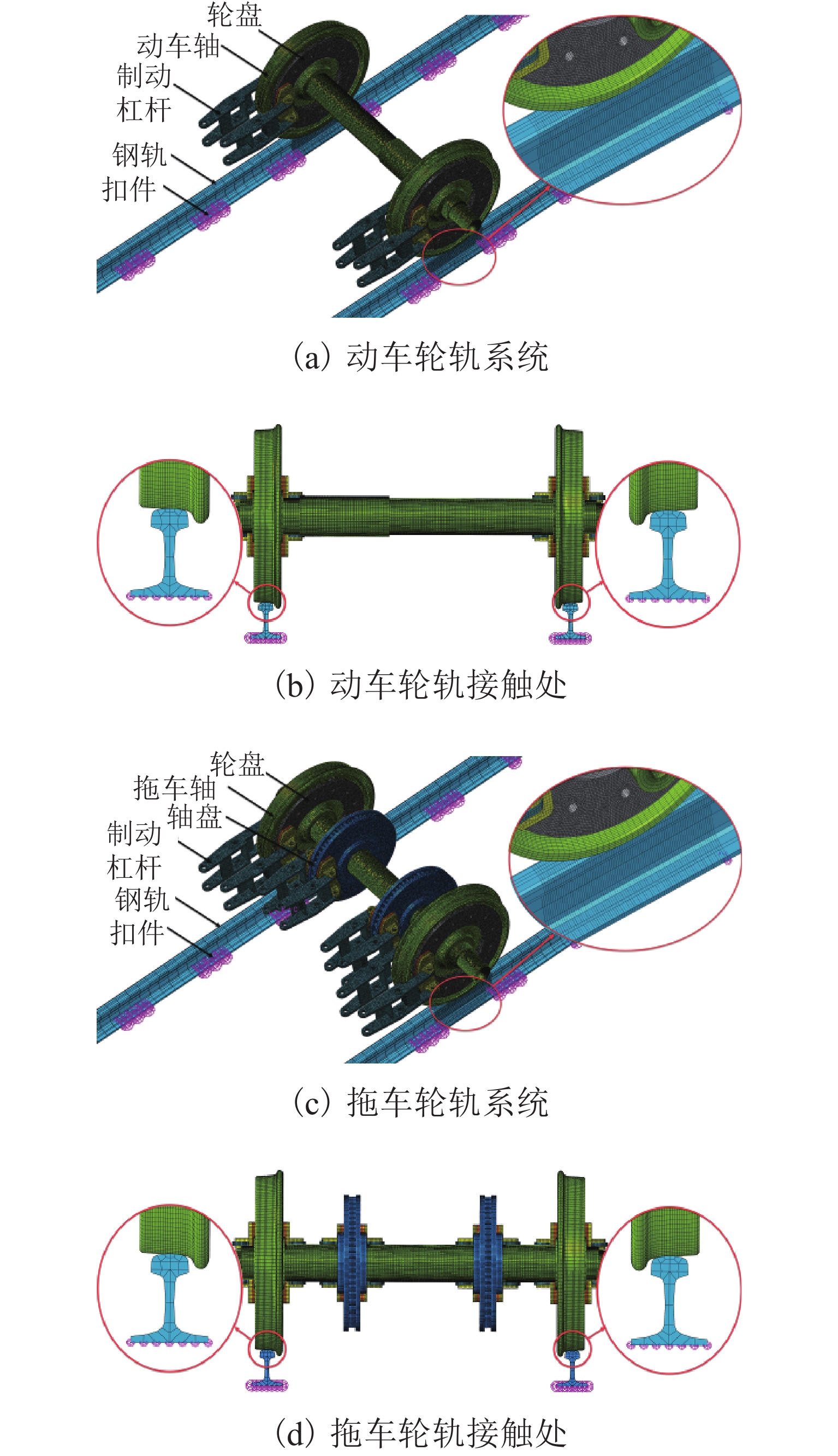
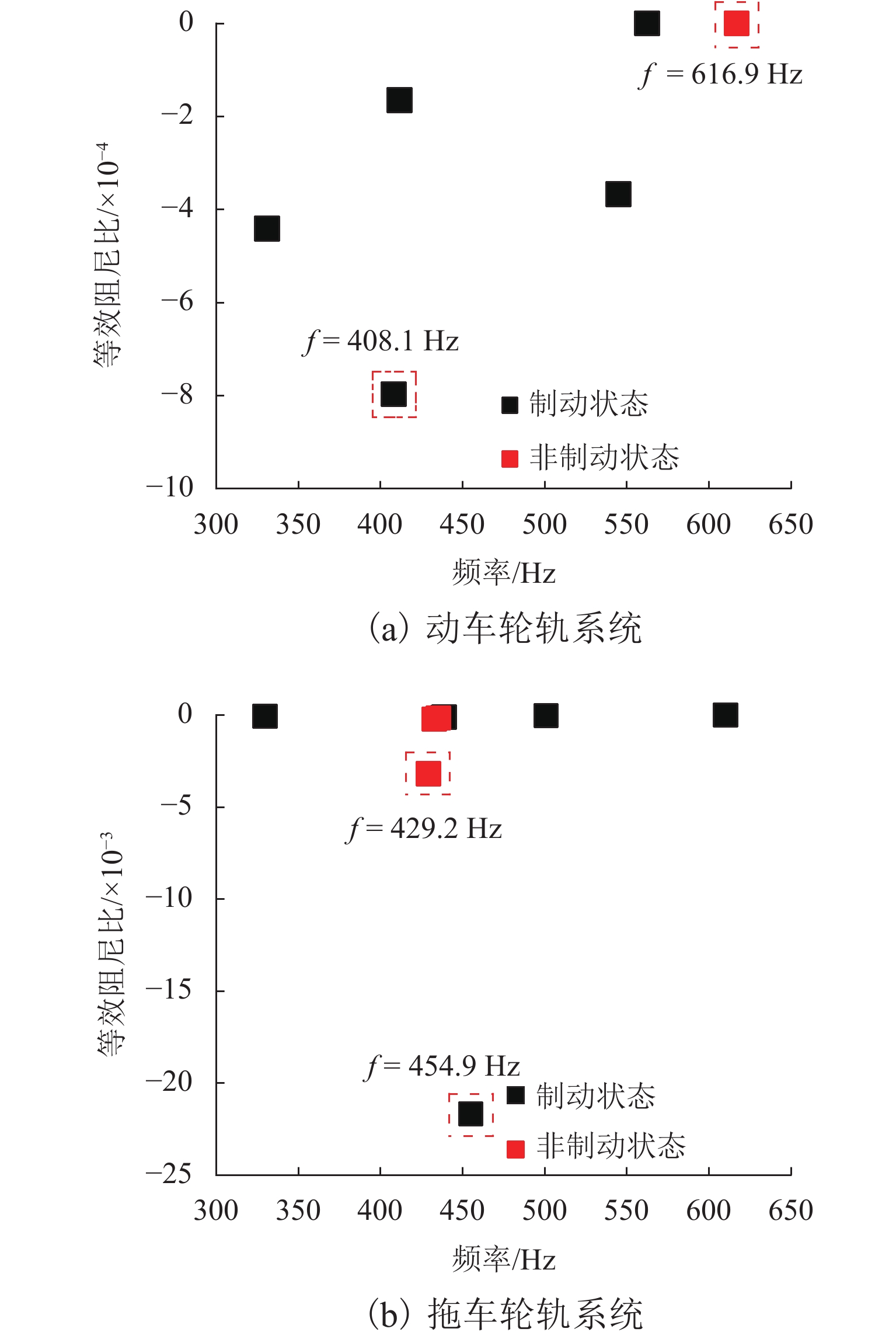
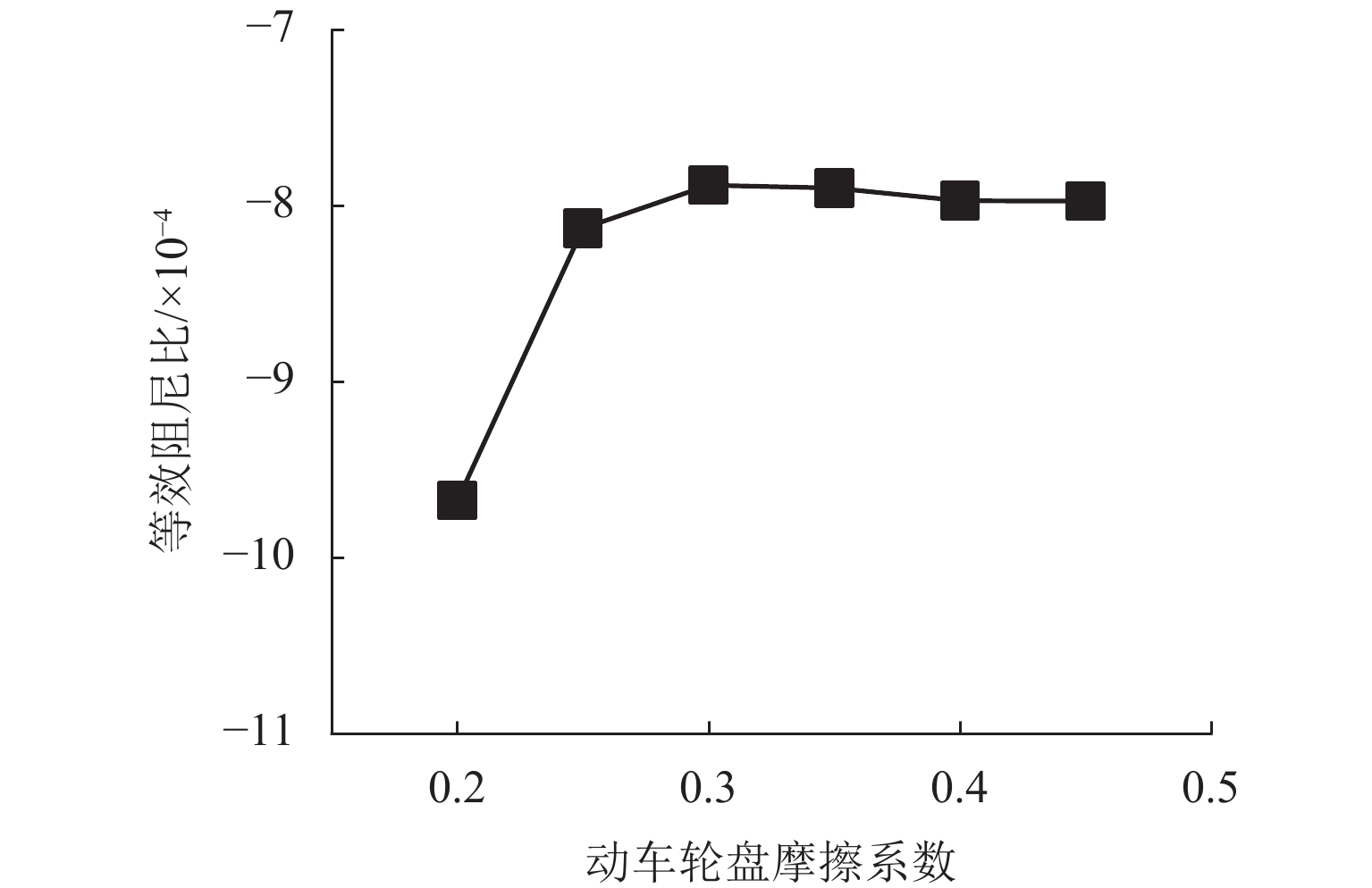
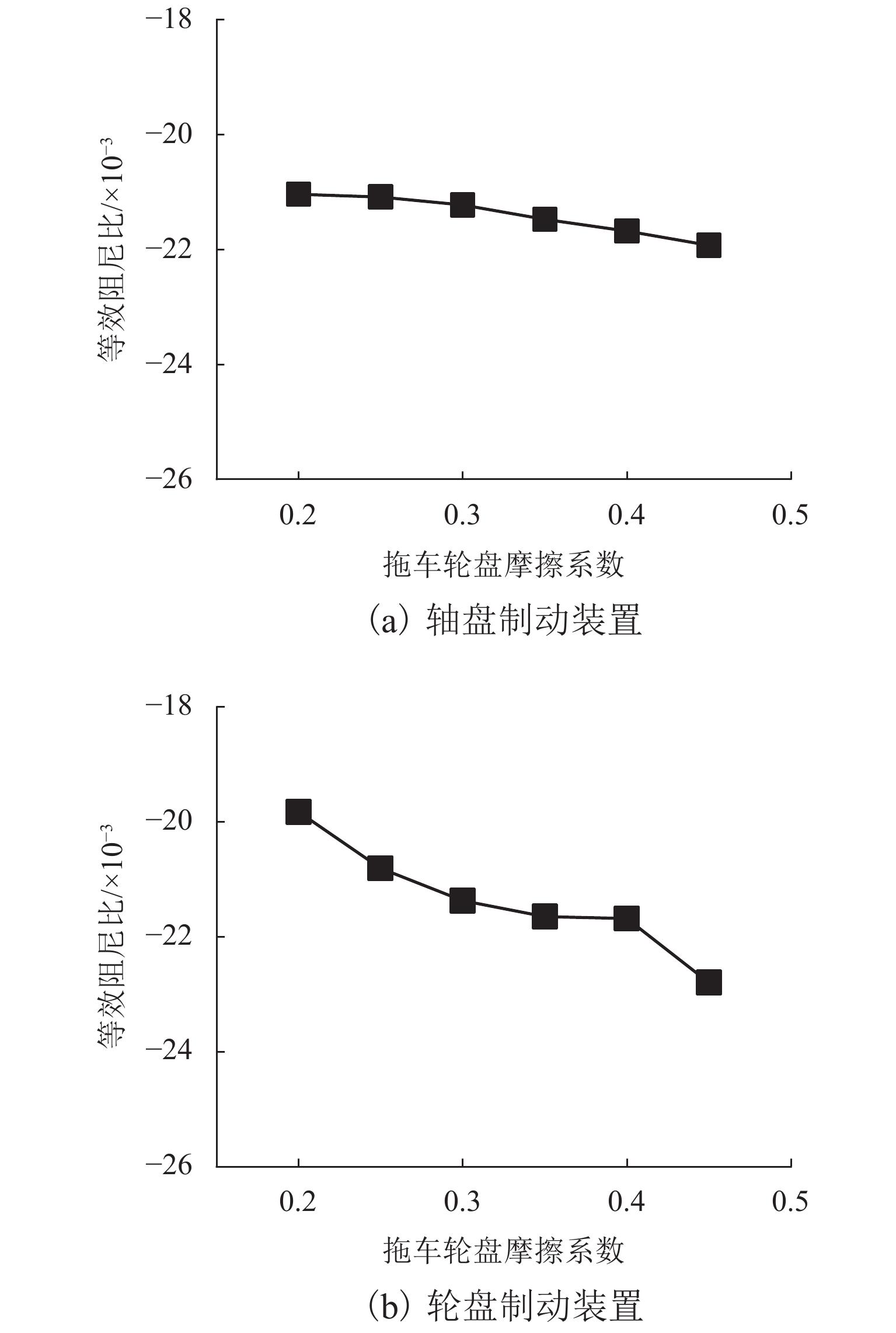
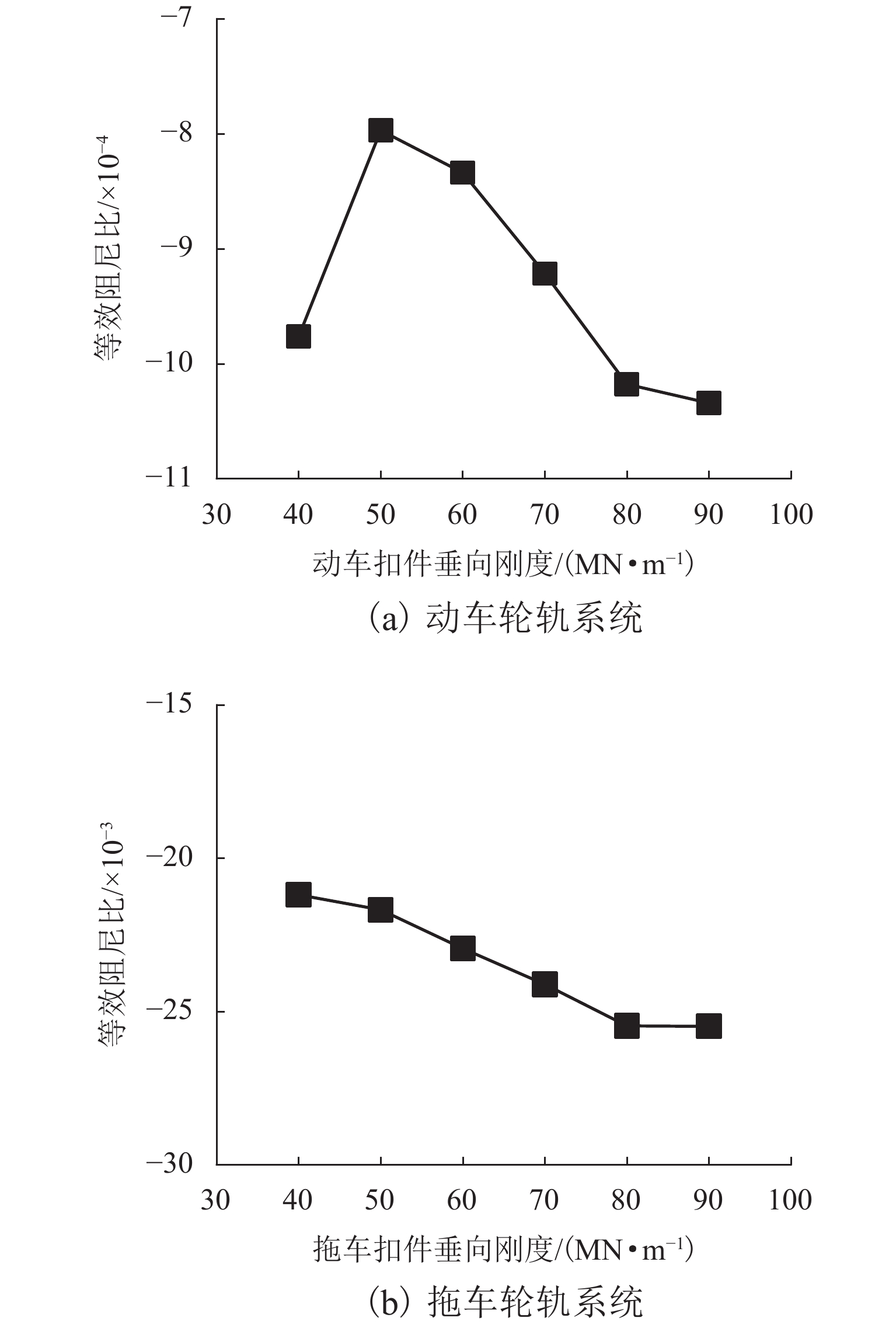
为了探究高速铁路制动区间的典型钢轨波磨现象，基于轮轨摩擦自激振动诱导钢轨波磨的观点展开了研究，通过武广高速铁路制动区段的现场调研，掌握该区段的波磨特征并采集相应的轨道不平顺；基于轮轨摩擦自激振动诱导钢轨波磨的观点分别建立制动区段高速列车的动/拖车轮对-轨道-制动系统的有限元模型，并利用复特征值法进行动/拖车轮轨系统的摩擦自激振动分析，比较动/拖车轮轨系统在制动和非制动工况下系统发生摩擦自激振动的可能性，以及在制动工况下动车轮轨和拖车轮轨系统的摩擦自激振动情况；使用控制变量法研究了制动系统摩擦系数和扣件垂向刚度对动/拖车轮轨系统摩擦自激振动的影响规律. 研究结果表明：制动工况更容易引起系统的摩擦自激振动；拖车轮轨系统更容易引起系统摩擦自激振动；控制制动装置摩擦系数约为0.30，扣件垂向刚度约为50 MN/m时能一定程度降低轮轨系统发生摩擦自激振动的可能性，进而抑制钢轨波磨的产生.
Abstract:This study investigates the typical rail corrugation phenomenon in the braking section of high-speed railways from the viewpoint that the self-excited vibration of wheel-rail friction induces rail corrugation. The corrugation characteristics of a braking section are first mastered and corresponding track irregularities are collected in a field investigation of the Wuhan Guangzhou high-speed railway. Then, from the viewpoint of the rail corrugation induced by the self-excited vibration of the wheel-rail friction, finite element models of the power/trailer wheelset-track-braking system of a high-speed train in the braking section are established. The friction self-excited vibration of the wheel-rail system of the power/trailer is analyzed using the complex eigenvalue method. The possibility of friction self-excited vibrations of the wheel-rail system of the power/trailer is compared under braking and non-braking conditions. The friction self-excited vibrations of the wheel-rail system of the power and trailer under braking conditions are then analyzed. Finally, the effects of the friction coefficient and fastener vertical stiffness on the friction self-excited vibration of the wheel-rail system are studied adopting the control variable method. The comparison between braking and non-braking conditions reveals that the braking condition is more likely to cause the friction self-excited vibrations of the system. Compared with the power/trailer wheel-rail system, the trailer wheel-rail system is more likely to cause the friction self-excited vibration of the system. It is concluded from parametric analysis that when the friction coefficient of the brake device is approximately 0.3 and the vertical stiffness of the fastener is approximately 50 MN·m−1, the possibility of the friction self-excited vibration of the wheel-rail system can be reduced to a certain extent, resulting in the suppression of rail corrugation.
-
图 3 动/拖车轮对-轨道-制动系统的接触模型
Figure 3. Contact models of wheelset-track-braking system of power/trailer
图 4 动/拖车轮对-轨道-制动系统的有限元模型
Figure 4. Finite element models of wheelset-track-braking system of power/trailer
图 6 动/拖车轮轨系统摩擦自激振动频率分布
Figure 6. Frequency distribution of friction self-excited vibration of wheel/rail system of power/trailer
图 7 制动参数变化对动车轮轨系统的影响
Figure 7. Influence of braking parameters variation on wheel/rail system of power
图 8 制动参数变化对拖车轮轨系统的影响
Figure 8. Influence of braking parameters variation on wheel/rail system of trailer
图 9 扣件参数变化对动/拖车轮轨系统的影响
Figure 9. Influence of fastener parameters variation on wheel/rail system of power/trailer
表 1 部件材料参数
Table 1. Material parameters of components
部件 密度/（kg•m−3） 弹性模量/MPa 泊松比 轮对 7800 210000 0.3 钢轨 7800 205900 制动闸片 2500 8100 制动托 5600 100000 制动杠杆 7000 190000 轮盘/轴盘 7300 207000 
下载: 导出CSV
-
[1] 金学松,李霞,李伟,等. 铁路钢轨波浪形磨损研究进展[J]. 西南交通大学学报,2016,51(2): 264-273. doi: 10.3969/j.issn.0258-2724.2016.02.006JIN Xuesong, LI Xia, LI Wei, et al. Review of rail corrugation progress[J]. Journal of Southwest Jiaotong University, 2016, 51(2): 264-273. doi: 10.3969/j.issn.0258-2724.2016.02.006 [2] CHEN G X, ZHOU Z R, OUYANG H J, et al. A finite element study on rail corrugation based on saturated creep force-induced self-excited vibration of a wheelset-track system[J]. Journal of Sound and Vibration, 2010, 329(22): 4643-4655. doi: 10.1016/j.jsv.2010.05.011 [3] GRASSIE S L. Rail irregularities,corrugation and acoustic roughness:characteristics,significance and effects of reprofiling[J]. Proceedings of the Institution of Mechanical Engineers,Part F: Journal of Rail and Rapid Transit, 2012, 226(5): 542-557. doi: 10.1177/0954409712443492 [4] OOSTERMEIJER K H. Review on short pitch rail corrugation studies[J]. Wear, 2008, 265(9/10): 1231-1237. doi: 10.1016/j.wear.2008.01.037 [5] 刘学毅,王平,万复光. 重载线路钢轨波形磨耗成因研究[J]. 铁道学报,2000,22(1): 98-103. doi: 10.3321/j.issn:1001-8360.2000.01.021LIU Xueyi, WANG Ping, WAN Fuguang. Formation mechanism of rail corrugations in heavy-haul railline[J]. Journal of The China Railway Society, 2000, 22(1): 98-103. doi: 10.3321/j.issn:1001-8360.2000.01.021 [6] LIU W, MA W H, LUO S H, et al. Research into the problem of wheel tread spalling caused by wheelset longitudinal vibration[J]. Vehicle System Dynamics, 2015, 53(4): 546-567. doi: 10.1080/00423114.2015.1008015 [7] WU B W, CHEN G X, LV J Z, et al. Generation mechanism and remedy method of rail corrugation at a sharp curved metro track with Vanguard fasteners[J]. Journal of Low Frequency Noise Vibration and Active Control, 2020, 39(2): 368-381. doi: 10.1177/1461348419845992 [8] 钱韦吉,黄志强. 蠕滑力饱和条件下钢轨吸振器抑制短波波磨的理论研究[J]. 振动与冲击,2019,38(14): 68-73, 111.QIAN Weiji, HUANG Zhiqiang. Theoretical study on the suppression of short pitch rail corrugation induced vibration by rail vibration absorbers under saturated creep forces condition[J]. Journal of Vibration and Shock, 2019, 38(14): 68-73, 111. [9] 陈光雄,金学松,邬平波,等. 车轮多边形磨耗机理的有限元研究[J]. 铁道学报,2011,33(1): 14-18. doi: 10.3969/j.issn.1001-8360.2011.01.003CHEN Guangxiong, JIN Xuesong, WU Pingbo, et al. Finite element study on the generation mechanism of polygonal wear of railway wheels[J]. Journal of The China Railway Society, 2011, 33(1): 14-18. doi: 10.3969/j.issn.1001-8360.2011.01.003 [10] 谷永磊,赵国堂,王衡禹,等. 轨道振动特性对高速铁路钢轨波磨的影响[J]. 中国铁道科学,2016,37(4): 42-47. doi: 10.3969/j.issn.1001-4632.2016.04.07GU Yonglei, ZHAO Guotang, WANG Hengyu, et al. Effect of track vibration characteristics on rail corrugation of high speed railway[J]. China Railway Science, 2016, 37(4): 42-47. doi: 10.3969/j.issn.1001-4632.2016.04.07 [11] ZHAO X, WEN Z F, WANG H Y, et al. Modeling of high-speed wheel-rail rolling contact on a corrugated rail and corrugation development[J]. Journal of Zhejiang University—Science A, 2014, 15(12): 946-963. [12] CUI X L, CHENG Z, YANG Z C, et al. Study on the phenomenon of rail corrugation on high-speed rail based on the friction-induced vibration and feedback vibration[J]. Vehicle System Dynamics, 2020, 9: 1-20. [13] YU M, WANG W D, LIU J Z, et al. The transient response of high-speed wheel/rail rolling contact on "roaring rails" corrugation[J]. Proceedings of the Institution of Mechanical Engineers,Part F: Journal of Rail and Rapid Transit, 2019, 233(10): 1068-1080. doi: 10.1177/0954409719825682 [14] CORREA N, OYARZABAL O, VADILLO E G, et al. Rail corrugation development in high speed lines[J]. Wear, 2011, 271(9/10): 2438-2447. doi: 10.1016/j.wear.2010.12.028 [15] BOGACZ R, KURNIK W. On some rotor-dynamical phenomena of high-speed trains[J]. Archive of Applied Mechanics, 2015, 85(9/10): 1343-1352. doi: 10.1007/s00419-014-0966-3 [16] 赵晓男,陈光雄,康熙,等. 兰新客运专线动车组车轮多边形磨耗的机理[J]. 西南交通大学学报,2020,55(2): 364-371. doi: 10.3969/j.issn.0258-2724.20190027ZHAO Xiaonan, CHEN Guangxiong, KANG Xi, et al. Mechanism of polygonal wear on wheels of electric multiple units on Lanzhou−Xinjiang passenger dedicated line[J]. Journal of Southwest Jiaotong University, 2020, 55(2): 364-371. doi: 10.3969/j.issn.0258-2724.20190027 [17] 乔青峰,杨伟东,朱琪,等. 铁路盘型制动噪声机理及其控制方法[J]. 西南交通大学学报,2021,56(1): 62-67.QIAO Qingfeng, YANG Weidong, ZHU Qi, et al. Generation mechanism of railway disc brake squeal and its suppression method[J]. Journal of Southwest Jiaotong University, 2021, 56(1): 62-67. [18] NIELSEN J C O, LUNDÉN R, JOHANSSON A, et al. Train-track interaction and mechanisms of irregular wear on wheel and rail surfaces[J]. Vehicle System Dynamics, 2003, 40(1/2/3): 3-54. [19] CHEN G X, CUI X L, QIAN W J. Investigation into rail corrugation in high-speed railway tracks from the viewpoint of the frictional self-excited vibration of a wheel-rail system[J]. Journal of Modern Transportation, 2016, 24(2): 124-131. doi: 10.1007/s40534-016-0106-6 [20] WU B W, QIAO Q F, CHEN G X, et al. Effect of the unstable vibration of the disc brake system of high-speed trains on wheel polygonalization[J]. Proceedings of the Institution of Mechanical Engineers, Part F: Journal of Rail and Rapid Transit, 2020, 234(1): 80-95. doi: 10.1177/0954409719833787 [21] ZHAO X X, CHEN G X, HUANG Z Y, et al. Study on the different effects of power and trailer wheelsets on wheel polygonal wear[J]. Shock and Vibration, 2020(5): 1-12. [22] YUAN Z W, TIAN C, WU M L. Modelling and parameter identification of friction coefficient for brake pair on urban rail vehicle[J]. International Journal of Rail Transportation, 2021, 9(4): 368-379. doi: 10.1080/23248378.2020.1807422 [23] PALIWAL M, MAHAJAN A, DON J, et al. Noise and vibration analysis of a disc-brake system using a stick-slip friction model involving coupling stiffness[J]. Journal of Sound and Vibration, 2005, 282(3/4/5): 1273-1284. [24] 陈光雄,崔晓璐,王科. 高速列车车轮踏面非圆磨耗机理[J]. 西南交通大学学报,2016,51(2): 244-250. doi: 10.3969/j.issn.0258-2724.2016.02.004CHEN Guangxiong, CUI Xiaolu, WANG Ke. Generation mechanism for plolygonalization of wheel treads of high-speed trains[J]. Journal of Southwest Jiaotong University, 2016, 51(2): 244-250. doi: 10.3969/j.issn.0258-2724.2016.02.004 [25] ABUBAKAR A R, OUYANG H J. Complex eigenvalue analysis and dynamic transient analysis in predicting disc brake squeal[J]. International Journal of Vehicle Noise and Vibration, 2006, 2(2): 143-155. doi: 10.1504/IJVNV.2006.011051 [26] LIU K, JING L. A finite element analysis-based study on the dynamic wheel-rail contact behaviour caused by wheel polygonization[J]. Proceedings of the Institution of Mechanical Engineers,Part F: Journal of Rail and Rapid Transit, 2020, 234(10): 1285-1298. doi: 10.1177/0954409719891549 [27] 范志勇,项载毓,谭德强,等. CRH380A型高速动车组制动闸片摩擦损伤分析[J]. 摩擦学学报,2020,40(2): 185-194.FAN Zhiyong, XIANG Zaiyu, TAN Deqiang, et al. Wear analysis of brake pad for CRH380A high-speed train[J]. Tribology, 2020, 40(2): 185-194. -
下载:
点击查看大图
计量
- 文章访问数: 329
- HTML全文浏览量: 139
- PDF下载量: 32
- 被引次数: 0