Simulation Calculation Method and Application for Relative Displacement of Heavy Hall Freight Suspension on Curved Track
-
摘要:
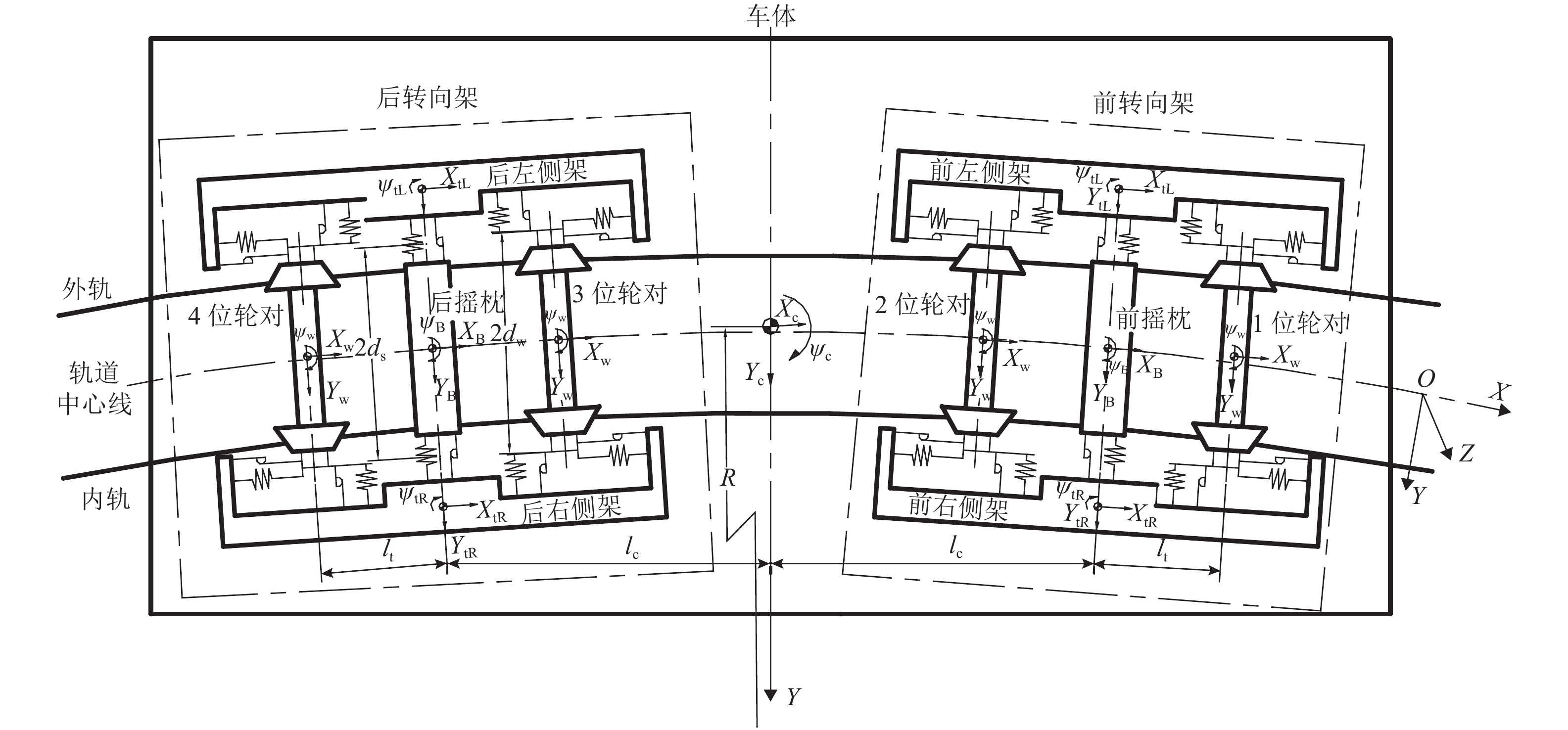
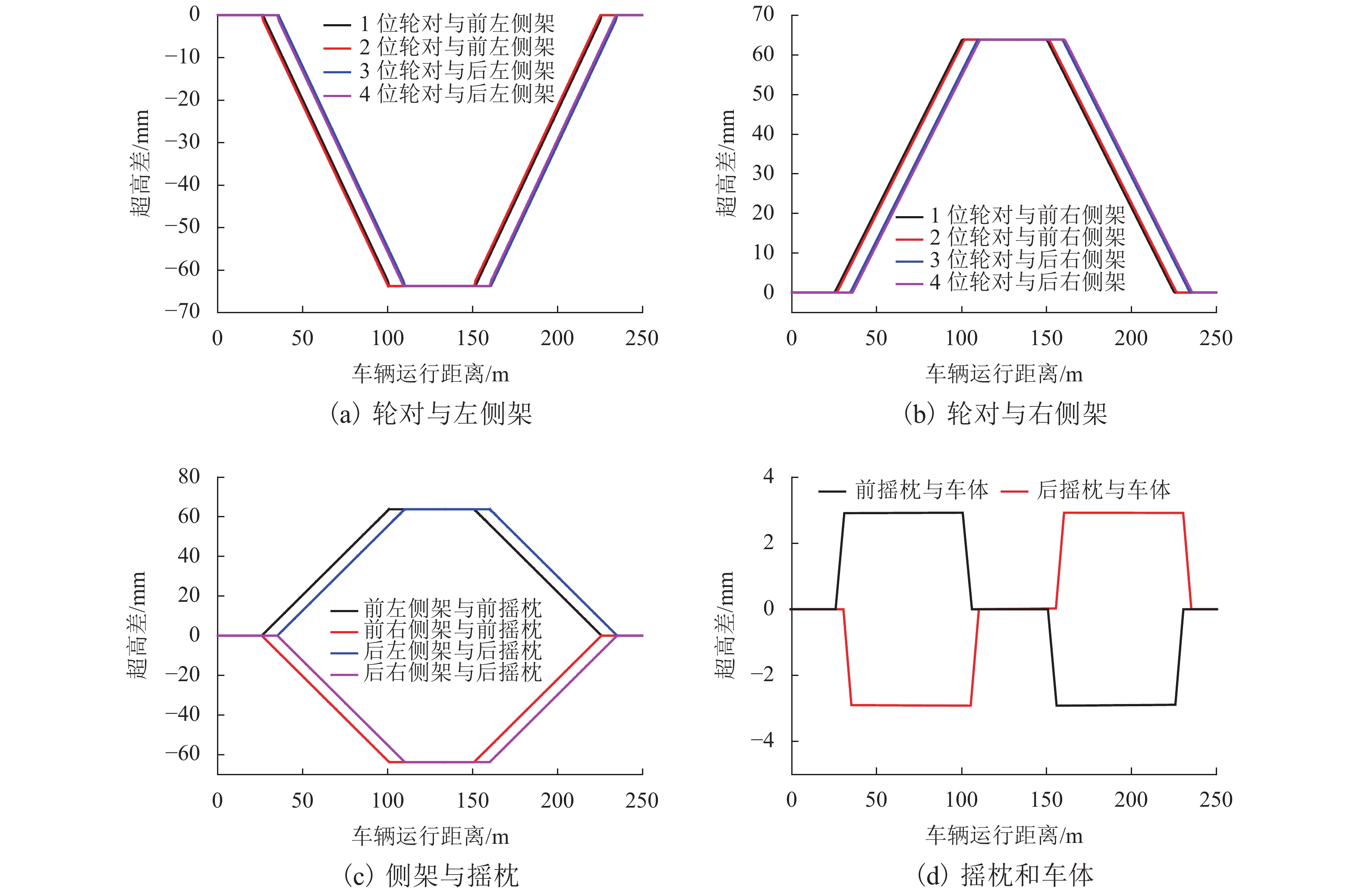
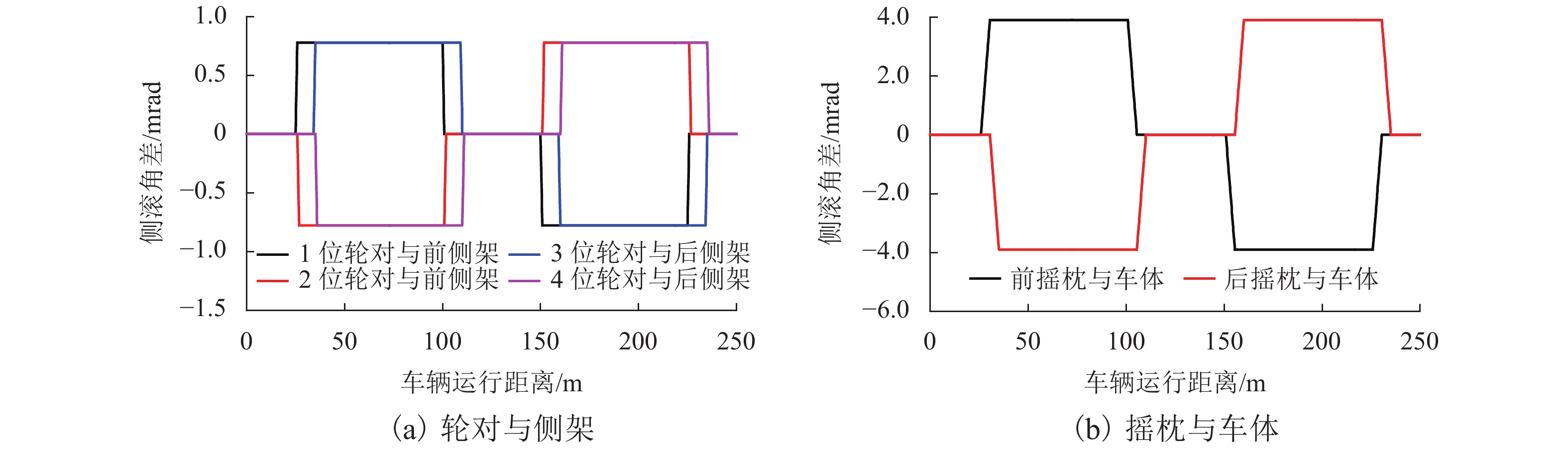
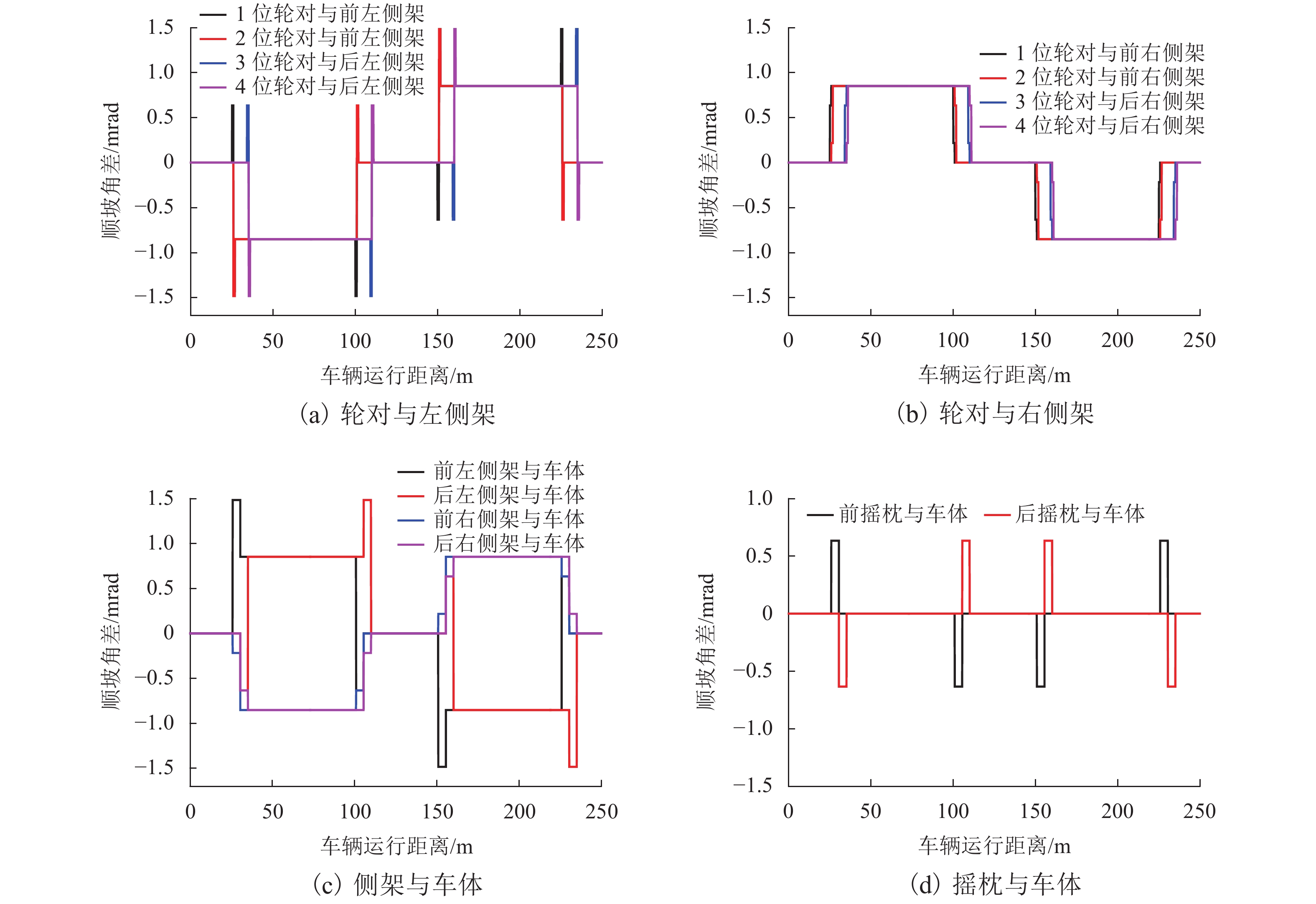
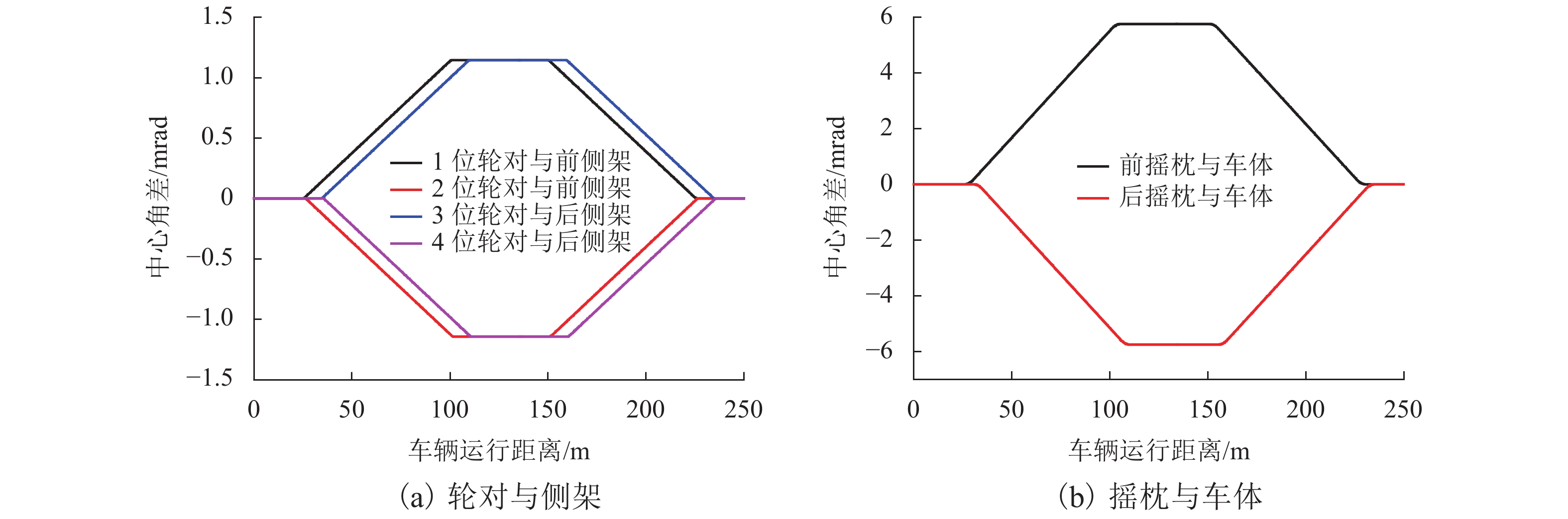
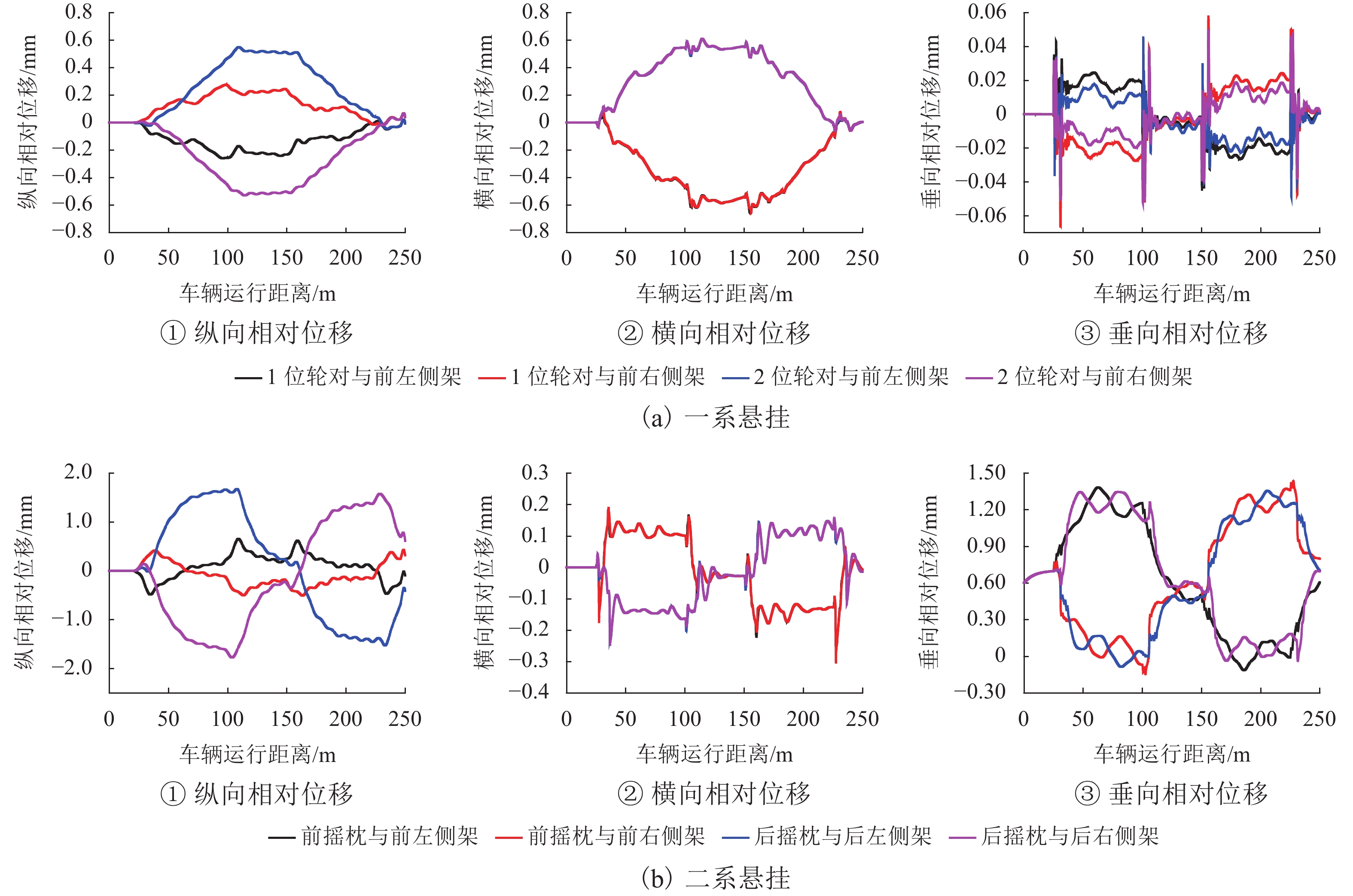
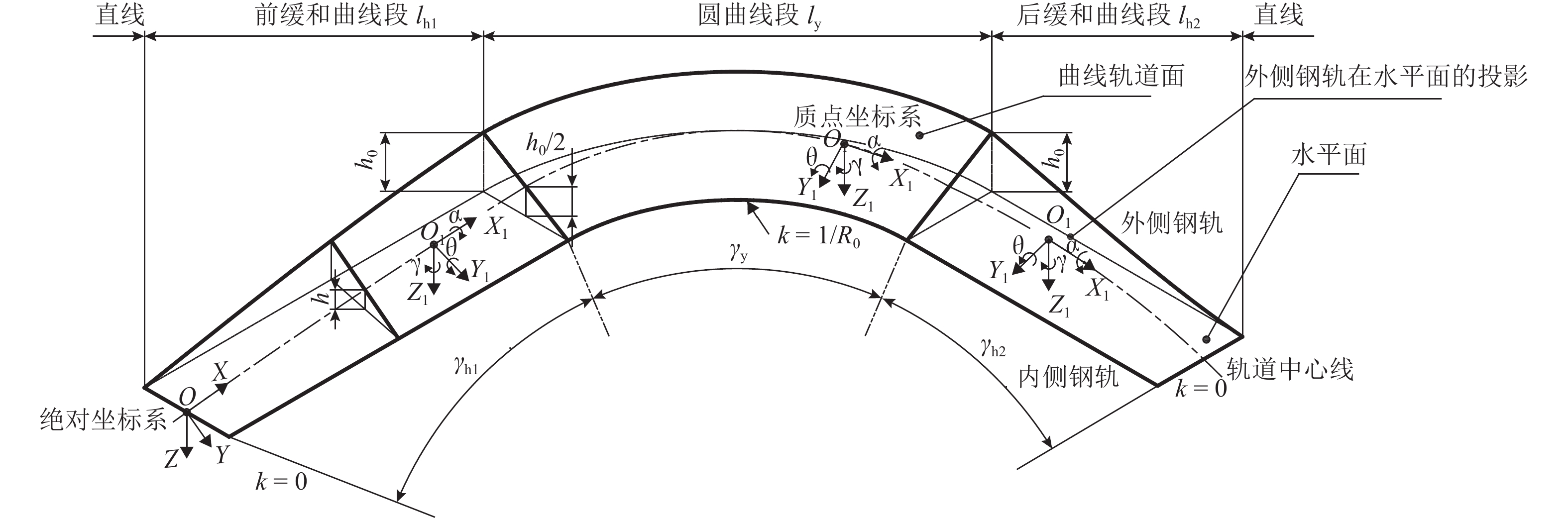
为准确求解曲线轨道上重载货车悬挂的相对位移，首先，建立曲线轨道数学模型，推导出曲线外轨超高、顺坡角、侧滚角和中心角随线路长度的变化公式，再根据车辆各刚体部件进出曲线的时间和所处曲线位置差异，编程计算悬挂点刚体间的超高及转角差；其次，以刚体质心为坐标原点建立本体坐标系，分别给出悬挂点在两刚体本体坐标系中的坐标表达式，通过坐标变换法将本体坐标转换到同一坐标系下，计算悬挂点瞬态相对位移；最后，结合车辆曲线动力学仿真程序计算，即可求出车辆曲线通过时各悬挂点的动态相对位移. 计算结果表明：车辆悬挂相对位移是车辆参数和曲线轨道参数综合作用的结果，当单独不计线路侧滚角差、顺坡角差、中心角差时，对应悬挂相对位移的最大偏差率可达42.85%、24.03%、71.42%；利用坐标变换结合动力学仿真计算的方法可全面考虑车辆和轨道参数，求解车辆悬挂相对位移更为准确.
Abstract:In order to accurately solve the relative displacements of heavy haul freight suspension on a curved track, firstly the mathematical model of curved track was established, and the formulas of outer rail superelevation, slope angle, roll angle and central angle with the length of curve were derived, then according to the time difference and the geometric position difference between the suspension components while the vehicle entering or leaving the curved track, programming to calculate the relative rail superelevation and angle difference of these rigid components. Secondly, the ontological coordinate system was established with the centroid of each rigid body as the origin, and the coordinate expressions of suspension points in the two ontology coordinate systems were given respectively, and converting these coordinates into a same coordinate system through coordinate transformation method, so the transient relative displacement of suspension points could be calculated. Finally, by combining the vehicle curving dynamics simulation, the dynamic relative displacements of suspension points could be calculated. The results indicate that the relative displacement of vehicle suspension is the result of the comprehensive action of vehicle parameters and curve track parameters, when the difference of roll angle difference, slope angle and central angle are excluded separately, the corresponding maximum deviation rate of relative suspension displacement can arrive at 42.85%, 24.03%, and 71.42%. The method of coordinate transformation combined with dynamic simulation can fully consider the vehicle and track parameters, and the relative displacement of vehicle suspension can be solved more accurately.
-
随着现代工业的不断发展，高速电机对轴承提出了更高的要求. 高速电机是依据电磁感应定律实现电能转换或传递的一种装置. 在高速运行过程中，对转子转速及稳定性有很高要求[1]. 为确保电磁轴承系统能够稳定运行，需要在5个自由度上施加控制力，一般需要两个径向磁轴承与一个推力磁轴承，两个径向磁轴承提供4个径向自由度，一个推力磁轴承提供一个轴向自由度. 但3个磁轴承增加了系统的轴向长度，限制了转子的临界转速，无法满足高速电机对高转速的要求.
因此，高速电机磁轴承通常采用轴向长度短、推力盘小的结构来提高转子临界转速，减少空气摩擦损失. 将径向磁轴承与推力磁轴承合并为一个混合磁轴承单元，该方法对由磁轴承支承的高速电机系统尤为重要[2]. 目前，轴-径向混合磁轴承主要有两种结构，一种是将径向磁轴承固定于推力磁轴承内部[3-4]，该结构关于径向平面对称，轴向长度短，能有效提高转子临界转速，但径向长度较长，不利于散热；另一种是将径向磁轴承与推力磁轴承并排放置[5-6]，结构紧凑，能够有效减少空气摩擦损失，但由于轴承轴向剖面在径向方向不对称，轴向控制磁通一部分会流过径向磁轴承，推力磁轴承与径向磁轴承之间存在交叉耦合[7-8].
针对现有的径向磁轴承与推力磁轴承并排布置结构中交叉耦合产生的不利影响，本文提出一种三自由度轴-径向混合磁轴承（ARHMB），建立了综合考虑涡流、漏磁及交叉耦合效应的动态特性模型，并采用不完全微分PID控制对ARHMB进行研究.
1. ARHMB结构设计
本文所提出的ARHMB结构被视为最适合高速电机的结构之一，其三维结构如图1所示. 它由推力磁轴承与径向磁轴承通过永磁环相连接. 永磁环是轴向磁化的，可以为径向磁轴承和推力磁轴承提供偏置磁通，有效减小线圈电流，从而降低功率损耗. 径向磁轴承包含径向叠片定子、径向叠片转子、径向线圈和导磁环，导磁环组装在径向定子外侧. 轴向磁轴承包含轴向定子、轴向线圈和推力盘.
为了减小涡流损耗，工程上常采用高电阻率磁性材料或叠片结构. 对于径向磁轴承，由于其磁路在垂直于转轴的平面内，可采用叠片硅钢材料制备其定子与转子，从而达到减小涡流损耗的目的. 但对于推力磁轴承，由于其磁路既包含轴向部分又包含径向部分，难以使用叠片结构来减小涡流损耗. 目前，在工业应用中，常使用碳钢材料制备推力磁轴承，但其电阻率约为1.0×10−7 Ω•m，实际工作时涡流损耗较为严重. 本文采用软磁复合材料（SMCs）[9-10]来制备推力磁轴承，其电阻率约为1.1×10−4 Ω•m，在工作时涡流损耗较小. 此外，由于许多高转速机械存在较大的轴向荷载，可在推力磁轴承内引入具有单边聚磁性的Halbach永磁阵列，将聚磁侧正对转子气隙部分，充分利用永磁体，从而增加轴向磁力.
2. ARHMB动态磁路模型
经典磁路模型基于静态电磁场，仅考虑气隙磁阻，忽略了铁芯磁阻与涡流效应的影响[11]. 但在电磁轴承实际运行过程中，涡流效应会引起电磁轴承相位滞后、电磁力减小，影响系统的动态特性. 因此，经典磁路模型不适用于高速磁轴承设计，实际分析中，涡流效应不可忽略. 如图1所示，该轴承结构紧凑，不同构件之间距离很小，相邻铁片之间的漏磁非常严重，轴向磁轴承与径向磁轴承之间还存在交叉耦合. 所以，为了精准预测电磁轴承的高频特性，需要同时考虑涡流、漏磁以及交叉耦合效应的影响，并通过替换材料或改变结构等方式来减小影响.
根据ARHMB结构特点与功能，将等效磁路分为以下3个部分：偏置磁通等效磁路、径向控制磁通等效磁路、轴向控制磁通等效磁路. ARHMB的结构参数如图2所示，图中：d1为轴向转子半径；d2为轴向磁极内径；d3为轴向转子外径；d4为轴向磁极外径；d5为轴向定子内径；d6为轴向定子内径与轴向定子外径之间的距离；d7为径向定子外径；d8为导磁环厚度；x为轴向磁极宽度；y为转子外径宽度；b为轴向定子腔宽度；c为径向磁极轴向宽度；l为径向磁极径向宽度；g为气隙宽度；hpm为永磁体厚度；e为转子与轴向磁极的距离；r1为径向转子内径；r2为径向转子外径；r3为径向磁极内径；r4为径向定子内径；r5为径向定子外径；r6为径向转子轴心与导磁环外径之间的距离；其余数值见表1.
表 1 ARHMB结构参数Table 1. ARHMB structure parametersmm 参数 数值 参数 数值 轴向磁极
宽度 x6 转子外径
宽度 y6 轴向定子腔
宽度 b20 径向磁极轴向
宽度 c25 径向磁极径向
宽度 l9 气隙宽度 g 0.4 转子半径 d1 15 轴向磁极
内径 d218 转子外径 d3 24 径向磁极
外径 d428 轴向定子
内径 d558 轴向定子内外径
间距 d67 径向定子
外径 d758 导磁环厚度 d8 6 2.1 偏置磁通等效磁路
图3所示为Halbach永磁阵列与轴径向定子之间永磁环共同作用下的偏置磁通分布. 从图3（a）中可以看出：偏置磁通不仅分布于轴承内部与转子内部，还存在8条漏磁路径. 其中：
$ {{\rm{LF}}}_{{\rm{pm1}}} $ 是从永磁体到自身的；$ {{\rm{LF}}}_{{\rm{pm2}}} $ 是从轴向定子到径向定子的；$ {{\rm{LF}}}_{{\rm{pm3}}} $ 、$ {{\rm{LF}}}_{{\rm{pm6}}} $ 是从轴向定子到转子的；$ {{\rm{LF}}}_{{\rm{pm4}}} $ 、$ {{\rm{LF}}}_{{\rm{pm5}}} $ 、$ {{\rm{LF}}}_{{\rm{pm7}}} $ 、$ {{\rm{LF}}}_{{\rm{pm8}}} $ 是从轴向定子到推力盘的. 漏磁路径$ {{\rm{LF}}}_{{\rm{pm1}}} $ ~${{\rm{LF}}}_{{\rm{pm8}}} $ 的漏磁效用可用漏磁阻$ {R}_{{\rm{lpm1}}} $ ~$ {R}_{{\rm{lpm8}}} $ 表示. 从图3（b）中可以看出：Halbach永磁阵列聚磁效果明显. 此外，由于永磁环产生的磁通是静态的，采用不考虑铁芯磁阻的静态磁路，对应的偏置磁通等效磁路如图4所示.在图4中：Rpm与Fpm分别为永磁环的磁阻和磁动势；
$ {R}_{{\rm{Hpm}}} $ 为Halbach永磁阵列的磁阻. 红色虚线区域总磁阻Rpt如式（1）所示.Rpt=Rrg4+Rzg2λpm1+RHpm, (1) 式中：Rrg和Rzg分别为径向、轴向气隙磁阻；为了描述漏磁的严重程度，定义
$ {\lambda }_{{\rm{pm1}}} $ 、$ {\lambda }_{{\rm{pm2}}} $ 为偏置磁通漏磁系数，如式（2）、（3），|表示两磁阻为并联关系.λpm1=Rlpm3|Rlpm4|Rlpm7Rzg+Rlpm3|Rlpm4|Rlpm7, (2) λpm2=Rlpm1|Rlpm2Rpt+Rlpm1|Rlpm2. (3) 偏置磁通磁路总磁阻可以表示为
Rp=Rpm+Rptλpm2. (4) 因此，径向气隙磁通
$ {\phi }_{{\rm{rpm}}} $ 与轴向气隙磁通$ {\phi }_{{\rm{z}}{\rm{pm}}} $ 可以表示为ϕrpm=14FpmRpλpm2, (5) ϕzpm=12FpmRpλpm1λpm2. (6) 2.2 径向控制磁通等效磁路
由于径向磁轴承关于x、y轴对称，以y方向为研究对象，其控制磁通分布如图5（a）所示，根据控制磁通分布可将该轴承分为3个单元，如图5（b）所示，
$ {\mathrm{L}\mathrm{F}}_{\mathrm{r}} $ 是径向漏磁. 其中：单元1为径向定子环部分；单元2为磁极部分；单元3为径向转子部分.根据径向控制磁通分布，可绘制出径向控制磁通等效磁路如图6所示.
图6中：Nx为x方向的线圈匝数；Ny为y方向的线圈匝数；
$ {R}_{x}^{ + } $ 、$ {R}_{x}^{-} $ 、$ {R}_{y}^{ + } $ 、$ {R}_{y}^{-} $ 分别为转子沿x + 、x−、y + 、y−向偏转时的磁阻；$ {i}_{x} $ 为x方向上的控制电流；$ {i}_{y} $ 为y方向上的控制电流；$ {{\rm{LF}}}_{{\rm{r}}} $ 为径向漏磁，用磁阻$ {R}_{{\rm{lr}}} $ 表示；$ {R}_{{\rm{re1}}} $ 为定子叠片动磁阻；$ {R}_{{\rm{re2}}} $ 为径向磁极动磁阻；$ {R}_{{\rm{re3}}} $ 为径向转子动磁阻，如式（7）.{Rre1=π(r5+r4)4μ0μrfl(r5−r4),Rre2=r5+r4−r2−r12μ0μrfAr,Rre3=π(r1+r2)4μ0μrfl(r2−r1), (7) 式中：
$ {A}_{{\rm{r}}} $ 为径向磁极的面积；$ {\mu }_{{\rm{rf}}}$ 为考虑了涡流效应的叠片磁导率；$ {\mu }_{0} $ 为真空磁导率.当控制电流沿y方向时，径向控制磁通总磁阻
$ {R}_{{\rm{r}}} $ 为Rr=Rre1|Rlr+2Rre2+2Rg+Rre3, (8) 式中：Rg为气隙磁阻，其大小与
$ {R}_{x}^{ + } $ 、$ {R}_{x}^{-} $ 、$ {R}_{y}^{ + } $ 、$ {R}_{y}^{-} $ 相同.x方向控制磁通总磁阻与y方向计算过程类似，在此不做过多赘述. 因此，径向控制磁通
$ {\phi }_{{\rm{r}}} $ 可以表示为ϕr=2NrirRr, (9) 式中：Nr为径向线圈匝数；ir为径向电流.
2.3 轴向控制磁通等效磁路
由于ARHMB轴向剖面在径向方向不对称，推力磁轴承产生的轴向控制磁通一部分会流经径向磁轴承部分，与径向轴承本身产生的磁通相互交叉，从而造成轴-径向交叉耦合效应. 因此，在实际分析中，应考虑径向磁轴承对推力磁轴承的影响. 轴向控制磁通分布如图7（a）所示，从图中可以看出，该系统除了轴承及转子内部的磁力线外，还包含9条漏磁路径（
$ {{\rm{LF}}}_{{\rm{z}}1} $ ~${{\rm{LF}}}_{{\rm{z}}9}$ ），其漏磁效用可用漏磁阻$ {R}_{{\rm{l}}{\rm{z}}1} $ ~${R}_{{\rm{l}}{\rm{z}}9} $ 表示. 根据轴向控制磁通分布，可将系统划分为12个单元，如图7（b），各单元磁阻可用$ {R}_{{\rm{z}}{\rm{1}}}$ ~${R}_{{\rm{z}}{\rm{12}}} $ 表示.根据文献[12]中的等效磁路分析方法和图7（a）中的控制磁通分布，建立如图8所示的轴向控制磁通等效磁路.
在图8中，虚线区 ① 与虚线区 ② 的总磁阻相等，用
$ {R}_{{\rm{z}}{\rm{t1}}} $ 与$ {R}_{{\rm{z}}{\rm{t2}}} $ 表示，如式（10）、（11）.Rzt1=Rlz3|Rlz4|Rlz7|Rz7, (10) Rzt2=Rlz6|Rlz5|Rlz8|Rz8. (11) 为了刻画轴向控制磁通路径中漏磁效应与交叉耦合效应的严重程度，定义
$ {\alpha }_{1} $ 、$ {\alpha }_{2} $ 、$ {\alpha }_{3} $ 为轴向控制磁通漏磁系数，如式（12） ~ （14），$\varepsilon$ 为交叉耦合系数[5]，如式（15）.α1=Rlz3|Rlz4|Rlz7Rlz3|Rlz4|Rlz7+Rz7, (12) α2=Rlz1|Rlz2Rlz1|Rlz2+Rz9, (13) α3=Rlz9Rlz9+Rzt3+2×Rzt1+RHpm+ε(Rz2+Rz4), (14) ε=Rz10+Rz11+Rz12+α2Rz9Rz10+Rz11+Rz12+α2Rz9+Rz2+Rz4, (15) 式中：
${R_{{\rm{z}}{\rm{t3}}}} = {R_{{\rm{z}}6}} + {R_{{\rm{z}}3}} + {R_{{\rm{z}}5}}$ ；$ R_{{\rm{Hpm}}} = R_{{\rm{Hpml}}} + R_{{\rm{Hpmr}}} $ ，$ {R}_{{\rm{Hpml}}} $ 与$ {R}_{{\rm{Hpmr}}} $ 分别为Halbach左侧磁阻与右侧磁阻.因此，轴向控制磁通的总磁阻
$ {R}_{{\rm{z}}} $ 为Rz=Rz1+α3[Rzt3+2Rzt1+RHpm+ε(Rz2+Rz4)]. (16) 轴向总控制磁通为
ϕz=NzizRzα1α2α3ε. (17) 式中：Nz为轴线线圈匝数；iz为轴向控制电流.
3. 动态特性分析
3.1 等效磁阻频率响应
为了获取材料类型及交叉耦合效应对等效磁阻频率响应的影响，基于ARHMB等效磁路图，分别分析了轴向和径向磁阻在0~10 kHz的频率响应图. 图9为碳钢材料和软磁复合材料制备的轴向磁阻频率响应. 由图9可知：随着频率的增加，等效磁阻幅值和相位均呈上升趋势；对于不同材料制备的相同轴承，未考虑交叉耦合效应时，碳钢轴承幅值从0到10 kHz增加了大约290%，SMCs轴承幅值基本没有发生变化，仅增加了大约21%；对比相同材料制备的轴承，考虑交叉耦合效应时，两类轴承等效磁阻幅值均有增加，SMCs轴承在10 kHz时幅值增加14%，碳钢轴承在10 kHz时幅值增加23%；此外，考虑交叉耦合效应时，碳钢轴承相位最大变化率约为30%，SMCs轴承相位最大变化率约为50%；在交变磁场的作用下，轴承损耗与等效磁阻成正比，并且随着频率的增加而变得明显. 因此，在较高的磁场下，由SMCs制备的轴承优于碳钢材料，为了使计算模型更加精确，交叉耦合效应不可忽略. 图10为ARHMB径向部分等效磁阻频率响应，当激励频率增加时，径向等效磁阻的幅值和相位在0~1 kHz上升缓慢，在1~10 kHz时上升较快. 因此，SMCs可以代替碳钢材料用于制造ARHMB轴向部分，能满足0~10 kHz的使用需求. 径向部分采用叠片结构，在0~1 kHz范围内涡流损耗较低，轴承发热较少，但在1~10 kHz时动态特性较差，能满足中低频工况.
3.2 动态刚度频率响应
为了验证ARHMB动态特性，分别给出轴向和径向的动态力-电流刚度、动态力-位移刚度频率响应. 图11为两种不同材料制备的ARHMB的轴向动态力-电流刚度的频率响应. 由图11可知：当激励频率为100 Hz时，碳钢及SMCs轴承电流刚度曲线相交；在100 Hz之后，SMCs轴承电流刚度远大于碳钢轴承；碳钢轴承下降趋势较快，当频率达到10 kHz时，其电流刚度已近似为0，这表明碳钢轴承在中高频磁场工况下不能提供支承作用；SMCs轴承在0~10 kHz时电流刚度下降较为缓慢，考虑交叉耦合效应时，该轴承电流刚度在10 kHz时降低了19%；对比相位图还能发现，SMCs制备的轴承相位与电流刚度幅值变化趋势一致，考虑交叉耦合效应时，SMCs轴承相位最大变化率约为48%.
将文献[5-6]中的静态刚度实验值与ARHMB进行比较. 在静态状态下，ARHMB的电流刚度分别比Ren和Le的模型刚度大20%和48%. 这是由于ARHMB轴向增加了Halbach永磁阵列，在静态状态下具有更大电磁力.
图12为两种不同材料制备的ARHMB的轴向动态力-位移刚度的频率响应. 由图12可知：与动态力-电流刚度变化规律类似，当频率增加时，位移刚度呈现下降趋势；此外，碳钢轴承的位移刚度和相位随频率变化很大，在高频状态下表现出极不稳定的特性，而SMCs轴承位移刚度更加稳定，拥有更加优良的动态特性；对比相同材料制备的轴承，考虑交叉耦合效应时，SMCs轴承电流刚度在10 kHz时降低20%，相位最大变化率约为48%；相比由SMCs制备3-DOF PMB[4]，该结构将径向磁轴承放置于永磁偏置磁轴承内部构成整体，在10 kHz前轴向动态位移刚度较本结构降低了17%. 因此，综合电流及位移刚度发现，交叉耦合效应影响电流及位移刚度的模型精度，且在高频时影响更加显著，不可忽略.
图13为径向动态刚度频率响应，由于混合磁轴承径向为叠片结构. 从图13中可以看出：激励频率在0~1 kHz范围内，径向动态电流刚度和相位、径向动态位移刚度和相位均由小幅下降. 因此，径向采用能够减小涡流损耗的叠片结构，能够使电流刚度和位移刚度在0~1 kHz范围内保持相对稳定，具有良好的动态特性.
4. ARHMB系统控制
传统PID控制因其原理简洁、运行方便、稳定可靠以及没有静态误差等许多优点而被广泛应用，其传递函数Gc（s）为
Gc(s)=kp(1+1TIs+TDs), (18) 式中：
$ {k}_{\mathrm{p}} $ 为比例系数；$ {T}_{\mathrm{I}} $ 为积分时间常数；$ {T}_{\mathrm{D}} $ 为积分时间常数；s为频域相关量.但当外界存在干扰时，传统PID控制的微分调节器容易受到影响. 因此为了系统可以正常工作，本文在PID算法的基础上添加用来抵抗干扰的一阶惯性环节
$ {G}_{\mathrm{d}}=1/\left[1 + {T}_{\mathrm{d}}s\right] $ ，从而得到如图14所示不完全微分形式的PID控制[13-14]. 其中：Td为滞后时间常数；E（s）为偏差输入；U（s）为控制器输出.对于多自由度系统，为了简化控制策略，通常的处理方式是对每个自由度进行分散独立的控制[15-16]. 由于ARHMB轴径向控制磁通相互影响，不完全微分PID控制参数考虑涡流、漏磁及交叉耦合效应，采用独立控制方法也可实现轴径向的控制磁通相互独立. 本文以轴向为例，采用不完全微分PID控制对ARHMB的推力磁轴承进行了研究.
系统传递函数可表示为
G（s）=kims2−kz, (19) 式中：m为转子系统质量；ki、kz分别为力-电流刚度与力-位移刚度.
对于ARHMB系统，假设转子系统质量为1 kg，电流刚度取301.8 N/A，位移刚度取−33070 N/m，选择微分时间常数
$ {T}_{{\rm{d}}}=0.000\;1 $ ，并对系统进行控制仿真，系统的阶跃响应如图15所示. 从图中可以看出：系统超调量约为26%，系统响应速度快，达到峰值所用时间约为0.000 4 s，达到稳定所需时间短，稳态误差近似为0，能够对ARHMB实现有效控制，提升系统的控制性能.图16为ARHMB控制系统误差变化曲线. 从图16中可以看出：随着系统开始工作，转子位移发生变化，系统的误差随之增加；随着控制器发挥作用，误差快速减小直至到稳态误差近似为零，达到系统稳定时间很短. 因此采用不完全微分PID控制能够有效地对ARHMB实现准确控制，具有优良的控制效果.
图 16 不完全微分形式的PID控制误差变化曲线Figure 16. Error curve of PID control in incomplete differential form5. 结 论
本文采用有限元与解析法对ARHMB的动态特性进行了分析，并在此基础上使用不完全微分PID控制对ARHMB进行仿真控制. 具体结论如下：
1） 建立了考虑涡流、漏磁及交叉耦合效应的动态特性模型，对比分析了材料类型及交叉耦合效应对混合磁轴承的影响，结果表明由SMCs制备的推力轴承涡流损耗低，高频动态特性优良，可以代替碳钢材料用于制备ARHMB的轴向部分.
2） 交叉耦合效应对SMCs制备的电磁轴承动态特性影响较大并在高频时影响更加显著，不可忽略，但对碳钢材料制备的电磁轴承影响较小.
3） 采用计及涡流、漏磁及交叉耦合效应的不完全微分PID控制对轴承系统进行了仿真控制. 结果表明，采用不完全微分PID控制可对轴承系统实现有效控制.
-
图 2 重载货车各刚体部件在曲线轨道上的位置关系
Figure 2. Position relationships of the freight car rigid bodies on a curved track
图 3 车辆系统悬挂点刚体间的超高差
Figure 3. Superelevation height differences between the rigid bodies of vehicle system suspension points
图 4 车辆系统悬挂点刚体间的侧滚角差
Figure 4. Rolling angle differences between the rigid bodies of vehicle system suspension points
图 5 车辆系统悬挂点刚体间的顺坡角差
Figure 5. Slope angle differences between the rigid bodies of vehicle system suspension points
图 6 车辆系统悬挂点刚体间的中心角差
Figure 6. Yawing angle differences between the rigid bodies of vehicle system suspension points
-
[1] 王福天. 车辆系统动力学[M]. 北京: 中国铁道出版社, 1994: 144-149. [2] 姚建伟. 机车车辆动力学[M]. 北京: 科学出版社, 2014: 251-257. [3] 刘学毅, 王平. 车辆-轨道-路基系统动力学[M]. 成都: 西南交通大学出版社, 2010: 51-55. [4] 翟婉明. 车辆-轨道耦合动力学（上册） [M]. 4版. 北京: 科学出版社, 2015: 57-64. [5] 王开云,翟婉明. 直线与曲线轨道上车辆悬挂相对位移的计算[J]. 西南交通大学学报,2003,38(2): 122-126. doi: 10.3969/j.issn.0258-2724.2003.02.002WANG Kaiyun, ZHAI Wanming. Calculation of displacements of vehicle suspension on tangent and curved tracks[J]. Journal of Southwest Jiaotong University, 2003, 38(2): 122-126. doi: 10.3969/j.issn.0258-2724.2003.02.002 [6] 刘鹏飞,翟婉明,王开云,等. 机车车辆通过缓和曲线时悬挂系统及轮重的动态特性[J]. 中国铁道科学,2013,34(1): 67-74. doi: 10.3969/j.issn.1001-4632.2013.01.10LIU Pengfei, ZHAI Wanming, WANG Kaiyun, et al. The dynamic characteristics of suspension system and wheel load for rolling stock passing through transition curve[J]. China Railway Science, 2013, 34(1): 67-74. doi: 10.3969/j.issn.1001-4632.2013.01.10 [7] 李亨利,李芾,潘树平,等. 新型货车径向转向架低动力性能与连接可靠性[J]. 交通运输工程学报,2013,13(5): 39-46. doi: 10.3969/j.issn.1671-1637.2013.05.006LI Hengli, LI Fu, PAN Shuping, et al. Low track force dynamic performance and connection reliability of new type radial bogie for freight car[J]. Journal of Traffic and Transportation Engineering, 2013, 13(5): 39-46. doi: 10.3969/j.issn.1671-1637.2013.05.006 [8] 张建全,黄运华,李芾. 缓和曲线线型对铁道车辆动力学性能的影响[J]. 交通运输工程学报,2010,10(4): 39-44. doi: 10.3969/j.issn.1671-1637.2010.04.007ZHANG Jianquan, HUANG Yunhua, LI Fu. Influence of transition curves on dynamics performance of railway vehicle[J]. Journal of Traffic and Transportation Engineering, 2010, 10(4): 39-44. doi: 10.3969/j.issn.1671-1637.2010.04.007 [9] 高亮,王璞,蔡小培,等. 基于多车精细建模的曲线地段重载列车-轨道系统动力性能研究[J]. 振动与冲击,2014,33(22): 1-6,12.GAO Liang, WANG Pu, CAI Xiaopei, et al. Dynamic characteristics of train-track system in curved track sections based on elaborate multi-vehicle model[J]. Journal of Vibration and Shock, 2014, 33(22): 1-6,12. [10] TSUJIE M, MIURA M, CHEN H, et al. A study on the initiation of head check of the low rail using multibody dynamics[J]. Wear, 2019, 436/437: 202989.1-202989.10. doi: 10.1016/j.wear.2019.202989 [11] WU L, YAO X S, VANDERMAREL J, et al. Effects of curve radius and rail profile on energy saving in heavy haul achieved by application of top of rail friction modifier[J]. Wear, 2016, 366/367: 279-286. doi: 10.1016/j.wear.2016.07.003 [12] ZHAI W M, GAO J M, LIU P F, et al. Reducing rail side wear on heavy-haul railway curves based on wheel-rail dynamic interaction[J]. Vehicle System Dynamics, 2014, 52(S1): 440-454. [13] ZBOIŃSKI K, WOŹNICA P. Optimisation of the railway transition curves' shape with use of vehicle-track dynamical model[J]. Archives of Transport, 2010, 22(3): 387-406. [14] ZBOINSKI K, GOLOFIT-STAWINSKA M. Investigation into nonlinear phenomena for various railway vehicles in transition curves at velocities close to critical one[J]. Nonlinear Dynamics, 2019, 98(3): 1555-1601. doi: 10.1007/s11071-019-05041-2 [15] 邵文东,李立东,周国东,等. 我国铁路重载货车转向架技术及发展[J]. 铁道车辆,2012,50(12): 15-18. doi: 10.3969/j.issn.1002-7602.2012.12.005SHAO Wendong, LI Lidong, ZHOU Guodong, et al. Technologies and development of railway heavy haul freight car bogies in our country[J]. Rolling Stock, 2012, 50(12): 15-18. doi: 10.3969/j.issn.1002-7602.2012.12.005 [16] 刘宏友,邵文东,王宝磊,等. 货车转向架60年的回顾与展望[J]. 铁道车辆,2013,51(12): 42-48. doi: 10.3969/j.issn.1002-7602.2013.12.006LIU Hongyou, SHAO Wendong, WANG Baolei, et al. Review and prospects of the freight car bogies in the recent 60 years[J]. Rolling Stock, 2013, 51(12): 42-48. doi: 10.3969/j.issn.1002-7602.2013.12.006 [17] 段仕会,徐世锋,李立东,等. DZ1型转向架的研制[J]. 铁道车辆,2016,54(6): 31-34. doi: 10.3969/j.issn.1002-7602.2016.06.010DUAN Shihui, XU Shifeng, LI Lidong et al. Development of DZ1 bogies[J]. Rolling Stock, 2016, 54(6): 31-34. doi: 10.3969/j.issn.1002-7602.2016.06.010 [18] 张志彬,刘爽,李华,等. C80E(H、F)型通用敞车研制[J]. 铁道车辆,2018,56(6): 22-24. doi: 10.3969/j.issn.1002-7602.2018.06.009ZHANG Zhibin, LIU Shuang, LI Hua, et al. Development of C80E(H, F) general purpose gondola cars[J]. Rolling Stock, 2018, 56(6): 22-24. doi: 10.3969/j.issn.1002-7602.2018.06.009 [19] 杨春雷. 重载货车轴重与速度匹配关系研究[D]. 成都: 西南交通大学, 2013: 30-45. -
下载:
下载:
点击查看大图
计量
- 文章访问数: 378
- HTML全文浏览量: 218
- PDF下载量: 33
- 被引次数: 0