Motion Characteristics Analysis of DC Arc on Arcing Horn
-
摘要:
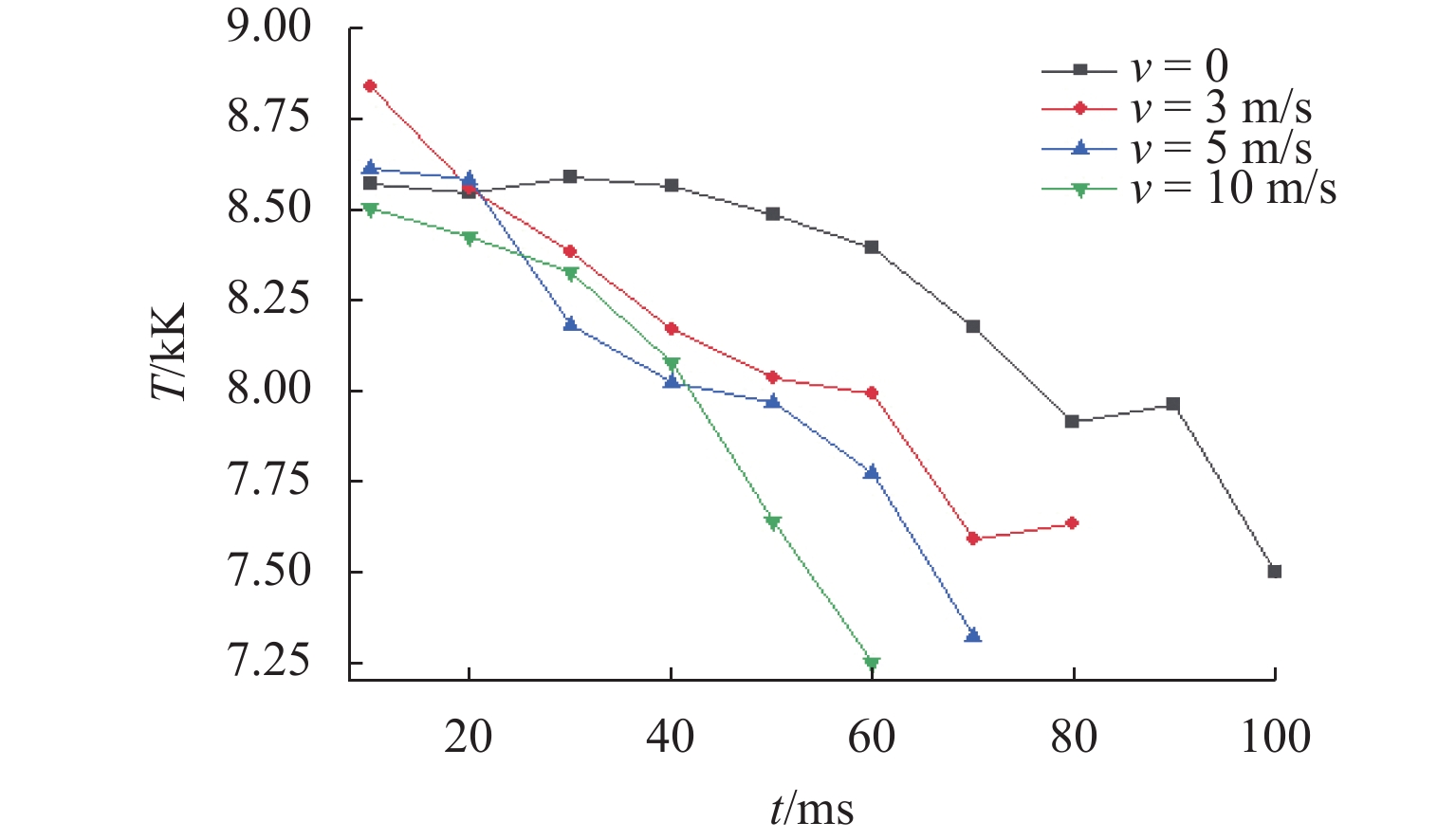
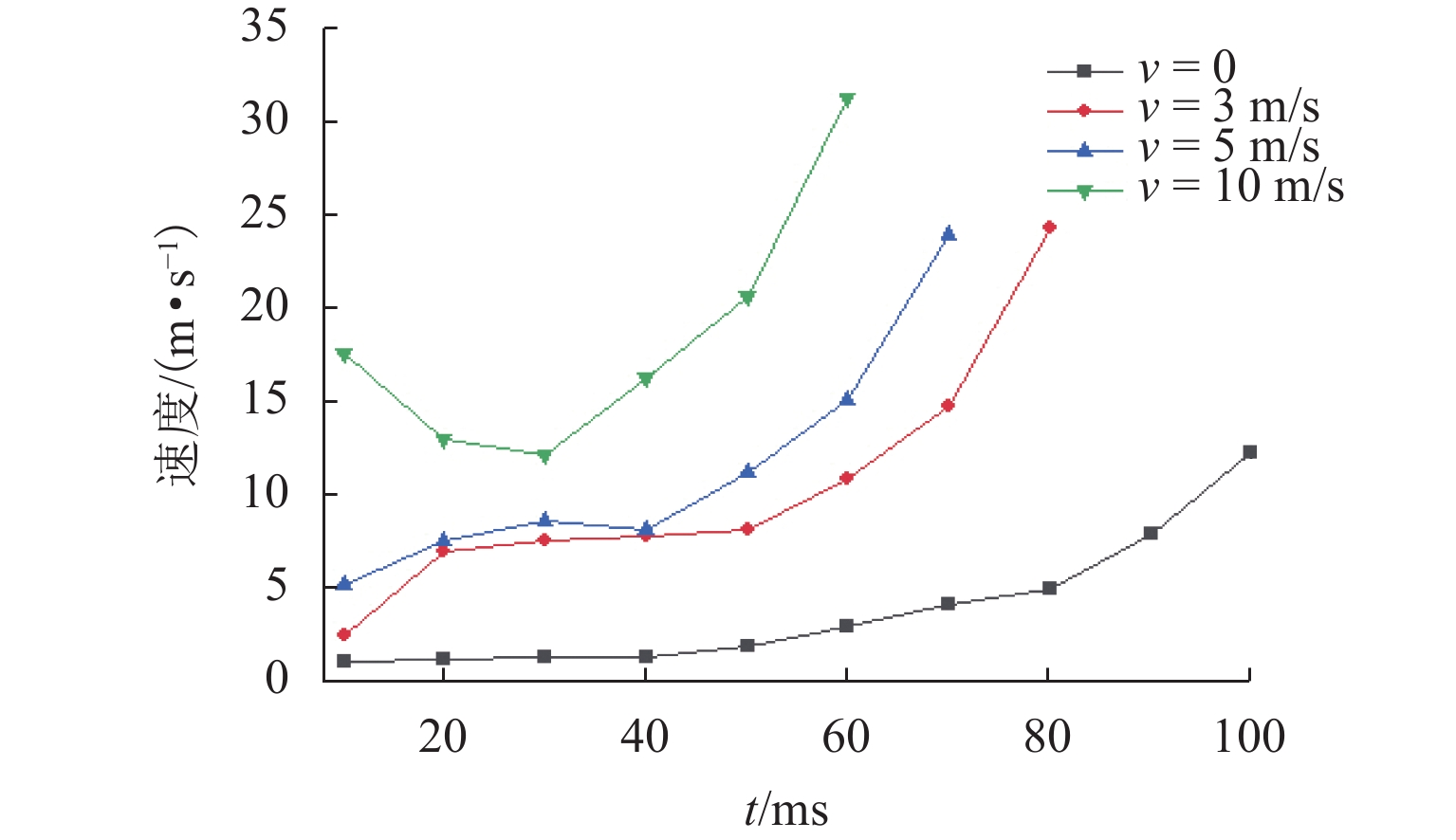
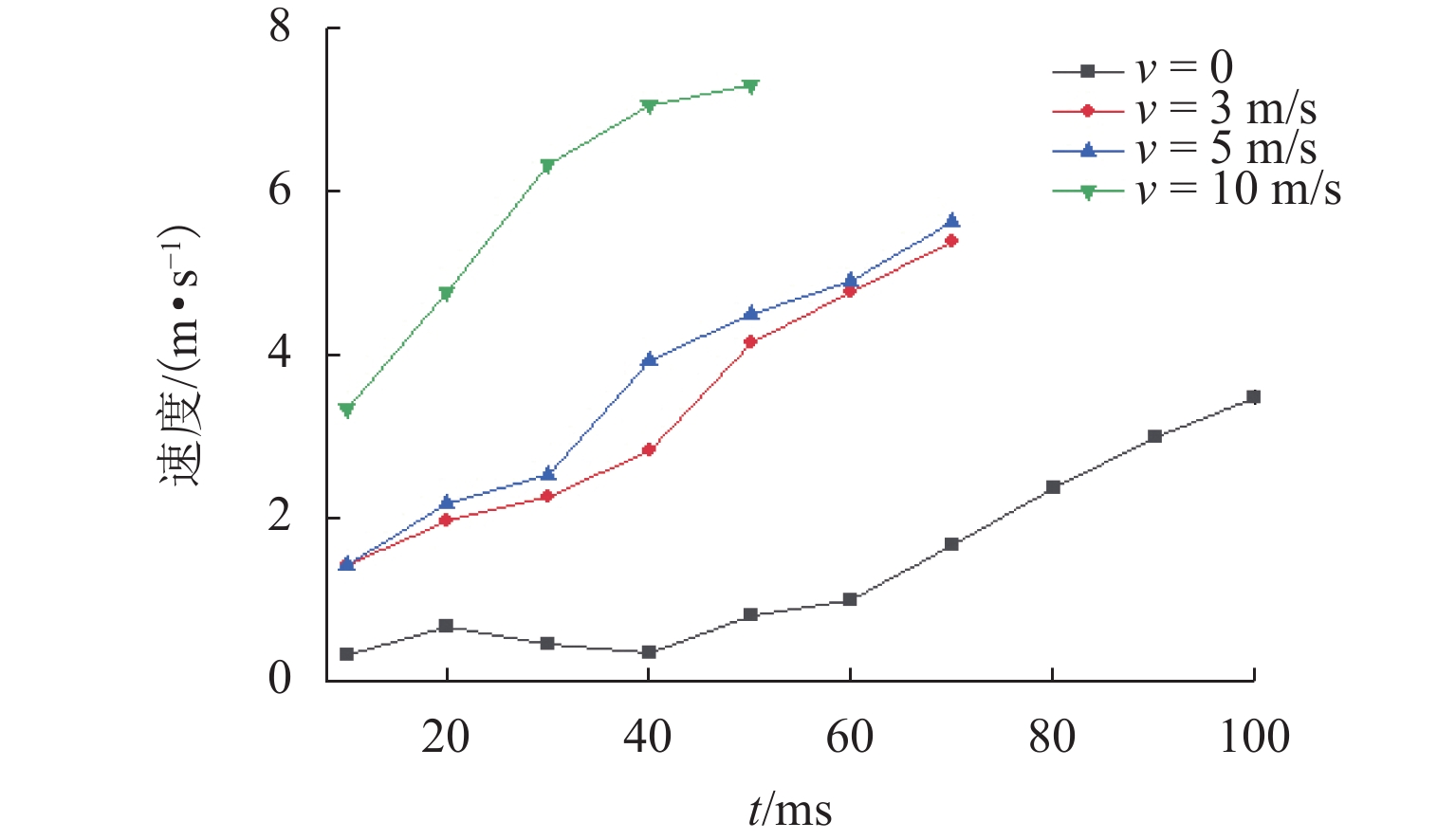
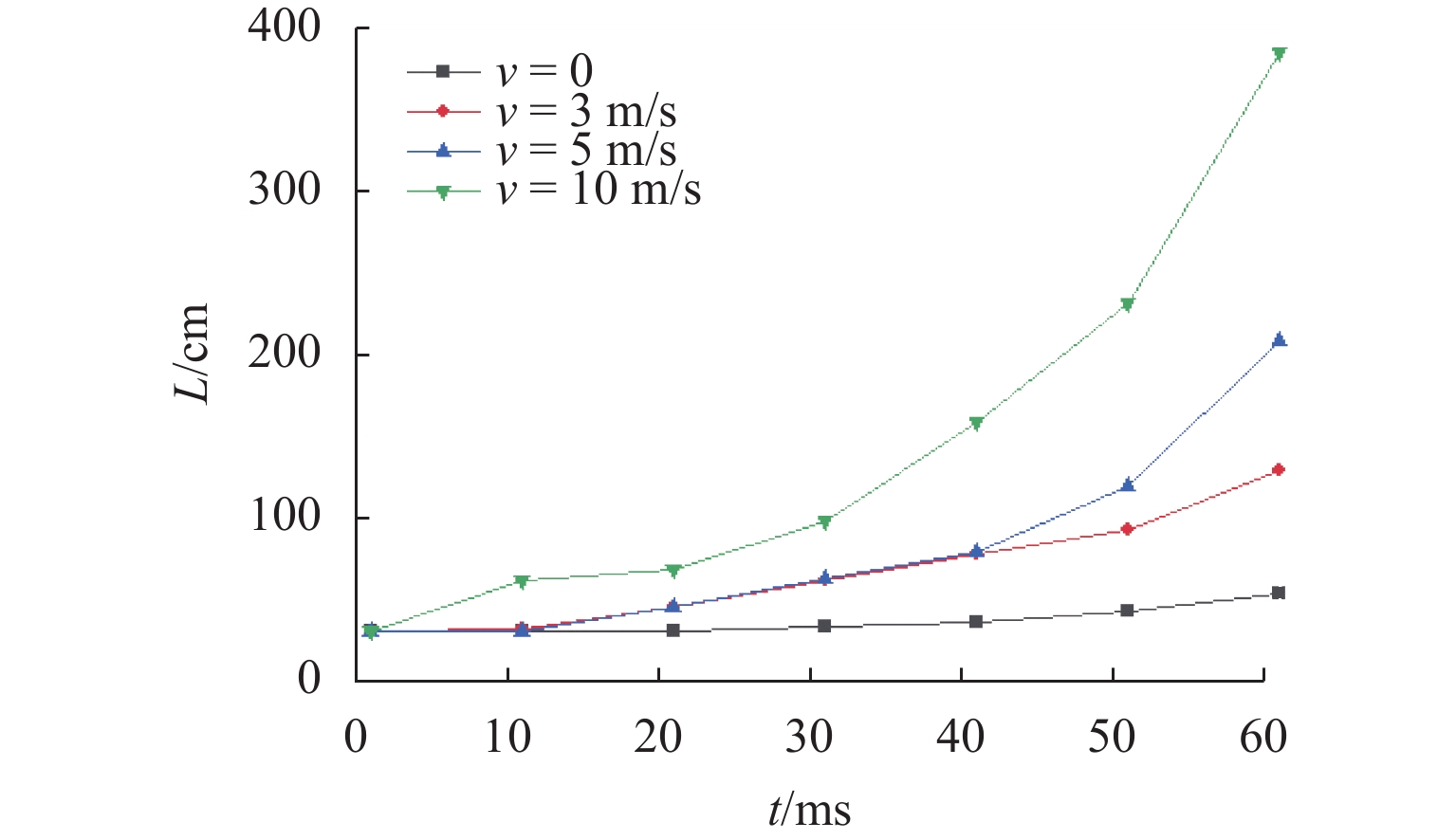
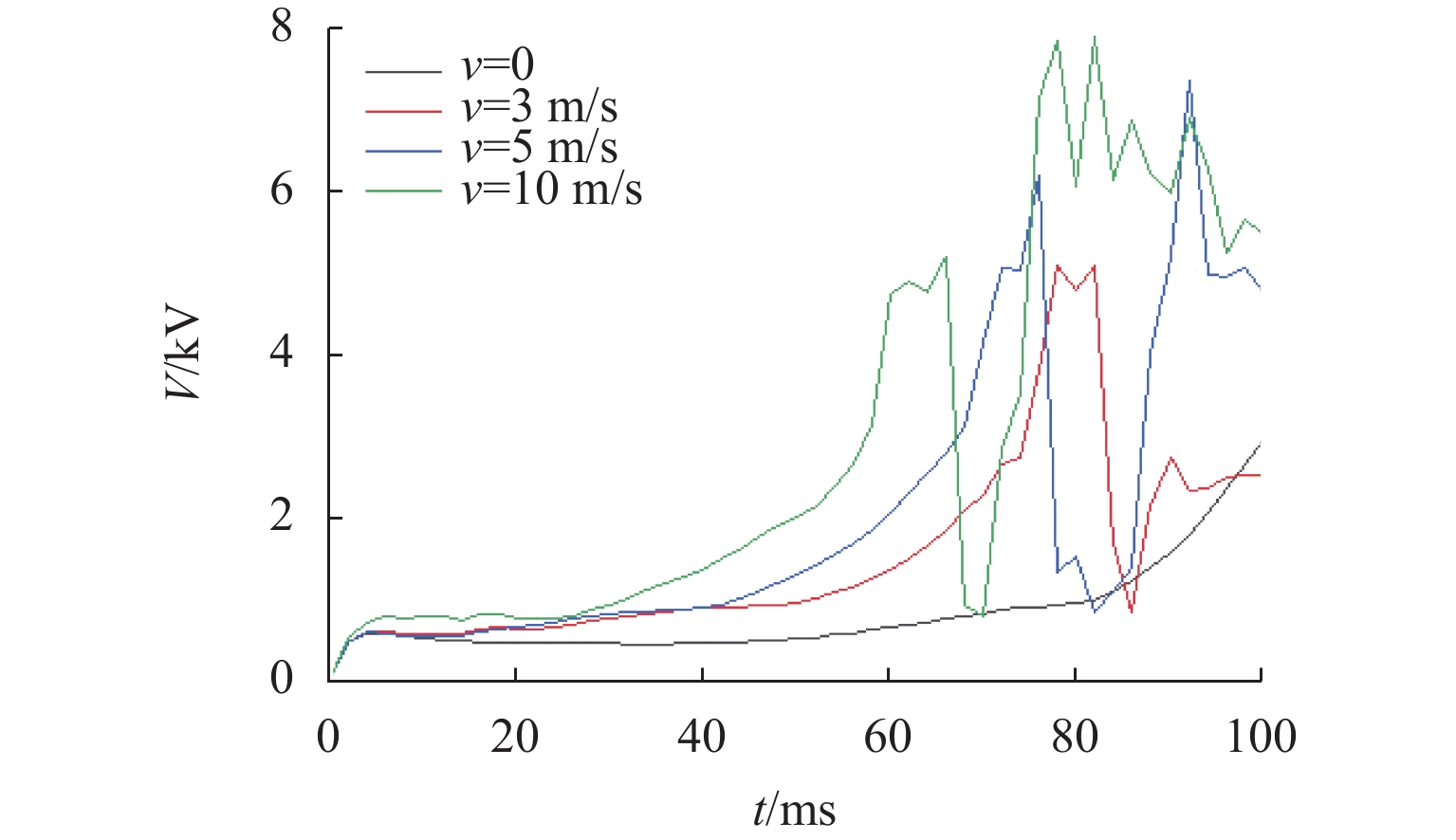
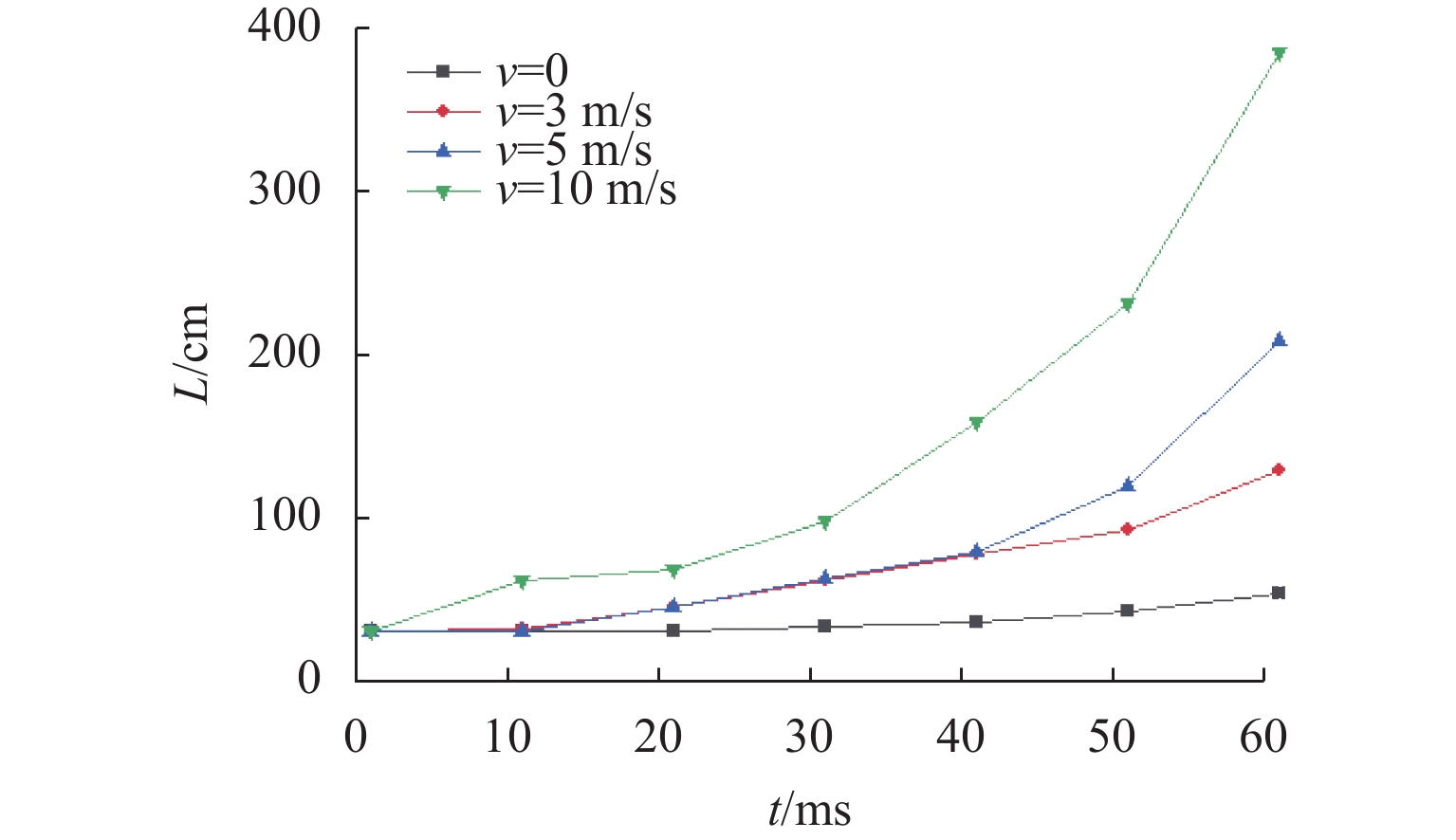
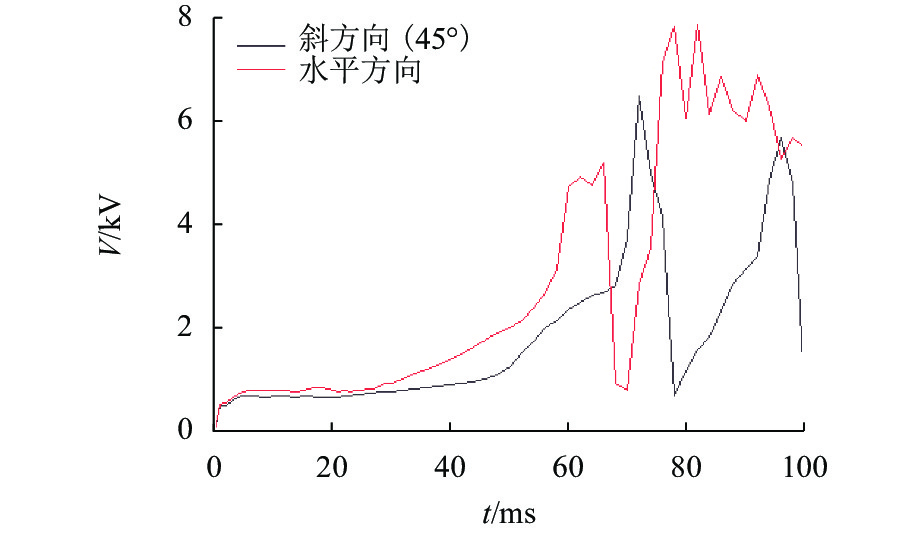
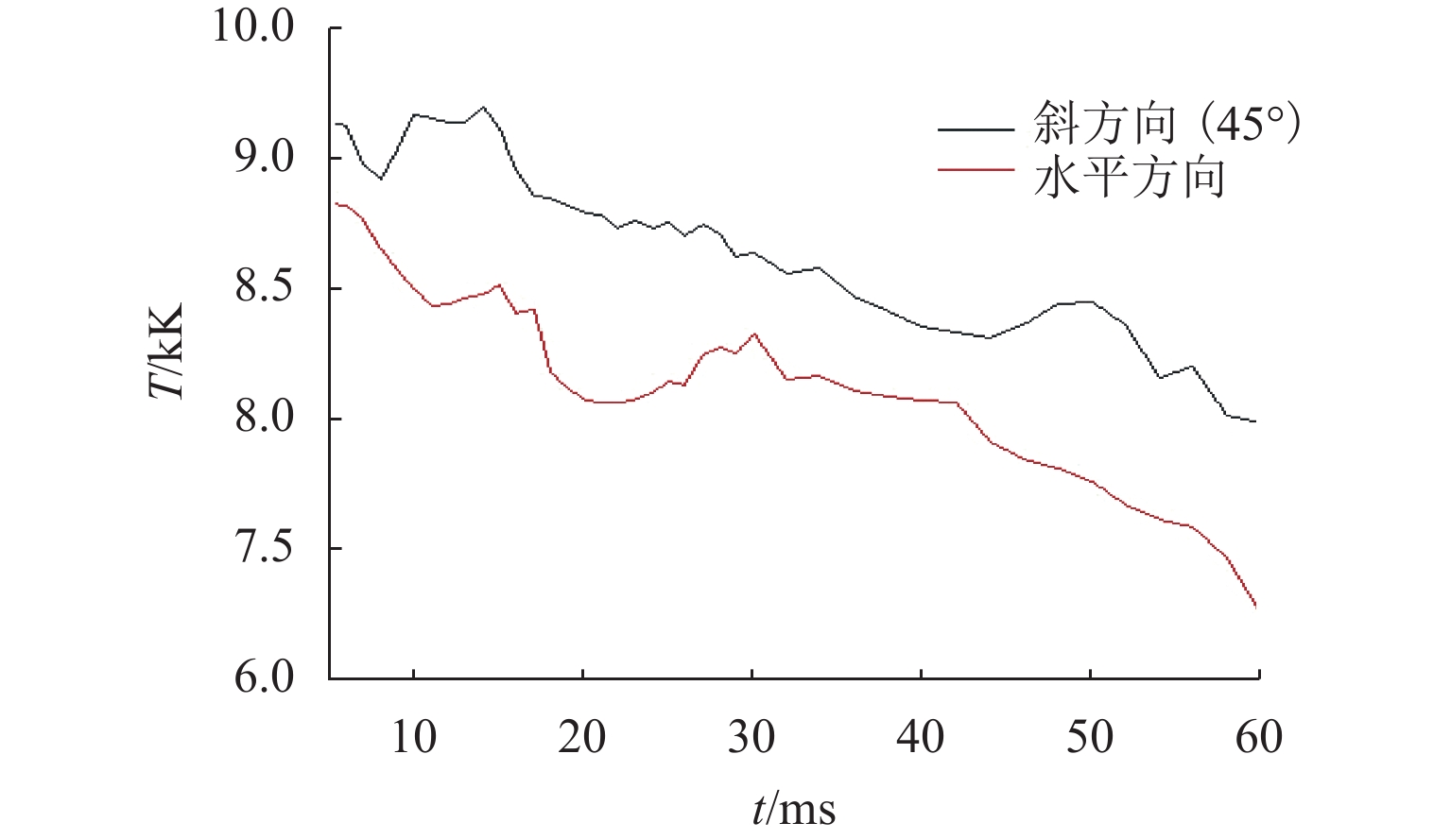
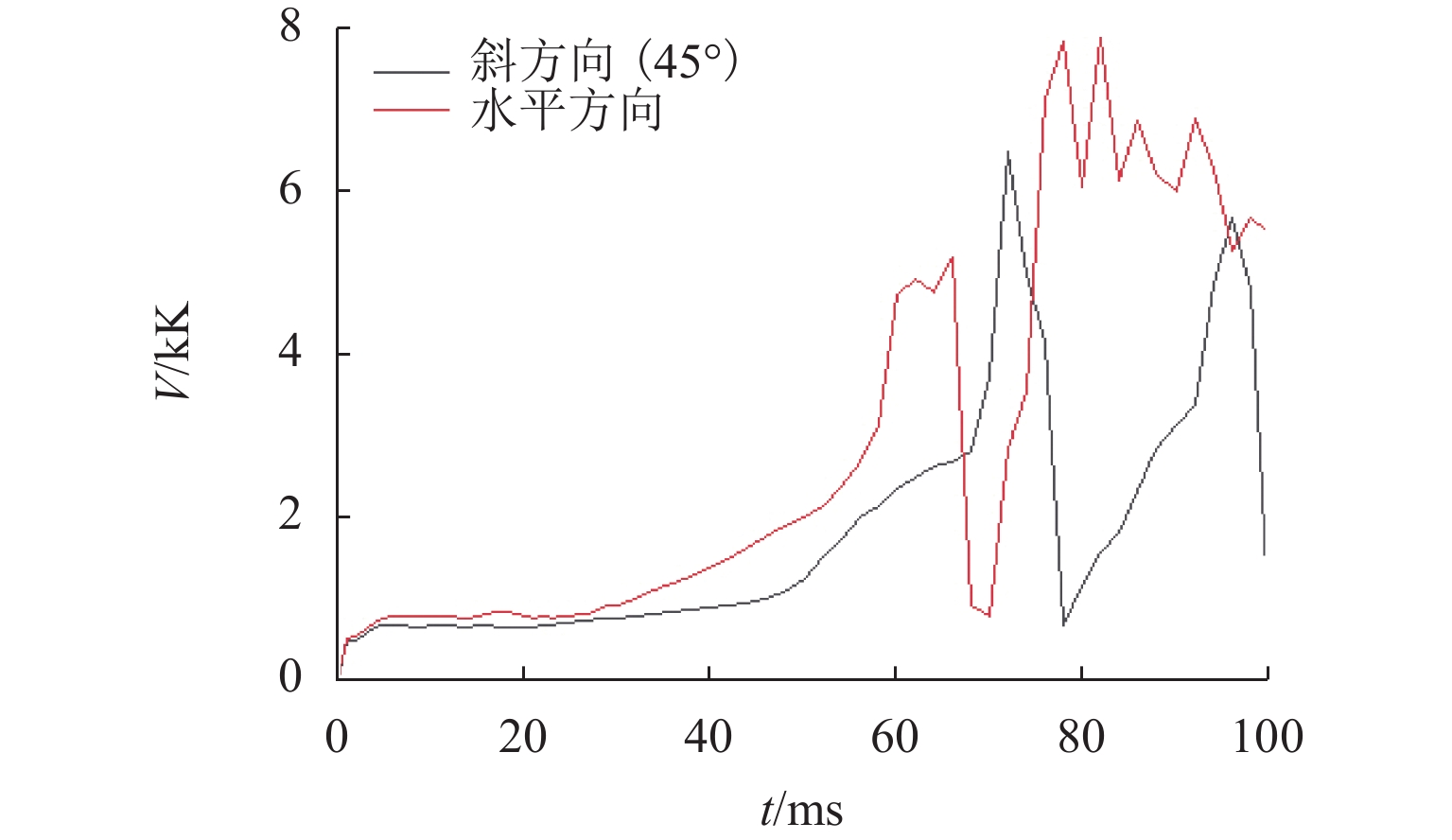
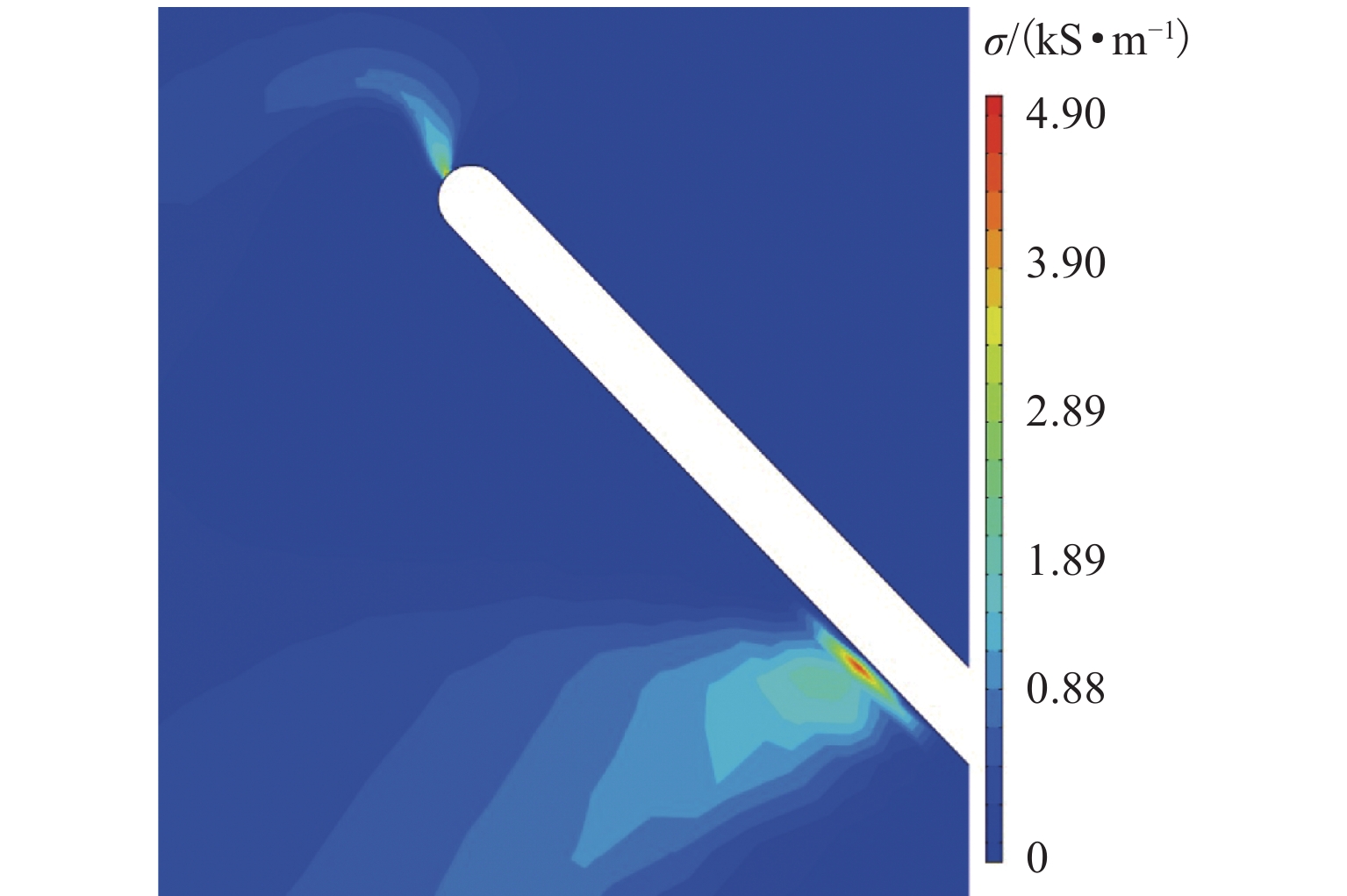
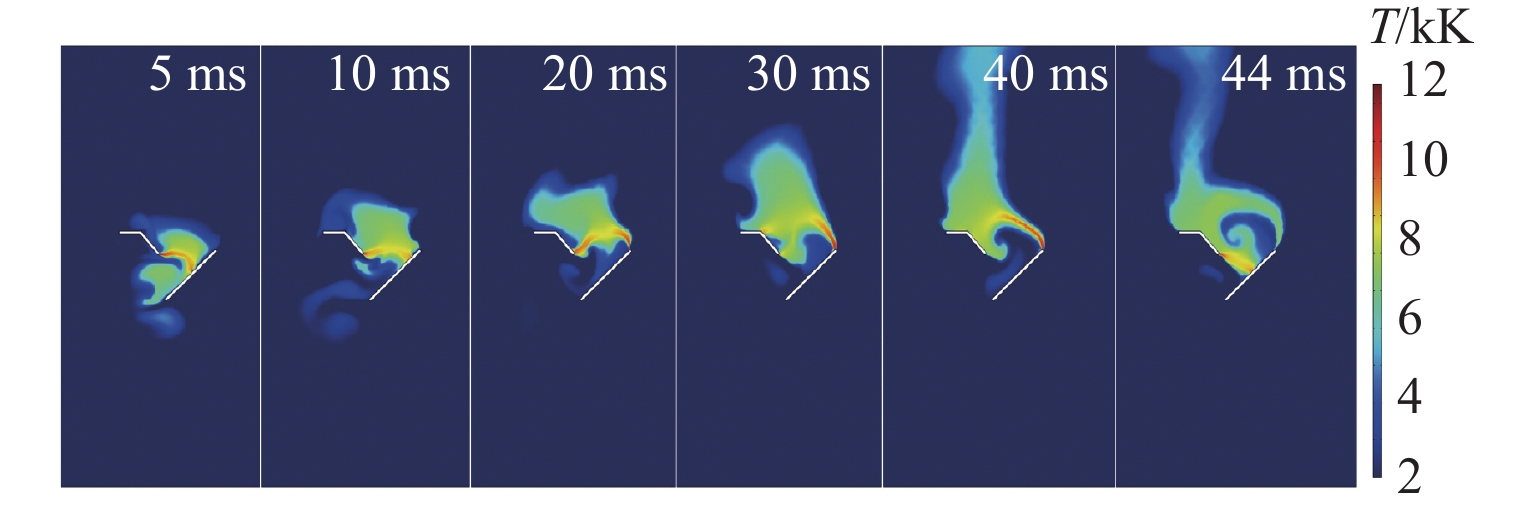
接地极线路是直流输电系统的重要组成部分，是直流系统不平衡电流和大地回流的入地通道. 接地极线路遭遇雷击时，入地电流会在招弧角间隙形成稳定电弧，由于直流电流不存在周期性过零点，直流电弧很难熄灭，进而破坏线路绝缘，严重威胁直流输电系统安全. 针对接地极线路招弧角处于野外开放空间、电弧运动受多场耦合影响的特点，建立了招弧角电弧磁流体动力学二维仿真模型，研究气流速度、方向以及招弧角结构对直流电弧运动特性的影响. 研究表明：招弧角电极电弧主要受电磁力作用沿电极扩张方向运动，通过吹弧和拉伸，降低电弧温度，提高电弧电压，使电弧更利于熄灭；气流环境对电弧动态特性产生较大影响，同方向风速有利于电弧的吹离和疏导；同等风速下，水平方向气流吹弧效果更显著；电极样式对电弧的拉伸有重要影响，同等间隙距离下，双羊角电极对电弧的拉伸作用比单羊角电极更强；在入地电流持续注入的情况下，电弧易重燃，且难以彻底熄灭.
Abstract:Grounding electrode line is an important part of the DC power transmission system, and it is a channel for the unbalanced current and the grounding current in the DC system. When the grounding electrode line is attacked by lightning, the grounding current will form a stable arc in the gap. Since the DC current has no periodic zero crossing point, the DC arc is difficult to extinguish, which damages the line insulation and seriously threatens the safety of the entire system. As the arcing horn of the grounding electrode line is in an open space, and the arc motion is affected by multi-field coupling, a two-dimensional simulation model of the arc horn based on magnetohydrodynamics is built to study the effects of the airflow velocity, direction and the structure of arcing horn on the DC arc motion. The results show that the arc is mainly driven by electromagnetic force and moves along the electrode. Through the arc blowing and stretching, the temperature is reduced, and the voltage is increased, which are beneficial to extinguishing arc. The airflow has a greater influence on the dynamic characteristics of the arc, and the wind speed in the same direction is beneficial to the blowing and dredging of the arc. At the same wind speed, the normal airflow plays a major role in the arc blowing. Electrode types have an important effect on the stretching of the arc. With the same gap distance, the double-horn electrode has a more significant stretching effect on the arc than the single-horn electrode. When the DC ground current is continuously injected, the arc is easy to reignite and difficult to extinguish completely.
-
Key words:
- grounding electrode line /
- arcing horn /
- DC arc /
- magneto hydro dynamics /
- motion characteristics
-
图 3 电弧电压与电极初始位置温度随时间变化情况
Figure 3. Arc voltage and temperature at electrode initial position changing over time
图 4 无风情况下不同时刻弧柱温度分布
Figure 4. Temperature field distribution of arc column without wind at different time points
图 5 不同风速下电弧温度分布（t=60 ms）
Figure 5. Temperature field distribution of arc under different wind speeds （t=60 ms）
图 6 不同风速下弧柱温度分布（t=60 ms）
Figure 6. Temperature field distribution of arc column under different wind speeds （t=60 ms）
图 7 不同风速下弧柱温度随时间变化趋势
Figure 7. Variation trend of arc column temperature with time under different wind speeds
图 12 45° 斜方向气流下电弧温度分布
Figure 12. Temperature field distribution of arc under oblique airflow of 45°
图 13 斜方向和水平方向风速下 弧柱温度对比（v=10 m/s）
Figure 13. Comparison of arc column temperature under oblique and horizontal directions of wind speed (v=10 m/s)
图 14 斜方向和水平方向风速下 电弧电压对比（v=10 m/s）
Figure 14. Comparison of arc voltage under oblique and horizontal directions of wind speed (v=10 m/s)
图 16 单羊角型电极电弧温度分布
Figure 16. Temperature field distribution of single-horn electrode arc
图 17 不同电极样式下弧柱温度对比
Figure 17. Comparison of arc column temperature under different electrode styles
图 18 不同电极样式下电弧电压对比
Figure 18. Comparison of arc voltage under different electrode styles
表 1 仿真模型几何尺寸
Table 1. Dimensions of simulation model
边界 类别 尺寸/cm AB、DE 电极 25 BC、EF 电极 40 GH、IJ 开放边界 250 GJ、HI 开放边界 250 BE 空气间隙 30 
下载: 导出CSV
表 2 电弧长度变化
Table 2. Arc lengths at different time points
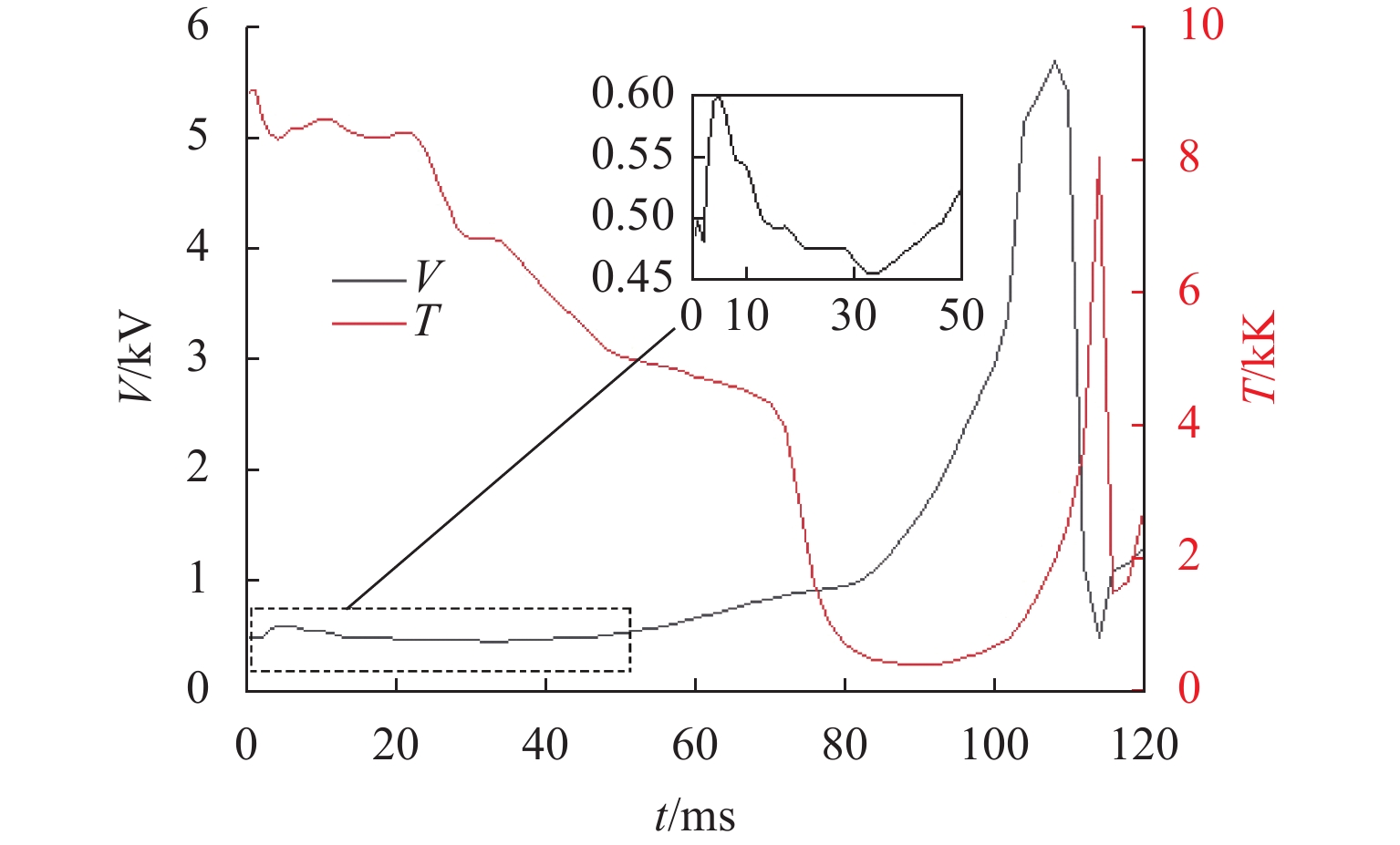
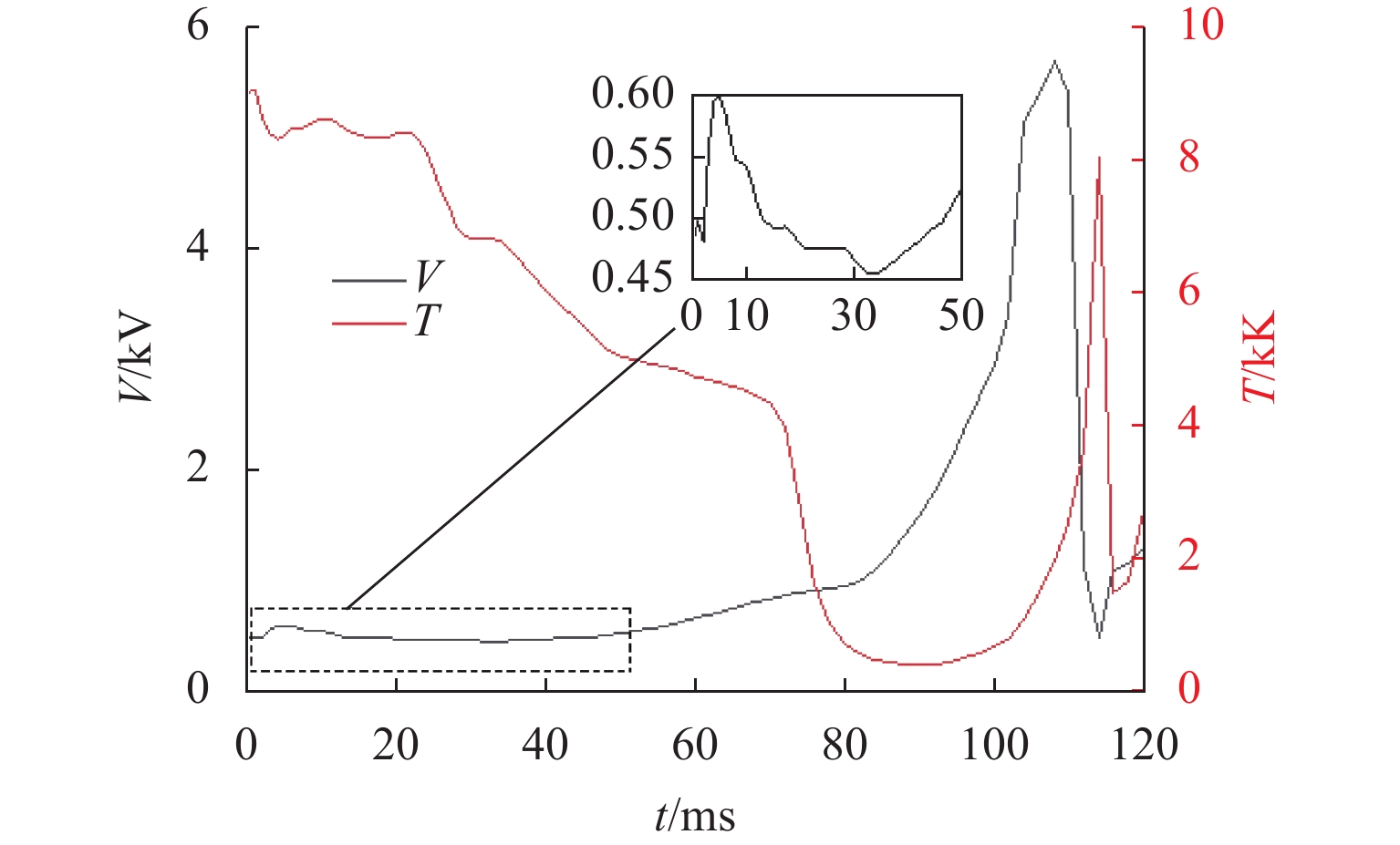
t/ms 电弧电压/
V电弧长度/
cm电位梯度/
（V·mm−1）20 478 30.9 1.5 40 476 36.3 1.3 60 671 53.9 1.2 80 956 89.0 1.1 100 2957 263.2 1.1 110 5409 505.9 1.1
下载: 导出CSV
-
[1] 刘振亚. 特高压交直流电网[M]. 北京: 中国电力出版社, 2013: 136-139. [2] 杨刚,李恒超,谭蓓,等. 层次极限学习机用于高光谱图像预测绝缘子污秽度[J]. 西南交通大学学报,2020,55(3): 579-587. doi: 10.3969/j.issn.0258-2724.20190093YANG Gang, LI Hengchao, TAN Bei, et al. Application of hierarchical extreme learning machine in prediction of insulator pollution degree using hyperspectral images[J]. Journal of Southwest Jiaotong University, 2020, 55(3): 579-587. doi: 10.3969/j.issn.0258-2724.20190093 [3] 刘守豹,皇甫成,余世峰,等. 特高压直流接地极线路过电压研究[J]. 高电压技术,2018,44(7): 2410-2417.LIU Shoubao, HUANGFU Cheng, YU Shifeng, et al. Study on overvoltage of UHV DC grounding line[J]. High Voltage Engineering, 2018, 44(7): 2410-2417. [4] 郑扬亮,冉学彬,刘更生. 直流输电接地极线路招弧角有关问题的分析[J]. 高电压技术,2008,34(7): 1513-1516.ZHENG Yangliang, RAN Xuebin, LIU Gengsheng. Research on arcing horns of HVDC electrode lines[J]. High Voltage Engineering, 2008, 34(7): 1513-1516. [5] 孙秋芹,周志成,刘洋,等. 特高压输电线路潜供电弧的燃弧特性[J]. 高电压技术,2014,40(12): 3895-3901.SUN Qiuqin, ZHOU Zhicheng, LIU Yang, et al. Arcing characteristics of secondary arc of UHV transmission lines[J]. High Voltage Engineering, 2014, 40(12): 3895-3901. [6] 廖一帆,胡传良,唐军,等. 污秽绝缘子安装并联间隙的雷电击穿特性分析[J]. 西南交通大学学报,2018,53(6): 1117-1122. doi: 10.3969/j.issn.0258-2724.2018.06.004LIAO Yifan, HU Chuanliang, TANG Jun, et al. Analysis of lightning breakdown characteristics of contaminated insulators in parallel clearance[J]. Journal of Southwest Jiaotong University, 2018, 53(6): 1117-1122. doi: 10.3969/j.issn.0258-2724.2018.06.004 [7] 陈维江,孙昭英,李国富,等. 110 kV和220 kV架空线路并联间隙防雷保护研究[J]. 电网技术,2006,30(13): 70-75. doi: 10.3321/j.issn:1000-3673.2006.13.013CHEN Weijiang, SUN Zhaoying, LI Guofu, et al. Development of parallel gap lightning protection device for 110 kV and 220 kV overhead lines[J]. Power System Technology, 2006, 30(13): 70-75. doi: 10.3321/j.issn:1000-3673.2006.13.013 [8] 雷潇,曾宏,刘小江,等. 特高压直流接地极线路雷击闪络风险研究[J]. 电瓷避雷器,2017(2): 59-63.LEI Xiao, ZENG Hong, LIU Xiaojiang, et al. Research on the lightning flashover risk of UHVDC electrode lines[J]. Insulators and Surge Arresters, 2017(2): 59-63. [9] 司马文霞,张智,杨庆,等. 110 kV复合绝缘子棒形并联间隙工频电弧疏导过程的试验研究[J]. 中国电机工程学报,2012,32(31): 114-121,226.SIMA Wenxia, ZHANG Zhi, YANG Qing, et al. Experimental research on power frequency arc movement process of 110 kV composite insulators in rod shape parallel gap lightning protection devices[J]. Proceedings of the CSEE, 2012, 32(31): 114-121,226. [10] 司马文霞,谭威,杨庆,等. 基于热浮力–磁场力结合的并联间隙电弧运动模型[J]. 中国电机工程学报,2011,31(19): 138-145.SIMA Wenxia, TAN Wei, YANG Qing, et al. Long AC arc movement model for parallel gap lightning protection device with consideration of thermal buoyancy and magnetic force[J]. Proceedings of the CSEE, 2011, 31(19): 138-145. [11] 谷山强,何金良,陈维江,等. 架空输电线路并联间隙防雷装置电弧磁场力计算研究[J]. 中国电机工程学报,2006,26(7): 140-145. doi: 10.3321/j.issn:0258-8013.2006.07.026GU Shanqiang, HE Jinliang, CHEN Weijiang, et al. Magnetic force computation for the electric arc of parallel gap lightning protection device on overhead transmission lines[J]. Proceedings of the CSEE, 2006, 26(7): 140-145. doi: 10.3321/j.issn:0258-8013.2006.07.026 [12] GODA Y, IWATA M, IKEDA K, et al. Arc voltage characteristics of high current fault arcs in long gaps[J]. IEEE Transactions on Power Delivery, 2000, 15(2): 791-795. doi: 10.1109/61.853021 [13] TERZIJA V, PRESTON G, POPOV M, et al. New static “AirArc” EMTP model of long arc in free air[J]. IEEE Transactions on Power Delivery, 2011, 26(3): 1344-1353. doi: 10.1109/TPWRD.2010.2086082 [14] 陈锡阳,尹创荣,杨挺,等. 110 kV输电线路并联间隙防雷装置的设计与运行[J]. 电力建设,2011,32(6): 57-61.CHEN Xiyang, YIN Chuangrong, YANG Ting, et al. Design and operation on parallel gap lightning protection device of composite insulators for 110 kV overhead transmission line[J]. Electric Power Construction, 2011, 32(6): 57-61. [15] 王巨丰,李世民,闫仁宝,等. 可主动快速熄灭工频续流电弧的灭弧防雷间隙装置设计[J]. 高电压技术,2014,40(1): 40-45.WANG Jufeng, LI Shimin, YAN Renbao, et al. Arc-quenching lightning protection gap for fast extinction of power frequency arcs[J]. High Voltage Engineering, 2014, 40(1): 40-45. [16] 高国强,许潘,魏文赋,等. 带载工况下降弓电弧磁流体建模分析[J]. 高电压技术,2019,45(12): 3916-3923.GAO Guoqiang, XU Pan, WEI Wenfu, et al. Magneto hydrodynamics modeling analysis of arc under lowering pantograph with load condition[J]. High Voltage Engineering, 2019, 45(12): 3916-3923. -
下载:
点击查看大图
计量
- 文章访问数: 485
- HTML全文浏览量: 156
- PDF下载量: 28
- 被引次数: 0