基于边权重图神经网络的一阶逻辑前提选择

刘清华; 徐扬; 吴贯锋; 李瑞杰

doi:10.3969/j.issn.0258-2724.20210134

基于边权重图神经网络的一阶逻辑前提选择

doi: 10.3969/j.issn.0258-2724.20210134

刘清华^{1, 2,},
徐扬^{2, 3, ,},
吴贯锋^{2, 3},
李瑞杰⁴

1.
西南交通大学信息科学与技术学院，四川成都 611756
2.
西南交通大学系统可信性自动验证国家地方联合工程实验室，四川成都 610031
3.
西南交通大学数学学院，四川成都 611756
4.
西南交通大学交通运输与物流学院，四川成都 611756

基金项目: 中央高校基本科研业务费专项资金（2682020CX59，2682021CX057）；教育部人文社会科学研究项目（20XJCZH016，19YJCZH048）；四川省科技计划（2020YJ0270，2020YFH0026）

详细信息

作者简介:
刘清华（1992—），女，博士研究生，研究方向自动推理、智能信息处理，E-mail：qhliu@my.swjtu.edu.cn

通讯作者:
徐扬（1956—），男，教授，博士，研究方向为逻辑代数、不确定性推理和自动推理，E-mail：xuyang@home.swjtu.edu.cn

中图分类号: TP391
计量
- 文章访问数: 421
- HTML全文浏览量: 242
- PDF下载量: 33
- 被引次数: 0
出版历程
- 收稿日期: 2021-02-23
- 修回日期: 2021-07-12
- 网络出版日期: 2022-08-24
- 刊出日期: 2021-11-17

Edge-Weighted-Based Graph Neural Network for First-Order Premise Selection

LIU Qinghua^{1, 2
,},
XU Yang^{2, 3
, ,},
WU Guanfeng^{2, 3},
LI Ruijie⁴

1.
School of Information Science and Technology, Southwest Jiaotong University, Chengdu 611756, China
2.
National-Local Joint Engineering Laboratory of System Credibility Automatic Verification, Southwest Jiaotong University, Chengdu 610031, China
3.
School ofMathematics, Southwest Jiaotong University, Chengdu 611756, China
4.
School of Transportation and Logistics, Southwest Jiaotong University, Chengdu 611756, China

摘要

摘要:
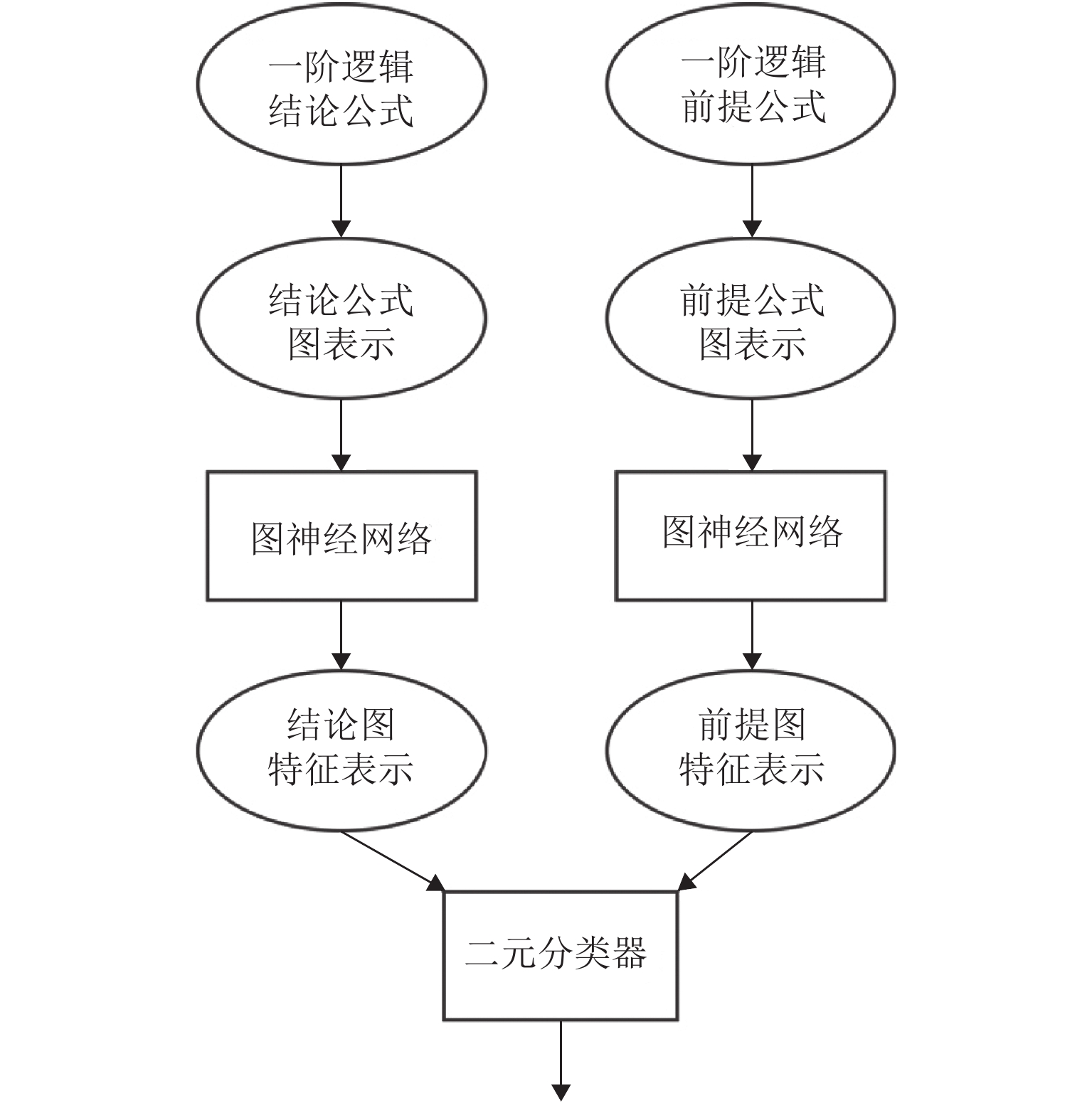
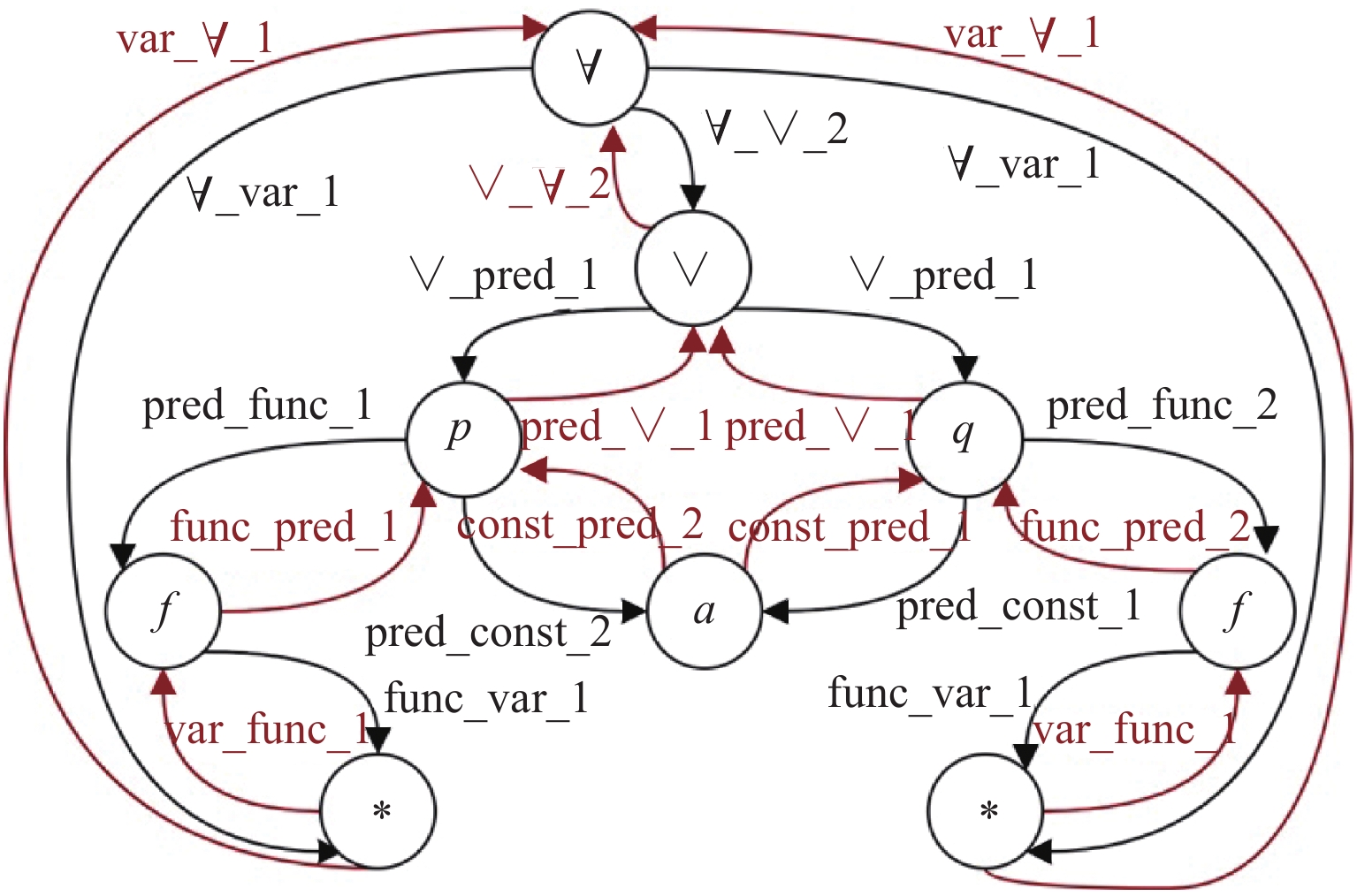
为提高自动定理证明器在大规模问题中证明问题的能力，前提选择任务应运而生. 由于公式图的有向性，主流的图神经网络框架只能单向地对节点进行更新，且无法编码公式图中子节点间的顺序. 针对以上问题，提出了带有边类型的双向公式图表示方法，并提出了一种基于边权重的图神经网络（edge-weight-based graph neural network，EW-GNN）模型用于编码一阶逻辑公式. 该模型首先利用相连节点的信息来更新对应边类型的特征表示，随后利用更新后的边类型特征计算邻接节点对中心节点的权重，最后利用邻接节点的信息双向地对中心节点进行更新. 实验比较分析表明：基于边权重的图神经网络模型在前提选择任务中表现得更加优越，其在相同的测试集上比当前最优模型的分类准确率高了约1%.
- 图神经网络 /
- 双向图 /
- 前提选择 /
- 一阶逻辑公式
Abstract:
In order to improve the ability of automated theorem provers, the premise selection task emerges. Due to the directional nature of formula graphs, most current graph neural networks can only update nodes in one direction, and cannot encode the order of sub-nodes in the formula graph. To address the above problems, a bidirectional graph with edge types to represent logical formulae and a edge-weight-based graph neural network (EW-GNN) model to encode first-order logic formulae are proposed. The model firstly uses the information of connected nodes to update the feature representation of the corresponding edge type, then calculates the weight of the adjacent node to the central node with the updated edge type feature, and finally uses the information of the adjacent node to update the target node in both directions. The experimental results show the edge-weighted-based graph neural network model performs better in the premise selection task, which can improve the classification accuracy by 1% compared to the best model on the same test dataset.
- graph neural network /
- bidirectional graph /
- premise selection /
- first-order logical formula

HTML全文

图 1 一阶逻辑公式的双向图表示

Figure 1. Bidirectional graph representation of first-order logical formula

下载: 全尺寸图片幻灯片

图 2 基于图神经网络的前提选择模型

Figure 2. Premise selection model based ongraph neural network

下载: 全尺寸图片幻灯片

表 1 MPTP2078问题库描述

Table 1. Description of MPTP2078 benchmark 条

名称	公式	结论	最小前提	最大前提	平均前提
数量	4 564	2 078	10	4 563	1 876

下载: 导出CSV

表 2 数据集划分

Table 2. Division of datasets 个

样本	训练集	验证集	测试集
正	27663	3417	3432
负	27556	3485	3471
总样本	55219	6902	6903

下载: 导出CSV

表 3 参数设置

Table 3. Setting of parameters

参数	设置
节点向量维度$ {d}_{{h}_{v}} $	64
边向量维度$ {d}_{{h}_{e}} $	32
迭代次数 K/次	1
学习率	0.0010
学习率衰减系数	0.1
学习率衰减步长	50
轮次/轮	100
权重衰减	0.0001
批量大小/个	8

下载: 导出CSV

表 4 数据集上的对比实验结果

Table 4. Comparision of experimental results on datasets

方法	准确率	精确率	召回率	F₁
GCN^[18]	0.8625	0.8669	0.8547	0.8608
GAT^[19]	0.858 0	0.862 9	0.851 8	0.857 3
GraphSAGE^[27]	0.8615	0.8686	0.8501	0.8592
SGC^[28]	0.8557	0.8579	0.8506	0.8543
Chebyshev^[29]	0.8608	0.8660	0.8518	0.8588
EW-GNN	0.8724	0.8701	0.8686	0.8641

下载: 导出CSV

参考文献(29)

[1]	KERN C, GREENSTREET M R. Formal verification in hardware design: a survey[J]. ACM Transactions on Design Automation of Electronic Systems (TODAES), 1999, 4(2): 123-193. doi: 10.1145/307988.307989
[2]	KLEIN G, ELPHINSTONE K, HEISER G, et al. seL4: Formal verification of an OS kernel[C]//Proceedings of the ACM SIGOPS 22nd Symposium on Operating Systems Principles. Big Sky: ACM, 2009: 207-220.
[3]	LEROY X. Formal verification of a realistic compiler[J]. Communications of the ACM, 2009, 52(7): 107-115. doi: 10.1145/1538788.1538814
[4]	KOVÁCS L, VORONKO A. First-order theorem proving and vampire[C]//25th International Conference on Computer Aided Verification. Saint Petersburg: [s.n.], 2013: 1-35.
[5]	SCHULZ S. E – a brainiac theorem prover[J]. Ai Communications, 2002, 15(2/3): 111-126.
[6]	SUTCLIFFE G. The TPTP problem library and associated infrastructure[J]. Journal of Automated Reasoning, 2017, 59(4): 483-502. doi: 10.1007/s10817-017-9407-7
[7]	KALISZYK C, URBAN J. MizAR 40 for mizar 40[J]. Journal of Automated Reasoning, 2015, 55(3): 245-256. doi: 10.1007/s10817-015-9330-8
[8]	MCCUNE W W. Otter 3.0 reference manual and guide[R]. Chicago: Argonne National Lab., 1994.
[9]	MENG J, PAULSON L C. Lightweight relevance filtering for machine-generated resolution problems[J]. Journal of Applied Logic, 2009, 7(1): 41-57. doi: 10.1016/j.jal.2007.07.004
[10]	HODER K, VORONKOV A. Sine qua non for large theory reasoning[C]//23th International Conference on Automated Deduction. Wroclaw: [s.n.], 2011: 299-314.
[11]	ALAMA J, HESKES T, KÜHLWEIN D, et al. Premise selection for mathematics by corpus analysis and kernel methods[J]. Journal of Automated Reasoning, 2014, 52(2): 191-213. doi: 10.1007/s10817-013-9286-5
[12]	KALISZYK C, URBAN J, VYSKOČIL J. Efficient semantic features for automated reasoning over large theories[C]//Proceedings of the 24th International Conference on Artificial Intelligence. [S.l.]: AAAI Press, 2015: 3084-3090.
[13]	PIOTROWSKI B, URBAN J. ATPboost: learning premise selection in binary setting with ATP feedback[C]//International Joint Conference on Automated Reasoning. Cham: Springer, 2018: 566-574.
[14]	ALEMI A A, CHOLLET F, EEN N, et al. DeepMath-deep sequence models for premise selection[C]// Proceedings of the 30th International Conference on Neural Information Processing Systems. Barcelona: Curran Associates Inc., 2016: 2243-2251.
[15]	WANG M, TANG Y, WANG J, et al. Premise selection for theorem proving by deep graph embedding[C]//Proceedings of the 31st International Conference on Neural Information Processing Systems. Long Beach: Curran Associates Inc., 2017: 2783-2793.
[16]	CROUSE M, ABDELAZIZ I, CORNELIO C, et al. Improving graph neural network representations of logical formulae with subgraph pooling[EB/OL]. (2019-11-15). https://arxiv.org/abs/1911.06904.
[17]	PALIWAL A, LOOS S, RABE M, et al. Graph representations for higher-order logic and theorem proving[C]//34th Proceedings of the AAAI Conference on Artificial Intelligence. Palo Alto: AAAI Press, 2020: 2967-2974.
[18]	KIPF T N, WELLING M. Semi-supervised classification with graph convolutional networks[DB/OL]. (2016-09-09). https://doi.org/10.48550/arXiv.1609.02907.
[19]	VELIČKOVIĆ P, CUCURULL G, CASANOVA A, et al. Graph attention networks[DB/OL]. (2017-10-30). https://doi.org/10.48550/arXiv.1710.10903.
[20]	ROBINSON A J, VORONKOV A. Handbook of automated reasoning[M]. [S.l.]: Elsevier, 2001.
[21]	Rudnicki P. An overview of the Mizar project[C]//Proceedings of the 1992 Workshop on Types for Proofs and Programs. [S.l.]: Chalmers University of Technology, 1992: 311-330.
[22]	JAKUBŮVJ, URBAN J. ENIGMA: efficient learning-based inference guiding machine[C]//International Conference on Intelligent Computer Mathematics. Cham: Springer, 2017: 292-302.
[23]	COVER T, HART P. Nearest neighbor pattern classification[J]. IEEE Transactions on Information Theory, 1967, 13(1): 21-27.
[24]	PASZKE A, GROSS S, MASSA F, et al. PyTorch: an imperative style, high-performance deep learning library[DB/OL]. (2019-12-03). https://arxiv.org/abs/1912.01703
[25]	FEY M, LENSSEN J E. Fast graph representation learning with PyTorch geometric[DB/OL]. (2019-03-06). https://arxiv.org/abs/1903.02428
[26]	KINGMA D P, BA J. Adam: a method for stochastic optimization[DB/OL]. (2014-12-22). https://arxiv.org/abs/1412.6980.
[27]	HAMILTON W L, YING R, LESKOVEC J. Inductive representation learning on large graphs[C]//Proceedings of the 31st International Conference on Neural Information Processing Systems. Long Beach: [s.n.], 2017: 1025-1035.
[28]	WU F L, SOUZA A H, ZHANG T Y, et al. Simplifying graph convolutional networks[C]// International Conference on Machine Learning. [S.l.]: PMLR, 2019: 6861-6871.
[29]	DEFFERRARD M, BRESSON X, VANDERGHEYNST P. Convolutional neural networks on graphs with fast localized spectral filtering[C]//Proceedings of the 30th International Conference on Neural Information Processing Systems. Barcelona: [s.n.], 2016: 3844-3852.