Automatic Path Planning Method Based on Terrain Adaptation for Freight Cableways
-
摘要:
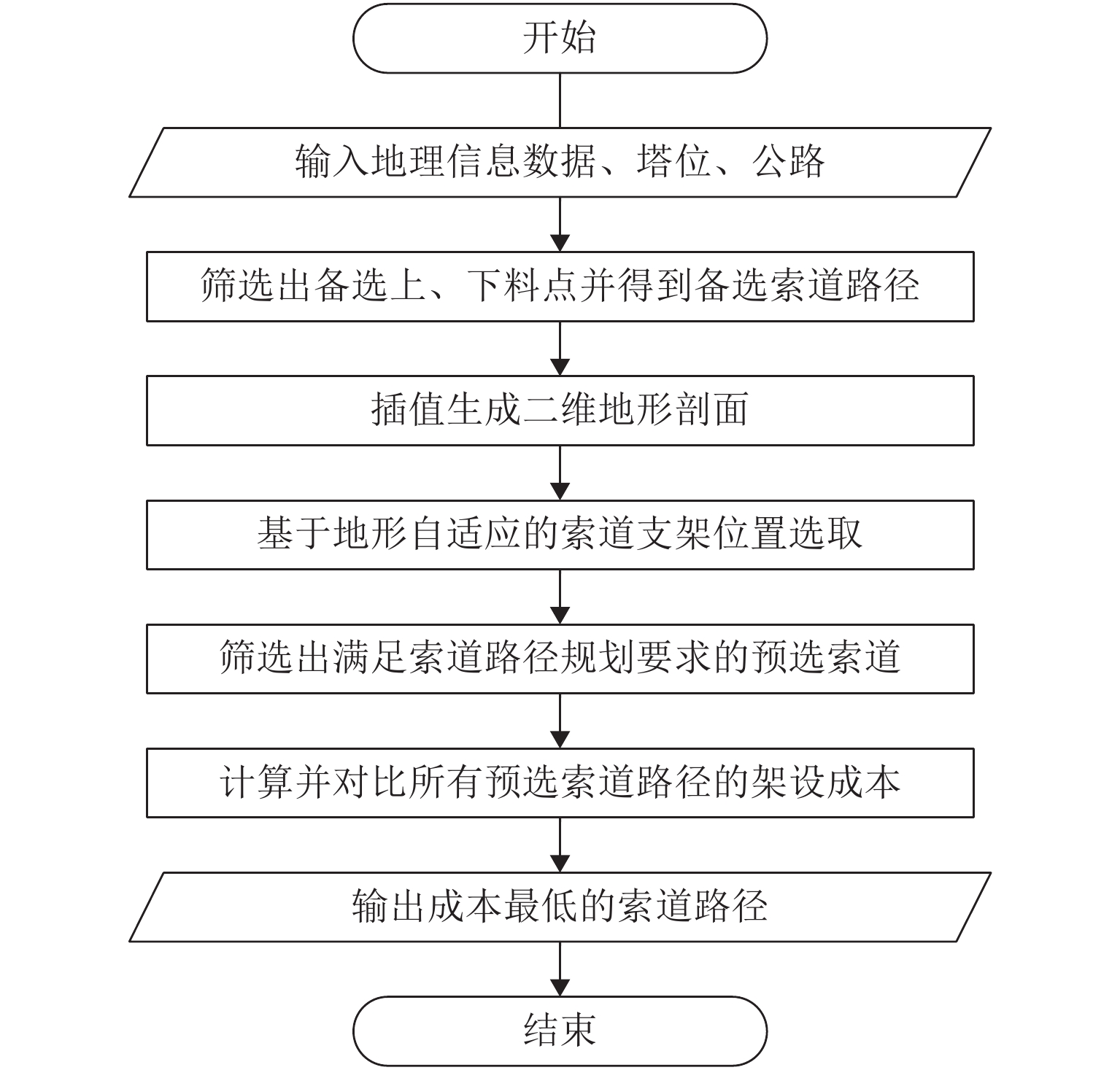
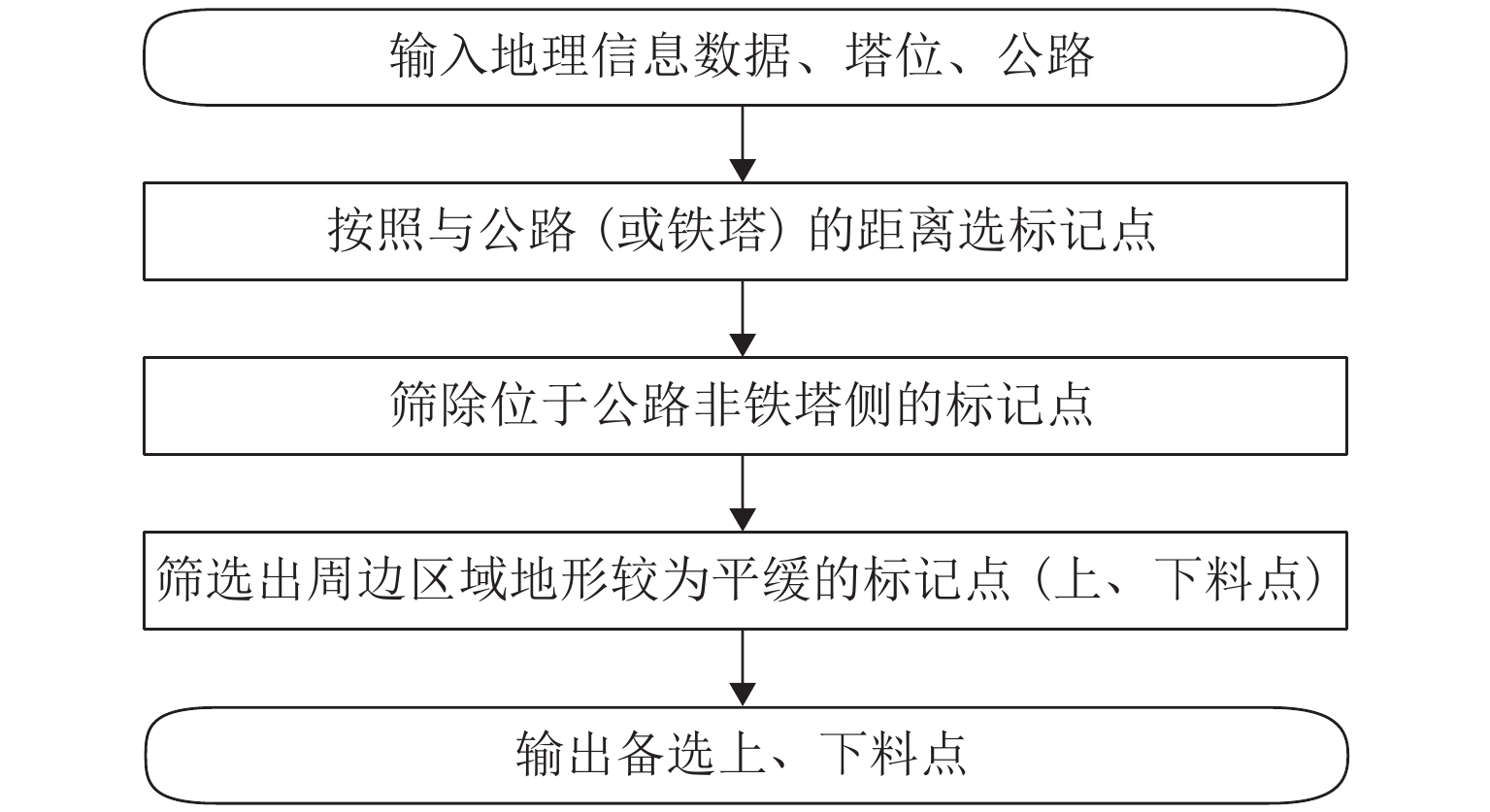
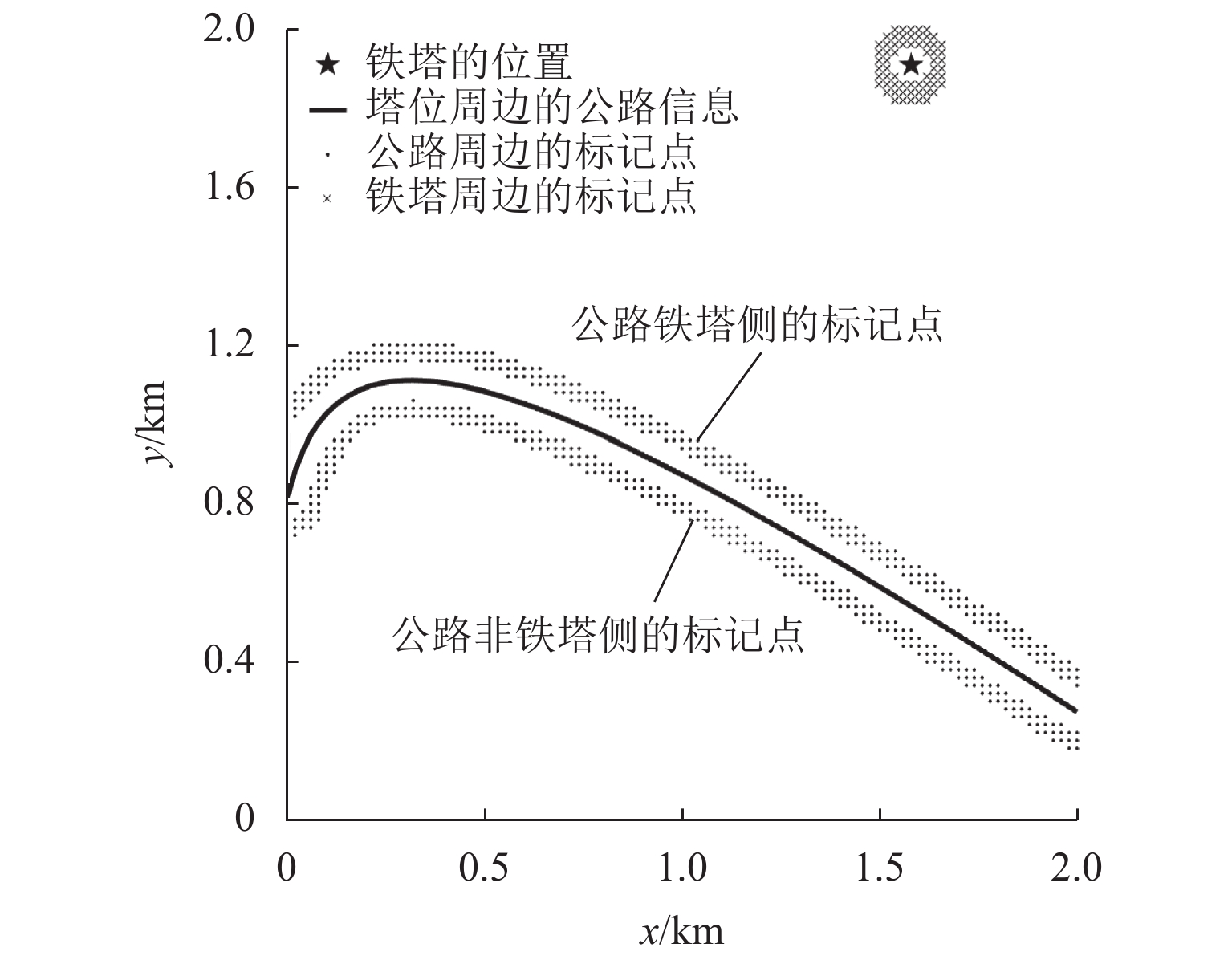
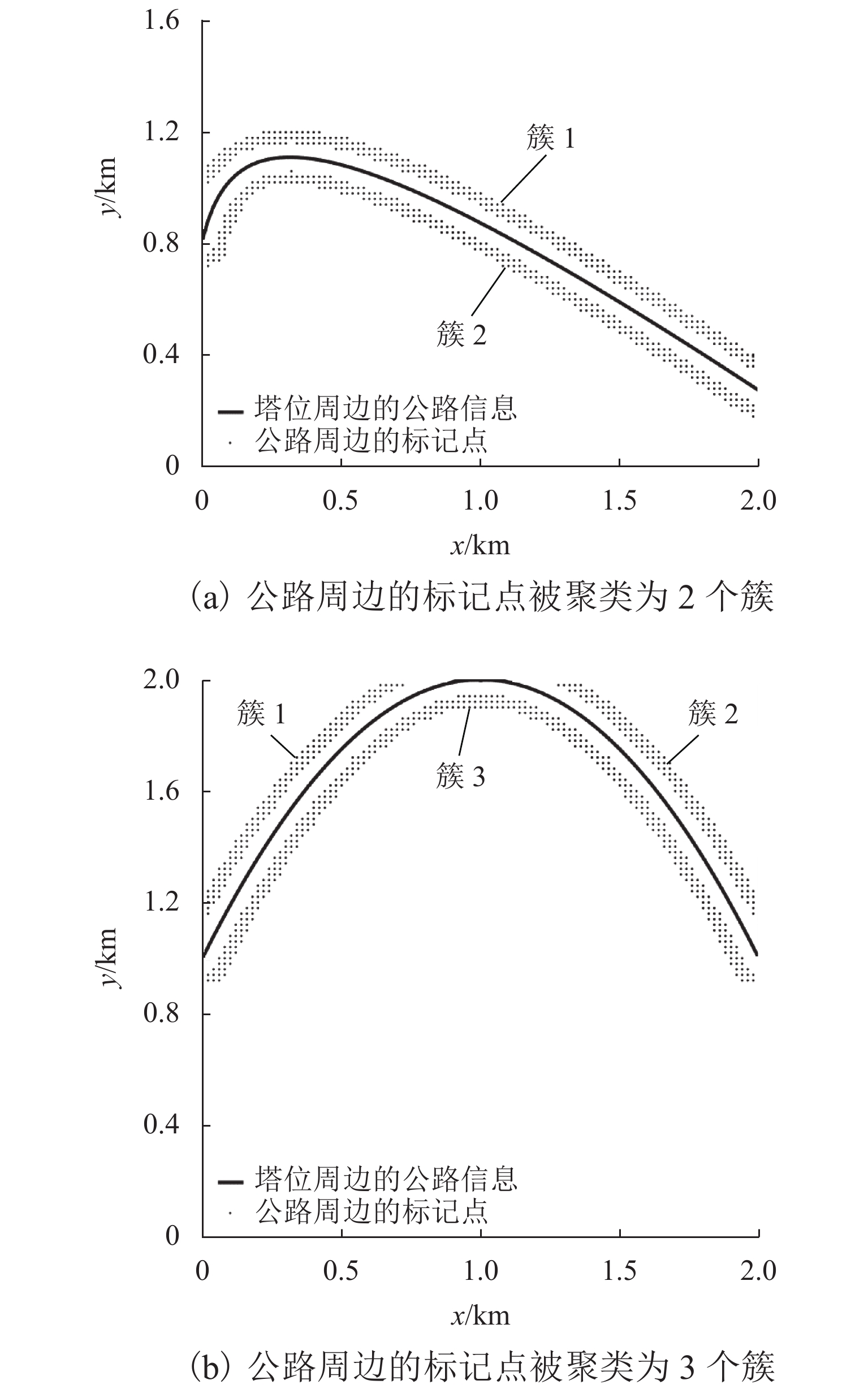
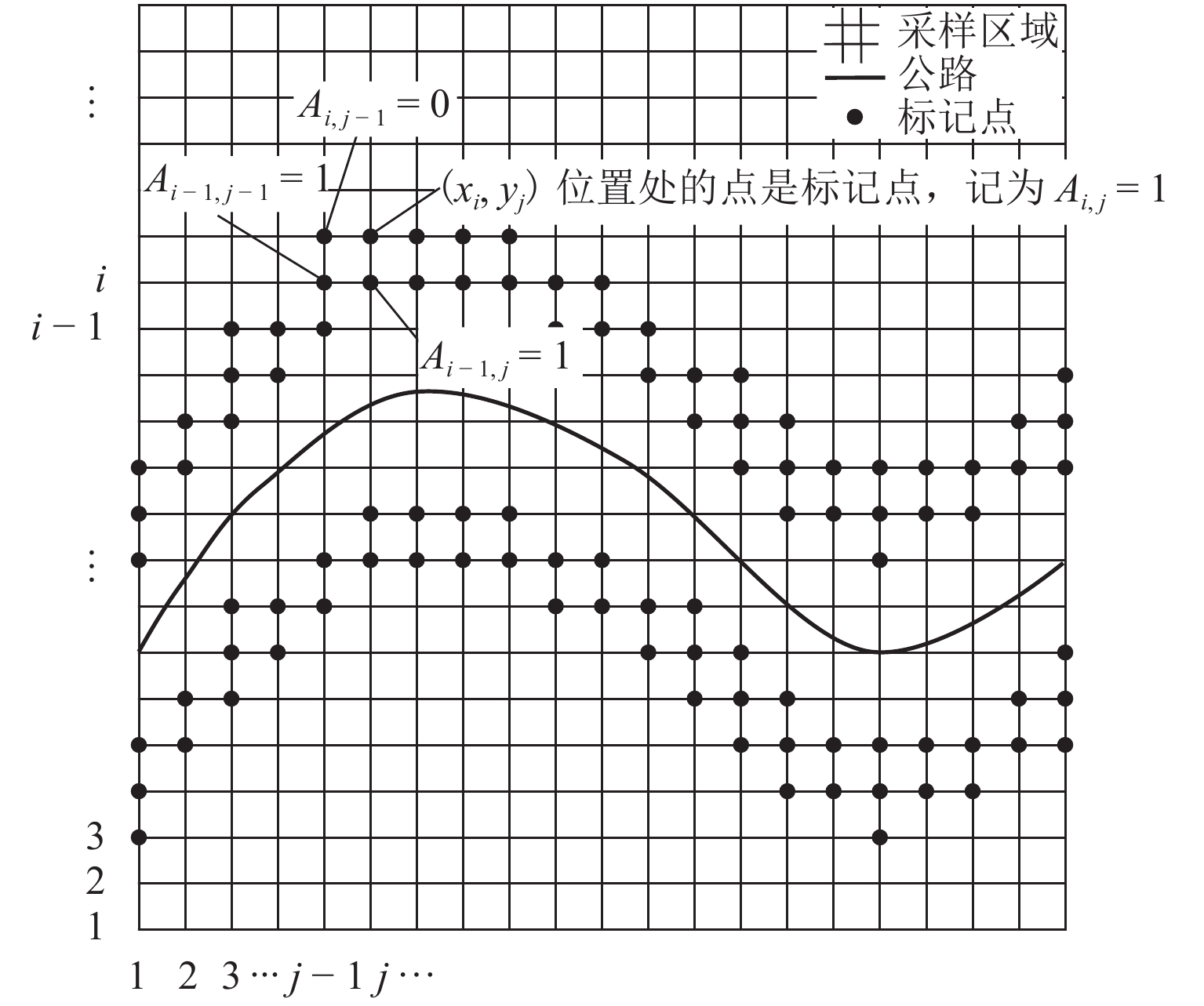
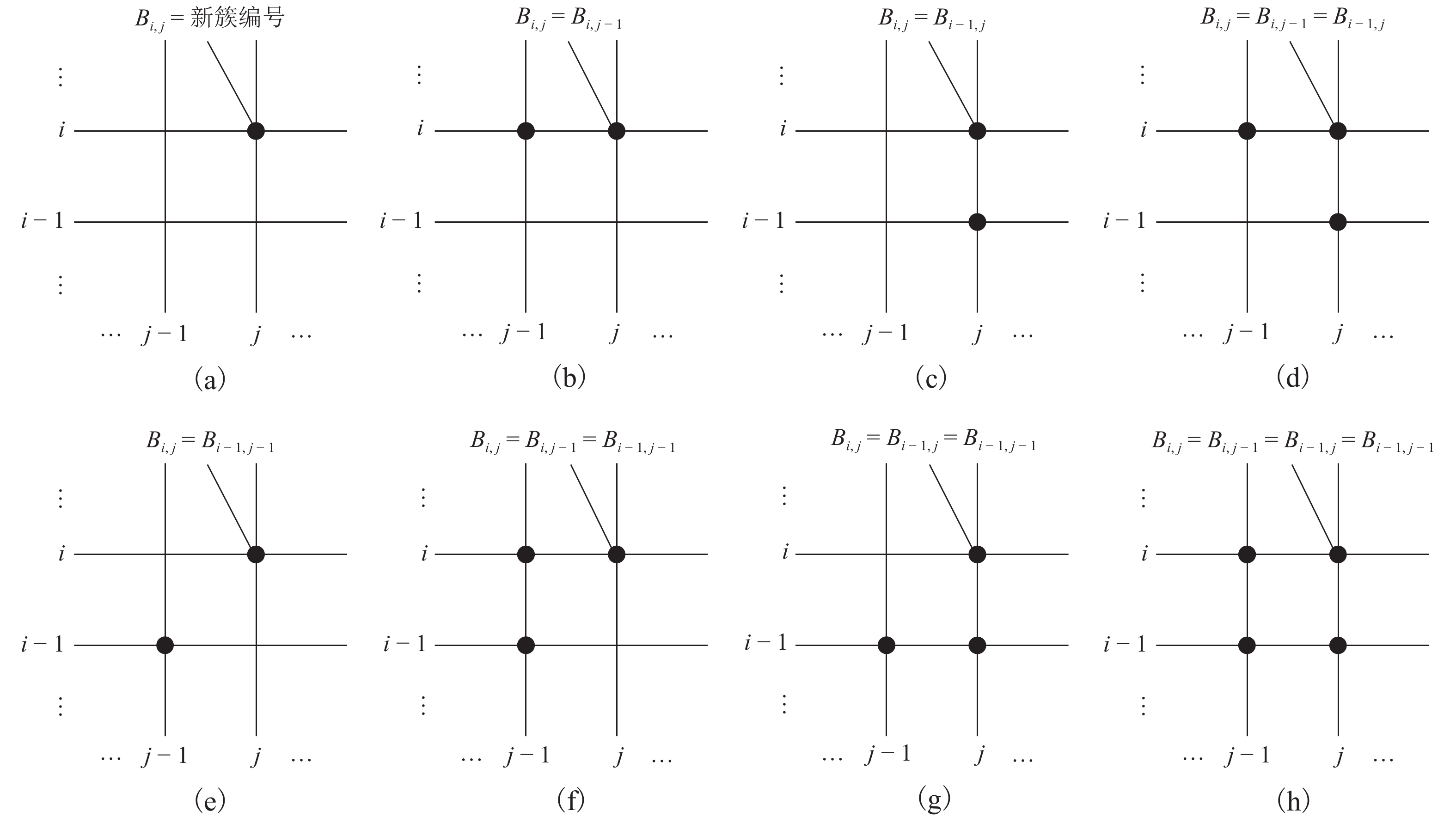
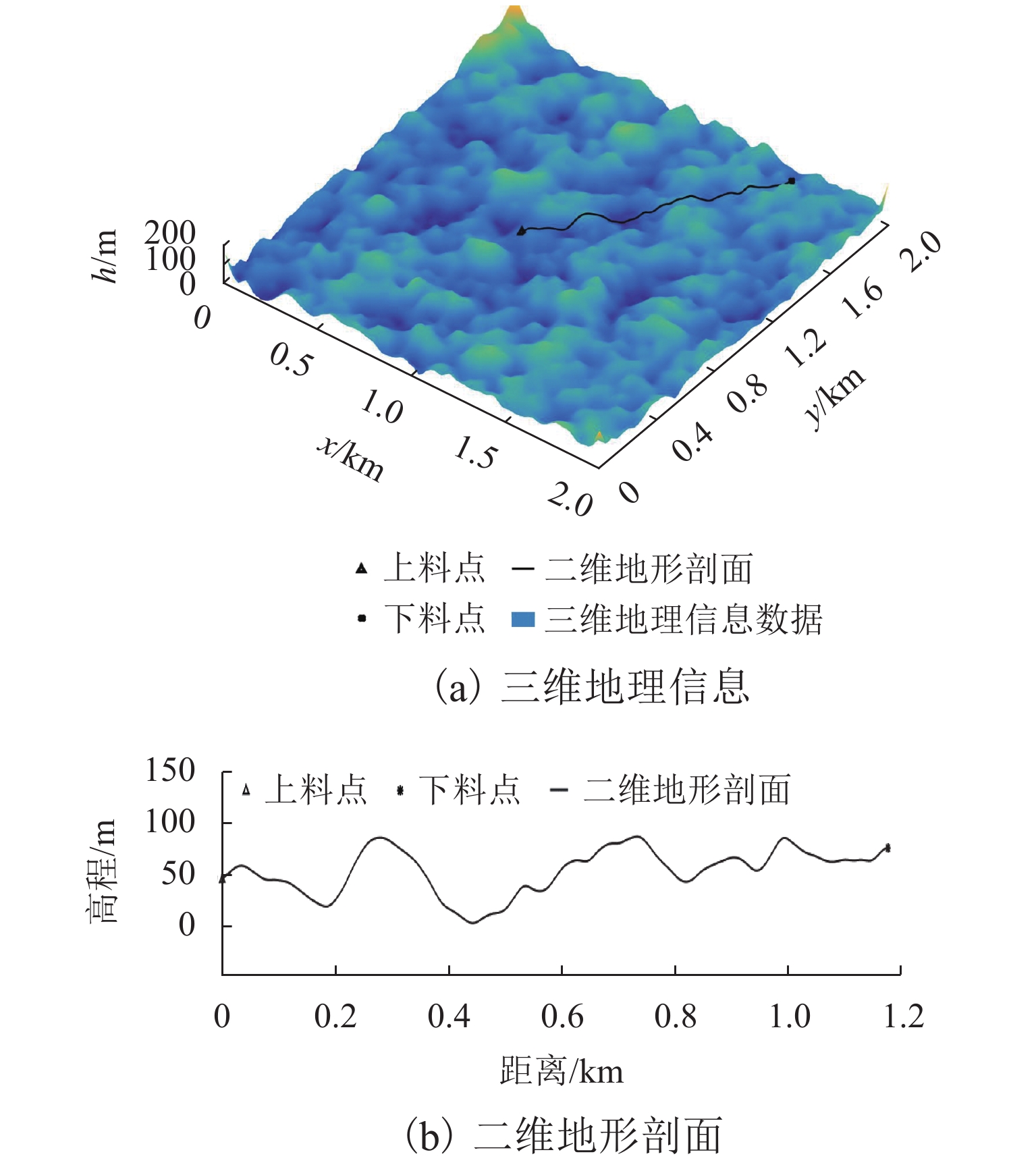
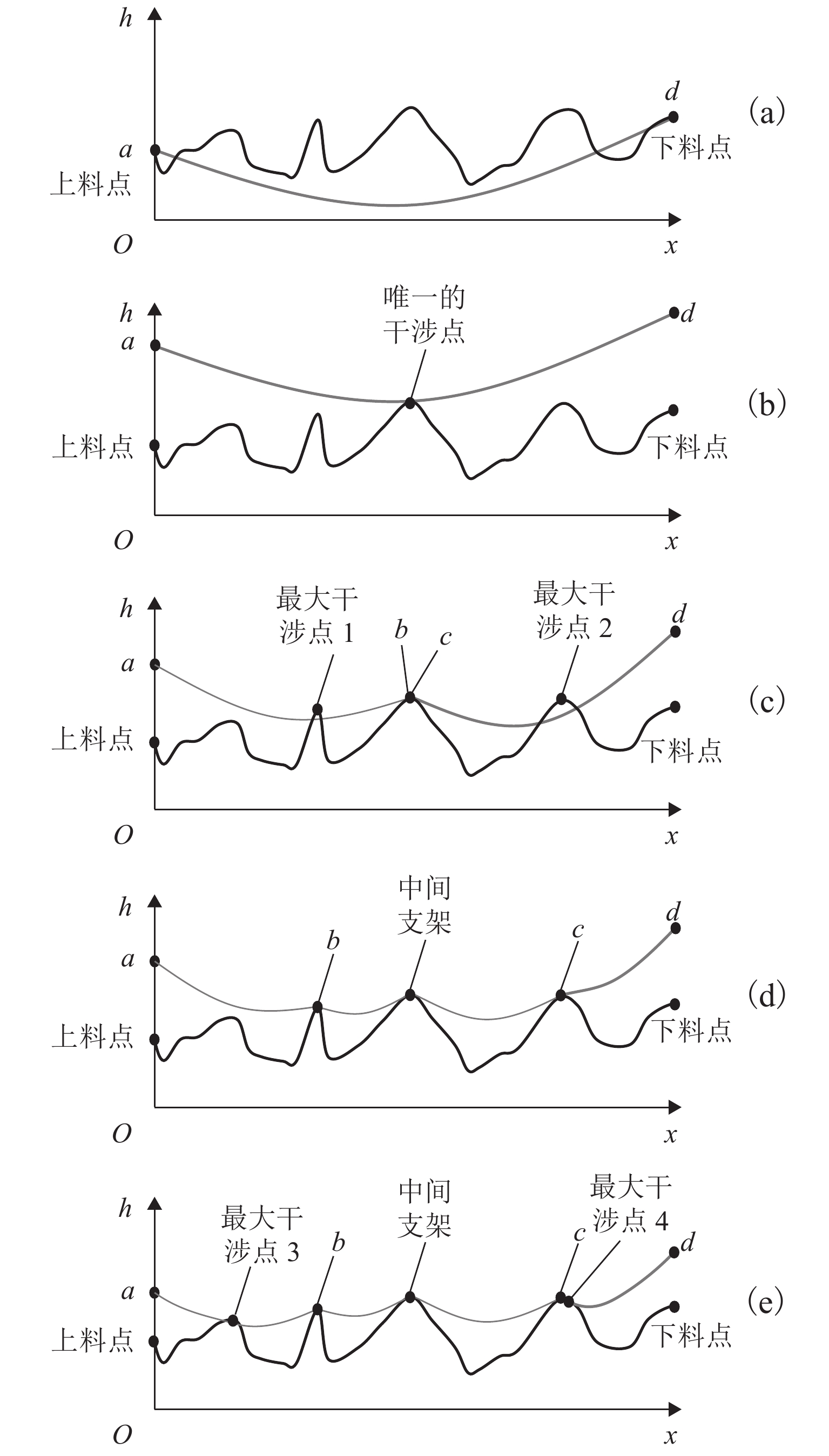
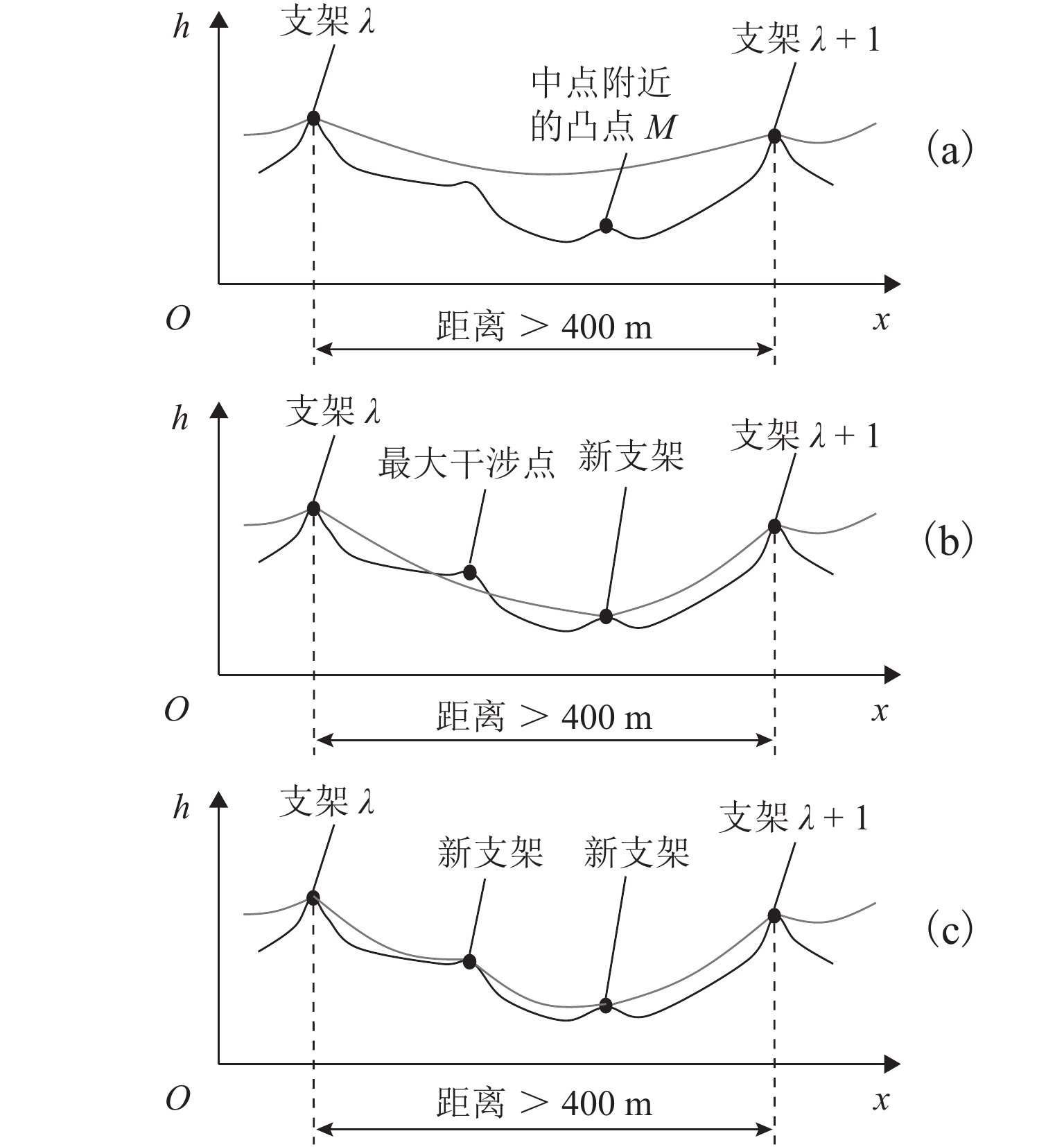
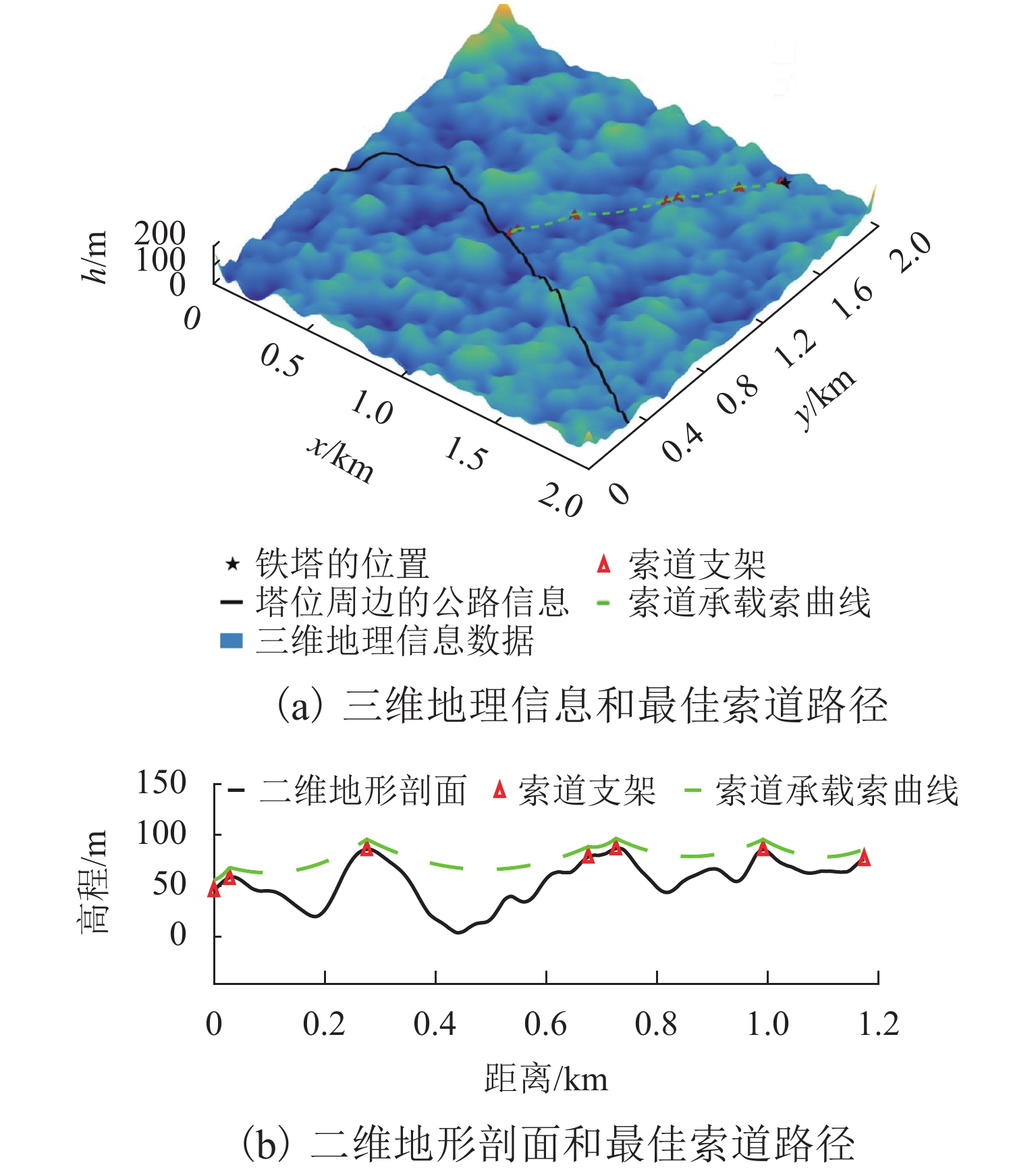
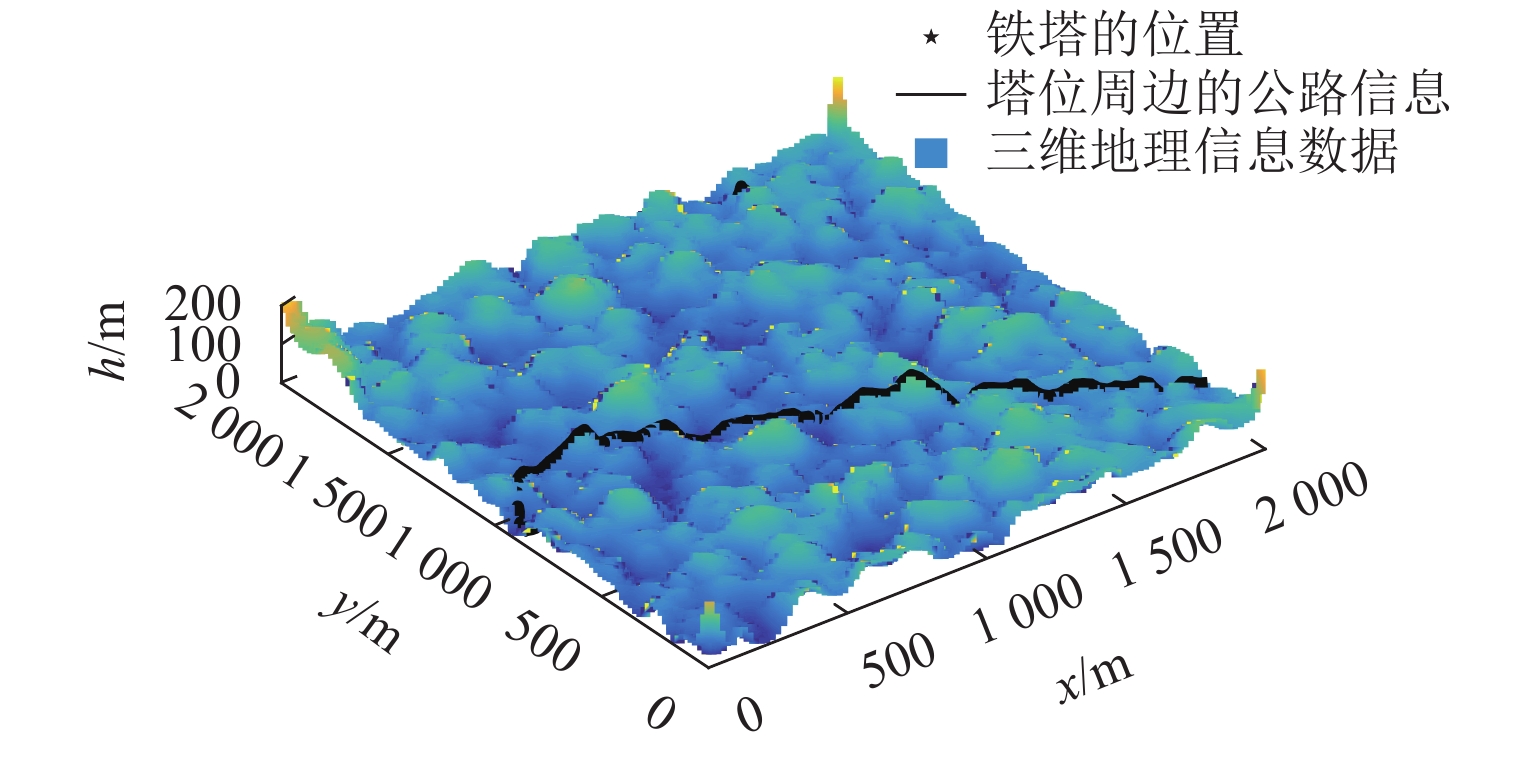
为降低货运索道路径规划工作的时间和经济成本，综合考虑地理信息、工程实际情况和索道架设与运营成本等多方面因素，提出了索道路径规划要求，形成自动化路径规划的技术流程. 针对索道架设要求，提出了基于聚类分簇思想的上、下料点自动筛选方法，实现索道对公路的避让；并根据三维地形数据提出了基于地形自适应的索道支架位置搜索方法，搜索的支架可保证索道承载索与地面的间距满足施工要求；通过支架位置优化，减少支架数量，实现索道成本的降低. 对实际工程的路径规划计算应用表明：该规划方法可在约半个小时的时间内自动获得的上千条索道路径及支架架设方案，规划速度快，数据分析全面.
Abstract:To reduce the time and economic costs of freight cableway path planning, according to factors such as geographical information, project requirements, and costs of cableway erection and operation, the requirements of cableway path planning are proposed, and the technical process of automatic path planning is developed. To meet the requirements of cableway erection, an automatic method for screening loading and unloading points based on clustering was presented to achieve the avoidance of cableway to highway, and by the use of three-dimensional terrain data, a search method for trestle positions based on terrain adaptation is proposed. The selected trestle positions can ensure that the distance between the bearing cable of the cableway and the ground meets the construction requirements, and in this way the number of trestles is optimized to reduce the cost of the cableway. The field applications of the proposed method demonstrate that it can provide thousands of cableway paths and trestle positions automatically in around half an hour, showing fast planning and comprehensive data analysis.
-
Key words:
- transmission line /
- freight cableway /
- path planning /
- terrain adaptation.
-
图 2 货运索道路径自动规划的主要流程
Figure 2. Flowchart of automatic path planning for freight cableways
图 9 基于地形自适应的货运索道中间支架自动搜索原理
Figure 9. Automatic search principle for intermediate trestle of freight cableway based on terrain adaptation
表 1 索道路径规划问题计算结果
Table 1. Results of cableway path planning problems
算例编号 备选上料点/个 备选下料点/个 备选索道路径/条 满足索道架设要求的索道/条 计算时长/min 1 1786 28 50008 3563 18.28 2 1514 18 27252 3760 10.47 3 3943 115 453445 0 165.90 4 163 3 489 14 0.56 5 1111 80 88880 0 32.15 6 69 31 2139 193 1.15 7 31 13 403 0 0.34 8 232 49 11368 443 4.66 9 971 3 2913 338 1.41 10 2229 80 178320 1850 66.62 均值 1205 42 81522 1016 30.16 
下载: 导出CSV
-
[1] 缪谦. 我国电网建设工程施工货运索道运输方式的研究[J]. 华北电力技术,2010(12): 12-15. doi: 10.3969/j.issn.1003-9171.2010.12.003MIAO Qian. Research of transportation way by cargo cableway in construction of power grid[J]. North China Electric Power, 2010(12): 12-15. doi: 10.3969/j.issn.1003-9171.2010.12.003 [2] 缪谦,白雪松. 货运索道运输技术与设备研究[J]. 电力建设,2009,30(12): 93-96. doi: 10.3969/j.issn.1000-7229.2009.12.025MIAO Qian, BAI Xuesong. Study on transportation technology and equipment in freight cableway system[J]. Electric Power Construction, 2009, 30(12): 93-96. doi: 10.3969/j.issn.1000-7229.2009.12.025 [3] 秦剑,乔良,江明,等. 多承载索货运索道计算方法及张力不平衡效应分析[J]. 中国安全生产科学技术,2019,15(9): 44-49. doi: 10.11731/j.issn.1673-193x.2019.09.007QIN Jian, QIAO Liang, JIANG Ming, et al. Calculation method of material ropeway with multiple carrying ropes and analysis of tension unbalance effect[J]. Journal of Safety Science and Technology, 2019, 15(9): 44-49. doi: 10.11731/j.issn.1673-193x.2019.09.007 [4] 江明. 考虑索间耦合效应的双索货运索道系统设计[J]. 机械设计与制造,2020(9): 80-84. doi: 10.3969/j.issn.1001-3997.2020.09.020JIANG Ming. Design of double cable freight ropeway system considering coupling effect between cables[J]. Machinery Design & Manufacture, 2020(9): 80-84. doi: 10.3969/j.issn.1001-3997.2020.09.020 [5] 秦剑,乔良,李其莹,等. 多索索道承载索耦合计算方法及安全性评估[J]. 安全与环境学报,2020,20(2): 433-440.QIN Jian, QIAO Liang, LI Qiying, et al. Calculation method of the coupled loading-cables and safety assessment for the multi-cable cableway[J]. Journal of Safety and Environment, 2020, 20(2): 433-440. [6] 秦剑,乔良,张映晖,等. 多档货运索道动力计算方法及结构冲击影响研究[J]. 动力学与控制学报,2020,18(2): 59-68.QIN Jian, QIAO Liang, ZHANG Yinghui, et al. Calculation method for dynamics of multi-span freight cableway and influence of structure impact[J]. Journal of Dynamics and Control, 2020, 18(2): 59-68. [7] 白雪松,缪谦,王立军,等. 货运施工索道工作索计算软件开发与应用[J]. 电力建设,2009,30(2): 41-44. doi: 10.3969/j.issn.1000-7229.2009.02.010BAI Xuesong, MIAO Qian, WANG Lijun, et al. Development and application of working cable computation software for construction cargo cableway[J]. Electric Power Construction, 2009, 30(2): 41-44. doi: 10.3969/j.issn.1000-7229.2009.02.010 [8] 李洋,李爱华,刘岭梅,等. 辅助索道方案优化设计平台的设计与应用[J]. 地理空间信息,2018,16(1): 115-118,9. doi: 10.3969/j.issn.1672-4623.2018.01.035LI Yang, LI Aihua, LIU Lingmei, et al. Design and application of the auxiliary ropeway scheme optimization and design platform[J]. Geospatial Information, 2018, 16(1): 115-118,9. doi: 10.3969/j.issn.1672-4623.2018.01.035 [9] 李攀,李志斌,谢芳毅,等. 三维GIS辅助山区输电线路货运索道选线系统设计[J]. 数字技术与应用,2016(5): 173-174. [10] 王刚, 李志斌. 基于GIS的输电线路路径智能选线研究[C]//第九届京港澳测绘地理信息技术交流会论文集. 北京: 中国地图出版社, 2015: 157-162. [11] 刘亮亮. 智能式GIS在超特高压输电路径规划中的优选与应用[D]. 昆明: 云南大学, 2017. [12] 谢景海,苏东禹,卢诗华,等. 基于改进蚁群算法的输电线路路径规划关键技术[J]. 电测与仪表,2020,57(4): 122-128.XIE Jinghai, SU Dongyu, LU Shihua, et al. Key technology of transmission line path planning based on improved ant[J]. Electrical Measurement & Instrumentation, 2020, 57(4): 122-128. [13] 贾乃文. 非线性空间结构力学[M]. 北京: 科学出版社, 2002. -
下载:
点击查看大图
计量
- 文章访问数: 394
- HTML全文浏览量: 142
- PDF下载量: 47
- 被引次数: 0