Experimental Study on Stress-Strain Relationship of Steel Slag Fine Aggregate Concrete Under Uniaxial Compression
-
摘要:
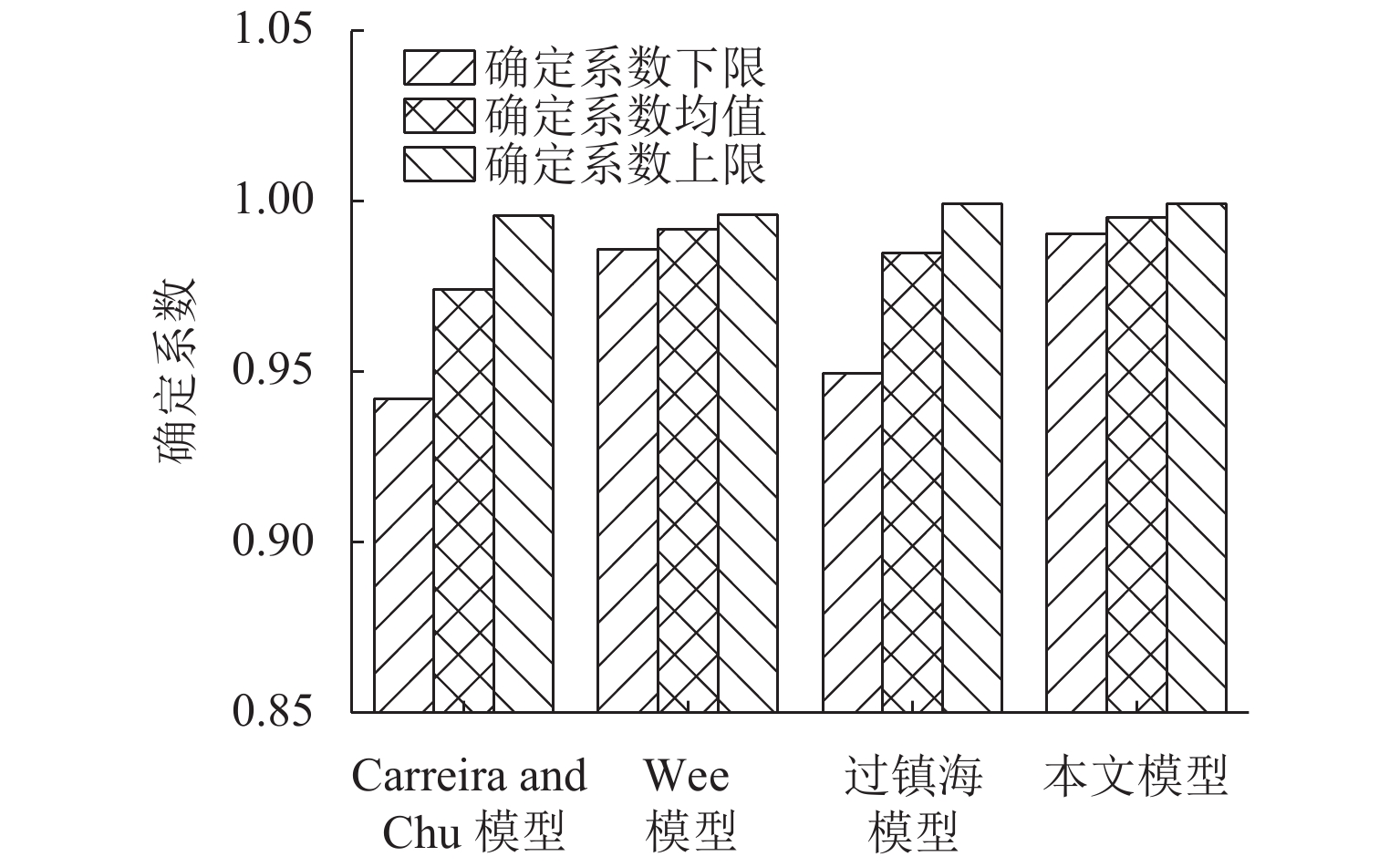
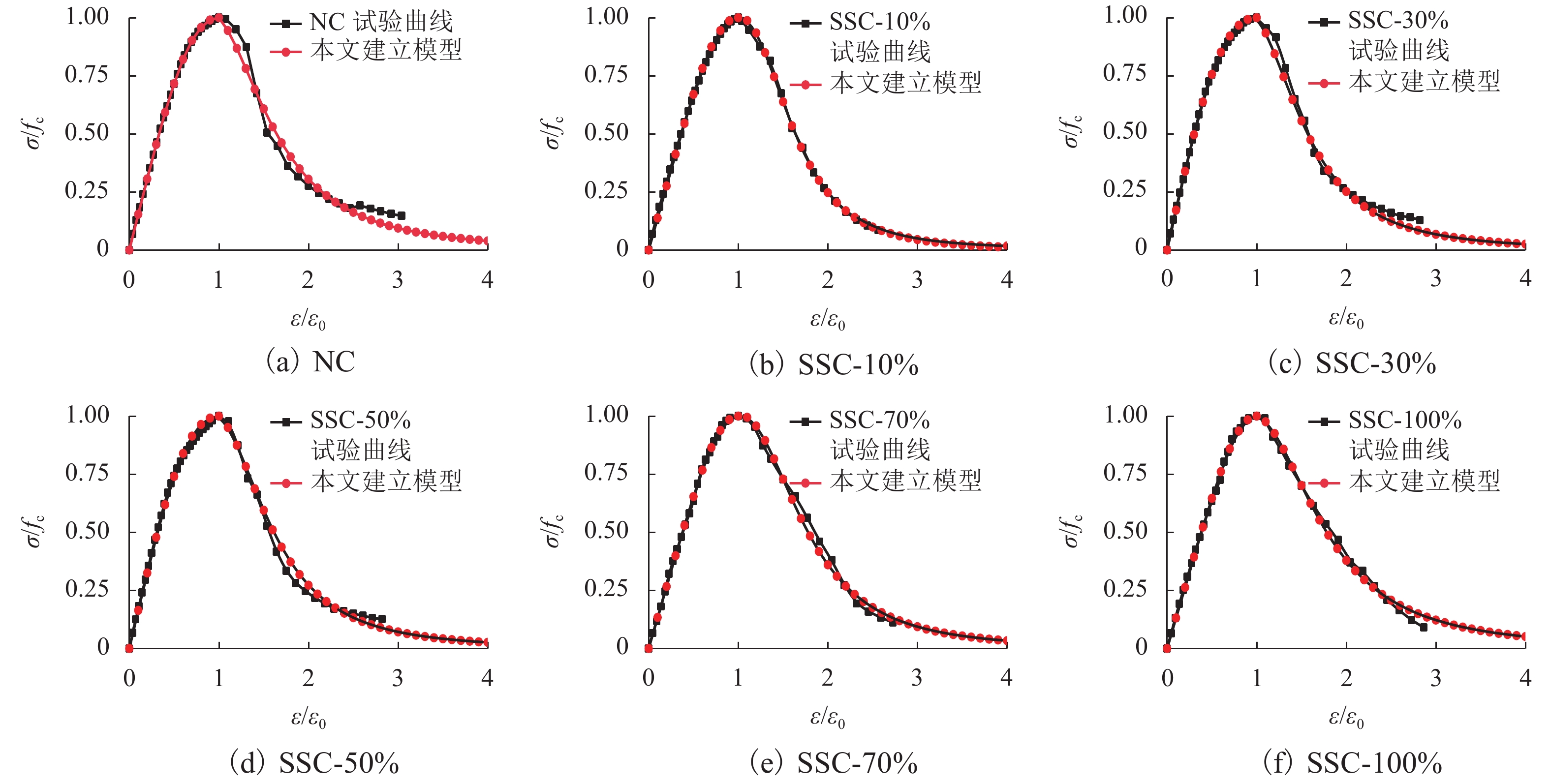
为研究钢渣细骨料在混凝土中的适用性及钢渣细骨料混凝土的轴压本构模型，进行了钢渣细骨料的物理化学性能试验，并对钢渣细骨料的稳定性进行测试分析；在此基础上，制备了6组不同钢渣细骨料掺量的钢渣混凝土立方体及棱柱体试件，研究了钢渣细骨料混凝土的单轴受压性能. 研究结果表明：本文选用钢渣的游离氧化钙含量、压蒸粉化率均满足相关规范要求，适用于混凝土细骨料；钢渣细骨料混凝土破坏的脆性特征更加明显，比普通混凝土的抗压强度有明显提高；钢渣混凝土棱柱体抗压强度与立方体抗压强度比值为0.80 ~ 0.86；可依据Carreira and Chu模型及Wee模型对钢渣混凝土本构关系进行分段描述，分段式本构模型与实测钢渣细骨料混凝土的应力-应变曲线基本吻合.
Abstract:In order to study the applicability of steel slag fine aggregate in concrete and the Axial compression constitutive model of steel slag concrete, the physical and chemical properties of steel slag fine aggregate were tested and the stability of steel slag fine aggregate was tested and analyzed. Six groups of steel slag concrete cube and prism specimens with different steel slag fine aggregate content were prepared, and the uniaxial compression performance of steel slag concrete was studied. The results show that the free calcium oxide and autoclaved pulverization rate of steel slag selected in this paper meet the requirements of relevant specifications and are suitable for concrete aggregate. The brittle characteristics of steel slag fine aggregate concrete are more obvious, which is significantly improved than ordinary concrete. The ratio of prism compressive strength of steel slag concrete to cube compressive strength is 0.80−0.86. The constitutive relationship of steel slag concrete can be described in sections according to the Carreira and Chu model and Wee model. The sectional constitutive model is basically consistent with the measured stress-strain curve of steel slag fine aggregate concrete.
-
Key words:
- steel slag fine aggregate /
- concrete /
- uniaxial compression /
- constitutive relationship
-
图 3 钢渣混凝土棱柱体轴心抗压试验装置
Figure 3. Axial compressive test apparatus for steel slag concrete prisms
图 5 普通混凝土及钢渣细骨料混凝土轴压破坏形态
Figure 5. Failure modes of ordinary concrete and steel slag fine aggregate concrete under axial compression
图 6 钢渣细骨料不同替代率下混凝土单轴受压应力-应变曲线
Figure 6. Stress-strain curves of concrete under uniaxial compression under different substitution rates of steel slag fine aggregate
图 10 上升段参数D与替代率关系
Figure 10. Relationship between the ascending stage parameter D and the substitution rate
图 11 下降段参数与替代率的关系
Figure 11. Relationships between the descending parameters and the substitution rate
图 12 试验曲线与本文建立模型曲线对比
Figure 12. Comparison of test curves and model curves established in this paper
表 1 钢渣主要化学成分
Table 1. Main chemical composition of steel slag
化学成分 CaO SiO2 Al2O3 Fe2O3 MgO f-CaO 其他 质量分数/% 36.5 23.0 9.0 10.0 7.5 1.2 12.8 
下载: 导出CSV
表 2 骨料物理性能指标
Table 2. Physical properties of aggregate
材料 表观密度/
（kg·m−3）细度模数 松散堆积密度/（kg·m−3） 吸水率/% 含水率/% 砂 2601 2.87 1566 0.90 0.50 钢渣细骨料 3440 2.94 1800 3.70 0.25 石子 2681 1450 0.80 0.50
下载: 导出CSV
表 3 钢渣细骨料混凝土配合比
Table 3. Mix proportion of steel slag fine aggregate concrete
kg 试验编号 水泥 粉煤灰 河砂 钢渣细
骨料碎石 水 减水剂 NC 323 57 795.0 0 1054 171 5.7 SSC-10% 715.5 79.5 SSC-30% 556.5 238.5 SSC-50% 397.5 397.5 SSC-70% 238.5 556.5 SSC-100% 0 795.0
下载: 导出CSV
表 4 棱柱体抗压强度与立方体抗压强度
Table 4. Prism compressive strength and cube compressive strength
试验编号 fc(ssc)/MPa fcu(ssc)/MPa fc(ssc)/fcu(ssc) NC 33.4 45.1 0.74 SSC-10% 37.9 47.4 0.80 SSC-30% 39.0 48.9 0.80 SSC-50% 41.8 50.5 0.83 SSC-70% 46.3 53.6 0.86 SSC-100% 41.4 49.2 0.84
下载: 导出CSV
-
[1] 左更. 中国钢铁正值“壮年”将引领全球钢铁进入新发展周期[N]. 中国冶金报, 2021-02-10. [2] 董静媚. 2019年钢铁行业形势分析与2020年展望[J]. 中国物价,2020(2): 9-11.DONG Jingmei. Steel industry situation analysis for 2019 and prospect for 2020[J]. China Price, 2020(2): 9-11. [3] 高本恒,郝以党,张淑苓,等. 钢渣综合利用现状及发展趋势[J]. 环境工程,2016,34(增1): 776-779.GAO Benheng, HAO Yidang, ZHANG Shuling, et al. Development trend and comprehensive utilization of steel slag[J]. Environmental Engineering, 2016, 34(S1): 776-779. [4] 刘洋,张春霞. 钢铁渣的综合利用现状及发展趋势[J]. 矿产综合利用,2019(2): 21-25. doi: 10.3969/j.issn.1000-6532.2019.02.004LIU Yang, ZHANG Chunxia. Comprehensive utilization situation and development trend of iron and steel slag in China and abroad[J]. Multipurpose Utilization of Mineral Resources, 2019(2): 21-25. doi: 10.3969/j.issn.1000-6532.2019.02.004 [5] BISKRI Y, ACHOURA D, CHELGHOUM N, et al. Mechanical and durability characteristics of high performance concrete containing steel slag and crystalized slag as aggregates[J]. Construction and Building Materials, 2017, 150: 167-178. doi: 10.1016/j.conbuildmat.2017.05.083 [6] ABU-EISHAH S I, EL-DIEB A S, BEDIR M S. Performance of concrete mixtures made with electric arc furnace (EAF) steel slag aggregate produced in the Arabian Gulf region[J]. Construction and Building Materials, 2012, 34: 249-256. doi: 10.1016/j.conbuildmat.2012.02.012 [7] 朱训国,王兆毅,何传琪,等. 低强度钢渣混凝土抗压及抗渗性能试验研究[J]. 西安理工大学学报,2019,35(2): 256-263.ZHU Xunguo, WANG Zhaoyi, HE Chuanqi, et al. Experimental study on compressive strength and impermeability of low strength slag concrete[J]. Journal of Xi’an University of Technology, 2019, 35(2): 256-263. [8] 韩艳丽,冯勇,肖磊. 粗细钢渣替代天然骨料对混凝土力学性能的影响[J]. 混凝土与水泥制品,2015(2): 96-98. doi: 10.3969/j.issn.1000-4637.2015.02.027HAN Yanli, FENG Yong, XIAO Lei. Effecting of coarse and fine steel slag replaced with natural aggregate on mechanical properties of concrete[J]. China Concrete and Cement Products, 2015(2): 96-98. doi: 10.3969/j.issn.1000-4637.2015.02.027 [9] QASRAWI H, SHALABI F, ASI I. Use of low CaO unprocessed steel slag in concrete as fine aggregate[J]. Construction and Building Materials, 2009, 23(2): 1118-1125. doi: 10.1016/j.conbuildmat.2008.06.003 [10] 于峰,王旭良,张扬,等. 补偿收缩钢渣混凝土应力-应变关系试验[J]. 建筑材料学报,2017,20(4): 527-534. doi: 10.3969/j.issn.1007-9629.2017.04.007YU Feng, WANG Xuliang, ZHANG Yang, et al. Stress-strain relationship of shrinkage compensating steel-slag concrete[J]. Journal of Building Materials, 2017, 20(4): 527-534. doi: 10.3969/j.issn.1007-9629.2017.04.007 [11] 李斌,力乙鹏,王晨霞,等. 水淬钢渣混凝土应力-应变全曲线试验研究[J]. 建筑结构学报,2019,40(8): 163-169. doi: 10.14006/j.jzjgxb.2017.0815LI Bin, LI Yipeng, WANG Chenxia, et al. Experimental study on stress-strain curve of granulated steel slag concrete[J]. Journal of Building Structures, 2019, 40(8): 163-169. doi: 10.14006/j.jzjgxb.2017.0815 [12] 中华人民共和国国家市场监督管理总局, 中国国家标准化管理委员会. 通用硅酸盐水泥: GB 175—2007[S].北京: 中国建筑工业出版社, 2009. [13] 中华人民共和国国家质量监督检验检疫总局, 中国国家标准化管理委员会. 建设用砂: GB/T 14684—2011[S]. 北京: 中国建筑工业出版社, 2012. [14] 中华人民共和国国家质量监督检验检疫总局, 中国国家标准化管理委员会. 建设用卵石、碎石: GB/T 14685—2001[S]. 北京: 中国建筑工业出版社, 2009. [15] 游润卫,郭月红. 钢渣用于填筑盐碱土地段路基的研究[J]. 天津城市建设学院学报,2008,14(2): 130-134.YOU Runwei, GUO Yuehong. Research of steel slag as subgrade filling at saline-alkali soil section[J]. Journal of Tianjin Institute of Urban Construction, 2008, 14(2): 130-134. [16] 中华人民共和国国家质量监督检验检疫总局, 中国国家标准化管理委员会. 钢渣稳定性试验方法: GB/T 24175—2009[S]. 北京: 中国标准出版社, 2009. [17] 中华人民共和国工业和信息化部. 普通预拌砂浆用钢渣砂: YB/T 4201—2009[S]. 北京: 中国建筑工业出版社, 2009. [18] 中华人民共和国工业和信息化部. 水泥混凝土路面用钢渣砂应用技术规程: YB/T 4329—2012[S]. 北京: 中国建筑工业出版社, 2012. [19] 中华人民共和国住房和城乡建设部. 普通混凝土配合比设计规程: JGJ 55—2011[S]. 北京: 中国建筑工业出版社, 2011. [20] 王强,曹丰泽,于超,等. 钢渣骨料对混凝土性能的影响[J]. 硅酸盐通报,2015,34(4): 1004-1010.WANG Qiang, CAO Fengze, YU Chao, et al. Influence of steel slag aggregate on the properties of concrete[J]. Bulletin of the Chinese Ceramic Society, 2015, 34(4): 1004-1010. [21] 刘华山. 钢渣水泥混凝土力学性能及耐久性研究[J]. 公路交通科技(应用技术版),2019,15(12): 84-86. [22] 中华人民共和国住房和城乡建设部. 混凝土物理力学性能试验方法标准: GB/T 50081—2019[S]. 北京: 中国建筑工业出版社, 2019. [23] 梁兴文, 史庆轩. 混凝土结构设计原理[M]. 4版. 北京: 中国建筑工业出版社, 2019: 84-96. [24] CARREIRA D J, CHU K H. Stress-strain relationship for plain concrete in compression[J]. ACI Journal Proceedings, 1985, 82(6): 797-804. [25] 过镇海. 混凝土的强度和本构关系: 原理与应用[M]. 北京: 中国建筑工业出版社, 2004. [26] WEE T H, CHIN M S, MANSUR M A. Stress-strain relationship of high-strength concrete in compression[J]. Journal of Materials in Civil Engineering, 1996, 8(2): 70-76. doi: 10.1061/(ASCE)0899-1561(1996)8:2(70) -
下载:
点击查看大图
计量
- 文章访问数: 356
- HTML全文浏览量: 144
- PDF下载量: 38
- 被引次数: 0