An Analytical Method for Train Dynamic Behavior on Long Steep Grades of High-Speed Railway
-
摘要:
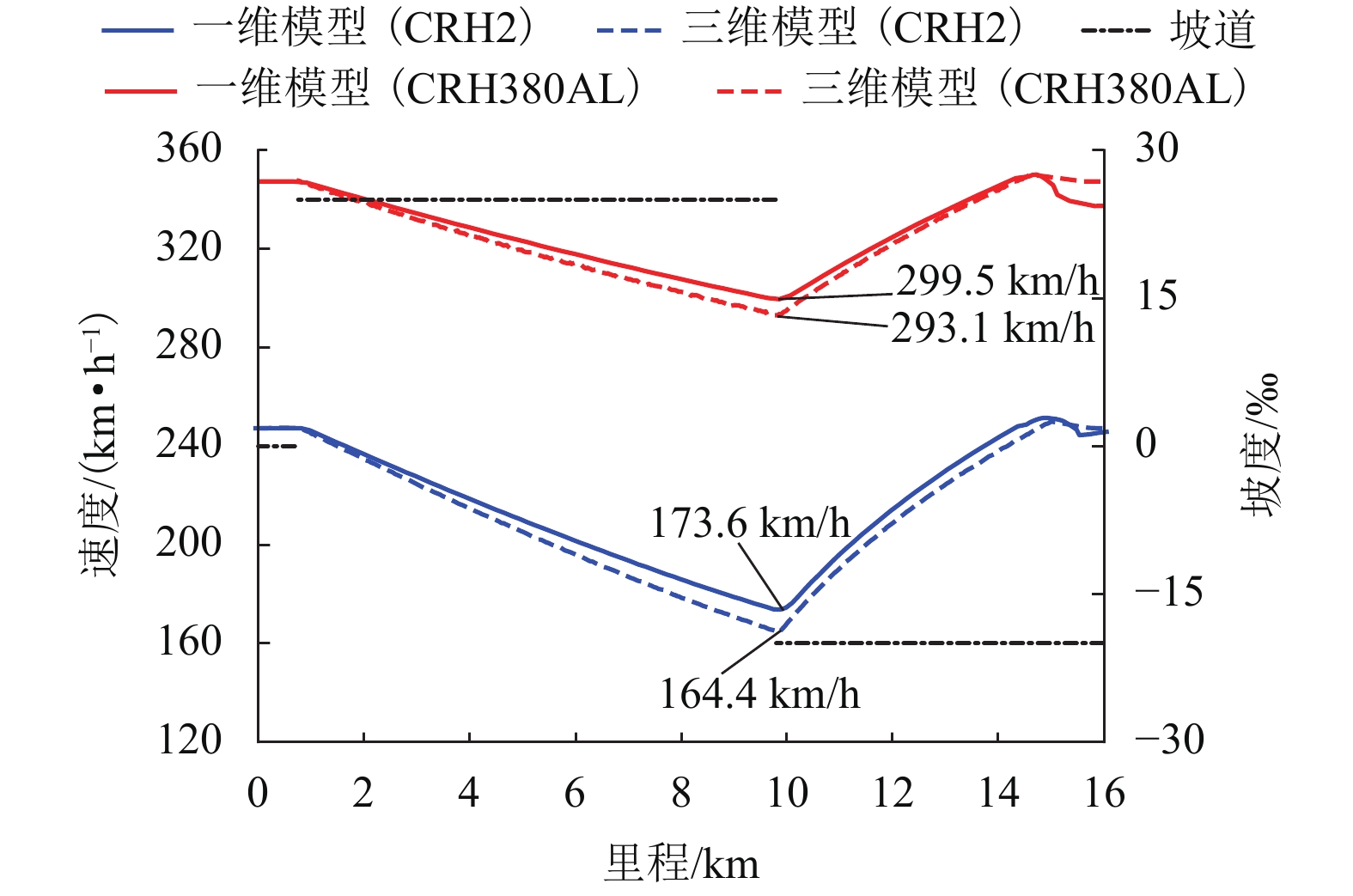
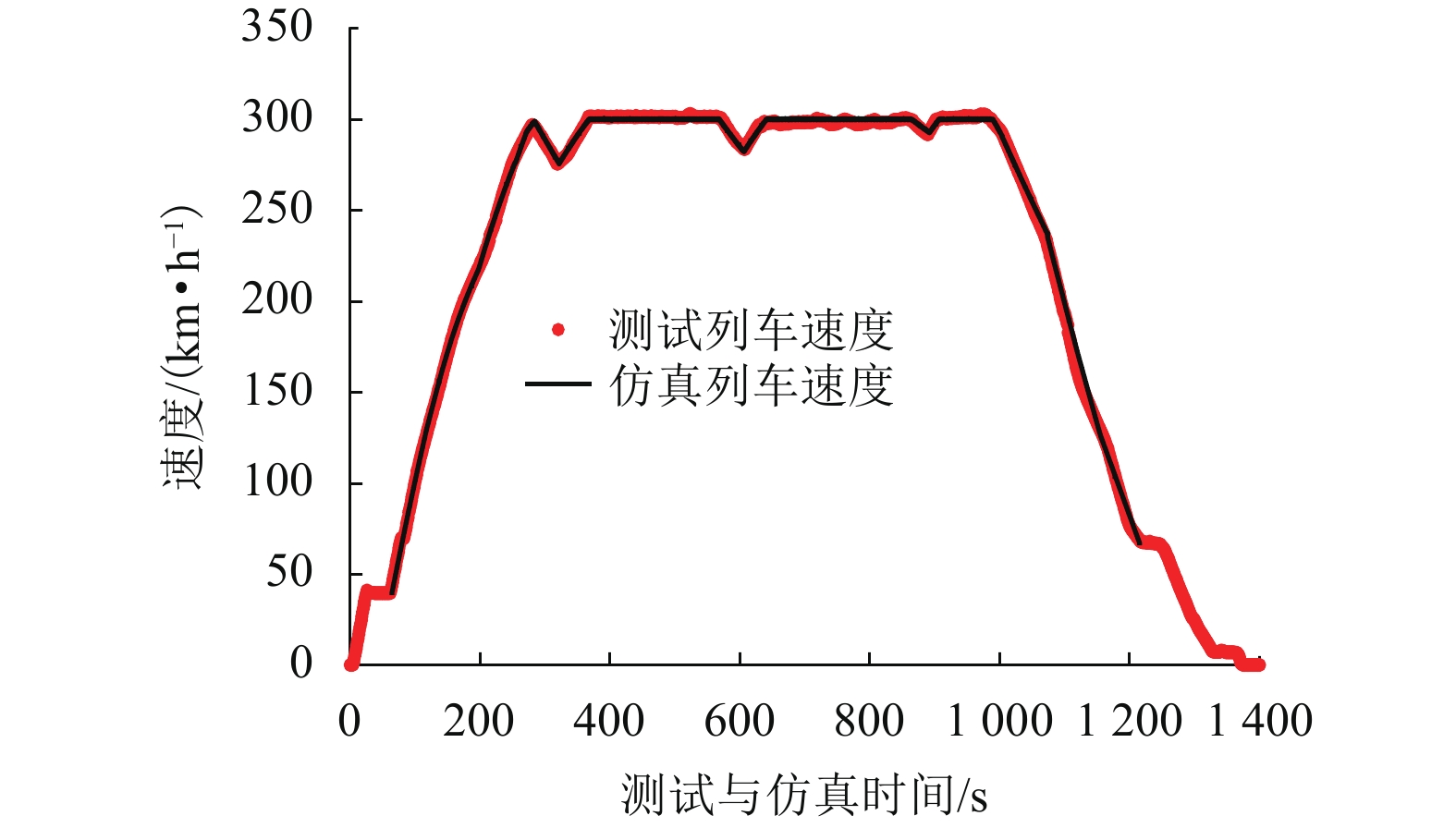
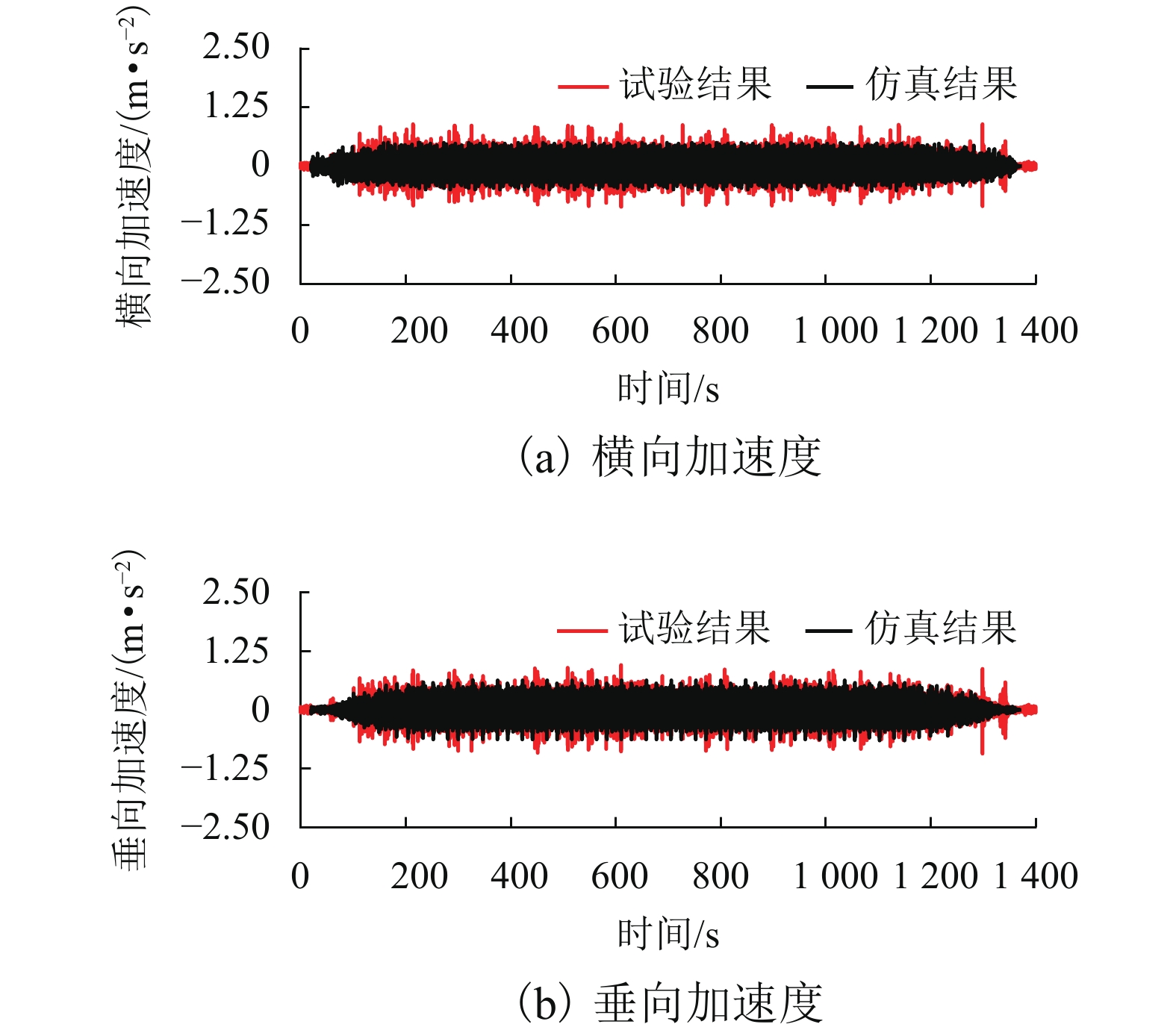
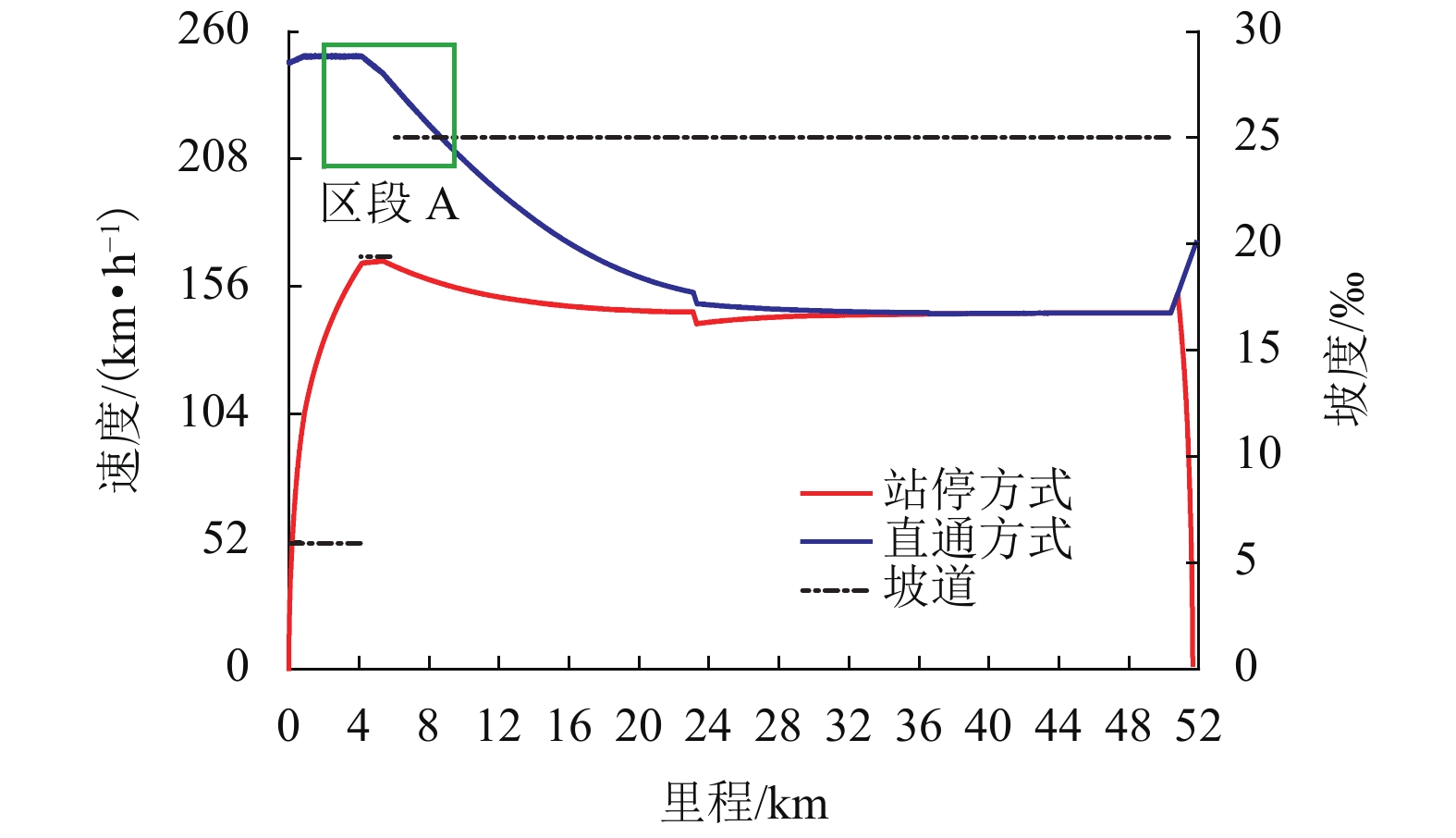
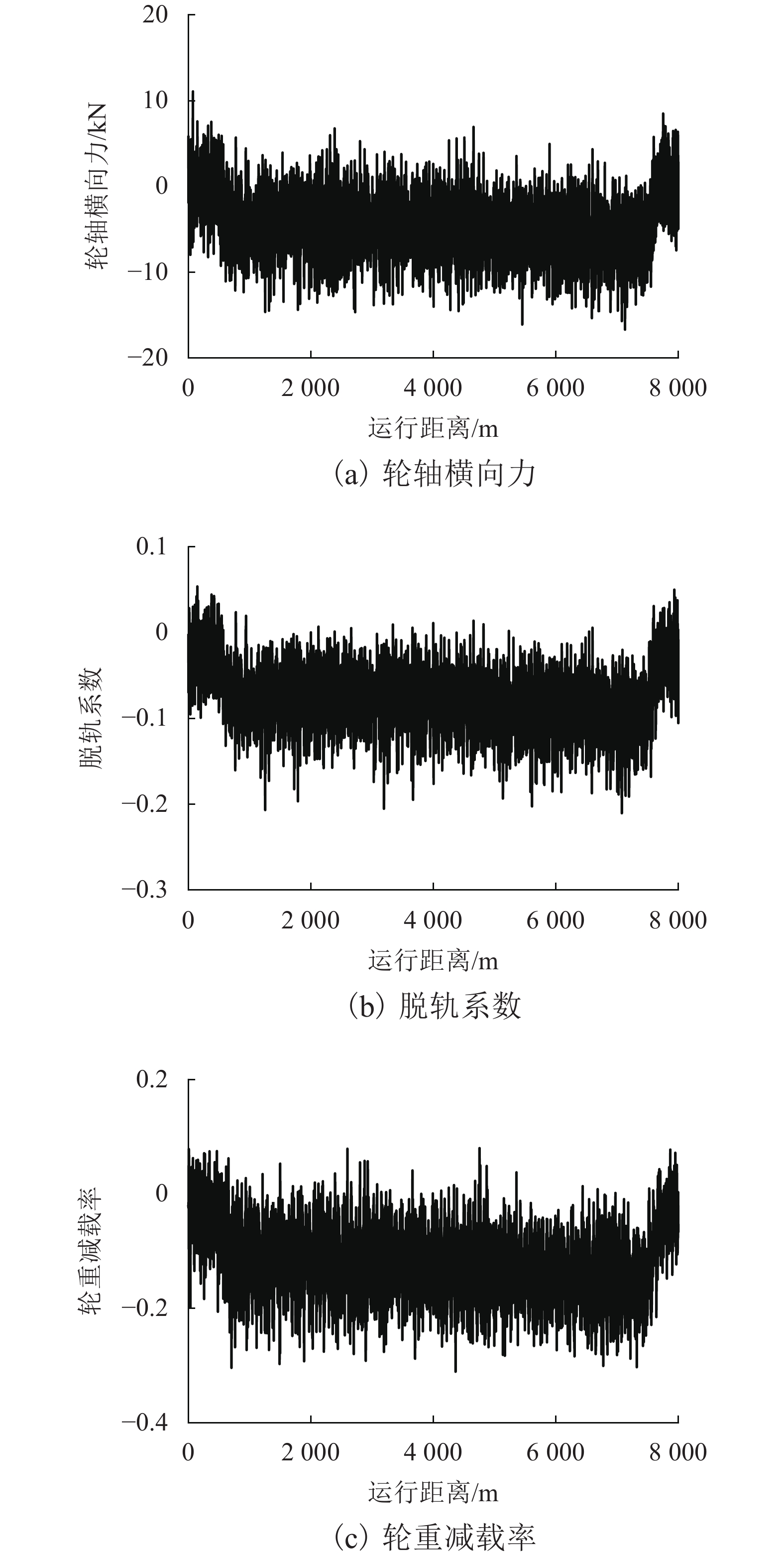
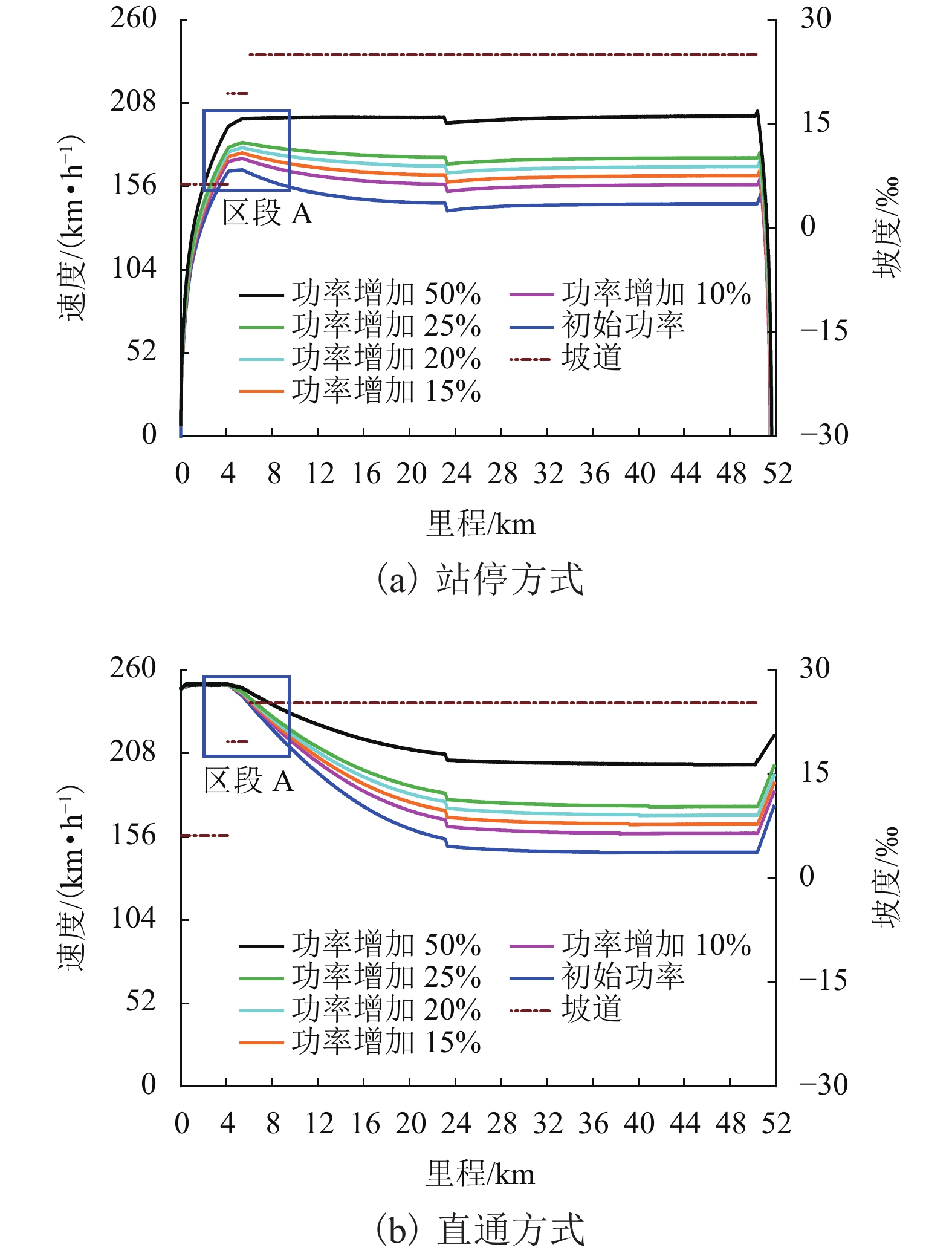
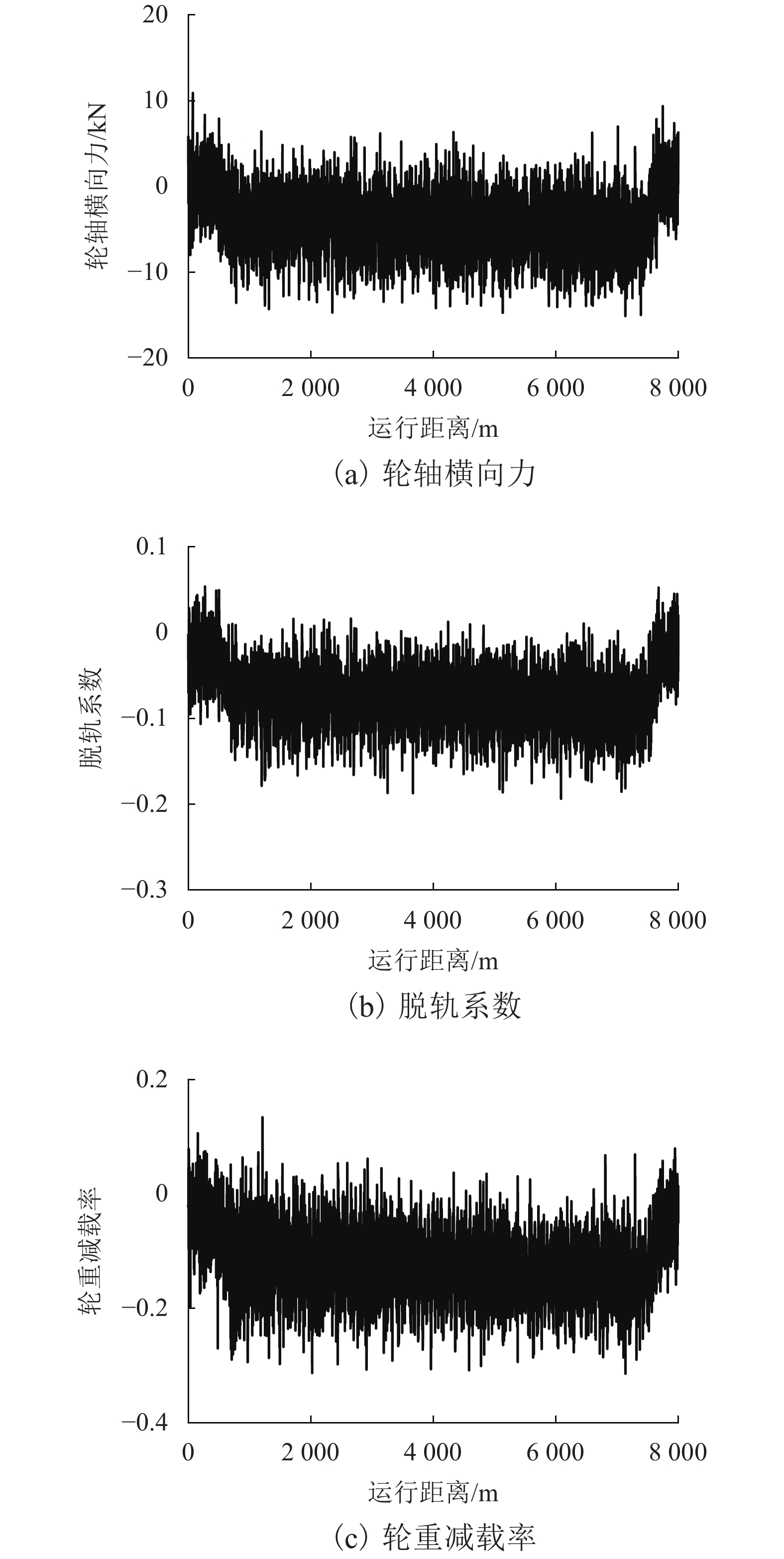
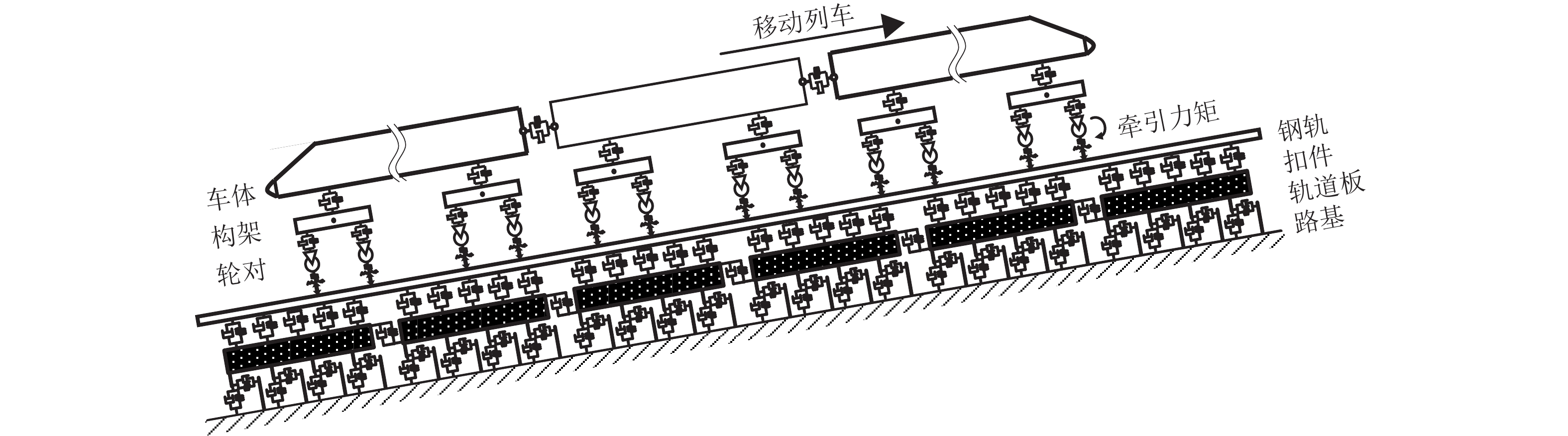
当动车组运行通过长大坡道时，车辆与轨道的耦合振动作用会对列车牵引制动效率产生重要的影响. 为更准确地分析动车组列车通过长大坡道时的运行性能，基于车辆-轨道耦合动力学理论，考虑列车牵引制动行为与线路平纵断面的影响，建立高速铁路长大坡道动车组运行性能分析模型，采用线路试验数据对模型进行验证，对比分析三维模型与传统一维模型的差异，并将模型应用到西安—成都高速铁路（西成高铁）动车组运行性能研究中. 结果表明：本文提出的方法能反映长大坡道对动车组运行速度和动力学性能的影响；传统的一维模型对长大坡道动车组的降速量评估不足，与本方法相比，两者差异为每10 km 5%左右；CRH3A型动车组在西成高铁长大坡道运行会出现严重的降速现象，列车功率提升50%后，降速超过20%的区间减少了7个，全线运行时长缩短了13%，为提高列车运营效率与曲线通过性能，需提高动车组牵引功率.
Abstract:The coupled vibration of vehicle and track has a significant effect on the traction and braking effectiveness of trains when they pass through long steep grades. A vehicle-track coupled dynamics model considering train traction/braking behavior and the horizontal/vertical profile of the track is formulated, which is applied to study the dynamic behavior of a train passing through long steep grades. The proposed numerical model is validated by experimental data, which is also validated by comparing with the traditional calculation method. The proposed model is then used to evaluate the running capability of a high-speed train on the steep grades of Xi’an−Chengdu high-speed railway. The result shows that the proposed three-dimensional (3D) method can predict the influences of steep grades on the speed variation and dynamic performances of the trains. Traditional one-dimensional (1D) model underestimates the speed reduction value of the trains travelling on steep grades. The estimated value of speed reduction calculated by 1D method was around 5% less for every 10 kilometers than that calculated by 3D method. A serious deceleration phenomenon occurs when the CRH3A train running through the long steep grades of Xi’an−Chengdu high-speed railway. When the traction power is increased by 50%, the amount of sections where the reduction of speed over 20% is reduced by 7, and the total running time of the trains is 13% fewer. The trains with higher power traction should be adopted to increase the operational efficiency and enhance curving performance when passing through Xi’an−Chengdu high-speed railway.
-
Key words:
- high-speed railway /
- high-speed train /
- long steep grades /
- numerical model /
- dynamic analysis
-
图 2 CRH2和CRH380AL通过25‰坡道的速度曲线
Figure 2. Speed curves of CRH2 and CRH380AL passing through section with the grade of 25‰
图 5 CRH3A按原功率通过鄠邑—新场街区间的速度曲线
Figure 5. Speed curves when CRH3A passing through Huyi−Xinchangjie with original power
图 6 CRH3A以原功率通过区段A的运行安全性指标
Figure 6. Wheel-rail safety index when CRH3A passing through section A with original power
图 7 CRH3A以不同功率通过鄠邑—新场街区间的速度曲线
Figure 7. Speed curves when CRH3A passing through Huyi−Xinchangjie with different powers
图 8 CRH3A功率提升50%后通过区段A的运行安全性指标
Figure 8. Wheel-rail safety index when CRH3A passing through section A with 1.5 times of power
表 1 西成高铁超长大坡道统计
Table 1. Statistical results of long steep grades in Xi’an−Chengdu high-speed railway
区间 区间长/km 长大坡道数/个 坡度/‰ （长度/km） 鄠邑—新街场 51.9 2 19.0 （1.2） ， 25.0 （45.1） 新街场—佛坪 42.8 4 −22.5 （10.5）， −23.0 （15.6）， −25.0 （3.6），−22.0 （2.5） 佛坪—洋县西 52.9 2 −25.0 （4.2）， −18.0 （9.0） 新集—宁强南 53.5 3 19.0 （5.6）， 25.0 （8.7）， −20.0 （12.5） 中子—广元 37.8 3 −18.0 （1.5）， −15.0 （8.5）， −20.0 （1.9） 剑门关—江油北 51.0 2 20.0 （7.3）， −16.0 （7.3） 
下载: 导出CSV
表 2 最小坡顶速度与区间用时统计结果
Table 2. Statistical results of minimum speeds on uphill and time cost
区间 区间长/km 上行 下行 速度/（km•h−1） 用时/min 速度/（km•h−1） 用时/min 西安北—阿方宫 21.55 206.6 7.45 224.9 7.30 阿方宫—鄠邑 23.60 233.6 7.90 180.2 8.20 鄠邑—新街场 51.85 145.2 22.10 250.0 14.00 新街场—佛坪 42.78 250.0 11.90 157.3 16.50 佛坪—洋县西 52.90 250.0 14.80 164.7 16.00 洋县西—城固北 20.83 184.6 7.30 202.7 7.20 城固北—汉中 28.60 247.5 9.20 185.2 9.23 汉中—新集 22.60 194.1 7.84 227.9 7.50 新集—宁强南 53.50 166.4 17.30 192.5 15.60 宁强南—中子 24.12 190.9 8.30 179.1 9.00 中子—广元 37.80 220.2 11.50 213.3 12.20 广元—剑门关 37.68 184.9 11.70 231.4 11.83 剑门关—江油北 51.03 177.8 15.60 189.6 15.40 江油北—江油 37.39 225.7 11.34 247.0 12.00 合计 506.23 164.23 161.96
下载: 导出CSV
表 3 坡顶降速超20%的区间数量（站停）
Table 3. Amount of sections where the reduction of speed over 20% while the train stop at every station
个 区间 动车组功率配置 100% 110% 115% 120% 125% 150% 上行（西安北—江油） 7 5 4 2 1 0 下行（江油—西安北） 7 5 4 3 2 0
下载: 导出CSV
表 4 CRH3A通过各区间的用时统计
Table 4. Statistics of time cost of CRH3A at each section
min 区间 动车组功率配置 100% 110% 115% 120% 125% 150% 上行（西安北—江油） 164.23 159.05 156.81 154.83 152.85 145.60 下行（江油—西安北） 161.69 152.96 154.73 152.86 150.86 143.77
下载: 导出CSV
-
[1] 石红国,彭其渊,郭寒英. 城市轨道交通牵引计算模型[J]. 交通运输工程学报,2005,5(4): 20-26. doi: 10.3321/j.issn:1671-1637.2005.04.005SHI Hongguo, PENG Qiyuan, GUO Hanying. Traction calculation model of urban mass transit[J]. Journal of Traffic and Transportation Engineering, 2005, 5(4): 20-26. doi: 10.3321/j.issn:1671-1637.2005.04.005 [2] 朱晓敏,徐振华. 基于单质点模型的城市轨道交通列车动力学仿真[J]. 铁道学报,2011,33(6): 14-19. doi: 10.3969/j.issn.1001-8360.2011.06.003ZHU Xiaomin, XU Zhenhua. Dynamic simulation of urban rail transit train based on single-particle model[J]. Journal of the China Railway Society, 2011, 33(6): 14-19. doi: 10.3969/j.issn.1001-8360.2011.06.003 [3] 王开云,黄超. 基于多质点模型的重载列车动能闯坡性能[J]. 交通运输工程学报,2015,15(5): 50-56. doi: 10.3969/j.issn.1671-1637.2015.05.007WANG Kaiyun, HUANG Chao. Kinetic energy uphill performance of heavy-haul train based on multi-particle model[J]. Journal of Traffic and Transportation Engineering, 2015, 15(5): 50-56. doi: 10.3969/j.issn.1671-1637.2015.05.007 [4] ALBRECHT A, HOWLETT P, PUDNEY P, et al. The key principles of optimal train control—part 1:formulation of the model,strategies of optimal type,evolutionary lines,location of optimal switching points[J]. Transportation Research Part B:Methodological, 2016, 94: 482-508. doi: 10.1016/j.trb.2015.07.023 [5] ALBRECHT A, HOWLETT P, PUDNEY P, et al. The key principles of optimal train control—part 2:existence of an optimal strategy,the local energy minimization principle,uniqueness,computational techniques[J]. Transportation Research Part B:Methodological, 2016, 94: 509-538. doi: 10.1016/j.trb.2015.07.024 [6] DING Y, ZHOU F M, BAI Y, et al. Train grade resistance calculation modification model based on measured data[J]. Journal of Transportation Systems Engineering and Information Technology, 2010, 10(6): 82-88. doi: 10.1016/S1570-6672(09)60075-1 [7] 易思蓉,聂良涛,秦方方. 基于动力学分析的高速铁路最小曲线半径研究[J]. 西南交通大学学报,2013,48(1): 16-20,35. doi: 10.3969/j.issn.0258-2724.2013.01.003YI Sirong, NIE Liangtao, QIN Fangfang. Study on minimum curve radius of high-speed railway based on dynamics analysis[J]. Journal of Southwest Jiaotong University, 2013, 48(1): 16-20,35. doi: 10.3969/j.issn.0258-2724.2013.01.003 [8] 王仲林,曾勇,易思蓉. 地铁正线40.0‰最大坡度对行车特性的影响[J]. 西南交通大学学报,2021,56(5): 937-944.WANG Zhonglin, ZENG Yong, YI Sirong. Influence of 40.0‰ maximum gradient of metro main line on running characteristics of trains[J]. Journal of Southwest Jiaotong University, 2021, 56(5): 937-944. [9] IWNICKI S, SPIRYAGIN M, COLE C, et al. Handbook of railway vehicle dynamics[M]. 2nd edition. Boca Raton: CRC Press, 2019. [10] 翟婉明. 车辆-轨道耦合动力学[M]. 4版. 北京: 科学出版社, 2015. [11] 王开云,周维俊,翟婉明,等. 基于动力学理论对高中速客运专线和高低速客货共线铁路平纵面合理匹配的研究[J]. 铁道标准设计,2005,49(7): 1-3. doi: 10.3969/j.issn.1004-2954.2005.07.001WANG Kaiyun, ZHOU Weijun, ZHAI Wanming, et al. Plan and profile matching research of passenger and freight traffic mixed railway based on dynamic theory[J]. Railway Standard Design, 2005, 49(7): 1-3. doi: 10.3969/j.issn.1004-2954.2005.07.001 [12] 凌亮. 高速列车-轨道三维刚柔耦合动力学研究[D]. 成都: 西南交通大学, 2015. [13] LING L, ZHANG Q, XIAO X B, et al. Integration of car-body flexibility into train-track coupling system dynamics analysis[J]. Vehicle System Dynamics, 2018, 56(4): 485-505. doi: 10.1080/00423114.2017.1391397 [14] XIAO X B, LING L, JIN X S. A Study of the derailment mechanism of a high speed train due to an earthquake[J]. Vehicle System Dynamics, 2012, 50(3): 449-470. doi: 10.1080/00423114.2011.597508 [15] HU Y L, LING L, WANG K Y, et al. Curving performance of high-speed trains running on steep grades[C]//Advanced in Dynamics of Vehicles on Roads and Tracks. Cham: Springer, 2019: 460-465. [16] 刘鹏飞. 纵向冲动作用下重载列车与轨道动态相互作用研究[D]. 成都: 西南交通大学, 2015. [17] 国家铁路局. 高速铁路无砟轨道不平顺谱: TB/T 3352—2014 [S]. 北京: 中国铁道出版社, 2015. -
下载:
点击查看大图
计量
- 文章访问数: 351
- HTML全文浏览量: 168
- PDF下载量: 29
- 被引次数: 0