Optimization for Joint Relocation of Carsharing Based on Modular Simulation
-
摘要:
运营商在调度车辆时单独采用员工或顾客调度策略均难以有效解决共享汽车分布不均衡导致的盈利难问题. 为此,在传统时空网络基础上,考虑道路拥堵和用车需求随时间变化对运营的影响,基于C# 语言和O2DES (object-oriented discrete event simulation)离散事件仿真框架,建立由模块化站点和路段模型组成、可高效率运行的共享汽车仿真系统;在此基础上,提出一个以运营商日均净收益最大化为目标,联合决策车辆库存量阈值和行程定价的仿真优化模型,并为解决随机环境下的全局优化问题,设计了EGA-OCBA (elitist genetic algorithm with optimal computing budget allocation)算法;最后,以成都市的5个共享汽车站点为例,验证了仿真优化模型的有效性. 仿真优化结果表明:在相同车队规模下,与采用固定价格的顾客调度策略相比,联合策略可使日均净收益提升10.37%~162.30%;与单独的员工调度策略相比,联合策略可使日均净收益提升15.34%.
-
关键词:
- 共享汽车 /
- 离散事件仿真 /
- 动态定价 /
- 阈值触发调度 /
- 精英遗传算法(EGA) /
- 最优计算量分配(OCBA)
Abstract:It is difficult for operators to effectively solve the profitable difficulty caused by the imbalanced distribution of shared vehicles when considering staff-based and customer-based relocation alone. Thus, based on the traditional space-time network, the impact of time-varying road congestion and trip demands on the operation is considered. Based on C# language and O2DES (object-oriented discrete event simulation) framework, an efficient carsharing system model composed of modular station and road segment models is built. Moreover, a simulation-optimization model that jointly determines vehicle inventory thresholds and trip pricing is proposed to maximize the daily net revenue of operators. In order to solve the global optimization problem in a random environment, an elitist genetic algorithm (EGA) with optimal computing budget allocation (OCBA) is designed. Finally, a case study in Chengdu with five sites is conducted to demonstrate the efficiency of the proposed simulation-optimization model. The results show that with the same fleet size, the optimal design can increase the average daily net revenue by 10.37%−162.30% compared with customer-based relocation (fixed pricing); the optimized scheme can increase the profit by 15.34% compared with separate staff-based relocation.
-
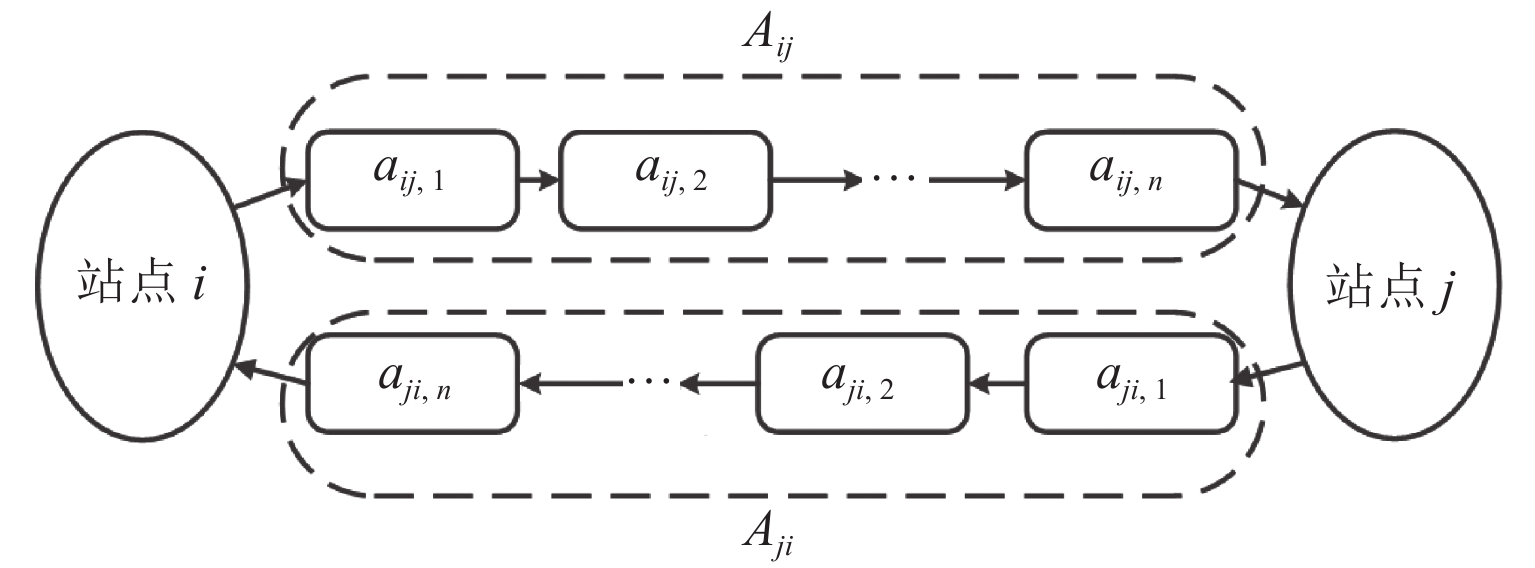
表 1 路径模块事件
Table 1. Events of path module
类型 符号 说明 输入 $\alpha _{ij,n}^{( { {\text{p} }1} )}$ 车辆 h 进入路段,$ \forall h \notin {H_{ij,n}}\left( \tau \right) $ 内部 $ \beta _{ij,n}^{( {{\text{p}}1} )} $ 更新车辆的剩余路程和时间戳 $\beta _{ij,n}^{( { {\text{p} }2} )}$ 车辆 h 加入到路段车辆集合 $ \beta _{ij,n}^{( {{\text{p}}3} )} $ 根据路径状态计算平均速度 $ \beta _{ij,n}^{( {{\text{p}}4} )} $ 更新共享汽车的预计离开时刻 $ \beta _{ij,n}^{( {{\text{p}}5} )} $ 共享汽车 h “尝试”离开路段 输出 $ \gamma _{ij,n}^{( {{\text{p}}1} )} $ 车辆 h 离开路段,$ \forall h \in {H_{ij,n}}( \tau ) $ 表 2 站点模块事件
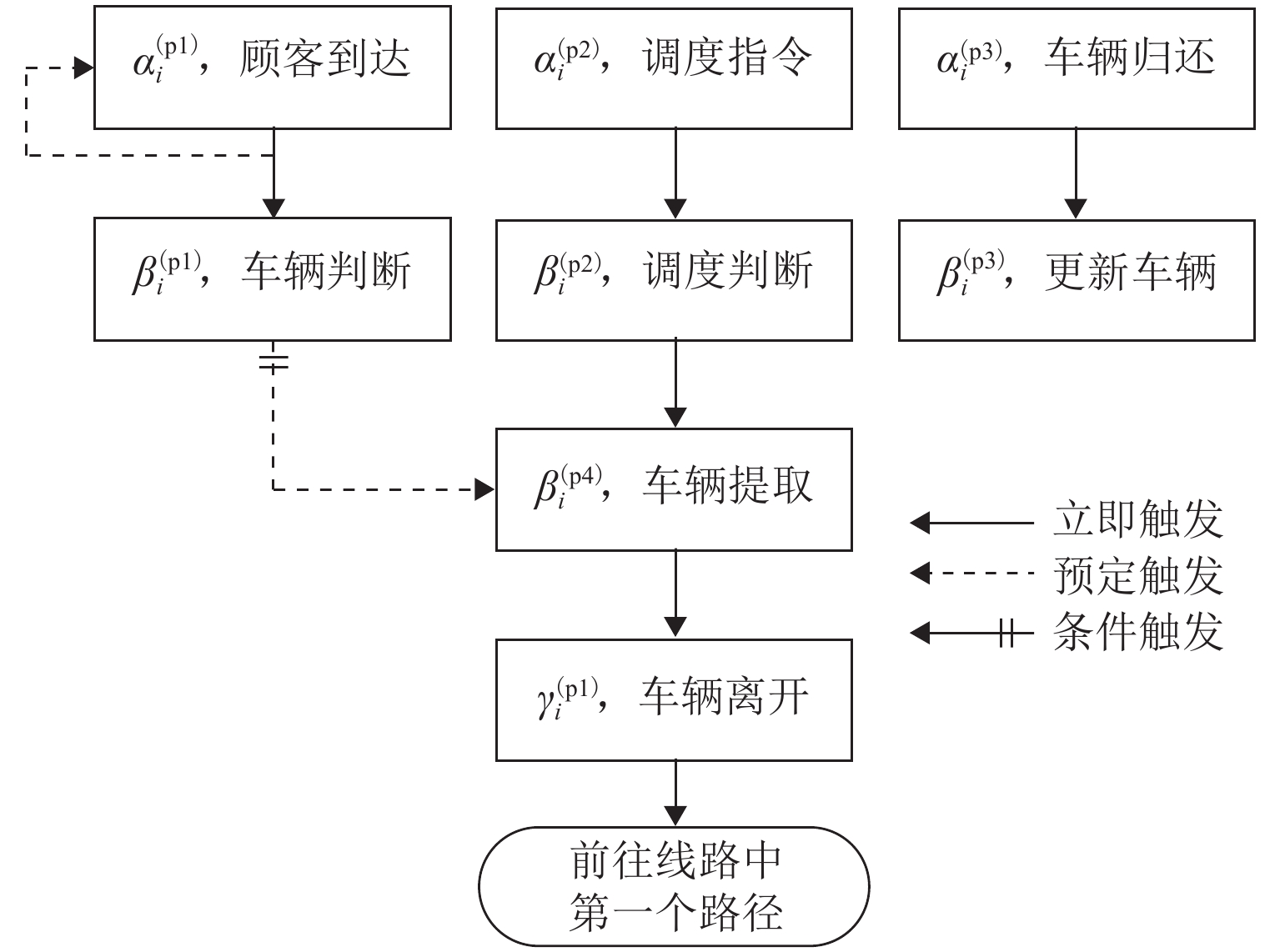
Table 2. Events of station module
类型 符号 说明 输入 $ \alpha _i^{( {{\text{p}}1} )} $ 顾客到达车站 $ \alpha _i^{( {{\text{p2}}} )} $ 下达调度指令,向车站 i 调车 $ \alpha _i^{( {{\text{p3}}} )} $ 表示车辆 h 归还到站点 i 内部 $ \beta _i^{( {{\text{p1}}} )} $ 判断车辆库存是否足够 $ \beta _i^{( {{\text{p2}}} )} $ 更新车辆集合,车辆选择去向 $ \beta _i^{( {{\text{p3}}} )} $ 判断是否执行调度指令 $ \beta _i^{( {{\text{p4}}} )} $ 更新车辆和调度员数量 输出 $ \gamma _i^{( {{\text{p1}}} )} $ 表示车辆 h 离开站点 i,$ \forall h \in {H_i\left( \tau \right)} $ 表 3 车站初始状态
Table 3. Initial state of stations
站点 车辆数/辆 调度员数/人 1 6 2 2 4 2 3 5 2 4 5 2 5 5 2 表 4 动态定价方案
Table 4. Dynamic pricing scheme
元 时段 $ {A_{12}} $ $ {A_{13}} $ $ {A_{14}} $ $ {A_{15}} $ $ {A_{21}} $ $ {A_{23}} $ $ {A_{24}} $ $ {A_{25}} $ $ {A_{31}} $ $ {A_{32}} $ 06:00—09:00 37.0 22.0 40.0 24.0 48.0 40.0 34.0 28.0 16.0 54.0 09:00—12:00 39.0 56.0 12.0 12.0 51.0 23.0 31.0 25.0 13.0 19.0 12:00—15:00 50.0 38.0 41.0 19.0 43.0 58.0 13.0 51.0 27.0 57.0 15:00—18:00 37.0 34.0 20.0 35.0 17.0 20.0 47.0 43.0 38.0 13.0 18:00—21:00 36.0 36.0 42.0 14.0 55.0 50.0 54.0 15.0 23.0 53.0 21:00—24:00 33.0 54.0 28.0 33.0 44.0 32.0 43.0 43.0 44.0 10.0 时段 $ {A_{34}} $ $ {A_{35}} $ $ {A_{42}} $ $ {A_{42}} $ $ {A_{43}} $ $ {A_{45}} $ $ {A_{51}} $ $ {A_{52}} $ $ {A_{53}} $ $ {A_{54}} $ 06:00—09:00 46.0 31.0 33.0 37.0 56.0 37.0 54.0 10.0 10.0 34.0 09:00—12:00 48.0 58.0 10.0 25.0 35.0 12.0 27.0 59.0 36.0 34.0 12:00—15:00 48.0 32.0 27.0 14.0 34.0 48.0 55.0 32.0 12.0 22.0 15:00—18:00 25.0 48.0 37.0 29.0 28.0 27.0 30.0 16.0 20.0 19.0 18:00—21:00 53.0 30.0 21.0 58.0 24.0 22.0 12.0 18.0 57.0 42.0 21:00—24:00 45.0 23.0 39.0 40.0 50.0 54.0 54.0 42.0 51.0 39.0 表 5 阈值触发调度方案
Table 5. Threshold-triggering relocation scheme
辆 时段 $S_{ 1}^{ {\text{up} } }\left( \tau \right)$ $S_{ 1}^{ {\text{low} } }\left( \tau \right)$ $S_{ 2}^{ {\text{up} } }\left( \tau \right)$ $S_{ 2}^{ {\text{low} } }\left( \tau \right)$ $S_{ 3}^{ {\text{up} } }\left( \tau \right)$ $S_{ 3}^{ {\text{low} } }\left( \tau \right)$ $S_{ 4}^{ {\text{up} } }\left( \tau \right)$ $S_{ 4}^{ {\text{low} } }\left( \tau \right)$ $S_{ 5}^{ {\text{up} } }\left( \tau \right)$ $S_{ 5}^{ {\text{low} } }\left( \tau \right)$ 06:00—09:00 19 18 17 5 17 6 15 12 9 6 09:00—12:00 23 13 11 7 12 5 24 4 17 2 12:00—15:00 13 11 20 19 4 2 21 20 21 2 15:00—18:00 15 5 15 6 19 1 7 5 22 0 18:00—21:00 9 6 12 6 13 2 24 4 23 7 21:00—24:00 12 6 17 16 7 0 22 1 23 15 表 6 策略净收益对比
Table 6. Net income comparison among strategies
元 策略 收益 策略 收益 联合调度策略 10374.68 动态定价无调度 8979.37 定价 15 元有调度 3955.25 定价 15 元无调度 3756.46 定价 20 元有调度 5888.43 定价 20 元无调度 5466.05 定价 25 元有调度 7055.95 定价 25 元无调度 6880.96 定价 30 元有调度 7863.41 定价 30 元无调度 7193.02 定价 35 元有调度 9234.57 定价 35 元无调度 8043.68 定价 40 元有调度 9826.50 定价 40 元无调度 8106.93 定价 45 元有调度 9504.22 定价 45 元无调度 7698.97 定价 50 元有调度 7973.05 定价 50 元无调度 7203.43 -
[1] MARTIN E W, SHAHEEN S A. Greenhouse gas emission impacts of carsharing in North America[J]. IEEE Transactions on Intelligent Transportation Systems, 2011, 12(4): 1074-1086. doi: 10.1109/TITS.2011.2158539 [2] DI FEBBRARO A, SACCO N, SAEEDNIA M. One-way carsharing[J]. Transportation Research Record: Journal of the Transportation Research Board, 2012, 2319(1): 113-120. doi: 10.3141/2319-13 [3] JORGE D, CORRELA G H D A. Carsharing systems demand estimation and defined operations: a literature review[J]. European Journal of Transport & Infrastructure Reaserch, 2013, 13(3): 201-220. [4] WANG L, LIU Q, MA W J. Optimization of dynamic relocation operations for one-way electric carsharing systems[J]. Transportation Research Part C: Emerging Technologies, 2019, 101: 55-69. doi: 10.1016/j.trc.2019.01.005 [5] BARTH M, TODD M. Simulation model performance analysis of a multiple station shared vehicle system[J]. Transportation Research Part C: Emerging Technologies, 1999, 7(4): 237-259. doi: 10.1016/S0968-090X(99)00021-2 [6] CATALANO M, CASTO B L, MIGLIORE M. Car sharing demand estimation and urban transport demand modelling using stated preference techniques[J]. European Transport, 2008, 40: 33-50. [7] CHEU R L, XU J X, KEK A G H, et al. Forecasting shared-use vehicle trips with neural networks and support vector machines[J]. Transportation Research Record: Journal of the Transportation Research Board, 2006, 1968(1): 40-46. doi: 10.1177/0361198106196800105 [8] KEK A G H, CHEU R L, CHOR M L. Relocation simulation model for multiple-station shared-use vehicle systems[J]. Transportation Research Record: Journal of the Transportation Research Board, 2006, 1986(1): 81-88. doi: 10.1177/0361198106198600111 [9] KEK A G H, CHEU R L, MENG Q, et al. A decision support system for vehicle relocation operations in carsharing systems[J]. Transportation Research Part E: Logistics and Transportation Review, 2009, 45(1): 149-158. doi: 10.1016/j.tre.2008.02.008 [10] CAO G Y, WANG L, JIN Y, et al. Determination of the vehicle relocation triggering threshold in electric car-sharing system[C]//Proceedings of 2016 Chinese Intelligent Systems Conference. [S.1.]: Spring, 2016: 11-22 [11] 王宁,舒雅静,唐林浩,等. 基于动态定价的共享汽车自适应调度策略[J]. 交通运输系统工程与信息,2018,18(5): 12-17,74. doi: 10.16097/j.cnki.1009-6744.2018.05.003WANG Ning, SHU Yajing, TANG Linhao, et al. Adaptive scheduling strategy in car-sharing system based on feedback dynamic pricing[J]. Journal of Transportation Systems Engineering and Information Technology, 2018, 18(5): 12-17,74. doi: 10.16097/j.cnki.1009-6744.2018.05.003 [12] 王宁,郑文晖,刘向,等. 基于用户激励的共享电动汽车调度成本优化[J]. 同济大学学报(自然科学版),2018,46(12): 1668-1675,1721. doi: 10.11908/j.issn.0253-374x.2018.12.008WANG Ning, ZHENG Wenhui, LIU Xiang, et al. Relocation cost optimization model of electric vehicle sharing based on user incentive[J]. Journal of Tongji University (Natural Science), 2018, 46(12): 1668-1675,1721. doi: 10.11908/j.issn.0253-374x.2018.12.008 [13] JORGE D, MOLNAR G, DE ALMEIDA CORREIA G H. Trip pricing of one-way station-based carsharing networks with zone and time of day price variations[J]. Transportation Research Part B: Methodological, 2015, 81: 461-482. doi: 10.1016/j.trb.2015.06.003 [14] XU M, MENG Q, LIU Z Y. Electric vehicle fleet size and trip pricing for one-way carsharing services considering vehicle relocation and personnel assignment[J]. Transportation Research Part B: Methodological, 2018, 111: 60-82. doi: 10.1016/j.trb.2018.03.001 [15] NOURINEJAD M, ROORDA M J. A dynamic carsharing decision support system[J]. Transportation Research Part E: Logistics and Transportation Review, 2014, 66: 36-50. doi: 10.1016/j.tre.2014.03.003 [16] CHEN C H, LEE L H. Stochastic simulation optimization: optimal computing budget allocation[M]. Singapore: World Scientific, 2010: 40-60. [17] LI H B, ZHOU C H, LEE B K, et al. Capacity planning for mega container terminals with multi-objective and multi-fidelity simulation optimization[J]. IISE Transactions, 2017, 49(9): 849-862. doi: 10.1080/24725854.2017.1318229 [18] LI H B, ZHU Y C, CHEN Y X, et al. The object-oriented discrete event simulation modeling: a case study on aircraft spare part management[C]//2015 Winter Simulation Conference (WSC). Piscataway: IEEE, 2015: 3514-3525. [19] ZEIGLER B P. Hierarchical, modular discrete-event modelling in an object-oriented environment[J]. Simulation, 1987, 49(5): 219-230. doi: 10.1177/003754978904900506 [20] ZEIGLER B P, PRAEHOFER H, KIM T G. Theory of modeling and simulation: integrating discrete event and continuous complex dynamic systems[M]. Pittsburgh: Academic Press, 2000: 4-5. [21] ZHOU C H, LEE L H, CHEW E P, et al. A modularized simulation for traffic network in container terminals via network of servers with dynamic rates[C]//Proceedings of 2017 Winter Simulation Conference (WSC). Las Vegas: IEEE, 2017: 3150-3161. [22] HU L, ZHAO B, ZHU J X, et al. Two time-varying and state-dependent fluid queuing models for traffic circulation systems[J]. European Journal of Operational Research, 2019, 275(3): 997-1019. doi: 10.1016/j.ejor.2019.01.020 [23] CHEN H C, CHEN C H, YUCESAN E. Computing efforts allocation for ordinal optimization and discrete event simulation[J]. IEEE Transactions on Automatic Control, 2000, 45(5): 960-964. doi: 10.1109/9.855560 [24] CHEN C H, LIN J W, YÜCESAN E, et al. Simulation budget allocation for further enhancing the efficiency of ordinal optimization[J]. Discrete Event Dynamic Systems, 2000, 10(3): 251-270. doi: 10.1023/A:1008349927281 [25] XIAO H, LEE L H. Simulation optimization using genetic algorithms with optimal computing budget allocation[J]. Journal of Simulation, 2014, 90(10): 1146-1157. doi: 10.1177/0037549714548095 [26] MANDL C E. Evaluation and optimization of urban public transportation networks[J]. European Journal of Operational Research, 1980, 5(6): 396-404. doi: 10.1016/0377-2217(80)90126-5 -




 下载:
下载: