Experimental Study on Vertical Bearing Capacity and Cyclic Compression Behavior of Soilbags
-
摘要:
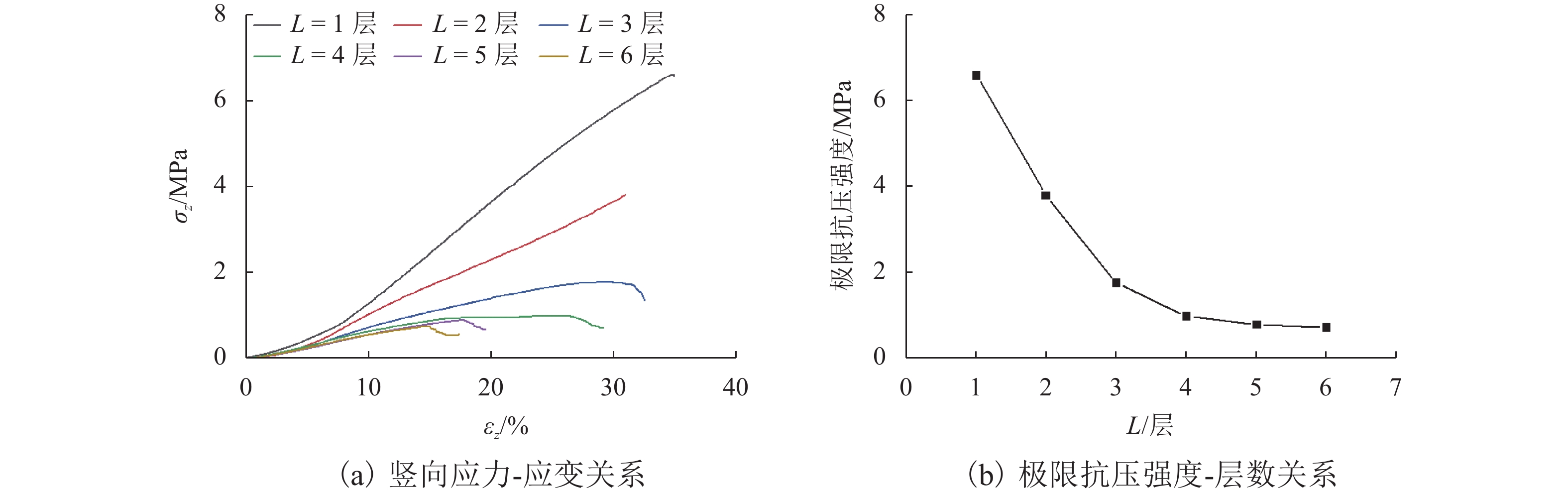
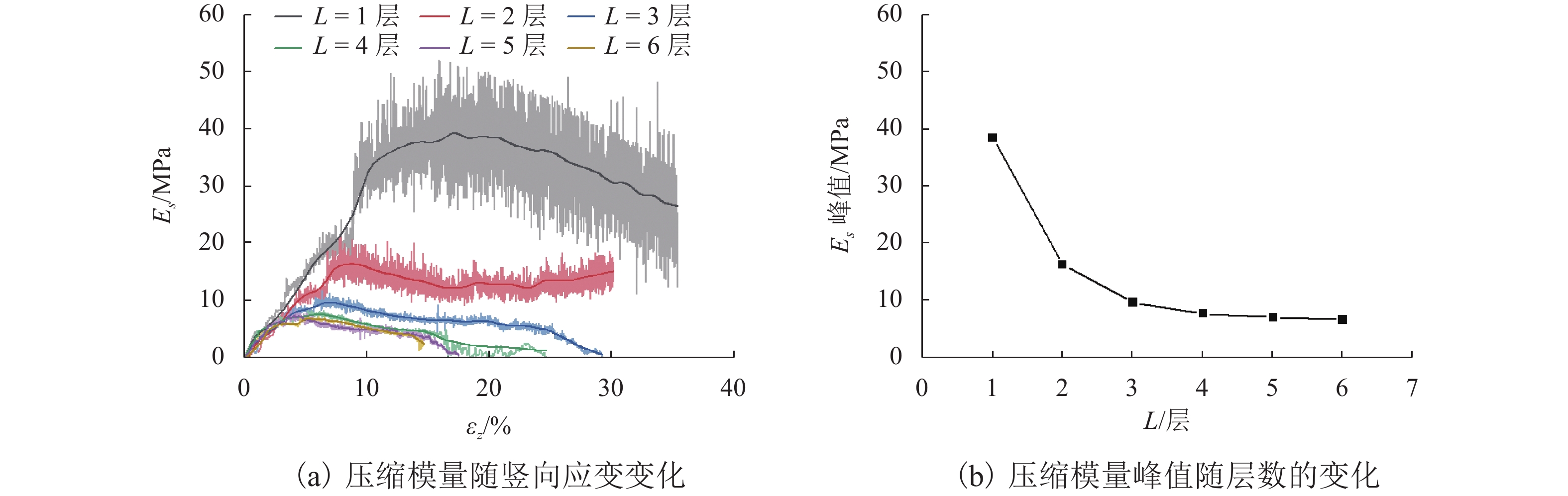
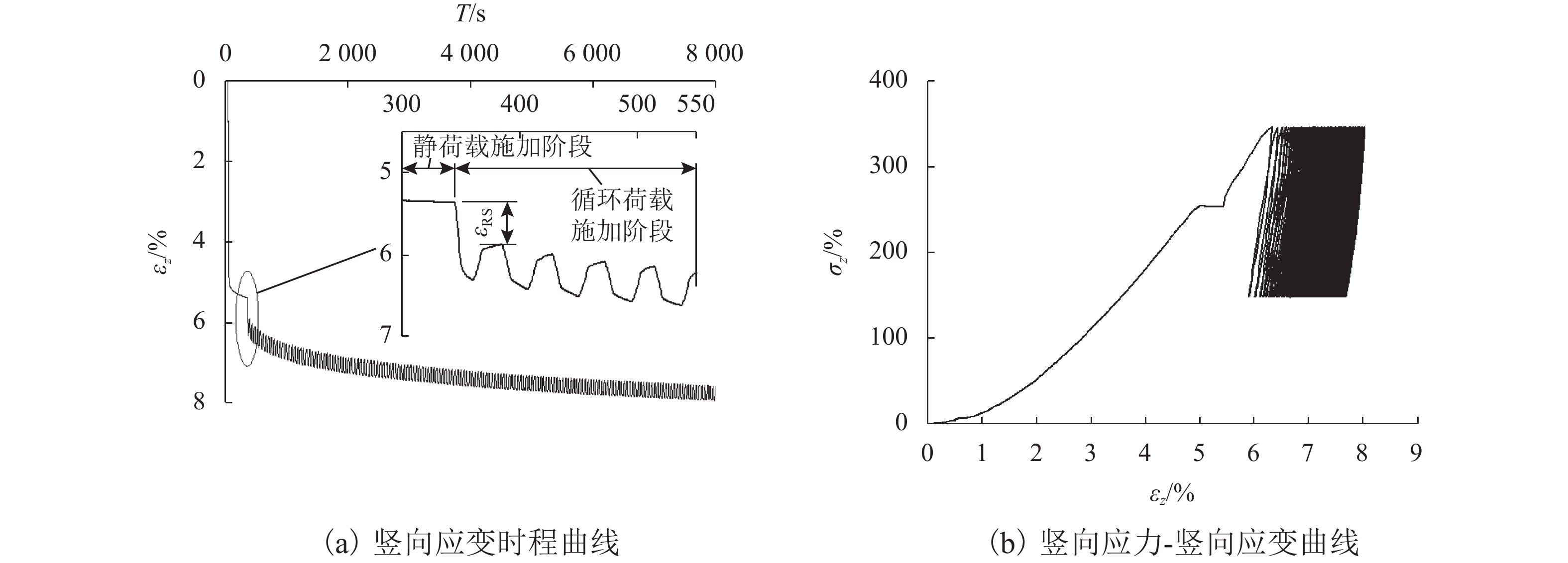
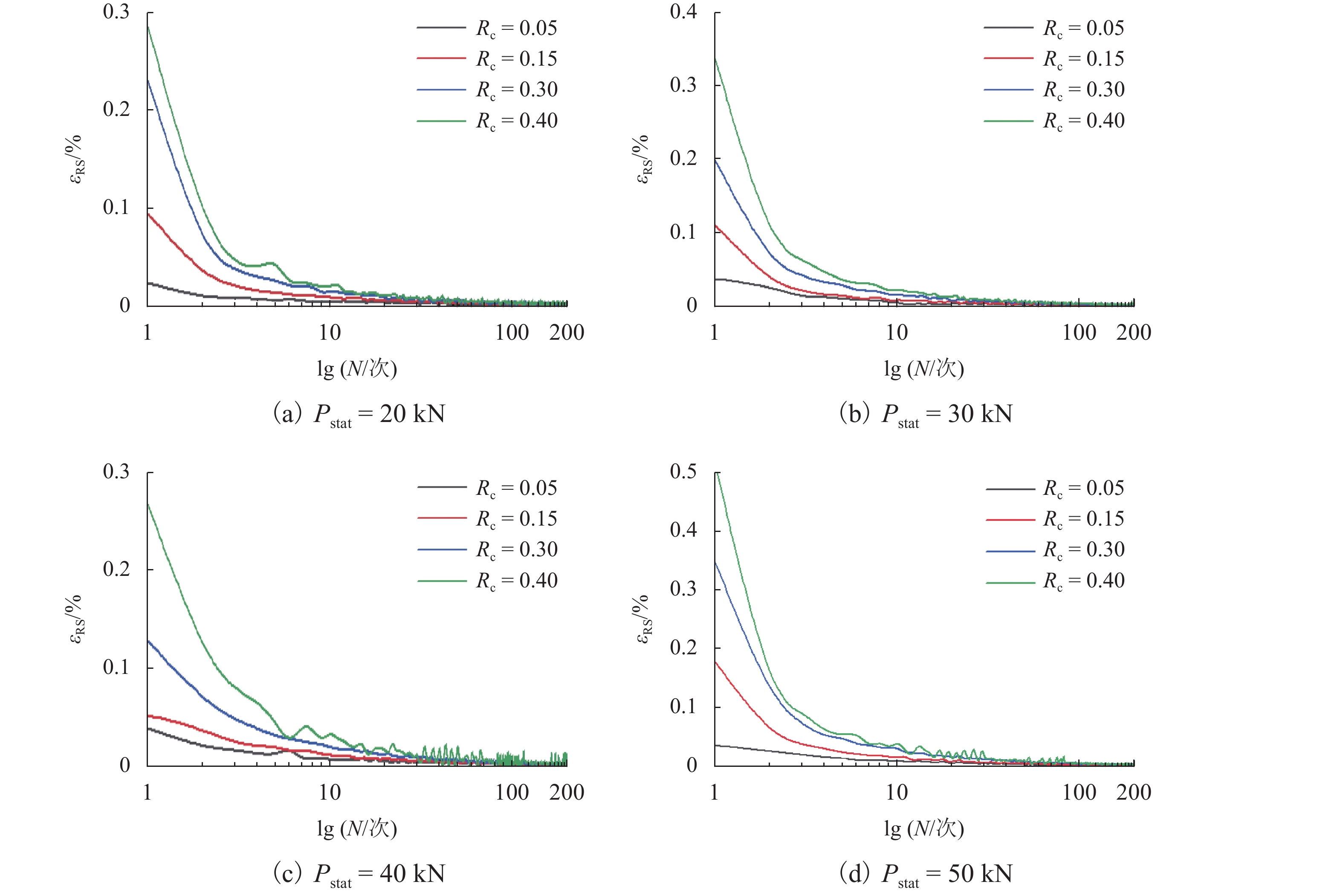
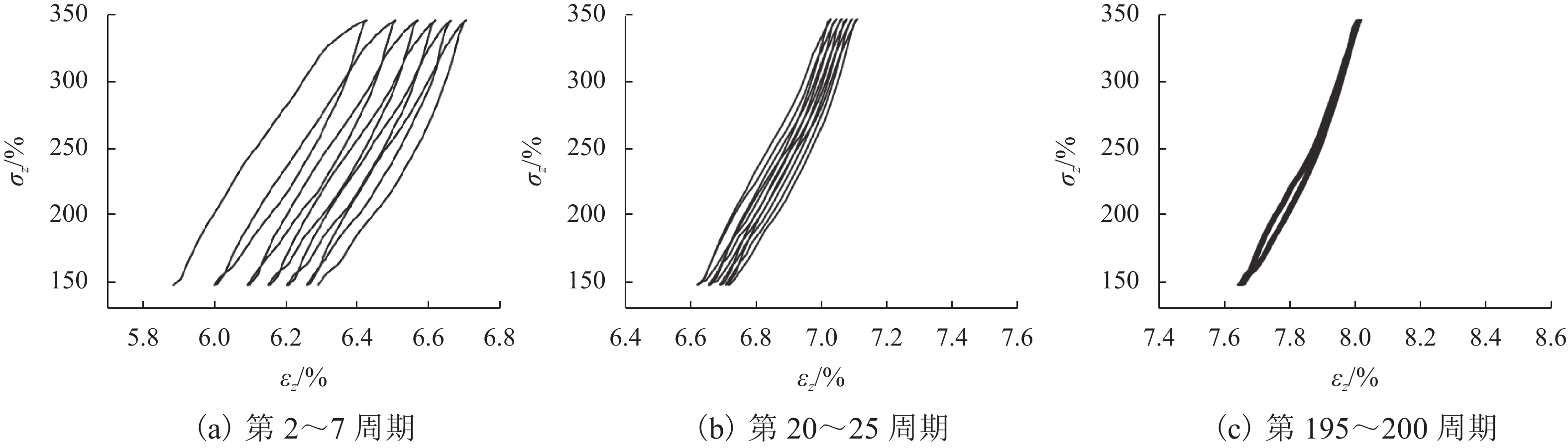
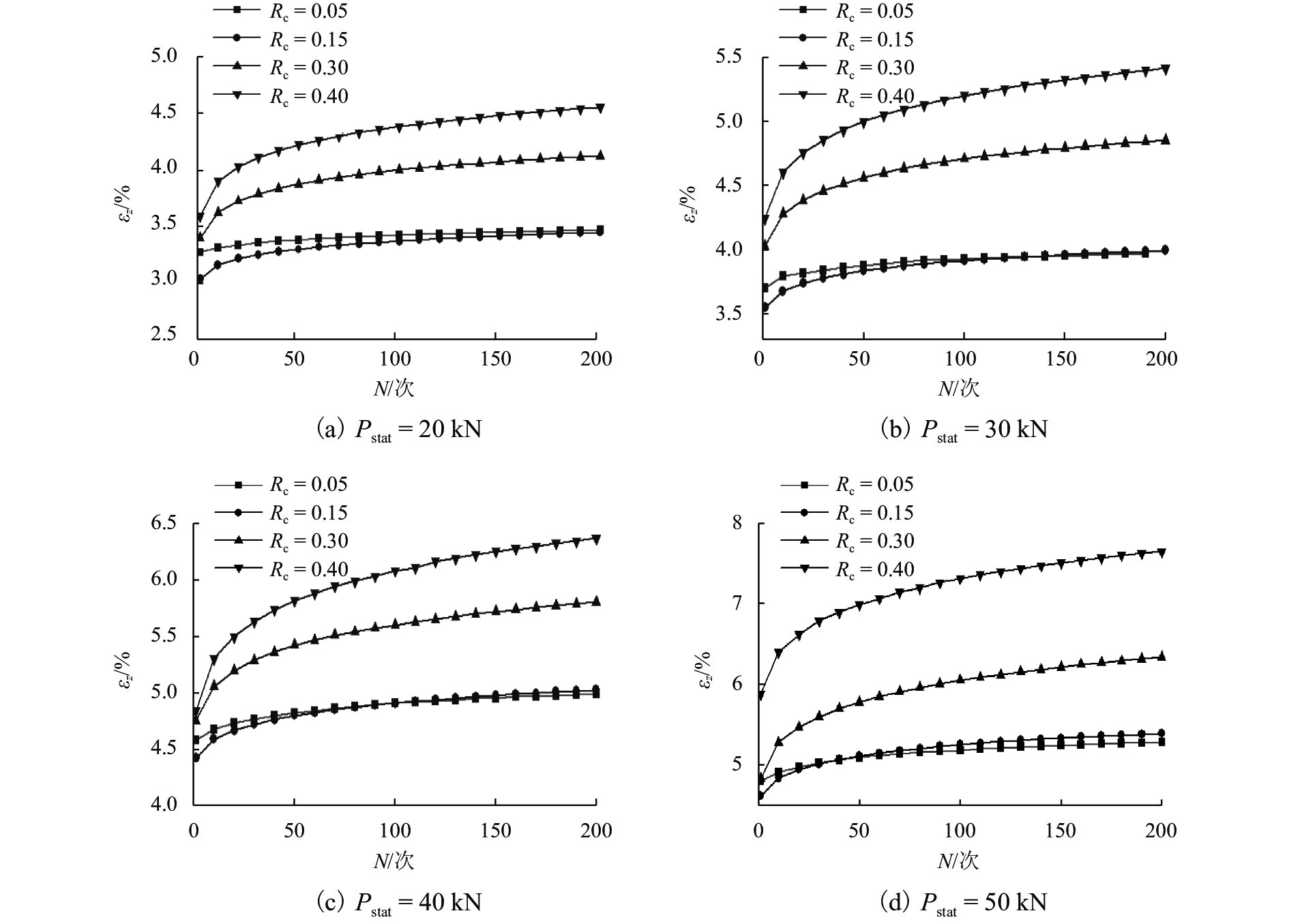
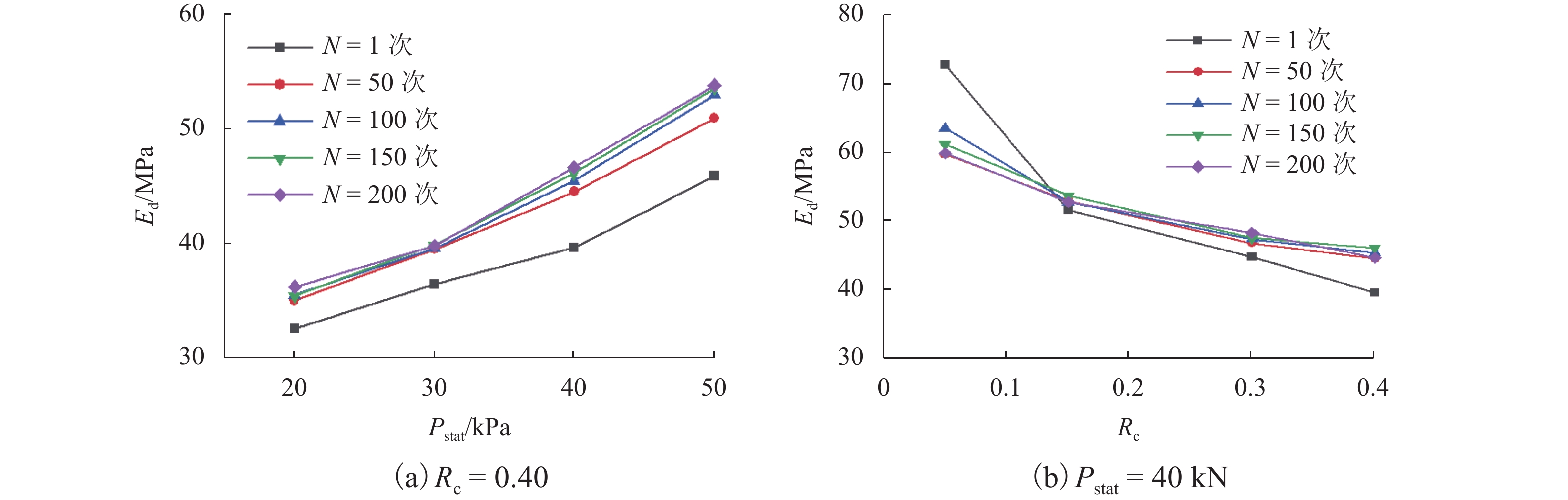
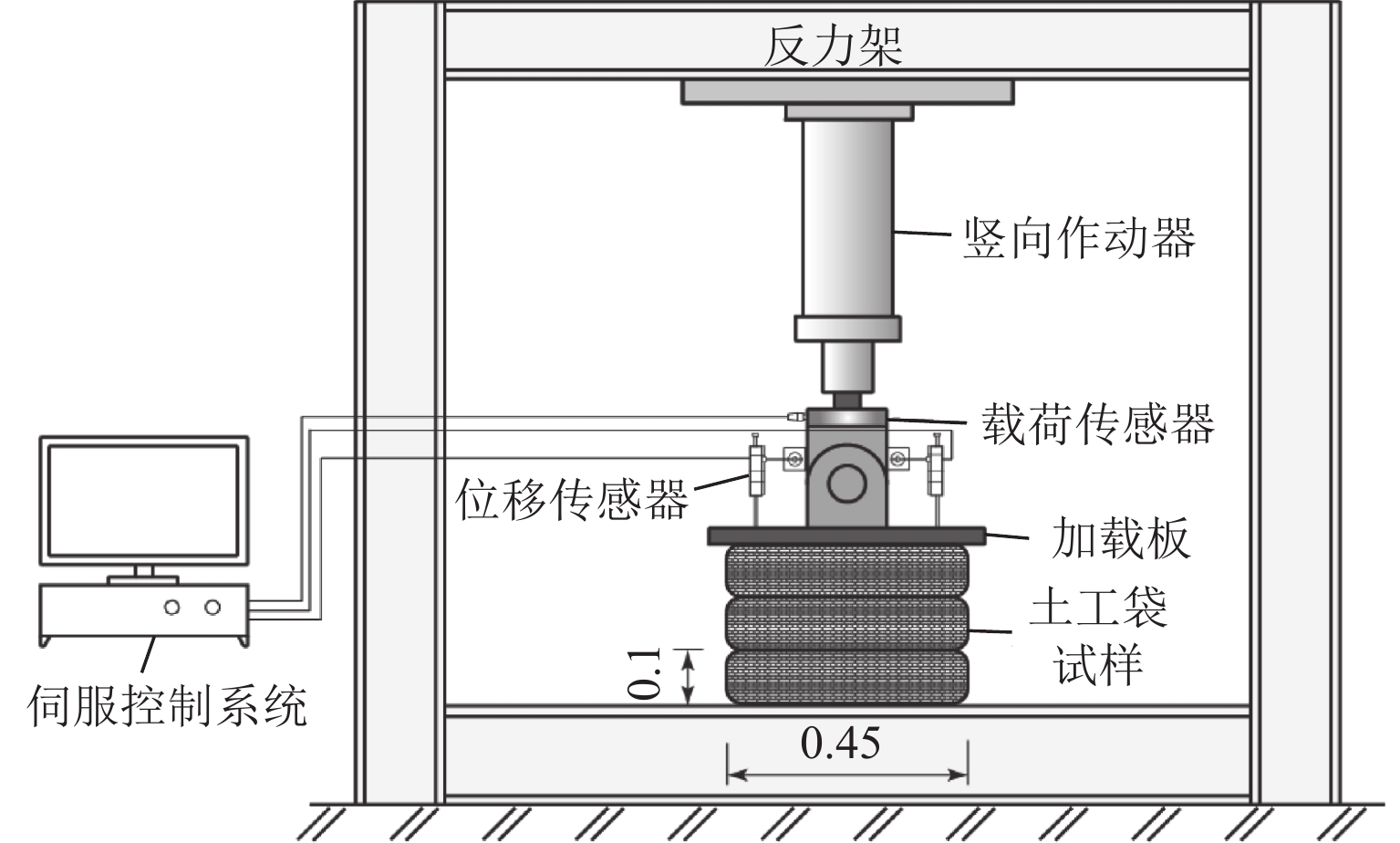
土工袋技术近年来已被成功应用于房屋地基加固，具有较好的隔震效果，但其在动荷载条件下的变形特性尚未深入研究. 为了进一步分析土工袋竖向承载能力及变形特性，开展一系列室内土工袋组合体无侧限极限抗压强度试验以及循环压缩试验，并通过控制循环次数、上部静荷载及循环荷载比值的大小研究其对土工袋组合体竖向应力、应变和动压缩模量的影响. 试验结果表明：随着层数的增加，土工袋组合体极限抗压强度逐渐减小并趋于稳定值0.7 MPa，压缩模量峰值也随之减小并稳定于6.73 MPa；循环压缩试验初期土工袋组合体塑性变形显著，每一循环周期产生的竖向残余应变随着循环次数的增加逐渐减小并趋于0；动压缩模量在试验过程中基本保持稳定，不受循环次数的影响；随着上部静荷载的增大，土工袋组合体动压缩模量逐渐增大，上部静荷载为50 kN的土工袋组合体经过200次循环荷载作用后动压缩模量达到53.87 MPa；反之，循环荷载比值越大，动压缩模量越小，循环荷载比值为0.4条件下土工袋组合体在200次循环荷载作用后仍能达到49.39 MPa；在竖向动荷载作用下，土工袋能够满足其作为隔震材料的承载能力及稳定性要求.
Abstract:Soilbags have been successfully applied to the reinforcement of building foundation with obvious effect on seismic isolation, but their deformation characteristics under dynamic load have not been studied in depth yet. In order to further analyze the vertical bearing capacity and deformation characteristics of soilbags, a series of laboratory unconfined ultimate loading tests and cyclic compression tests were conducted, and the effect of the number of loading cycles, the static load, and the cyclic load ratio on the dynamic characteristics of soilbags was studied in terms of the vertical stress-strain variation and the dynamic compression modulus. The test results show that with the increase of the number of layers, the ultimate strength of stacked soilbags decreased gradually and tended to a stable value of 0.7 MPa, and the peak compression modulus also decreased and stabilized at 6.73 MPa. An obvious plastic deformation of stacked soilbags was observed at the beginning of the cyclic compression test, and the vertical residual strain generated in each cycle decreased gradually and tended to zero with the increase of the number of cycles. The dynamic compression modulus was basically stable throughout the whole testing process, and was not affected by the number of cyclic loads. With the increase of the upper static load, the dynamic compression modulus of the stacked soilbags increased gradually. After 200 cycles of loading, the dynamic compression modulus of soilbags with the static load of 50 kN reached 53.87 MPa. However, it significantly decreased with the increased cyclic load ratio. When the cyclic load ratio was 0.4, the dynamic compression modulus of soilbags could still reached 49.39 MPa after 200 cycles of loading. In general, under the action of vertical dynamic load, the soilbags can satisfy the requirements of bearing capacity and stability as a kind of seismic isolation material.
-
Key words:
- soilbags /
- compressive strength /
- cyclic loads /
- residual strain /
- dynamic compression modulus
-
图 1 土工袋循环压缩试验装置示意（单位：m）
Figure 1. Schematic of cyclic compression experiment device for soilbags (unit： m)
图 4 循环压缩试验第i个循环周期竖向应力-应变示意
Figure 4. Schematic of vertical stress-strain relation during the ith loading cycle
图 5 不同层数条件下土工袋竖向承载特性试验结果
Figure 5. Test results of bearing capacities of soilbags with different layers
图 6 不同层数条件下土工袋组合体压缩模量
Figure 6. Development of compression modulus of stacked soilbags with different layers
图 7 Pstat=50 kN，Rc=0.4条件下土工袋组合体循环压缩试验结果
Figure 7. Results of cyclic compression tests of stacked soilbags under Pstat=50 kN and Rc=0.4
图 8 竖向残余应变随循环次数的变化
Figure 8. Variation of vertical residual strain of stacked soilbags with loading cycles
图 9 不同循环阶段滞回圈演化（Pstat=50 kN, Rc=0.40）
Figure 9. Evolution of hysteresis loops through different cyclic stages （Pstat=50 kN, Rc=0.40）
图 10 累积竖向应变随循环次数的变化
Figure 10. Variation of accumulated vertical strain of stacked soilbags with loading cycles
图 11 土工袋组合体动压缩模量随循环次数的变化
Figure 11. Variation of dynamic compression modulus of stacked soilbags with loading cycles
-
[1] 李杰, 李国强. 地震工程学导论[M]. 北京: 地震出版社, 1992. [2] KELLY J M, KONSTANTINIDIS D A. Mechanics of rubber bearings for seismic and vibration isolation[M]. Manhattan: Wiley, 2011. [3] 尚守平,张斌,肖逸夫,等. 基础隔震低层框架结构振动台试验研究[J]. 地震工程与工程振动,2019,39(4): 30-40. doi: 10.13197/j.eeev.2019.04.30.shangsp.004SHANG Shouping, ZHANG Bin, XIAO Yifu, et al. Shaking table test of base isolation low-rise frame structure[J]. Earthquake Engineering and Engineering Dynamics, 2019, 39(4): 30-40. doi: 10.13197/j.eeev.2019.04.30.shangsp.004 [4] 周福霖. 隔震、消能减震与结构控制体系——终止我国城乡地震灾难的必然技术选择[J]. 城市与减灾,2016(5): 1-10. [5] 窦远明,刘晓立,赵少伟,等. 砂垫层隔震性能的试验研究[J]. 建筑结构学报,2005,26(1): 125-128. doi: 10.14006/j.jzjgxb.2005.01.020DOU Yuanming, LIU Xiaoli, ZHAO Shaowei, et al. An experimental study of isolating properties of sand cushion[J]. Journal of Building Structures, 2005, 26(1): 125-128. doi: 10.14006/j.jzjgxb.2005.01.020 [6] 尹志勇,景立平,孙海峰,等. 农村房屋地基砂垫层隔震系统振动台试验研究[J]. 建筑结构学报,2020,41(6): 30-37. doi: 10.14006/j.jzjgxb.2019.0901YIN Zhiyong, JING Liping, SUN Haifeng, et al. Experimental study on sand cushion isolation system for foundations of rural house by shaking table test[J]. Journal of Building Structures, 2020, 41(6): 30-37. doi: 10.14006/j.jzjgxb.2019.0901 [7] 刘斯宏, 王艳巧, 胡晓平, 等. 一种土工袋减震隔震建筑基础及其施工方法和应用: CN 101914922 B[P]. 2011-12-14. [8] 白福青,刘斯宏,王艳巧. 土工袋加固原理与极限强度的分析研究[J]. 岩土力学,2010,31(增1): 172-176. doi: 10.16285/j.rsm.2010.s1.054BAI Fuqing, LIU Sihong, WANG Yanqiao. Research on reinforcement mechanism and failure strength of soilbags[J]. Rock and Soil Mechanics, 2010, 31(S1): 172-176. doi: 10.16285/j.rsm.2010.s1.054 [9] DING G Y, WU J L, WANG J, et al. Experimental study on vibration reduction by using soilbag cushions under traffic loads[J]. Geosynthetics International, 2018, 25(3): 322-333. doi: 10.1680/jgein.18.00010 [10] LIU S H, JIA F, CHEN X L, et al. Experimental study on seismic response of soilbags-built retaining wall[J]. Geotextiles and Geomembranes, 2020, 48(5): 603-613. doi: 10.1016/j.geotexmem.2020.03.006 [11] SHENG T, BIAN X C, LIU G B, et al. Experimental study on the sandbag isolator of buildings for subway-induced vertical vibration and secondary air-borne noise[J]. Geotextiles and Geomembranes, 2020, 48(4): 504-515. doi: 10.1016/j.geotexmem.2020.02.008 [12] LIU S H, GAO J J, WANG Y Q, et al. Experimental study on vibration reduction by using soilbags[J]. Geotextiles and Geomembranes, 2014, 42(1): 52-62. doi: 10.1016/j.geotexmem.2013.12.007 [13] WANG Y Q, LI X, LIU K, et al. Experiments and DEM analysis on vibration reduction of soilbags[J]. Geosynthetics International, 2019, 26(5): 551-562. doi: 10.1680/jgein.19.00045 [14] 中华人民共和国住房和城乡建设部. 建筑地基基础设计规范: GB 50007—2011[S]. 北京: 中国建筑工业出版社, 2012. [15] 于海英,王栋,杨永强,等. 汶川8.0级地震强震动加速度记录的初步分析[J]. 地震工程与工程振动,2009,29(1): 1-13. doi: 10.13197/j.eeev.2009.01.001YU Haiying, WANG Dong, YANG Yongqiang, et al. The preliminary analysis of strong ground motion records from the Ms 8.0 Wenchuan Earthquake[J]. Journal of Earthquake Engineering and Engineering Vibration, 2009, 29(1): 1-13. doi: 10.13197/j.eeev.2009.01.001 [16] MARTIN G R, FINN W D L, SEED H B. Fundamentals of liquefaction under cyclic loading[J]. Journal of the Geotechnical Engineering Division, 1975, 101(5): 423-438. doi: 10.1061/AJGEB6.0000164 [17] 谢定义. 土动力学[M]. 北京: 高等教育出版社, 2011. [18] MOGHADDAS TAFRESHI S N, RAHIMI M, DAWSON A R, et al. Cyclic and post-cycling anchor response in geocell-reinforced sand[J]. Canadian Geotechnical Journal, 2019, 56(11): 1700-1718. doi: 10.1139/cgj-2018-0559 [19] 焦贵德,赵淑萍,马巍,等. 循环荷载下冻土的滞回圈演化规律[J]. 岩土工程学报,2013,35(7): 1343-1349.JIAO Guide, ZHAO Shuping, MA Wei, et al. Evolution laws of hysteresis loops of frozen soil under cyclic loading[J]. Chinese Journal of Geotechnical Engineering, 2013, 35(7): 1343-1349. 期刊类型引用(5)
1. 张伟杰，盛广侠，王兰心，王赟程，王立国，刘志勇，蒋金洋，张嘉文. 复杂服役环境下无砟轨道水泥基材料性能演变的研究综述. 材料导报. 2024(22): 143-160 . 
百度学术2. 冯博，刘青，钱永久. 高性能混凝土在氯盐侵蚀和冻融循环作用下的耐久性分析. 西南交通大学学报. 2023(05): 1083-1089 . 
本站查看3. 苗帅杰，钟阳龙，高亮，蔡小培，肖一雄，张芷寒. 列车循环荷载下完全装配式无砟轨道结构疲劳性能试验研究. 中南大学学报(自然科学版). 2023(12): 4933-4945 . 百度学术4. 任娟娟，张书义，许雪山，杜俊宏，杜威. 寒区无砟轨道服役性能演化与提升技术研究进展. 中国铁路. 2022(08): 76-87 . 百度学术5. 杨志强，李化建，温家馨，黄法礼，王振，易忠来. 疲劳荷载作用下无砟轨道混凝土轨道板氯离子传输与服役寿命. 铁道建筑. 2022(12): 24-29 . 百度学术其他类型引用(3)
-
下载:
百度学术
点击查看大图
计量
- 文章访问数: 394
- HTML全文浏览量: 142
- PDF下载量: 21
- 被引次数: 8