Calculation Method of Hertz Normal Contact Stiffness
-
摘要: 轮轨之间的弹性接触变形是车辆-轨道耦合动力学中计算轮轨力的核心，以基于Hertz接触理论的非线性接触刚度来描述轮轨之间的压缩量与轮轨法向力之间的关系. 目前的轮轨Hertz接触刚度计算公式为经验公式，来源于20世纪70年代英国铁路技术研究所的研究工作，分锥形踏面和磨耗型踏面两种类型，局限于特定的轮径范围和钢轨廓形. 基于三维弹性体Hertz接触理论，推导了满足Hertz接触条件的弹性体法向接触刚度通用计算公式，并结合轮轨几何外形特点，给出了轮轨接触斑大小及接触刚度参数的直接确定方法和数表，并以LM车轮踏面和CN60钢轨踏面匹配为例，对比分析了典型工况下计算结果与经验公式的差异. 分析结果表明：基于本文计算公式制定的Hertz弹性接触数表弥补了现有数表中缺乏接触刚度的不足，可直接用于弹性体接触计算；对于轮轨接触，与本文公式计算结果相比，以往经验公式中磨耗型踏面的接触常数计算结果仅在车轮名义中心圆弧与轨顶中心圆弧接触时的误差较小，约为0.40%～0.44%；其他接触位置时，经验公式计算结果与本文公式计算结果相差较大，误差范围可达 −25.97%～131.42%.Abstract: Elastic contact deformation between the wheel and rail is pivotal in the computation of the wheel-rail contact force in the vehicle-track coupled dynamics. Based on the Hertz contact theory, the nonlinear contact stiffness is used to depict the relation of the wheel-rail normal contact force and their relative compression. The current empirical formulas of the Hertz contact stiffness for the wheel-rail contact are based on the work of British Railway in 1970 s, and are classified into two categories, i.e., coned profile and worn profile. However, they are restricted to specific wheel radii and rail profiles. In this work, based on Hertz contact theory, the general formulas of the elastic normal contact stiffness are deduced, which can satisfy the Hertz contact conditions. According to the characteristics of the wheel-rail geometry, the dimension of wheel-rail contact spots and contact stiffness parameters are tabulated and determined. Finally, an example of LM wheel profile and CN60 rail profile is used to compare the results of the empirical formulas and those of the proposed formulas. The results show that the Hertz contact parameter table formed by the proposed contact formula makes up the absence of the contact stiffness in the current ones, and can be used directly in elastic contact calculation. When the circle around the nominal center of the wheel profile and the central circle of the rail head are in contact, the results calculated by empirical formulas have less error in the contact stiffness deviation of the worn tread, which varies in 0.40% − 0.44%. Otherwise, there is a significant difference between the results of empirical formulas and those of the proposed formulas, the range of which is −25.97% −131.42%.
-
Key words:
- Hertz contact /
- contact stiffness /
- contact ellipse /
- contact table /
- wheel/rail force
-
图 3 LM车轮踏面和CN60钢轨匹配下的接触常数
Figure 3. Contact constants for LM wheel profile and CN60 rail profile
-
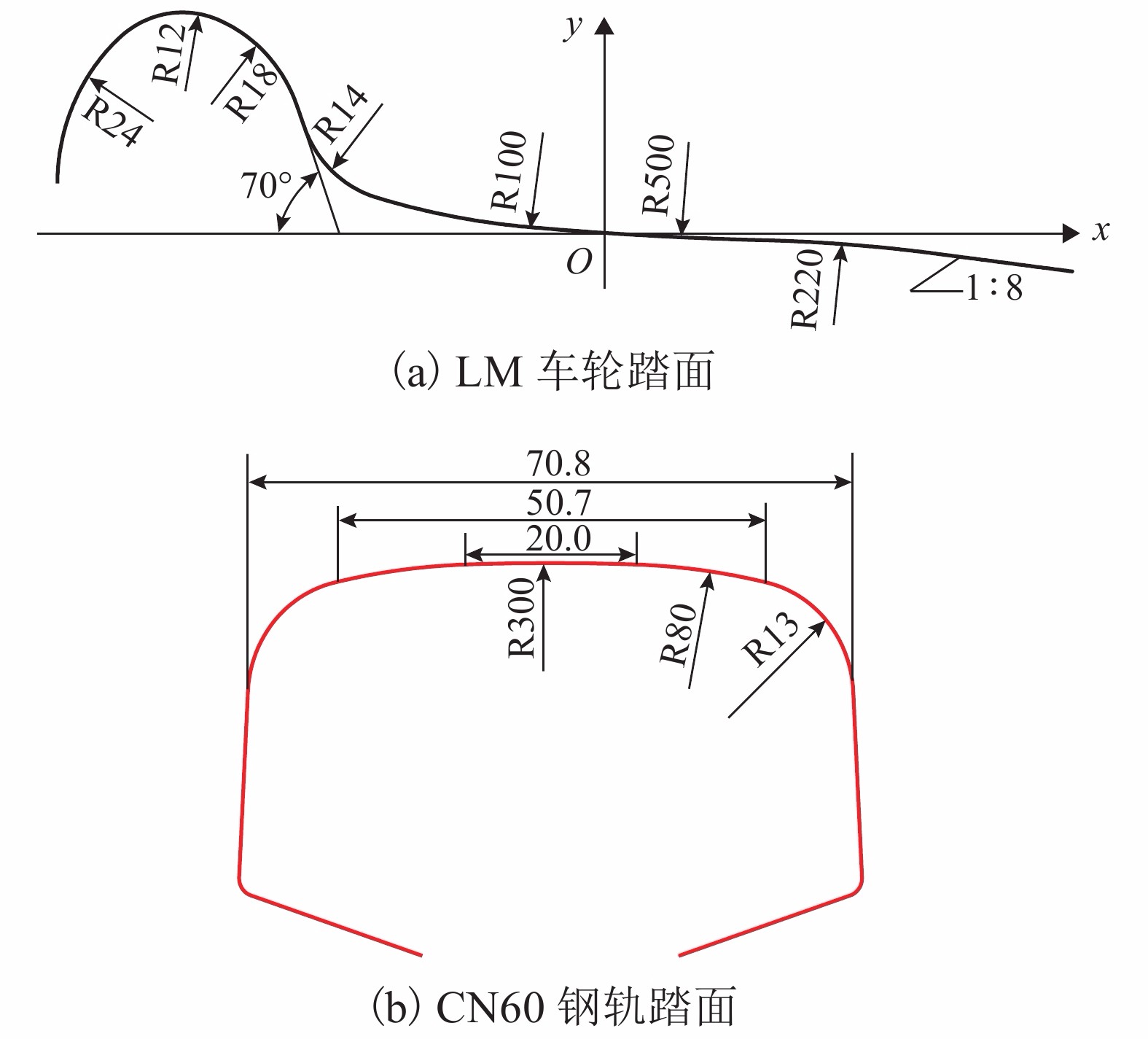
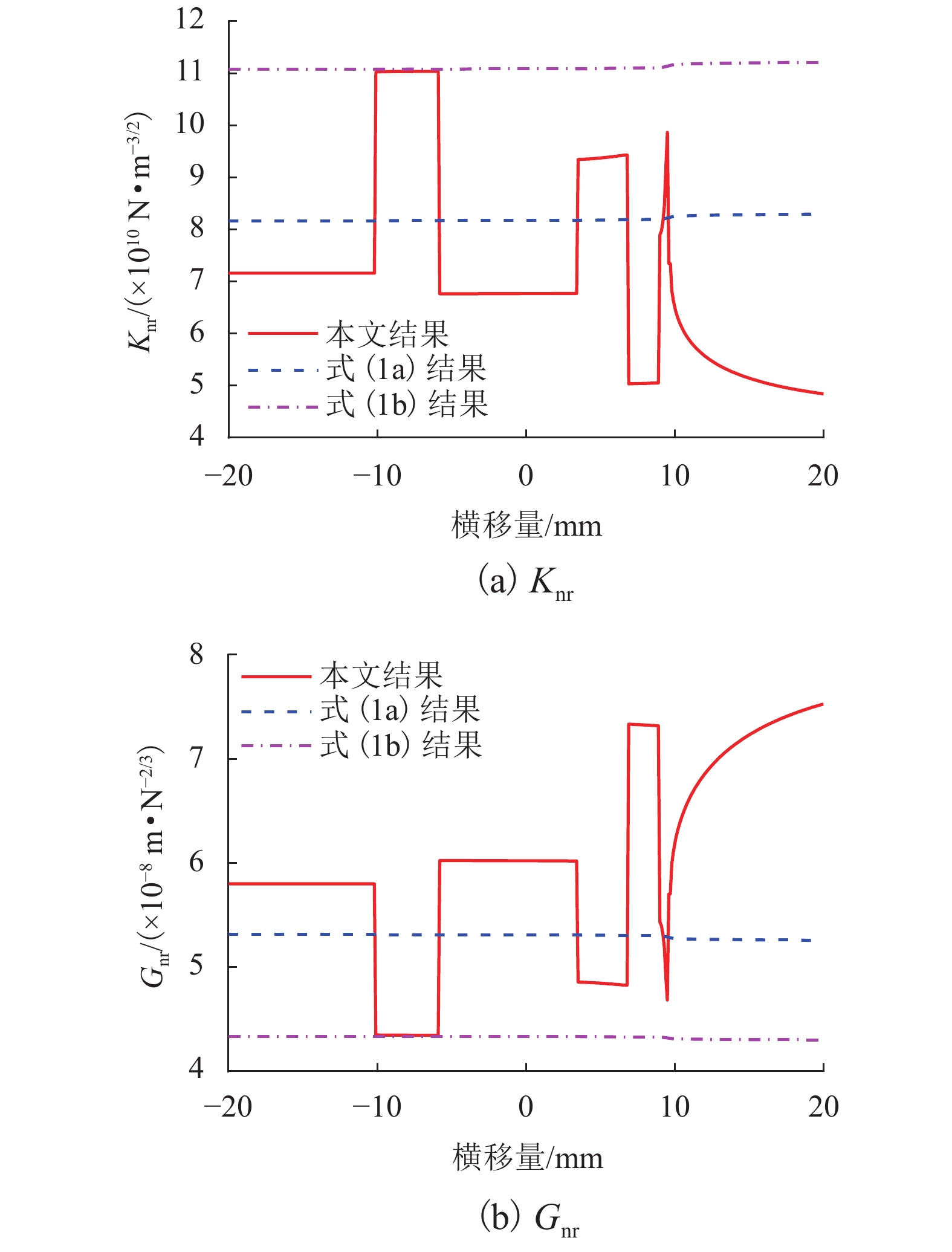
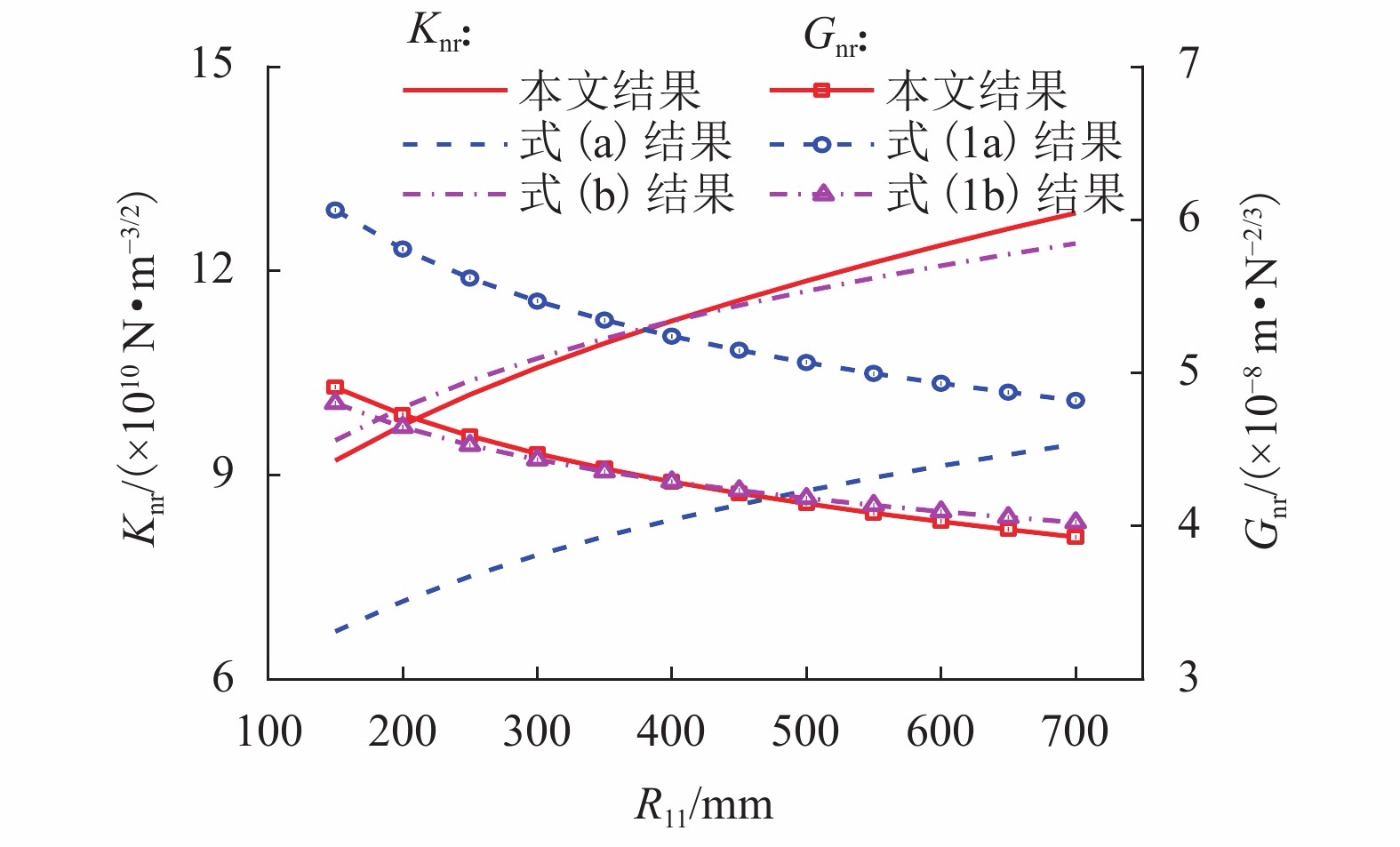
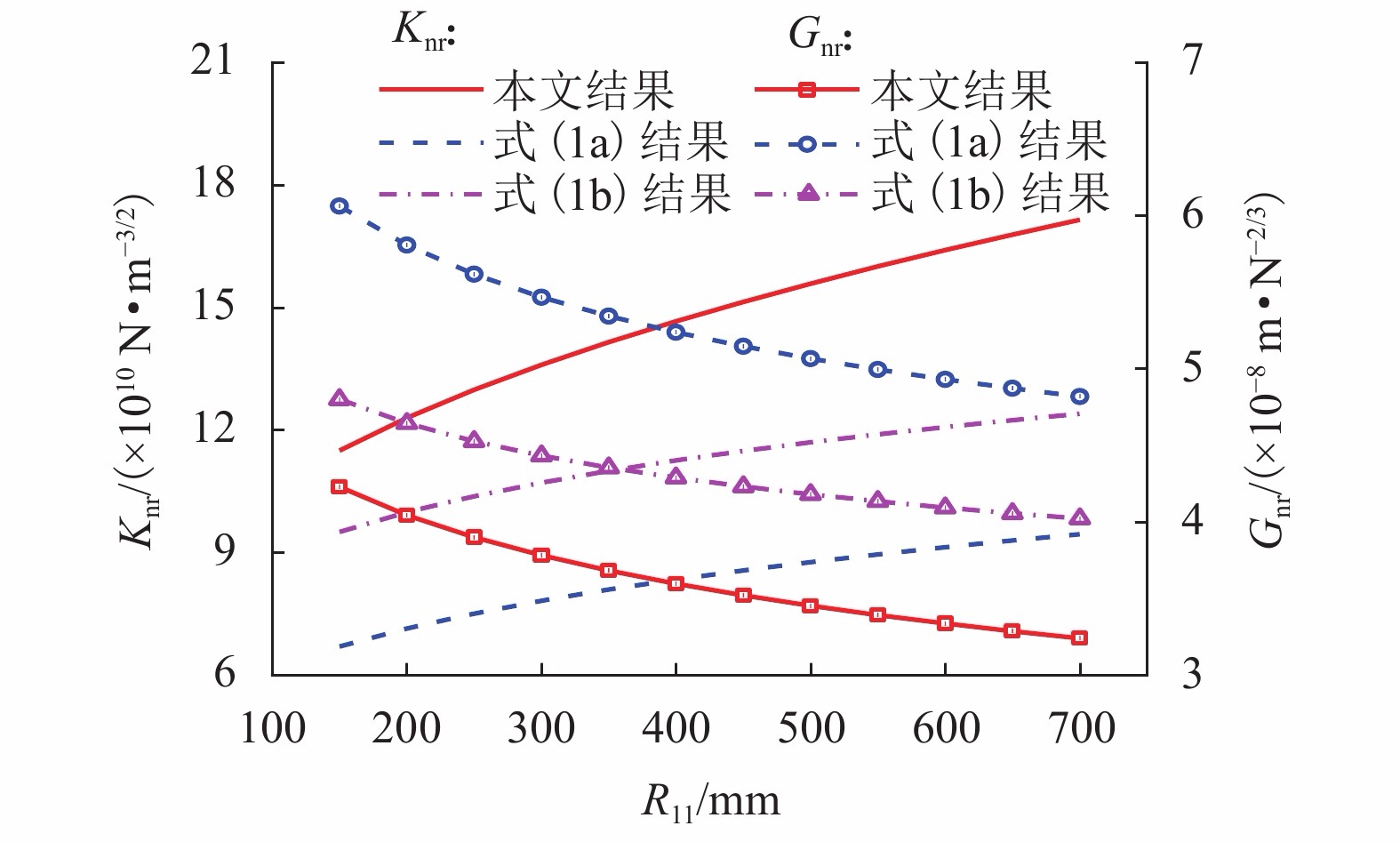
ZHAI Wanming. Vehicle-track coupled dynamics: theory and application[M]. Singapore: Science Press and Springer Nature Singapore Pte Ltd., 2020. 金学松, 刘启跃. 轮轨摩擦学[M]. 北京: 中国铁道出版社, 2004: 47-63. GOLDSMITH W. Impact: the theory and physical behavior of colliding solids[M]. New York: Dover Publications, Inc., 2001: 82-87. 张鹏,赵鑫,凌亮,等. 轮轨高频动力作用模拟中接触模型的影响分析[J]. 机械工程学报,2020,56(12): 124-132. doi: 10.3901/JME.2020.12.124ZHANG Peng, ZHAO Xin, LING Liang, et al. Influence of contact modeling on numerical analyses of high frequency wheel-rail interactions[J]. Journal of Mechanical Engineering, 2020, 56(12): 124-132. doi: 10.3901/JME.2020.12.124 徐井芒,王凯,高原,等. 高速铁路无缝钢轨断缝瞬态冲击行为分析[J]. 西南交通大学学报,2020,55(6): 1348-1354. doi: 10.3969/j.issn.0258-2724.20190312XU Jingmang, WANG Kai, GAO Yuan, et al. Transient impact behavior analysis of rail broken gap on high-speed continuous welded rail[J]. Journal of Southwest Jiaotong University, 2020, 55(6): 1348-1354. doi: 10.3969/j.issn.0258-2724.20190312 CHENG Gong, HE Yuanpeng, HAN Jian, et al. An investigation into the effects of modelling assumptions on sound power radiated from a high-speed train wheelset[J]. Journal of Sound and Vibration, 2021, 495: 115910.1-115910.20. JENKINS H H, STEPHENSON J E, CLAYTON G A, et al. The effect of track and vehicle parameters on wheel/rail vertical dynamic forces[J]. Railway Engineering Journal, 1974, 3(1): 2-16. 孙翔. 确定轮轨接触椭圆的直接方法[J]. 西南交通大学学报,1985(4): 8-21.SUN Xiang. A direct method to determine the wheel/rail contact ellipse[J]. Journal of Southwest Jiaotong University, 1985(4): 8-21. JOHNSON K L. Contact mechanics[M]. Cambridge: Cambridge University Press, 1985: 119-124. SHABANA A A, ZAAZAA K E, ESCALONA J L, et al. Development of elastic force model for wheel/rail contact problems[J]. Journal of Sound and Vibration, 2004, 269(1/2): 295-325. FLORES P, AMBROSIO J, CLARO J C P, et al. Influence of the contact-impact force model on the dynamic response of multi-body systems[J]. Proceedings of the Institution of Mechanical Engineering,Part K:Journal of Multi-Body Dynamics, 2006, 220(1): 21-34. doi: 10.1243/146441906X77722 SKRINJAR L, SLAVIC J, BOLTEZAR M. A review of continuous contact-force models in multibody dynamics[J]. International Journal of Mechanical Sciences, 2018, 145: 171-187. doi: 10.1016/j.ijmecsci.2018.07.010 HU S, GUO X. A dissipative contact force model for impact analysis in multibody dynamics[J]. Multibody System Dynamics, 2015, 35: 131-151. doi: 10.1007/s11044-015-9453-z ZHANG J, LI W, ZHAO L, et al. A continuous contact force model for impact analysis in multibody dynamics[J]. Mechanism and Machine Theory, 2020, 153: 103946.1-103946.25. ISMAIL K A, STRONGE W J. Impact of viscoplastic bodies:dissipation and restitution[J]. Journal of Applied Mechanics, 2008, 75: 061011-1-061011-5. YIGIT A S, CHRISTOFOROU A P, MAJEED M A. A nonlinear visco-elastoplastic impact model and the coefficient of restitution[J]. Nonlinear Dynamics, 2011, 66: 509-521. doi: 10.1007/s11071-010-9929-6 -
下载:
点击查看大图
图(5)
计量
- 文章访问数: 784
- HTML全文浏览量: 1798
- PDF下载量: 430
- 被引次数: 0