Analytical Solution of Mechanical Response inShallow Non-circular Tunnels
-
摘要:
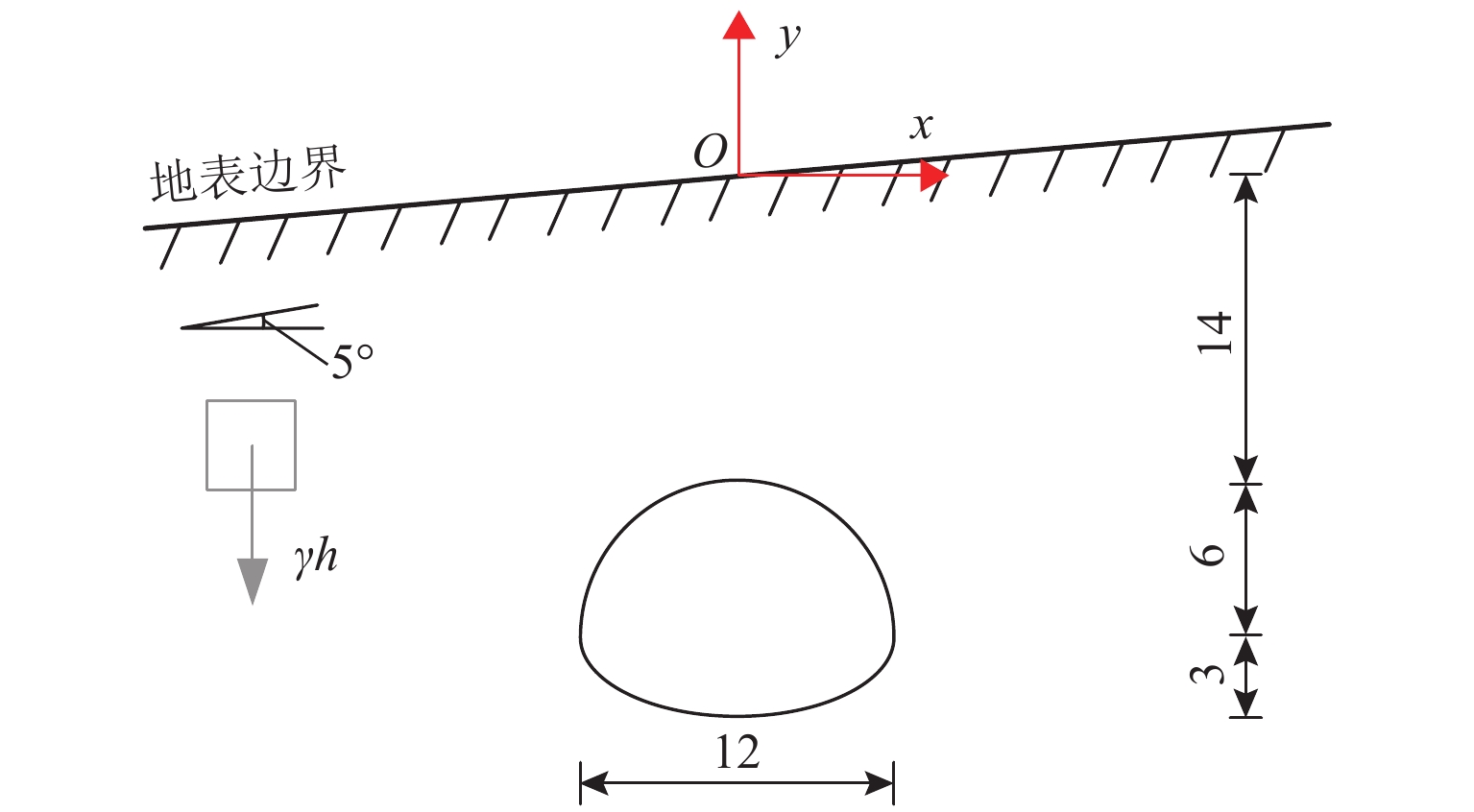
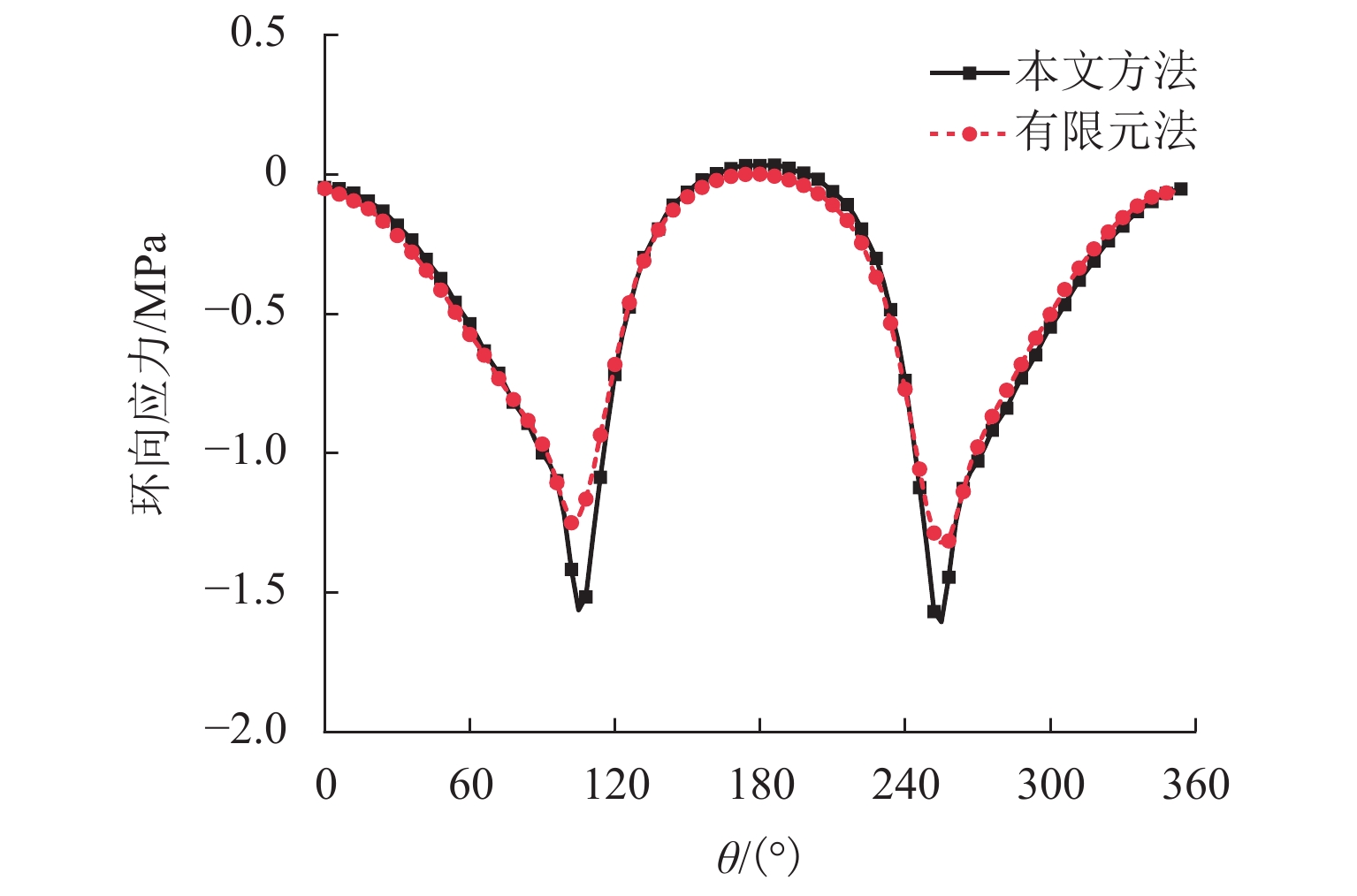
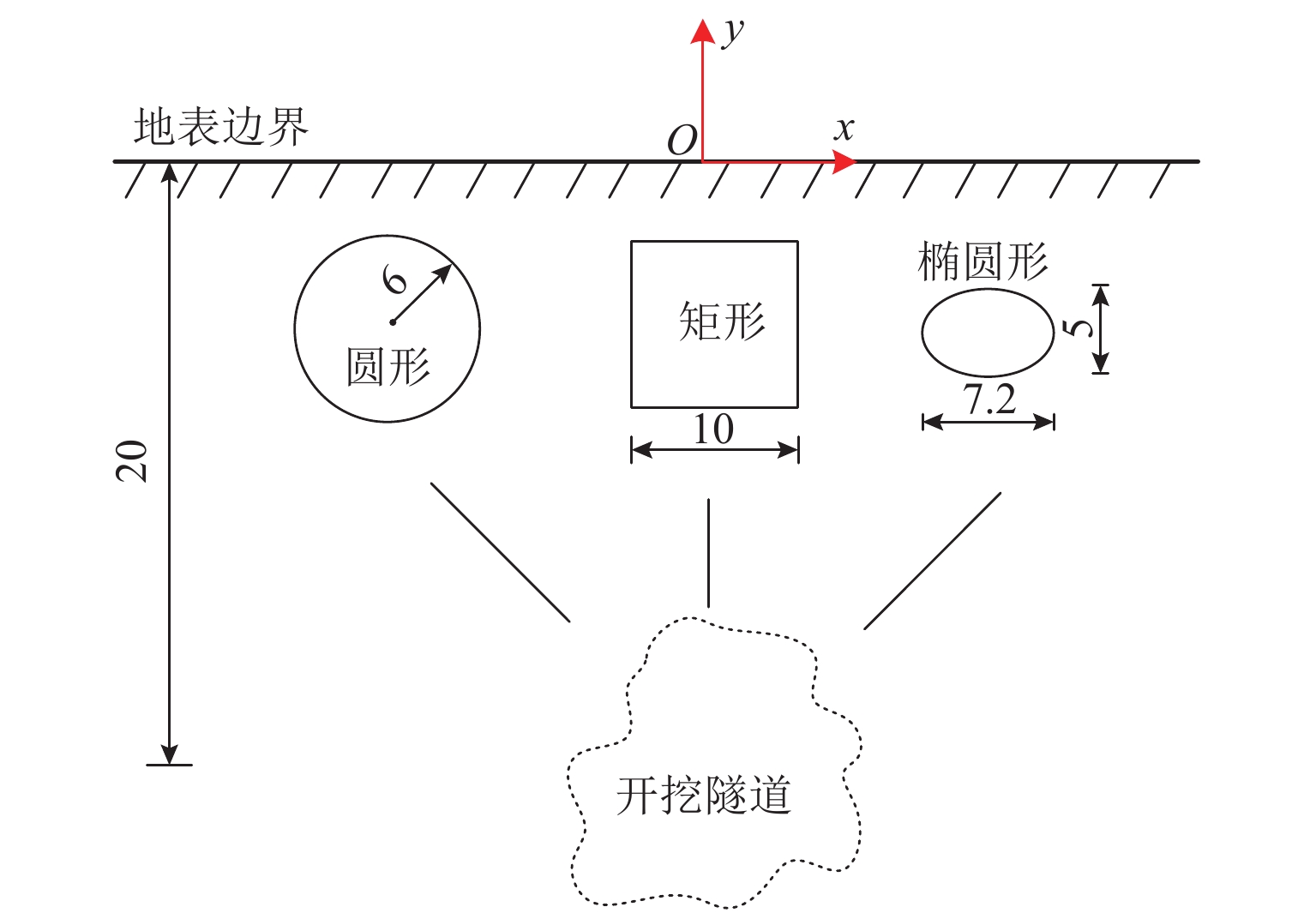
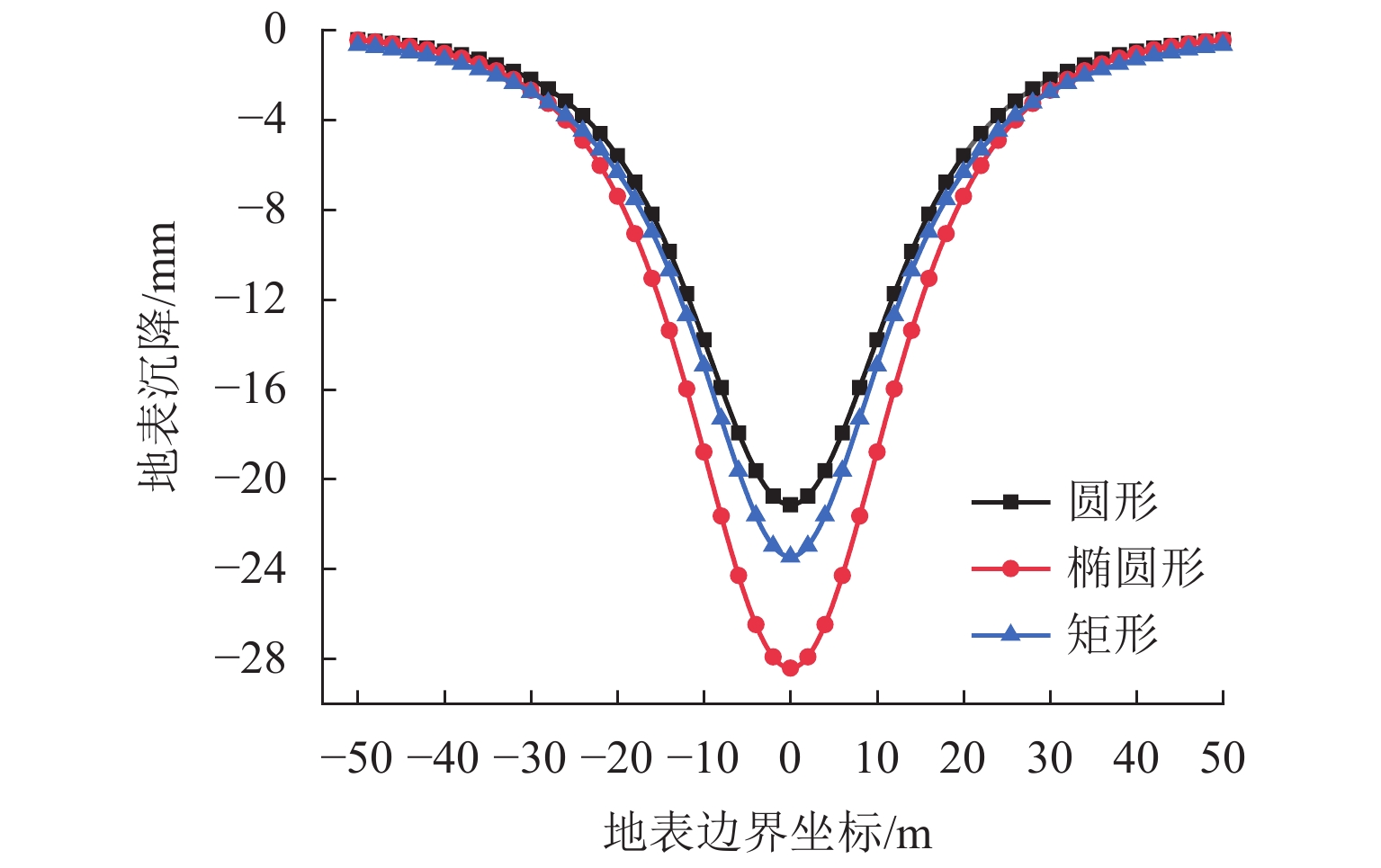
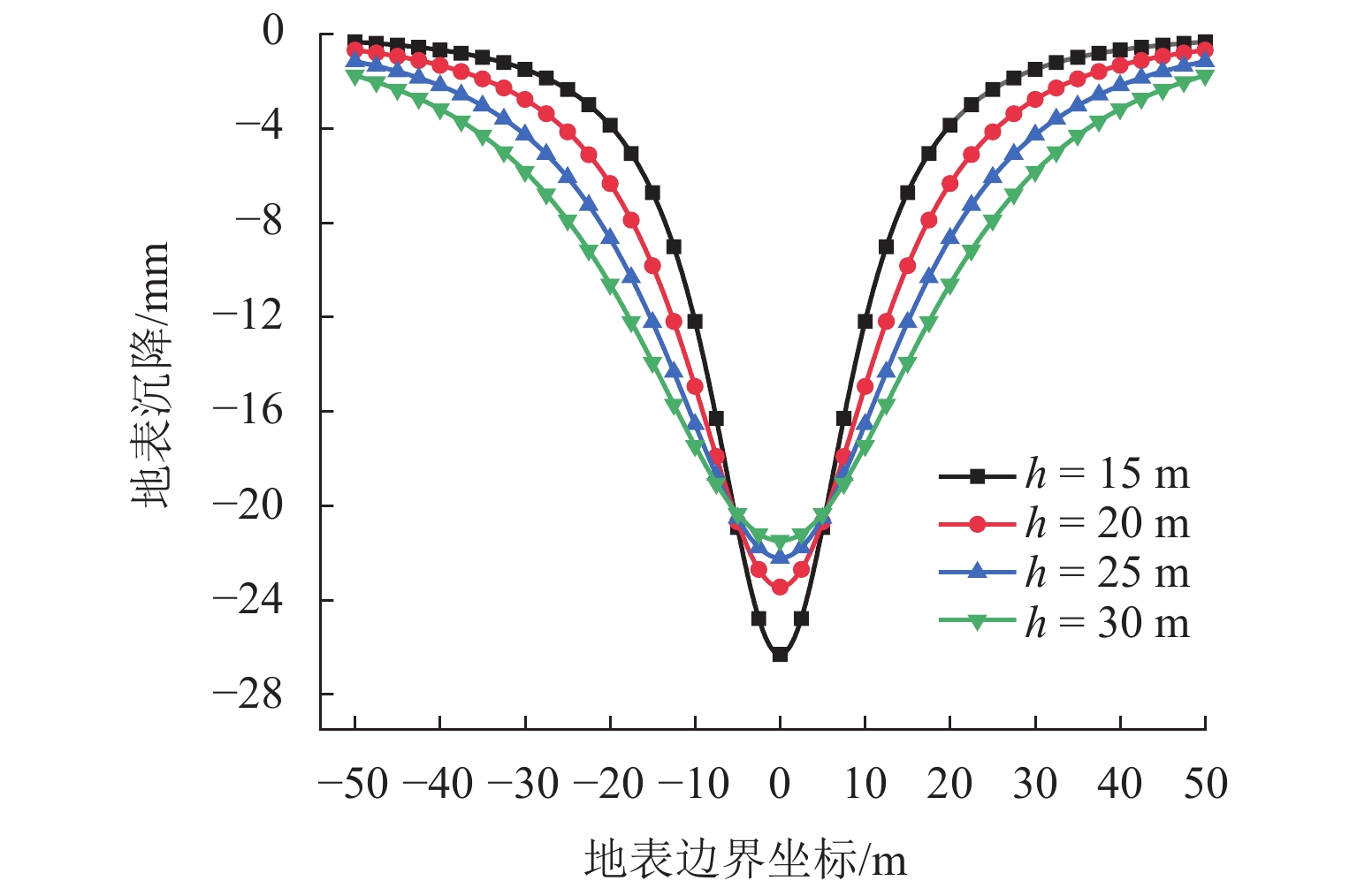
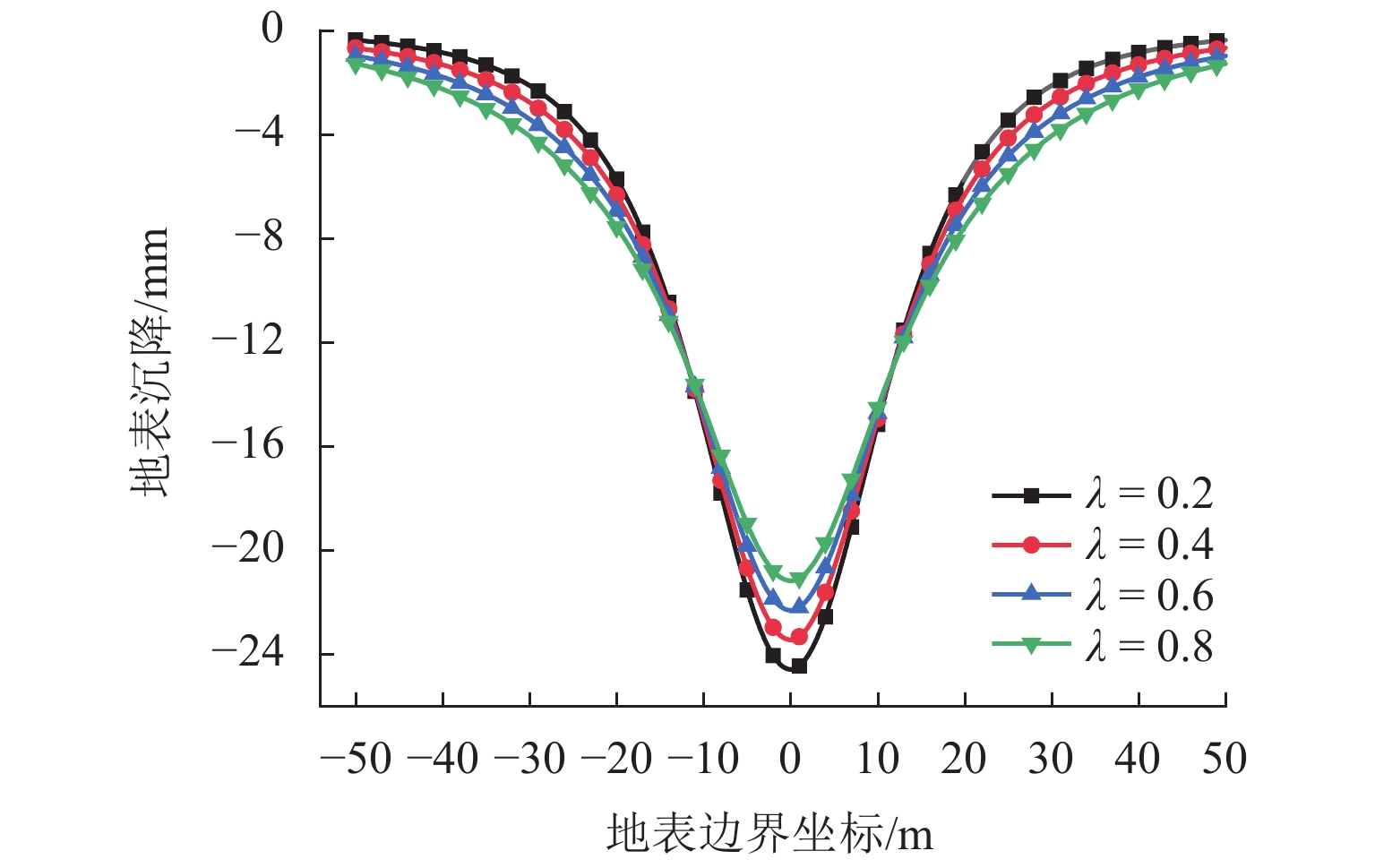
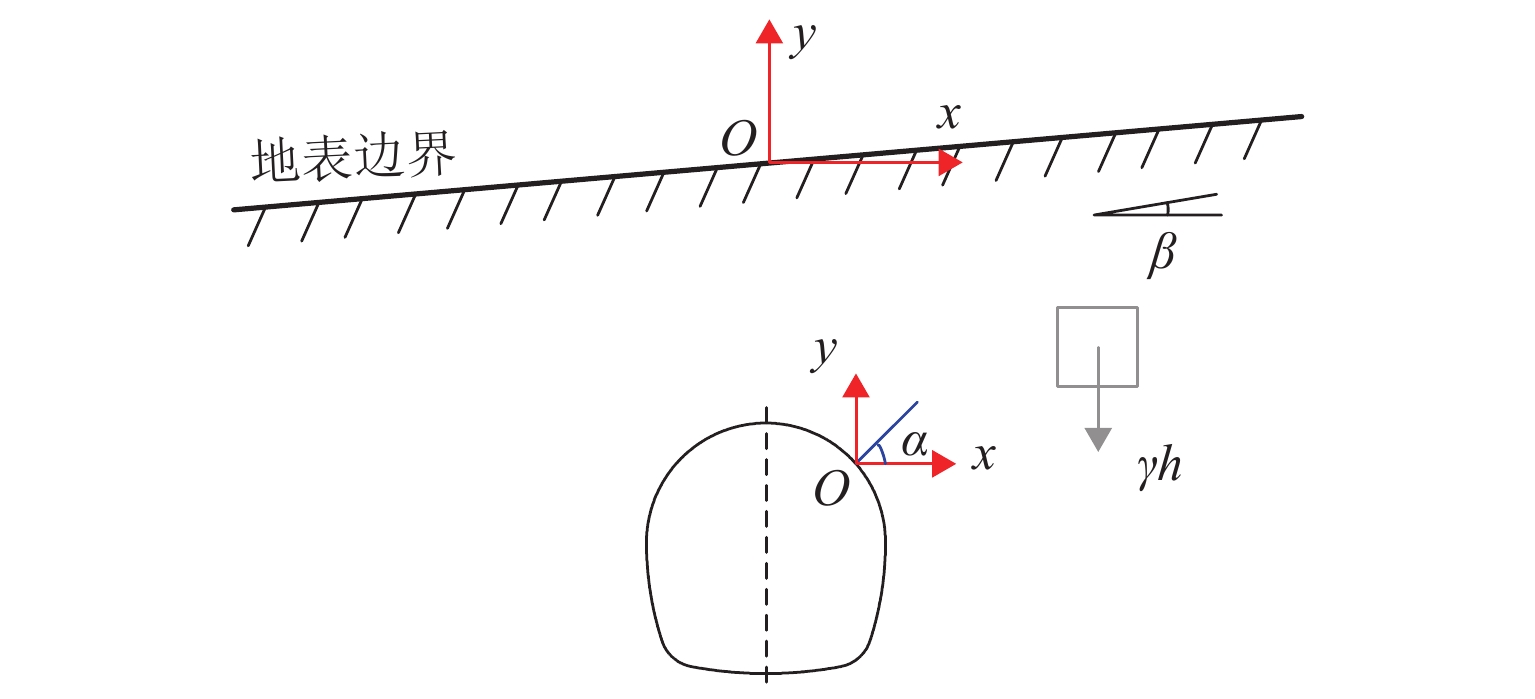
浅埋非圆形隧道的力学分析对城市地铁隧道的施工安全具有重要意义，其求解难点在于如何考虑重力场的影响以及圆环域保角映射函数的确定.为此，在复变函数理论框架下通过重构解析函数的表达，提出了重力条件下浅埋非圆形隧道力学分析的解耦保角映射方法，该方法将解析函数拆分成两组子函数，并采用不同的局部坐标系进行表达，两组子函数可以分别表达地表边界内与隧道边界外的应力与位移场，同时地表边界与隧道边界也可以单独进行保角映射；利用快速Fourier变换将用于确定解析函数的边界条件方程转化为频域方程进行求解；将本文方法应用于浅埋隧道开挖引起的地表沉降分析. 研究结果表明：隧道形状会对地表沉降的大小造成显著影响，其主因素来源于隧道的高跨比；隧道埋深会同时对地表沉降量以及沉降槽宽度产生影响，埋深越小其敏感程度越大；侧压力系数的改变对地表沉降槽的宽度影响较小；与有限元方法相比，本文方法的程序体量极小、计算速度更快且精度更高.
Abstract:The mechanical analysis of shallow noncircular tunnels is of great significance to the construction safety of urban subway tunnels. The difficulty in solving this problem originates from the influence of gravity and the determination of conformal mapping. To this end, a decoupling conformal mapping method with the framework of complex variable theory was proposed. In this method, the analytic function was decomposed into two groups of sub-functions, which were expressed in different local coordinate systems. These two sub-functions can exactly express the mechanical field of the computational domains inside the ground surface and outside the tunnel boundary. Then the ground and tunnel boundaries can be mapped independently by conformal transformation. Furthermore, the boundary condition equation used to determine the analytic function was transformed into the frequency equation using the fast Fourier transform method. Finally, the proposed method is applied to the analysis of ground settlement caused by the shallow tunnel excavation. From the results, the following conclusions can be drawn: 1) The tunnel shape has a significant effect on the ground settlement, and its main factor is the height-to-span ratio. 2) The buried depth affects both the ground settlement and the width of the settlement trough. Its sensitivity increases with the decrease of buried depth. 3) The lateral pressure coefficient has little effect on the width of the ground settlement trough. 4) Compared with the finite element method, the proposed method can obtain high-precision results at a small computational cost.
-
Key words:
- tunnel engineering /
- decoupling conformal mapping method /
- complex variable theory /
- shallow /
-
图 4 浅埋非圆形隧道力学分析（单位：m）
Figure 4. Mechanical analysis of shallow non-circular tunnel (unit：m)
图 6 隧道开挖引起地表沉降的影响因素分析（单位：m）
Figure 6. Influencing factors analysis of the ground settlement due to tunnel excavation (unit：m)
图 9 侧压力系数对地表沉降的影响
Figure 9. Influence of lateral pressure coefficient on ground settlement
表 1 矩形隧道应力计算结果对比
Table 1. Comparison of stress for rectangular tunnel
有限元法 本文方法 网格尺寸/m 应力/MPa 项数/项 应力/MPa 0.12 0.13 30 1.80 0.06 1.80 60 2.70 0.03 2.40 120 2.70 
下载: 导出CSV
-
[1] 张子新,朱叶艇,朱雁飞,等. 1∶1站立式大断面异形盾构管片力学试验系统的研发与应用[J]. 岩石力学与工程学报,2017,36(12): 2895-2905.ZHANG Zixin, ZHU Yeting, ZHU Yanfei, et al. Development and application of a 1∶1 mechanical test system for special-shaped shield lining with a large cross-section[J]. Chinese Journal of Rock Mechanics and Engineering, 2017, 36(12): 2895-2905. [2] 方黄城,张顶立,文明,等. 任意多孔条件下围岩力学分析的非迭代解析方法[J]. 岩石力学与工程学报,2020,39(11): 2204-2212.FANG Huangcheng, ZHANG Dingli, WEN Ming, et al. A non-iterative analytical method for mechanical analysis of surrounding rock with arbitrary shape holes[J]. Chinese Journal of Rock Mechanics and Engineering, 2020, 39(11): 2204-2212. [3] VERRUIJT A. A complex variable solution for a deforming circular tunnel in an elastic half-plane[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 1997, 21(2): 77-89. doi: 10.1002/(SICI)1096-9853(199702)21:2<77::AID-NAG857>3.0.CO;2-M [4] 晏莉,阳军生,刘宝琛. 浅埋双孔平行隧道开挖围岩应力和位移分析[J]. 岩土工程学报,2011,33(3): 413-419.YAN Li, YANG Junsheng, LIU Baochen. Stress and displacement of surrounding rock with shallow twin-parallel tunnels[J]. Chinese Journal of Geotechnical Engineering, 2011, 33(3): 413-419. [5] 韩凯航,张成平,王梦恕. 浅埋隧道围岩应力及位移的显式解析解[J]. 岩土工程学报,2014,36(12): 2253-2259. doi: 10.11779/CJGE201412013HAN Kaihang, ZHANG Chengping, WANG Mengshu. Explicit analytical solutions for stress and displacement of surrounding rock in shallow tunnels[J]. Chinese Journal of Geotechnical Engineering, 2014, 36(12): 2253-2259. doi: 10.11779/CJGE201412013 [6] 张治国,张成平,奚晓广. 双线隧道不同布置方式下相互作用影响的地层位移解析[J]. 岩土工程学报,2019,41(2): 262-271.ZHANG Zhiguo, ZHANG Chengping, XI Xiaoguang. Closed solutions to soil displacements induced by twin-tunnel excavation under different layout patterns[J]. Chinese Journal of Geotechnical Engineering, 2019, 41(2): 262-271. [7] 曾癸森,吕爱钟. 考虑构造应力作用下浅埋圆形隧洞的解析解[J]. 岩土力学,2017,38(增1): 79-86. doi: 10.16285/j.rsm.2017.S1.009ZENG Guisen, LÜ Aizhong. Analytical solution for shallow circular tunnel under action of tectonic stress[J]. Rock and Soil Mechanics, 2017, 38(S1): 79-86. doi: 10.16285/j.rsm.2017.S1.009 [8] ZHANG Z G, ZHANG M X, JIANG Y J, et al. Analytical prediction for ground movements and liner internal forces induced by shallow tunnels considering non-uniform convergence pattern and ground-liner interaction mechanism[J]. Soils and Foundations, 2017, 57(2): 211-226. doi: 10.1016/j.sandf.2017.03.004 [9] ZENG G S, CAI H, LU A Z. An analytical solution for an arbitrary cavity in an elastic half-plane[J]. Rock Mechanics and Rock Engineering, 2019, 52(11): 4509-4526. doi: 10.1007/s00603-019-01844-2 [10] 李新源,刘国彬. 半无限体任意开挖断面外域到同心圆环域共形映射的计算方法[J]. 岩石力学与工程学报,2018,37(增1): 3507-3514. doi: 10.13722/j.cnki.jrme.2017.0180LI Xinyuan, LIU Guobin. Calculating method for conformal mapping from exterior of cavern with arbitrary excavation cross-section in half-plane to the area between two concentric circles[J]. Chinese Journal of Rock Mechanics and Engineering, 2018, 37(S1): 3507-3514. doi: 10.13722/j.cnki.jrme.2017.0180 [11] MUSKHELISHVILI N I. Some basic problems of the mathematical theory of elasticity[M]. Noordhoff Groningen: Springer, 1963: 5-20. [12] 陈子荫. 围岩力学分析中的解析方法[M]. 北京: 煤炭工业出版社, 1994: 89-105. [13] 吕爱钟, 张路青. 地下隧洞力学分析的复变函数方法[M]. 北京: 科学出版社, 2007: 128-129. -
下载:
点击查看大图
计量
- 文章访问数: 448
- HTML全文浏览量: 147
- PDF下载量: 48
- 被引次数: 0