Theoretical Design Method for Composite Stiffness under Baseplate of Elastic Indirect Fasteners
-
摘要:
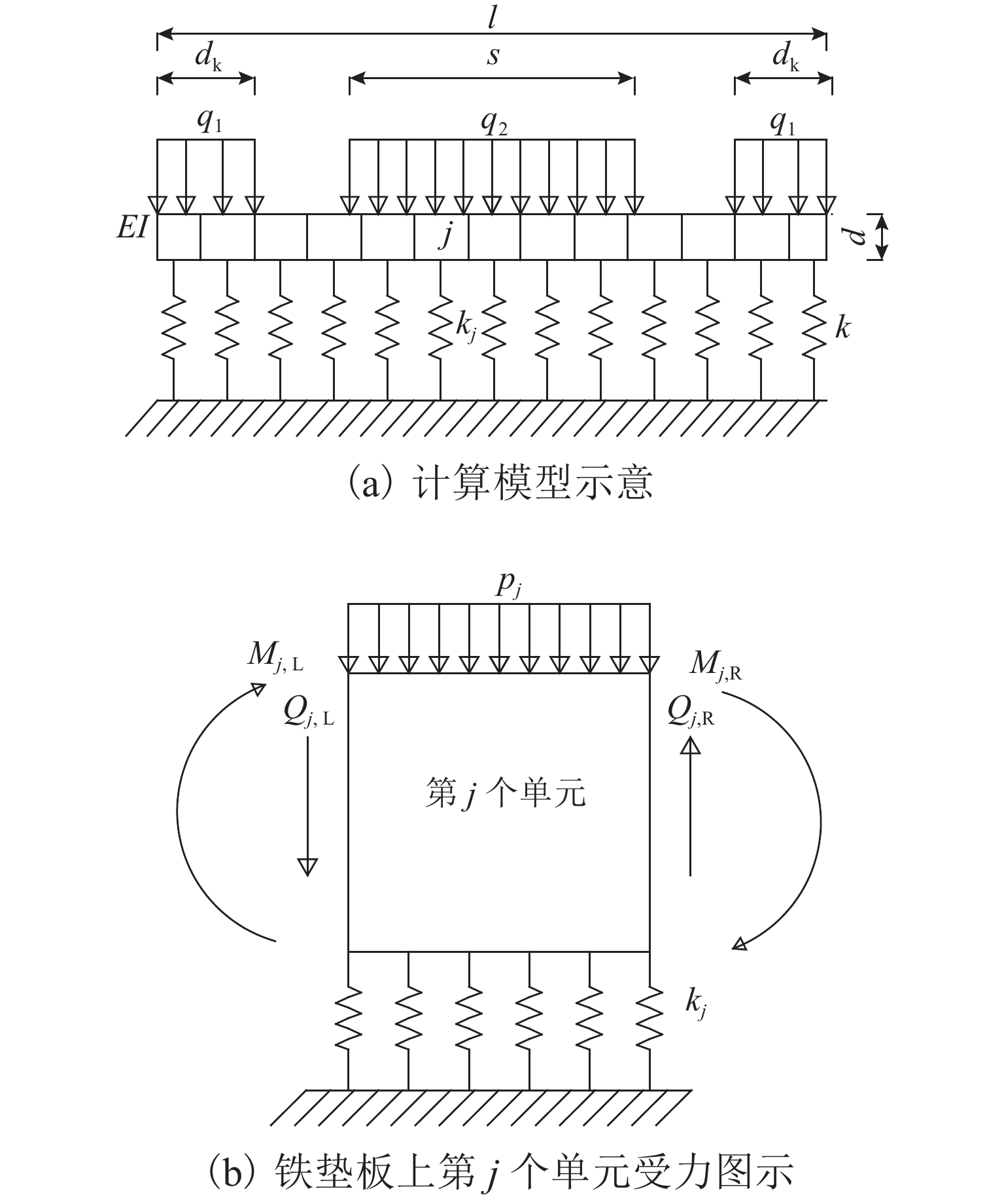
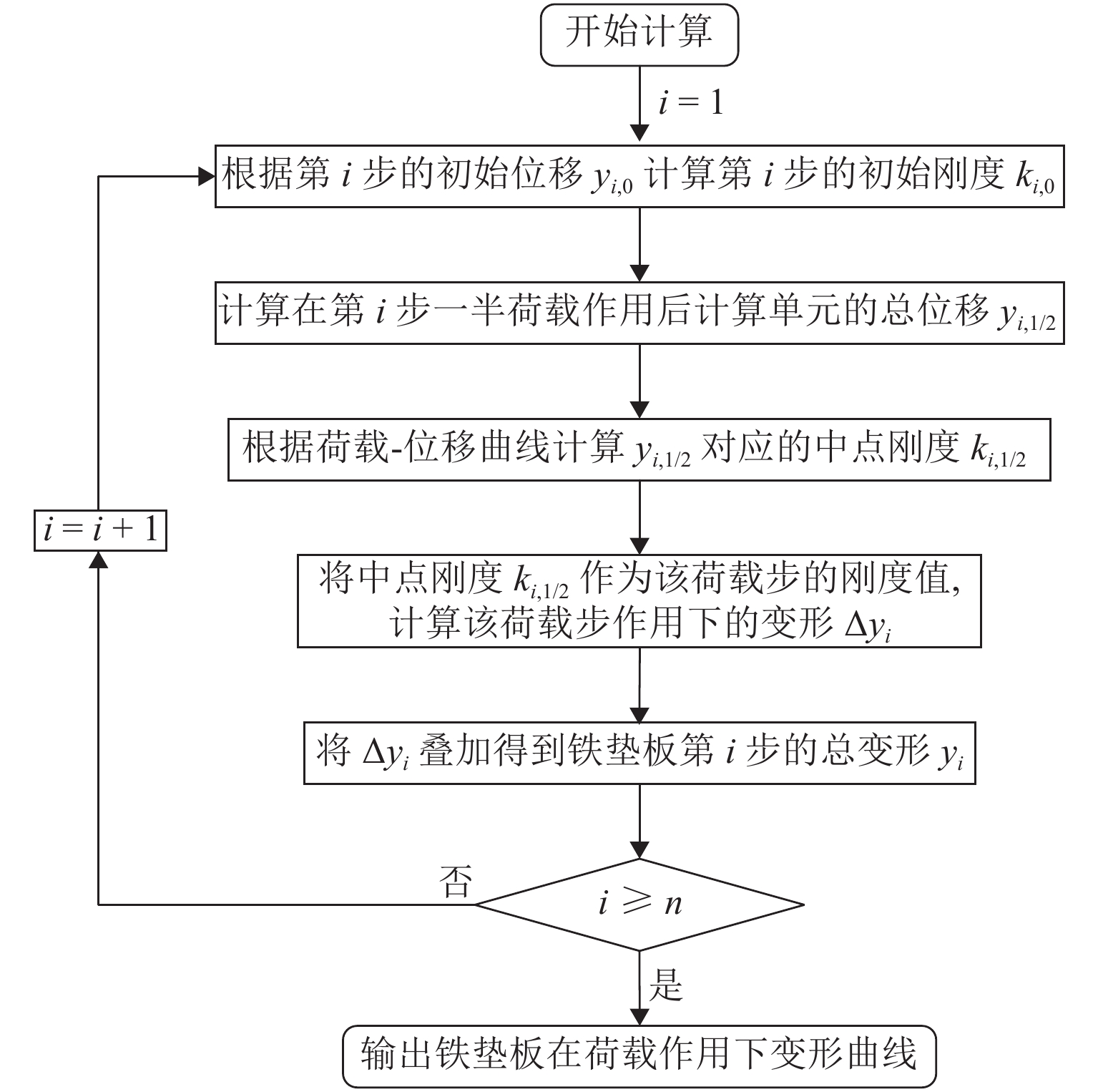
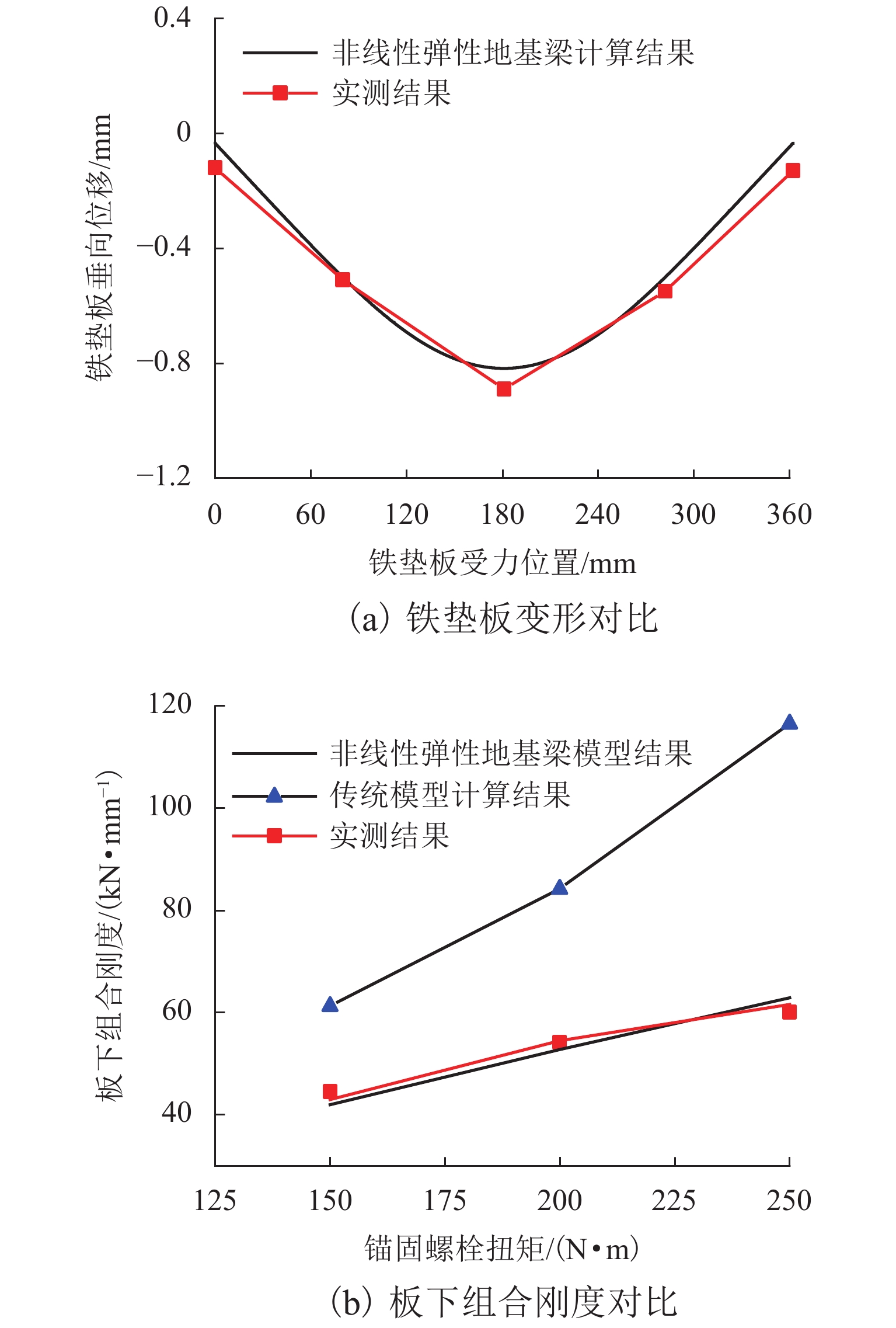
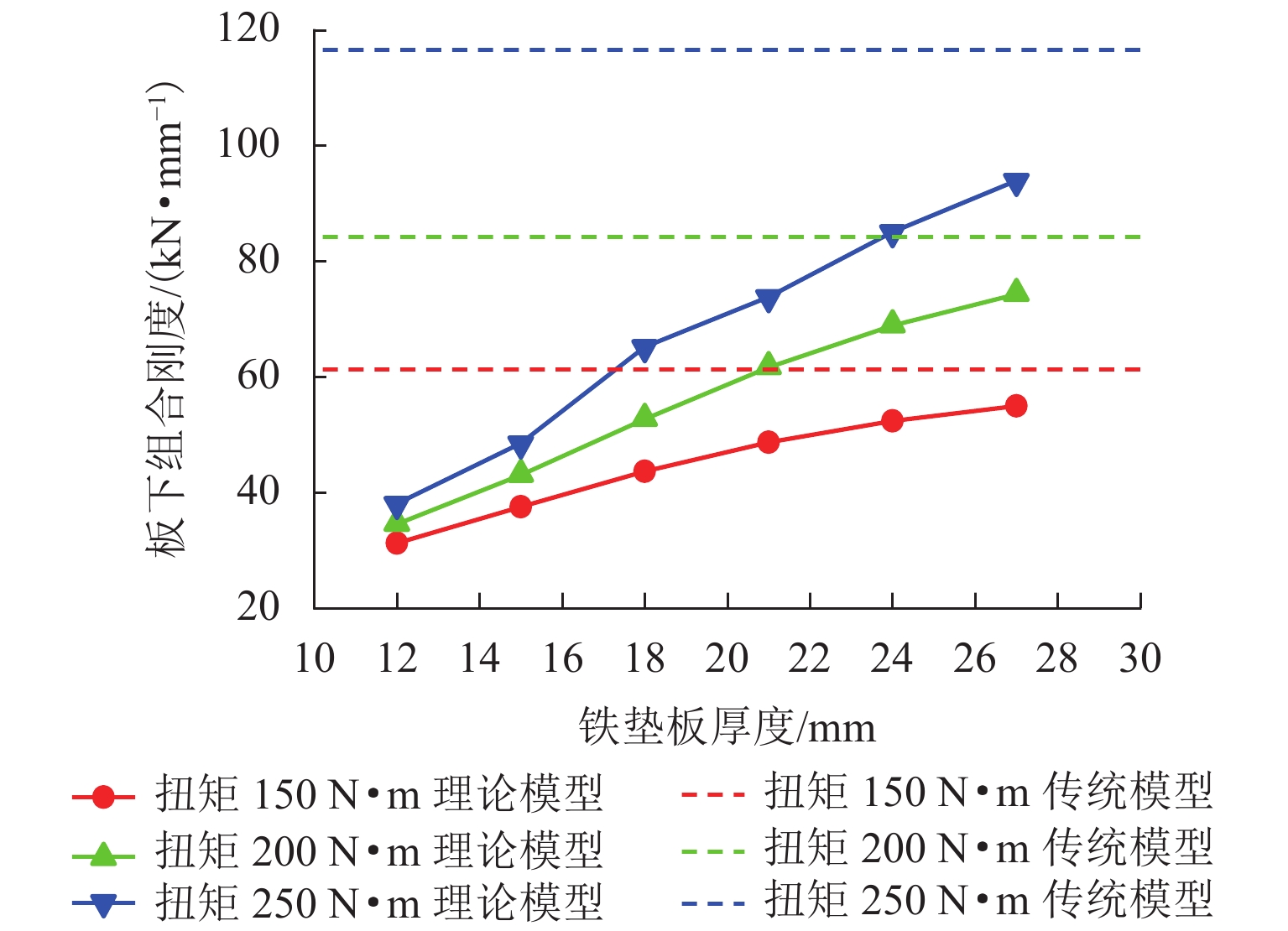
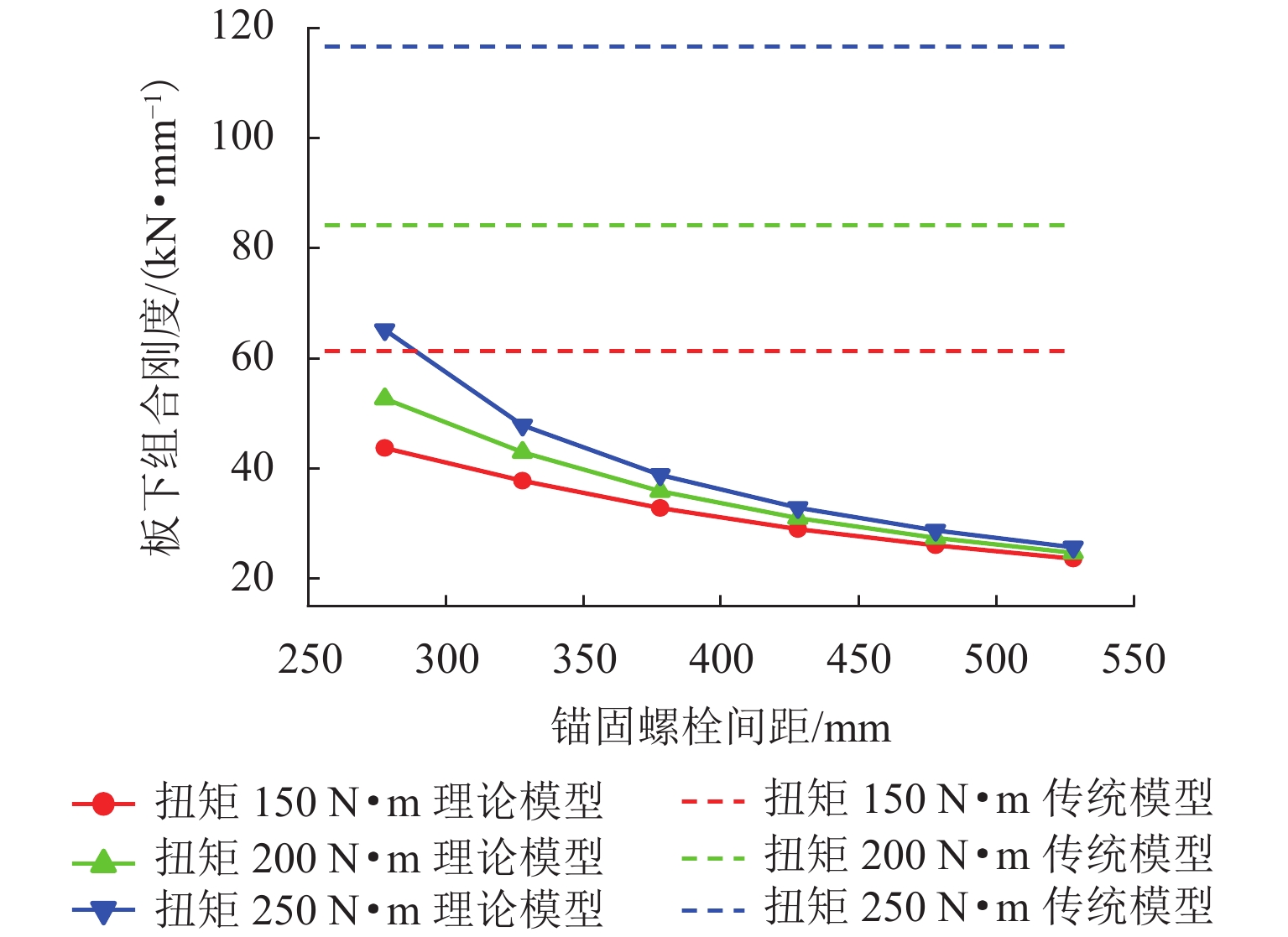
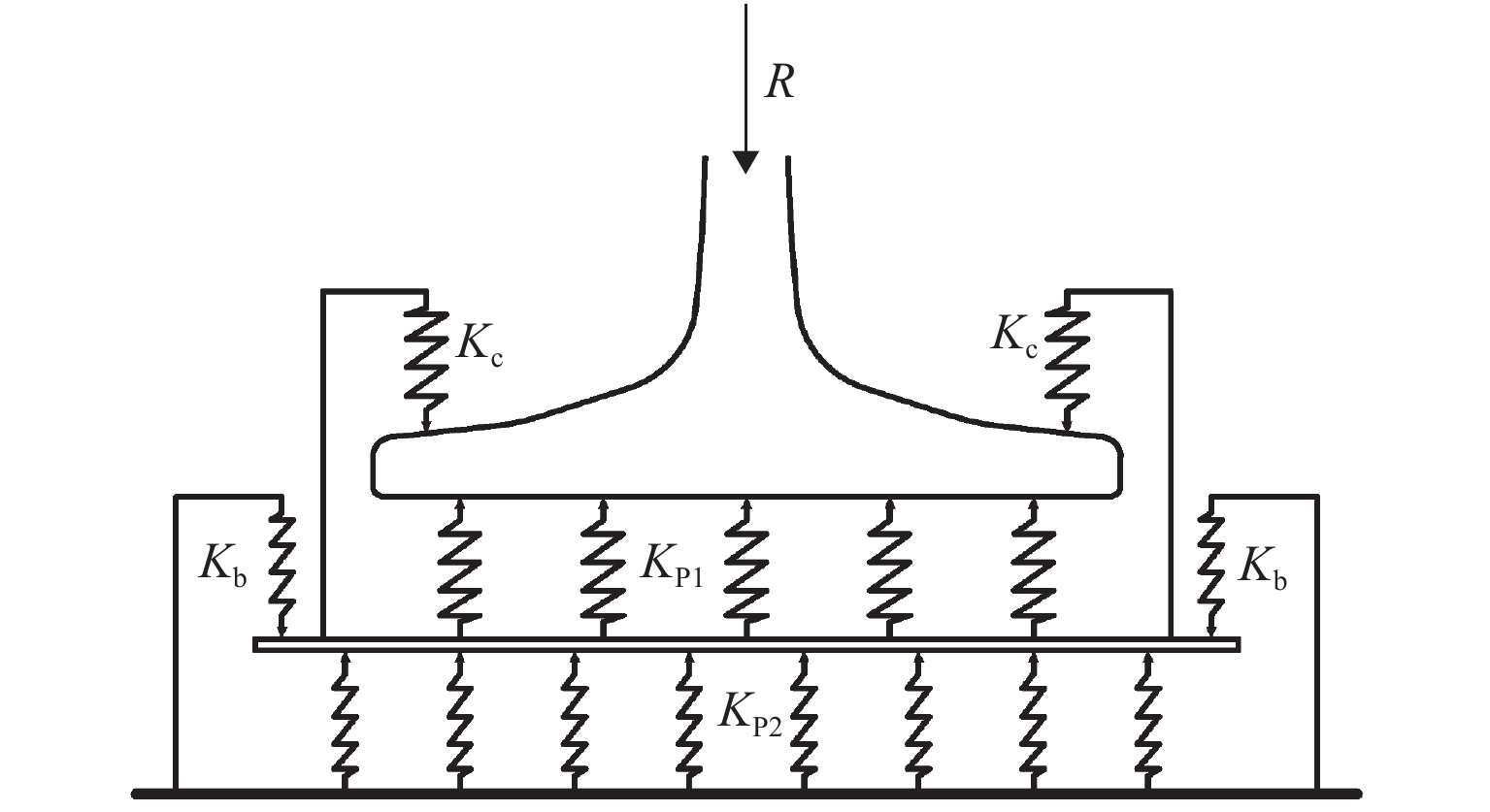
为探究弹性分开式扣件系统板下组合刚度的科学设计方法，明确传统计算模型（简称传统模型）的设计误差并提高设计精度，提出了一种基于非线性弹性地基梁的板下组合刚度理论计算模型（简称理论模型）. 首先，将弹性垫板非线性弹性引入地基梁系统中，并将梁段划分为多个计算单元，从而建立反映铁垫板实际变形特征与板下支承特征的板下组合刚度理论模型，并采用中点刚度法求解锚固螺栓紧固扭矩与列车荷载施加过程中铁垫板的变形曲线与板下组合刚度；其次，采用力学试验机测试DZ Ⅲ型扣件系统在真实服役状态下铁垫板的变形与组合刚度，验证本文理论模型的正确性；最后，分析传统模型与理论模型在不同安装状态（螺栓扭矩）、铁垫板设计参数（铁垫板厚度、锚固螺栓间距）下的板下组合刚度，明确传统模型设计误差在不同铁垫板设计参数下的变化规律. 对比分析表明：由于未考虑铁垫板变形与板下垫板非线性弹性的影响，传统模型在安装扭矩范围（150 ~ 250 N•m）内的设计误差范围为37.75% ~ 94.27%，已无法满足工程设计的误差要求；本文提出的理论模型最大误差仅为2.91%，符合工程设计要求；铁垫板厚度较低或螺栓间距较宽时，铁垫板实际变形状态与传统模型中的计算假设差异将被放大，传统模型的设计误差也将进一步变大.
Abstract:In order to explore the design method of the combined stiffness under the baseplate of the elastic indirect fastener system, improve the error and accuracy in the design of the traditional model, based on nonlinear elastic foundation beam, a theoretical calculation model of composite stiffness under baseplate is proposed. First, the nonlinear elasticity of the baseplate pad is introduced into the continuous foundation beam model, and the beam is divided into multiple calculation elements, so as to establish a theoretical analysis model of the composite stiffness under baseplate reflecting the actual deformation and support characteristics of the baseplate. Moreover, the midpoint stiffness method is adopted to solve the deformation of the baseplate and the composite stiffness under baseplate during imposing the installation torque of anchor bolts and the train load. Secondly, mechanical testing machine is used to test the deformation and composite stiffness of DZ Ⅲ fastener system in the real service state, and validate the theoretical model. Finally, the composite stiffness under baseplate of traditional and theoretical calculation models are calculated in different installation conditions (bolt torque) and baseplate design parameters (thickness and bolt distance), and the design error variation of traditional calculation model under different design baseplate parameters is summarized. The comparative analysis shows that, due to neglecting the iron baseplate deformation and nonlinear elasticity under baseplate, the traditional calculation model has a design error range of 37.75%－94.27% within the installation torque range (150－250 N•m), which fails to meet the error requirements of engineering design. The maximum error of the proposed theoretical calculation model is only 2.91%, which meets the requirements of engineering design. When the thickness of the iron baseplate is low or the bolt spacing is wide, the difference between the actual deformation of the iron baseplate and the calculation assumptions in the traditional calculation model will magnify, and the design error of the traditional calculation model will be further increased.
-
图 1 传统弹性分开式扣件组装静刚度模型
Figure 1. Traditional model for static stiffness of elastic indirect fastener assemblies
图 3 板下组合结构变形计算流程
Figure 3. Flow chart of deformation calculation forcombined structure under baseplate
图 8 理论模型计算结果与实测对比
Figure 8. Comparison between results of theoretical model and actual measurement
图 9 不同铁垫板厚度不同扭矩下的板下组合刚度
Figure 9. Combined stiffness under baseplate with different baseplate thicknesses and torques
图 10 不同螺栓间距不同扭矩的板下组合刚度
Figure 10. Combined stiffness under baseplate with different bolt distances and torques
表 1 铁垫板相关参数
Table 1. Related parameters of baseplate
mm 铁垫板参数 值 长度 l 362 厚度 d 18 宽度 b 170 调距垫板长度 dk 84 列车荷载作用宽度 s 169 
下载: 导出CSV
表 2 荷载工况参数
Table 2. Load condition parameters
荷载工况 螺栓预紧力/kN 列车荷载/kN 螺栓扭矩 150 N•m 36 50 螺栓扭矩 200 N•m 48 螺栓扭矩 250 N•m 60
下载: 导出CSV
表 3 计算工况表
Table 3. Calculation conditions
计算工况 铁垫板
厚度/mm锚固螺栓
间距/mm锚固螺栓
扭矩/（N•m）Ⅰ 12，15，18，
21，24，27194 150，200，250 Ⅱ 18 278，328，378，428，478，528
下载: 导出CSV
-
[1] 赵汝康. 铁路钢轨扣件[M]. 北京: 中国铁道出版社, 2018: 159-162. [2] 韦凯,王丰,赵泽明,等. 弹性分开式扣件弹性垫板静刚度测试评价方法[J]. 铁道工程学报,2018,35(11): 32-36,86. doi: 10.3969/j.issn.1006-2106.2018.11.006WEI Kai, WANG Feng, ZHAO Zeming, et al. The methodology research on the test and evaluation of static stiffness of elastic pads in elastic separated fastener[J]. Journal of Railway Engineering Society, 2018, 35(11): 32-36,86. doi: 10.3969/j.issn.1006-2106.2018.11.006 [3] 韦凯,王丰,牛澎波,等. 钢轨扣件弹性垫板的动态黏弹塑性力学试验及理论表征研究[J]. 铁道学报,2018,40(12): 115-122. doi: 10.3969/j.issn.1001-8360.2018.12.015WEI Kai, WANG Feng, NIU Pengbo, et al. Experimental investigation and theoretical model of viscoelastic and plastic dynamic properties of rail pads[J]. Journal of the China Railway Society, 2018, 40(12): 115-122. doi: 10.3969/j.issn.1001-8360.2018.12.015 [4] 陈家照, 黄闽翔, 王学仁, 等. 几种典型的橡胶材料本构模型及其适用性[J]. 材料导报, 2015, 29（增1）: 118-120, 124.CHEN Jiazhao, HUANG Minxiang, WANG Xueren, et al. Typical constitutive models of rubber materials and their ranges of application[J]. Materials Review, 2015, 29(S1): 118-120, 124. [5] 张琦,时剑文,索双富,等. 基于Mooney-Rivlin模型和Yeoh模型的橡胶材料有限元分析[J]. 合成橡胶工业,2020,43(6): 468-471. doi: 10.3969/j.issn.1000-1255.2020.06.006ZHANG Qi, SHI Jianwen, SUO Shuangfu, et al. Finite element analysis of rubber materials based on Mooney-Rivlin models and Yeoh models[J]. China Synthetic Rubber Industry, 2020, 43(6): 468-471. doi: 10.3969/j.issn.1000-1255.2020.06.006 [6] ANNIN B D, BAGROV K V. Numerical simulation of the hyperelastic material using new strain measure[J]. Acta Mechanica, 2021, 232(5): 1809-1813. doi: 10.1007/s00707-020-02904-3 [7] 陈侃,沈景凤,余关仁,等. 轨道用橡胶扣件Mooney-Rivlin模型参数确定及压缩变形的有限元模拟[J]. 机械工程材料,2016,40(4): 89-92. doi: 10.11973/jxgccl201604020CHEN Kan, SHEN Jingfeng, YU Guanren, et al. Parameter determination of Mooney-Rivlin model and finite element simulation of the compression deformation of rubber rail fastener[J]. Materials for Mechanical Engineering, 2016, 40(4): 89-92. doi: 10.11973/jxgccl201604020 [8] 龙驭球. 弹性地基梁的计算[M]. 北京: 人民教育出版社, 1981: 27-67. [9] 铁科院铁建所. 高速铁路扣件系统试验方法 第3部分 组装静刚度的测定: TB/T 3395.1—2015[S]. 北京: 国家铁路局, 2015. [10] 铁道科学研究院金属及化学研究所, 北京市化工产品质量监督检验站. 轨道交通扣件系统弹性垫板: GB/T 21527—2008[S]. 北京: 中国标准出版社, 2008. [11] WANG M J. The role of filler networking in dynamic properties of filled rubber[J]. Rubber Chemistry and Technology, 1999, 72(2): 430-448. doi: 10.5254/1.3538812 [12] 赵泽明,胡小刚,韦凯,等. 弹性分开式扣件板下弹性垫板静刚度试验及评价[J]. 铁道建筑,2018,58(8): 127-131. doi: 10.3969/j.issn.1003-1995.2018.08.31ZHAO Zeming, HU Xiaogang, WEI Kai, et al. Experiment and evaluation on static stiffness of resilient pad under tie plate in elastic separated rail fastening[J]. Railway Engineering, 2018, 58(8): 127-131. doi: 10.3969/j.issn.1003-1995.2018.08.31 -
下载:
点击查看大图
计量
- 文章访问数: 276
- HTML全文浏览量: 98
- PDF下载量: 21
- 被引次数: 0