Distortion Effect of Single Box Double-Cell Box Girders with Rectangular Cross Section
-
摘要:
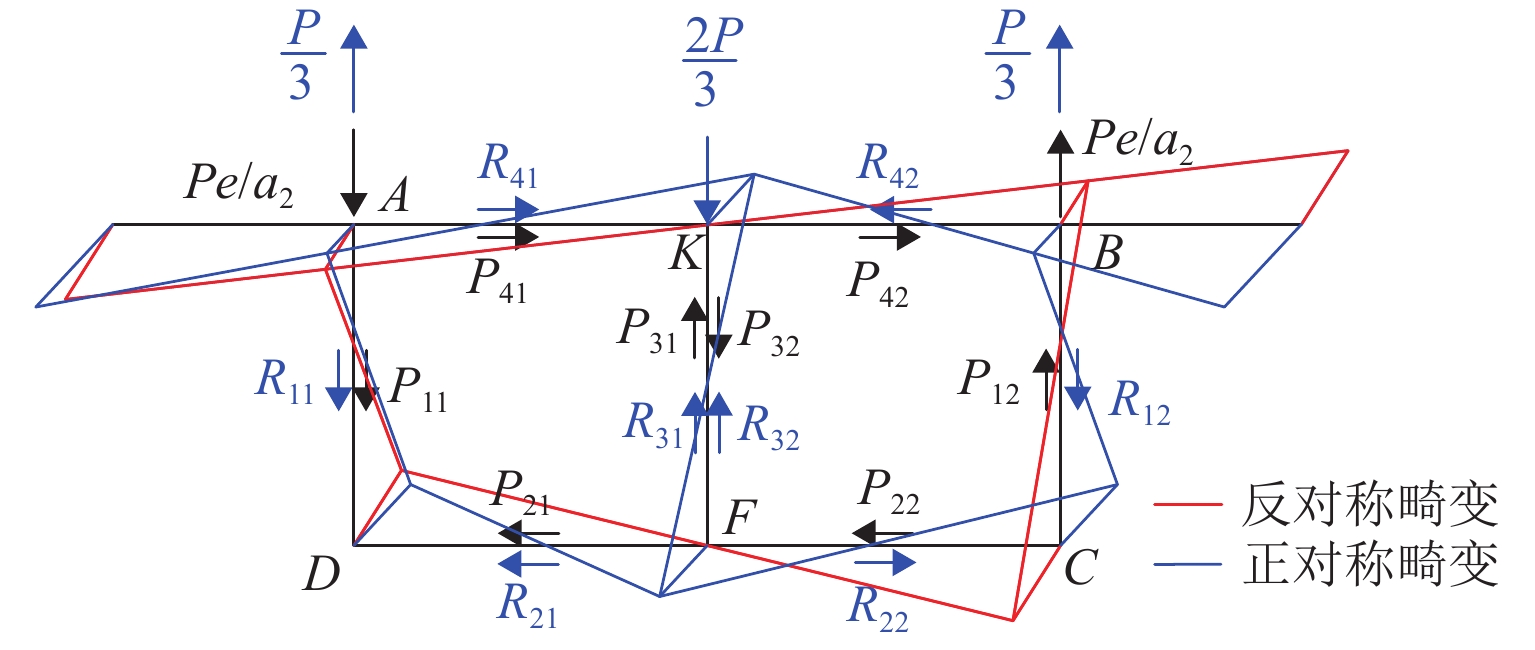
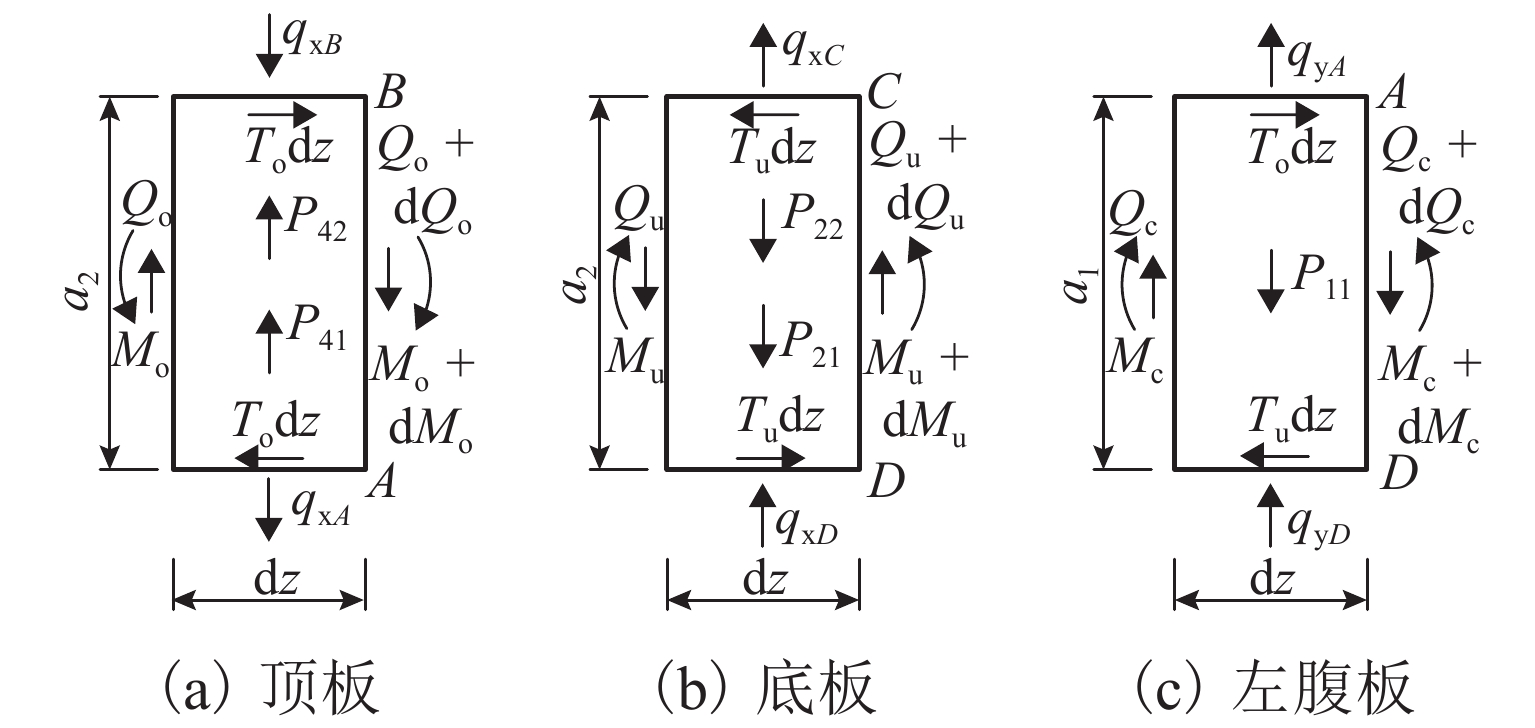
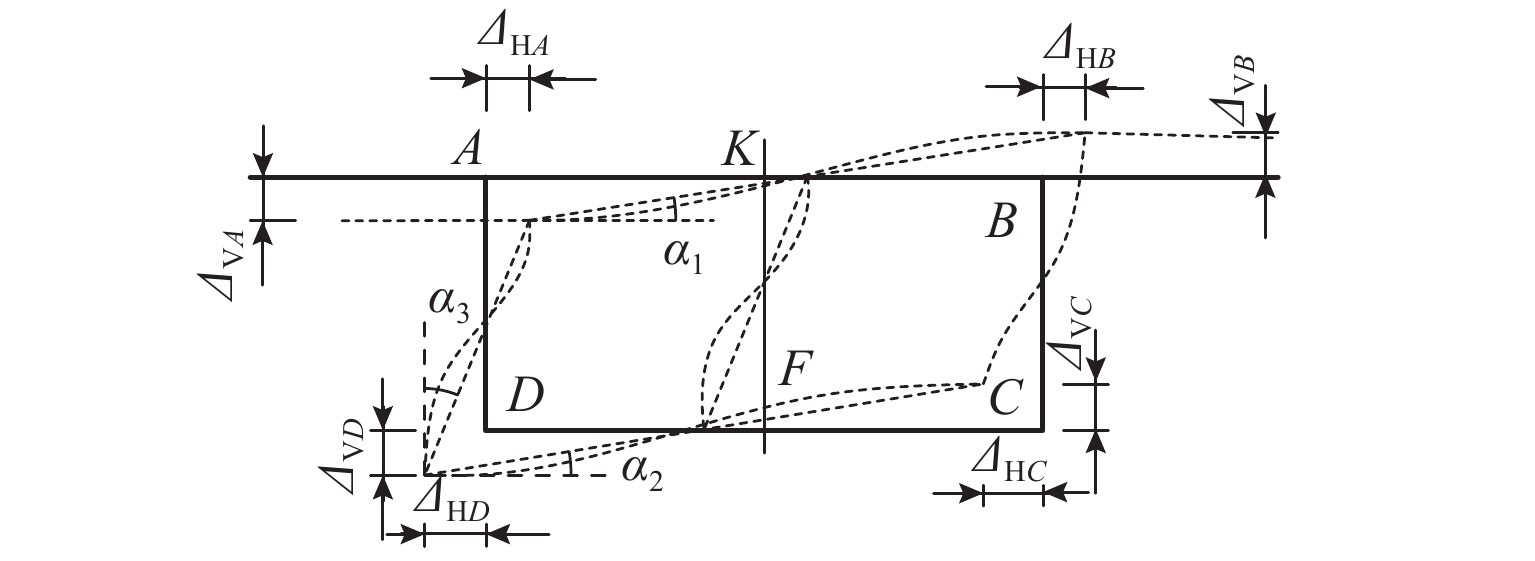
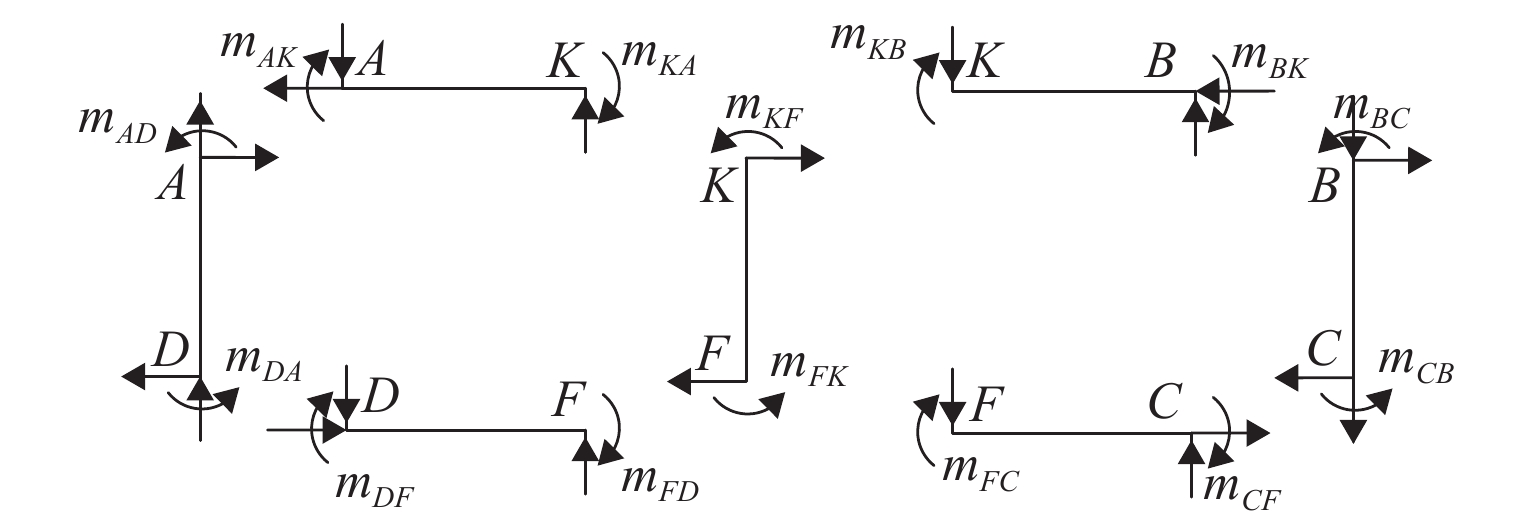
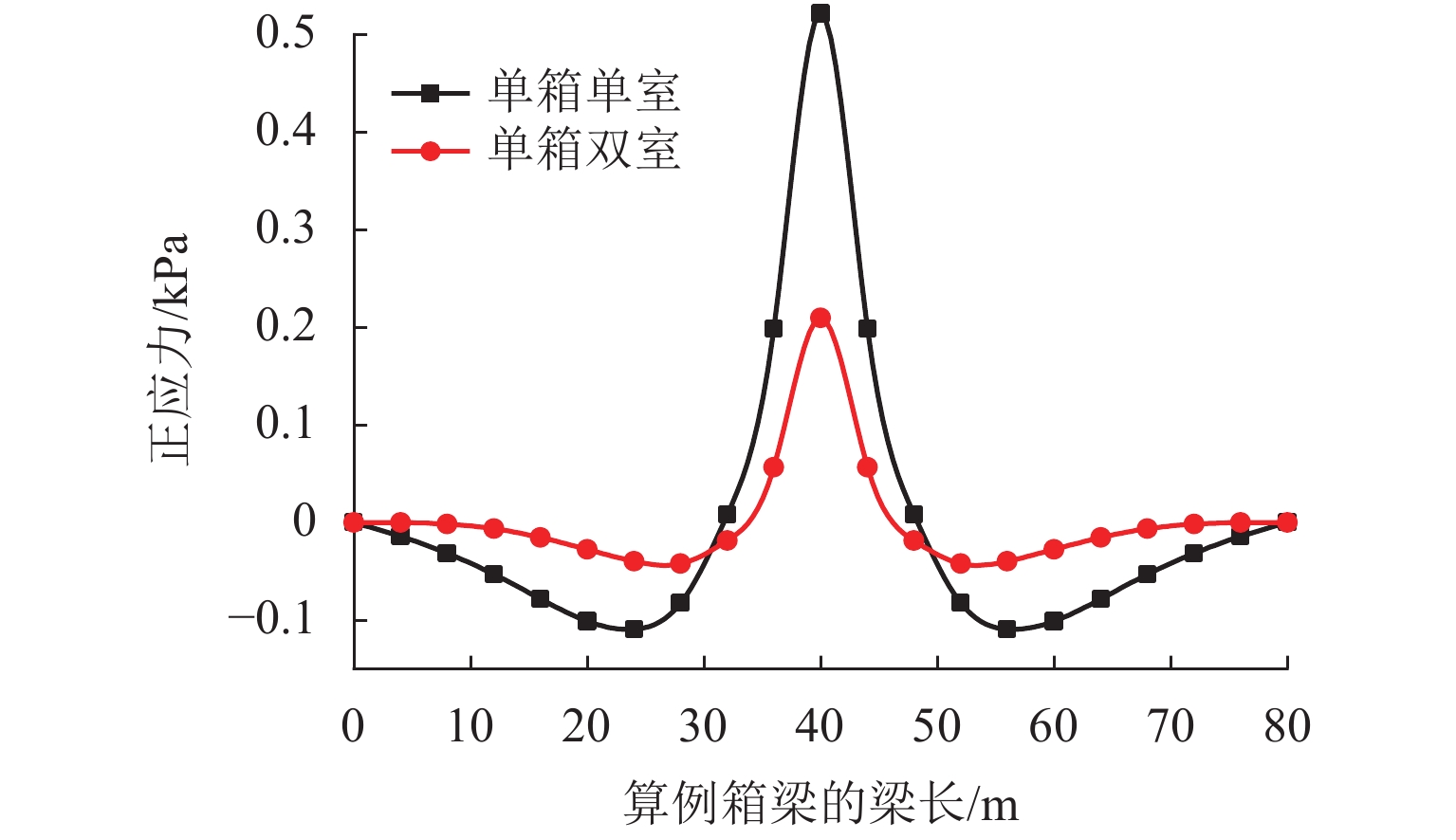
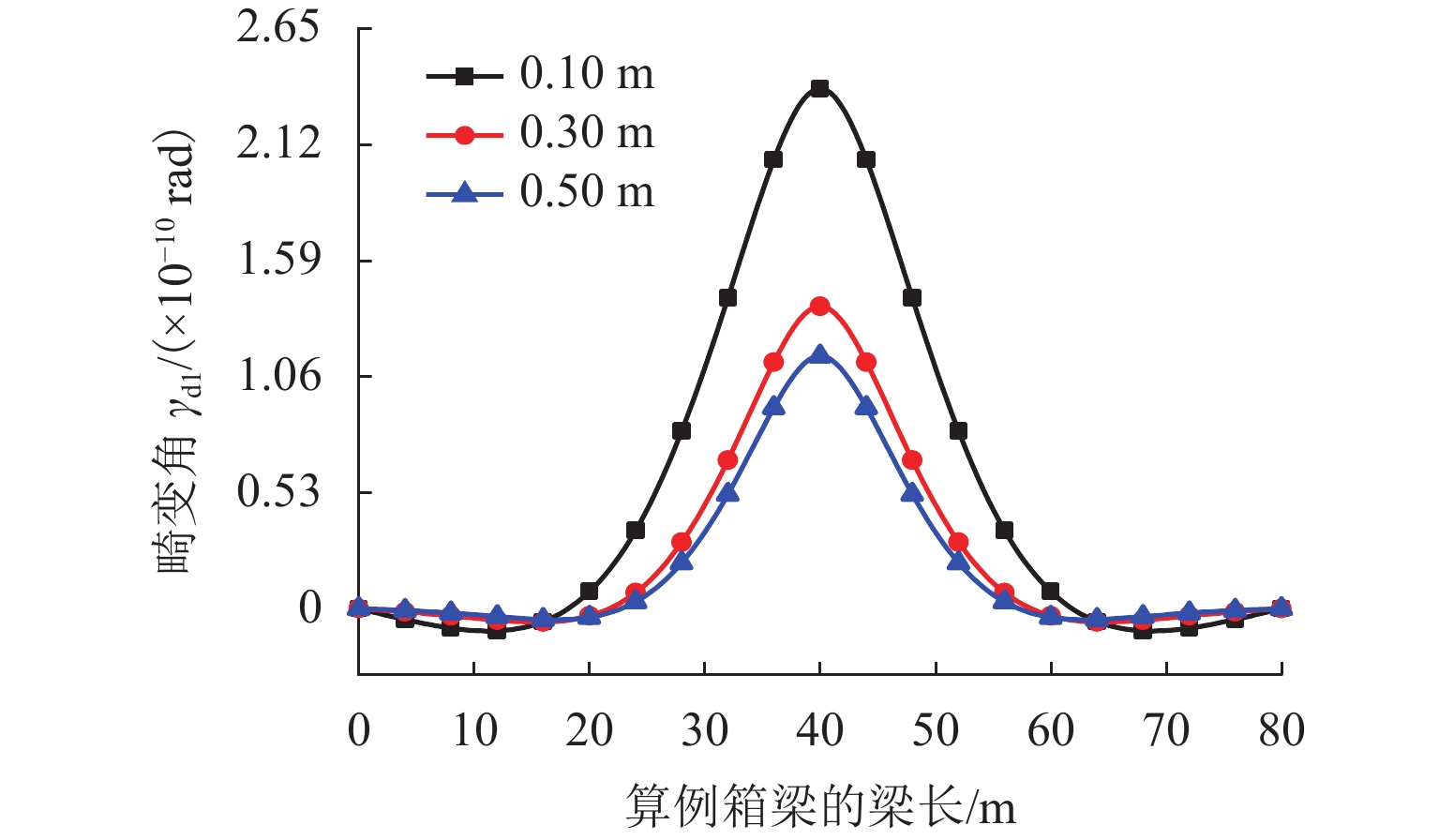
为准确研究单箱双室箱梁在偏心竖向荷载作用下的畸变效应，引入双室箱梁反对称和正对称畸变的概念，补充矩形截面单箱双室箱梁畸变研究的假定. 采用不同定义的畸变角分别描述箱梁的反、正对称畸变，用板元分析法和能量变分法分析单箱双室箱梁的畸变；采用2个参数分别描述顶板、底板和腹板上的畸变正应力分布，以适应双室箱梁正对称畸变；考虑正对称畸变对双室箱梁畸变效应的影响，比较对应单室和双室箱梁的畸变效应，研究中腹板厚度改变时双室箱梁畸变角沿梁长的变化. 研究结果表明：考虑了正对称畸变影响的单箱双室箱梁畸变正应力的解析解和有限元数值解更吻合，误差不超过8.71%；正对称畸变正应力较小，最大只占反对称畸变正应力的28.08%；箱梁中腹板能有效减弱偏心竖向荷载作用引起的箱梁畸变，可使角点处的畸变正应力降低到对应单室箱梁的49.09%；采用2个参数描述箱梁正对称畸变时各板件上畸变正应力的分布比传统方法的更合理；改变中腹板厚度可使单箱双室箱梁畸变发生明显的变化，厚度增大时畸变逐渐减小.
Abstract:To accurately investigate the distortional effect of single box double-cell box girders (SBDBG) under vertical eccentric load, the concepts of antisymmetrical and positive-symmetrical distortion were introduced, and the distortional assumption of rectangular cross section of SBDBG was supplemented. The antisymmetrical and positive-symmetrical distortion of SBDBG were described by different definitions of distortional angles. The distortion of SBDBG was researched by plate element analysis and energy variation methods. Two parameters were used to describe the distribution of stress on top, bottom, and web plates respectively to adapt to the positive-symmetrical distortion. The influence of positive-symmetrical distortion on SBDBG was considered, compared difference of distortion effect between single-cell and double-cell box girder, discussed variation of distortional angle along the length of SBDBG with the change of mid-web thickness. The results show that the analytical solution of SBDBG distortion is more consistent with the finite element solution when considering the influence of positive-symmetrical distortion, the error is less than 8.71%. The normal stress of positive-symmetrical distortion is small, and the maximum is only 28.08% of the antisymmetrical distortion. The mid-web can effectively reduce distortion effect caused by eccentric vertical load, and make the distortion normal stress decrease to 49.09% of the single-cell box girder. The distribution of the distortional normal stress on each plate is more reasonable when using two parameters to describe the positive-symmetrical distortion. The change of the mid-web thickness can make the SBDBG distortion alter obviously, and distortion will gradually decrease when the thickness increases.
-
与内燃机车相比，电力机车运输能力更强、综合性能也更优越，广泛应用于干线铁路运营和城市轨道交通[1]. 电力动车组将动力装置分散到各节车厢，可以达到更高的运营速度，近10多年来在我国得到了快速发展. 牵引变压器负责向动力装置提供电能，关系到列车运行安全，是动车组关键技术之一[2]. 相比于传统电力变压器，动车组牵引变压器发热功率大、运行条件恶劣、内部绕组容易过热[3]. 变压器绕组过热会加速绝缘材料老化，严重时，甚至烧损绝缘材料、引起短路停车事故. 热电类比常用来计算变压器工作温度，采用集中总参数分析方法，分别建立绕组和油的等效电路及相应的微分方程. IEEE Std C57.91—2011导则给出了基于热电类比的变压器绕组温升计算模型[4]. Swift等[5-6]考虑环境温度变化对变压器散热性能的影响，对导则中的热电类比分析模型进行了改进，实验表明，改进后的模型可以比较准确地预测变压器顶层油温升. 为考虑油黏度随温度变化的影响，滕黎等[7]建立变压器热电类比模型时定义了非线性热阻和集总热容. 热电类比法计算简便，但没有充分考虑变压器绕组和油温度在空间分布上的差异. 另外，变压器启动阶段，油流量不断增加，可能对变压器的温升特性产生显著影响. 随着数值传热学和计算机技术的快速发展，计算流体动力学（CFD）技术逐渐进入了变压器热特性研究领域[8-12]. 这类方法通过求解流场和温度场控制微分方程组，获得变压器内部绕组和油温度分布情况. 陈伟根等[8]采用控制体积方法对油自然循环的电力变压器进行数值模拟，预测了稳态条件下绕组温度分布情况；谢蓉等[10]利用商业CFD软件ANSYS Fluent建立了强迫油循环冷却的变压器流固耦合传热的数值模型，并研究了进出口位置、进口速度和导向结构对冷却效果的影响；Torriano等[11]利用商业Fluent软件研究了质量流量和进口条件对盘式绕组内部流动和温度的影响. CFD技术可以比较准确地预测变压器内部流场和温度场，进而替代和削减物理实验，但计算量大，不太适合做非稳态计算，对复杂多设备散热系统的适应性也不强.
牵引变压器发热功率很大，需要采用强迫油循环风冷的方式进行散热. 对这种散热方式进行数值模拟，除了要求解变压器内部油与绕组间复杂流固耦合传热外，还需要考虑高温油通过油泵输送到换热器的二次冷却. 基于已有的分析，本文拟将变压器（含绕组和油）、油冷却器、油泵和管道等看做一个完整系统，对变压器和油冷却器分别做一维假设，建立强油循环风冷变压器散热系统的数学模型，并提出合适的算法进行数值求解. 鉴于动车组运行时牵引变压器温度随时间、空间显著变化，笔者拟借助该数值模型研究变压器动态温度场特性. 为了检验模型的预测精度，本文以一台车载牵引变压器及其配套散热系统进行动态温升实验.
1. 数学模型
1.1 物理模型
某型牵引变压器绕组焦耳热比较大，为防止其温度过高，采用强迫油循环风冷方式进行散热. 该变压器散热系统工作原理如图1，由变压器（内含2个线圈柱）、油泵、油冷却器、风机、管道和冷却油等组成. 工作时，冷却油在油泵驱动下，进入绕组内部油道进行冷却；吸热后的高温油经管道流入油冷却器，被常温空气所冷却；降温后的冷却油再次进入变压器构成循环.
图 1 强迫油循环风冷变压器散热示意Figure 1. Heat dissipation for air-cooling transformer with forced oil circulation该变压器线圈柱采用层式结构，低压绕组在里侧，外侧为高压绕组，如图2所示. 鉴于高压和低压绕组的结构和工作参数相差较大，本模型对其单独建模，两绕组的冷却油在变压器出口处混合.
图 2 高、低压绕组和油流道结构示意Figure 2. High- and low-voltage windings together with oil channels1.2 控制方程组
牵引变压器工作时，冷却油不断流过绕组层间狭缝流道，吸收绕组工作损耗所释放的热量. 这一过程可以抽象为带固体内热源的平行通道流固耦合传热问题. 考虑到铜线绕组热导率很大，单层绕组厚度又比较小，可以忽略垂直于油流动方向温度梯度，因此，采用一维空间流体（冷却油）和固体（绕组）双能量方程来描述 [13-14]，如式（1）、（2）.
ρfcp,f∂Tf∂t+ρfucp,f∂Tf∂x=kf∂2Tf∂x2+αas(Ts−Tf), (1) ρscp,s∂Ts∂t=ks∂2Ts∂x2+αas(Tf−Ts)+SJH, (2) 式中：u为流体速度；t和x分别为时间和绕组轴向位移；ρ、cp、k和T依次为密度、比热、热导率和温度，下标f和s分别表示流体和固体；as为比表面积；α为油与绕组间对流传热系数，由经验关联式确定[14]； SJH为绕组运行的焦耳热，与工作电流和导线截面积等有关，数值由焦耳定律确定.
为了考虑换热面和液体热容对变压器动态温度场特性的影响，油冷却器传热模型包括固体换热面及其两侧流体（冷却油和空气）的非稳态能量守恒方程. 与变压器模型类似，油冷却器也采用一维非稳态模型，即冷热流体能量方程形式与式（1）相同，固体换热面的微分方程与式（2）类似，但需要同时考虑两侧表面的对流传热，另外，其内部无内热源项（即无右侧第3项）.
变压器油流量与油泵供油特性有关，还依赖于油泵实际工作扬程. 油泵工作扬程等于变压器、油冷却器和管道等流动阻力之和，变压器与油冷却器的流动阻力Δp用式（3）计算，管道油流阻力还需考虑局部损失的影响[15].
Δp=fLρu22Dh, (3) 式中：L和Dh分别为流道长度和特征尺寸；f为摩擦因子，由经验关联式确定.
油冷却器采用板翅式结构，空气侧采用波纹翅片，油侧采用锯齿形翅片. 数值求解油冷却器能量微分方程时，首先按冷却器结构和工作参数确定空气侧和油侧的雷诺数（Re数），然后采用j因子和f因子关联式（式（4）~（7））确定α和
Δp .空气侧波纹翅片（1000 < Re < 15000）[15-16]：
f=10.628Re−0.359(H/s)0.264(2A/s)−0.848(l/2A)−1.931， (4) j=0.242Re−0.375(H/s)0.235(2A/s)−0.288(l/2A)−0.553， (5) 式中：H、s分别为翅片高度、间距； A和l分别为波纹波幅、波长.
油侧锯齿翅片（300 < Re < 7500）[16-17]：
lnf=0.132856(lnRe)2−2.28042lnRe+6.79634， (6) lnj=−0.0264136(lnRe)3+0.555843(lnRe)2−4.09241lnRe+6.21681. (7) 高、低压绕组结构尺寸和工作电流有显著差异，其传热特性明显不同，为提高预测精度，分别对高、低压区绕组和油的能量方程进行离散. 根据层间油道并联的特点，按照高压和低压绕组油道流动阻力相等的原则来分配两者油流量.
2. 数值求解
强迫油循环风冷变压器散热的数值模型由变压器、油泵、油冷却器和管道等模块组成. 这些模块通过进出口压力、温度和流量连续耦合在一起，借助迭代计算进行数值求解. 变压器和油冷却器采用分布参数，数值计算时，沿油流方向离散成若干单元，并采用有限差分法将其控制微分方程组（即式（1）、式（2））转变为代数方程组. 方程离散时，空间导数采用中心差分格式，时间维度采用全隐格式. 在MATLAB平台上进行数值计算，采用稀疏矩阵方法求解代数方程组.
图3为牵引变压器散热数值计算流程框图. 求解过程由内、外两个循环组成：内循环用于计算当前时刻变压器（含冷却油和绕组）温度和流阻、油冷却器油温和流阻、油泵流量等参数，由于冷却油黏度和绕组电阻等参数与温度密切相关，内循环通过迭代计算确定绕组内热源和油泵流量；外循环为时间域循环，用于模拟变压器和油冷却器温度场和油循环流量等参数随时间的变化. 通过比较相邻时刻温度相对变化量来判断散热过程是否进入稳态工况，一旦进入稳定工况，输出计算结果并终止程序.
图 3 强迫油循环风冷式变压器散热数值计算流程Figure 3. Flow chart for heat dissipation of air-cooling transformer with forced oil circulation3. 变压器温升实验与模型验证
3.1 变压器温升实验
为验证本文变压器散热模型的准确性，搭建了变压器温升实验平台，对一台牵引变压器在典型工况下进行了测试，如图4所示. 实验平台包括一台牵引变压器样机及其强油循环风冷散热系统、供电系统、数据监测采集系统等. 变压器高、低压绕组均采用层式结构，轴向长度约为750 mm. 低压和高压绕组铜导线额定电流分别为966 A和147 A，额定工况发热密度约为0.82 MW/m3和1.40 MW/m3. 变压器进口和出口设置了油温探头，以便实时监测变压器工作时油温变化情况，同时依据断电时刻直流电阻值来推断绕组平均温度. 实验开始时，变压器内部温度与环境温度相同，约为31.2 ℃. 通电后，数据采集系统自动监测记录变压器各监测点数据. 连续运行3 h左右，系统温度达到稳定并已持续一段时间，停止实验.
图 4 牵引变压器温升实验台Figure 4. Experimental rig for temperature rise of traction transformer3.2 模型验证
采用1.2节建立的变压器散热模型对牵引变压器动态温升实验进行数值模拟，并将模型预测的变压器进、出口油温度变化情况与实验值进行对比，如图5（a）所示. 从图5（a）曲线可以看出：高压绕组和低压绕组出口油温呈现同样的变化趋势，即通电初始阶段（约27 min），油温度急剧上升，随后油温上升速度显著减慢，最后趋于稳定. 出口油温的变化规律与变压器内部非稳态传热和油冷却器中油二次散热有关，即在变压器初始运行阶段，由于油温度较低、黏度较大，油泵工作扬程较大、流量较小，因此，在相同绕组发热量条件下，绕组和油温度上升都比较快；另一方面，在初始阶段，油流量较少，且油与空气间温差较小，油冷却器中油-空气换热量较少，因此，油从绕组获得的热量不能及时散发到大气中，导致油和绕组温度快速上升. 运转一段时间后，油温度已经显著上升，其黏度明显下降，此时，油流量较大，绕组能够得到有效冷却，同时由于油冷却器内传热也显著变强，油从绕组得到的热量能够及时排放大气，因而油和绕组温度上升速度明显减慢，最终趋于稳定. 对比图5（a）中温度曲线可以看出：本文模型预测的变压器进、出口油温曲线与实验值吻合较好，稳定运行的误差分别为1.8 ℃和0.7 ℃，整个动态过程的最大误差小于5.0 ℃，能够满足工程实践需求；本文预测的油温稳定时间（与稳定后温度相差1.0 ℃所需运行时间）与实验值接近，即58 min和61 min.
图 5 变压器油和绕组温度模型预测值与计算值对比Figure 5. Comparisons of oil and winding temperatures of current model against experimental counterparts绕组断电时刻直流电阻反推高压和低压绕组平均温度数值见图5（b）右上角数值点. 为便于与实验值进行比较，对变压器模型计算的高、低压绕组温度场分别做平均处理，并将其随时间的变化情况绘于图5（b）中. 从图5（b）看出：变压器初始运行阶段，绕组温度快速升高，经过一段时间后温度上升速度显著减慢，最后趋于稳定. 显然，由于绕组发热量需要通过油带走，绕组温度上述变化规律与图5（a）中进、出口油温变化曲线一致. 定量比较图5（b）中稳态条件下高、低压绕组温度的模型预测值与实验值可以看出：两者比较接近，相对误差分别为3.2% 和0.6%.
为方便读者参考，表1总结了模型预测油温和绕组温度的实验测量值与预测值的相对大小.
表 1 油和绕组稳态温度预测值与实验值的对比Table 1. Comparison of oil and winding temperatures of current model against experimental counterparts参数 进口油温/℃ 出口油温/℃ 稳定时间/min 高压绕组温度/℃ 低压绕组温度/℃ 模型预测值 68.5 73.9 58 81.4 92.7 实验值 66.7 73.2 61 78.9 92.1 偏差 1.8 0.7 −3 2.5 0.6 上述对比分析表明：本文强迫油循环风冷变压器散热模型具有较好的预测精度，可以用于牵引变压器动态温度场研究.
4. 变压器温度场分析
为进一步了解变压器内部温度情况，图6给出了典型时刻高压和低压绕组以及相应流道内油温度沿轴向的分布曲线，横坐标0和750分别代表绕组线柱底部和顶部. 由于低温油从线圈柱底部进入绕组层间流道，吸收绕组损耗热后从顶部流出，因此油温度沿绕组轴向不断升高；另一方面，随着轴向油温的升高，油冷却能力变弱，为此绕组温度也会沿轴向不断增加，与图6温度曲线一致. 铜导线电阻值随温度升高而增大，所以绕组顶部发热强度比较大，然而图6绕组曲线显示其顶部温度变化率比较小. 绕组的这种温度分布特点可能与油热容量（等于油流量与比热的乘积）的大小有关. 当油热容量较大时，吸收同样损耗热后温度变化较小；当油轴向温升速度比绕组慢时，轴向传热温差将增加，此时即便下游绕组发热强度较大，其轴向温升速度也可能比上游慢. 根据图6中可以看出：本文变压器油热容量比较大，其轴向温度增加速度明显低于绕组，证实了图6绕组温度轴向增加速度逐渐减慢的合理性. 实际上，绕组温度的变化趋势与文献[18]报道一致.
图 6 变压器内高、低压绕组和油轴向温度分布Figure 6. Axial temperature profiles of high-and low-voltage windings and oils对比图6中实心方块和圆标记的曲线可以看出：高压和低压绕组流道进口处（轴向位移为0）油温度相同，但两者油温轴向变化速率明显不同，高压区流道油轴向温升速度明显高于低压区，另外，低压绕组的温度则明显高于高压绕组. 变压器高压区和低压区的这种温度差异与高低压绕组结构和工作参数有关.
5. 结 论
牵引变压器供电功率大且随时间波动，需要采用先进的强迫油循环风冷方式进行散热，然而，相关的变压器动态温度场研究报道比较有限. 本文将变压器（含绕组和冷却油）、油冷却器、油泵和管道等视为一个完整系统，建立了强迫油循环风冷型牵引变压器分布参数的动态温度场数学模型，并提出一套数值求解算法. 为了检验模型预测精度，对一台动车组牵引变压器样机进行动态温升性能实验. 此外，借助该模型对绕组内部温度场情况进行了分析.
研究表明，本文变压器数值模型有较好的精度，预测的牵引变压器稳态条件进、出口油温（68.5 ℃和73.9 ℃）和平均过渡时间（58 min）均与对应的实验值（66.7 ℃和73.2 ℃，61 min） 吻合较好. 另外，模型预测的高压绕组平均温度与实验值偏差大于低压绕组，约为2.5 ℃.
牵引变压器动态温度场与其结构和工作参数密切相关，借助本文模型可以对其几何结构和工况条件进行优化.
-
图 7 结构AKFD的变形和横向弯矩
Figure 7. Deformation and transverse bending moment of structure AKFD
图 11 中腹板厚度对箱梁畸变角的影响
Figure 11. Influence of mid-web thickness on distortional angle of box girder
表 1 箱梁反对称畸变计算值
Table 1. Antisymmetrical distortional values
方法 Iωd1/m6 IR1/m2 ωdD/m2 ωdA/m2 β1 γd1/（ × 10−10 rad） Bd/（N·m2） σdA/kPa σdD/kPa 单箱单室箱梁畸变 12.1728 0.0040 2.5426 1.2075 0.4749 3.3961 2.6279 0.5213 1.0978 单箱双室箱梁反对称畸变 12.1728 0.0096 2.5426 1.2075 0.4749 1.7660 2.1110 0.2094 0.4409 
下载: 导出CSV
表 2 箱梁正对称畸变计算值
Table 2. Positive-symmetrical distortional values
方法 角点应力比 γd/（ × 10−10 rad） σdA/kPa σdD/kPa 单箱双室箱梁正对称畸变 β1 = 0.5000， β2 = 0.6241 0.0160 0.05897 0.11795 单箱单室箱梁畸变 0.3229 3.7516 0.28055 0.86898
下载: 导出CSV
表 3 箱梁角点畸变正应力
Table 3. Corner distortion normal stress of box girder
畸变正应力 单箱双室箱梁畸变解析解/kPa 有限元解 ②/kPa 误差（（①−②）/② × 100） /% 反对称畸变 正对称畸变 最终结果 ① σdA 0.20940 0.05897 0.26837 0.26380 1.73 σdD 0.44090 0.11795 0.55885 0.61220 −8.71
下载: 导出CSV
-
[1] 张元海,刘泽翔,林丽霞,等. 基于势能驻值原理的薄壁箱梁畸变效应分析[J]. 中南大学学报(自然科学版),2016,47(10): 3461-3468.ZHANG Yuanhai, LIU Zexiang, LIN Lixia, et al. Analysis on distortion effect of thin-walled box girders based on principle of stationary potential energy[J]. Journal of Central South University (Science and Technology), 2016, 47(10): 3461-3468. [2] 徐勋,强士中. 薄壁箱梁畸变分析理论的研究[J]. 工程力学,2013,30(11): 192-201.XU Xun, QIANG Shizhong. Research on distortion analysis theory of thin-walled box girder[J]. Engineering Mechanics, 2013, 30(11): 192-201. [3] 鲍永方,黄文彬. 矩形箱梁约束扭转理论的分析与比较[J]. 工程力学,1997,14(3): 132-137.BAO Yongfang, HUANG Wenbin. Analysis and comparision of restrained torsion theories for rectangular box shaped beam[J]. Engineering Mechanics, 1997, 14(3): 132-137. [4] 王兆南,张元海. 基于板元分析法的梯形截面箱梁畸变效应研究[J]. 铁道学报,2020,42(2): 102-109.WANG Zhaonan, ZHANG Yuanhai. Research on distortion effect of box girder with trapezoidal cross section based on plate element analytic method[J]. Journal of the China Railway Society, 2020, 42(2): 102-109. [5] PEZESHKY P, MOHAREB M. Distortional theory for the analysis of wide flange steel beams[J]. Engineering Structures, 2014, 75: 181-196. doi: 10.1016/j.engstruct.2014.05.024 [6] YOO C H, KANG J, KIM K. Stresses due to distortion on horizontally curved tub-girders[J]. Engineering Structures, 2015, 87: 70-85. doi: 10.1016/j.engstruct.2015.01.011 [7] TSIPTSIS I N, SAPOUNTZAKIS E J. Generalized warping and distortional analysis of curved beams with isogeometric methods[J]. Computers & Structures, 2017, 191: 33-50. [8] KOLEKOVÁ Y, KOVÁČ M, BALÁŽ I. Influence lines of bridges with box-girder cross-section under torsion and distortion[J]. Procedia Engineering, 2017, 190: 603-610. doi: 10.1016/j.proeng.2017.05.386 [9] 刘保东,冯文章,任红伟,等. 波纹钢腹板连续刚构桥扭转与畸变的试验研究[J]. 中国铁道科学,2015,36(4): 40-46. doi: 10.3969/j.issn.1001-4632.2015.04.07LIU Baodong, FENG Wenzhang, REN Hongwei, et al. Experimental study on torsion and distortion of continuous rigid frame bridge with corrugated steel webs[J]. China Railway Science, 2015, 36(4): 40-46. doi: 10.3969/j.issn.1001-4632.2015.04.07 [10] 狄谨,周绪红,游金兰,等. 波纹钢腹板预应力混凝土组合箱梁抗扭性能[J]. 长安大学学报(自然科学版),2009,29(3): 58-63,76.DI Jin, ZHOU Xuhong, YOU Jinlan, et al. Torsional property of prestressed concrete composite beam with corrugated steel webs[J]. Journal of Chang’an University (Natural Science Edition), 2009, 29(3): 58-63,76. [11] 杨丙文,黎雅乐,万水,等. 波形钢腹板箱梁畸变应力分析[J]. 东南大学学报(自然科学版),2011,41(5): 1065-1069. doi: 10.3969/j.issn.1001-0505.2011.05.032YANG Bingwen, LI Yale, WAN Shui, et al. Stress analysis of box girders with corrugated steel webs under distortion[J]. Journal of Southeast University (Natural Science Edition), 2011, 41(5): 1065-1069. doi: 10.3969/j.issn.1001-0505.2011.05.032 [12] LI L F, ZHOU C, WANG L H. Distortion analysis of non-prismatic composite box girders with corrugated steel webs[J]. Journal of Constructional Steel Research, 2018, 147: 74-86. doi: 10.1016/j.jcsr.2018.03.030 [13] REN Y Z, CHENG W M, WANG Y Q, et al. Distortional analysis of simply supported box girders with inner diaphragms considering shear deformation of diaphragms using initial parameter method[J]. Engineering Structures, 2017, 145: 44-59. doi: 10.1016/j.engstruct.2017.05.004 [14] CAMBRONERO-BARRIENTOS F, DÍAZ-DEL-VALLE J, MARTÍNEZ-MARTÍNEZ J A. Beam element for thin-walled beams with torsion, distortion, and shear lag[J]. Engineering Structures, 2017, 143: 571-588. doi: 10.1016/j.engstruct.2017.04.020 [15] 蔺鹏臻,阳放,雒敏,等. 单箱双室箱梁对称弯曲时的局部扭转效应[J]. 建筑结构学报,2017,38(7): 68-77.LIN Pengzhen, YANG Fang, LUO Min, et al. Analysis on local torsional behavior of twin-cell box girder under symmetrical bending[J]. Journal of Building Structures, 2017, 38(7): 68-77. [16] CHIDOLUE C A, AMADOU A, EZEAGU C A. Torsional-distortional performance of multi-cell trapezoidal box girder with all inclined web members[J]. Journal of Engineering Research and Applications, 2015, 5(2): 45-51. -
下载:
下载:
点击查看大图
计量
- 文章访问数: 490
- HTML全文浏览量: 268
- PDF下载量: 44
- 被引次数: 0