受约束的过道布置问题建模及优化方法

刘俊琦; 张则强; 龚举华; 张裕

doi:10.3969/j.issn.0258-2724.20200803

受约束的过道布置问题建模及优化方法

doi: 10.3969/j.issn.0258-2724.20200803

西南交通大学机械工程学院，四川成都 610031

基金项目: 国家自然科学基金（51205328，51675450）；教育部人文社会科学研究青年基金（18YJC630255）；四川省科技计划（2022YFG0245）

详细信息

作者简介:
刘俊琦（1995—），男，博士研究生，研究方向为设施布局与智能优化，E-mail：junqi5497@163.com

通讯作者:
张则强（1978—），男，教授，研究方向为制造系统与智能优化，E-mail：zzq_22@163.com

中图分类号: TH165；TP301.6
计量
- 文章访问数: 280
- HTML全文浏览量: 75
- PDF下载量: 30
- 被引次数: 0
出版历程
- 收稿日期: 2020-12-01
- 修回日期: 2021-03-22
- 网络出版日期: 2022-08-13
- 刊出日期: 2021-03-26

Modeling and Optimization Method of Constrained Corridor Allocation Problem

School of Mechanical Engineering, Southwest Jiaotong University, Chengdu 610031, China

摘要

摘要:
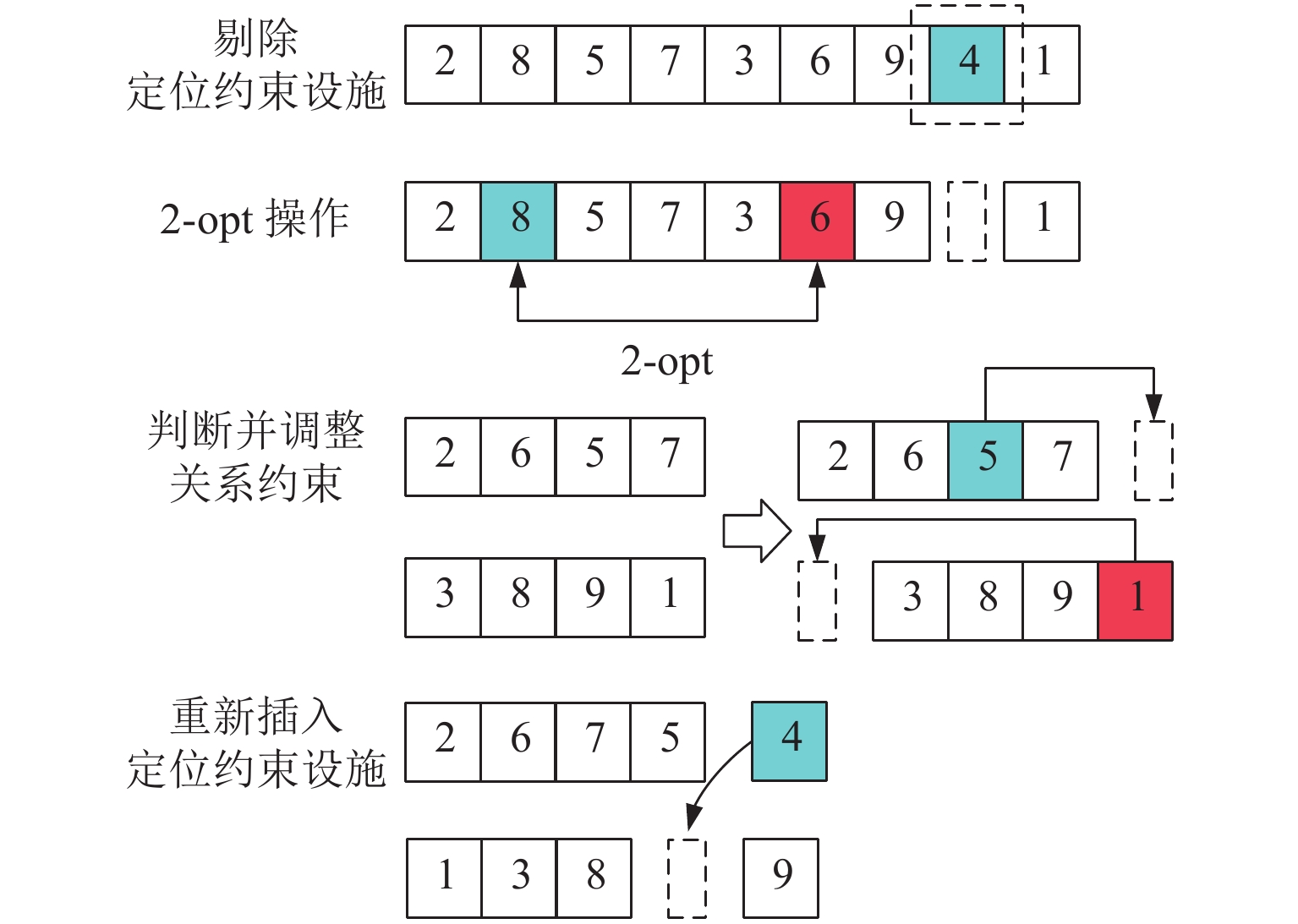
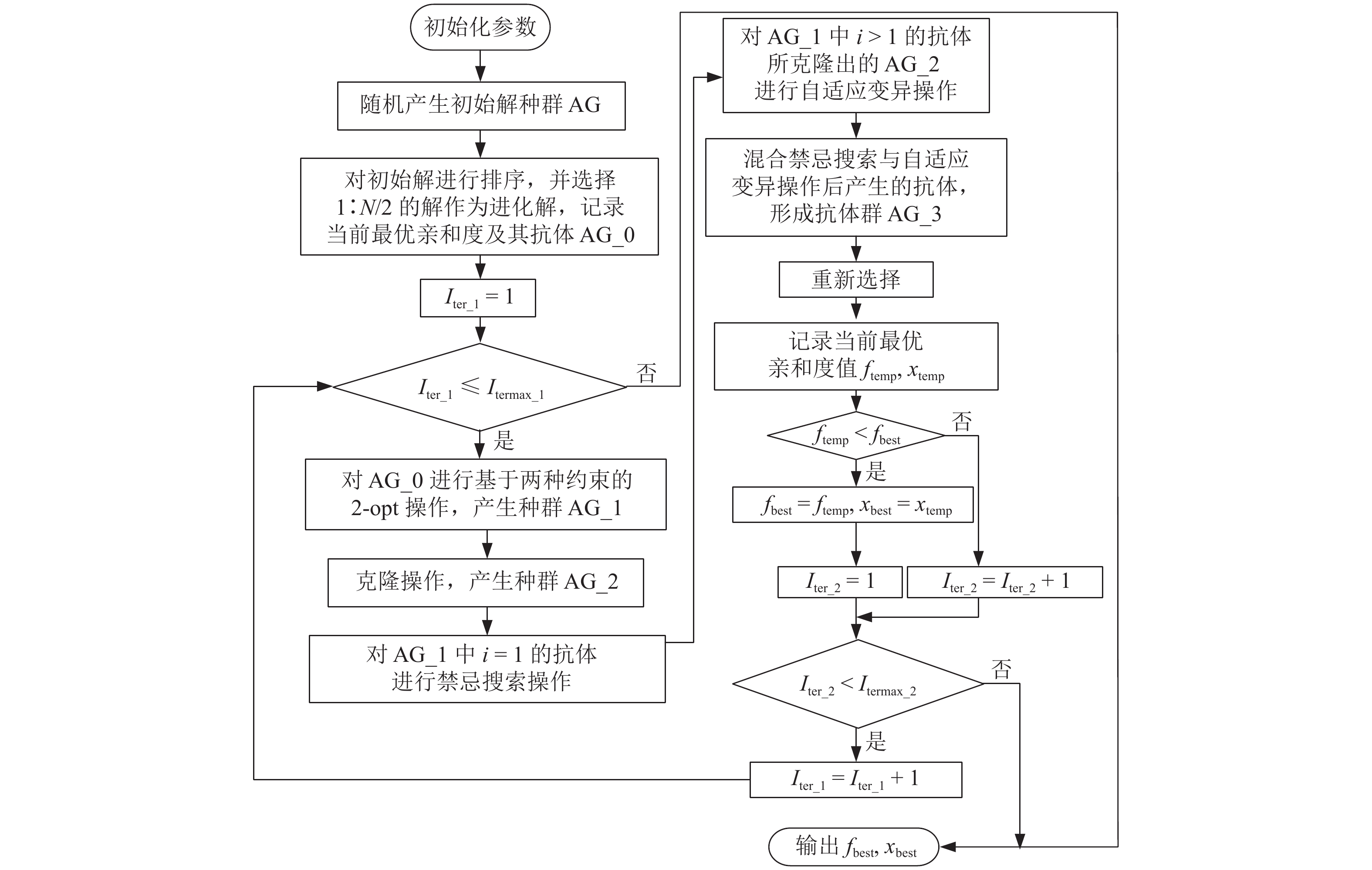
为了研究过道布置问题中设施关系对布局的影响，首先，考虑定位约束与排序约束，构建过道布置问题混合整数规划模型，并提出一种求解该问题的自适应混合克隆选择算法，在克隆操作之前新增符合受约束过道布置问题特性的2-opt操作，随后对所产生种群中最优个体进行禁忌搜索操作，对其他个体进行变异操作并设置自适应变异概率；然后，对模型进行精确求解以验证模型的正确性且求解结果为算法提供了理论依据；最后，应用所提算法分别对受约束过道布置问题与基本过道布置问题的42 ~ 49规模实例进行测试，并将求解结果与克隆选择算法、遗传算法、分散搜索算法、花授粉算法以及烟花算法进行对比，结果表明：混合克隆选择算法可以达到当前先进算法的求解效果且在算例sko-42-04与算例sko49-03上表现更优.
- 设施布局 /
- 受约束的过道布置问题 /
- 克隆选择算法 /
- 禁忌搜索操作 /
- 自适应变异
Abstract:
In order to study the influence of facility relationship on layout in corridor allocation problem, An integer programming model considering location and relationship constraints is constructed, and a hybrid clonal selection algorithm based on clonal selection algorithm is proposed to solve the problem. Before clonal operation, a new 2-opt operation based on problem characteristics is added. Then, tabu search operation is carried out for the optimal individuals in the generated population, mutation operation is carried out for other individuals and adaptive mutation probability is set. The model is accurately solved to verify the correctness of the model and the solution results provide a theoretical basis for the algorithm. Applying the proposed algorithm to test 42−49 scale examples of constrained corridor allocation problem and basic corridor allocation problem respectively. The results are compared with clonal selection algorithm, genetic Algorithm, Scatter Search, flower pollination algorithm and fireworks algorithm. The results show that the hybrid clone selection algorithm can achieve the solution effect of the current advanced algorithm and perform better in the examples sko-42-04 and sko-49-03.
- facility layout /
- constrained corridor allocation problem /
- clone selection algorithm /
- tabu search operation /
- adaptive mutation

HTML全文

图 1 过道布置问题距离计算方式

Figure 1. Distance calculation method of CAP

下载: 全尺寸图片幻灯片

图 2 基于两种约束的2-opt操作示意

Figure 2. Improved 2-opt operation diagram based on two kinds of constraints

下载: 全尺寸图片幻灯片

图 3 ACSATS 流程

Figure 3. Flow chart of ACSATS

下载: 全尺寸图片幻灯片

图 4 CSA与ACSATS在9~15规模下问题求解结果箱线图

Figure 4. Box-plot of the solution results of CSA and ACATS in the scale of 9−15

下载: 全尺寸图片幻灯片

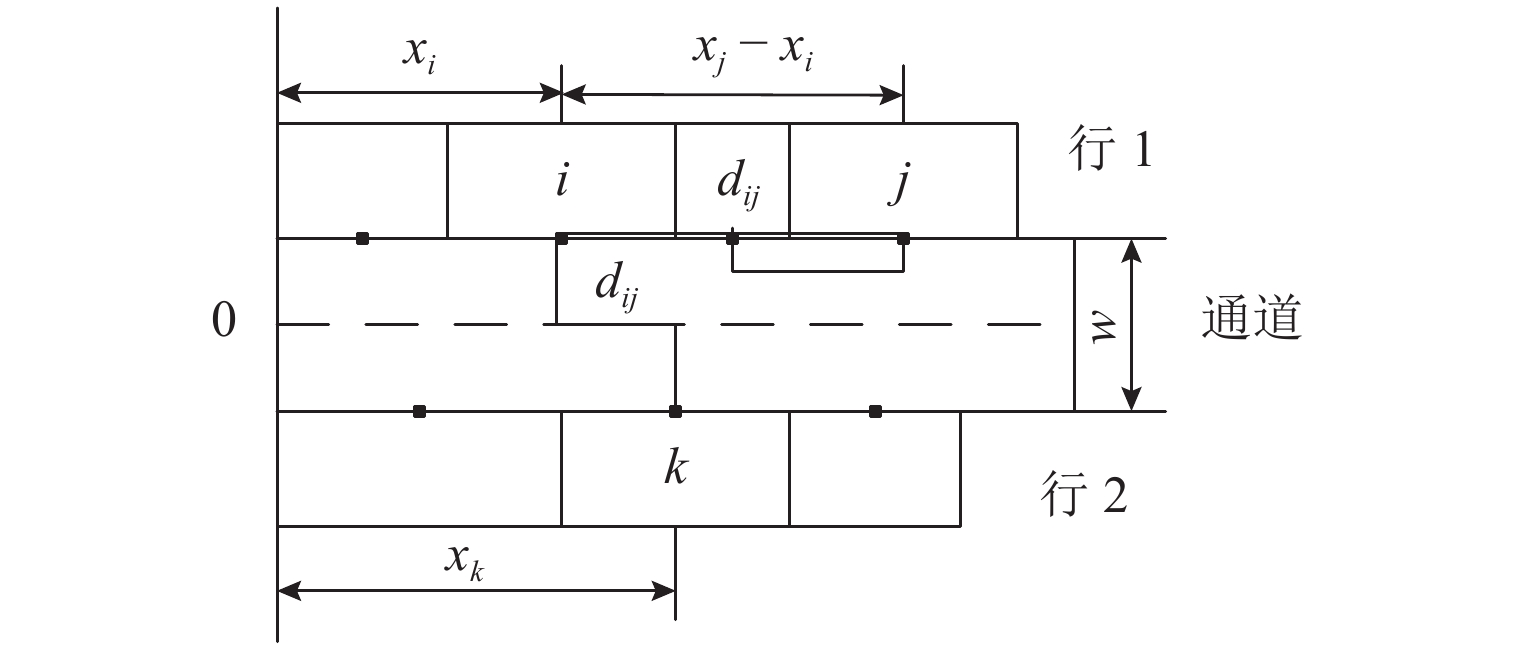
表 1 参数名称与定义

Table 1. Parameter names and definition

变量	意义
n	问题规模，即布置的设施数目
I	所有设施的集合，I={1, 2, 3, …, n}
i, j, h, k	设施编号，i, j, h∈ I
c_ij	设施 i 与设施 j 之间的物流成本，$\forall $i∈{1,2,…, n−1}，$\forall $j∈ {1,2,…,n−1}
d_ij	设施 i, j 之间物流交互点在 X 轴方向的距离
l_i	设施 i 沿 X 轴边线的长度
w	通道宽度
α_ij	二进制变量，i, j 分配在同一行，且设施 i 被放置在设施 j 的左侧 α_ij= 1，否则 α_ij= 0
q_ij	二进制决策变量，若设施 i 与设施 j 被布置于同一行，则 q_ij= 1，否则 q_ij= 0
β_hi	二进制决策变量，若设施 h 的物料搬运点在设施 i 的左侧，则 β_hi= 1，否则 β_hi= 0
f	设施间的总物流成本

下载: 导出CSV

表 2 CSA与ACSATS算法求解CCAP与CAP的参数

Table 2. Algorithm parameters of CSA and ACSATS in solving CCAP and CAP

问题	算法	n	N	I_{termax_1}	G	α	S/个	搜索次数/次
CCAP	ACSATS	9~15	200	200	0.01	1	20	200
		25	400	600	0.01	1.2	40	400
		30	600	800	0.02	1.6	80	800
		36	800	1000	0.02	1.6	80	800
	CSA	42~49	1000	1000	0.02	1.6	100	800
		9~15	200	200	0.01	1	—	—
		9~15	200	200	0.01	0.8	20	200
CAP	ACSATS	30	600	800	0.02	1.6	80	600
		36	800	1000	0.02	1.6	80	600
		42	1000	1000	0.02	1.6	100	800
		49	1000	1200	0.02	1.8	110	800

下载: 导出CSV

表 3 LINGO精确解与ACSATS算法的计算结果

Table 3. LINGO exact solution and solving results of ACSATS

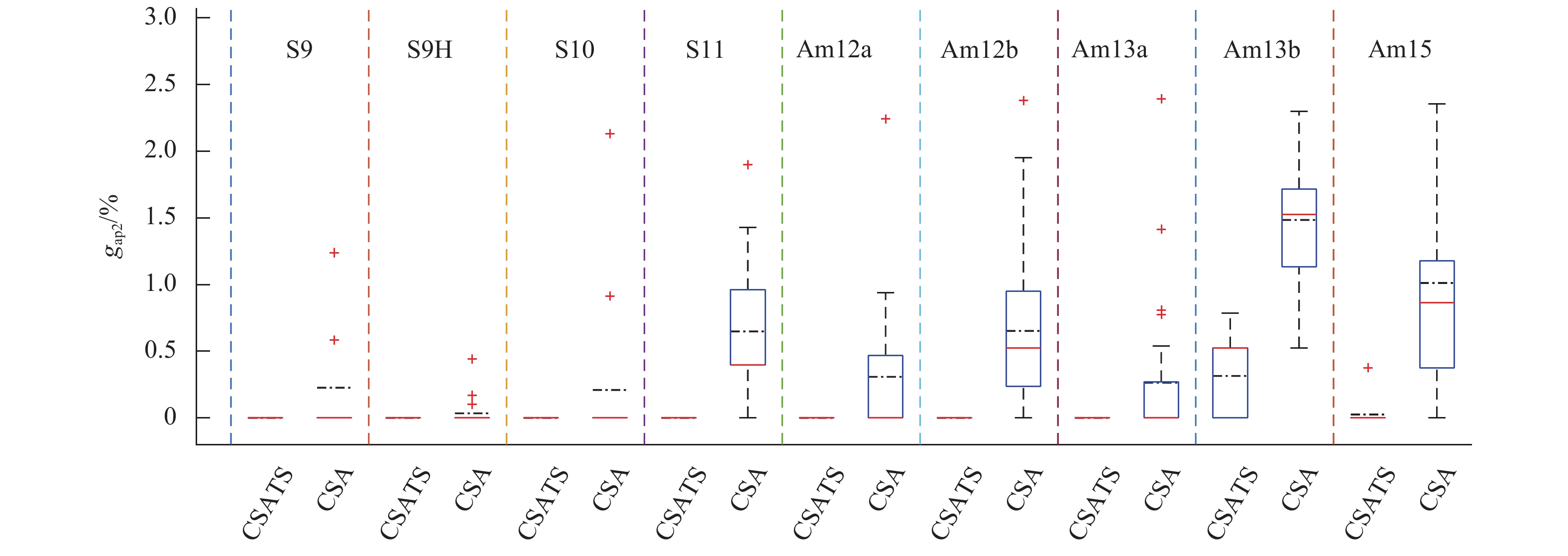
问题	n	LINGO		ACSATS
问题	n	F₀	t/s	F_min	t/s	g_ap1
S9	9	1372.5	900	1372.5	1.34	0
S9H	9	2946.5	900	2946.5	1.42	0
S10	10	1642.5	900	1642.5	1.77	0
S11	11	4812.5	900	4268.5	2.06	−11.30
Am12 a	12	2269.0	900	1919.0	2.38	−15.43
Am12 b	12	2400.5	900	2101.5	2.45	−12.46
Am13 a	13	3401.5	900	2968.5	2.61	−12.73
Am13 b	13	4291.0	900	3439.0	3.11	−19.86
Am15	15	5146.0	900	3989.0	3.05	−22.48
N-25-05	25	—	900	8408.0	44.78	—
ste-36-05	36	—	900	50210.5	798.67	—
sko-42-05	42	—	900	125647.5	1355.99	—
注：下划线表示LINGO与算法ACSATS的求解结果较优的一方.

下载: 导出CSV

表 4 CSA算法与ACSATS算法对CCAP的求解结果

Table 4. Solving results of CSA and ACSATS for CCAP

问题	CSA		ACSATS
问题	F_CSA	标准偏差	F_ACSATS	标准偏差
S9	1372.5	6.49	1372.5	0
S9H	2946.5	2.63	2946.5	0
S10	1642.5	11.60	1642.5	0
S11	4268.5	22.97	4268.5	0
Am12 a	1919.0	9.51	1919.0	0
Am12 b	2101.5	13.11	2101.5	0
Am13 a	2968.5	15.40	2968.5	0
Am13 b	3457.0	20.29	3439.0	10.68
Am15	3989.0	37.57	3989.0	3.81

下载: 导出CSV

表 5 SS、GA、IDFPA、IFWA与ACSATS在42与49规模问题下测试CAP的求解结果

Table 5. Results of solving CAP with SS, GA, IDFPA, IFWA and ACSATS in 42 and 49 scale instances

算例	SS^[4]		GA^[4]		IDFPA^[11]		IFWA^[9]		ACSATS
算例	f	t/s	f	t/s	f	t/s	f	t/s	f	t/s
42-1	12731.0	1249.04	12731.0	7174.64	12731.0	279.37	12731.0	321.29	12731.0	322.38
42-2	108020.5	1249.04	108049.5	6815.77	108006.5	681.43	108020.5	604.61	108006.5	489.94
42-3	86667.5	956.28	86667.5	6854.25	86644.5	427.61	86655.5	621.45	86644.5	497.01
42-4	68733.0	1141.34	68769.0	6509.35	68708.0	493.77	68722.0	867.15	68701.0	517.67
42-5	124058.5	1236.47	124099.5	7052.59	124017.5	546.72	124017.5	554.07	124017.5	519.47
49-1	20479.0	2683.93	20472.0	14934.38	20470.0	515.02	20470.0	542.13	20470.0	598.67
49-2	208081.0	2733.87	208270.0	14338.86	208068.0	760.20	208078.0	1009.45	208068.0	1007.99
49-3	162196.0	2877.19	162267.0	14351.91	162187.0	822.33	162187.0	1173.59	162183.0	1006.58
49-4	118264.5	3716.16	118311.5	14290.03	118260.5	1809.86	118260.5	1193.88	118260.5	843.93
49-5	332855.0	2596.39	332990.0	14913.18	332836.0	821.67	332811.0	989.91	332836.0	799.05

下载: 导出CSV

参考文献(32)

[1]	ANJOS M F, VIEIRA M V C. Mathematical optimization approaches for facility layout problems: the state-of-the-art and future research directions[J]. European Journal of Operational Research, 2017, 261(1): 1-16. doi: 10.1016/j.ejor.2017.01.049
[2]	HOSSEINI-NASAB H, FEREIDOUNI S, FATEMI GHOMI S M T, et al. Classification of facility layout problems: a review study[J]. The International Journal of Advanced Manufacturing Technology, 2018, 94(1/2/3/4): 957-977.
[3]	AMARAL A R S. The corridor allocation problem[J]. Computers and Operations Research, 2012, 39(12): 3325-3330.
[4]	GHOSH D, KOTHARI R. Population heuristics for the corridor allocation problem[J]. Iima Working Papers, 2012, 98(2): 33-40.
[5]	AHONEN H, DE ALVARENGA A G, AMARAL A R S. Simulated annealing and tabu search approaches for the corridor allocation problem[J]. European Journal of Operational Research, 2014, 232(1): 221-233. doi: 10.1016/j.ejor.2013.07.010
[6]	KALITA Z, DATTA D. Solving the bi-objective corridor allocation problem using a permutation-based genetic algorithm[J]. Computers & Operations Research, 2014, 52: 123-134.
[7]	KALITA Z, DATTA D, PALUBECKIS G. Bi-objective corridor allocation problem using a permutation-based genetic algorithm hybridized with a local search technique[J]. Soft Computing, 2019, 23(3): 961-986. doi: 10.1007/s00500-017-2807-0
[8]	ZHANG Z Q, MAO L L, GUAN C, et al. An improved scatter search algorithm for the corridor allocation problem considering corridor width[J]. Soft Computing, 2020, 24(1): 461-481. doi: 10.1007/s00500-019-03925-4
[9]	刘思璐,张则强,管超,等. 考虑设施深度的过道布置问题及改进烟花算法求解方法[J]. 控制与决策,2020,35(1): 45-54. doi: 10.13195/j.kzyjc.2018.0720 LIU Silu, ZHANG Zeqiang, GUAN Chao, et al. Improved fireworks algorithm for the corridor allocation problem with facility depth[J]. Control and Decision, 2020, 35(1): 45-54. doi: 10.13195/j.kzyjc.2018.0720
[10]	管超,张则强,毛丽丽,等. 双层过道布置问题的混合整数规划模型及启发式求解方法[J]. 计算机集成制造系统,2018,24(8): 1972-1982. doi: 10.13196/j.cims.2018.08.009 GUAN Chao, ZHANG Zeqiang, MAO Lili, et al. Mixed integer programming model and heuristic method for double-layer corridor allocation problem[J]. Computer Integrated Manufacturing Systems, 2018, 24(8): 1972-1982. doi: 10.13196/j.cims.2018.08.009
[11]	GUAN C, ZHANG Z Q, LI Y P. A flower pollination algorithm for the double-floor corridor allocation problem[J]. International Journal of Production Research, 2019, 57(20): 6506-6527. doi: 10.1080/00207543.2019.1566673
[12]	管超,张则强,朱立夏,等. 双层过道布置问题的混合整数非线性规划模型及两阶段改进模拟退火算法[J]. 中国机械工程,2019,30(8): 975-983. doi: 10.3969/j.issn.1004-132X.2019.08.014 GUAN Chao, ZHANG Zeqiang, ZHU Lixia, et al. A MINLP model and improved simulated annealing algorithm for double-layer corridor allocation problem[J]. China Mechanical Engineering, 2019, 30(8): 975-983. doi: 10.3969/j.issn.1004-132X.2019.08.014
[13]	刘俊琦,张则强,管超,等. 基于多纵向传输通道的双层过道布置问题建模与优化[J]. 计算机集成制造系统,2022,28(2): 481-494. doi: 10.13196/j.cims.2022.02.013 LIU Junqi, ZHANG Zeqiang, GUAN Chao, et al. Modeling and optimization of double floor corridor allocation problem based on multi-longitudinal transmission channels[J]. Computer Integrated Manufacturing Systems, 2022, 28(2): 481-494. doi: 10.13196/j.cims.2022.02.013
[14]	王沙沙,张则强,刘俊琦,等. 多路径交互环形过道布置问题建模及改进蚁狮算法优化[J]. 计算机集成制造系统,2021,27(8): 2237-2247. doi: 10.13196/j.cims.2021.08.007 WANG Shasha, ZHANG Zeqiang, LIU Junqi, et al. Modeling of multi-path interactive annular corridor allocation problem and optimization of improved ant-lion algorithm[J]. Computer Integrated Manufacturing Systems, 2021, 27(8): 2237-2247. doi: 10.13196/j.cims.2021.08.007
[15]	陈凤, 张则强, 刘俊琦. 考虑设施方向的双目标过道布置问题建模与优化[J]. 计算机集成制造系统, 2022, 28（6）: 1717-1734. CHEN Feng, ZHANG Zeqiang, LIU Junqi, et al. Modeling and optimization of bi-objective corridor layout problem considering facility orientation [J]. Computer Integrated Manufacturing Systems, 2022, 28（6）: 1717-1734.
[16]	KALITA Z, DATTA D. Corridor allocation as a constrained optimization problem using a permutation-based multi-objective genetic algorithm[J]. Nature-Inspired Methods for Metaheuristics Optimization: Algorithms and Applications in Science and Engineering, 2020, 16: 335-358.
[17]	LIU J Q, ZHANG Z Q, CHEN F, et al. A novel hybrid immune clonal selection algorithm for the constrained corridor allocation problem[J]. Journal of Intelligent Manufacturing, 2020, 33(4): 953-972.
[18]	GUO Y W, MILEHAM A R, OWEN G W, et al. Operation sequencing optimization using a particle swarm optimization approach[J]. Proceedings of the Institution of Mechanical Engineers, Part B:Journal of Engineering Manufacture, 2006, 220(12): 1945-1958. doi: 10.1243/09544054JEM647
[19]	张则强,汪开普,朱立夏,等. 多目标U型拆卸线平衡问题的Pareto蚁群遗传算法[J]. 西南交通大学学报,2018,53(3): 628-637,660. doi: 10.3969/j.issn.0258-2724.2018.03.026 ZHANG Zeqiang, WANG Kaipu, ZHU Lixia, et al. Pareto hybrid ant colony and genetic algorithm for multi-objective U-shaped disassembly line balancing problem[J]. Journal of Southwest Jiaotong University, 2018, 53(3): 628-637,660. doi: 10.3969/j.issn.0258-2724.2018.03.026
[20]	KALITA Z, DATTA D. A constrained single-row facility layout problem[J]. The International Journal of Advanced Manufacturing Technology, 2018, 98(5/6/7/8): 2173-2184.
[21]	LIU S L, ZHANG Z Q, GUAN C, et al. An improved fireworks algorithm for the constrained single-row facility layout problem[J]. International Journal of Production Research, 2021, 59(8): 2309-2327. doi: 10.1080/00207543.2020.1730465
[22]	高锋阳,李昭君,袁成,等. 含特殊负荷的配电网分层故障定位方法[J]. 西南交通大学学报,2020,55(3): 570-580. GAO Fengyang, LI Zhaojun, YUAN Cheng, et al. Hierarchical fault location method for distribution network with special load[J]. Journal of Southwest Jiaotong University, 2020, 55(3): 570-580.
[23]	徐长安,倪少权,陈钉均. 基于两阶段算法的运行图与天窗协同优化[J]. 西南交通大学学报,2020,55(4): 882-888. XU Changan, NI Shaoquan, CHEN Dingjun. Collaborative optimization for timetable and maintenance window based on two-stage algorithm[J]. Journal of Southwest Jiaotong University, 2020, 55(4): 882-888.
[24]	XIA Y K, FU Z. An adaptive tabu search algorithm for the open vehicle routing problem with split deliveries by order[J]. Wireless Personal Communications, 2018, 103(1): 595-609. doi: 10.1007/s11277-018-5464-4
[25]	ZHOU B H, WU Q. An improved immune clonal selection algorithm for bi-objective robotic assemble line balancing problems considering time and space constraints[J]. Engineering Computations, 2019, 36(6): 1868-1892. doi: 10.1108/EC-11-2018-0512
[26]	左兴权,王春露,赵新超. 一种结合多目标免疫算法和线性规划的双行设备布局方法[J]. 自动化学报,2015,41(3): 528-540. ZUO Xingquan, WANG Chunlu, ZHAO Xinchao. Combining multi-objective immune algorithm and linear programming for double row layout problem[J]. Acta Automatica Sinica, 2015, 41(3): 528-540.
[27]	贾林,张则强,李六柯,等. 考虑面积成本的双目标环形过道布置建模及改进禁忌搜索优化[J]. 信息与控制,2019,48(4): 477-485. JIA Lin, ZHANG Zeqiang, LI Liuke, et al. Modeling and improved tabu search optimization for double objective annular corridor allocation considering area cost[J]. Information and Control, 2019, 48(4): 477-485.
[28]	任子武,伞冶. 自适应遗传算法的改进及在系统辨识中应用研究[J]. 系统仿真学报,2006,18(1): 41-43,66. doi: 10.3969/j.issn.1004-731X.2006.01.011 REN Ziwu, SAN Ye. Improved adaptive genetic algorithm and its application research in parameter identification[J]. Journal of System Simulation, 2006, 18(1): 41-43,66. doi: 10.3969/j.issn.1004-731X.2006.01.011
[29]	徐岩,郅静. 基于改进自适应遗传算法的PMU优化配置[J]. 电力系统保护与控制,2015,43(2): 55-62. doi: 10.7667/j.issn.1674-3415.2015.02.009 XU Yan, ZHI Jing. Optimal PMU configuration based on improved adaptive genetic algorithm[J]. Power System Protection and Control, 2015, 43(2): 55-62. doi: 10.7667/j.issn.1674-3415.2015.02.009
[30]	耿敬,覃天意,李明伟,等. 基于进化ANSYS的防波堤结构智能优化方法[J]. 华中科技大学学报(自然科学版),2020,48(10): 86-91. GENG Jing, QIN Tianyi, LI Mingwei, et al. Intelligent optimization method of breakwater structure based on evolutionary ANSYS[J]. Journal of Huazhong University of Science and Technology (Natural Science Edition), 2020, 48(10): 86-91.
[31]	LIU J Q, ZHANG Z Q, ZENG Y Q. Modeling and optimization of double floor corridor allocation problem considering double channel unidirectional elevator[C]//Conference Proceedings of the 8th International Symposium on Project Management, China (ISPM2020). Beijing: [s.n.], 2020: 482-493.
[32]	魏彤辉,左文杰,郑宏伟,等. 基于降维算法的车身可靠性优化[J]. 汽车工程,2020,42(7): 941-948. WEI Tonghui, ZUO Wenjie, ZHENG Hongwei, et al. Reliability-based design optimization of car BodyBased on dimension reduction method[J]. Automotive Engineering, 2020, 42(7): 941-948.