外置可更换耗能装置的节段拼装CFST桥墩抗震性能分析

赵建锋; 刘雪飞; 孟庆一; 李晰

doi:10.3969/j.issn.0258-2724.20200796

外置可更换耗能装置的节段拼装CFST桥墩抗震性能分析

doi: 10.3969/j.issn.0258-2724.20200796

青岛理工大学土木工程学院，山东青岛 266033

基金项目: 国家自然科学基金（51778314）；四川省科技计划（2019YJ0239）

详细信息

作者简介:
赵建锋（1976—），男，副教授，博士，研究方向为预制拼装桥梁结构抗震， E-mail：zhaojf@qut.edu.cn

通讯作者:
李晰（1984—），男，副教授，博士，研究方向为桥梁抗震及减震，E-mail：xi.li@qut.edu.cn

中图分类号: U443.22
计量
- 文章访问数: 351
- HTML全文浏览量: 191
- PDF下载量: 29
- 被引次数: 0
出版历程
- 收稿日期: 2020-12-01
- 修回日期: 2021-04-23
- 网络出版日期: 2022-07-15
- 刊出日期: 2021-04-29

Seismic Performance of Precast Segmental CFST Bridge Piers with External Replaceable Energy Dissipation Devices

School of Civil Engineering, Qingdao University of Technology, Qingdao 266033, China

摘要

摘要:
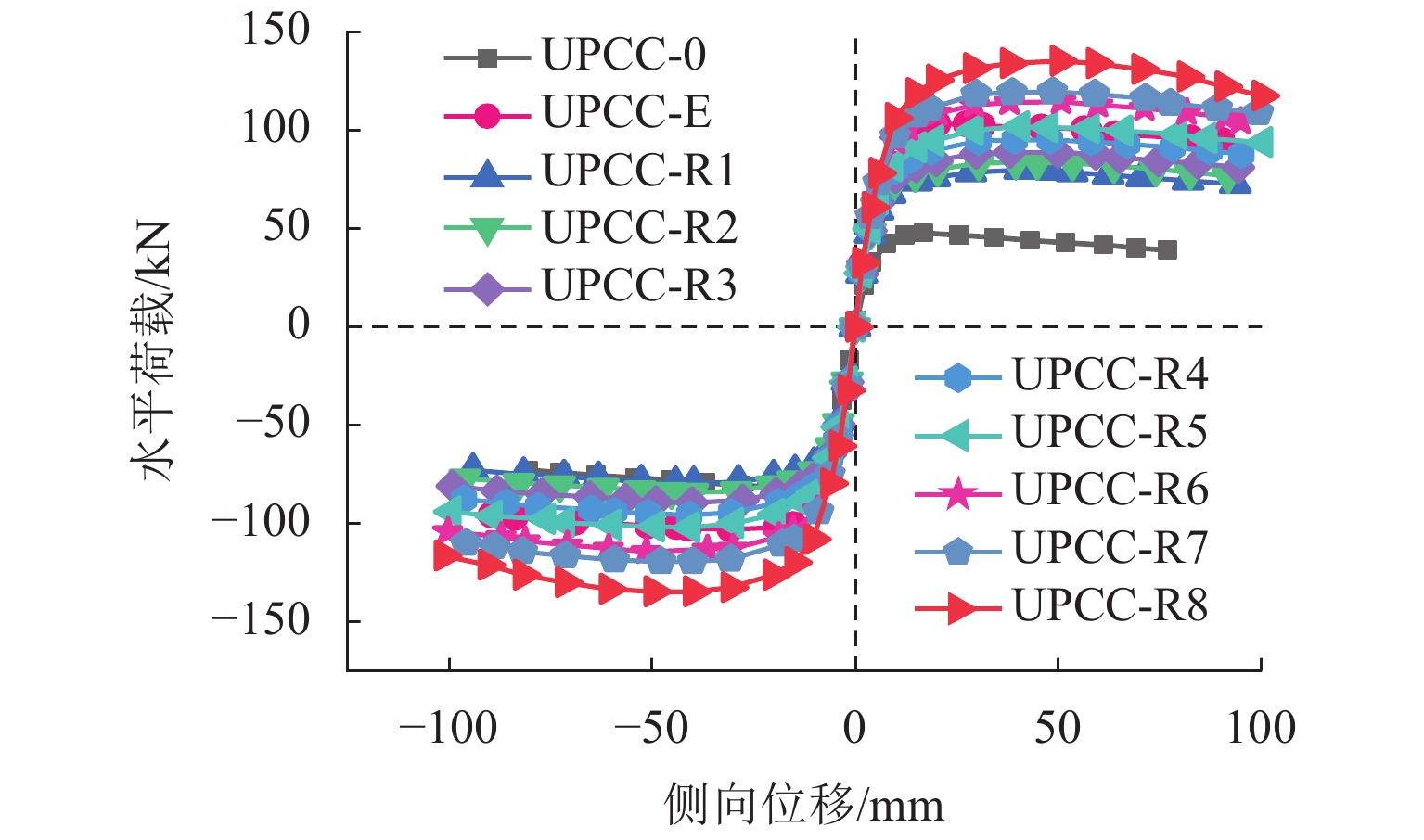
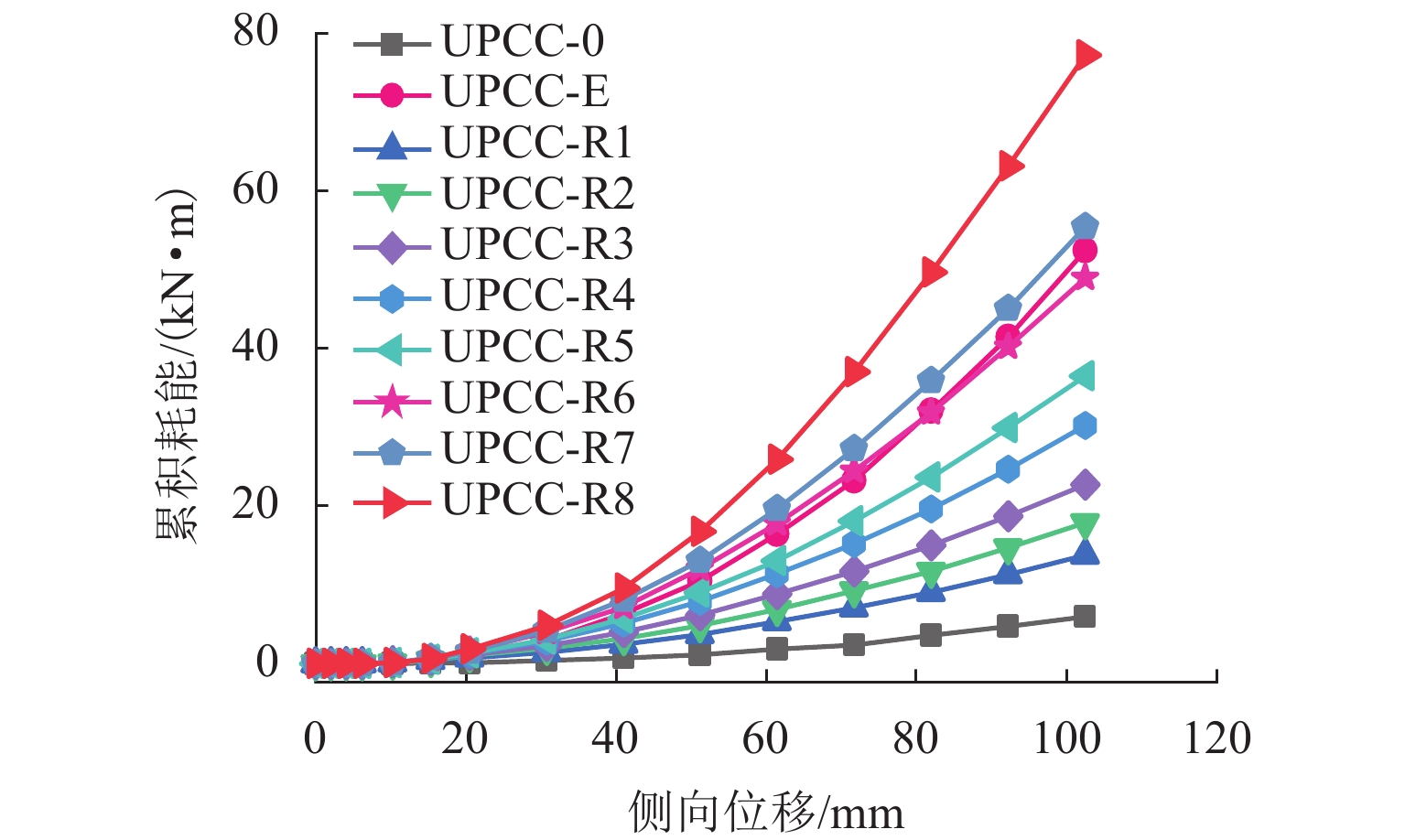
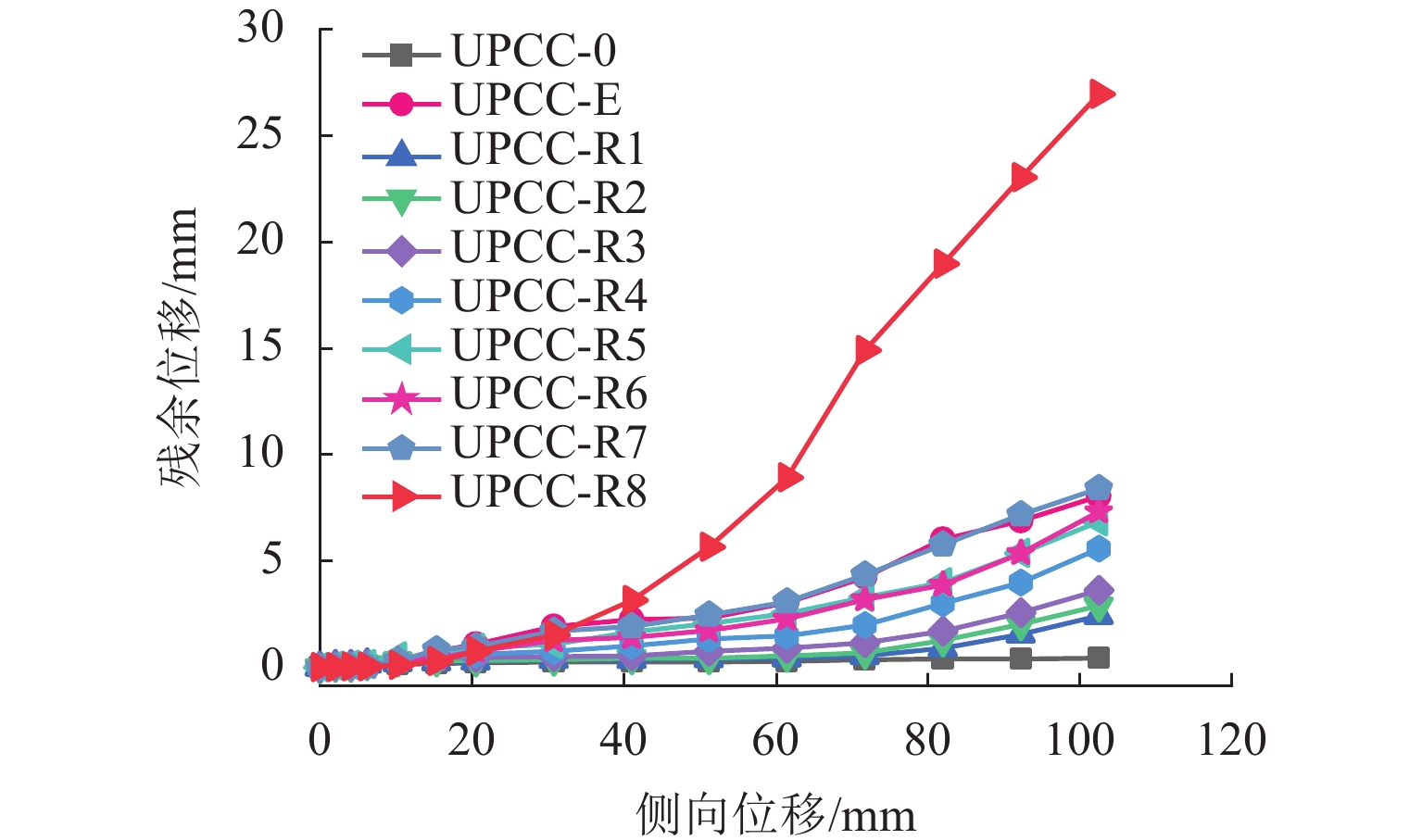
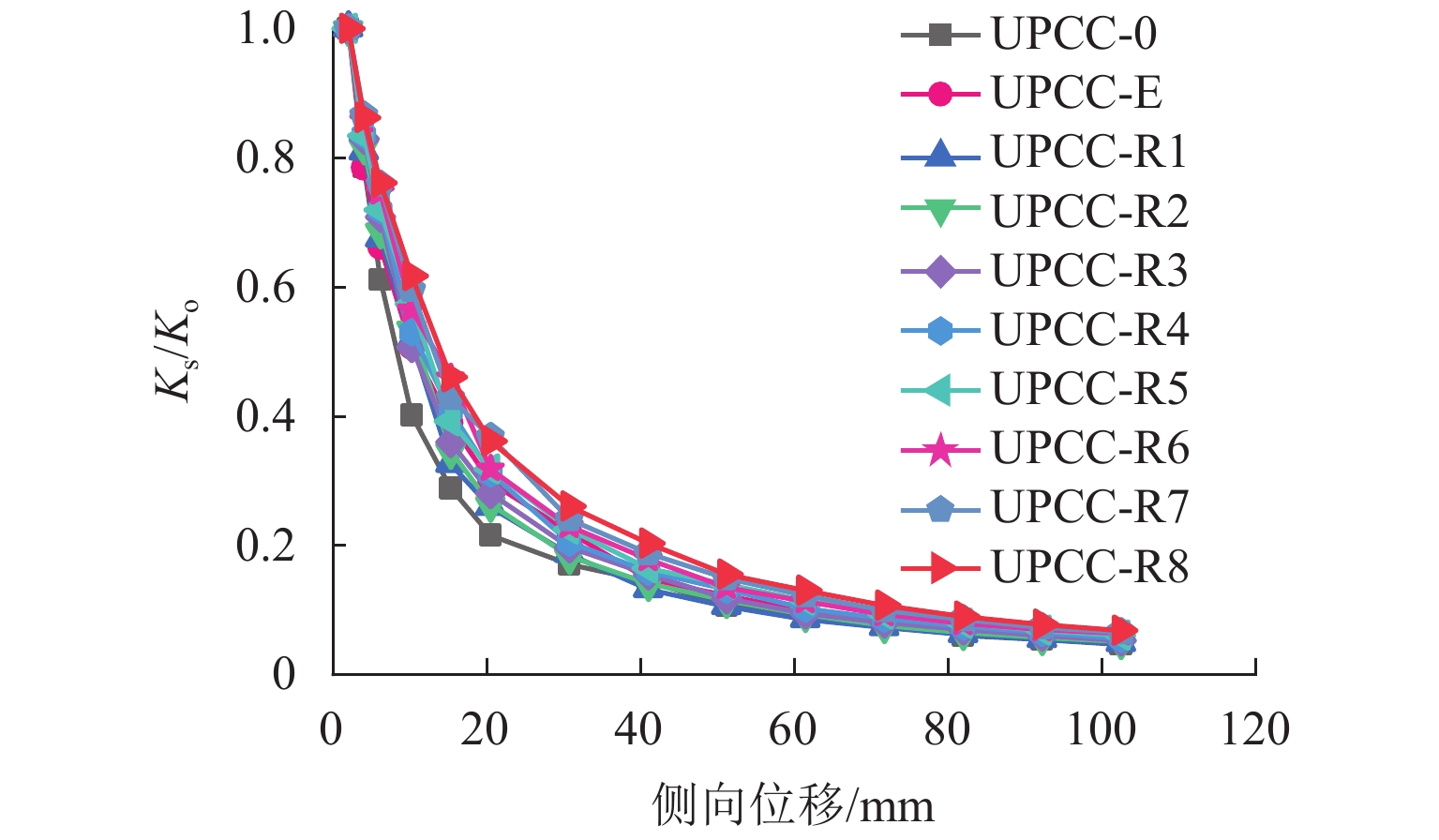
为顺应桥墩震后使用功能快速修复的新要求，提高预制拼装桥墩在中、高烈度地震区的适用性能，提出了一种外置可更换耗能装置的节段拼装钢管混凝土（CFST）桥墩. 基于ABAQUS有限元分析软件建立了三节段后张预应力预制拼装CFST桥墩分析模型，对外置3种不同控制参数（截面贡献率、耗能钢棒长细比及其布置方式）耗能装置的桥墩模型在往复加载作用下的抗震性能进行了分析. 研究结果表明：外置耗能装置的节段拼装CFST桥墩墩身损伤可控，能够通过更换耗能装置等措施实现震后的快速修复；与未设置耗能装置的桥墩相比，该类桥墩的侧向承载力、初始刚度和耗能能力分别提升了11%~88%、2.86%~6.87%和2.3倍~12.9倍；为保证震后修复的可行性，建议耗能装置的截面贡献率宜低于1.9%；中部接缝处设置的耗能钢棒直径过小将阻碍墩底处耗能钢棒充分发挥耗能作用，耗能装置沿墩高方向布置的折减系数大于0.5；耗能钢棒长细比的改变会影响墩柱的抗侧强度和延性，长细比减小，桥墩耗能能力逐渐提升，但残余位移也逐渐增大，建议耗能钢棒长细比的取值宜大于4.5.
- 桥梁抗震 /
- 预制拼装桥墩 /
- 可更换耗能装置 /
- 震后修复 /
- 拟静力分析
Abstract:
To meet the new requirements of bridge piers for rapid repair after earthquake and improve the suitability of precast segmental bridge piers in medium and high intensity areas, a precast segmental concrete filled steel tube (CFST) bridge pier with external replaceable energy dissipation devices was proposed. Based on the ABAQUS software, the analysis models of the post-tensioned prestressing precast segmental CFST piers with three segments were established. The seismic performance of the precast segmental CFST piers with the energy dissipation devices of three different control parameters (section contribution rate, slenderness ratio and arrangement) was analyzed under cyclic loading. The results show that the precast segmental CFST piers can be rapidly repaired by replacing energy dissipation devices and other measures due to the damage level of piers can be controlled by using external energy dissipation devices. Compared with the pier without energy dissipation device, the lateral strength, initial stiffness and energy dissipation capacity of the precast segmental CFST piers with external energy dissipation devices are increased 11%−88%, 2.86%−6.87% and 2.3 times−12.9 times, respectively. Meanwhile, to ensure the feasibility of repair after an earthquake, it is suggested that the section contribution rate of the external energy dissipation devices should not exceed 1.9%. Due to the small diameter of the energy dissipation bar on the middle joint which will cause the energy dissipation bar at pier bottom to not be fully utilized, it is suggested that the reduction factor of the energy dissipation devices along the pier height should not be less than 0.5. The change of slenderness ratio of energy dissipation bars has an effect on the lateral strength and ductility of the piers. With the decrease of the slenderness ratio, the energy dissipation capacity increases but the residual displacement of the piers also increases gradually. It is suggested that the slenderness ratio of energy dissipation bars should be greater than 4.5.
- bridge seismic /
- precast segmental pier /
- replaceable energy dissipation devices /
- renovation after earthquake /
- quasi-static analysis

HTML全文

图 1 耗能装置构造示意

Figure 1. Structure of the energy dissipation device

下载: 全尺寸图片幻灯片

图 2 限位钢板构造示意

Figure 2. Structure of the steel backing plate

下载: 全尺寸图片幻灯片

图 3 模拟结果与试验结果滞回曲线对比

Figure 3. Comparison between simulation results and test results

下载: 全尺寸图片幻灯片

图 4 底节段损伤变形对比

Figure 4. Comparison of damage and deformation at the bottom segment

下载: 全尺寸图片幻灯片

图 5 预制拼装CFST桥墩构造

Figure 5. Structure of precast CFST pier

下载: 全尺寸图片幻灯片

图 6 UPCC-R桥墩有限元模型

Figure 6. Finite element model of UPCC-R bridge pier

下载: 全尺寸图片幻灯片

图 7 不同模型骨架曲线对比

Figure 7. Skeleton curves of different models

下载: 全尺寸图片幻灯片

图 8 不同模型累积耗能曲线

Figure 8. Cumulative energy consumption curves of different models

下载: 全尺寸图片幻灯片

图 9 不同模型残余位移对比

Figure 9. Residual displacement curves of different models

下载: 全尺寸图片幻灯片

图 10 不同模型刚度退化曲线对比

Figure 10. Stiffness degradation curves of different models

下载: 全尺寸图片幻灯片

图 11 沿墩高不同布置方式的骨架曲线和累积耗能曲线

Figure 11. Skeleton curves and cumulative energy consumption curves of different arrangements along pier height

下载: 全尺寸图片幻灯片

图 12 不同长细比骨架曲线、累积耗能曲线、残余位移曲线对比

Figure 12. Residual displacement curves of different slenderness ratios

下载: 全尺寸图片幻灯片

图 13 应力损伤云图

Figure 13. Stress damage nephogram

下载: 全尺寸图片幻灯片

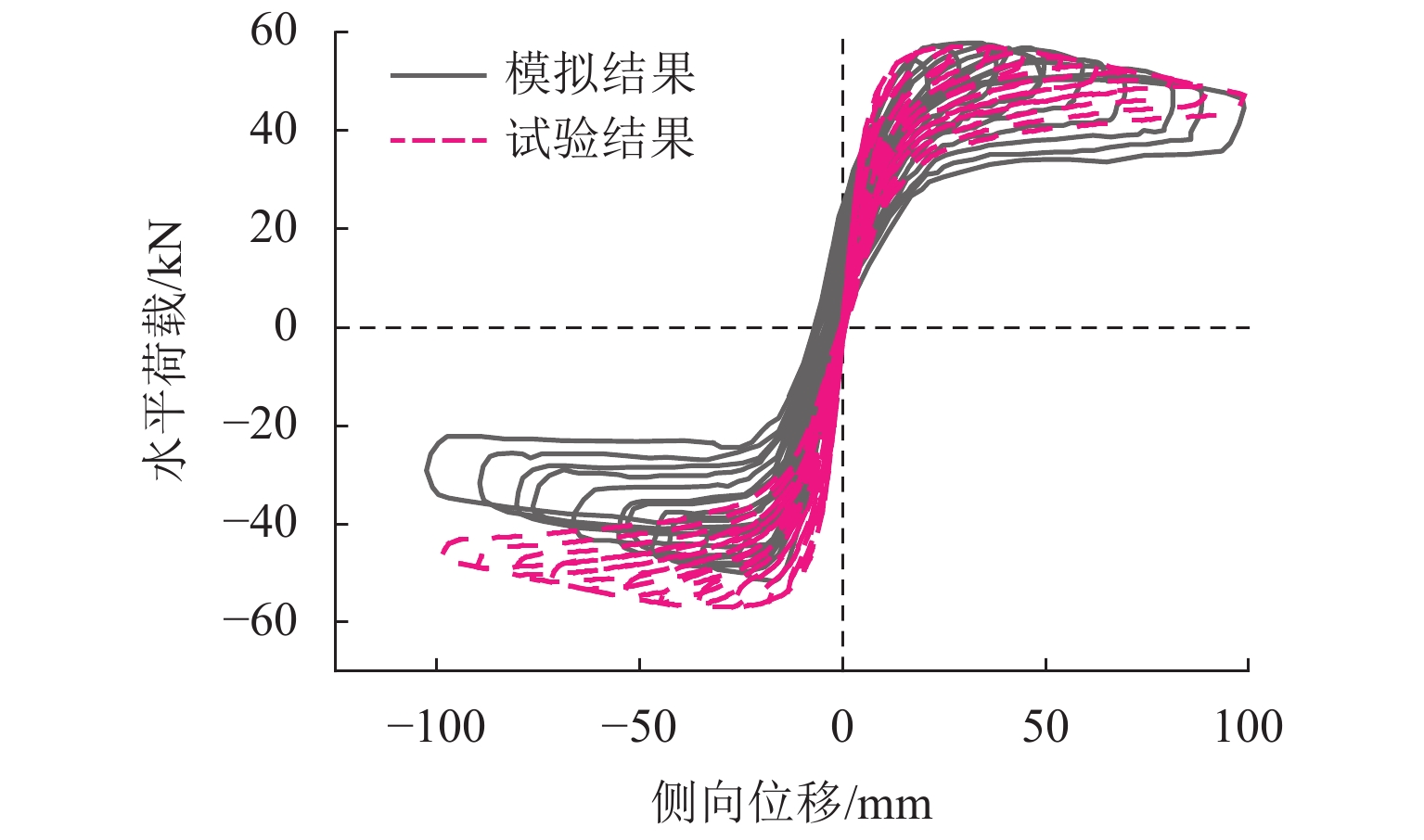
表 1 模拟结果与试验结果

Table 1. Simulation results and test results

对比项	侧向承载力/ kN	初始刚度/ （kN·mm⁻¹）	耗能能力/ （kN·m）
试验结果	58.00	9.06	3.31
模拟结果	56.07	8.83	3.58
差异率/%	3.3	2.5	8.2

下载: 导出CSV

表 2 不同截面贡献率的设计参数

Table 2. Parameters for section contribution rate %

模型编号	耗能钢棒	耗能钢筋配筋率	底接缝处 η_ed
UPCC-0	无
UPCC-E	内置	1.3
UPCC-R1	外置		0.3
UPCC-R2			0.5
UPCC-R3			0.6
UPCC-R4			0.8
UPCC-R5			1.1
UPCC-R6			1.3
UPCC-R7			1.6
UPCC-R8			1.9

下载: 导出CSV

表 3 沿墩高不同布置方式的设计参数

Table 3. Parameters for arrangement along pier height

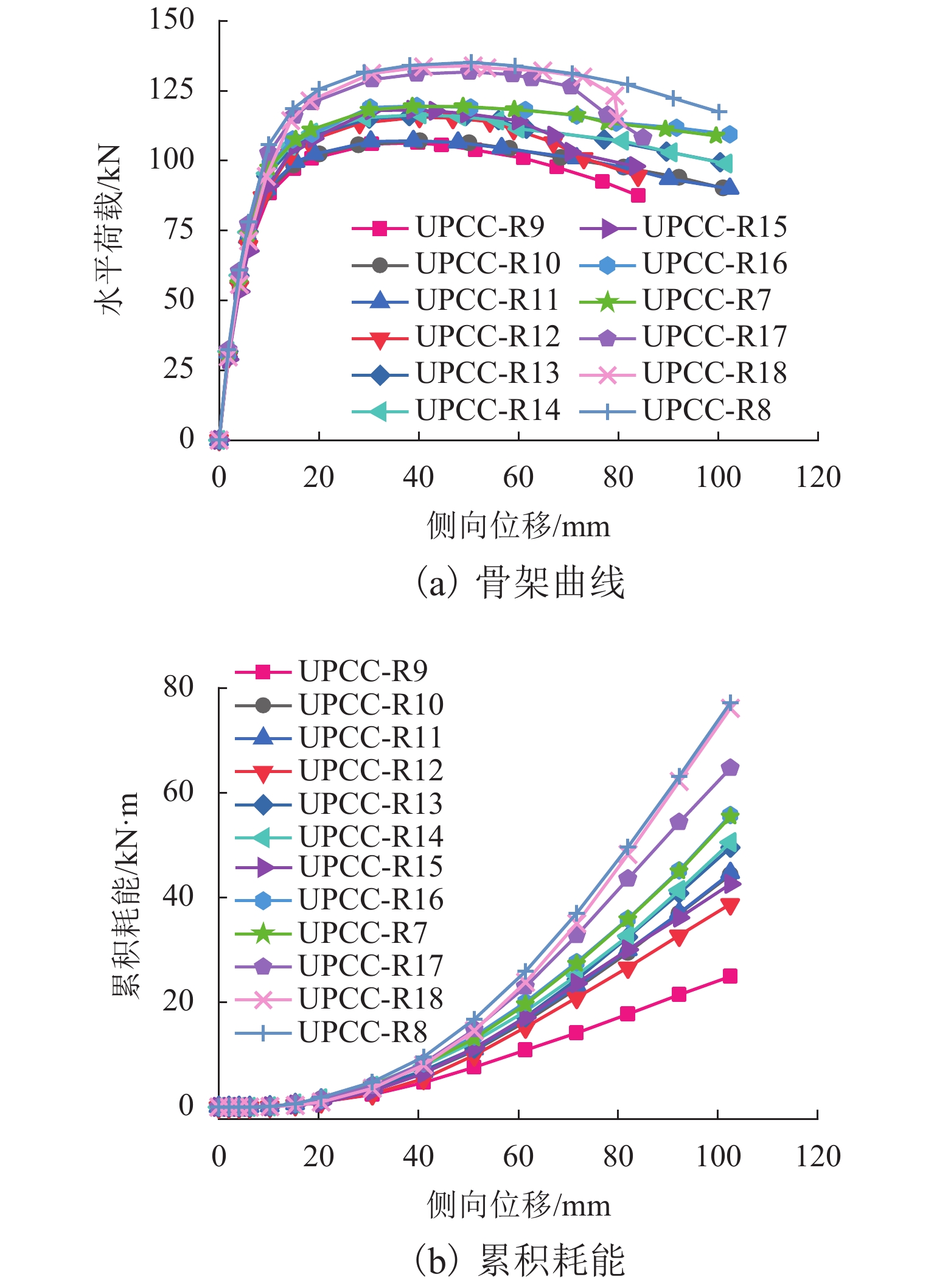
模型编号	S1−S2 接缝 D_ed/mm	底接缝			α
模型编号	S1−S2 接缝 D_ed/mm	D_ed/mm	η_ed/%	h/mm	α
UPCC-R9	12	18	1.1	200	0.2
UPCC-R10	14				0.3
UPCC-R11	16				0.4
UPCC-R12	16	20	1.3		0.3
UPCC-R13	18				0.4
UPCC-R14	20				0.5
UPCC-R15	18	22	1.6	250	0.3
UPCC-R16	20				0.4
UPCC-R7	22				0.5
UPCC-R17	20	24	1.9		0.3
UPCC-R18	22				0.4
UPCC-R8	24				0.5

下载: 导出CSV

表 4 不同长细比的参数设计

Table 4. Parameters for slenderness ratio

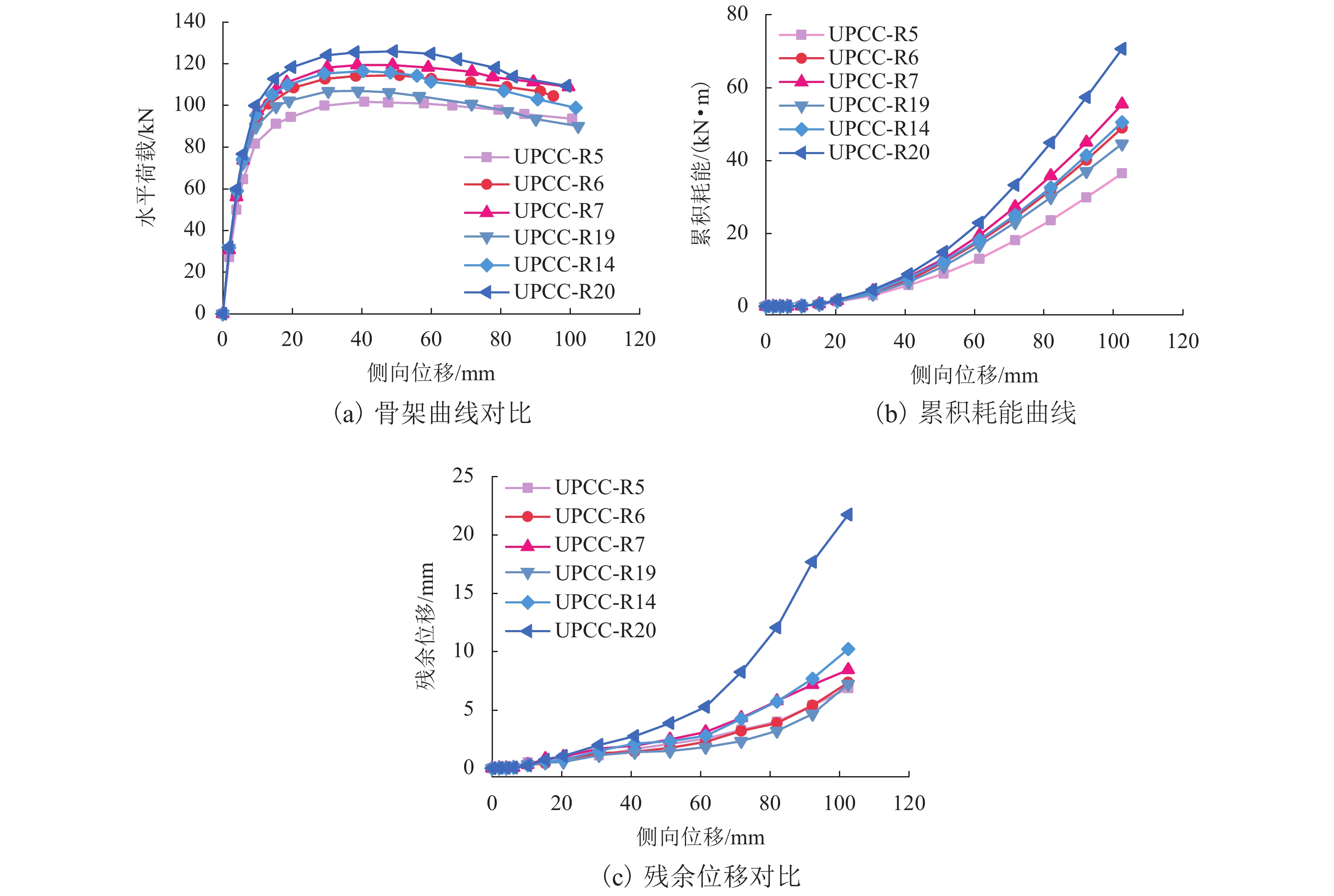
模型编号	S1-S2 接缝处/mm			底接缝处/mm			η_ed/%	h/mm	λ	α
模型编号	D_ed	L_ed	D_ted	D_ed	L_ed	D_ted	η_ed/%	h/mm	λ	α
UPCC-R5	18	150	26	18	150	26	1.1	250	8.3	0.5
UPCC-R6	20		28	20		28	1.3		7.5
UPCC-R7	22		32	22		32	1.6		6.8
UPCC-R19	18	100	26	18	100	26	1.1	200	5.6
UPCC-R14	20		28	20		28	1.3		5.0
UPCC-R20	22		32	22		32	1.6		4.5

下载: 导出CSV

参考文献(24)

[1]	王景全,王震,高玉峰,等. 预制桥墩体系抗震性能研究进展:新材料、新理念、新应用[J]. 工程力学,2019,36(3): 1-23. WANG Jingquan, WANG Zhen, GAO Yufeng, et al. Review on aseismic behavior of precast piers: new material, new concept, and new application[J]. Engineering Mechanics, 2019, 36(3): 1-23.
[2]	赵建锋,孟庆一,薛振兴,等. 基于不同隔震体系的预制拼装桥墩桥梁结构地震响应分析[J]. 建筑科学与工程学报,2020,37(4): 97-107. ZHAO Jianfeng, MENG Qingyi, XUE Zhenxing, et al. Seismic response analysis of bridge structures with precast segmental bridge piers based on different isolation systems[J]. Journal of Architecture and Civil Engineering, 2020, 37(4): 97-107.
[3]	杜修力,周雨龙,韩强,等. 摇摆桥墩的研究综述[J]. 地震工程与工程振动,2018,38(5): 1-11. DU Xiuli, ZHOU Yulong, HAN Qiang, et al. State-of-the-art on rocking piers[J]. Earthquake Engineering and Engineering Dynamics, 2018, 38(5): 1-11.
[4]	王震,王景全. 预应力节段预制拼装桥墩抗震性能研究综述[J]. 建筑科学与工程学报,2016,33(6): 88-97. doi: 10.3969/j.issn.1673-2049.2016.06.012 WANG Zhen, WANG Jingquan. Review of seismic performance of prestressed segmental precast and assembled piers[J]. Journal of Architecture and Civil Engineering, 2016, 33(6): 88-97. doi: 10.3969/j.issn.1673-2049.2016.06.012
[5]	CHOU C C, CHEN Y C. Cyclic tests of post-tensioned precast CFT segmental bridge columns with unbonded strands[J]. Earthquake Engineering and Structural Dynamics, 2006, 35(2): 159-175.
[6]	OU Y C, WANG P H, TSAI M S, et al. Large-scale experimental study of precast segmental unbonded posttensioned concrete bridge columns for seismic regions[J]. Journal of Structural Engineering, 2010, 136(3): 255-264. doi: 10.1061/(ASCE)ST.1943-541X.0000110
[7]	OU Y C, TSAI M S, CHANG K C, et al. Cyclic behavior of precast segmental concrete bridge columns with high performance or conventional steel reinforcing bars as energy dissipation bars[J]. Earthquake Engineering and Structural Dynamics, 2010, 39(11): 1181-1198.
[8]	WANG J C, OU Y C, CHANG K C, et al. Large-scale seismic tests of tall concrete bridge columns with precast segmental construction[J]. Earthquake Engineering and Structural Dynamics, 2008, 37(12): 1449-1465.
[9]	ELGAWADY M A, DAWOOD H M. Analysis of segmental piers consisted of concrete filled FRP tubes[J]. Engineering Structures, 2012, 38: 142-152. doi: 10.1016/j.engstruct.2012.01.001
[10]	VARELA S, SAIIDI M. A bridge column with superelastic NiTi SMA and replaceable rubber hinge for earthquake damage mitigation[J]. Smart Materials and Structures, 2016, 25(7): 075012.1-075012.34.
[11]	SIDERIS P, AREF A J, FILIATRAULT A. Large-scale seismic testing of a hybrid sliding-rocking posttensioned segmental bridge system[J]. Journal of Structural Engineering, 2014, 140(6): 04014025.1-04014025.14. doi: 10.1061/(ASCE)ST.1943-541X.0000961
[12]	李建中,管仲国. 桥梁抗震设计理论发展: 从结构抗震减震到震后可恢复设计[J]. 中国公路学报,2017,30(12): 1-9,59. doi: 10.3969/j.issn.1001-7372.2017.12.001 LI Jianzhong, GUAN Zhongguo. Research progress on bridge seismic design: target from seismic alleviation to post-earthquake structural resilience[J]. China Journal of Highway and Transport, 2017, 30(12): 1-9,59. doi: 10.3969/j.issn.1001-7372.2017.12.001
[13]	HAN Q, JIA Z L, XU K, et al. Hysteretic behavior investigation of self-centering double-column rocking piers for seismic resilience[J]. Engineering Structures, 2019, 188: 218-232. doi: 10.1016/j.engstruct.2019.03.024
[14]	LI C, BI K M, HAO H, et al. Cyclic test and numerical study of precast segmental concrete columns with BFRP and TEED[J]. Bulletin of Earthquake Engineering, 2019, 17(6): 3475-3494. doi: 10.1007/s10518-019-00597-1
[15]	WANG Z, WANG J Q, TANG Y C, et al. Seismic behavior of precast segmental UHPC bridge columns with replaceable external cover plates and internal dissipaters[J]. Engineering Structures, 2018, 177: 540-555. doi: 10.1016/j.engstruct.2018.10.012
[16]	WANG Z, WANG J Q, ZHAO G T, et al. Design criterion for the self-centering capacity of precast segmental UHPC bridge columns with unbonded post-tensioning tendons[J]. Engineering Structures, 2019, 200: 109706.1-109706.14.
[17]	WANG Z, WANG J Q, ZHU J Z, et al. Energy dissipation and self-centering capacities of posttensioning precast segmental ultra-high performance concrete bridge columns[J]. Structural Concrete, 2020, 21(2): 517-532. doi: 10.1002/suco.201900024
[18]	贾俊峰,赵建瑜,张强,等. 后张预应力节段拼装CFST桥墩抗侧力学行为试验[J]. 中国公路学报,2017,30(3): 236-245. doi: 10.3969/j.issn.1001-7372.2017.03.026 JIA Junfeng, ZHAO Jianyu, ZHANG Qiang, et al. Experiment on lateral bearing behavior of post-tensioned segmental CFST bridge pier columns[J]. China Journal of Highway and Transport, 2017, 30(3): 236-245. doi: 10.3969/j.issn.1001-7372.2017.03.026
[19]	SARTI F, PALERMO A, PAMPANIN S. Fuse-type external replaceable dissipaters:experimental program and numerical modeling[J]. Journal of Structural Engineering, 2016, 142(12): 04016134.1-04016134.12.
[20]	张于晔,吴刚,孙泽阳,等. 采用混合体系的预制拼装桥墩抗震性能分析[J]. 长安大学学报(自然科学版),2019,39(1): 70-80. doi: 10.19721/j.cnki.1671-8879.2019.01.009 ZHANG Yuye, WU Gang, SUN Zeyang, et al. Analysis of seismic performance of a hybrid prefabricated bridge pier system[J]. Journal of Chang’an University (Natural Science Edition), 2019, 39(1): 70-80. doi: 10.19721/j.cnki.1671-8879.2019.01.009
[21]	SUSANTHA K A S, GE H B, USAMI T. Uniaxial stress-strain relationship of concrete confined by various shaped steel tubes[J]. Engineering Structures, 2001, 23(10): 1331-1347. doi: 10.1016/S0141-0296(01)00020-7
[22]	徐有邻,王晓锋,刘刚,等. 混凝土结构理论发展及规范修订的建议[J]. 建筑结构学报,2007,28(1): 1-6. doi: 10.3321/j.issn:1000-6869.2007.01.001 XU Youlin, WANG Xiaofeng, LIU Gang, et al. The proposal of concrete structure theory development and code amendment[J]. Journal of Building Structures, 2007, 28(1): 1-6. doi: 10.3321/j.issn:1000-6869.2007.01.001
[23]	石永久,王萌,王元清. 循环荷载作用下结构钢材本构关系试验研究[J]. 建筑材料学报,2012,15(3): 293-300. doi: 10.3969/j.issn.1007-9629.2012.03.001 SHI Yongjiu, WANG Meng, WANG Yuanqing. Experimental study of structural steel constitutive relationship under cyclic loading[J]. Journal of Building Materials, 2012, 15(3): 293-300. doi: 10.3969/j.issn.1007-9629.2012.03.001
[24]	ZHANG Y Y, WU G, DIAS-DA-COSTA D. Cyclic loading tests and analyses of posttensioned concrete bridge columns combining cast-in-place and precast segments[J]. Bulletin of Earthquake Engineering, 2019, 17(11): 6141-6163. doi: 10.1007/s10518-019-00714-0