Suspension Parameters Optimum Matching of High-Speed Locomotive Based on Frequency Domain Stationarity
-
摘要:
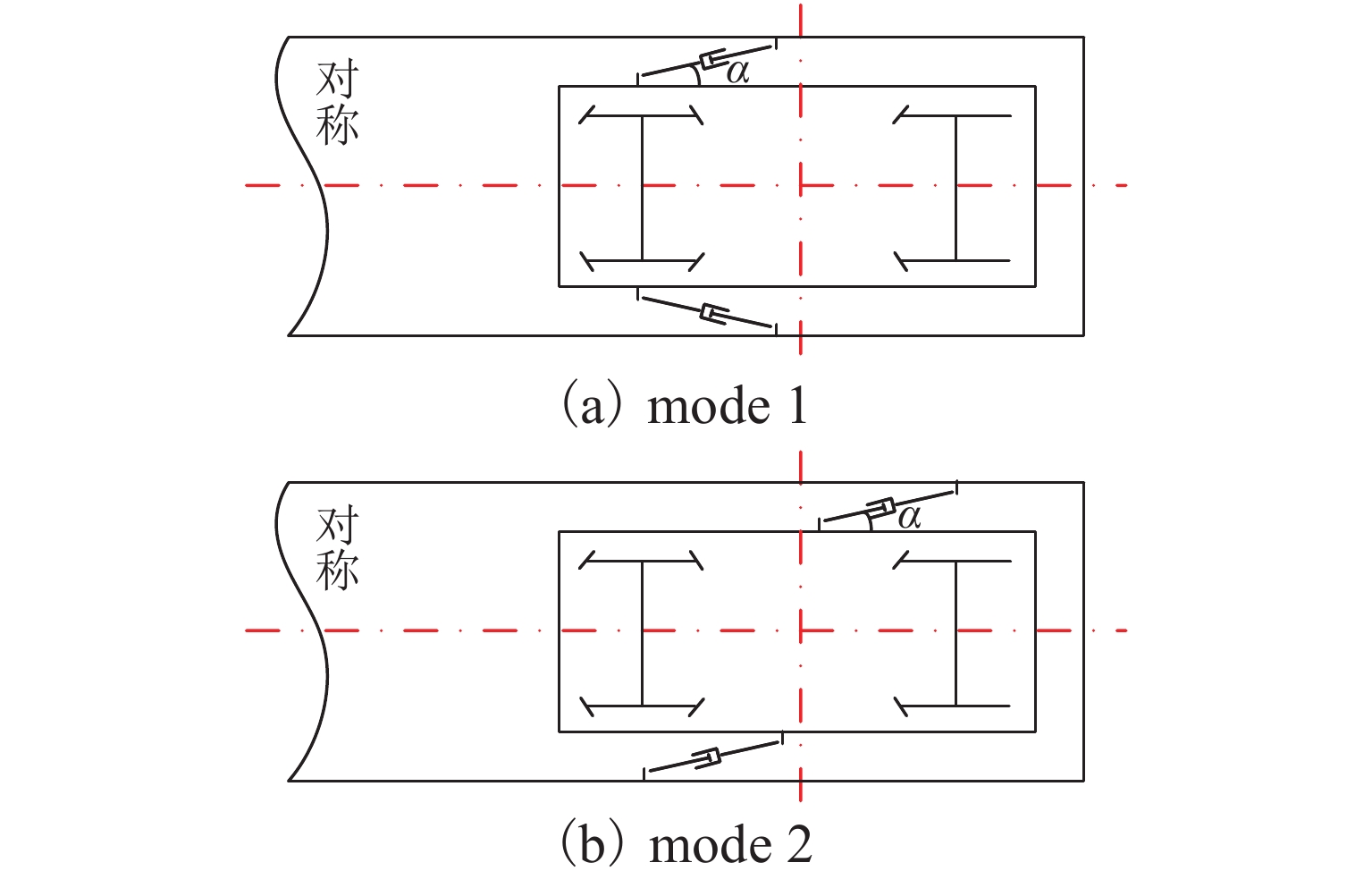
为合理优化匹配悬挂参数以提升高速机车动力学性能,针对某高速机车,采用虚拟激励法计算频域横向平稳性指标,提出了考虑频域横向平稳性和稳定性多目标性能的关键悬挂参数多参数协同优化方法;分别以2种抗蛇行减振器布置方式和3种轮轨接触状态运行工况为例,验证了该方法对机车横向动力学性能的提升效果. 结果表明:低轮轨接触锥度工况机车一次蛇行稳定性较差,尤其采用抗蛇行减振器斜对称布置方式,机车后司机室横向平稳性显著变差;对于低锥度工况,需以提高机车稳定性为优化目标,而高锥度工况则更需关注其横向平稳性;为兼顾不同轮轨接触条件下机车动力学性能,以提高线路适应性,机车一系纵向刚度、抗蛇行减振器阻尼和二系横向减振器阻尼值在文中给定的优化范围内应尽量选取较小值,建议分别选取12 kN/mm、600 kN·s/m和25 kN·s/m.
Abstract:In order to reasonably optimize and match the suspension parameters to improve the dynamic performance of high-speed locomotives, the pseudo-excitation method was used to calculate the lateral riding quality index in the frequency domain for a high-speed locomotive, and a collaborative multi-parameter optimization method for the key suspension parameters was proposed considering the multi-objective performance of lateral riding quality in the frequency domain and lateral stability. Taking the operational scenarios as examples in which two yaw damper layouts and three wheel-rail contact conditions were considered, the improvement effect of this method on the lateral dynamic performance of the locomotive was illustrated. The results show that the primary hunting stability of the locomotive is poor in the low equivalent conicity condition. The lateral riding quality of the rear cab is significantly deteriorated, especially when the skewed symmetrical arrangement of the yaw damper is adopted. For the case of low equivalent conicity, it's necessary to regard improving locomotive lateral stability as the optimization objective, while for the case of high equivalent conicity, more attention should be paid to lateral riding quality. In order to give consideration to the dynamic performance of the locomotive under different wheel-rail contact states, thus improving the adaptability to track lines, the values of primary longitudinal stiffness, yaw damper damping and secondary lateral damping should be designed as small as possible in the given optimization range, it is recommended to choose them as 12 kN/mm, 600 kN·s/m, and 25 kN·s/m, respectively.
-
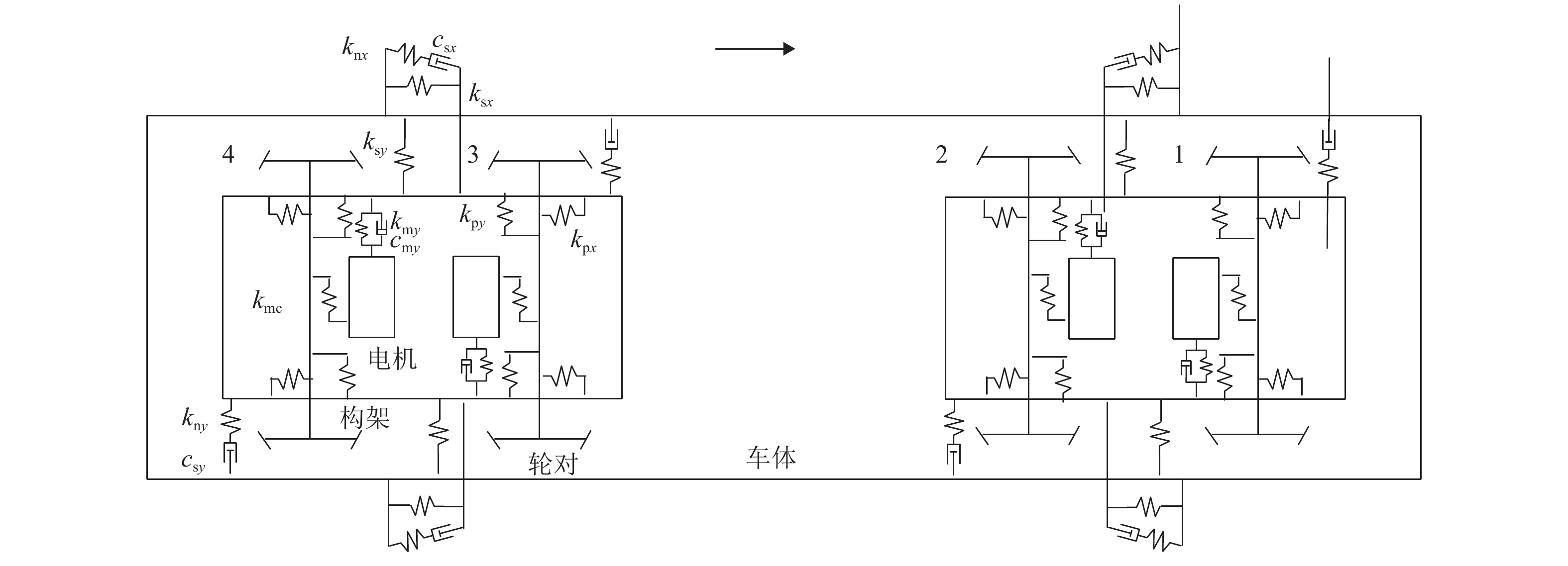
表 1 模型部分参数
Table 1. Partial parameters of model
参数 符号 数值 速度 V/(km·h−1) 160 新轮轨接触等效锥度 λ 0.1 轴重 Ld/t 19.5 轴距 b/m 2.8 车辆定距 l/m 10.2 车体质量 mc/t 42 转向架质量 mb/t 18 电机质量 md/t 3.5 转向架单侧二系横向刚度 ksy/(kN·mm−1) 0.24 表 2 悬挂参数优化范围
Table 2. Optimization range of suspension parameters
参数 优化范围 kpx/ (kN·mm−1) 12 ~ 100 kpy/ (kN·mm−1) 2 ~ 8 csx/ (kN·s·m−1) 300 ~ 2000 csy/ (kN·s·m−1) 10 ~ 60 kncsx/(kN·mm−1) 10 ~ 25 α/(°) 0 ~ 10 表 3 横向动力学性能指标阀值
Table 3. Threshold of dynamic performance index
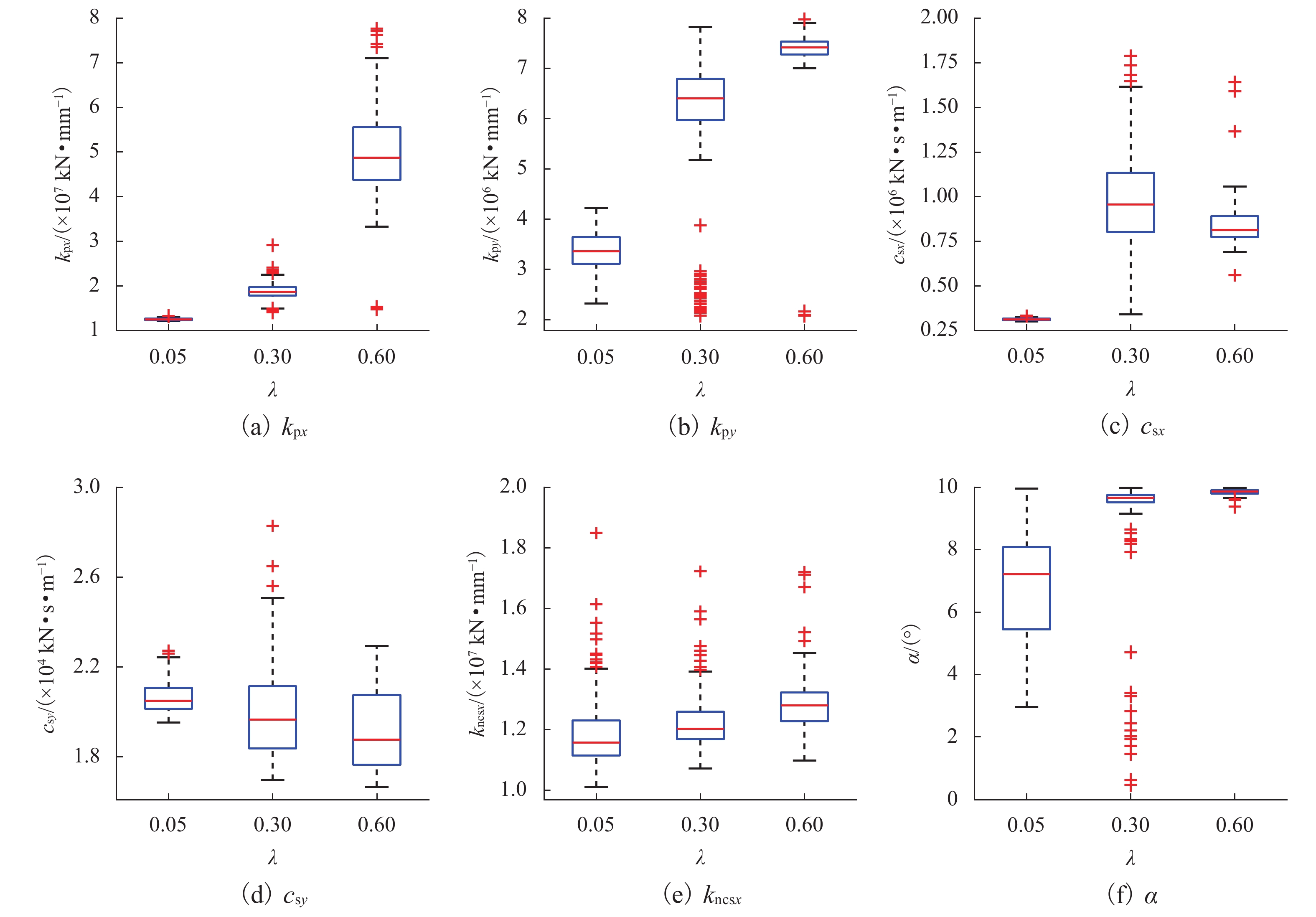
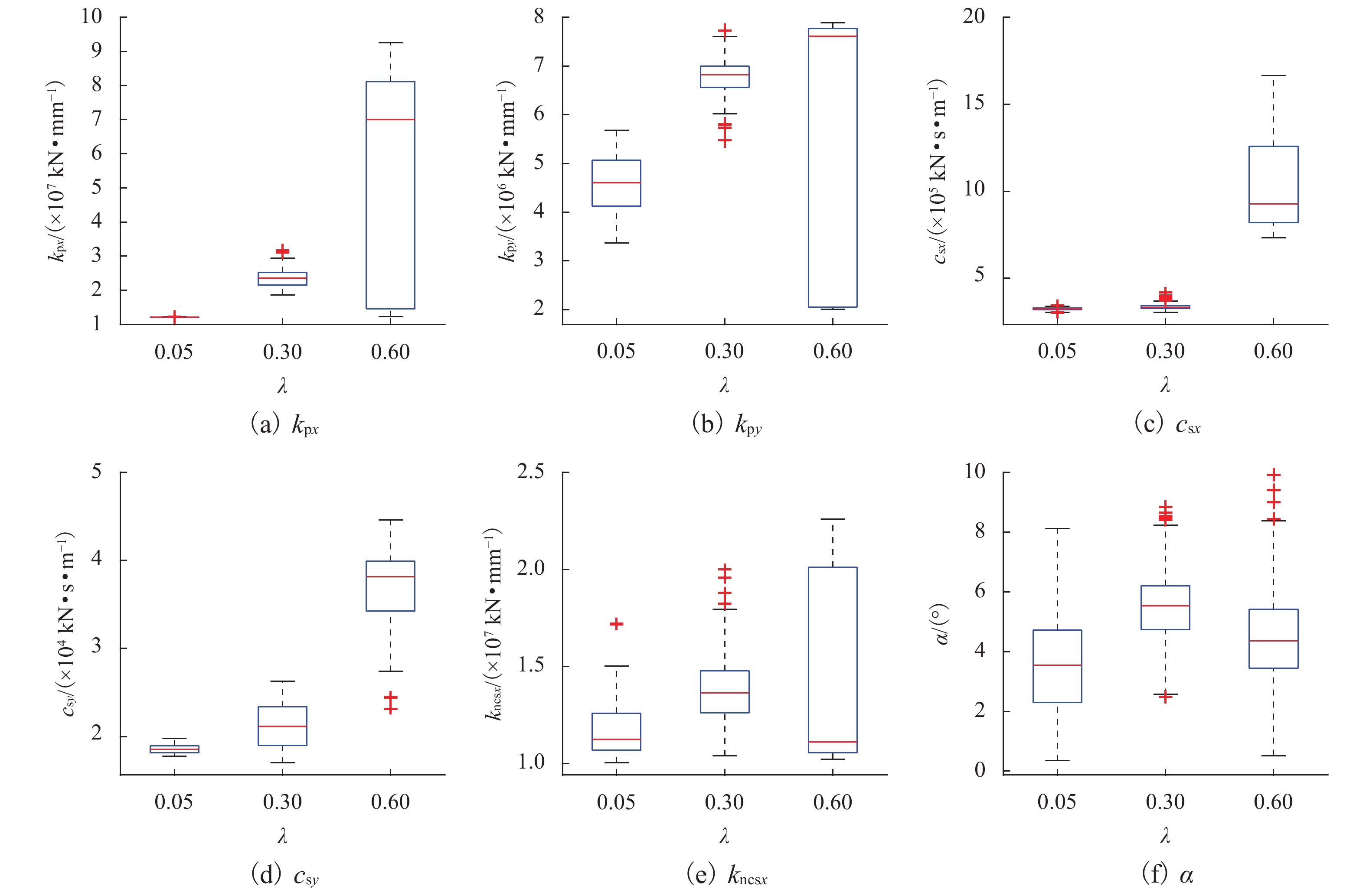
λ ζmax Wf Wb 0.05 ≤−0.10 ≤2.5 ≤2.5 0.30 [−0.25, −0.16] ≤2.5 ≤2.5 0.60 [−0.25, −0.16] ≤2.5 ≤2.5 表 4 悬挂参数、Wf与Wb的相关系数
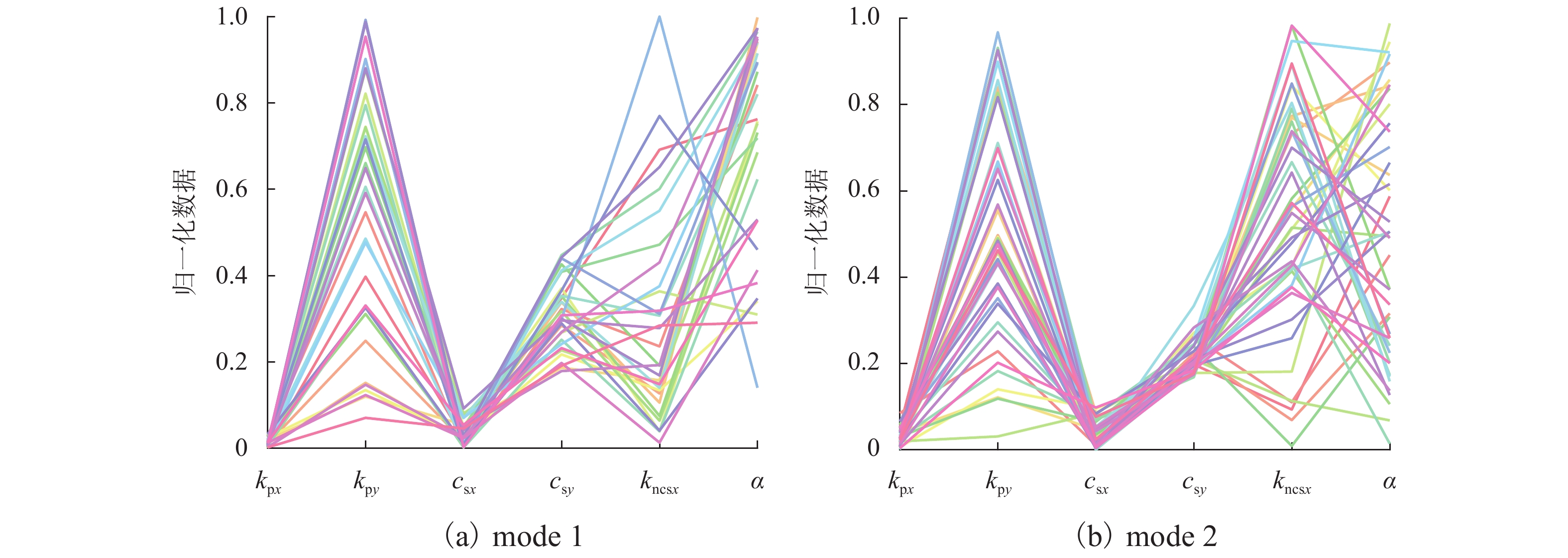
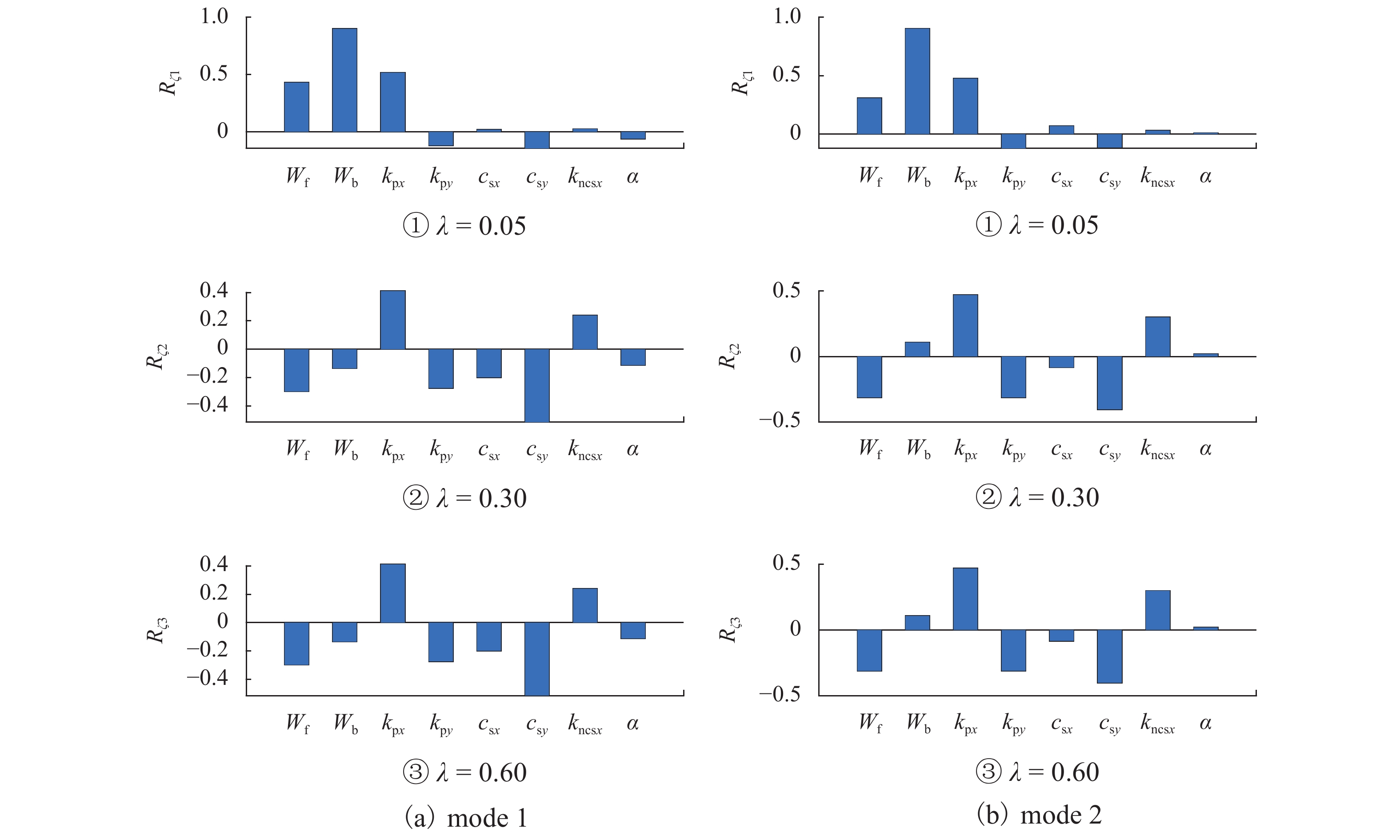
Table 4. Correlation coefficients of suspension parameters and Wf with Wb
mode Wf kpx kpy csx csy kncsx α 1 0.90 0.31 −0.25 0.24 0.88 0.08 −0.12 2 0.81 0.25 −0.29 0.28 0.83 0.15 0.01 -
[1] BRAGHIN F, BRUNI S, RESTA F. Active yaw damper for the improvement of railway vehicle stability and curving performances: simulations and experimental results[J]. Vehicle System Dynamics, 2006, 44(11): 857-869. doi: 10.1080/00423110600733972 [2] YAO Y, LI G, SARDAHI Y, et al. Stability enhancement of a high-speed train bogie using active mass inertial actuators[J]. Vehicle System Dynamics, 2019, 57(3): 389-407. doi: 10.1080/00423114.2018.1469776 [3] YAO Y, WU G S, SARDAHI Y, et al. Hunting stability analysis of high-speed train bogie under the frame lateral vibration active control[J]. Vehicle System Dynamics, 2018, 56(2): 297-318. doi: 10.1080/00423114.2017.1375128 [4] JIANG J Z, MATAMOROS-SANCHEZ A Z, GOODALL R M, et al. Passive suspensions incorporating inerters for railway vehicles[J]. Vehicle System Dynamics, 2012, 50(S1): 263-276. doi: 10.1080/00423114.2012.665166 [5] 金天贺,刘志明,任尊松,等. 高速列车半主动悬挂可变刚度和阻尼减振器适应性研究[J]. 振动工程学报,2020,33(4): 772-783. doi: 10.16385/j.cnki.issn.1004-4523.2020.04.016JIN Tianhe, LIU Zhiming, REN Zunsong, et al. Adaptability of variable stiffness and damping shock absorber for semi-active suspension of high speed train[J]. Journal of Vibration Engineering, 2020, 33(4): 772-783. doi: 10.16385/j.cnki.issn.1004-4523.2020.04.016 [6] 李响,任尊松,徐宁. 基于转向架悬挂参数与踏面锥度优化的高速车辆动力学性能分析[J]. 铁道学报,2018,40(3): 39-44. doi: 10.3969/j.issn.1001-8360.2018.03.006LI Xiang, REN Zunsong, XU Ning. Dynamic performance analysis of high-speed vehicle based on optimization of bogie suspension parameters and tread conicity[J]. Journal of the China Railway Society, 2018, 40(3): 39-44. doi: 10.3969/j.issn.1001-8360.2018.03.006 [7] YAO Y, LI G, WU G S, et al. Suspension parameters optimum of high-speed train bogie for hunting stability robustness[J]. International Journal of Rail Transportation, 2020, 8(3): 195-214. doi: 10.1080/23248378.2019.1625824 [8] HE Y P, MCPHEE J. Multidisciplinary optimization of multibody systems with application to the design of rail vehicles[J]. Multibody System Dynamics, 2005, 14(2): 111-135. doi: 10.1007/s11044-005-4310-0 [9] JOHNSSON A, BERBYUK V, ENELUND M. Pareto optimisation of railway bogie suspension damping to enhance safety and comfort[J]. Vehicle System Dynamics, 2012, 50(9): 1379-1407. doi: 10.1080/00423114.2012.659846 [10] MOUSAVI-BIDELEH S M, BERBYUK V. Multi-objective optimisation of bogie suspension to boost speed on curves[J]. Vehicle System Dynamics, 2016, 54(1): 58-85. doi: 10.1080/00423114.2015.1114655 [11] 解欢,杨岳,童林军,等. 基于混合代理模型的高速轨道车辆悬挂参数多目标优化[J]. 铁道科学与工程学报,2016,13(10): 2056-2063. doi: 10.3969/j.issn.1672-7029.2016.10.025XIE Huan, YANG Yue, TONG Linjun, et al. Multi-objective optimization of the suspension parameters for high speed rail vehicle based on a hybrid surrogate model[J]. Journal of Railway Science and Engineering, 2016, 13(10): 2056-2063. doi: 10.3969/j.issn.1672-7029.2016.10.025 [12] MOUSAVI BIDELEH S M, BERBYUK V, PERSSON R. Wear/comfort Pareto optimisation of bogie suspension[J]. Vehicle System Dynamics, 2016, 54(8): 1053-1076. doi: 10.1080/00423114.2016.1180405 [13] MOHEBBI M, REZVANI M A. Multi objective optimization of aerodynamic design of high speed railway windbreaks using Lattice Boltzmann Method and wind tunnel test results[J]. International Journal of Rail Transportation, 2018, 6(3): 183-201. doi: 10.1080/23248378.2018.1463873 [14] 姚远,陈相旺,李广,等. 高速列车抗蛇行减振器参数的多目标优化研究[J]. 西南交通大学学报,2021,56(6): 1298-1304.YAO Yuan, CHEN Xiangwang, LI Guang, et al. Multi-objective optimization of yaw damper parameters for high-speed train[J]. Journal of Southwest Jiaotong University, 2021, 56(6): 1298-1304. [15] 中华人民共和国铁道部. 铁道机车动力学性能试验鉴定方法及评定标准: TB/T 2360—1993[S]. 北京: 中国铁道出版社, 1994. [16] 林家浩, 张亚辉. 随机振动的虚拟激励法[M]. 北京: 科学出版社, 2004. [17] 王平,杨帆,韦凯. 扣件胶垫刚度频变的车-线-隧垂向耦合随机振动虚拟辛分析[J]. 西南交通大学学报,2017,52(2): 209-215. doi: 10.3969/j.issn.0258-2724.2017.02.001WANG Ping, YANG Fan, WEI Kai. Symplectic random vibration analysis of vertically coupled vehicle-track-tunnel system considering frequency-dependent stiffness of rail pads[J]. Journal of Southwest Jiaotong University, 2017, 52(2): 209-215. doi: 10.3969/j.issn.0258-2724.2017.02.001 [18] LIU X X, ZHANG Y H, GUO H F, et al. Random vibration analysis procedure of railway vehicle[J]. Vehicle System Dynamics, 2020, 58(12): 1873-1892. doi: 10.1080/00423114.2019.1656813 [19] DEB K, PRATAP A, AGARWAL S, et al. A fast and elitist multiobjective genetic algorithm: NSGA-II[J]. IEEE Transactions on Evolutionary Computation, 2002, 6(2): 182-197. doi: 10.1109/4235.996017 -




 下载:
下载: