一年龄期内超高泵送SCC力学性能时变研究

周济; 陈宗平; 唐际宇; 陈宇良

doi:10.3969/j.issn.0258-2724.20200746

一年龄期内超高泵送SCC力学性能时变研究

doi: 10.3969/j.issn.0258-2724.20200746

周济^1,,
陈宗平^{1, 2, ,},
唐际宇^{1, 3},
陈宇良⁴

1.
广西大学土木建筑工程学院，广西南宁 530004
2.
南宁学院土木与建筑工程学院，广西南宁 530200
3.
中建八局广西分公司，广西南宁 530004
4.
广西科技大学土木建筑工程学院，广西柳州 545006

基金项目: 国家自然科学基金（51578163）；八桂学者专项研究经费项目（[2019]79号）；广西科技基地与人才专项（桂科AD21075031）；中央引导地方科技发展资金项目（桂科ZY21195010）；南宁市科学研究与技术开发计划重大专项（20223024）

详细信息

作者简介:
周济（1995—），男，博士研究生，研究方向为钢-混凝土组合结构、海洋及近海混凝土结构，E-mail：zhouji_1995@163.com

通讯作者:
陈宗平（1975—），男，教授，博士，研究方向为钢-混凝土组合结构、海洋及近海混凝土结构、再生混凝土结构，E-mail：zpchen@gxu.edu.cn

中图分类号: TU528.53
计量
- 文章访问数: 263
- HTML全文浏览量: 127
- PDF下载量: 21
- 被引次数: 0
出版历程
- 收稿日期: 2020-11-03
- 修回日期: 2021-02-28
- 网络出版日期: 2022-08-08
- 刊出日期: 2021-03-02

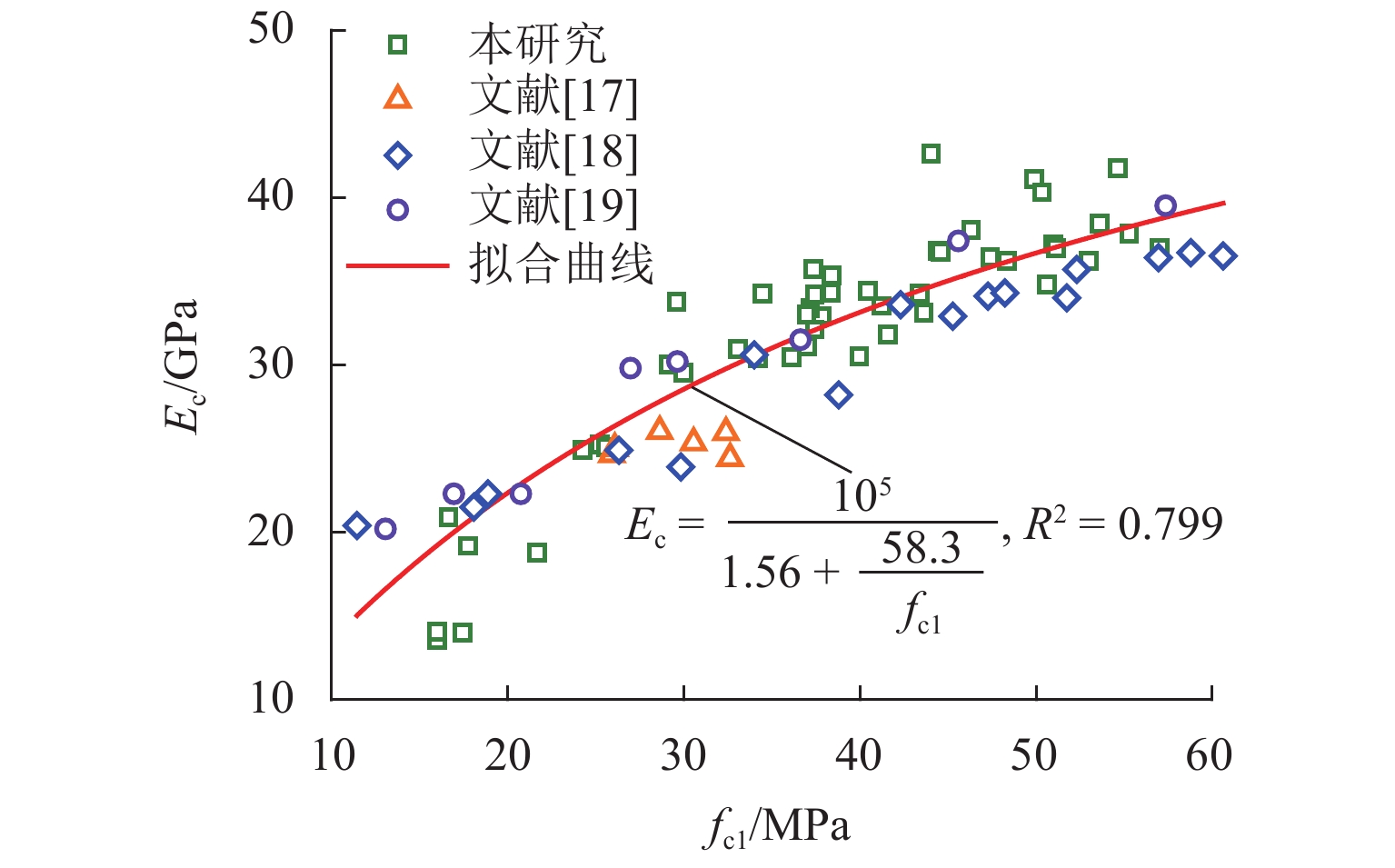
Time Variation of Mechanical Properties of Ultra-High Pumped Self-Compacting Concrete Within One Year of Age

ZHOU Ji^1
,,
CHEN Zongping^{1, 2
, ,},
TANG Jiyu^{1, 3},
CHEN Yuliang⁴

1.
College of Civil Engineering and Architecture, Guangxi University, Nanning 530004, China
2.
College of Architecture and Civil Engineering, Nanning University, Nanning 530200, China
3.
China Construction Eighth Engineering Division Co., Guangxi Branch, Nanning 530004, China
4.
College of Civil Engineering and Architecture, Guangxi University of Science and Technology, Liuzhou 545006, China

摘要

摘要:
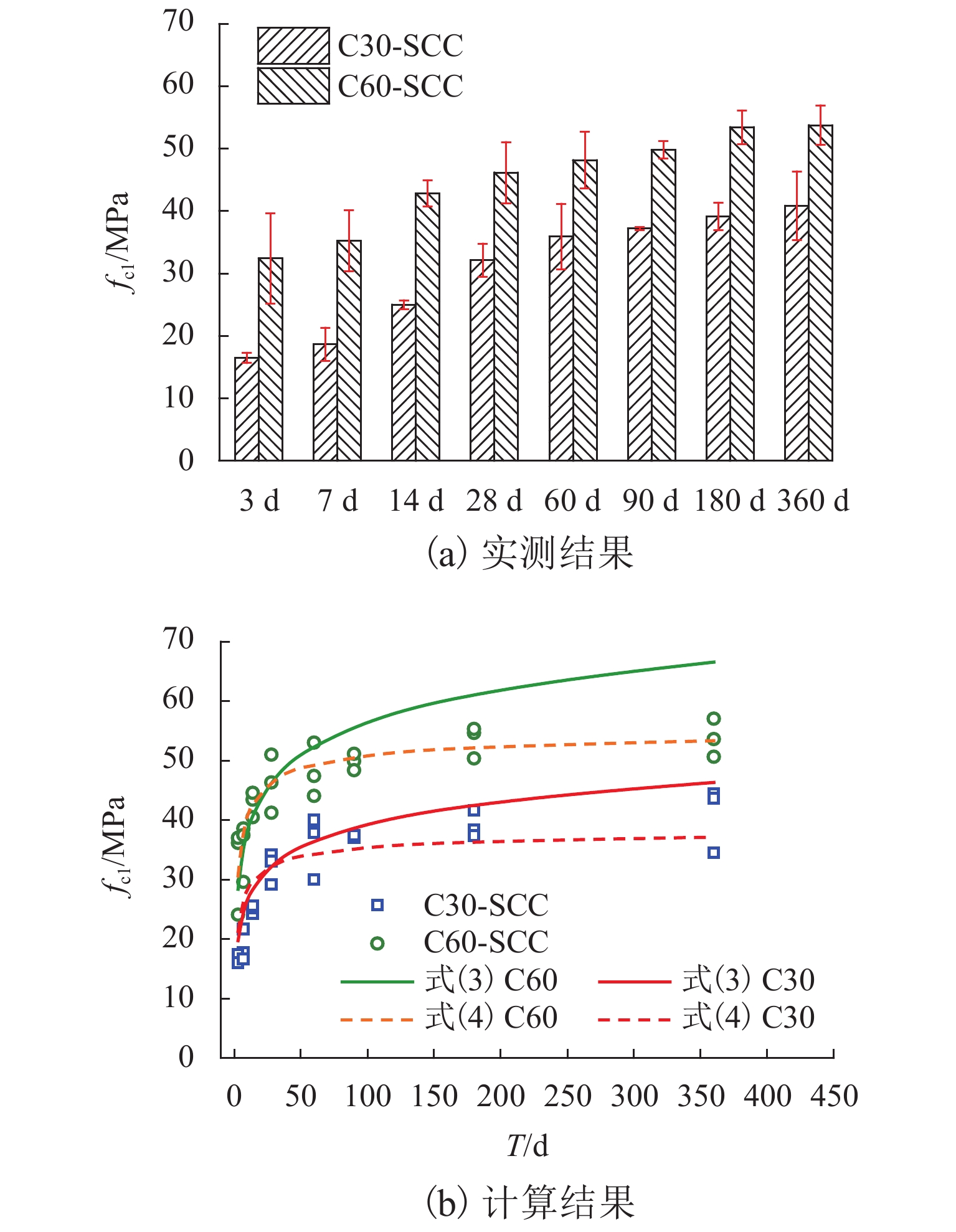
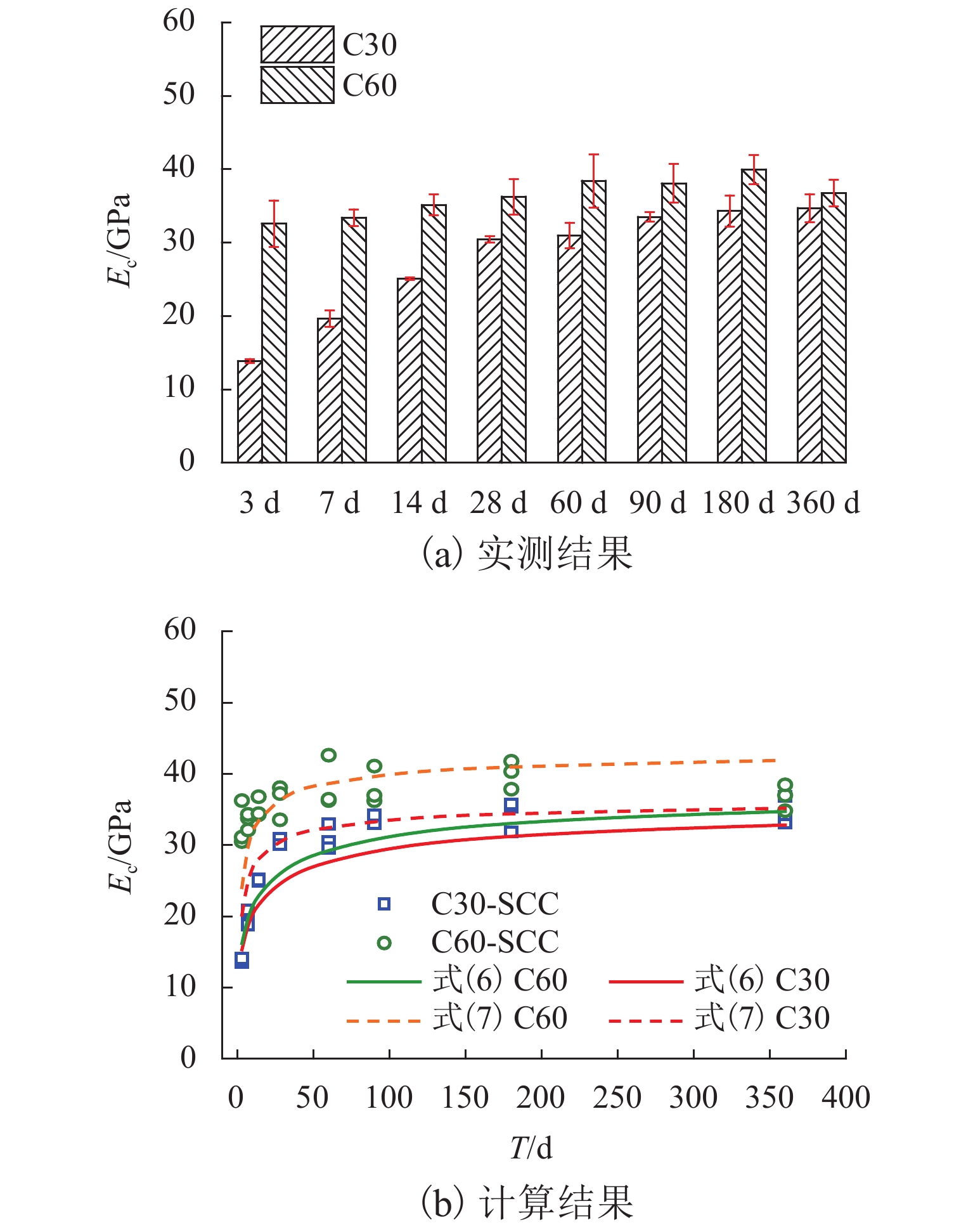
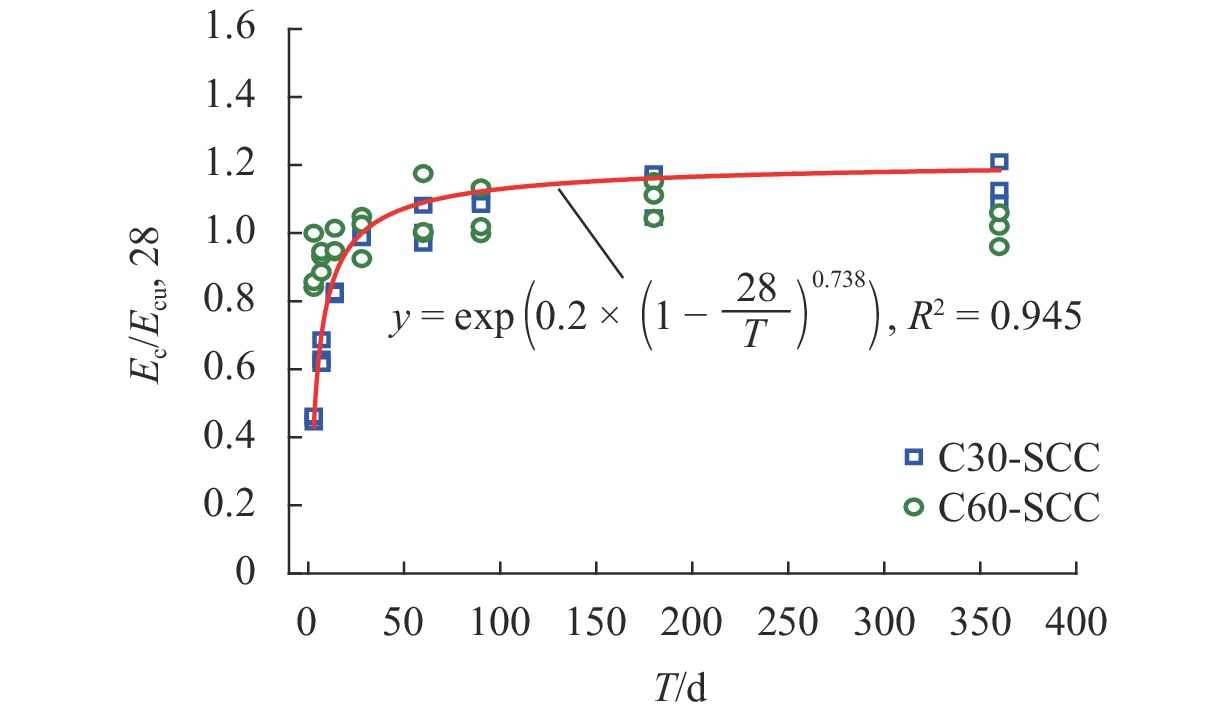
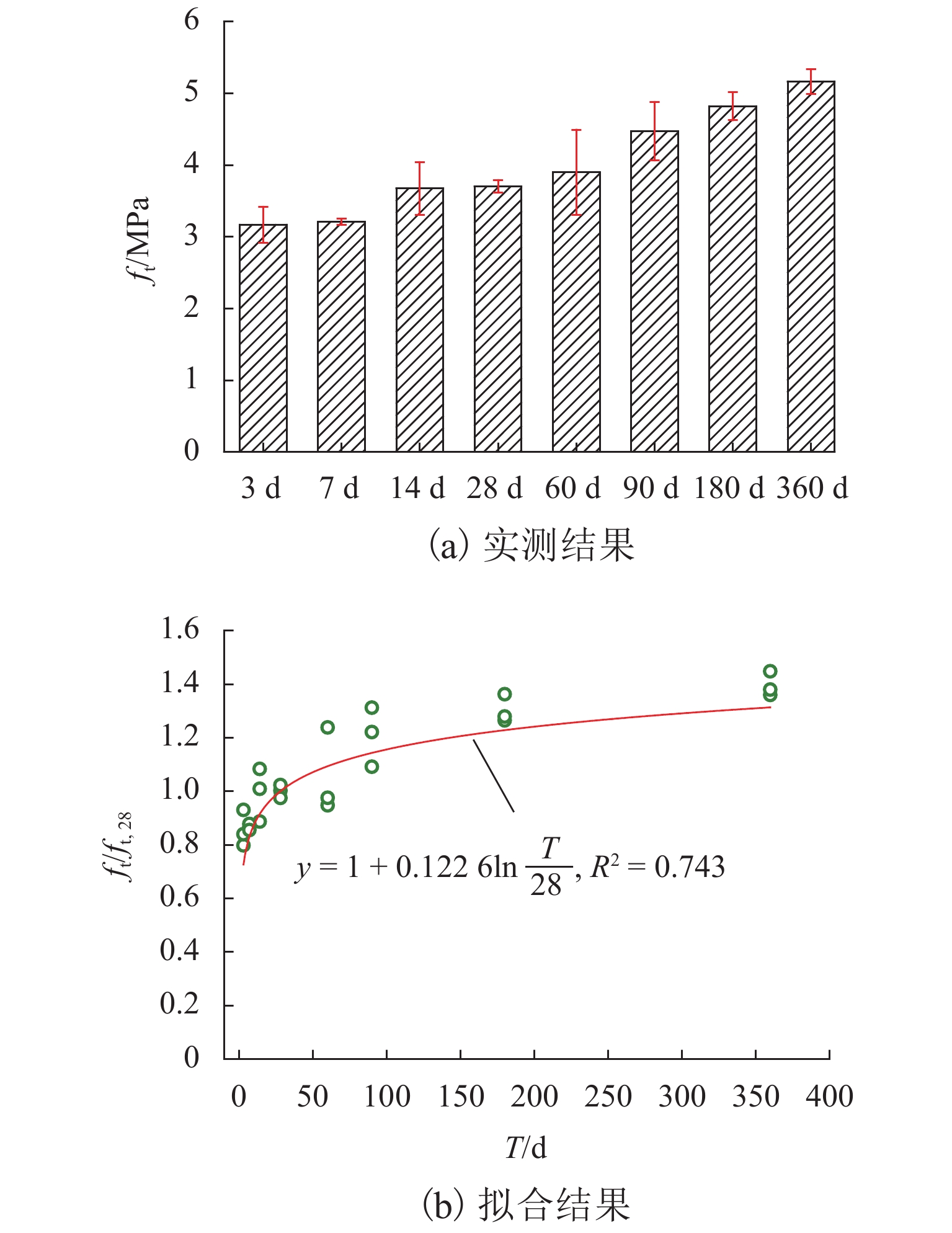
为揭示施工龄期内超高层建筑泵送自密实混凝土（SCC）轴心抗压强度、弹性模量以及劈裂抗拉强度等力学性能的时变规律，提供超高层建筑施工阶段力学性能分析的基础依据，依托某一超400 m高层建筑泵送SCC制作了120个试件，包括96个圆柱体件和24个立方体试件，并对其进行了不同时间龄期的力学性能测试，获取了超高层建筑泵送SCC的应力-应变曲线，提出了各力学性能指标时变及关系计算公式. 研究结果表明：超高层建筑泵送SCC在免振条件下具有良好的密实性；随着龄期的增长，超高层建筑泵送SCC的峰值应力增大，且其峰值应变显著大于普通混凝土的；早期14 d内为各项性能增长的关键阶段，弹性模量在90 d后趋于稳定，而轴心抗压强度和劈裂抗拉强度在28 d后仍有大幅增长；龄期T ≤ 60 d时，超高层建筑泵送SCC的轴压刚度随龄期增长呈增大趋势，而相对韧性则呈减小趋势，龄期T > 60 d时，二者均变化较小趋于稳定；超高层建筑泵送SCC强度的提高能增快早期性能的发展，且能增大轴压刚度和相对韧性；提出的各力学性能指标时变计算公式能为超高层建筑泵送SCC的力学性能预测与评估提供可靠依据.
- 超400 m高层建筑 /
- 自密实混凝土 /
- 施工龄期 /
- 力学性能 /
- 时变规律
Abstract:
In order to reveal the time-varying laws of the axial compressive strength, elastic modulus and splitting tensile strength of the pumped self-compacting concrete (SCC) in super high-rise buildings during the construction period, and to provide a basis for mechanical performance analysis of super high-rise buildings in construction stage, 120 specimens, including 96 cylindrical specimens and 24 cube specimens, were fabricated by pumping the SCC of a high-rise building over 400 m, their mechanical properties were tested at different ages, and the stress-strain curves of the ultra-high pumped SCC were obtained. Based on the tested results, formulas for calculating the time-varying relationship of the mechanical properties were proposed. The results show that the ultra-high pumped SCC has good compactness under vibration-free conditions. With the increase of age, the peak stress of the ultra-high pumped SCC increases, and the peak strain is significantly greater than that of ordinary concrete. The period of early 14 d is the key stage for the growth of various properties; the elastic modulus tends to stabilize after 90 d, while the axial compressive strength and split tensile strength still increase significantly after 28 d. When the age T ≤ 60 d, the axial compressive stiffness of the ultra-high pumped SCC increases with time, while the relative toughness decreases. When T > 60 d, both of them change little and tend to be stable. The improvement of strength of the pumped SCC in super high-rise buildings can accelerate the development of its early performance, and increase the axial compressive stiffness and relative toughness. The proposed calculation formulas of time-varying mechanical properties can provide a reliable basis for prediction and evaluation of mechanical performance of the pumped SCC in super high-rise buildings.
- high-rise buildings over 400 m /
- SCC /
- construction age /
- mechanical properties /
- time-varying regularity

HTML全文

图 1 轴压试件应力-应变曲线

Figure 1. Stress-strain curves of specimens underaxial compression

下载: 全尺寸图片幻灯片

图 2 轴心抗压强度随龄期的变化

Figure 2. Variations of axial compressive strength with age

下载: 全尺寸图片幻灯片

图 3 相对轴压强度随龄期变化的拟合结果

Figure 3. Fitting results of relative axial compression strength changing with age

下载: 全尺寸图片幻灯片

图 4 弹性模量随龄期的变化

Figure 4. Variations of elastic modulus with age

下载: 全尺寸图片幻灯片

图 5 相对弹性模量随龄期变化的拟合结果

Figure 5. Fitting results of relative elastic modulus changing with age

下载: 全尺寸图片幻灯片

图 6 C60劈裂抗拉强度随龄期的变化

Figure 6. Variations of splitting tensile strength with age

下载: 全尺寸图片幻灯片

图 7 E_c和f_c1间的换算关系

Figure 7. Conversion relationship between E_c and f_c1

下载: 全尺寸图片幻灯片

图 8 f_c和f_c1间的换算关系

Figure 8. Conversion relationship between E_c and f_c1

下载: 全尺寸图片幻灯片

表 1 泵送SCC配合比

Table 1. Mix proportion of the pumped SCC

品种及规格	质量配合比		用量/（kg·m⁻³）
品种及规格	C30	C60	C30	C60
海螺 P•O42.5 水流	1.00	1.00	220	380
河砂（优质）	2.60	1.32	571	500
碎石机制砂	1.72	0.66	379	250
5 ~ 25 mm（优质）石子	4.27	2.50	940	950
自来水	0.70	0.42	155	158
S95 矿粉	0.23	0.17	50	65
Ⅱ级粉煤灰	0.27	0.21	60	80
四川朗天硅灰	0.14	0.09	30	35
聚羧酸 PCA 外加剂	0.03	0.03	7.2	13.0

下载: 导出CSV

表 2 各试件力学性能指标

Table 2. Mechanical property indexes of each specimen

试件编号	f_cu /MPa		f_c1 /MPa		E_c /GPa		试件编号	f_cu /MPa		f_c1 /MPa		E_c /GPa		f_t /MPa
试件编号	实测	平均	实测	平均	实测	平均	试件编号	实测	平均	实测	平均	实测	平均	实测	平均
C30-3 d	20.0	20.6	16.0	16.5	13.5	13.9	C60-3 d	45.2	40.5	36.2	32.4	30.5	32.6	3.0	3.2
	21.8		17.5		14.0			46.3		37.0		31.1		3.1
	20.0		16.0		14.1			30.1		24.1		36.2		3.4
C30-7 d	22.2	23.4	17.8	18.7	19.2	19.6	C60-7 d	37.0	43.9	29.6	35.2	33.8	33.4	3.2	3.2
	27.1		21.7		18.8			48.0		38.4		34.3		3.2
	20.8		16.7		20.9			46.8		37.5		32.1		3.2
C30-14 d	30.3	31.3	24.3	25.0	24.9	25.1	C60-14 d	54.3	53.6	43.4	42.8	34.2	35.1	3.3	3.7
	31.5		25.2		25.3			55.7		44.6		36.8		4.0
	32.0		25.6		25.1			50.6		40.5		34.4		3.7
C30-28 d	42.8	40.2	34.2	32.1	30.4	30.4	C60-28 d	57.9	57.7	46.3	46.2	38.0	36.3	3.7	3.7
	41.3		33.1		30.9			51.5		41.2		33.5		3.6
	36.4		29.2		30.0			63.7		51.0		37.2		3.8
C30-60 d	50.0	44.9	40.0	35.9	30.5	31.0	C60-60 d	66.3	60.2	53.0	48.2	36.2	38.4	4.6	3.9
	37.5		30.0		29.5			59.3		47.4		36.4		3.5
	47.3		37.8		32.9			55.1		44.1		42.6		3.6
C30-90 d	46.5	46.5	37.2	37.2	33.4	33.5	C60-90 d	62.4	62.3	49.9	49.8	41.1	38.1	4.5	4.5
	46.2		37.0		33.0			60.5		48.4		36.2		4.0
	46.8		37.5		34.2			63.9		51.1		36.9		4.9
C30-180 d	48.0	48.9	38.4	39.1	35.3	34.3	C60-180 d	68.3	66.8	54.6	53.4	41.7	40.0	4.7	4.8
	46.7		37.4		35.7			62.9		50.4		40.3		4.7
	52.0		41.6		31.8			69.1		55.3		37.8		5.0
C30-360 d	55.5	51.1	44.4	40.9	36.8	34.7	C60-360 d	71.3	67.2	57.0	53.8	37.0	36.7	5.0	5.2
	54.6		43.6		33.1			63.3		50.7		34.8		5.4
	43.1		34.5		34.3			67.0		53.6		38.4		5.1

下载: 导出CSV

表 3 轴压刚度及相对韧性

Table 3. Axial compressive stiffness and relative toughness

龄期/d	强度等级	轴压刚度 /MN	相对韧性 /×10⁻³
3	C30	64.35	3.61
3	C60	90.62	3.87
7	C30	62.91	3.23
7	C60	155.61	2.97
14	C30	99.31	3.08
14	C60	161.13	3.55
28	C30	106.67	2.86
28	C60	170.34	3.50
60	C30	149.31	2.76
60	C60	168.08	3.34
90	C30	165.49	2.60
90	C60	148.43	3.82
180	C30	155.88	2.33
180	C60	180.99	2.97
360	C30	163.55	2.55
360	C60	196.37	2.92

下载: 导出CSV

参考文献(19)

[1]	KAMAL M M, SAFAN M A, BASHANDY A A, et al. Experimental investigation on the behavior of normal strength and high strength self-curing self-compacting concrete[J]. Journal of Building Engineering, 2018, 16: 79-93. doi: 10.1016/j.jobe.2017.12.012
[2]	刘运华,谢友均,龙广成. 自密实混凝土研究进展[J]. 硅酸盐学报,2007,35(5): 671-678. doi: 10.3321/j.issn:0454-5648.2007.05.028 LIU Yunhua, XIE Youjun, LONG Guangcheng. Progress of research on self-compacting concrete[J]. Journal of the Chinese Ceramic Society, 2007, 35(5): 671-678. doi: 10.3321/j.issn:0454-5648.2007.05.028
[3]	HAZAREE C, MAHADEVAN V. Single stage concrete pumping through 2.432 km (1.51 miles): weather and execution challenges[J]. Case Studies in Construction Materials, 2015, 3: 56-69. doi: 10.1016/j.cscm.2015.05.001
[4]	TAN Y Q, ZHANG H, YANG D M, et al. Numerical simulation of concrete pumping process and investigation of wear mechanism of the piping wall[J]. Tribology International, 2012, 46(1): 137-144.
[5]	ROZIÈRE E, GRANGER S, TURCRY P, et al. Influence of paste volume on shrinkage cracking and fracture properties of self-compacting concrete[J]. Cement and Concrete Composites, 2007, 29(8): 626-636. doi: 10.1016/j.cemconcomp.2007.03.010
[6]	ZHAO Y, MA J, WU Z, et al. Study on fracture properties of self-compacting concrete using wedge splitting test[C]//Proceedings of the 1st International Symposium on Design, Performance and Use of Self-Consolidating Concrete. Paris: RILEM Publication SARL, 2005: 421-428
[7]	OMRANE M, KENAI S, KADRI E H, et al. Performance and durability of self-compacting concrete using recycled concrete aggregates and natural pozzolan[J]. Journal of Cleaner Production, 2017, 165: 415-430. doi: 10.1016/j.jclepro.2017.07.139
[8]	SANTOS S, DA SILVA P R, DE BRITO J. Self-compacting concrete with recycled aggregates-A literature review[J]. Journal of Building Engineering, 2019, 22: 349-371. doi: 10.1016/j.jobe.2019.01.001
[9]	ZHU W Z, BARTOS P J M. Permeation properties of self-compacting concrete[J]. Cement and Concrete Research, 2003, 33(6): 921-926. doi: 10.1016/S0008-8846(02)01090-6
[10]	元强,李白云,史才军,等. 混凝土泵送性能的流变学表征及预测综述[J]. 材料导报,2018,32(17): 2976-2985. doi: 10.11896/j.issn.1005-023X.2018.17.011 YUAN Qiang, LI Baiyun, SHI Caijun, et al. An overview on the prediction and rheological characterization of pumping concrete[J]. Materials Review, 2018, 32(17): 2976-2985. doi: 10.11896/j.issn.1005-023X.2018.17.011
[11]	中华人民共和国建设部, 国家质量监督检验检疫总局. 普通混凝土力学性能试验方法标准: GB/T 50081—2002[S]. 北京: 中国建筑工业出版社, 2003.
[12]	LI L, HWANG C L. Analysis on the stress-strain behavior of self-consolidating concrete[C]//SCC2005-China: 1st International Symposium on Design, Performance and Use of Self-Consolidating Concrete. [S.l.]: RILEM Publications SARL, 2005: 517-522.
[13]	朱伯芳. 大体积混凝土温度应力与温度控制[M]. 北京: 中国电力出版社, 2003.
[14]	TAERWE L. Fib model code for concrete structures 2010[M]. [S.l.]: Ernst & Sohn, Wiley, 2013.
[15]	杨久俊,刘俊霞,韩静宜,等. 大流动度超高强钢纤维混凝土力学性能研究[J]. 建筑材料学报,2010,13(1): 1-6. doi: 10.3969/j.issn.1007-9629.2010.01.001 YANG Jiujun, LIU Junxia, HAN Jingyi, et al. Studies on mechanical property of high fluidity steel fiber reinforced ultra-high strength concrete[J]. Journal of Building Materials, 2010, 13(1): 1-6. doi: 10.3969/j.issn.1007-9629.2010.01.001
[16]	中华人民共和国住房和城乡建设部. 混凝土结构设计规范: GB 50010—2010[S]. 北京: 中国建筑工业出版社, 2011.
[17]	赵军,高丹盈. 高性能自密实混凝土的力学及变形性能试验研究[J]. 中外公路,2006,26(2): 161-165. doi: 10.3969/j.issn.1671-2579.2006.02.045
[18]	王建新. 高性能自密实混凝土力学性能及抗冻性能研究[D]. 长春: 吉林大学, 2019.
[19]	NIKBIN I M, BEYGI M H A, KAZEMI M T, et al. A comprehensive investigation into the effect of aging and coarse aggregate size and volume on mechanical properties of self-compacting concrete[J]. Materials & Design, 2014, 59: 199-210.