Characteristics of Chloride Ion Permeation in Concrete of Type Ⅰ Fracture Crack Propagation
-
摘要:
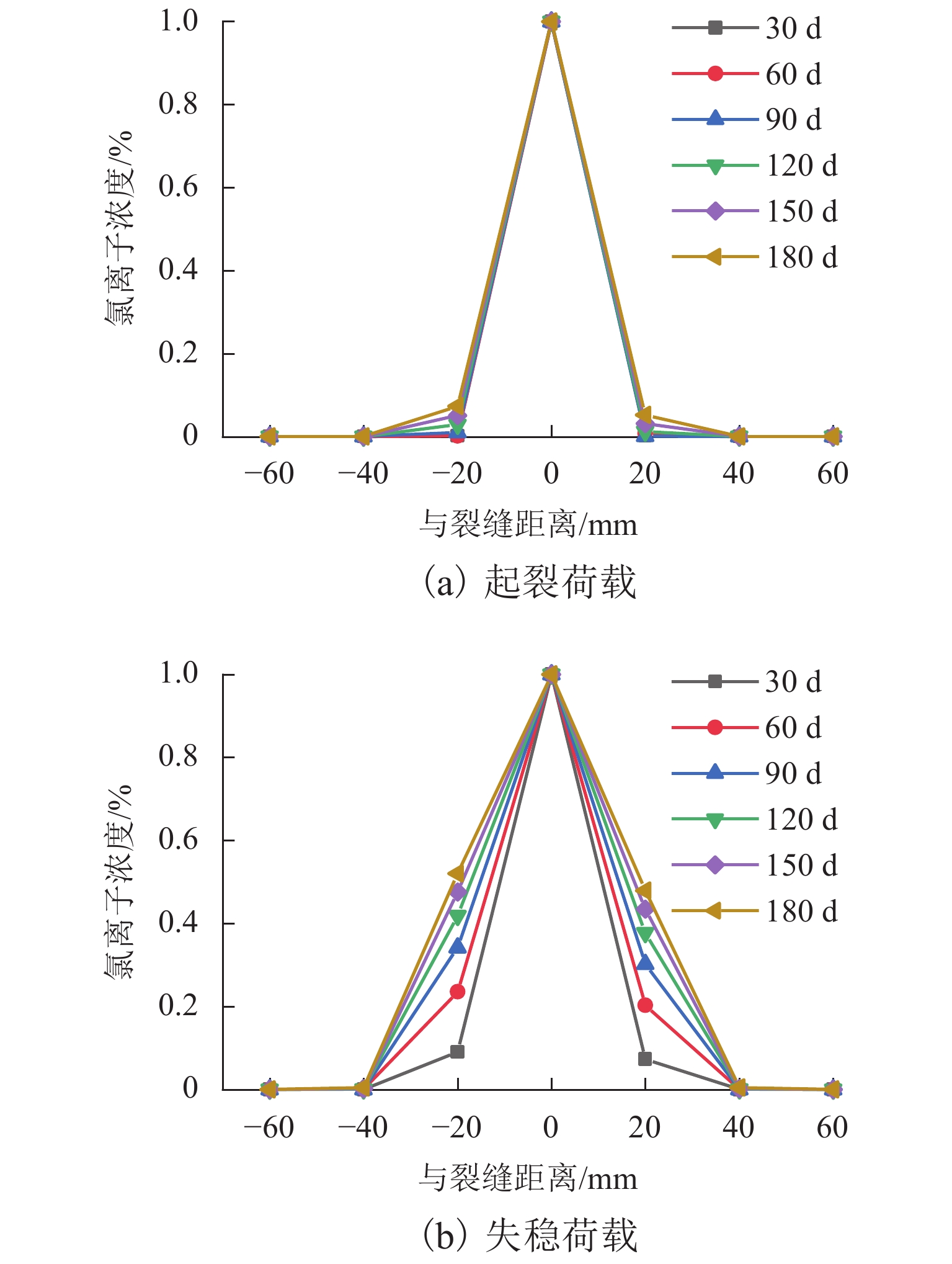
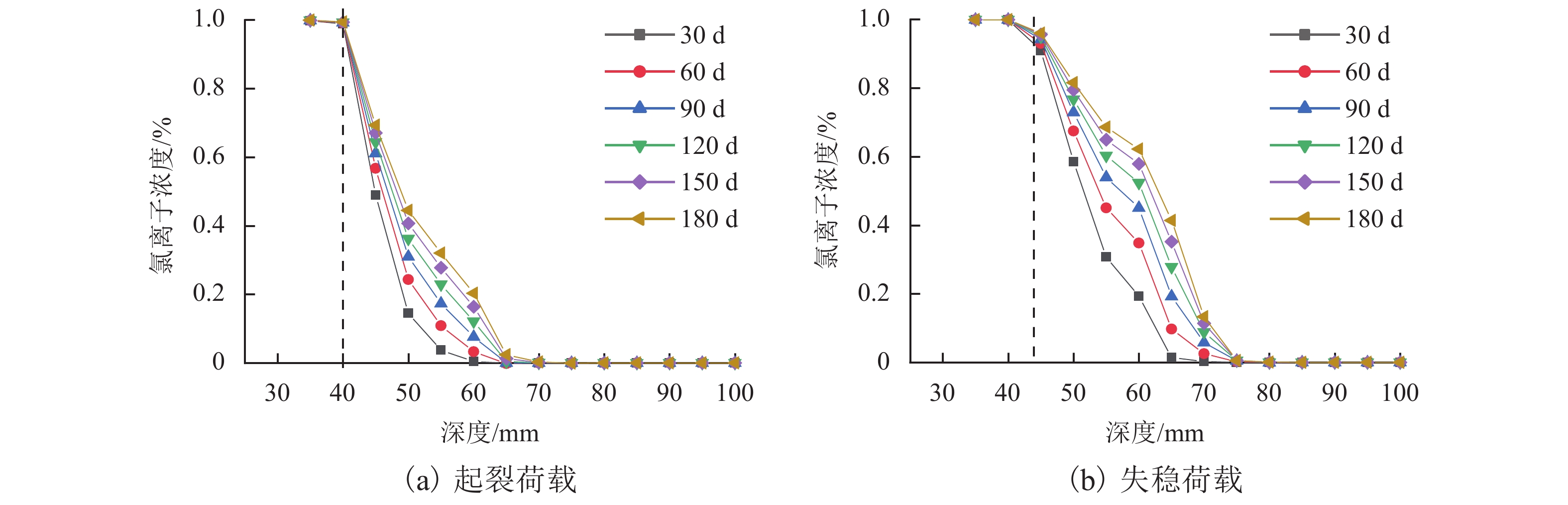
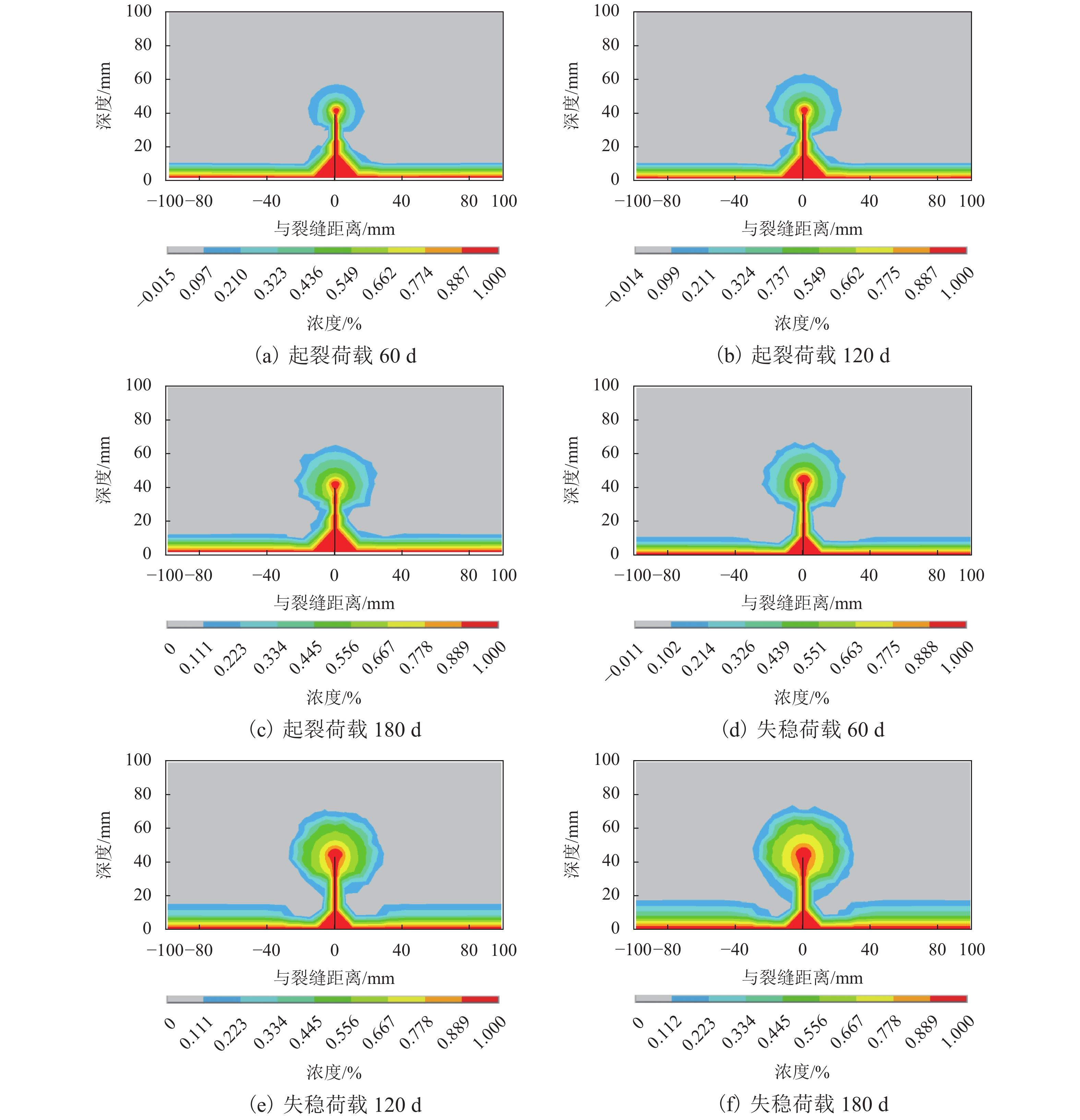
为了研究荷载作用下混凝土结构裂缝扩展过程中的氯离子侵蚀问题,更加准确地描述不同扩展阶段裂缝周边的氯离子侵蚀特征,依据混凝土断裂准则,采用ANSYS参数化设计语言APDL进行二次开发,自编程序模拟了混凝土小梁Ⅰ型断裂裂缝开展过程;在断裂分析的基础上通过参数等效,采用结构-热分析方法,基于体应变-损伤变量-氯离子扩散系数一一映射关系,实现了混凝土裂缝扩展过程中各个阶段氯离子侵蚀的数值分析. 结果表明:不同裂缝扩展阶段,三点弯曲混凝土小梁裂缝周边氯离子侵蚀结果与试验结果吻合,荷载作用下混凝土裂缝尖端氯离子侵蚀呈现加剧现象,在混凝土结构耐久性寿命分析中起决定性作用;双
K 断裂准则和基于损伤参数的氯离子扩散模型能够模拟混凝土开裂过程氯离子侵蚀问题.Abstract:To explore chloride ion erosion in the crack propagation process of concrete structures under loads, and more accurately describe the characteristics of chloride ion erosion around cracks at different stages, the development process of concrete trabeculae type Ⅰ fracture, based on the concrete fracture criteria, was simulated by self-programming, and redeveloped by ANSYS parametric design language APDL. Given the mapping relationship between volume strain, damage variable and chloride ion diffusion coefficient, the parameter equivalence method and the structure-thermal analysis method are used for numerical analysis of chloride ion erosion at various stages of concrete crack propagation. The results show that chloride ion erosion around the crack of a three-point bending concrete trabecular is consistent with the experimental one at different crack-expanding stages. The chloride ion erosion at the crack tip of concrete is intensified under loads; therefore, it plays a decisive role in the durability life analysis of concrete structures. Furthermore, the double-
K fracture criterion and the chloride ion diffusion model based on damage parameters can simulate the chloride ion erosion in the concrete cracking process.-
Key words:
- fracture /
- crack /
- chloride ion /
- erosion /
- numerical analysis
-
表 1 混凝土基本力学性能
Table 1. Basic mechanical properties of concrete
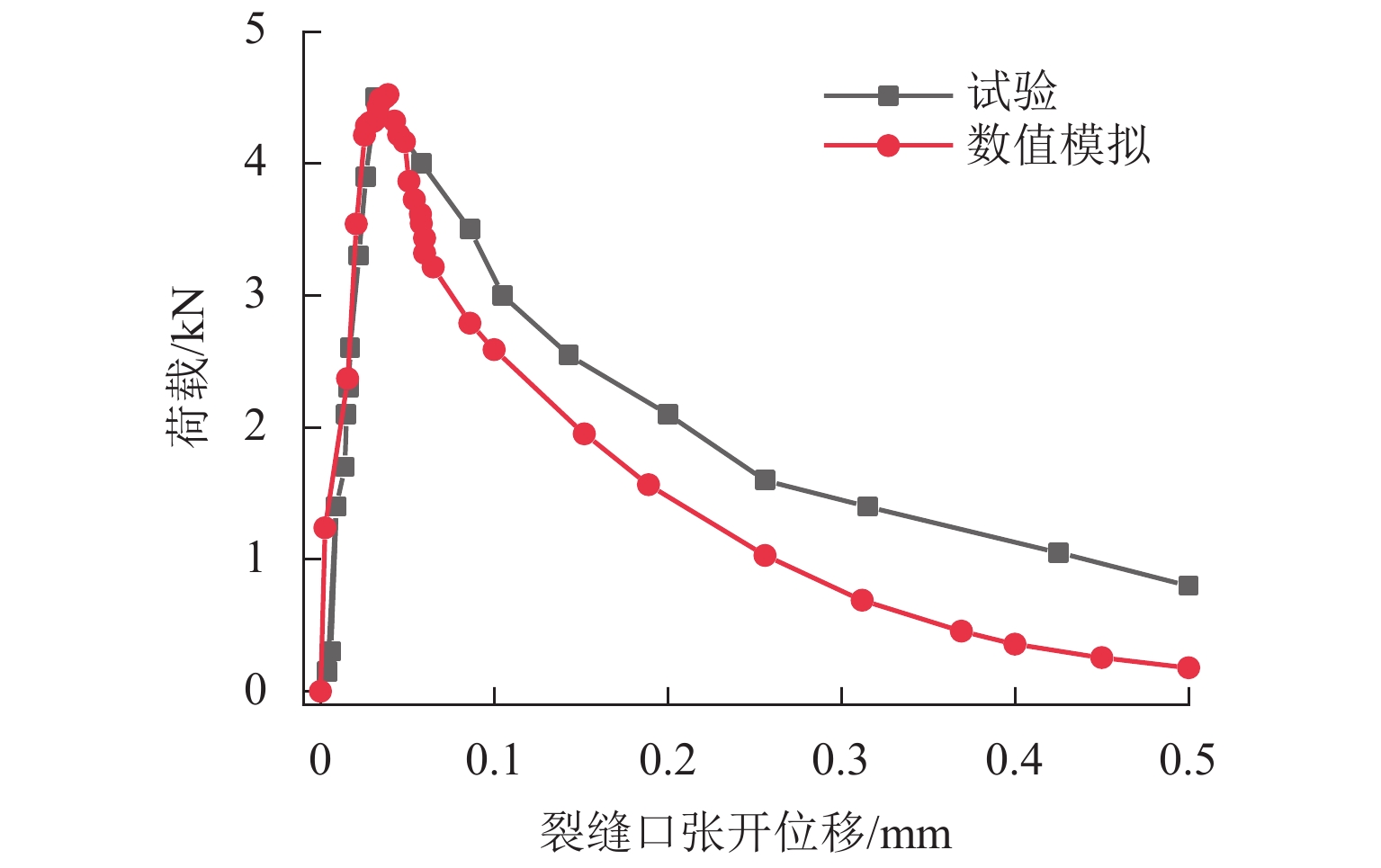
参量 E/GPa ft /MPa fc /MPa Pmin/kN Pmax/kN 数值 29.2 2.7 34.8 3.14 4.50 -
[1] 金伟良,延永东,王海龙. 氯离子在受荷混凝土内的传输研究进展[J]. 硅酸盐学报,2010,38(11): 2217-2224. doi: 10.14062/j.issn.0454-5648.2010.11.035JIN Weiliang, YAN Yongdong, WANG Hailong. Research progress on the chloride transportation in stressed concrete[J]. Journal of the Chinese Ceramic Society, 2010, 38(11): 2217-2224. doi: 10.14062/j.issn.0454-5648.2010.11.035 [2] DJERBI A, BONNET S, KHELIDJ A, et al. Influence of traversing crack on chloride diffusion into concrete[J]. Cement and Concrete Research, 2008, 38(6): 877-883. doi: 10.1016/j.cemconres.2007.10.007 [3] ISMAIL M, TOUMI A, FRANÇOIS R, et al. Effect of crack opening on the local diffusion of chloride in cracked mortar samples[J]. Cement and Concrete Research, 2008, 38(8/9): 1106-1111. doi: 10.1016/j.cemconres.2008.03.009 [4] 张菊辉,刘颖慧,时哲敏. 氯离子在开裂混凝土中的扩散特性研究[J]. 建筑材料学报,2018,21(2): 299-303. doi: 10.3969/j.issn.1007-9629.2018.02.020ZHANG Juhui, LIU Yinghui, SHI Zhemin. Diffusion property of chloride in cracked concrete[J]. Journal of Building Materials, 2018, 21(2): 299-303. doi: 10.3969/j.issn.1007-9629.2018.02.020 [5] 徐义洪,范颖芳,殷雨时. 带裂缝混凝土内氯离子的输运规律[J]. 混凝土,2016(11): 68-72,82. doi: 10.3969/j.issn.1002-3550.2016.11.019XU Yihong, FAN Yingfang, YIN Yushi. Transport regularity of in load cracked concrete[J]. Concrete, 2016(11): 68-72,82. doi: 10.3969/j.issn.1002-3550.2016.11.019 [6] 何世钦,贡金鑫. 弯曲荷载作用对混凝土中氯离子扩散的影响[J]. 建筑材料学报,2005,8(2): 134-138. doi: 10.3969/j.issn.1007-9629.2005.02.004HE Shiqin, GONG Jinxin. Influence of flexural loading on permeability of chloride ion in concrete[J]. Journal of Building Materials, 2005, 8(2): 134-138. doi: 10.3969/j.issn.1007-9629.2005.02.004 [7] 邢锋,冷发光,冯乃谦,等. 长期持续荷载对素混凝土氯离子渗透性的影响[J]. 混凝土,2004(5): 3-8. doi: 10.3969/j.issn.1002-3550.2004.05.001XING Feng, LENG Faguang, FENG Naiqian, et al. The influence of long-term sustaining load on the permeability of plain concrete to chloride ion[J]. Concrete, 2004(5): 3-8. doi: 10.3969/j.issn.1002-3550.2004.05.001 [8] ZHANG Y S, SUN W, LIU Z Y, et al. One and two dimensional chloride ion diffusion of fly ash concrete under flexural stress[J]. Journal of Zhejiang University—SCIENCE A, 2011, 12(9): 692-701. doi: 10.1631/jzus.A1100006 [9] 董伟. 混凝土Ⅰ-Ⅱ复合型裂缝起裂准则的试验研究与裂缝扩展过程的数值模拟[D]. 大连: 大连理工大学, 2008. [10] HILLERBORG A, MODÉER M, PETERSSON P E. Analysis of crack formation and crack growth in concrete by means of fracture mechanics and finite elements[J]. Cement and Concrete Research, 1976, 6(6): 773-781. doi: 10.1016/0008-8846(76)90007-7 [11] 董伟,肖魁,何化南,等. 全级配混凝土Ⅰ型裂缝扩展全过程数值模拟[J]. 工程力学,2013,30(4): 228-234. doi: 10.6052/j.issn.1000-4750.2011.11.0805DONG Wei, XIAO Kui, HE Huanan, et al. Numerical simulation on complete process of model Ⅰ crack propagation of fully-graded concrete[J]. Engineering Mechanics, 2013, 30(4): 228-234. doi: 10.6052/j.issn.1000-4750.2011.11.0805 [12] REINHARDT H W, CORNELISSEN H A W, HORDIJK D A. Tensile tests and failure analysis of concrete[J]. Journal of Structural Engineering, 1986, 112(11): 2462-2477. doi: 10.1061/(ASCE)0733-9445(1986)112:11(2462) [13] 吴智敏,董伟,刘康,等. 混凝土Ⅰ型裂缝扩展准则及裂缝扩展全过程的数值模拟[J]. 水利学报,2007,38(12): 1453-1459. doi: 10.3321/j.issn:0559-9350.2007.12.007WU Zhimin, DONG Wei, LIU Kang, et al. Mode Ⅰ crack propagation criterion of concrete and numerical simulation on complete process of cracking[J]. Journal of Hydraulic Engineering, 2007, 38(12): 1453-1459. doi: 10.3321/j.issn:0559-9350.2007.12.007 [14] 张云国,魏锐,刘康. 弯曲荷载作用下混凝土氯离子渗透数值分析[J]. 材料科学与工程学报,2018,36(6): 941-946,980.ZHANG Yunguo, WEI Rui, LIU Kang. Numerical analysis on chloride permeability of concrete under bending loads[J]. Journal of Materials Science and Engineering, 2018, 36(6): 941-946,980. [15] 王显利. 氯离子侵蚀的钢筋混凝土结构锈蚀损伤[D]. 大连: 大连理工大学, 2008. [16] GERARD B, PIJAUDIER-CABOT G, LABORDERIE C. Coupled diffusion-damage modelling and the implications on failure due to strain localisation[J]. International Journal of Solids and Structures, 1998, 35(31/32): 4107-4120. [17] 中华人民共和国住房和城乡建设部. 混凝土结构设计规范: GB 50010—2010[S]. 北京: 中国建筑工业出版社, 2011. [18] 中华人民共和国交通部. 水运工程混凝土试验规程: JTJ 270—1998[S]. 北京: 人民交通出版社, 1999. [19] 延永东. 氯离子在损伤及开裂混凝土内的输运机理及作用效应[D]. 杭州: 浙江大学, 2011. -




 下载:
下载: