Effects of Thermal Stress of Rock Masses Generated by Geothermal Gradient on Rockburst Prediction
-
摘要:
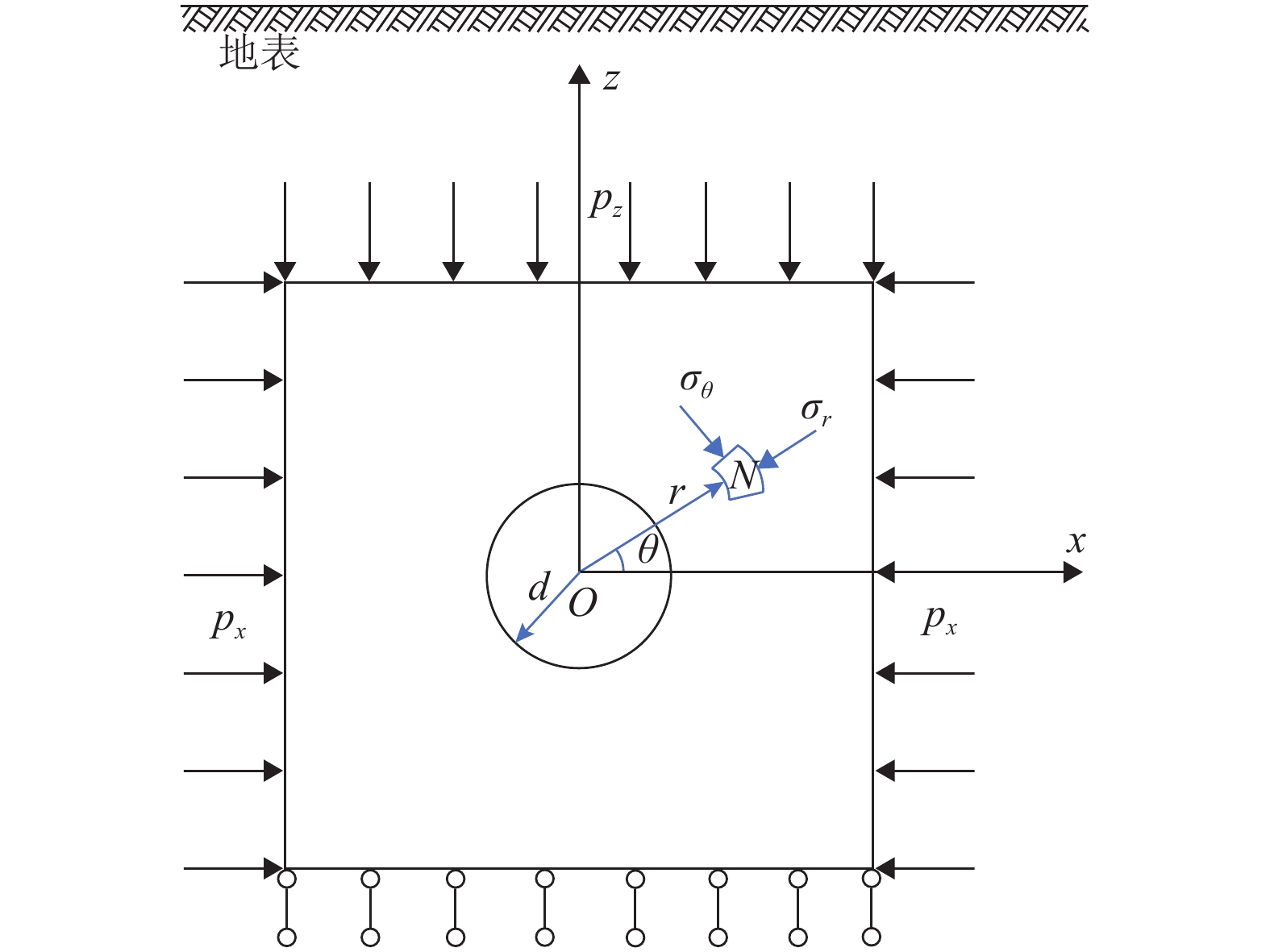
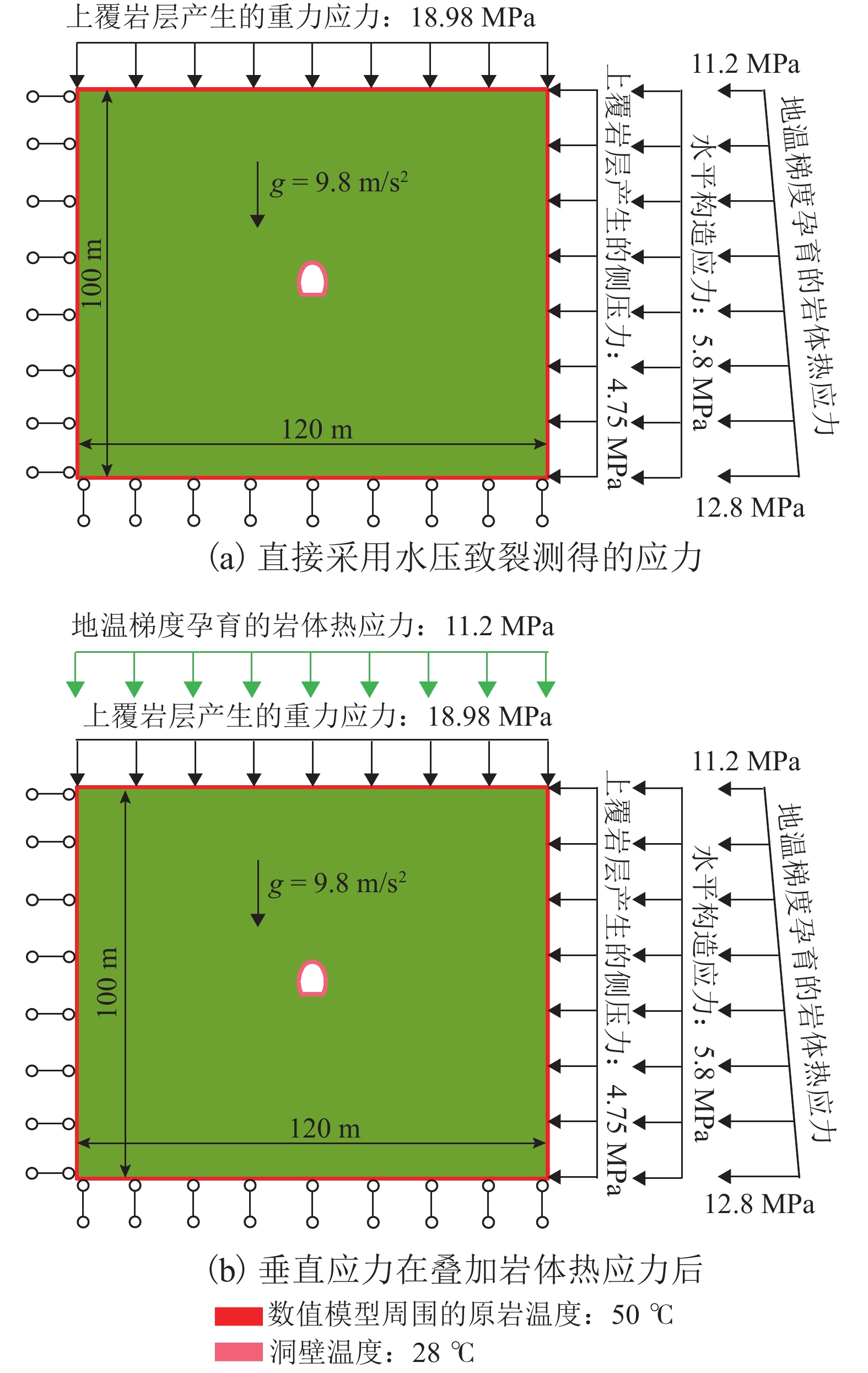
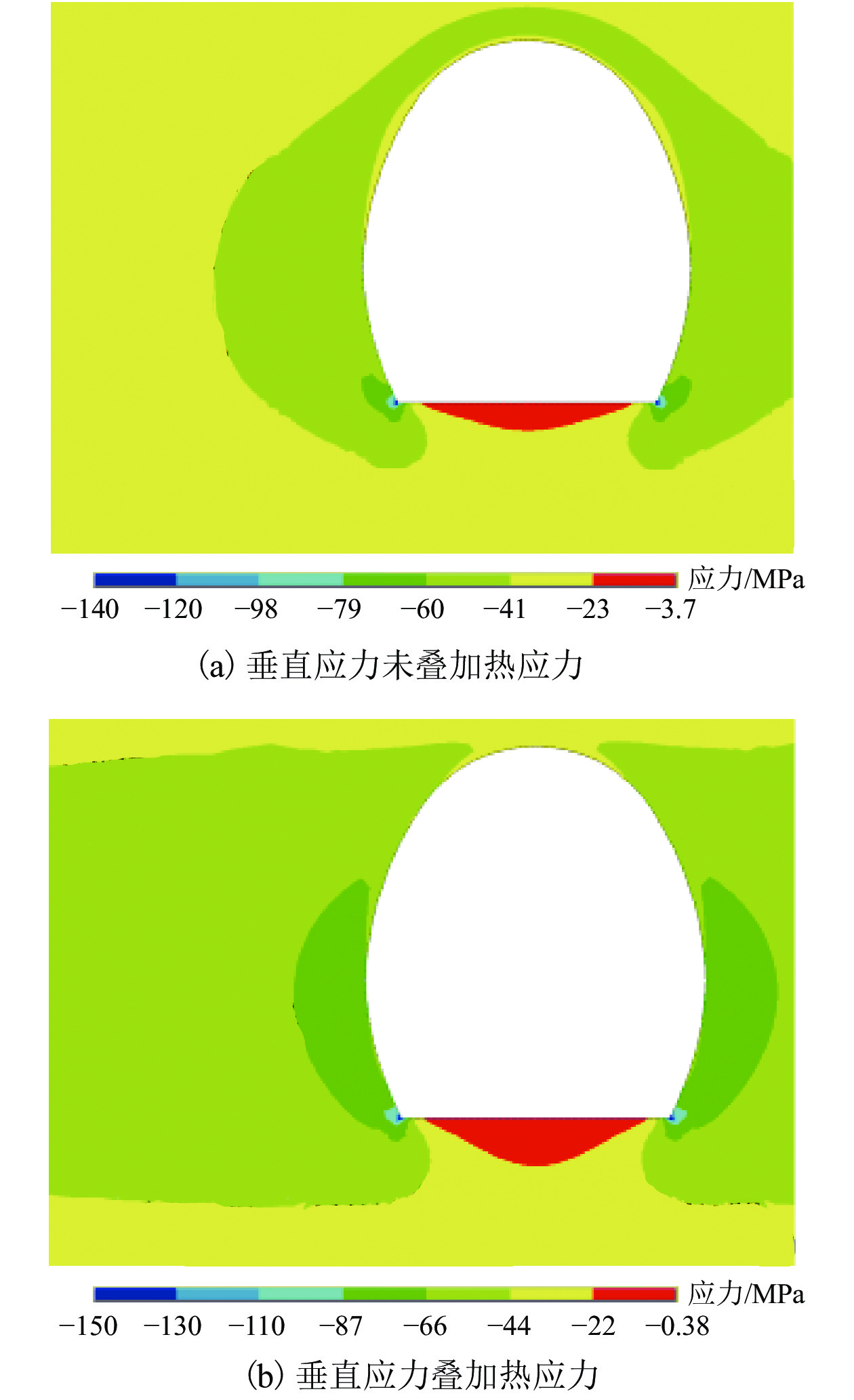
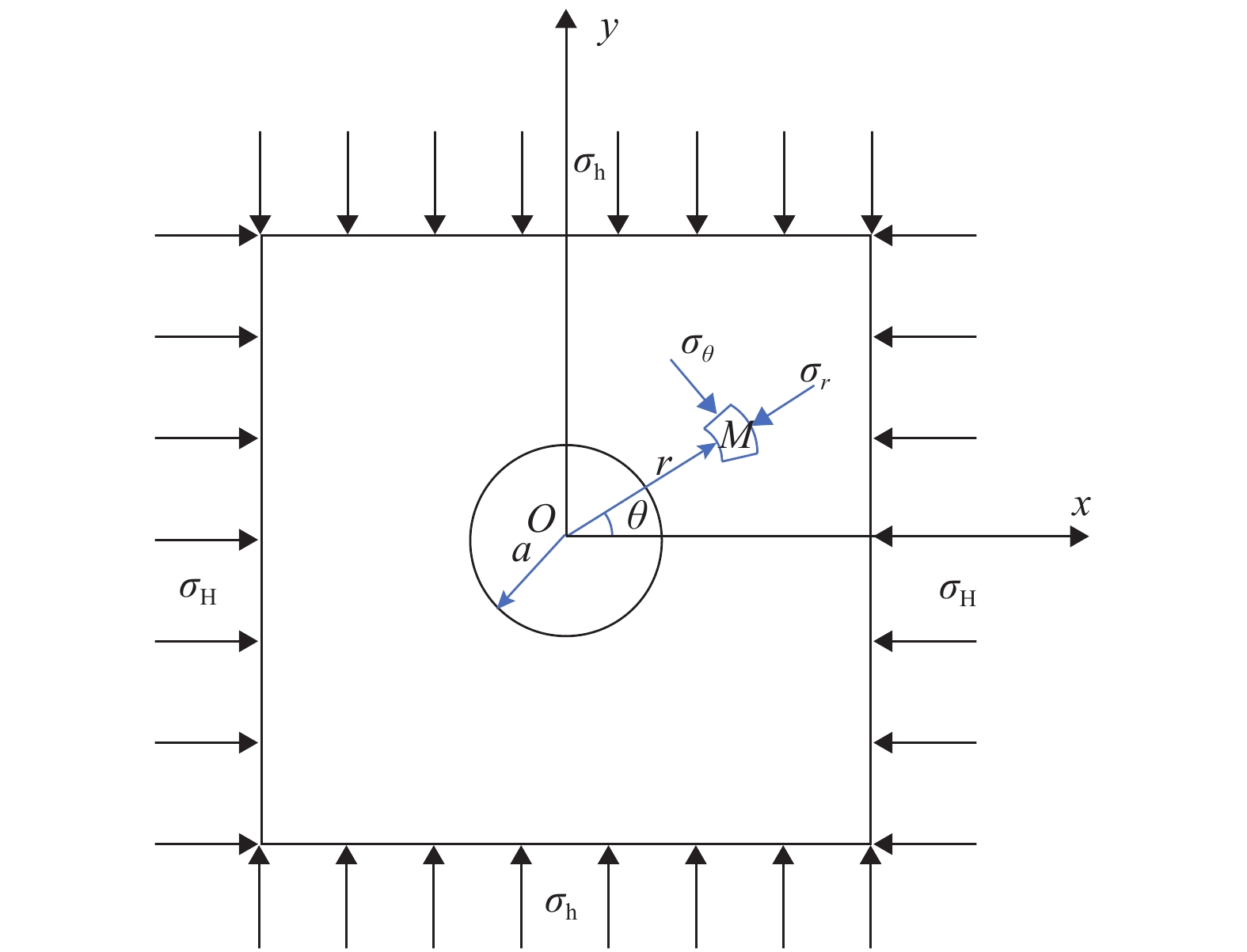
为使在高地温环境下通过水压致裂获得的应力更加真实地预测岩爆，提出在岩爆预测过程中应考虑地温梯度孕育的岩体热应力. 结合弹性理论获得了在高地温环境下水压致裂的理论应力解；基于此理论应力解对圆形隧道进行了岩爆预测；应用岩体热应力公式对桑珠岭隧址区的岩爆进行了预测. 研究结果表明：在高地温环境下，恒定压力和水平主应力会增加约一倍的岩体热应力，裂隙重开压力会增加约两倍的岩体热应力，垂直应力不变；如果在高地温环境下直接采用水压致裂测得的应力进行岩爆预测，当水平原位地应力大于竖向原位地应力时，得到的岩爆等级偏高，当水平原位地应力在重力应力和竖向原位地应力之间时，得到的岩爆预测位置与实际不一致，当水平原位地应力小于重力应力时，得到的岩爆等级偏低；桑珠岭隧址区的岩体热应力约为重力应力的61%，若不考虑此热应力进行岩爆预测会导致严重的错误.
Abstract:To make the stress obtained by hydraulic fracturing in a high geo-temperature environment more truly predict rockbursts, it is proposed that the thermal stress of rock masses generated by geothermal gradients should be considered during the rockburst prediction. Combined with the theory of elasticity, the theoretical stress solution of hydraulic fracturing in a high geo-temperature environment was obtained firstly. Then the rockburst prediction of a circular tunnel was conducted based on this theoretical stress solution. Finally, according to the thermal stress formula of rock masses, the rockburst prediction for the Sangzhuling tunnel was applied. The results show that the instantaneous shut-in pressure and the horizontal principal stress are increased by about one time the thermal stress of rock masses, and the reopening pressure is increased by about two times the thermal stress of rock masses. In addition, vertical stresses do not change. If the stress measured by hydraulic fracturing in a high geo-temperature environment is directly used for rockburst prediction, the estimated grade of rockbursts is high when horizontal in-situses are greater than vertical in-situ stresses, and the predicted position of rockbursts is inconsistent with reality when horizontal in-situ stresses are between gravitational stresses and vertical in-situ stresses. In addition, the estimated grade of rockbursts is low when horizontal in-situ stresses are less than gravitational stresses. The thermal stress of rock masses for the Sangzhuling tunnel is about 61% of the gravitational stress of rock masses. The rockburst prediction can lead to serious errors if the thermal stress is not considered.
-
Key words:
- high geo-temperature /
- rock burst /
- thermal stress /
- geothermal gradient /
- hydraulic fracturing
-
图 1 水压致裂应力测量的力学模型
Figure 1. Mechanical model of hydraulic fracturing stress measurement
图 2 垂直应力不考虑岩体热应力的圆形隧道计算模型
Figure 2. Calculated model of a circular tunnel that vertical stresses do not add the thermal stress of rock masses
表 1 计算参数
Table 1. Calculation parameters
参数 数值 单位 弹性模量 36 GPa 泊松比 v 0.2 重度$\gamma $ 26 kN·m−3 黏聚力 15 MPa 内摩擦角 50 （°） 热膨胀系数$\beta $ 8 × 10−6 ℃−1 导热系数 3.69 W·（m·K）−1 比热容 630 J·（kg·℃）−1 
下载: 导出CSV
-
[1] HE M C, MIAO J L, FENG J L. Rock burst process of limestone and its acoustic emission characteristics under true-triaxial unloading conditions[J]. International Journal of Rock Mechanics and Mining Sciences, 2010, 47(2): 286-298. doi: 10.1016/j.ijrmms.2009.09.003 [2] 李天斌,潘皇宋,陈国庆,等. 热-力作用下隧道岩爆温度效应的物理模型试验[J]. 岩石力学与工程学报,2018,37(2): 261-273.LI Tianbin, PAN Huangsong, CHEN Guoqing, et al. Physical model tests on thermo-mechanical effects in rockbursts around tunnels[J]. Chinese Journal of Rock Mechanics and Engineering, 2018, 37(2): 261-273. [3] 严健,何川,汪波,等. 雅鲁藏布江缝合带深埋长大隧道群岩爆孕育及特征[J]. 岩石力学与工程学报,2019,38(4): 769-781.YAN Jian, HE Chuan, WANG Bo, et al. Inoculation and characters of rockbursts in extra-long and deep-lying tunnels located on Yarlung Zangbo suture[J]. Chinese Journal of Rock Mechanics and Engineering, 2019, 38(4): 769-781. [4] CHEN G Q, LI T B, ZHANG G F, et al. Temperature effect of rock burst for hard rock in deep-buried tunnel[J]. Natural Hazards, 2014, 72(2): 915-926. doi: 10.1007/s11069-014-1042-6 [5] 苏国韶,陈智勇,尹宏雪,等. 高温后花岗岩岩爆的真三轴试验研究[J]. 岩土工程学报,2016,38(9): 1586-1594. doi: 10.11779/CJGE201609005SU Guoshao, CHEN Zhiyong, YIN Hongxue, et al. True triaxial tests on rockburst of granite after high temperatures[J]. Chinese Journal of Geotechnical Engineering, 2016, 38(9): 1586-1594. doi: 10.11779/CJGE201609005 [6] AKDAG S, KARAKUS M, TAHERI A, et al. Effects of thermal damage on strain burst mechanism for brittle rocks under true-triaxial loading conditions[J]. Rock Mechanics and Rock Engineering, 2018, 51(6): 1657-1682. doi: 10.1007/s00603-018-1415-3 [7] 王庆武,巨能攀,黄健,等. 桑珠岭特长隧道初始地应力场反演分析[J]. 科学技术与工程,2016,16(25): 137-143. doi: 10.3969/j.issn.1671-1815.2016.25.023WANG Qingwu, JU Nengpan, HUANG Jian, et al. Regression analysis of initial geostress field of sangzhuling super-long tunnel[J]. Science Technology and Engineering, 2016, 16(25): 137-143. doi: 10.3969/j.issn.1671-1815.2016.25.023 [8] 于学馥, 郑颖人, 刘怀恒, 等. 地下工程围岩稳定分析[M]. 北京: 煤炭工业出版社, 1983: 51-52. [9] 郑颖人, 朱合华, 方正昌, 等. 地下工程围岩稳定分析与设计理论[M]. 北京: 人民交通出版社, 2012: 17-21 [10] 岑衍强, 侯祺棕. 矿内热环境工程[M]. 武汉: 武汉工业大学出版社, 1989. [11] 蔡美峰, 乔兰, 李华斌. 地应力测量原理和技术[M]. 北京: 科学出版社, 1995: 38-40. [12] 周总瑛,刘世良,刘金侠. 中国地热资源特点与发展对策[J]. 自然资源学报,2015,30(7): 1210-1221. doi: 10.11849/zrzyxb.2015.07.013ZHOU Zongying, LIU Shiliang, LIU Jinxia. Study on the characteristics and development strategies of geothermal resources in China[J]. Journal of Natural Resources, 2015, 30(7): 1210-1221. doi: 10.11849/zrzyxb.2015.07.013 [13] 严健,何川,汪波,等. 热力耦合作用下拉林铁路桑珠岭隧道岩爆预测[J]. 西南交通大学学报,2018,53(3): 434-441. doi: 10.3969/j.issn.0258-2724.2018.03.002YAN Jian, HE Chuan, WANG Bo, et al. Prediction of rock bursts for sangzhuling tunnel located on Lhasa-Nyingchi railway under coupled thermo-mechanical effects[J]. Journal of Southwest Jiaotong University, 2018, 53(3): 434-441. doi: 10.3969/j.issn.0258-2724.2018.03.002 [14] 李天斌, 孟陆波, 王兰生. 高地应力隧道稳定性及岩爆、大变形灾害防治[M]. 北京: 科学出版社, 2016. [15] 吴枋胤,何川,汪波,等. 基于洞壁实测信息的FA-PP岩爆预测模型应用研究[J]. 中国公路学报,2020,33(11): 215-225. doi: 10.3969/j.issn.1001-7372.2020.11.020WU Fangyin, HE Chuan, WANG Bo, et al. Application research of FA-PP rockburst prediction modelfor tunnel walls[J]. China Journal of Highway and Transport, 2020, 33(11): 215-225. doi: 10.3969/j.issn.1001-7372.2020.11.020 -
下载:
点击查看大图
计量
- 文章访问数: 341
- HTML全文浏览量: 143
- PDF下载量: 22
- 被引次数: 0