Numerical Simulation Method for Vertical Vibration of Heavy Vehicle-Expansion Joint Coupled System
-
摘要:
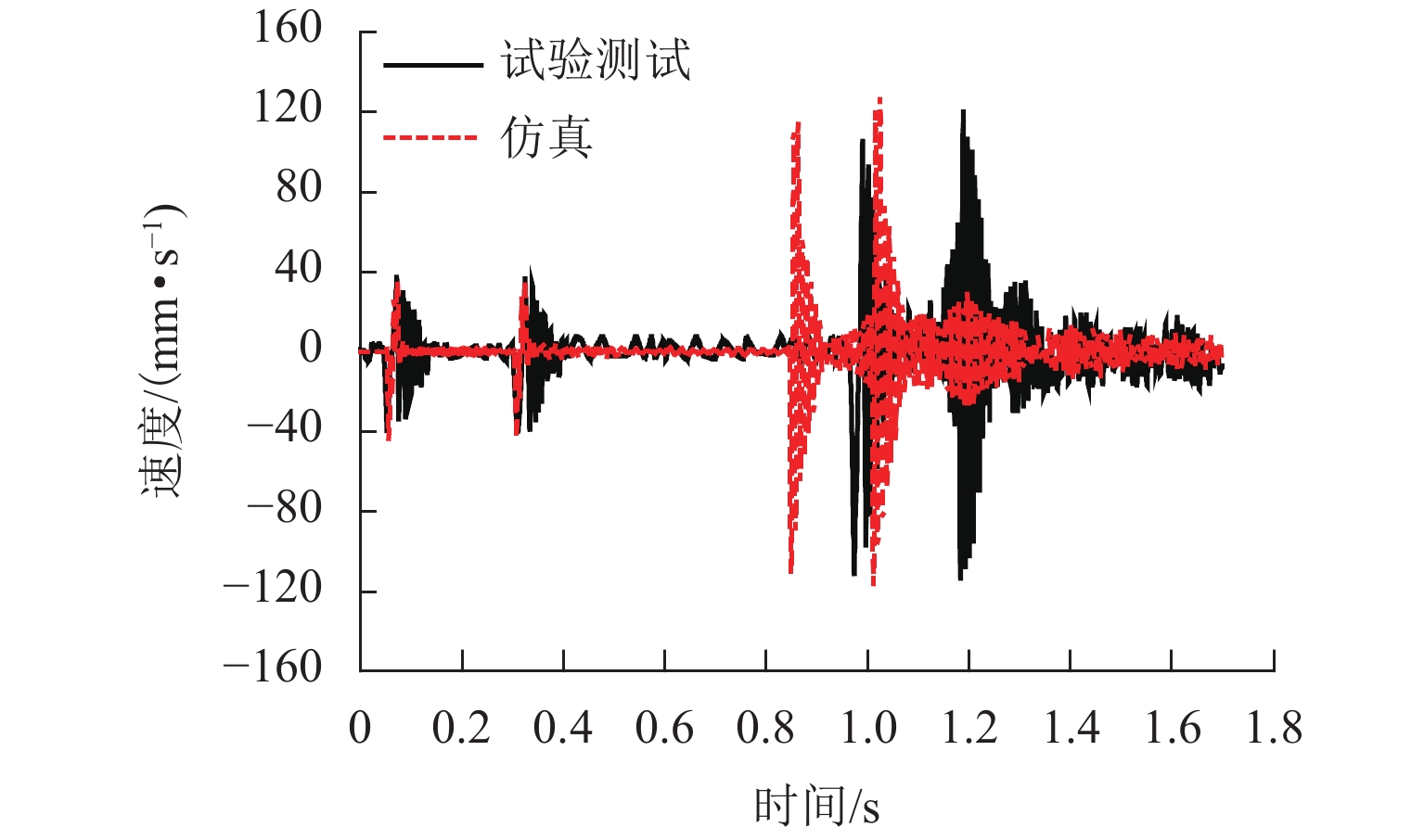
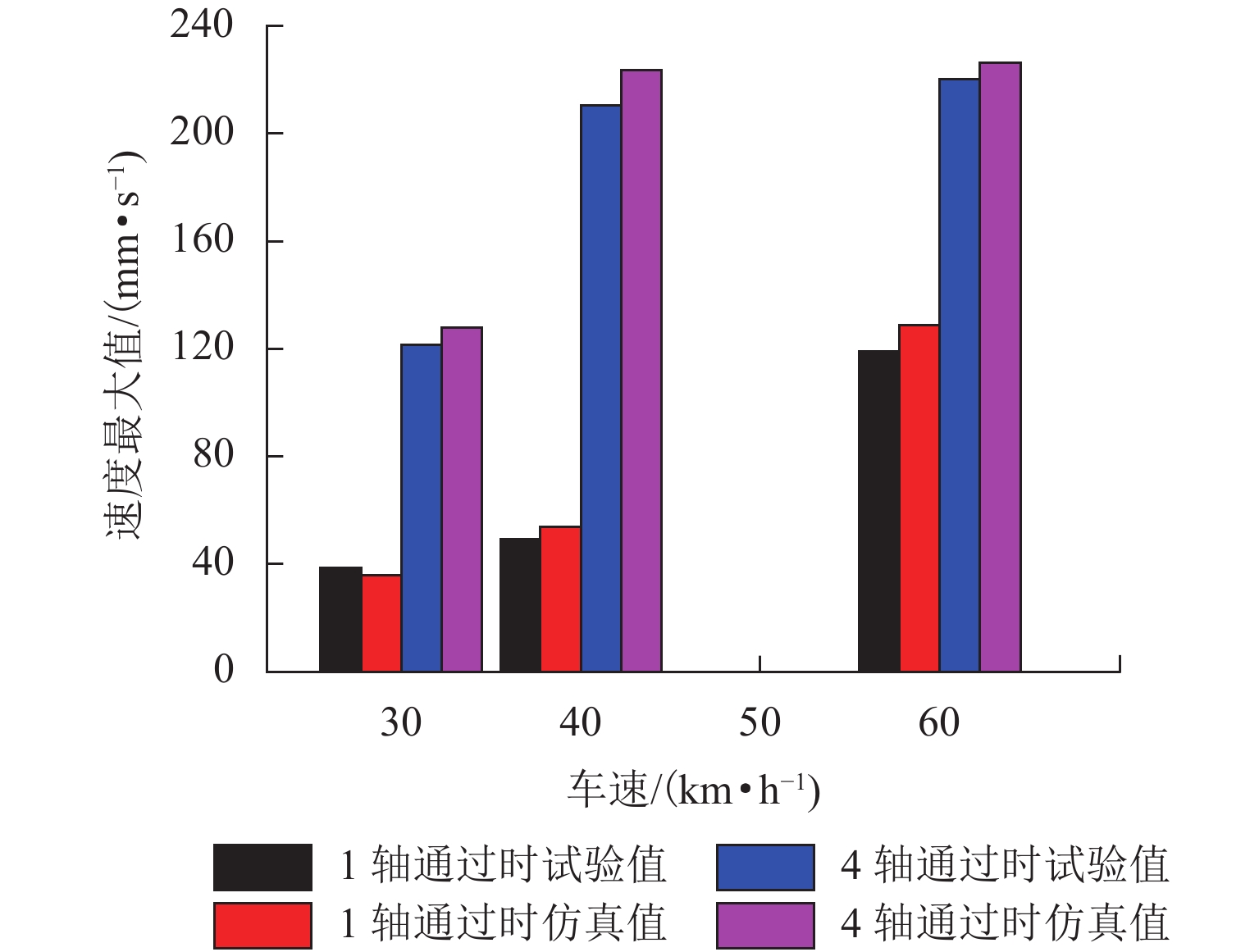
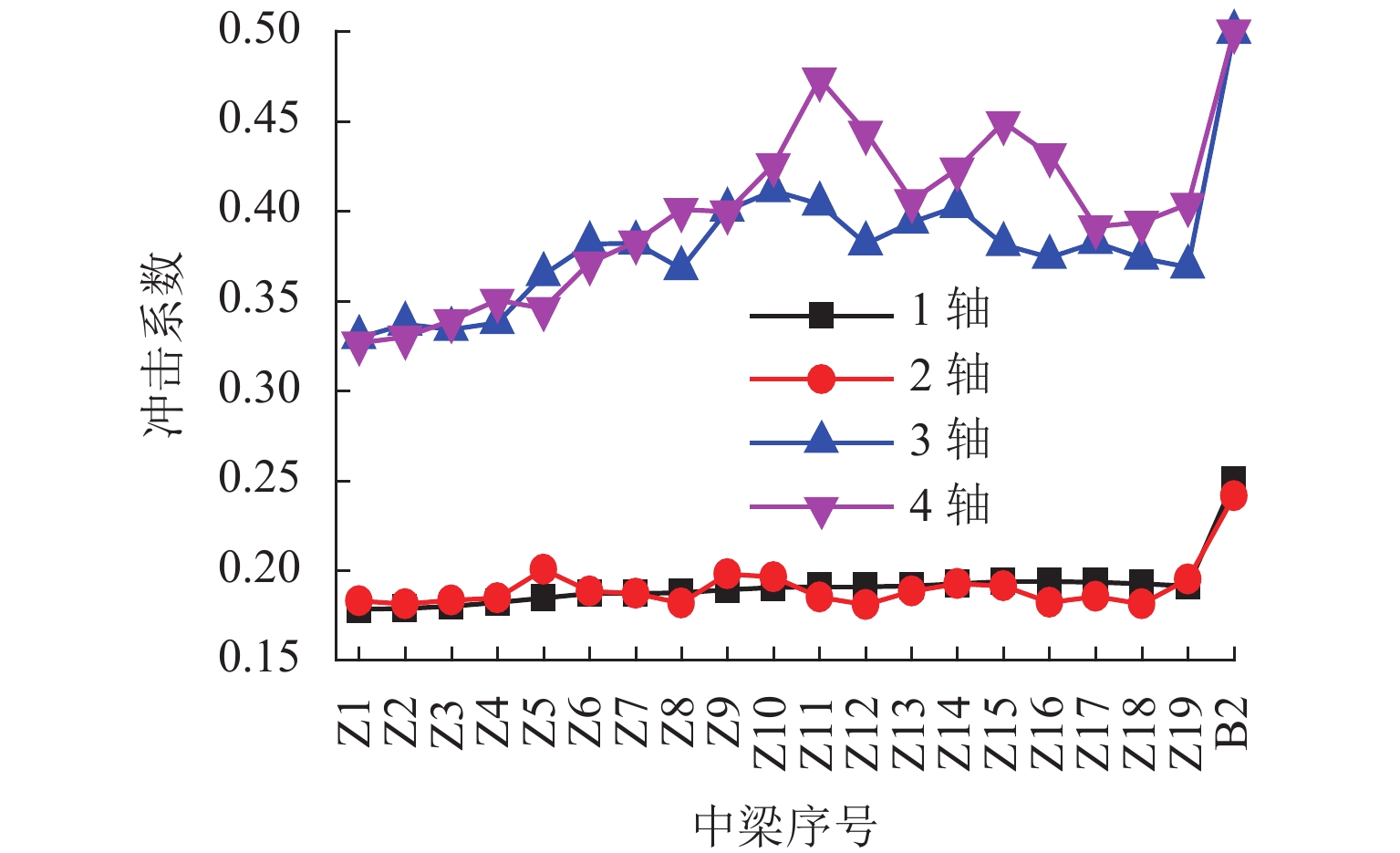
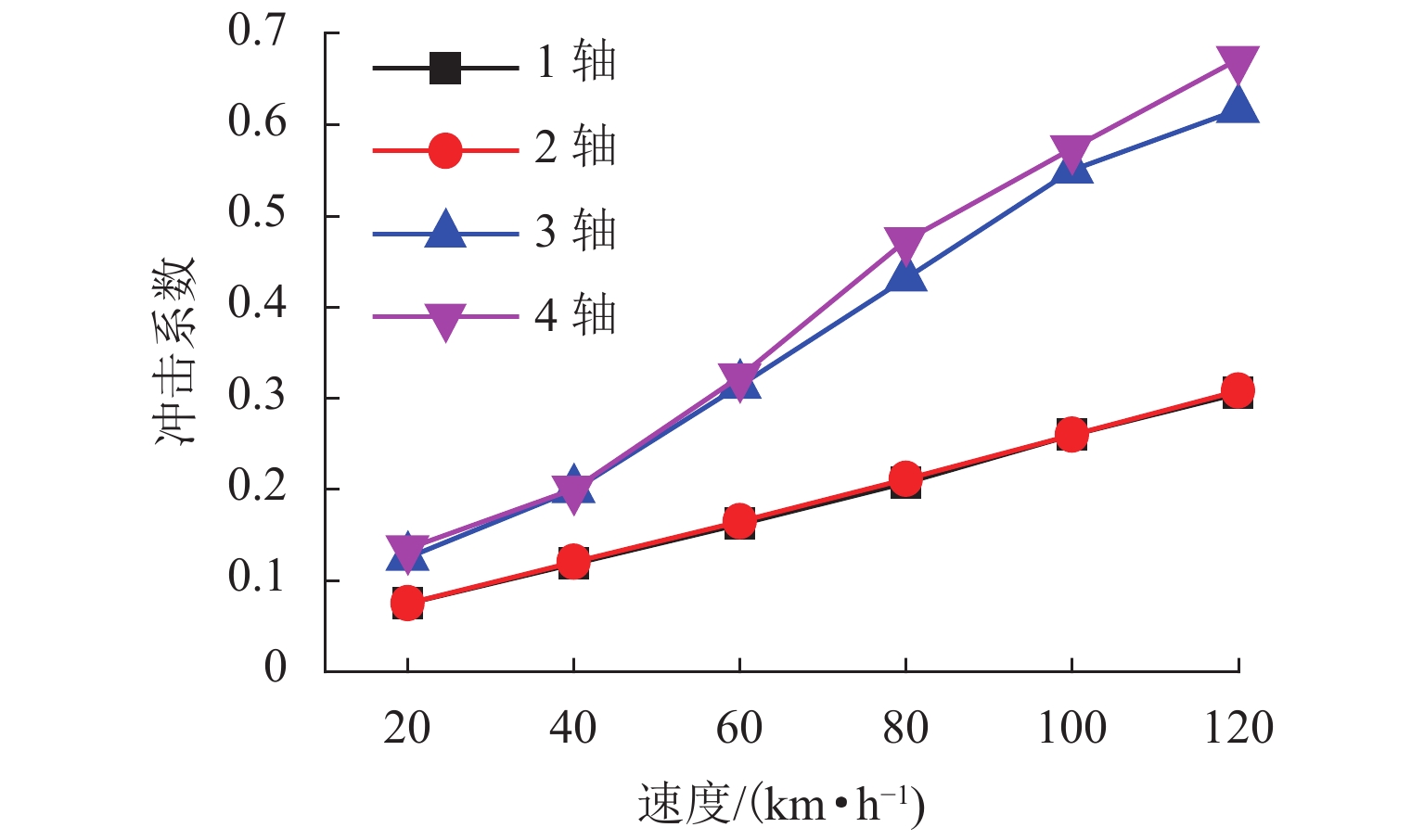
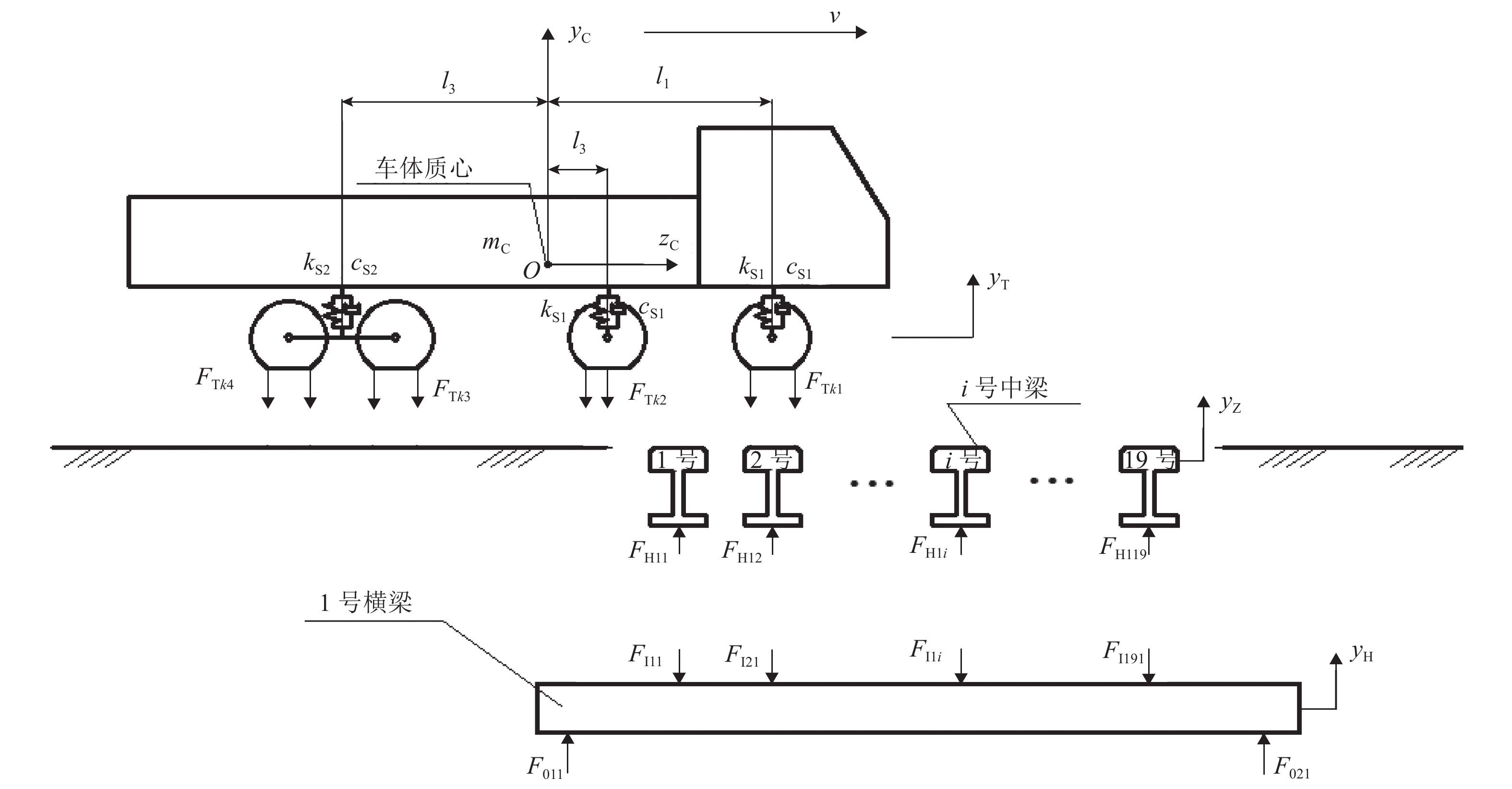
为研究车辆对大位移伸缩缝振动特性的影响，考虑轮胎载重车辆过大位移桥梁伸缩缝时的真实激励特性，提出了一种载重车辆-伸缩缝耦合系统垂向动力学模型，同时引入新型快速积分法对数值模型进行求解. 以ZL1600模数式大位移伸缩缝为研究对象，通过仿真结果与试验测试结果的对比验证模型有效性，并基于此模型分析了轮胎载重车辆对大位移伸缩缝的冲击效应. 研究结果表明：中梁测点垂向速度的动力学模型仿真结果能较好地匹配试验测试结果，仿真得到中梁测点最大下沉位移的偏差均小于10.0%，表明该模型具有较高的计算精度；车辆轮胎力的最大冲击系数出现在车轮驶上伸缩缝后方桥面时，需要考虑对此处结构进行加强；车辆轮胎对伸缩缝中梁和后方桥面的冲击系数均随车速的增大而增大，最大冲击系数分别为0.67和0.82，均超过了国内现行规范的推荐值0.45，应得到重视.
Abstract:To study the influence of vehicles on vibration characteristics of large displacement expansion joints, a vertical dynamic model of heavy vehicle-expansion joint coupled system is established, considering the real load characteristics of a wheeled heavy vehicle when passing a large displacement bridge expansion joint. The new fast integration method is introduced to solve the numerical model. Taking ZL1600 modular large displacement expansion joint as the research object, the validity of the model is verified by comparing simulation results with test results. Based on the model, the impact effect of wheeled heavy vehicle on expansion joint is analyzed. The results show that the dynamic model simulation results of vertical velocity at the center beam test points can be well matched with the test results. The deviations of center beam maximum sinking displacements between simulation results and test results are less than 10.0%, which indicates that the model has high calculation accuracy. The maximum impact factor of tire loads occurs when the wheel drives on the bridge deck behind the expansion joint. Therefore, it is necessary to strengthen the nearby structure. The impact factor of tire loads on the center beams and the rear bridge deck increases with speed. The maximum impact factors are 0.67 and 0.82 respectively, both exceeding the recommended value of 0.45 in the current Chinese standard. It should be given more attention.
-
Key words:
- vehicles /
- expansion joints /
- numerical simulation /
- experimental verification /
- coupled vibration
-
岩体是经过漫长地质作用形成的具有稳定外形的固态集合体，岩石自人类文明诞生以来便是人类生存的重要环境之一. 在当代，岩体作为一种工程介质，是采矿、土木建筑、路桥、地下工程等学科及领域重点研究的对象，这些领域中岩体工程的稳定和安全，与绿色宜居环境以及经济建设息息相关.
岩体工程相关的设计、施工、稳定性评价及灾害处治等均直接依赖于对岩体强度、变形、渗透性、破坏规律等特征的研究. 岩体强度、变形以及破裂特征是岩土工程研究的核心问题. 岩石因其特有的组成成分与所处的特定地质环境，其构造上呈现出高度的非连续性、非均匀性和各向异性，在力学性质上也表现出强烈的非线性、非弹性和黏滞性. 随着科技的进步发展，对岩石力学行为的研究与认识不断加深，采用的分析方法历经理想弹塑性介质、连续弹塑性介质、非连续介质模型等，目前离散元分析方法[1-3]已经基本成熟，成为研究岩石力学行为、完善岩石力学基础理论的重要工具之一[4-7]，并已初步应用于工程领域各类复杂现象的机制研究[8-10].
颗粒离散元方法将介质整体离散为圆盘形或球形颗粒单元进行分析，不受变形量限制，可方便地处理非连续介质力学问题，可有效模拟介质的开裂、分离等非连续现象. 颗粒离散元法可通过设置不同大小颗粒、随机颗粒簇以及不同规律分布的接触强度来构建非均匀性介质模型，也可通过离散裂隙网络技术（discrete fracture network，DFN）设置不同产状及密度的节理，从而体现岩体的各向异性.
颗粒离散元法作为研究岩石材料物理力学性质及破坏机制的有效方法，是近年来比较热门的一种数值模拟研究方法，但其有着较高的计算要求. 当进行室内岩石力学试验模拟时，为提高模拟的精确度需要将颗粒尺寸设置为极小，但颗粒总数过大会导致计算速度十分缓慢. 目前，颗粒离散元法在工程中的大规模应用相对较少，主要原因之一便是构建大型岩体模型所需颗粒数量较多，迭代计算量超出一般计算机能力范围[11].
因此，本文提出一种基于颗粒离散元的分层建模法，针对分层建模法存在的关键问题（尺寸效应问题）进行单轴抗压、巴西劈裂试验，并对试验相关内容进行分析、讨论，探究分层建模法模拟室内力学试验的可行性.
1. 分层建模法中的关键问题
分层建模方法，即对岩石试样裂纹主要扩展区域、岩体破坏大变形区域或关注区域采用小尺寸颗粒进行精细化模拟，外侧非破坏或非关注区域采用大尺寸颗粒建模以扩大计算区域. 图1为采用分层建模法构建含预制裂隙单轴压缩模型示意，在预制裂隙及裂纹扩展区域采用小颗粒填充，可得到更准确的裂纹连续发展轨迹.
分层建模法能够成功计算的关键在于各层颗粒构建的材料力学性质相同. 颗粒离散元法中模型宏观力学性质由材料细观参数决定，因此，各层颗粒需设置同种接触模型，并且颗粒及接触的各细观参数应相同（粒径除外）.
大多数基于颗粒离散元法的研究都是根据试验需求或计算机能力和效率来选择模型尺寸及细观结构特征（主要是颗粒尺寸和尺寸分布），而没有研究这些对最终结果的影响. 然而，一些研究表明，模型的细观结构特征对颗粒流模拟结果有着显著影响[12-14]. Ding等[15]开展了多组不同颗粒尺寸的三维单轴压缩模拟，重点分析了单轴抗压强度、弹性模量和泊松比的变化规律，并给出了颗粒与模型尺寸比的建议；Xu等[16]通过三维巴西劈裂模拟认为，颗粒尺寸以及尺寸分布的非均匀性对巴西劈裂强度以及变异系数具有一定的影响.
因此，分层建模法中各区域平均粒径的不同，也就是细观结构的不同，是否导致计算结果与常规建模法计算结果出现差异、计算结果离散程度是否变大、破裂模式是否发生变化，是分层建模法成功应用需解决的一个关键问题.
2. 单轴压缩试验及颗粒尺寸效应分析
2.1 模拟方案设计及参数选取
采用分层建模法与常规建模法分别构建室内单轴压缩试验模型，如图2所示，圆柱的直径D = 50 mm，高H = 100 mm. 因含孔、结构面或其他类型缺陷的岩石试样、岩体工程尺度的研究中，缺陷大多设置在试样中央，故单轴压缩试验模型中内层设置在中央有利于研究完整试样分层模型的力学性质，匹配宏观力学性质，进而开展更多研究. 内层模型形状与模型整体形状相同，避免因力不均匀传递造成的结果误差. 内层模型高度与直径均设为模型整体的一半，是为了方便计算内外层体积比.
颗粒间接触模型统一采用三维平节理接触模型（flat-joint model 3D，FJM3D）[17-18]，FJM3D的接触力学行为通过抽象面之间的等体积单元描述，单元类型分3种（类型B、类型S和类型G）并表示不同的接触状态，且FJM3D还植入了与应力相关的剪切强度. 因此，FJM3D在研究脆性岩石破裂机制方面具有一定的优势. 需要提及的是，通常模型中颗粒间是否可以赋予黏结取决于安装间距g，g ≤g'mean(dA,dB)，其中：g' 为一定值；mean(•)为均值函数；dA、dB分别为任意颗粒A、B的粒径. 采用分层建模法时，这种安装间距的设定存在问题，层与层交界处粒径差值较大，定值g' 无论设置何值都会影响颗粒间自锁效应，进而使模型实际强度非均匀. 故引入文献[18]提出的安装间距比gratio，即g＝gratio min{dA,dB}，gratio的范围是(0, dmin/dmax)，其中， dmin和dmax分别为最小和最大粒径.
接触细观力学参数需满足模型宏观力学参数与试样力学性质相匹配. 细观参数的调试原则是优先匹配影响参数少、敏感度低的宏观参数. 对于FJM3D，Wu等[18]通过对锦屏大理岩的校核调试过程和前期参数敏感性分析结论的总结，提出了一套完善的校核方法. 该方法首先考虑岩石的抗压-抗拉强度比、内摩擦角和应力-应变曲线峰后行为，然后再匹配变形属性和强度参数，具体调试步骤详见文献[18].
经室内岩石力学试验测得的试样宏观力学参数包括：单轴抗压强度47.64 MPa，弹性模量29.13 MPa，泊松比0.2，巴西抗拉强度2.06 MPa，是具有高压拉比的典型脆性岩石. 最终，通过采用颗粒平均直径d = 2.00 mm、dmax/dmin = 1.66的常规模型进行参数调试，采用表1所示的接触细观力学参数可得到与试样相匹配的宏观力学参数.
表 1 FJM3D各细观力学参数取值Table 1. FJM3D meso-mechanical parameters细观力学参数 数值 安装间距比 gratio 0.3 类型 B 单元比例 φB 0.9 类型 S 单元比例 φS 0.1 接触单元数 N/个 3 颗粒的有效模量 Ec/GPa 30 黏结的有效模量¯Ec/GPa 30 颗粒的法向与切向刚度比 kn/ks 1.9 黏结的法向与切向刚度比¯kn/¯ks 1.9 摩擦系数 μ1 0.3 黏结张拉强度平均值和标准偏差 σb/MPa 3.5, 0 黏结内聚力平均值和标准偏差 cb/MPa 36, 0 摩擦角 Фb/ （°） 10 Ding等[15]认为，在一定的粒径比dmax/dmin下，模型分辨率L/d （试样的最小尺寸L与d的比值）对单轴抗压强度σucs、弹性模量E和泊松比μ均有影响，但此影响在L/d超过一定量时会变小. 所以，在进行分层模型与常规模型对比前，首先需确定模型粒径设置范围. 对dmax/dmin均为1.66，不同L/d的5组常规模型进行计算，每组包含5种不同的颗粒排列. 经计算得到，L/d分别为10.00、12.50、16.70、20.00、25.00的5组常规模型σucs平均值分别为35.91、40.41、43.96、45.38、47.23 MPa，E平均值分别为28.58、28.64、28.79、28.98、29.02 GPa，μ平均值分别为0.186、0.188、0.189、0.193、0.193. 可见L/d小于16.70时，常规模型的各力学参数受较颗粒尺寸效应影响较大，对探究分层模型的颗粒尺寸效应已无太大对照意义.
所以共设计6组试验，包括L/d分别为16.70、20.00、25.00的3组常规模型以及3组分层模型，分层模型的内外层平均粒径两两对应3组常规模型. 常规模型采用5个随机种子数生成5种不同的颗粒排列，分层模型采用10个随机种子数生成10种不同的颗粒排列，模型材料密度为2 690 kg/m3. 常规模型以及分层模型内、外层颗粒的最大与最小粒径比dmax/dmin均为1.66，颗粒尺寸均匀分布，各组模型粒径设置如表2所示.
表 2 单轴压缩模型粒径设置Table 2. Particle size setting for uniaxial compression model模型 组号 dmin/mm dmax/mm d
/mmL/d 备注 常规 1 1.50 2.50 2.00 25.00 2 1.88 3.12 2.50 20.00 3 2.26 3.74 3.00 16.67 分层 4 1.50 2.50 2.00 25.00 内层 1.88 3.12 2.50 20.00 外层 5 1.50 2.50 2.00 25.00 内层 2.26 3.74 3.00 16.67 外层 6 1.88 3.12 2.50 20.00 内层 2.26 3.74 3.00 16.67 外层 2.2 模拟结果分析
对模型进行单轴压缩模拟，比较常规模型与分层模型的应力-应变曲线、单轴抗压强度σucs、起裂应力σcis和弹性模量E，以及这些宏观力学参数的离散程度，以此分析分层模型受颗粒尺寸效应的影响. 数据的离散程度以变异系数（coefficient of variation, COV）为衡量标准.
2.2.1 应力-应变曲线
分别从第1、3、5组模型中抽取1个模型，导出其单轴加载应力-应变曲线进行对比. 从图3中可看出：在弹性变形阶段、微弹性裂隙稳定发展及累进性破裂阶段、峰后阶段，分层模型的应力-应变曲线变化趋势与常规模型基本一致，峰前无局部峰值点，峰后表现出相同的脆性特征. 3个模型弹性阶段斜率基本相同. 分层模型峰值强度与外层粒径对应的常规模型接近，而相比内层粒径对应的常规模型减少了6.6%. 整体上，分层模型单轴抗压强度与弹性模量的变化在离散元尺寸效应[12, 15]可解释的范围内.
图 3 分层模型与常规模型应力-应变曲线对比Figure 3. Comparison of stress-strain curves between layered model and conventional model2.2.2 单轴抗压强度
6组模型的单轴压缩强度σucs计算结果如图4所示.
从图4（a）可看出：在常规模型中，σucs随着平均粒径的增大而减小，最小值与最大值相比减小6.9%，这与Potyondy等[12]、Ding等[15]的研究结论相同. 在分层模型中，σucs同样随着平均粒径的增大而减小. 横向对比可以发现，第4组分层模型的σucs更接近平均粒径为2.50 mm （第4组外层平均粒径）的第2组常规模型，而不是平均粒径为2.00 mm （第4组内层平均粒径）的第1组常规模型. 第5组、第6组分层模型的σucs结果也表现了相同的规律. 由图2分层模型内层区域尺寸设置可知，内外层体积比为13 : （23−1）＝1 : 7，所以分层模型的实际σucs更接近体积更大的外层模型，而不是组成颗粒密度更大的内层模型. 第4 ~ 6组分层模型σucs与外层平均粒径对应的常规模型相比，最多仅减小2.7%，从FJM3D的角度来看，大粒径模型的接触数量较少，单个接触承受的应力相比小粒径模型中的接触更大，在接触强度相同的条件下，大粒径模型中的接触在加载过程中会首先发生断裂，并且更快达到峰值应力. 在分层模型中，外层区域中接触会像大粒径模型一样提前发生破裂，且因外层区域体积较大，故而峰值强度与大粒径模型接近. 但内层区域小颗粒间的接触发生断裂较外层区域更慢，使峰值应变增加，所以，分层模型的峰值应变与内层对应的小粒径模型接近，如图3所示.
所以在匹配分层模型的单轴抗压强度时，建议以外层对应的常规模型作参照，也就是先采用大粒径模型进行参数匹配，再构建分层模型进行微调，这样比直接构建分层模型进行参数匹配效率更高.
从图4（b）可看出：在常规模型中，单轴抗压强度的COV随着平均粒径的减小而减小，并可能收敛到一特定值. 在分层模型中单轴抗压强度的COV无明显规律，但均比第3组常规模型单轴抗压强度的COV大. 这是因为COV体现的是模型中颗粒组装排列的不同以及材料强度的非均匀性，只有模型中颗粒的数量足够多，才能减弱这些影响，得到较为一致的σucs. 在分层模型中，内外层交界的存在使局部颗粒组装排列更具多样性，材料强度的非均匀性比常规模型更强. 所有分层模型的COV均小于2.00%，属于可以接受的范围.
2.2.3 起裂应力
6组模型的起裂应力σcis计算结果如图5所示.
图5（a）中常规模型、分层模型的σcis呈现出与单轴抗压强度σucs相同的规律，即σcis随着平均粒径的增大而减小. 常规模型σcis最小值与最大值相比减小了5.1%. 每组分层模型σcis略小于其外层平均粒径对应的常规模型，最多仅减小1.9%. 虽然室内单轴抗压试验测得的σucs受外部加载条件（加载速率、加载设备刚度等）影响较大，但在模拟中加载条件完全稳定不变，多次加载、以相同标准测得的σucs与σcis可视作相同细观参数下材料的稳定属性，所以，σcis与σucs在相同的粒径变化下会呈现相同的规律. 从接触模型的角度，同样是因为大粒径对应的接触承受更大的应力，外层区域中接触会像大粒径模型一样在加载过程中更快发生断裂.
图5（b）中常规模型起裂应力的COV随着平均粒径的增大而增大，分层模型起裂应力的COV均比外层平均粒径对应起裂应力的COV大，这也是由于分层结构的存在，颗粒呈不同排列方式的分层模型内部强度非均匀性更大. 起裂应力的COV最大仅为1.54%，可认为各组测得起裂应力的COV都很精确.
2.2.4 弹性模量
6组模型的弹性模量E计算结果如图6所示.
从图6（a）中可看：出6组E的差别极其微小，在常规模型中，E随着平均粒径的增大而减小，但最小值与最大值相比仅减小0.8%，远小于σucs的6.9%. σucs的变化值大于E是合理的，因为σucs涉及到大量的颗粒相互作用以及破裂形成，而E衡量的是模型在发生任何重大破裂之前的可变形性. 分层模型的E与外层对应的常规模型相比减小了1.3% ~ 2.3%，说明常规模型在弹性阶段抗变形性略强于分层模型，这也是由于颗粒尺度非均匀性而产生[15].
图6（b）中常规模型弹性模量的COV的变化规律与σucs、σcis相同，分层模型弹性模量的COV也随着平均粒径的增大而增大，总体弹性模量的COV均小于1.00%，可认为数据精确度较高.
3. 巴西劈裂试验及颗粒尺寸效应分析
3.1 模拟方案设计及参数选取
采用分层建模法与常规建模法分别构建巴西劈裂试验圆盘模型，圆盘厚度为 25 mm，直径为 50 mm. 大量的巴西圆盘试验及模拟结果表明[19-20]，试样的破裂集中在过圆心加载方向上. 在巴西劈裂模拟试验中，圆盘试样表面，特别是与加载板接触部位的光滑度，对计算结果有很大的影响[21]，减小颗粒尺寸，可以相对改善圆盘试样表面光滑度. 所以，巴西劈裂圆盘分层模型按图7所示设置.
共设计7组试验，分别为4组常规模型以及3组分层模型，每组采用10个随机种子数生成10种不同的颗粒排列，模型材料密度为2 690 kg/m3. 常规模型的最小分辨率参考Xu等[16]的建议，最低为16.7，也就是最大平均粒径为3.00 mm. 由于巴西劈裂加载用时较短，且圆盘模型尺寸较小，可容纳颗粒数更多，所以将常规模型中最小平均粒径设为1.50 mm，分层模型中内层颗粒平均直径一律设为1.50 mm. 常规模型以及分层模型内、外层颗粒的最大与最小粒径比均为1.66，颗粒尺寸均匀分布，各组模型粒径设置如表3所示. 颗粒间接触接触细观力学参数见表1.
表 3 巴西劈裂模型粒径设置Table 3. Particle size setting for Brazilian splitting model模型 组号 dmin/mm dmax/mm d/mm L/d 备注 常规 1 1.13 1.87 1.50 33.33 2 1.50 2.50 2.00 25.00 3 1.88 3.12 2.50 20.00 4 2.26 3.74 3.00 16.67 分层 5 1.13 1.87 1.50 33.33 内层 1.50 2.50 2.00 25.00 外层 6 1.13 1.87 1.50 33.33 内层 1.88 3.12 2.50 20.00 外层 7 1.13 1.87 1.50 33.33 内层 2.26 3.74 3.00 16.67 外层 3.2 加载设置
在平板加载条件下，加载板宽度是影响巴西劈裂试验结果的重要外部因素. 2016年，Xu等[16]将加载板设置为不同宽度进行巴西劈裂试验，分析应力-应变曲线，认为当加载板宽度小于平均粒径时，会使加载板与颗粒之间产生不充分接触，导致应力-应变曲线表现出低弹性模量，峰值应力相对较小，且出现局部峰值点；当加载板宽度大于平均粒径时，应力-应变曲线峰后在应力降至峰值应力约1/3处表现为延性特征，与室内试验结果不符. Xu等[16]建议将加载板宽度设为与平均粒径相等，然而，如此设置仍会有颗粒粒径大于加载板宽度，使加载板与颗粒之间产生不充分接触.
对第1组常规模型进行巴西劈裂加载，加载板宽度分别设为1.50 mm （平均粒径）和1.87 mm （最大粒径），测得的巴西劈裂抗拉强度σbt平均值分别为1.95 MPa和2.02 MPa，变异系数COV分别为3.86%、2.04%. 加载板宽度为1.50 mm时峰值应力较小，是因为在不同的颗粒排列下，与加载板接触的颗粒直径不同，当颗粒直径大于平均粒径，加载板与颗粒之间也会产生不充分接触. 加载板宽度为1.50 mm时COV较大，正说明测得的σbt存在不稳定性.
据以上分析，在各组常规模型进行巴西劈裂模拟时将加载板宽度设为与最大粒径相同，在各组分层模型进行模拟时将加载板宽度设为与内层最大粒径相同.
3.3 模拟结果分析
3.3.1 巴西劈裂抗拉强度
7组模型的巴西劈裂抗拉强度σbt计算结果如图8所示. 图8（a）中，常规模型σbt随平均粒径的增大而增大，最大值相比最小值的增加幅度为1.98%. σbt与σucs呈现出不同的规律，是因为Ⅰ型断裂韧度
KⅠc 与抗拉强度呈正向线性关系[22]，而KⅠc 和颗粒尺寸呈正相关[12]. 分层模型σbt虽然也是随着平均粒径的增大而增大，但超过了外层平均粒径对应的σbt，如第5组分层模型σbt超过了外层平均粒径2.00 mm对应的第2组常规模型，但第5组模型的平均粒径要小于第2组模型，这一点无法依据断裂韧度来解释. 3组分层模型σbt与其外层平均粒径对应的常规模型相比，分别增加了1.32%、2.35%、1.50%，虽然增加幅度不大，但在分层建模测定模型σbt时要考虑到这一影响.从接触模型的角度也可以解释常规模型σbt随平均粒径的增大而增大. 因为粒径较大时，接触的破裂可能不会沿着实际的宏观破裂轨迹扩展，而是因大颗粒的存在，接触的破裂角（破裂与加载方向的夹角）产生了一定的偏差. 需要更大的加载力才能使破裂贯通整个模型. 从接触模型的角度同样无法解释分层模型σbt大于其外层对应的常规模型σbt，此问题需要度进一步探究. 但是在匹配分层模型的σbt时，也可以外层对应的常规模型作参照，也就是先采用大粒径模型进行参数匹配，再构建分层模型进行微调. 因为，分层模型σbt相对外层对应的常规模型σbt增幅较小.
图8（b）中，平均粒径为1.50 mm和2.00 mm的常规模型，其巴西抗拉强度的COV基本相同，但平均粒径超过2.00 mm巴西抗拉强度的COV会有较大的增加，最大达到了5.15%. 可以说随着平均粒径的减小，巴西抗拉强度的COV有收敛的趋势. 分层模型抗拉强度的COV较小，与小粒径常规模型COV接近. 所以从变异系数的角度看，采用分层建模法测模型σbt是可行的.
3.3.2 宏观破裂特征
为探究分层模型与常规模型巴西劈裂试验宏观破裂是否存在较大差别，从平均粒径相差最大的第1组（d = 1.50 mm）、第4组（d = 3.00 mm）以及对应的分层模型第7组中各选择一种排列方式进行加载. 加载至峰后阶段峰值强度的60%时，试样宏观破裂情况如图9所示.
从图9中可以看出：与d = 1.50 mm的模型相比，d = 3.00 mm的模型宏观破裂带较宽. 这是因为在加载至峰值强度后，粒径小的模型裂纹延伸路径受颗粒影响较小，会迅速延伸至贯通，峰后阶段应力也会迅速下降. 而具有较大直径的颗粒会影响裂纹的延伸，应力最大、最易开裂处是颗粒而不是颗粒间的接触，裂纹延伸方向发生改变，应力-应变曲线在峰后历经几个局部峰值点后才会彻底下降. d = 1.50 mm的常规模型与分层模型宏观破裂基本相同，均呈“中间细，两头粗”的特征，但分层模型在加载板附近裂纹更多，说明分层模型需在更高的应力条件下，加载板附近发生更大范围宏观破裂后裂纹才能上下贯通. 所以，分层模型的巴西劈裂宏观破裂特征与小粒径常规模型相似，而颗粒数量较少，计算时间较短，也说明了分层建模法在巴西劈裂模拟中具有较高的可行性.
4. 讨 论
以上分析证明了分层模型同常规模型一样存在颗粒尺寸效应，且具有一定的规律. 在计算效率方面，将分层模型与同内层粒径常规模型颗粒数量、计算时长进行对比（表4）. 从表4中可看出：当分层模型外层平均粒径至少超过内层平均粒径0.50 mm时，颗粒数与常规模型相比大量减少，计算时长降低超过50%. 所以，分层建模法可以极大地提升计算效率，降低颗粒离散元法对计算能力的要求.
表 4 分层模型与常规模型颗粒数、计算时长对比Table 4. Comparison of particle number and calculation time between layered model and conventional model模型 d/mm 颗粒数/
个计算
时长/h计算时长
降低率/%单轴
压缩2.00 27 324 9.57 0 2.00（内），2.50（外） 15 721 4.72 50.68 2.00（内），3.00（外） 10 622 2.98 68.86 巴西
劈裂1.50 16 966 5.02 0 1.50（内），2.00（外） 11 085 2.28 54.58 1.50（内），2.50（外） 8 994 2.24 55.38 1.50（内），3.00（外） 8 042 2.13 57.57 通过试验与对比证明了分层建模法的有效性与高效性，但仍存在一些需要完善的问题：
1） 常规建模时模型需要的颗粒数是由孔隙率决定，生成颗粒后经过循环计算、调整使颗粒减少重叠并充满整个模型. 而分层建模时，先按照相同的孔隙率在不同区域生成不同粒径的颗粒，在循环计算、调整时区域界面处会有个别小颗粒移动至大颗粒区域，这样最终生成的模型孔隙率与最初设置的孔隙率存在细微差别，而孔隙率对模型试验结果也存在一定的影响. Ding等[15]认为，随着粒径非均匀性或dmax/dmin的增加，模型孔隙率降低，模型会有更高的σucs. 所以，在建模后需重新测定孔隙率，选择具有相同孔隙率的模型进行计算、分析.
2） 本文是分层建模法应用于小尺寸力学模拟中的可行性初探，文中分层模型外层颗粒平均粒径最大设置为内层平均粒径的2倍，在此条件下得到的分层模型计算结果是准确可接受的，但关于内外层粒径差对模型宏观力学参数的影响只是做了定性分析. 由颗粒离散元模型生成原理可知，相邻两层粒径差距不能过大，否则会使模型重叠率过高而难以达到力学平衡. 分层模型内外层颗粒粒径差最大可达何值，超过该值会发生怎样的现象，也是需要探究的一个问题. 只有解决这一问题，才能将分层建模法应用于更大尺度的模拟研究中.
3） 分层模型中交界面的存在是其力学属性与常规模型存在较小偏差的重要原因，若将两层之间的交界面附近设为中间层，中间层粒径分布范围小于外层平均粒径、大于内层平均粒径，能否减少局部应力集中，使裂纹在两层之间顺利过渡，此问题值得进一步研究.
在大规模工程尺度试验模拟中应用分层建模法，与室内试验尺度模拟有着同样的思路，首先，采用大颗粒模型进行预试验得到关键区域的方位，然后，在关键区域采用小尺寸颗粒，外侧采用大尺寸颗粒建模. 因相邻两层粒径差不能过大，需要设置多层用以过渡. 需要特别注意的是，工程尺度模拟存在模型尺寸效应，即室内试样匹配得到的细观参数应用于大尺度模型中时，大尺度模型的宏观力学性质会有一定的折减，因此，在校准细观参数时，还需对模型、颗粒的尺寸效应进行综合评估与对比. 图10为采用分层建模法构建的岩体，以及巷道开挖后在内层出现的分区破裂现象，详细研究见文献[10].
5. 结 论
1） 分层建模法与常规建模一样受颗粒尺寸效应影响，但可以减少颗粒流模型中的颗粒数量，极大地提高计算效率，一定程度上可提高各类尺度模拟精度，降低颗粒离散元法对计算能力的要求.
2） 分层模型的单轴抗压强度和起裂应力略小于其外层平均粒径对应的常规模型，匹配单轴抗压强度时可以外层材料常规模型作参照. 单轴抗压强度和起裂应力的变异系数普遍大于常规模型，但依然在可接受范围内.
3） 分层模型中粒径分布的不均匀性对模型弹性阶段的变形性质影响较小，分层模型的弹性模量与常规模型相差不大.
4） 分层模型的巴西劈裂抗拉强度整体略大于常规模型，宏观破裂特征与小颗粒常规模型相似，但在加载板附近有更多的裂纹.
-
图 1 车辆-伸缩缝耦合系统受力分析
Figure 1. Force analysis of the vehicle-expansion joint coupled system
图 4 1号中梁A组测点的速度时程曲线（v = 30 km/h）
Figure 4. Speed time history curves of group A measuring points of No.1 middle beam（v = 30 km/h）
图 5 1号中梁A组测点振动速度最大值对比
Figure 5. Comparison results of maximum speed at group A measuring points of No.1 middle beam
图 6 车辆驶过伸缩缝时轮胎力冲击系数（v = 80 km/h）
Figure 6. Impact factors of tire force when vehicle passing through expansion joint （v = 80 km/h）
图 7 车辆驶上伸缩缝时的最大冲击系数与车速的关系
Figure 7. Relationships between maximum impact factor and speed when vehicle getting on the expansion joint
图 8 车辆驶上桥梁时的最大冲击系数与车速的关系
Figure 8. Relationship between maximum impact factor and speed when vehicle getting on the bridge
表 1 大位移伸缩缝主要结构参数
Table 1. Main structural parameters of large displacement expansion joint
项目 数值 项目 数值 弹性模量 E/GPa 205 泊松比 ν 0.3 材料密度 ρ/（kg·m−3） 7800 缝宽 B/mm 0~80 中梁单位长度质量 mZ/（kg·m−1） 49.33 横梁单位长度质量 mH/（kg·m−1） 315.9 中梁长度 LZ/m 10.2 横梁长度 LH/m 4.2 中梁截面惯性矩 IZ/m4 1.24 × 10−5 横梁截面惯性矩 IH/m4 2.46 × 10−4 中梁、横梁弹性元件刚度/（kN·mm−1） 80 中梁、横梁弹性元件阻尼/（N·s·mm−1） 5 
下载: 导出CSV
表 2 四轴载重车辆动力学参数
Table 2. Dynamic parameters of four-axle vehicle
参数 数值 参数 数值 车体质量 mC/kg 6450 1 轴至车体质心
的距离 l1/m3.327 车体俯仰惯量JCx/（kg·m2） 88327 2 轴至车体质心
的距离 l2/m1.227 车体侧滚惯量JCz/（kg·m2） 17665 后悬架中心至车体质心的距离 l3/m 3.948 后悬架平衡
杆质量 mS/kg200 3、4 轴之间的
距离 l4/m1.35 后悬架平衡杆俯仰惯量 JS/（kg·m2） 380 1、2 轴的轮距
一半 b1/m1.0135 1、2 轴非簧载
的质量 mT1 /kg500 3、4 轴的轮距
一半 b2/m0.93 3、4 轴非簧载
的质量 mT2/kg800 1、2 悬架阻尼
cS1/（kN·s·m−1）25.32 1、2 轴悬架刚
度 kS1 /（kN·m−1）284 后悬架阻尼cS2/（kN·s·m−1） 50.636 后悬架刚度kS2/（kN·m−1） 2064 1、2 轴轮胎阻尼
cT1/（kN·s·m−1）3.5 1、2 轴轮胎刚
度 kT1 /（kN·m−1）1402 3、4 轴轮胎阻尼 cT2/（kN·s·m−1） 7 3、4 轴轮胎刚
度 kT2 /（kN·m−1）2804 轮胎型号 11.00R20-18RP
下载: 导出CSV
表 3 中梁测点最大下沉量对比结果
Table 3. Comparison results of maximum sinking displacement of center beam test points
传感器
位置车速/
（km·h−1）1 号中梁 10 号中梁 13 号中梁 19 号中梁 试验
值/mm仿真
值/mm偏差/
%试验
值/mm仿真
值/mm偏差/
%试验
值/mm仿真
值/mm偏差/
%试验
值/mm仿真
值/mm偏差/
%A 组 30 0.42 0.41 2.4 0.49 0.51 4.1 0.54 0.56 3.7 0.55 0.58 5.5 40 0.50 0.48 4.0 0.56 0.60 7.1 0.58 0.61 5.2 0.64 0.69 7.8 60 0.54 0.51 5.6 0.58 0.59 1.7 0.62 0.65 4.8 0.60 0.64 6.7 B 组 30 0.14 0.13 7.1 0.23 0.24 4.3 0.20 0.21 5.0 0.22 0.21 4.5 40 0.18 0.17 5.6 0.25 0.27 8.0 0.29 0.31 6.9 0.26 0.28 7.7 60 0.20 0.19 5.0 0.29 0.31 6.9 0.31 0.30 3.2 0.23 0.25 8.7
下载: 导出CSV
-
[1] 赵健. 高速公路桥梁伸缩缝病害的成因及防治[J]. 公路交通科技(应用技术版),2007,3(12): 128-129, 133.ZHAO Jian. Causes and prevention of expansion joint disease for expressway bridge[J]. Highway Transportation Technology (Application Technology Edition), 2007, 3(12): 128-129, 133. [2] XIA Q, XIA Y, WAN H P, et al. Condition analysis of expansion joints of a long-span suspension bridge through metamodel-based model updating considering thermal effect[J]. Structural Control and Health Monitoring, 2020, 27(5): 1-16. [3] HU J H, WANG L H, SONG X P, et al. Field monitoring and response characteristics of longitudinal movements of expansion joints in long-span suspension bridges[J]. Measurement: Journal of the International Measurement Confederation, 2020, 162: 1-13. [4] 孙正峰,王少华,吴昊,等. 大位移桥梁伸缩缝耦合动力学研究[J]. 公路工程,2014,39(2): 59-62,104.SUN Zhengfeng, WANG Shaohua, WU Hao, et al. Coupling dynamic research of the large displacement bridge expansion joints[J]. Highway Engineering, 2014, 39(2): 59-62,104. [5] 严情木,王少华,杨刚,等. 大位移桥梁伸缩缝的垂向动力学响应研究[J]. 机械设计与制造,2013(7): 41-43,46. doi: 10.3969/j.issn.1001-3997.2013.07.014YAN Qingmu, WANG Shaohua, YANG Gang, et al. Research of vertical dynamic response of the large displacement bridge expansion joint[J]. Machinery Design & Manufacture, 2013(7): 41-43,46. doi: 10.3969/j.issn.1001-3997.2013.07.014 [6] LI B, WANG S H, WU X, et al. Dynamic response of continuous beams with discrete viscoelastic supports under sinusoidal loading[J]. International Journal of Mechanical Sciences, 2014, 86: 76-82. doi: 10.1016/j.ijmecsci.2014.02.005 [7] 谢旭,吴冬雁,王建峰,等. 伸缩缝车辆冲击引起的钢箱梁桥振动特性[J]. 浙江大学学报(工学版),2009,43(10): 1923-1930. doi: 10.3785/j.issn.1008-973X.2009.10.030XIE Xu, WU Dongyan, WANG Jianfeng, et al. Dynamical behavior of steel box girder bridges due to vehicle-induced vibration at expansion joint[J]. Journal of Zhejiang University (Engineering Science), 2009, 43(10): 1923-1930. doi: 10.3785/j.issn.1008-973X.2009.10.030 [8] SUN Z, ZHANG Y F. Vehicle-induced dynamic response of expansion joints in long span bridges[J]. Applied Mechanics and Materials, 2014, 584/585/586: 2117-2120. [9] FRIEDL R, MANGERIG I. Dynamic amplification of bridge-expansion-joints considering roughness induced vehicle vibrations[J]. Procedia Engineering, 2017, 199: 2651-2656. doi: 10.1016/j.proeng.2017.09.515 [10] MANGERIG I, FRIEDL R. Dynamic interaction between vehicles and bridge expansion joints[C]// Proceedings of the International Conference on Structural Dynamic Porto. [S.l.]: European Association for Structural Dynamics, 2014: 1153-1160. [11] 丁勇,谢旭,区达光,等. 基于分布式弹簧-阻尼单元的桥头跳车动力荷载分析[J]. 土木工程学报,2012,45(12): 127-135.DING Yong, XIE Xu, AU FRANCIS T K, et al. Analysis of dynamic load of vehicle bumping at bridge-head using distributed spring-damper element[J]. China Civil Engineering Journal, 2012, 45(12): 127-135. [12] DING Y, ZHANG W, AU F T K. Effect of dynamic impact at modular bridge expansion joints on bridge design[J]. Engineering Structures, 2016, 127: 645-662. doi: 10.1016/j.engstruct.2016.09.007 [13] 张纬. 车辆荷载作用下桥梁伸缩缝强度与疲劳问题研究[D]. 宁波: 宁波大学, 2017. [14] 吴延平,吴冬雁,谢旭,等. 车辆通过钢箱梁桥伸缩缝的振动响应及减振[J]. 噪声与振动控制,2013,33(2): 95-100.WU Yanping, WU Dongyan, XIE Xu, et al. Response and vibration control of steel box-girder bridge when vehicles passing through the expansion joint[J]. Noise and Vibration Control, 2013, 33(2): 95-100. [15] 张锋. 深季节冻土区重载汽车荷载下路基动力响应与永久变形[D]. 哈尔滨: 哈尔滨工业大学, 2012. [16] 翟婉明. 车辆-轨道耦合动力学[M]. 4版. 北京: 科学出版社, 2015. [17] 郭孔辉,刘青,丁国峰. 轮胎包容特性分析及其在汽车振动系统建模中的应用[J]. 汽车工程,1999,21(2): 65-71,80.GUO Konghui, LIU Qing, DING Guofeng. Analysis of tire enveloping properties and its application in modeling of vehicle vibration systems[J]. Automotive Engineering, 1999, 21(2): 65-71,80. [18] YANG S P, LI S H, LU Y J. Dynamics of vehicle-pavement coupled system based on a revised flexible roller contact tire model[J]. Science in China Series E:Technological Sciences, 2009, 52(3): 721-730. doi: 10.1007/s11431-009-0053-0 [19] 崔志博. 子午线轮胎接地特性可控设计理论及实验研究[D]. 哈尔滨: 哈尔滨工业大学, 2016. [20] 林楠,李东升,李宏男. 基于零初值的测试加速度积分速度与位移的方法[J]. 中国科学:技术科学,2016,46(6): 602-614. doi: 10.1360/N092015-00282LIN Nan, LI Dongsheng, LI Hongnan. Novel integration method of measured acceleration to velocity and displacement based on zero initial condition[J]. Scientia Sinica (Technologica), 2016, 46(6): 602-614. doi: 10.1360/N092015-00282 [21] 中华人民共和国交通运输部. 公路桥涵设计通用规范: JTG D60—2015[S]. 北京: 人民交通出版社, 2015 期刊类型引用(6)
1. 胡建林，薛金昊，郭江峰，孟志鹏，刘洋，郑瑞海. 不同围压下锚杆–土体界面剪切特性影响因素的试验研究. 工业建筑. 2024(03): 200-205 . 
百度学术2. 白晓宇，吴泽坤，王凤姣，孙淦，张明义，闫楠. BFRP抗浮锚杆抗拔性能现场试验与荷载传递特性. 岩石力学与工程学报. 2024(06): 1335-1346 . 百度学术3. 陈向琳，王超圣，许战波，孙晓刚. 砾石地层中自钻式锚杆锚固特性现场试验与数值仿真. 科学技术与工程. 2024(20): 8655-8662 . 百度学术4. 胡玉超. 冻融环境下树脂混凝土与玻璃纤维锚杆粘结性能的试验研究. 水利技术监督. 2023(05): 231-233 . 百度学术5. 白晓宇，苏悦，闫楠，杲晓东，于风波，李伟奇，赵文强，宋波，苑振. 抗浮锚杆受力特性试验研究进展. 科学技术与工程. 2023(15): 6290-6302 . 百度学术6. 韩有强. 体育护具用玄武岩纤维复合材料的制备与性能分析. 塑料助剂. 2022(02): 38-40 . 百度学术其他类型引用(5)
-
下载:
下载:
百度学术
点击查看大图
计量
- 文章访问数: 354
- HTML全文浏览量: 155
- PDF下载量: 17
- 被引次数: 11