Bond-Slip of Connecting Bolts Between Tunnel Segments and Metro Station Portal Ring Beam
-
摘要:
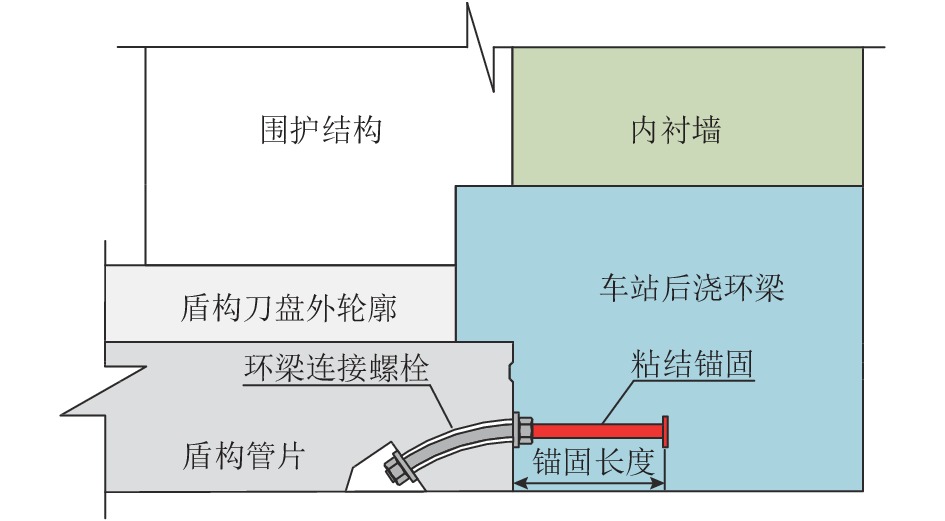
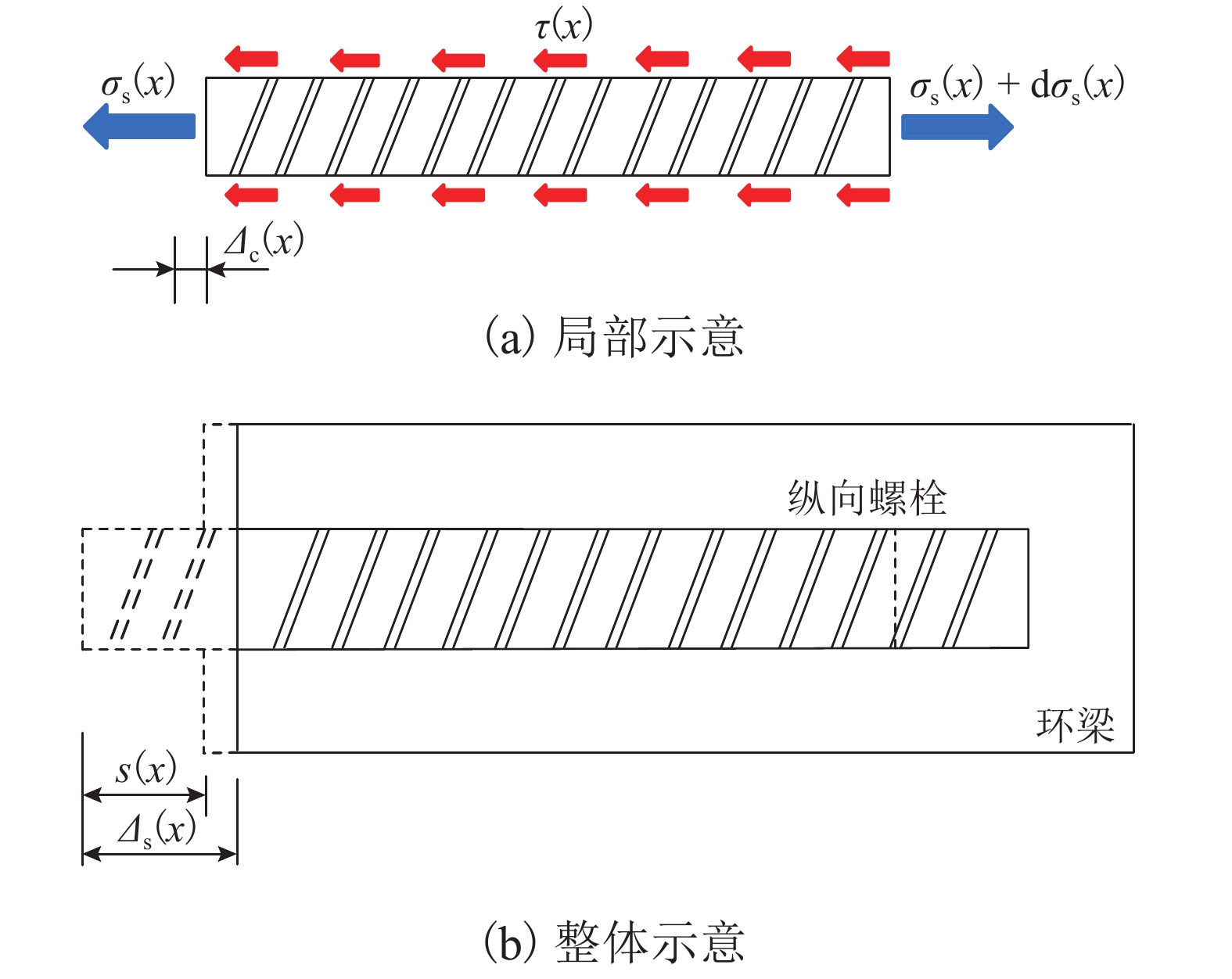
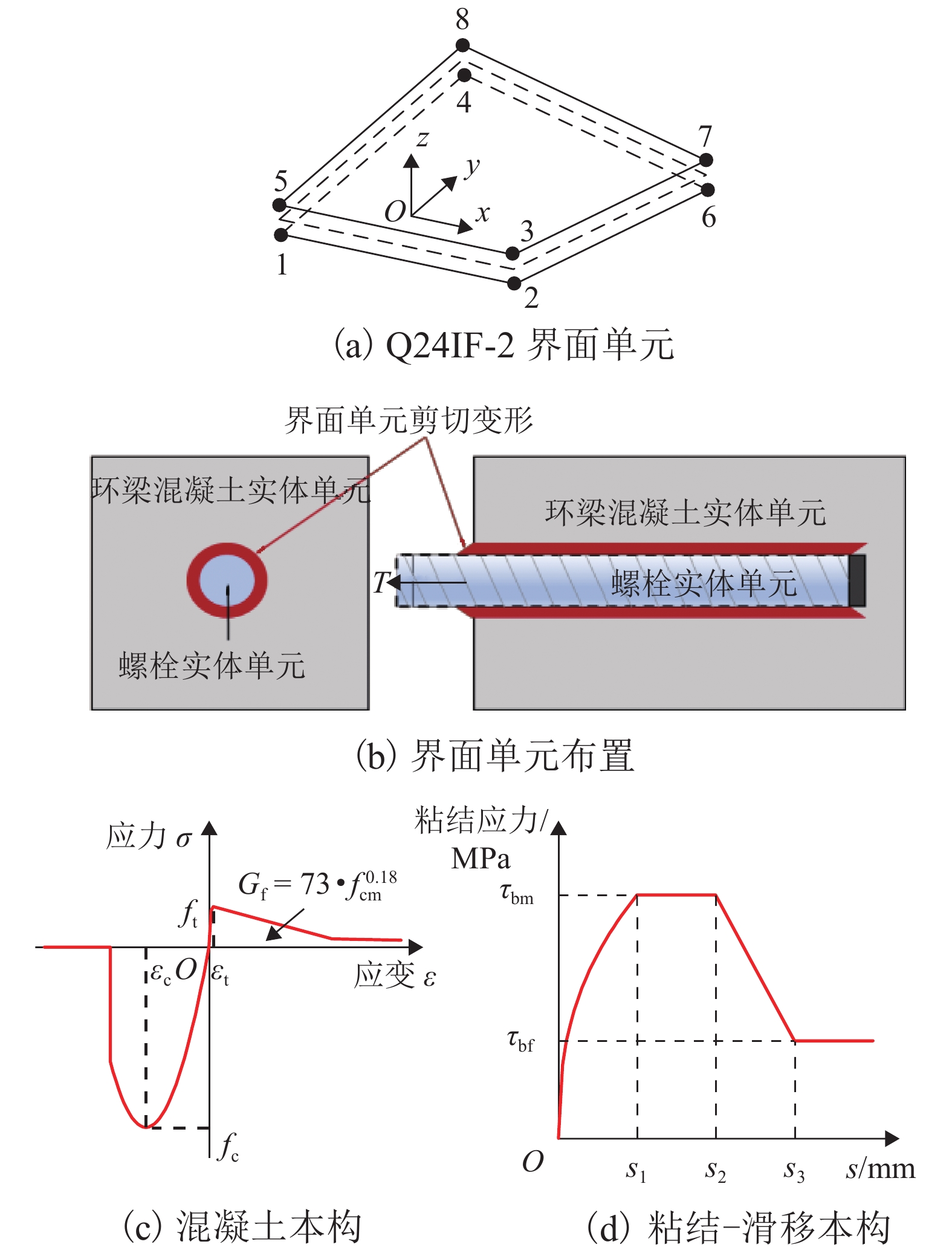
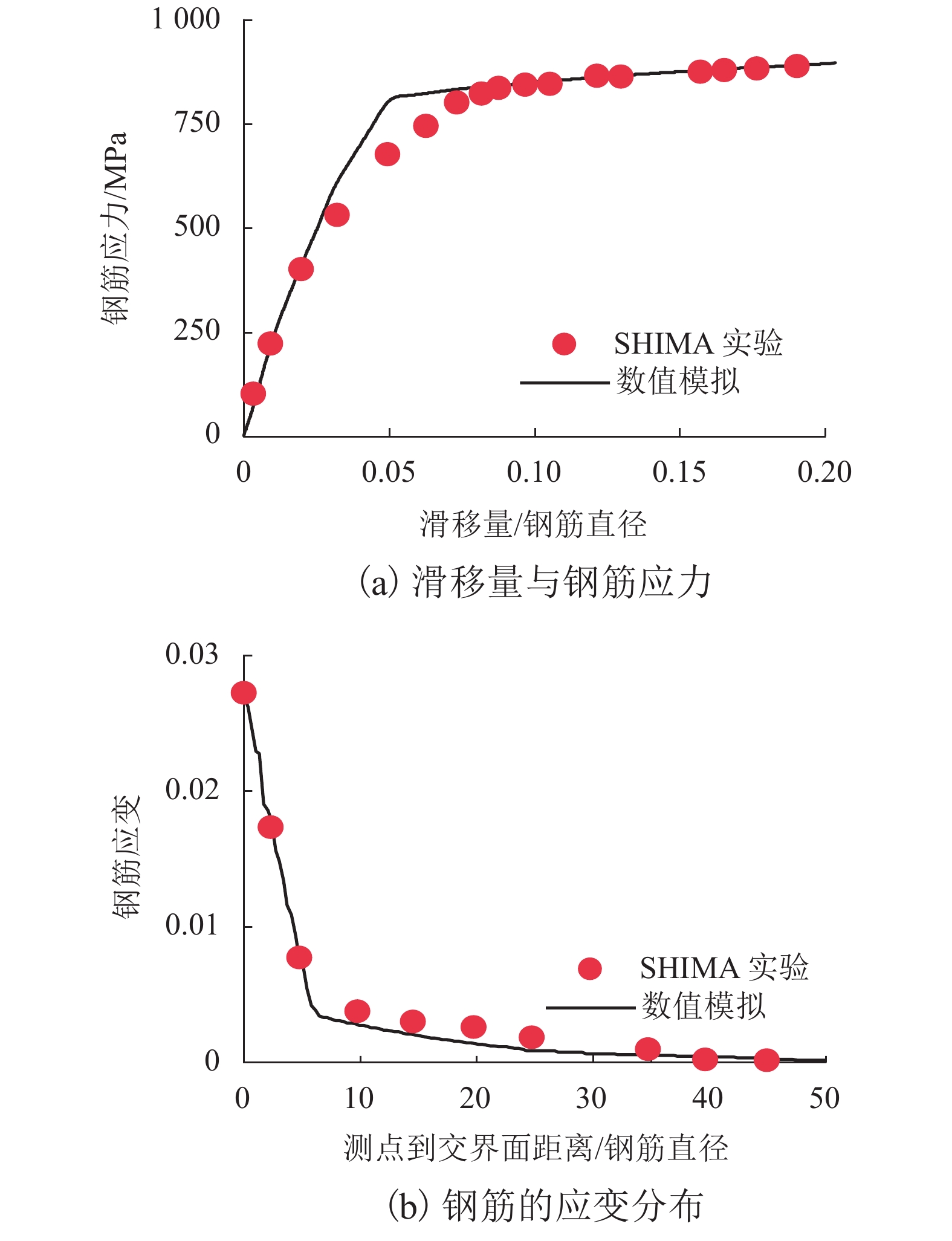
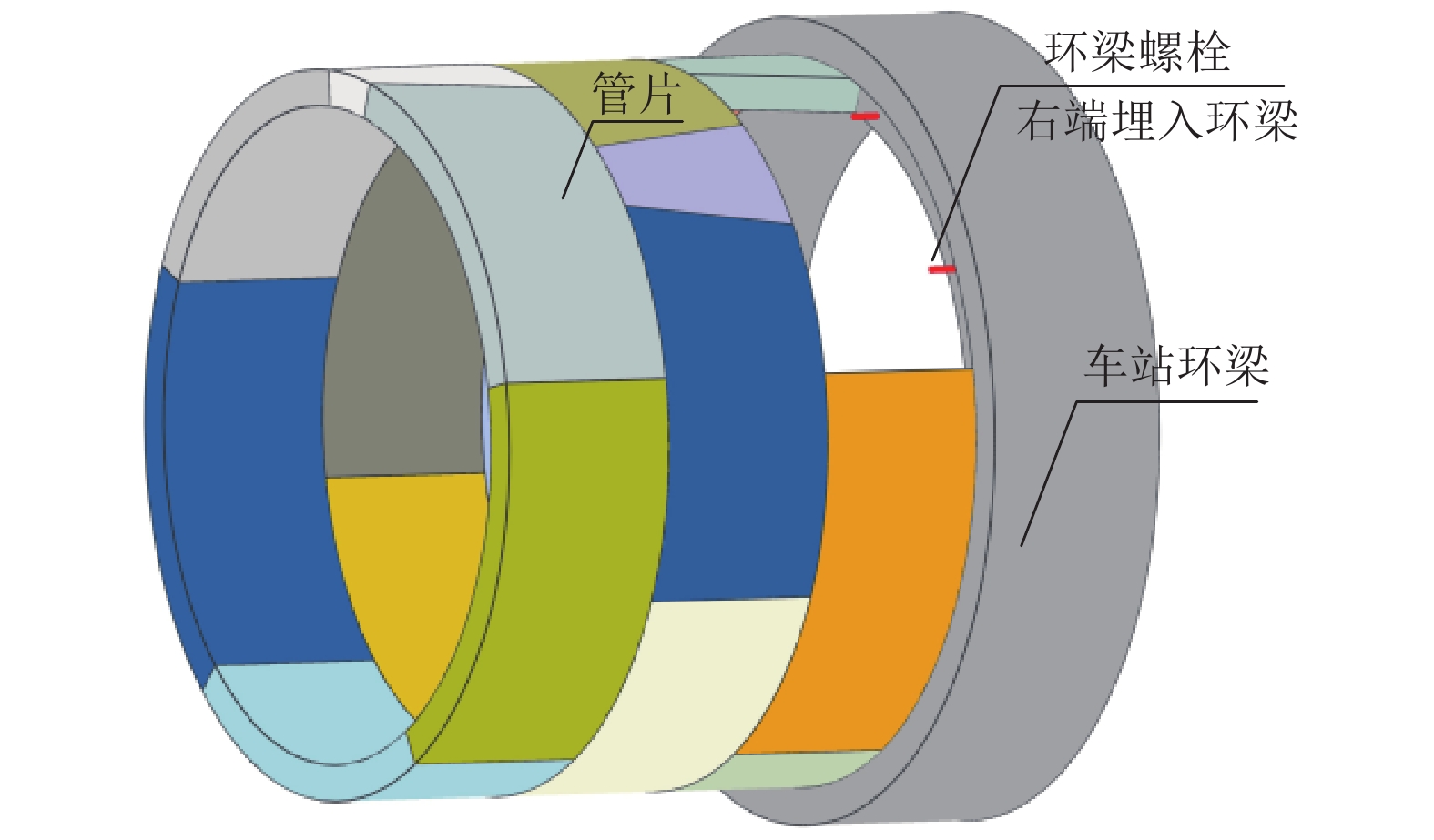
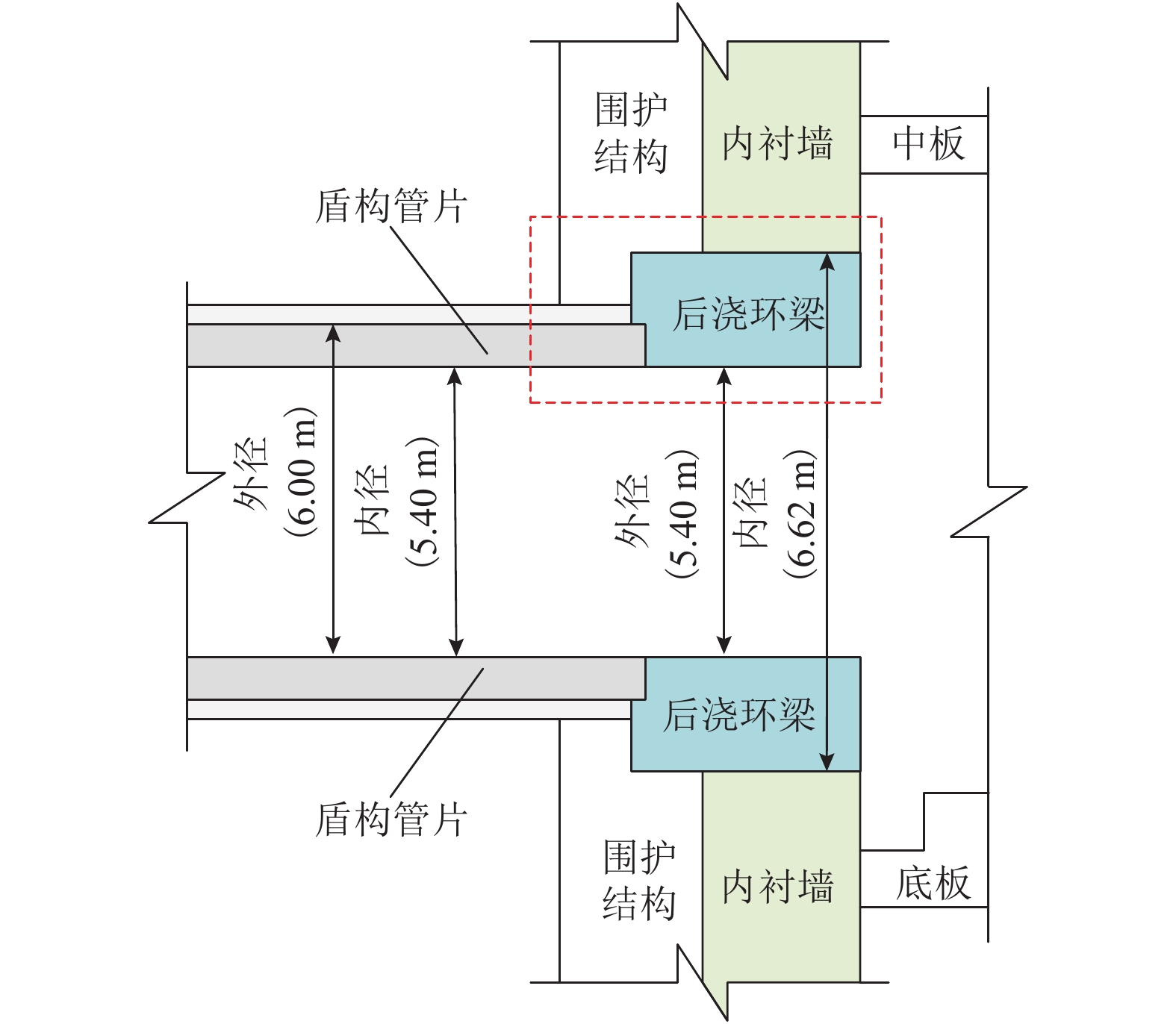
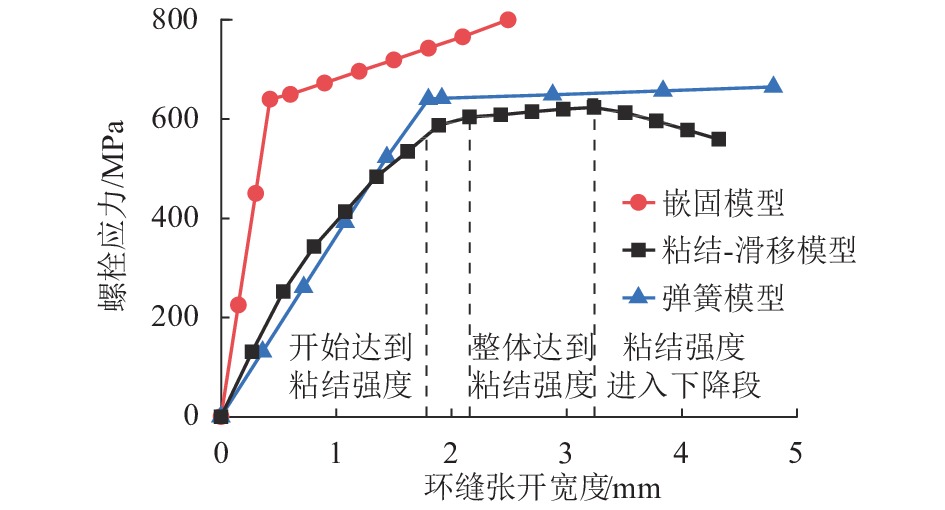
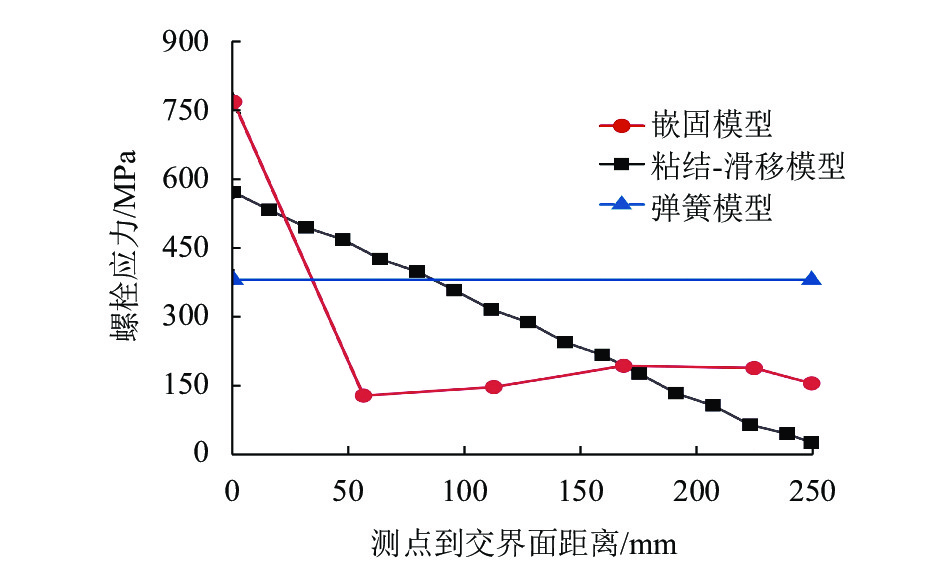
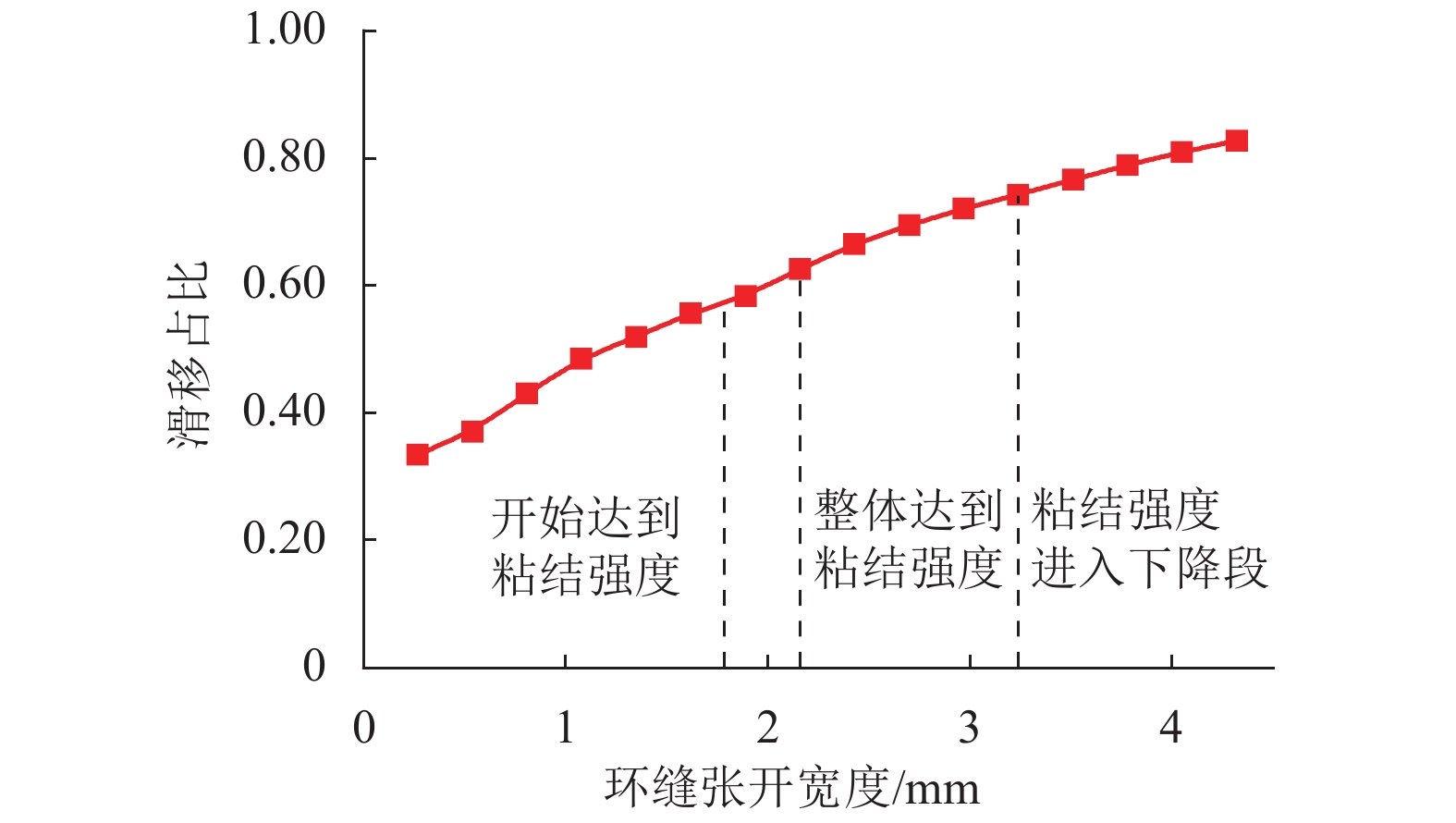
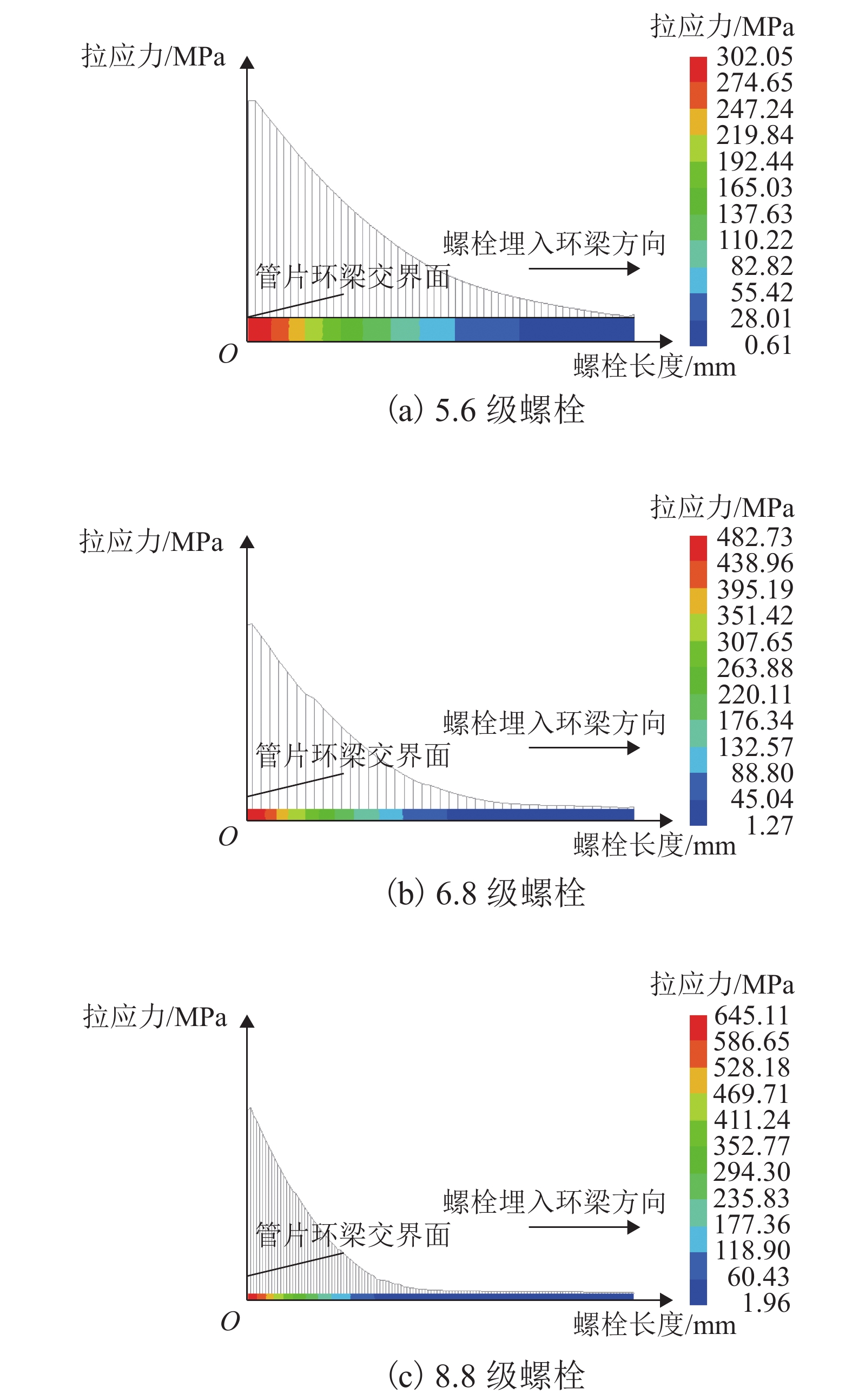
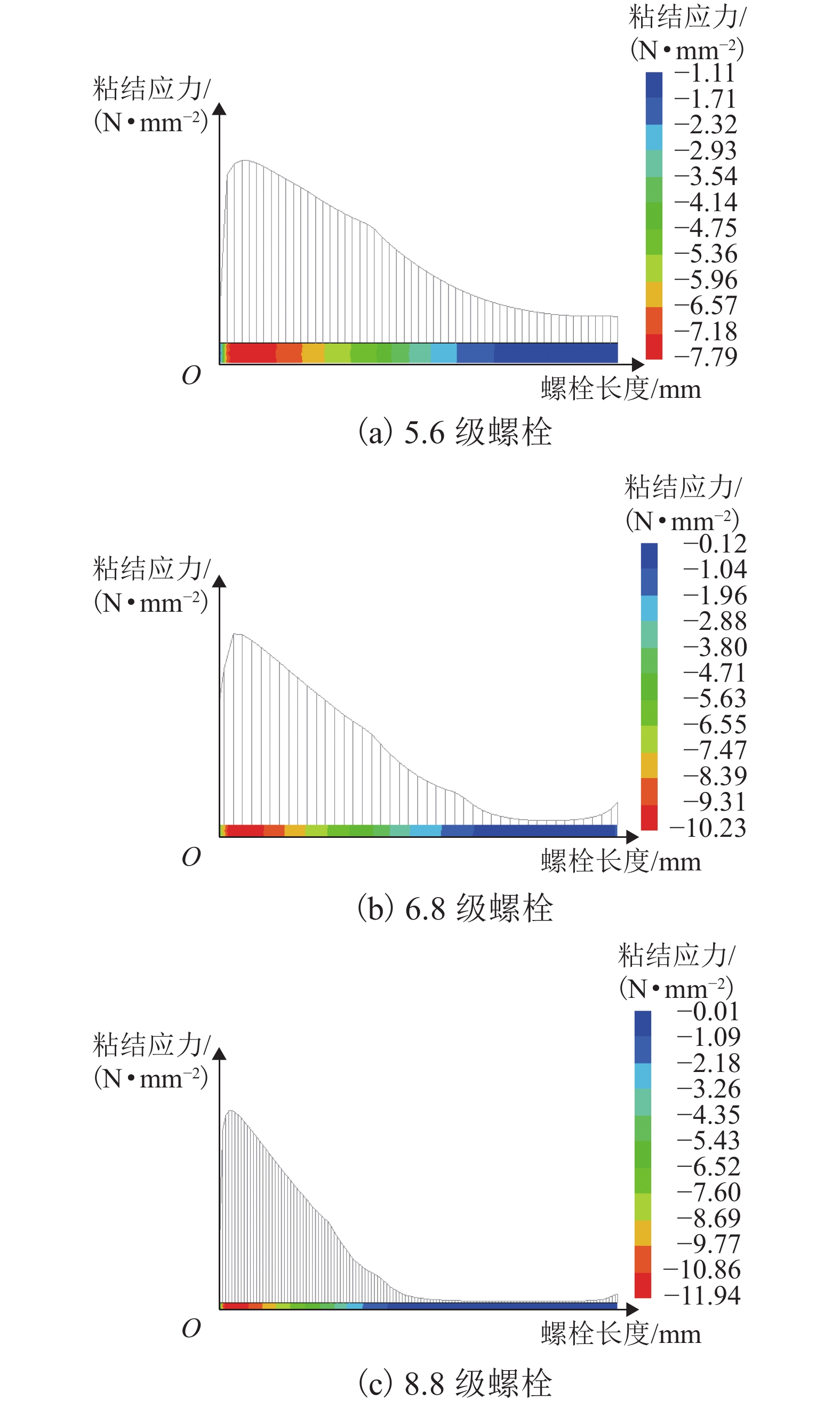
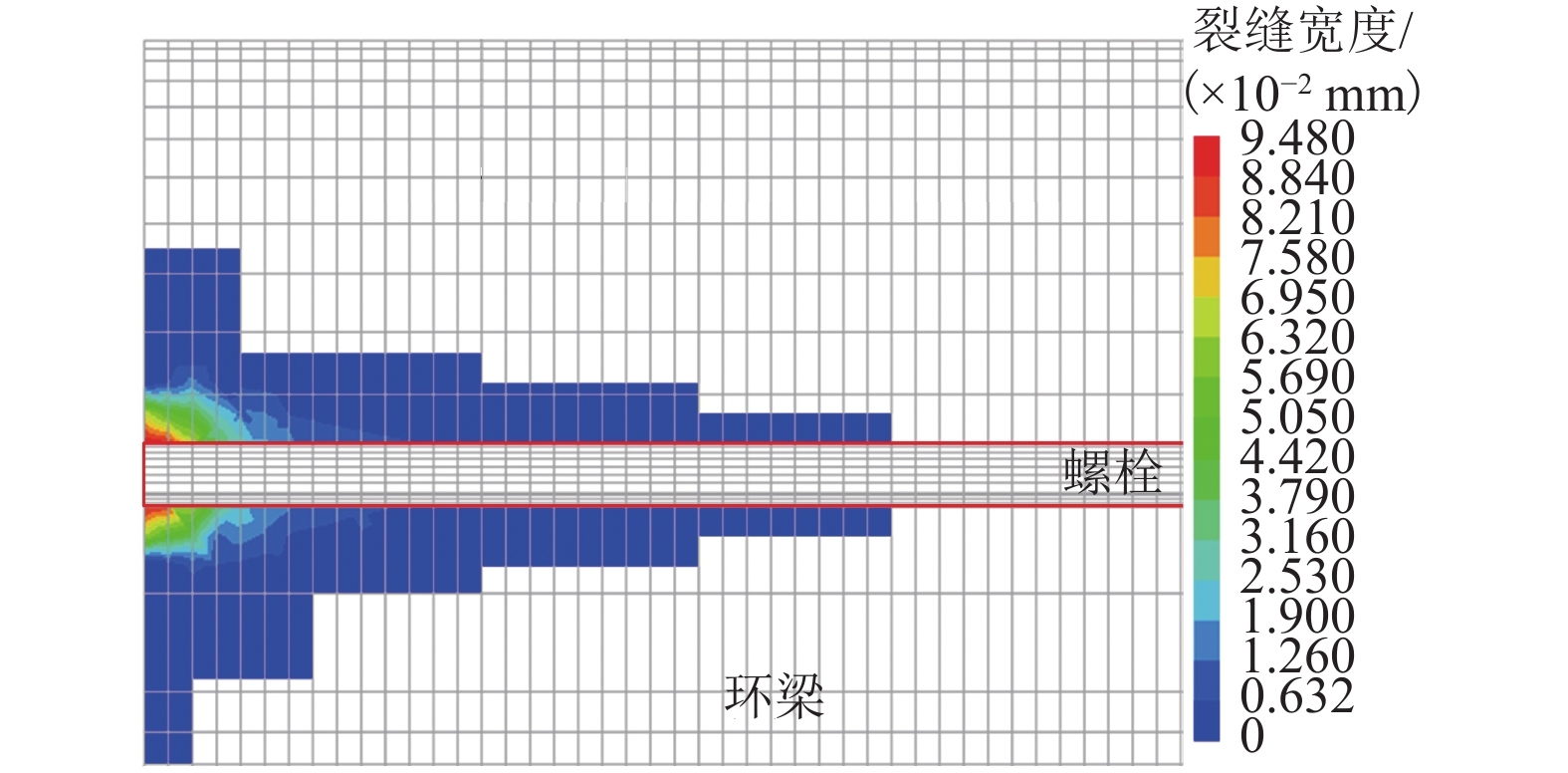
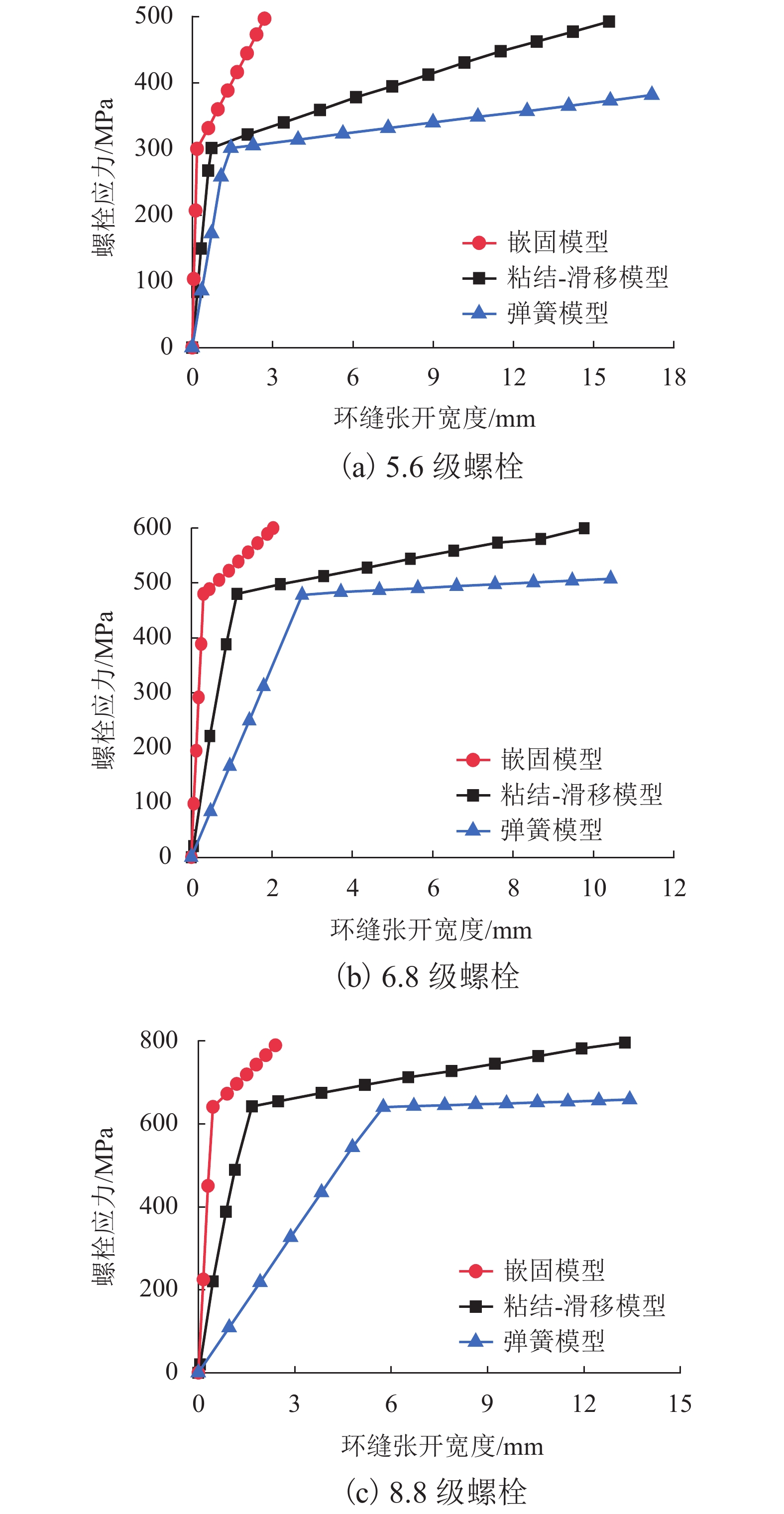
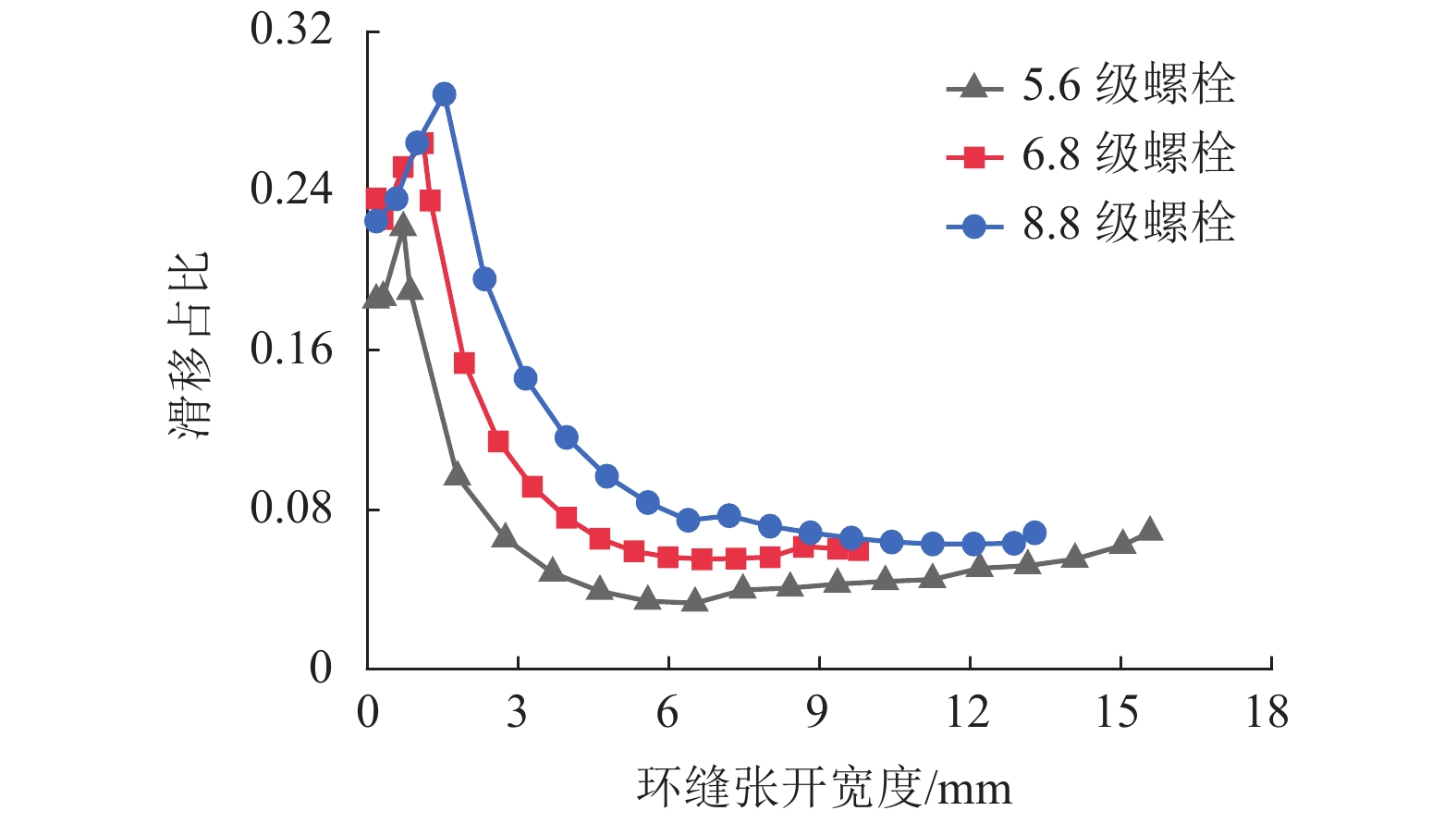
地铁车站洞口的混凝土环梁与隧道管片之间一般通过螺栓连接,螺栓往往以预埋的方式锚入车站环梁内,并且与握裹它的混凝土之间存在粘结-滑移变形,这对环缝张开宽度和环梁结构损伤发展都可能产生影响,为进一步明确其中的机理及影响程度,参考既有的粘结-滑移本构模型,利用可细化分析粘结-滑移的有限元分析平台,在充分考虑材料非线性特征的基础上,针对3种不同型号螺栓,分别考虑锚固长度足够和不足两种情况,分析了螺栓在环梁内的粘结-滑移,以及环缝宽度增大的过程;通过量化分析粘结应力和螺栓应力沿螺栓长度的分布,揭示了粘结-滑移对环缝宽度发展的影响机制. 分析表明:采用粘结-滑移模型时,得到的螺栓连接刚度介于嵌固模型和弹簧模型之间,粘结-滑移变形对盾构管片和车站环梁之间环缝宽度的影响不可忽略;仅考虑受拉影响,即便在锚固长度足够的情况下,当螺栓接近屈服时,螺栓与环梁间的粘结-滑移变形在环缝张开宽度中占比最大可达30%,螺栓屈服后,这个滑移占比会随环缝扩展降至8%以下,受此影响,考虑粘结-滑移的螺栓抗拉刚度最低约为完全嵌固模型的1/3.
Abstract:The concrete ring beam at the entrance of subway station is generally connected with the tunnel segment by bolts. The bolts are often embedded in the ring beam of subway station, and there is bond-slip deformation between the bolts and the concrete wrapping them. This may have an impact on the opening width of the ring joint and the damage development of the ring beam structure. Based on the existing constitutive model of bond-slip between concrete and steel, a high-precision finite element program function was utilized to investigate the concrete nonlinear behavior and cracking mechanism, and a model describing the behavior of bond-slip mechanism was built up to measure the influence of the slip displacement on the width of ring gap. For three different types of connection bolts with long anchorage and short anchorage, simulations were performed to analyze the bond-slip behaviors of these bolts in the ring beam concrete and the width increasing of the gap between ring beam and segment. Meanwhile, through quantitative analysis of distributions of bond stress and bolt stress along the bolt length, the mechanism for the contribution from the displacement and deformation of connecting blots to the width increasing of the gap was revealed. Results show that the bolt connection stiffness derived from the bond-slip models is between those derived from the completely fixed model and the spring model, and the influence of the bond-slip deformation on the width of the annular gap between the shield segment and the station ring beam cannot be ignored. In the case of long anchorages, the contribution of bond-slip to the gap width can reach up to about 30% when the bolt begins to yield. After the bolt yields, the slip proportion will decrease to less than 8% with the expansion of the circumferential seam. Affected by this, the tensile stiffness of the bolt considering bond slip is at least about 1/3 of the fully fixed model
-
Key words:
- shield tunnel /
- segments /
- concrete ring beam /
- bolts /
- bond-slip
-
表 1 某城市地铁站台附近隧道测点曲率半径分布情况
Table 1. Statistics of measurement results of curvature radius of tunnel near platform in a city
% 站台
名称R >
15.0 km5.0 km < R ≤ 15.0 km 2.5 km < R ≤ 5.0 km R ≤
2.5 kmA 83.00 11.14 4.00 1.86 B 88.43 8.29 2.42 0.86 C 90.43 7.14 2.29 0.14 D 92.85 6.14 0.72 0.29 E 88.57 8.86 2.43 0.14 -
[1] SHEN S L, WU H N, CUI Y J, et al. Long-term settlement behaviour of metro tunnels in the soft deposits of Shanghai[J]. Tunnelling and Underground Space Technology, 2014, 40: 309-323. doi: 10.1016/j.tust.2013.10.013 [2] 何川,封坤,方勇. 盾构法修建地铁隧道的技术现状与展望[J]. 西南交通大学学报,2015,50(1): 97-109. doi: 10.3969/j.issn.0258-2724.2015.01.015HE Chuan, FENG Kun, FANG Yong. Review and prospects on constructing technologies of metro tunnels using shield tunnelling method[J]. Journal of Southwest Jiaotong University, 2015, 50(1): 97-109. doi: 10.3969/j.issn.0258-2724.2015.01.015 [3] 翟婉明,赵春发. 现代轨道交通工程科技前沿与挑战[J]. 西南交通大学学报,2016,51(2): 209-226. doi: 10.3969/j.issn.0258-2724.2016.02.001ZHAI Wanming, ZHAO Chunfa. Frontiers and challenges of sciences and technologies in modern railway engineering[J]. Journal of Southwest Jiaotong University, 2016, 51(2): 209-226. doi: 10.3969/j.issn.0258-2724.2016.02.001 [4] 耿萍,陈枰良,张景,等. 轴力和弯矩共同作用下盾构隧道纵向非线性等效抗弯刚度研究[J]. 岩石力学与工程学报,2017,36(10): 2522-2534.GENG Ping, CHEN Pingliang, ZHANG Jing, et al. Nonlinear longitudinal equivalent bending stiffness of shield tunnel under the combined effect of axial force and bending moment[J]. Chinese Journal of Rock Mechanics and Engineering, 2017, 36(10): 2522-2534. [5] WANG Z, WANG L Z, LI L L, et al. Failure mechanism of tunnel lining joints and bolts with uneven longitudinal ground settlement[J]. Tunnelling and Underground Space Technology, 2014, 40: 300-308. doi: 10.1016/j.tust.2013.10.007 [6] WU H N, HUANG R Q, SUN W J, et al. Leaking behavior of shield tunnels under the Huangpu River of Shanghai with induced hazards[J]. Natural Hazards, 2014, 70(2): 1115-1132. doi: 10.1007/s11069-013-0863-z [7] ZHONG X C, ZHU W, HUANG Z R, et al. Effect of joint structure on joint stiffness for shield tunnel lining[J]. Tunnelling and Underground Space Technology, 2006, 21(3/4): 407-408. [8] 王如路. 上海软土地铁隧道变形影响因素及变形特征分析[J]. 地下工程与隧道,2009(1): 1-6,52.WANG Rulu. Factors influencing deformation of Shanghai soft soil metro tunnel and deformation analysis[J]. Underground Engineering and Tunnels, 2009(1): 1-6,52. [9] 郑永来,韩文星,童琪华,等. 软土地铁隧道纵向不均匀沉降导致的管片接头环缝开裂研究[J]. 岩石力学与工程学报,2005,24(24): 4552-4558. doi: 10.3321/j.issn:1000-6915.2005.24.025ZHENG Yonglai, HAN Wenxing, TONG Qihua, et al. Study on longitudinal crack of shield tunnel segment joint due to asymmetric settlement in soft soil[J]. Chinese Journal of Rock Mechanics and Engineering, 2005, 24(24): 4552-4558. doi: 10.3321/j.issn:1000-6915.2005.24.025 [10] 张冬梅,樊振宇,黄宏伟. 考虑接头力学特性的盾构隧道衬砌结构计算方法研究[J]. 岩土力学,2010,31(8): 2546-2552. doi: 10.3969/j.issn.1000-7598.2010.08.033ZHANG Dongmei, FAN Zhenyu, HUANG Hongwei. Mechanical characteristics of joints calculation method of shield tunnel lining considering[J]. Rock and Soil Mechanics, 2010, 31(8): 2546-2552. doi: 10.3969/j.issn.1000-7598.2010.08.033 [11] JIN H, YU S, ZHOU S H, et al. Research on mechanics of longitudinal joint in shield tunnel by the nonlinear spring equivalent method[J]. KSCE Journal of Civil Engineering, 2019, 23(2): 902-913. doi: 10.1007/s12205-018-0667-5 [12] 赵武胜,何先志,陈卫忠,等. 盾构隧道地震响应分析方法及工程应用[J]. 岩土力学,2012,33(8): 2415-2421. doi: 10.3969/j.issn.1000-7598.2012.08.027ZHAO Wusheng, HE Xianzhi, CHEN Weizhong, et al. Method for analyzing seismic response of shield tunnel and its application[J]. Rock and Soil Mechanics, 2012, 33(8): 2415-2421. doi: 10.3969/j.issn.1000-7598.2012.08.027 [13] 艾辉军,彭立敏,施成华. 基于三维非连续接触模型的管片接头静动力特性分析[J]. 岩土工程学报,2013,35(11): 2023-2029.AI Huijun, PENG Limin, SHI Chenghua. Static and dynamic characteristic analysis of segment joints based on three-dimensional discontinuous contact model[J]. Chinese Journal of Geotechnical Engineering, 2013, 35(11): 2023-2029. [14] 耿萍,王琦,郭翔宇,等. 地震作用下盾构隧道纵向接头的受力特征[J]. 西南交通大学学报,2020,55(4): 704-712. doi: 10.3969/j.issn.0258-2724.20180634GENG Ping, WANG Qi, GUO Xiangyu, et al. Force characteristics of longitudinal joints of shield tunnel under seismic action[J]. Journal of Southwest Jiaotong University, 2020, 55(4): 704-712. doi: 10.3969/j.issn.0258-2724.20180634 [15] 何川. 大直径盾构隧道掘进对周边地层扰动特征及施工关键技术[R]. 成都: 西南交通大学, 2019. [16] 上海市市政工程管理局. 上海市地铁沿线建筑施工保护地铁技术管理暂行规定: 沪市政法(94)第854号[S]. 上海: 上海市市政工程管理局, 1994. [17] 同济大学数学系. 高等数学[M]. 7版. 北京: 高等教育出版社, 2014. [18] 徐有邻,沈文都,汪洪. 钢筋砼粘结锚固性能的试验研究[J]. 建筑结构学报,1994,15(3): 26-37.XU Youlin, SHEN Wendu, WANG Hong. An experimental study of bond-anchorage properties of bars in concrete[J]. Journal of Building Structures, 1994, 15(3): 26-37. [19] DIANA. DIANA FEA user’s manual[EB/OL]. [2020-10-13]. https://dianafea.com/manuals/d103/Diana.html. [20] International Federation for Structural Concrete. FIB model code for concrete structures 2010[S]. Berlin: Wilhelm Ernst & Sohn, 2013. [21] VECCHIO F J, COLLINS M P. The modified compression-field theory for reinforced concrete elements subjected to shear[J]. ACI Structural Journal, 1986, 83(2): 219-231. [22] RUSSO G, PAULETTA M. A simple method for evaluating the maximum slip of anchorages[J]. Materials and structures, 2006, 39(5): 533-546. [23] BRANTSCHEN F, FARIA D M V, FERNÁNDEZ RUIZ M, et al. Bond behaviour of straight,hooked,U-shaped and headed bars in cracked concrete[J]. Structural Concrete, 2016, 17(5): 799-810. doi: 10.1002/suco.201500199 [24] SHIMA H, CHOU L L, OKAMURA H. Micro and macro models for bond in reinforced concrete[J]. Journal of the Faculty of Engineering, 1987, 39(2): 133-194. [25] RUSSO G, ZINGONE G, ROMANO F. Analytical solution for bond-slip of reinforcing bars in R. C. joints[J]. Journal of Structural Engineering, 1990, 116(2): 336-355. doi: 10.1061/(ASCE)0733-9445(1990)116:2(336) [26] 刘学山. 盾构隧道的纵向抗震分析研究[J]. 地下空间与工程学报,2003,23(2): 166-172,226.LIU Xueshan. Analysis and study of longitudinal earthquake resistance of shield tunnel[J]. Underground Space, 2003, 23(2): 166-172,226. [27] 郭瑞,何川,苏宗贤,等. 盾构隧道管片接头抗剪力学性能研究[J]. 现代隧道技术,2011,48(4): 72-77.GUO Rui, HE Chuan, SU Zongxian, et al. Study of shearing mechanical properties of segment joints of shield tunnels[J]. Modern Tunnelling Technology, 2011, 48(4): 72-77. [28] 中华人民共和国住房和城乡建设部. 钢筋锚固板应用技术规程: JGJ 256—2011[S]. 北京: 中国建筑工业出版社, 2011. [29] American Concrete Institute. Building code requirements for structural concrete (ACI 318-19) and commentary[S]. Farminton Hills Michigan: ACI Concrete, 2019. -




 下载:
下载: