Free Vibration Analysis of Thin-Walled Box Beam of Crane Considering Distortion
-
摘要:
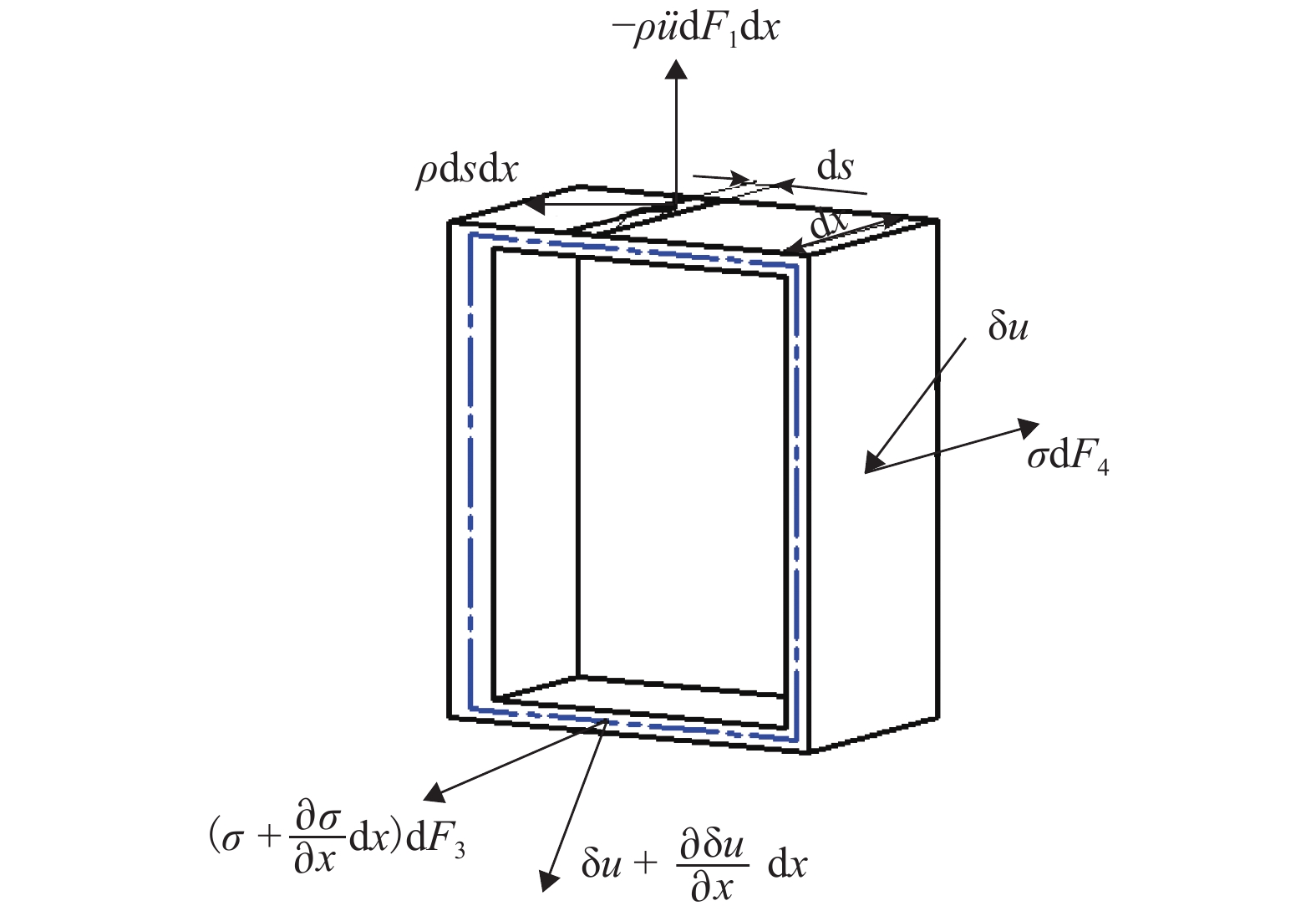
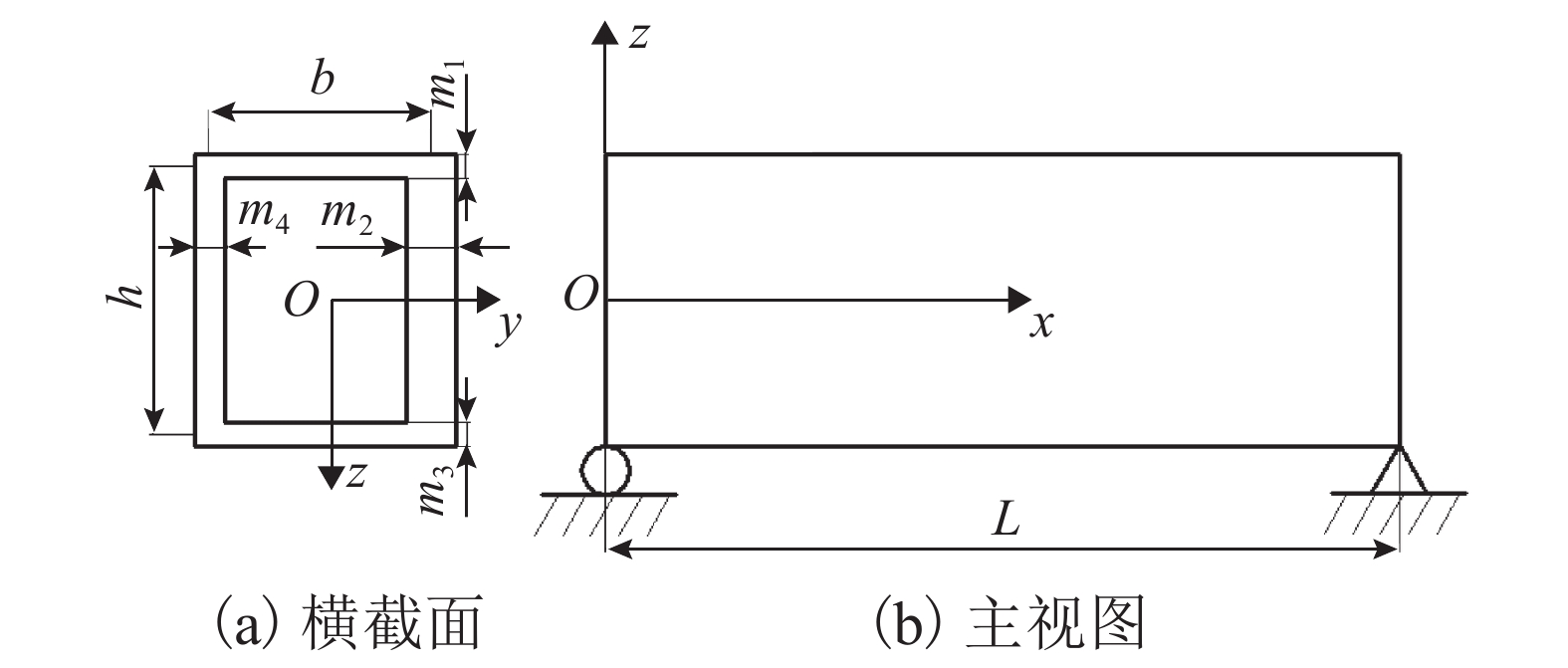
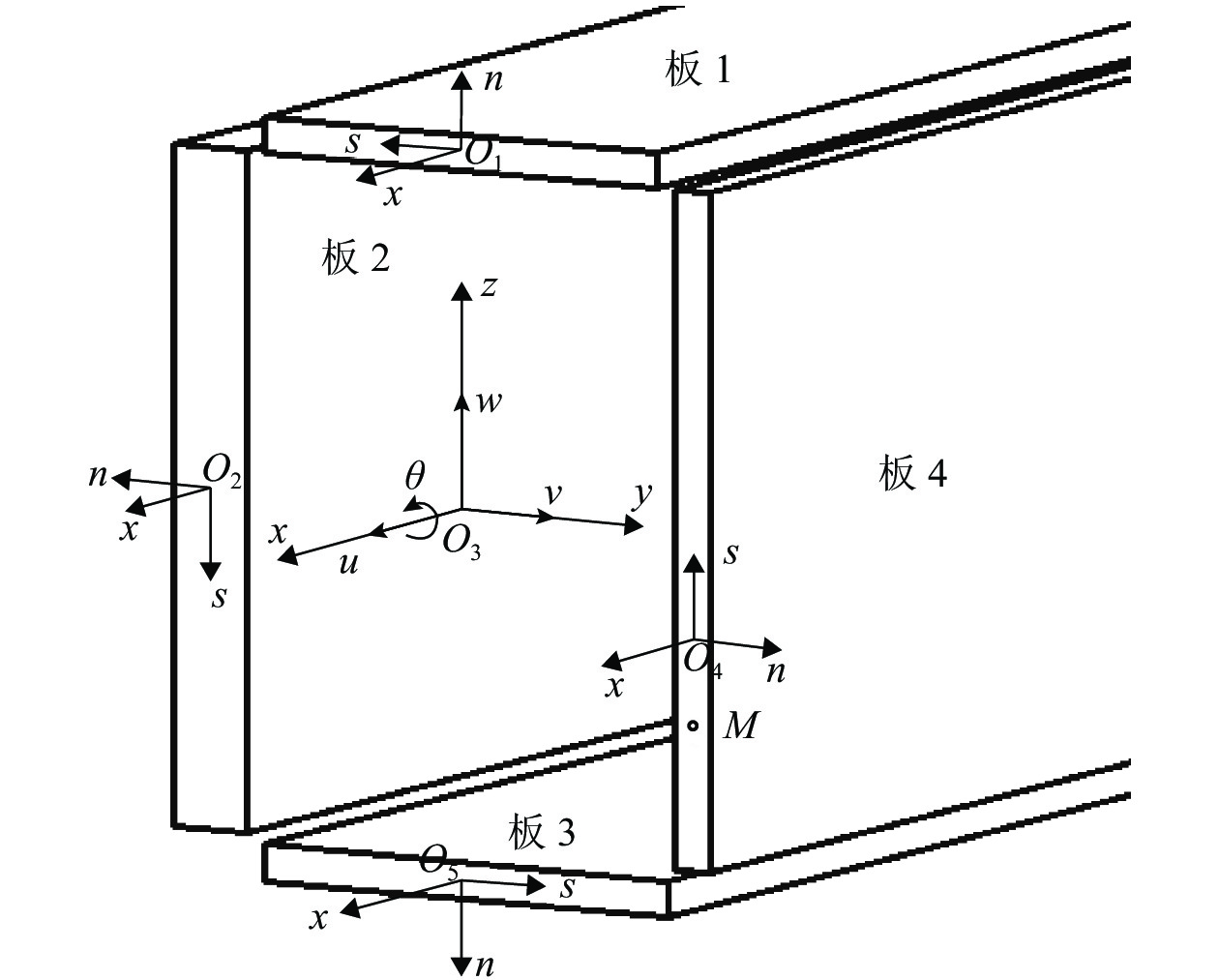
为了提高薄壁箱梁固有频率的计算精确度,基于广义坐标原理,对薄壁箱梁的动力特性进行了分析. 首先,通过虚功原理且考虑畸变形变的影响,获取了5种高度耦合模态(延伸、弯曲、扭转、翘曲和畸变)的自由振动微分方程组;其次,考虑转动惯性运动项的影响,建立了简支边界条件下的运动学模型,获得了薄壁箱形梁自由振动固有频率的四阶代数方程,进而求得固有频率的精确解;最后,通过算例将考虑畸变的固有频率精确解与Prokić 理论以及有限元分析方法的结果进行比较,验证了该方法的有效性和准确性. 结果表明:考虑畸变效应能够更准确地反映高阶状态下薄壁箱形梁的自由振动固有频率;对自由振动的4阶固有频率进行比较,当箱形梁长度为3 m时,本文理论的相对误差相较于Prokić 理论的0.42%下降至0.38%;当箱梁长度分别为4 m和5 m时,相对误差进一步下降至0.30% 和0.40%.
Abstract:In order to improve the calculation accuracy of the natural frequency of thin-walled box beams, the dynamic characteristics of thin-walled box beams are analyzed using the generalized coordinate principle. Firstly, the free vibration differential equations of five highly coupled modes (i.e., extension, bending, torsion, warping and distortion) are obtained by the virtual work principle and considering the influence of the distortion deformation. Secondly, considering the influence of the rotational inertial motion term, the kinematics model under the simply supported boundary condition is established. The fourth order algebraic equation of free vibration of the thin-walled box beam and the exact solution of the natural frequency are obtained. Finally, a numerical example is provided to compare the exact solution of natural frequency considering distortion with the results of Prokić theory and finite element analysis, so that the effectiveness and accuracy of present method are verified. The results show that when taking the distortion effect into consideration, the natural frequency of free vibration of the thin-walled box beam can be more accurately reflected in high-order modes. Comparison of natural frequencies at four orders of the free vibration indicates that when the length of the box girder is 3 m, the relative error of the present theory was reduced to 0.38% from Prokić’s 0.42%; when the length of the box girder is 4 and 5 m, the relative error can be further reduced to 0.30% and 0.40%, respectively.
-
Key words:
- bending /
- torsion /
- distortion /
- thin-walled box beam /
- free vibration
-
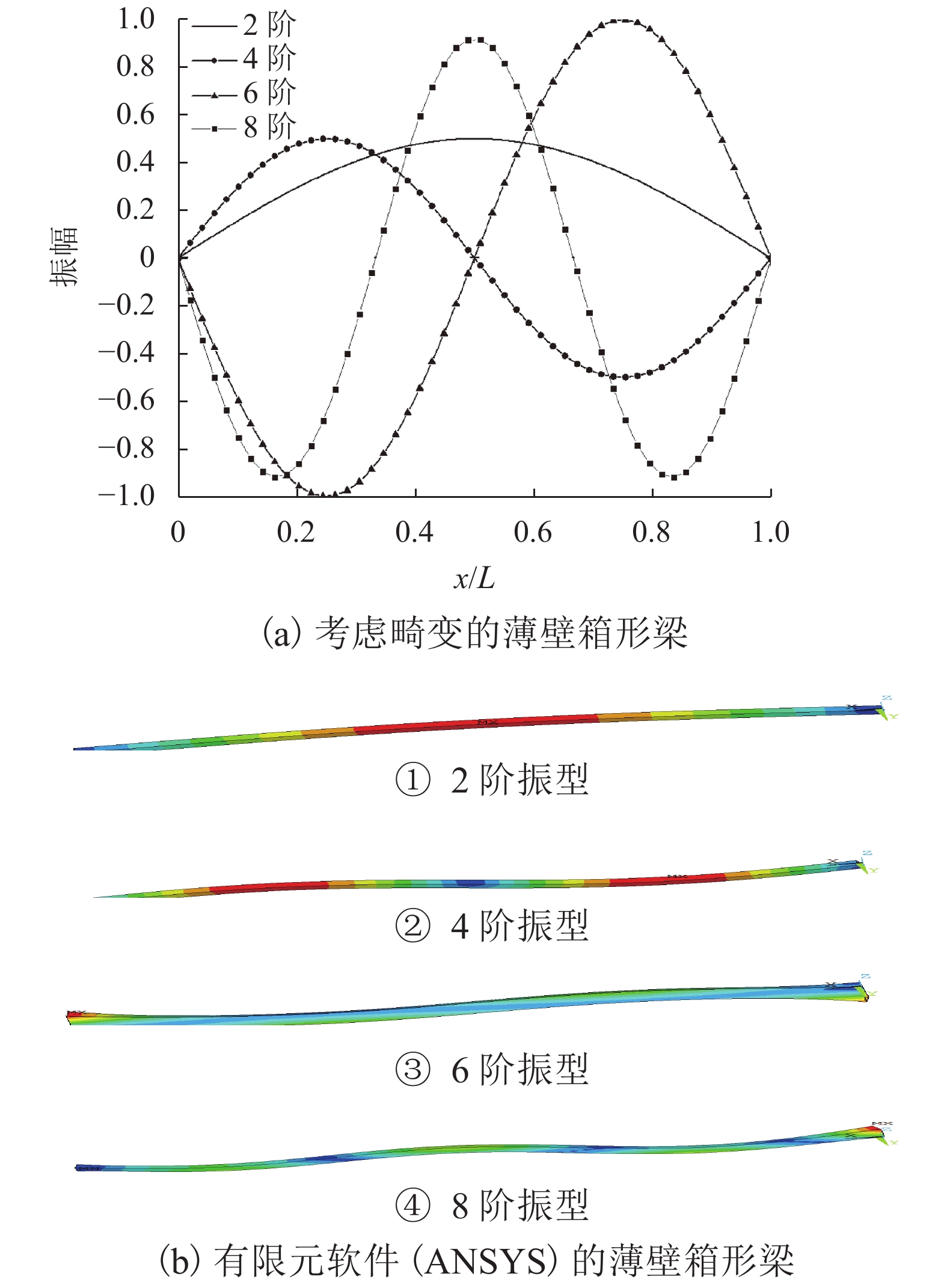
表 1 薄壁箱形梁其中4阶的固有频率比较
Table 1. Comparison of 2-, 4-, 6-, and 8-order natural frequencies of thin-walled box beams
阶数 ω1/Hz ωFEA/Hz Δ/% 2 9.36 9.34 0.18 4 36.99 36.90 0.25 6 54.30 54.11 0.36 8 89.46 88.67 0.89 表 2 简支薄壁箱形梁的固有频率
Table 2. Natural frequencies of simply supported thin-walled box beams
L/m 阶数 ω1/Hz ω2/Hz ωFEA/Hz Δ1/% Δ2/% 3 1 11.92 11.91 11.91 0.06 0 2 63.16 63.12 63.03 0.20 0.14 3 64.90 64.08 64.67 0.35 0.20 4 114.41 114.36 113.93 0.42 0.38 4 1 7.33 7.33 7.33 0 0 2 36.87 36.86 36.83 0.10 0.08 3 50.04 50.01 49.91 0.26 0.20 4 76.63 76.57 76.34 0.38 0.30 5 1 5.11 5.11 5.11 0 0 2 25.79 25.79 25.77 0.08 0.06 3 35.72 35.71 35.64 0.23 0.19 4 61.68 61.64 61.47 0.34 0.28 -
[1] GERE J M, LIN Y K. Coupled vibrations of thin-walled beams of open cross section[J]. Journal of Applied Mechanics, 1958, 25(3): 373-378. doi: 10.1115/1.4011830 [2] DOKUMACI E. An exact solution for coupled bending and torsion vibrations of uniform beams having single cross-sectional symmetry[J]. Journal of Sound and Vibration, 1987, 119(3): 443-449. doi: 10.1016/0022-460X(87)90408-1 [3] FRIBERG P O. Coupled vibrations of beams−an exact dynamic element stiffness matrix[J]. International Journal for Numerical Methods in Engineering, 1983, 19(4): 479-493. doi: 10.1002/nme.1620190403 [4] OHGA M, TAKAO H, HARA T. Natural frequencies and mode shapes of thin-walled members[J]. Computers & Structures, 1995, 55(6): 971-978. [5] ADAM C. Forced vibrations of elastic bending-torsion coupled beams[J]. Journal of Sound and Vibration, 1999, 221(2): 273-287. doi: 10.1006/jsvi.1998.2005 [6] ARPACI A, BOZDAG E. On free vibration analysis of thin-walled beams with nonsymmetrical open cross-sections[J]. Computers & Structures, 2002, 80(7/8): 691-695. [7] TANAKA M, BERCIN A N. Free vibration solution for uniform beams of nonsymmetrical cross section using Mathematica[J]. Computers & Structures, 1999, 71(1): 1-8. [8] JRAD W, MOHRI F, ROBIN G, et al. Analytical and finite element solutions of free and forced vibration of unrestrained and braced thin-walled beams[J]. Journal of Vibration and Control, 2020, 26(5/6): 255-276. [9] GÖKDAĞ H, KOPMAZ O. Coupled bending and torsional vibration of a beam with in-span and tip attachments[J]. Journal of Sound and Vibration, 2005, 287(3): 591-610. doi: 10.1016/j.jsv.2004.11.019 [10] RAFEZY B, HOWSON W P. Exact dynamic stiffness matrix for a thin-walled beam of doubly asymmetric cross-section filled with shear sensitive material[J]. International Journal for Numerical Methods in Engineering, 2007, 69(13): 2758-2779. doi: 10.1002/nme.1864 [11] 李海超,庞福振,李玉慧,等. 复杂边界条件圆柱壳自由振动特性分析[J]. 振动工程学报,2020,33(1): 56-63.LI Haichao, PANG Fuzhen, LI Yuhui, et al. Free vibration characteristics analysis of circular cylindrical shell under complex boundary conditions[J]. Journal of Vibration Engineering, 2020, 33(1): 56-63. [12] 蒲育,周凤玺. 基于一种广义梁理论的弹性地基FGM简支梁自由振动解析解[J]. 应用力学学报,2020,37(2): 840-845,946.PU Yu, ZHOU Fengxi. Exact solutions for free vibration of FGM simply supported beams on elastic foundation based on a generalized beam theory[J]. Chinese Journal of Applied Mechanics, 2020, 37(2): 840-845,946. [13] OVESY H R, KHANEH MASJEDI P. Investigation of the effects of constitutive equations on the free vibration behavior of single-celled thin-walled composite beams[J]. Mechanics of Advanced Materials and Structures, 2014, 21(10): 836-852. doi: 10.1080/15376494.2012.725266 [14] VO T P, THAI H T. Vibration and buckling of composite beams using refined shear deformation theory[J]. International Journal of Mechanical Sciences, 2012, 62(1): 67-76. doi: 10.1016/j.ijmecsci.2012.06.001 [15] FILIPPI M, PAGANI A, PETROLO M, et al. Static and free vibration analysis of laminated beams by refined theory based on Chebyshev polynomials[J]. Composite Structures, 2015, 132: 1248-1259. doi: 10.1016/j.compstruct.2015.07.014 [16] WANG S, ZHANG C. Structure mechanical modeling of thin-walled closed-section composite beams, part 2: multi-cell cross section[J]. Composite Structures, 2014, 113: 56-62. doi: 10.1016/j.compstruct.2014.03.002 [17] KIM Y Y, KIM J H. Thin-walled closed box beam element for static and dynamic analysis[J]. International Journal for Numerical Methods in Engineering, 1999, 45(4): 473-490. doi: 10.1002/(SICI)1097-0207(19990610)45:4<473::AID-NME603>3.0.CO;2-B [18] KAYA M O, OZGUMUS O O. Flexural-torsional-coupled vibration analysis of axially loaded closed-section composite Timoshenko beam by using DTM[J]. Journal of Sound and Vibration, 2007, 306(3/4/5): 495-506. [19] KIM N I. Dynamic stiffness matrix of composite box beams[J]. Steel and Composite Structures, 2009, 9(5): 473-497. doi: 10.12989/scs.2009.9.5.473 [20] PROKIĆ A, LUKIĆ D. Dynamic analysis of thin-walled closed-section beams[J]. Journal of Sound and Vibration, 2007, 302(4/5): 962-980. [21] DANCILA D S, ARMANIOS E A, LENTZ W K. Free vibration of thin-walled closed-section composite beams with optimum and near-optimum coupling[J]. Journal of Thermoplastic Composite Materials, 1999, 12(1): 2-12. doi: 10.1177/089270579901200101 [22] TAN M Y, CHENG W M. Non-linear lateral buckling analysis of unequal thickness thin-walled box beam under an eccentric load[J]. Thin-Walled Structures, 2019, 139: 77-90. doi: 10.1016/j.tws.2019.02.028 -




 下载:
下载: