Calculation Method of Axial Compression Capacity for Rectangular Short Reinforced Concrete Columns Confined with Innovative Five-Spiral Stirrups
-
摘要:
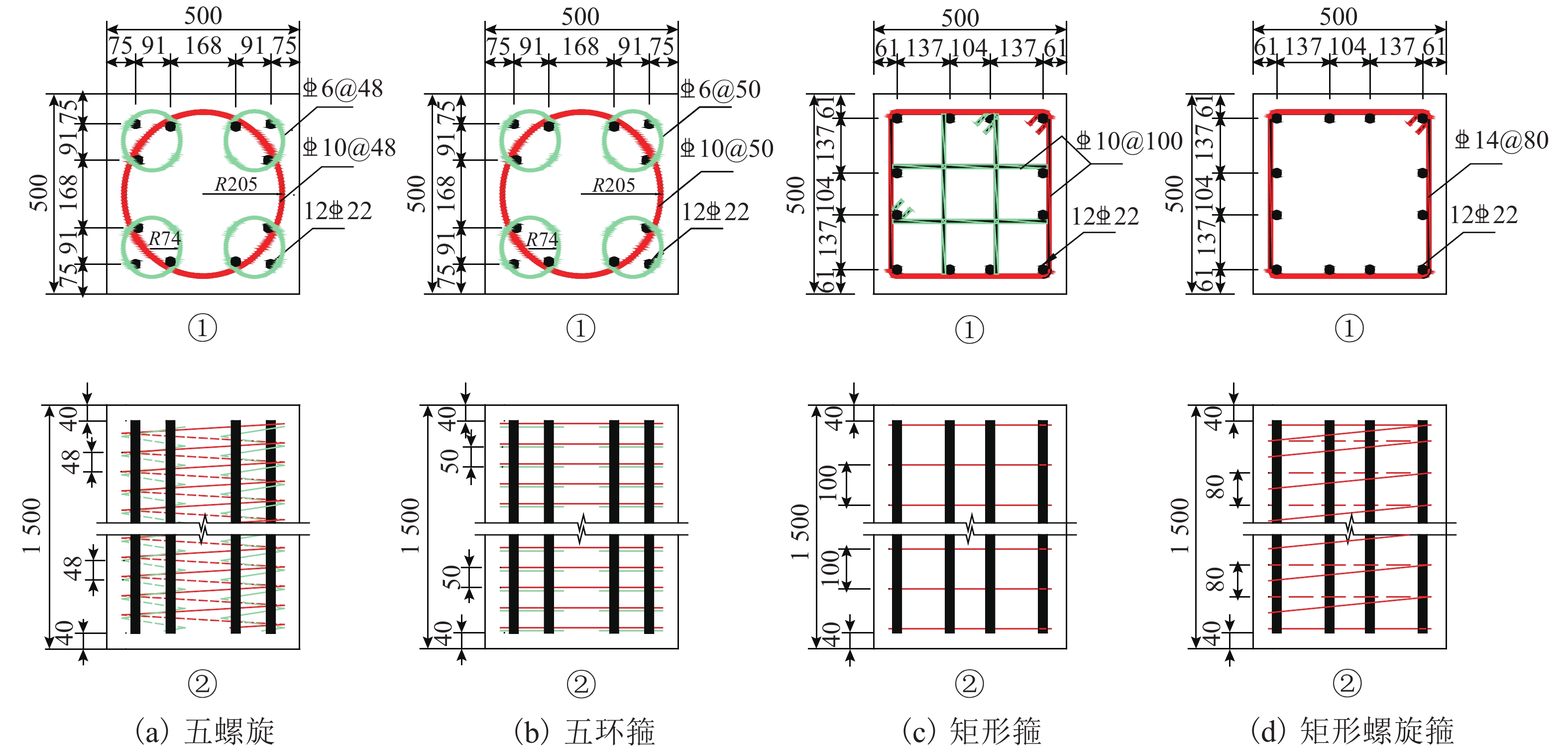
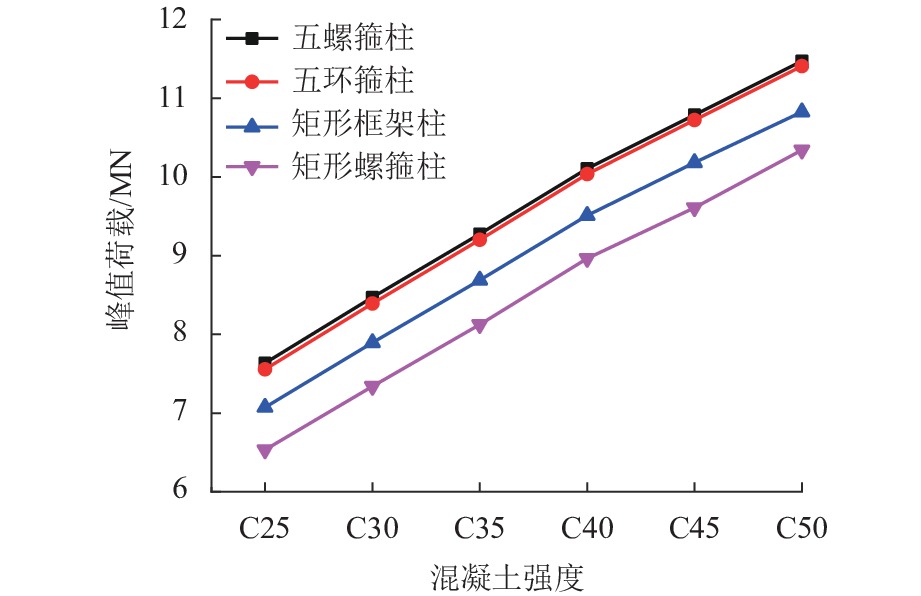
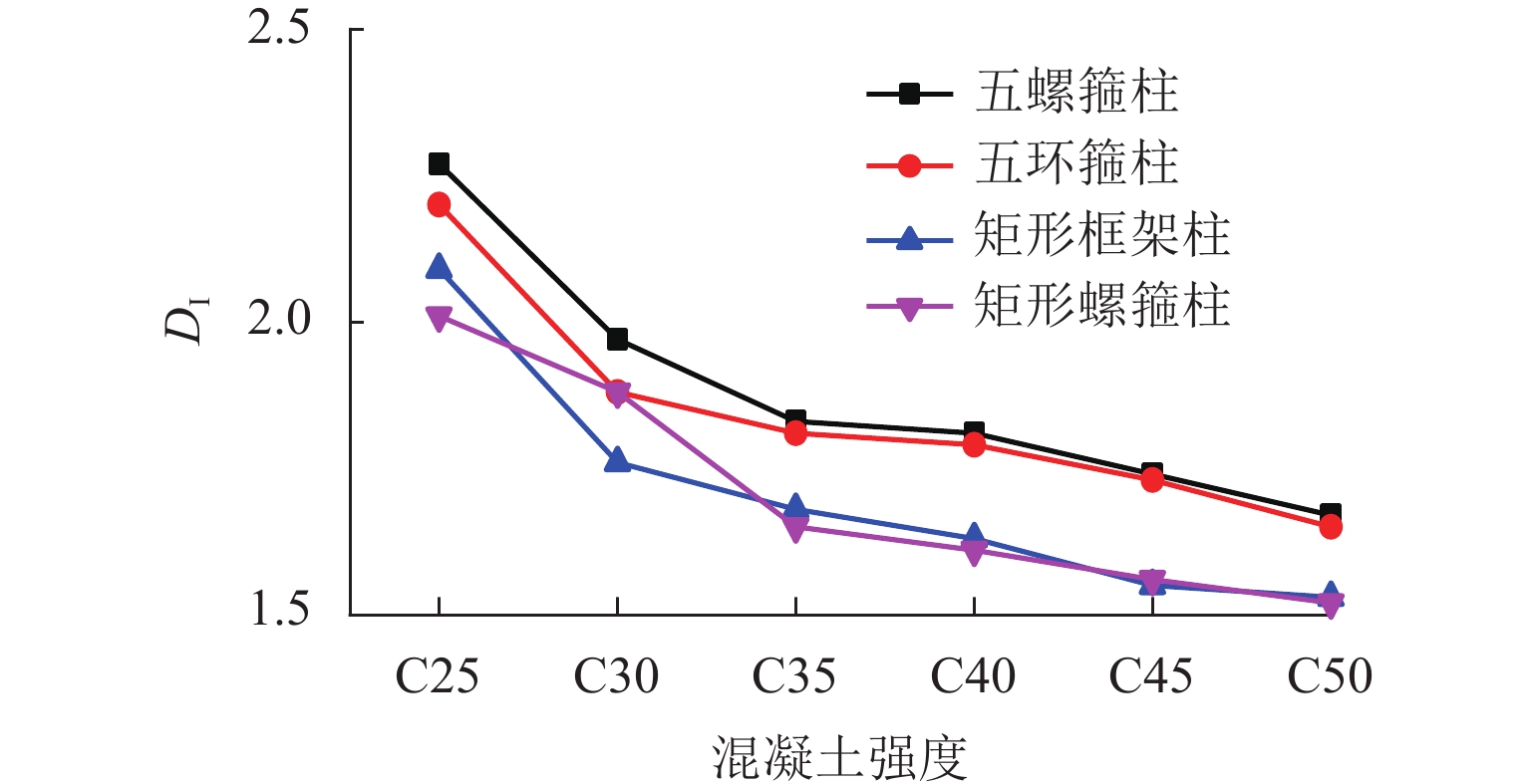
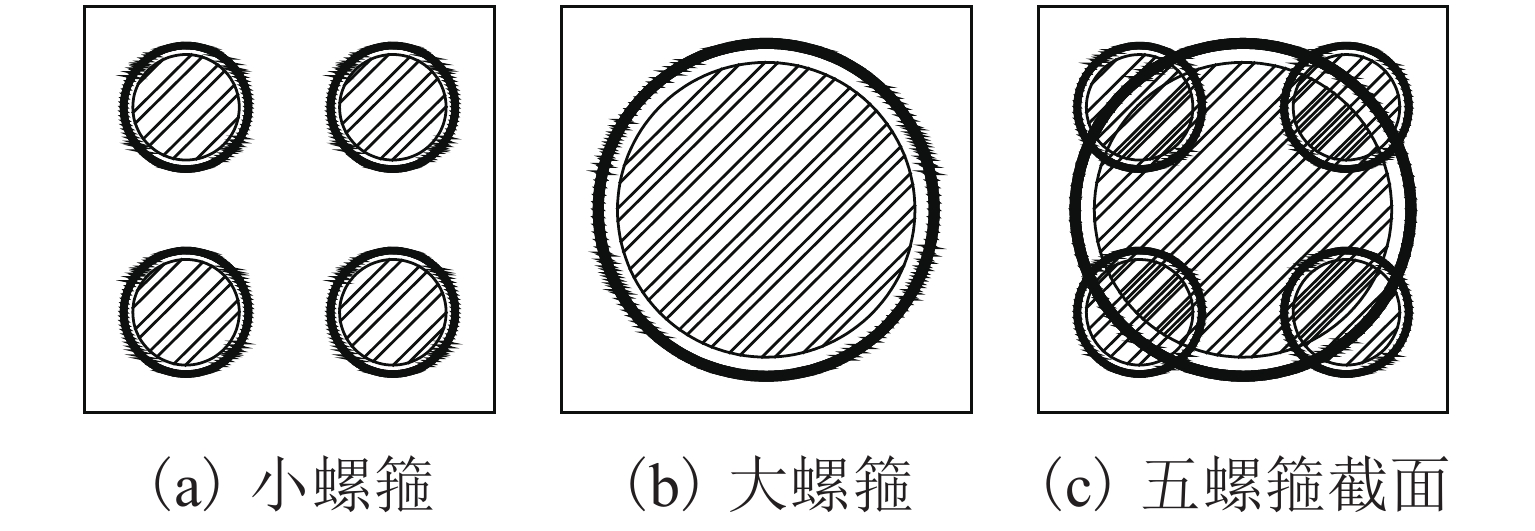
螺旋箍筋应用于钢筋混凝土柱能明显提高柱的承载力及延性，为了研究五螺箍矩形混凝土短柱在轴心受压荷载作用下的力学性能和轴压承载力计算方法，首先，结合已有文献中的试验建立有限元模型，并将有限元分析结果与试验结果进行对比，以验证有限元模型的正确性；其次，基于材料用量相等的原则，设计了4种不同配箍形式的矩形截面柱，基于已验证了的有限元模型开展了不同混凝土强度对上述4种柱的轴压承载力和延性的影响研究；最后，通过对五螺箍柱进行参数分析，提出了基于体积配箍率的轴压承载力计算方法. 研究结果表明：五螺箍较五环箍、矩形箍和矩形螺旋箍柱构件承载力均值分别提高0.78%、6.70%和13.73%，延性系数均值分别提高2.00%、10.32%和10.41%，说明五螺箍柱有较高的承载力和延性；与各国规范提出的公式进行对比，本文建议的轴压承载力计算方法较为简便，且与试验值的误差均值仅为2.83%.
Abstract:Application of spiral stirrups can obviously improve the axial bearing capacity and ductility of reinforced concrete (RC) columns. This paper aims to study the mechanical properties of rectangular short RC columns confined with five-spiral stirrups under axial compression and to present a calculation method for the axial compression bearing capacity by finite element analysis of a number of concrete short column specimens under axial compressive loading. Firstly, a finite element model is established on the basis of experiments available in the literature, and the finite element analytical results are compared with experimental values to verify the correctness of the finite element model. Subsequently, the finite element model is used in a parametric analysis to study the likely influence of concrete strength on the axial bearing capacity and ductility of rectangular short columns with 4 different stirrup configurations which are designed in a principle of equal material consumption. Finally, through analysis of influencing factors for the rectangular short RC columns confined with five-spiral stirrups, a calculation method of axial compression bearing capacity based on volume-stirrup ratio is proposed. The analysis results show that compared with those of RC columns with five-hoop stirrups, rectangular stirrups and rectangular-spiral stirrups, the average bearing capacity of the RC columns with the five-spiral stirrups is increased by 0.78%, 6.70%, and 13.73%, respectively; and the average ductility coefficient is increased by 2.00%, 10.32%, and 10.41%, respectively. It demonstrats that the five-spiral stirrup columns have higher bearing capacity and ductility. In addition, compared to the formulas recommended by codes of different countries, the calculation method of axial compression bearing capacity proposed in this paper is relatively simple, and the average error between calculation and experimental values is only 2.83%.
-
图 2 4种不同配箍形式矩形截面柱
Figure 2. Four types of rectangular columns with different stirrup configurations
图 7 约束作用系数-体积配箍率关系
Figure 7. Relationship between confinement coefficients and volume-stirrup ratios
表 1 试验和有限元计算结果对比
Table 1. Comparison of experiment and finite element calculation results
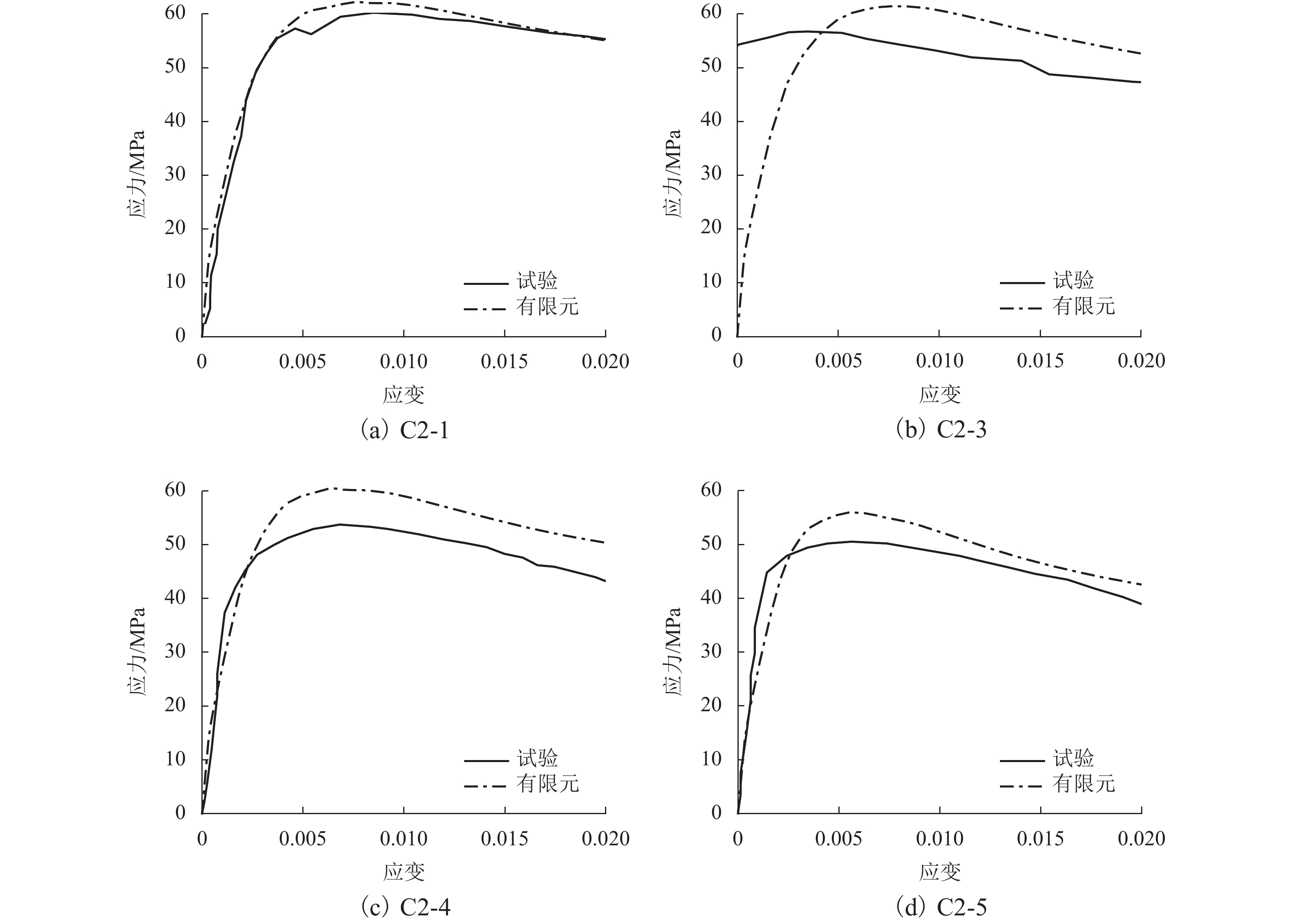
试件编号 材料强度/MPa 钢筋配置/mm 轴压承载力/kN 混凝土 纵筋 大螺箍 小螺箍 纵筋 大螺箍 小螺箍 试验值 模拟值 误差/% C2-1 39.4 420 280 280 D25 D13@50 D13@50 21670 22378 3.26 C2-3 40.3 D16@70 D13@70 20411 22109 8.32 C2-4 40.3 D13@60 D13@60 19336 21749 12.47 C2-5 39.4 D10@50 D10@50 18181 20128 10.70 
下载: 导出CSV
表 2 有限元模型主要参数
Table 2. Main parameters of finite element models
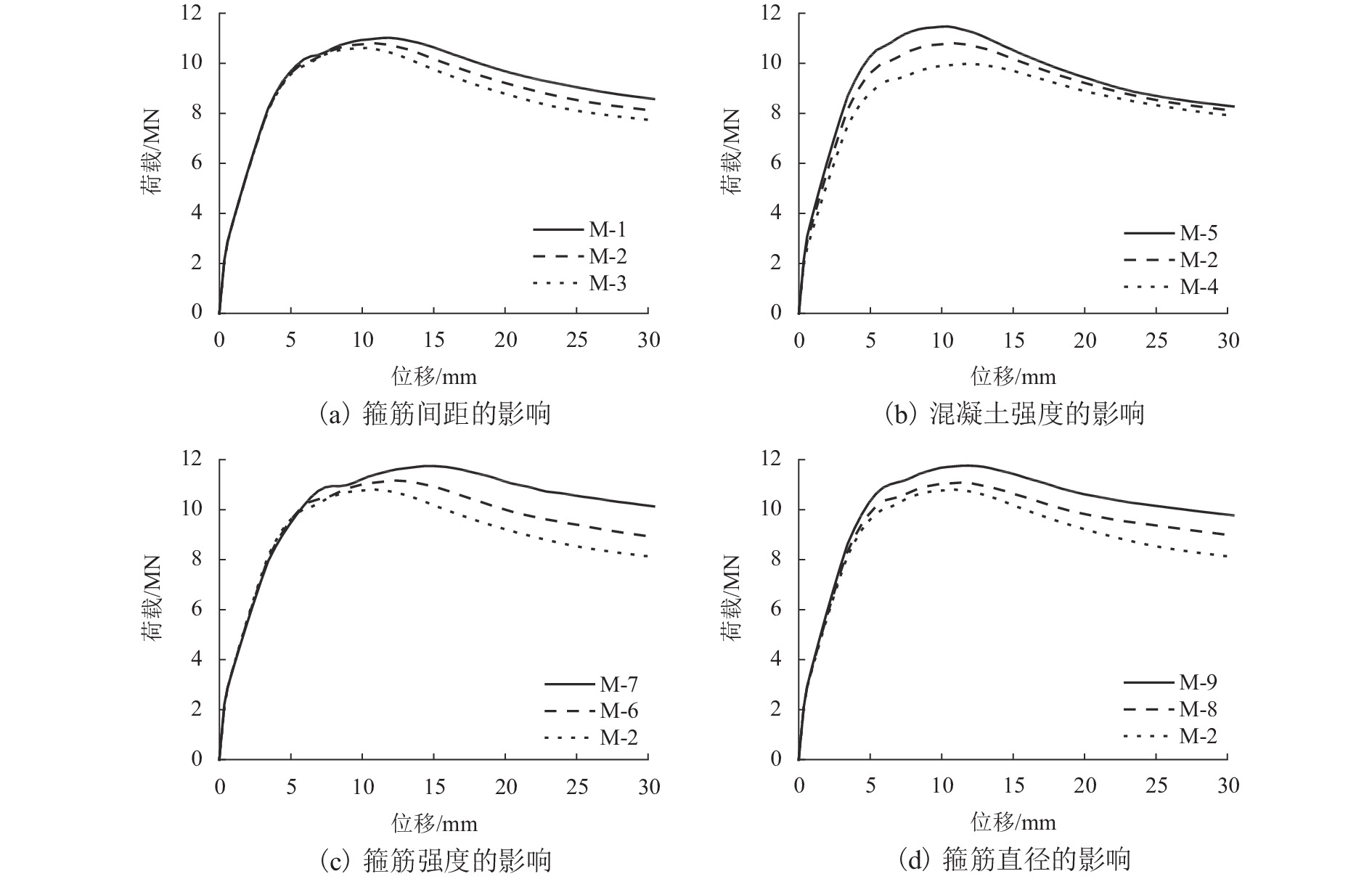
编号 螺旋箍筋
间距/mm螺旋箍筋
强度/MPa混凝土
强度/MPa大（小）螺箍
直径/mm体积配箍率/% 峰值荷载/kN DI M-1 45 335 26.8 10(6) 2.15 11020.60 1.84 M-2 50 335 26.8 10(6) 1.93 10779.40 1.78 M-3 55 335 26.8 10(6) 1.76 10613.50 1.76 M-4 50 335 23.4 10(6) 1.93 9979.90 1.97 M-5 50 335 29.6 10(6) 1.93 11472.50 1.75 M-6 50 400 26.8 10(6) 1.93 11163.90 1.94 M-7 50 500 26.8 10(6) 1.93 11744.80 2.16 M-8 50 335 26.8 10(8) 2.45 11078.90 2.13 M-9 50 335 26.8 12(8) 3.01 11756.80 2.27
下载: 导出CSV
表 3 9个模型的轴压承载力计算
Table 3. Axial compression bearing capacity calculation of nine models
编号 模拟值 Nue/kN 计算值/kN 相对误差/% ${N_{{\text{u1}}}}$ ${N_{{\text{u2}}}}$ ${N_{{\text{u3}}}}$ ${N_{{\text{u4}}}}$ ${N_{{\text{u5}}}}$ ${\delta _{\text{1}}}$ $ {\delta _{\text{2}}} $ ${\delta _{\text{3}}}$ ${\delta _{\text{4}}}$ ${\delta _{\text{5}}}$ M-1 11020.60 10024.25 10459.24 6543.56 7871.88 11039.23 −9.04 −5.09 −40.62 −28.57 0.17 M-2 10779.40 9601.01 10019.12 6543.56 7871.88 10675.10 −10.93 −7.05 −39.30 −26.97 −0.97 M-3 10613.50 9258.53 9656.58 6543.56 7871.88 10373.72 −12.77 −9.02 −38.35 −25.83 −2.26 M-4 9979.90 9001.25 9362.72 6002.76 7162.57 9610.15 −9.81 −6.18 −39.85 −28.23 −3.70 M-5 11472.50 10094.93 10555.22 6988.93 8456.03 11552.11 −12.01 −8.00 −39.08 −26.29 0.69 M-6 11163.90 10104.07 10515.16 6543.56 7871.88 11386.56 −9.49 −5.81 −41.39 −29.49 1.99 M-7 11744.80 10878.01 11257.04 6543.56 7871.88 12481.12 −7.38 −4.15 −44.29 −32.98 6.27 M-8 11078.90 10056.88 10453.68 6543.56 7871.88 11110.52 −9.22 −5.64 −40.94 −28.95 0.29 M-9 11756.80 10962.58 11334.17 6543.56 7871.88 11579.44 −6.76 −3.59 −44.34 −33.04 −1.51 绝对值均值 9.71 6.06 40.91 28.93 1.98 标准差 0.0197 0.0175 0.0215 0.0261 0.0195
下载: 导出CSV
表 4 4个试验构件的轴压承载力
Table 4. Axial compression bearing capacity calculation of four test members
编号 试验值[16]/kN 计算值/kN 相对误差/% ${N_{{\text{u1}}}} $ ${N_{{\text{u2}}}} $ ${N_{{\text{u3}}}} $ ${N_{{\text{u4}}}} $ ${N_{{\text{u5}}}} $ ${\delta _{\text{1}}} $ ${\delta _{\text{2}}} $ ${\delta _{\text{3}}} $ ${\delta _{\text{4}}} $ ${\delta _{\text{5}}} $ C2-1 21672.00 20569.22 21094.45 12090.38 11518.40 22156.09 −5.09 −2.66 −44.21 −46.85 2.23 C2-2 20412.00 19005.14 19508.17 12291.21 11706.16 20390.35 −6.89 −4.43 −39.78 −42.65 −0.11 C2-4 19332.00 19334.76 19871.39 12291.21 11706.16 20319.01 0.01 2.79 −36.42 −39.45 5.11 C2-5 18181.00 17305.58 17781.27 12090.38 11518.40 18883.65 −4.82 −2.20 −33.50 −36.65 3.86 绝对值均值 4.20 3.02 38.48 41.40 2.83 标准差 0.029 4 0.009 7 0.046 0 0.043 9 0.021 6
下载: 导出CSV
-
[1] 尹衍梁,王瑞祯,吴子良,等. 自动化加工五螺旋箍筋柱研发试验综述[J]. 城市住宅,2015(10): 114-118.YIN Yanliang, WANG Ruizhen, WU Ziliang, et al. The survey of experiments in automated forming multi-spiral stirrup columns[J]. City & House, 2015(10): 114-118. [2] American Concrete Institute. Building code requirements for structural concrete and commentary: ACI 318-08[S]. Farminton Hills: ACI Committee 318, 2008. [3] ABDEL-HALIM MOHAMED A H, ABU-LEBDEH TAHEY M. Analytical study for concrete confinement in tied columns[J]. Journal of Structural Engineering, 1989, 115(11): 2810-2828. doi: 10.1061/(ASCE)0733-9445(1989)115:11(2810) [4] MANDER J B, PRIESTLEY M J N, PARK R. Theoretical stress-strain model for confined concrete[J]. Journal of Structural Engineering, 1988, 114(8): 1804-1826. doi: 10.1061/(ASCE)0733-9445(1988)114:8(1804) [5] ASSA B, NISHIYAMA M, WATANABE F. New approach for modeling confined concrete II: rectangular columns[J]. Journal of Structural Engineering, 2001, 127(7): 751-757. doi: 10.1061/(ASCE)0733-9445(2001)127:7(751) [6] BING L, PARK R, TANAKA H. Stress-strain behavior of high-strength concrete confined by ultra-high and normal-strength transverse reinforcements[J]. ACI Structural Journal, 2001, 98(3): 395-406. [7] 过镇海, 张秀琴, 张达成, 等. 混凝土应力-应变全曲线的试验研究[J]. 建筑结构学报, 1982, 3(1): 1-12. GUO Zhenhai, ZHANG Xiuqin, ZHANG Dacheng, et al. Experimental investigation of the complete stress-strain curve of concrete[J]. Journal of Building Structures, 1982, 3(1): 1-12. [8] 张秀琴,过镇海,王传志. 反复荷载下箍筋约束混凝土的应力-应变全曲线方程[J]. 工业建筑,1985(12): 16-20. [9] 唐琼,李易,陆新征,等. 多螺箍筋柱轴压承载力研究[J]. 工程力学,2018(增1): 166-171. doi: 10.6052/j.issn.1000-4750.2017.06.S033TANG Qiong, LI Yi, LU Xinzheng, et al. Study on axial compression capacity of multi-spiral hoops confined concrete columns[J]. Engineering Mechanics, 2018(S1): 166-171. doi: 10.6052/j.issn.1000-4750.2017.06.S033 [10] 史庆轩,杨坤,刘维亚,等. 高强箍筋约束高强混凝土轴心受压力学性能试验研究[J]. 工程力学,2012,29(1): 141-149.SHI Qingxuan, YANG Kun, LIU Weiya, et al. Experimental study on mechanical behavior of high strength concrete confined by high-strength stirrups under concentric loading[J]. Engineering Mechanics, 2012, 29(1): 141-149. [11] 翁正強,尹衍樑,王瑞禎,等. 五螺箍矩形RC柱之軸壓試驗與優化設計研究[J]. 結構工程,2010,25(1): 71-105.WENG Zhengqiang, YIN Yanliang, WANG Ruizhen, et al. Experimental studies of reinforced concrete confined by multi-spiral hoops[J]. Structural Engineering, 2010, 25(1): 71-105. [12] 郑亮. 配螺旋箍筋方钢管混凝土柱计算方法及试验研究[D]. 天津: 天津大学, 2013. [13] 傅明月. 五螺箍预制混凝土方柱受力性能分析[D]. 广州: 广州大学, 2018. [14] LIANG C Y, CHEN C C, WENG C C, et al. Axial compressive behavior of square composite columns confined by multiple spirals[J]. Journal of Constructional Steel Research, 2014, 103: 230-240. doi: 10.1016/j.jcsr.2014.09.006 [15] 张战廷,刘宇锋. ABAQUS中的混凝土塑性损伤模型[J]. 建筑结构,2011,41(增2): 229-231.ZHANG Zhanting, LIU Yufeng. Concrete damaged plasticity model in ABAQUS[J]. Building Structure, 2011, 41(S2): 229-231. [16] 王柄雄. 新矩形混凝土柱约束型式之研究[D]. 台湾: 台湾大学, 2004. [17] 中华人民共和国建设部. 建筑抗震试验方法规程: JGJ 101—96 [S]. 北京: 中国建筑工业出版社, 1997. [18] 中华人民共和国住房和城乡建设部. 混凝土结构设计规范: GB 50010—2010[S]. 北京: 中国建筑工业出版社, 2011. [19] 方登甲,杜永峰,刘成清,等. 复杂多层隔震结构近场地震动位移响应特征分析[J]. 西南交通大学学报,2020,55(1): 158-166, 192. doi: 10.3969/j.issn.0258-2724.20181038FANG Dengjia, DU Yongfeng, LIU Chengqing, et al. Analysis for displacement response characteristics of complex multi-layer base-isolated structure under near-field ground motion[J]. Journal of Southwest Jiaotong University, 2020, 55(1): 158-166, 192. doi: 10.3969/j.issn.0258-2724.20181038 [20] HOBBS D W. Strength of concrete under combined stress[J]. Cement and Concrete Research, 1971, 1(1): 41-56. doi: 10.1016/0008-8846(71)90082-2 -
下载:
点击查看大图
计量
- 文章访问数: 437
- HTML全文浏览量: 188
- PDF下载量: 81
- 被引次数: 0