Deformation Recognition and Prediction of Track Slabs Based on Track Inspection Data
-
摘要:
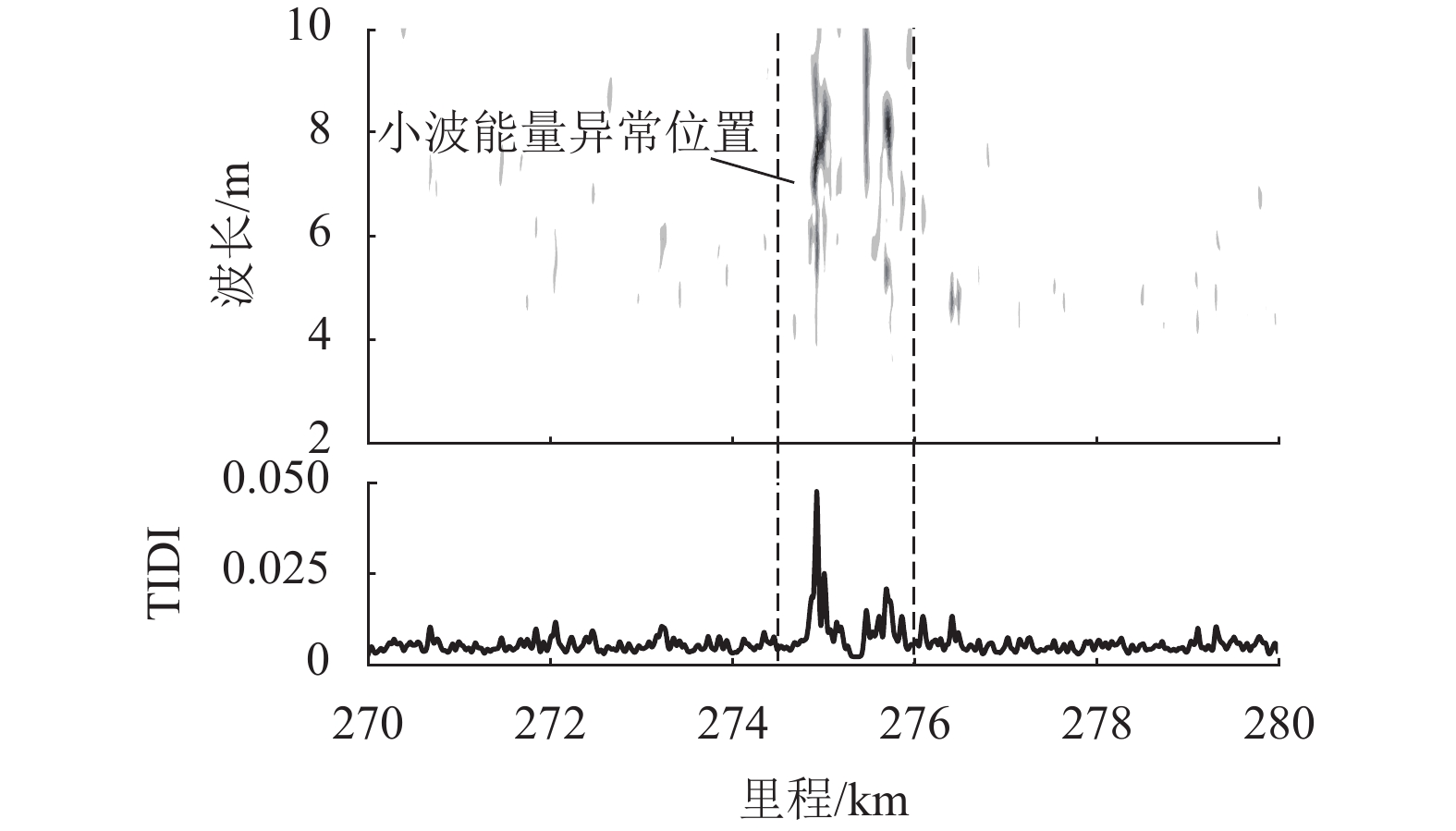
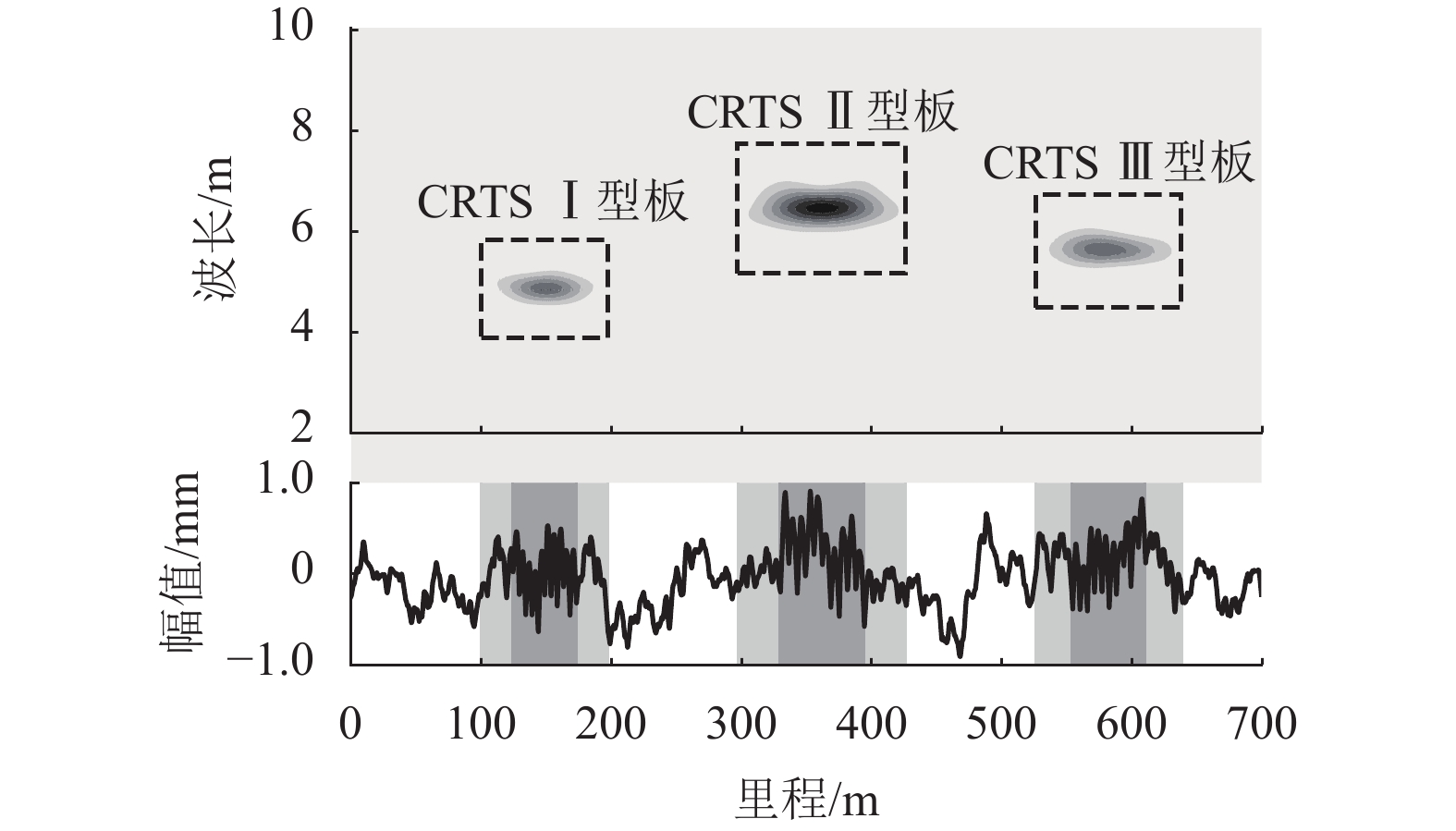
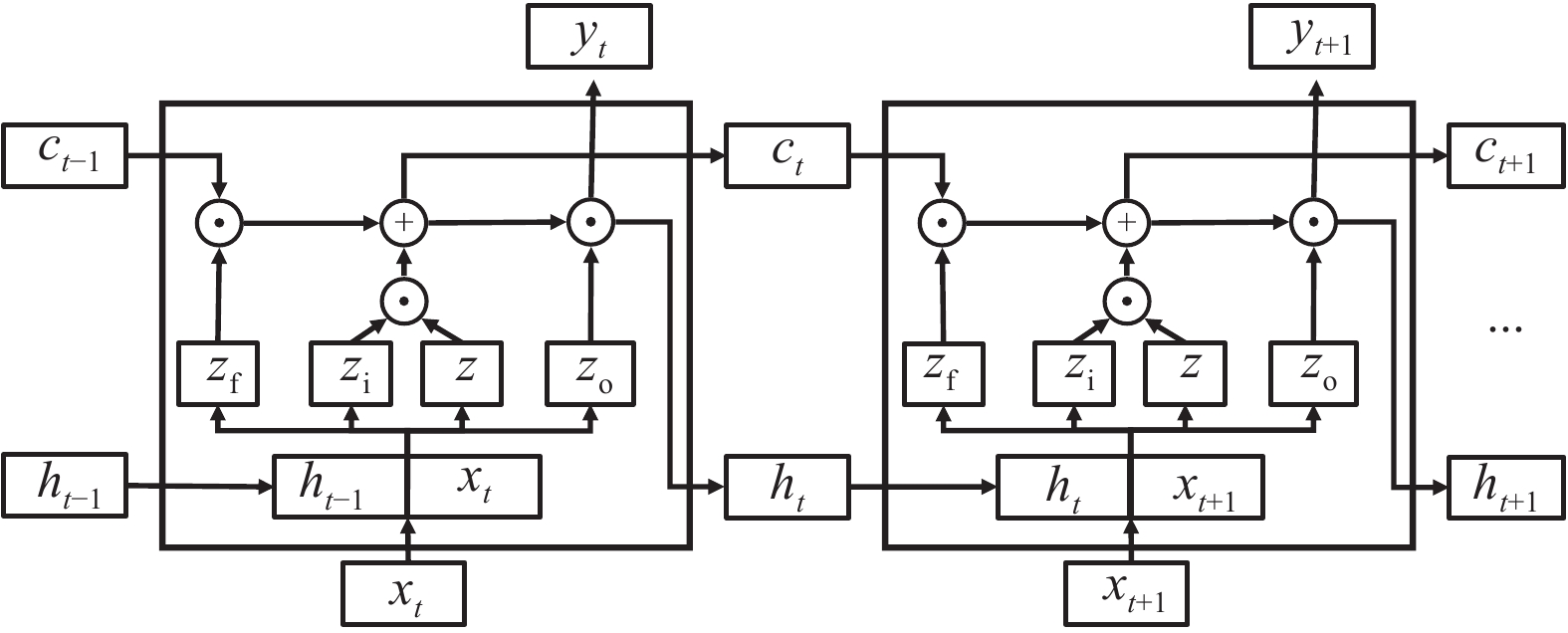
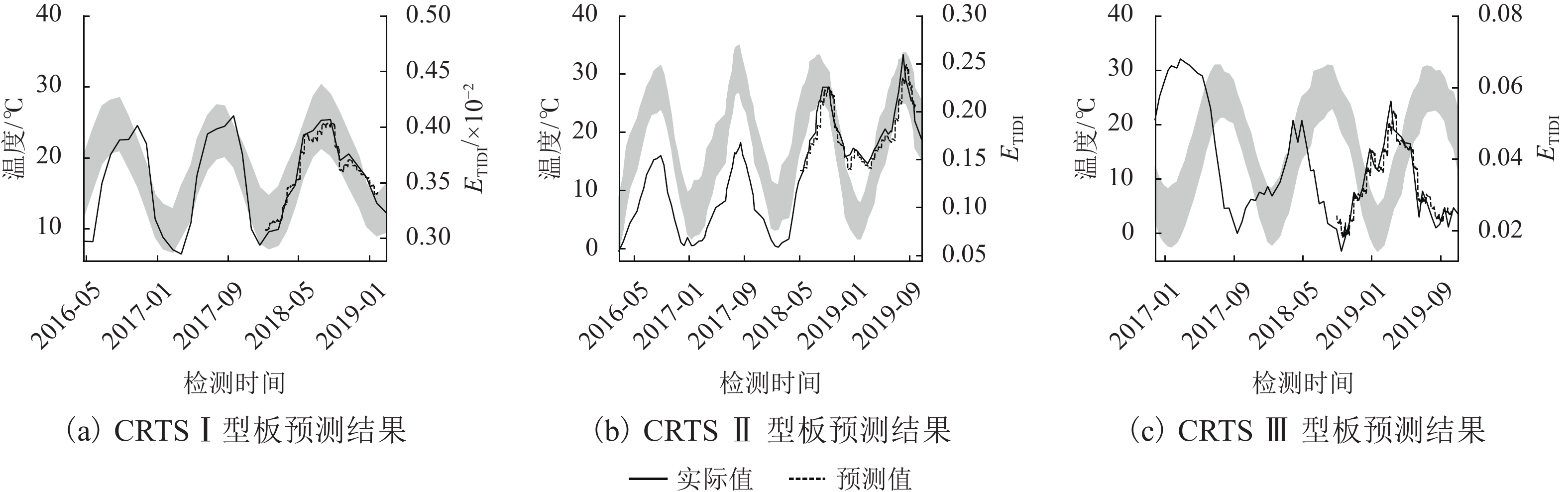
现有对高速铁路板式无砟轨道变形病害的检测效率不足，检测成本过高，而通过轨道动检数据能够一定程度上反映轨道板变形程度. 因此，搜集了CRTS Ⅰ、Ⅱ、Ⅲ型板线路3 a内的动检数据，引入小波能量作为轨道板变形评价指标，通过建立时空数据挖掘模型实现了不同轨道板的变形定位识别和劣化预测. 研究结果表明：受当地气温影响，轨道板变形程度具有一定的季节性规律，Ⅰ、Ⅱ型板在高温环境下出现翘曲或上拱，Ⅲ型板在低温环境下出现冻胀；3种轨道板中Ⅰ型板变形程度最小，Ⅱ型板最大，Ⅱ型板的残余变形会随时间累积，最终导致高低不平顺超限；长短期记忆网络能够实现对轨道板变形指标15～30 d内的短中期预测，Ⅰ型板变形的最佳预测结果R-square值接近0.9，而Ⅱ型板、Ⅲ型板变形的最佳预测R-square值均超过0.9.
Abstract:Existing methods for detecting deformation of high-speed railway slab ballastless tracksis low in efficiency and high in cost, while the track dynamic geometry inspection data can reflect the deformation level of slabs in a way.In this work, the track dynamic inspection data of railway lines of CRTS Ⅰ, Ⅱ, Ⅲ slabs within three years were collected and the wavelet energy was used as the deformation evaluation index of track slab. Finally, a temporal-spatial data mining model was proposed to realize the recognition and degradation prediction of track slabs. The results show that, affected by the local air temperature, the deformationlevel of track slabs has a seasonal pattern.Type-Ⅰ and type-Ⅱ slabs display warping and arching deformation in a high-temperature environment, while type-Ⅲ slab shows frost heavingin a low-temperature environment. Of the three types of track slabs, the deformation level of type-Ⅰ slab is mild, while the type-Ⅱ slab is most severe. The residual deformation of type-Ⅱ slab will accumulate over time, which may eventually lead to surface irregularity exceeding the limit. The long-term and short-term memory network can realize short- and mid-term prediction of the track slab deformation within 15 to 30 days. The the best predictionR-square value of the type-Ⅰ platedeformation is close to 0.9, while that of the type-Ⅱ and type-Ⅲ plate deformations exceeds 0.9.
-
图 1 不同轨道板的变形特征波长统计结果
Figure 1. Statistical results of deformation characteristic wavelength for different track slabs
图 6 温度与各类轨道板变形相关性分析
Figure 6. Correlation analysis between temperature and deformation of different track slabs
表 1 工况设置参数
Table 1. Parameters of operation condition
参数 CRTS Ⅰ
型板CRTS Ⅱ
型板CRTS Ⅲ
型板结构跨数/个 20 20 20 结构长度/mm 4856 6450 5600 异常位置/m 124～172 329～393 554～610 正常幅值（最大
值）/mm0.2 0.2 0.2 异常幅值（最大
值）/mm0.6 0.6 0.6 
下载: 导出CSV
表 2 不同轨道板预测结果的R-square值
Table 2. R-square values of prediction results for different track slabs
历史数据时间长度/d CRTS Ⅰ型板 CRTS Ⅱ型板 CRTS Ⅲ型板 15 d 30 d 45 d 15 d 30 d 45 d 15 d 30 d 45 d 15 0.85 0.66 0.61 0.92 0.81 0.76 0.92 0.84 0.64 30 0.88 0.75 0.57 0.91 0.82 0.74 0.93 0.85 0.65 45 0.88 0.75 0.67 0.91 0.80 0.76 0.93 0.86 0.74
下载: 导出CSV
-
[1] 王继军,尤瑞林,王梦,等. 单元板式无砟轨道结构轨道板温度翘曲变形研究[J]. 中国铁道科学,2010,31(3): 9-14.WANG Jijun, YOU Ruilin, WANG Meng, et al. Research on the slab temperature warping of the unit slab track system[J]. China Railway Science, 2010, 31(3): 9-14. [2] 孙加林,宣俊伟. 高速铁路CTRSⅡ型板式无砟轨道温度场效应分析[J]. 青岛大学学报(自然科学版),2016,29(2): 86-89.SUN Jialin, XUAN Junwei. Study on temperature responses of CTRSⅡslab ballastless track of high-speed railway[J]. Journal of Qingdao University (Natural Science Edition), 2016, 29(2): 86-89. [3] 肖威,郭宇,高建敏,等. 高速铁路路基不均匀沉降对CRTS Ⅲ板式轨道受力变形的影响[J]. 铁道科学与工程学报,2015,12(4): 724-730. doi: 10.3969/j.issn.1672-7029.2015.04.002XIAO Wei, GUO Yu, GAO Jianmin, et al. Effect of uneven subgrade settlement on the CRTS Ⅲ slab track stress and deformation of high-speed railway[J]. Journal of Railway Science and Engineering, 2015, 12(4): 724-730. doi: 10.3969/j.issn.1672-7029.2015.04.002 [4] 邵丕彦,李海燕,吴韶亮,等. CRTSⅠ型轨道板温度变形及与砂浆垫层间离缝的测试研究[J]. 中国铁道科学,2013,34(2): 18-22. doi: 10.3969/j.issn.1001-4632.2013.02.04SHAO Piyan, LI Haiyan, WU Shaoliang, et al. Measurement and research on temperature warping of CRTSⅠ track slab and crack between track slab and cement asphalt mortar cushion[J]. China Railway Science, 2013, 34(2): 18-22. doi: 10.3969/j.issn.1001-4632.2013.02.04 [5] GOU H Y, YANG L C, LENG D, et al. Effect of bridge lateral deformation on track geometry of high-speed railway[J]. Steel and Composite Structures, 2018, 29(2): 219-229. [6] 杨静静,高芒芒,杨飞,等. CRTSⅡ型轨道板上拱变形及对钢轨的影响[J]. 铁道建筑,2019,59(10): 104-108. doi: 10.3969/j.issn.1003-1995.2019.10.25YANG Jingjing, GAO Mangmang, YANG Fei, et al. Heaving deformation of CRTSⅡ track slab and its influence on rail[J]. Railway Engineering, 2019, 59(10): 104-108. doi: 10.3969/j.issn.1003-1995.2019.10.25 [7] 杨静静,张楠,高芒芒,等. CRTSⅡ型无砟轨道温度翘曲变形及其对车线动力响应的影响[J]. 工程力学,2016,33(4): 210-217.YANG Jingjing, ZHANG Nan, GAO Mangmang, et al. Temperature warping and it's impact on train-track dynamic response of CRTS Ⅱ ballastless track[J]. Engineering Mechanics, 2016, 33(4): 210-217. [8] SONG X L, ZHAO C F, ZHU X J. Temperature-induced deformation of CRTS Ⅱ slab track and its effect on track dynamical properties[J]. Science China Technological Sciences, 2014, 57(10): 1917-1924. doi: 10.1007/s11431-014-5634-x [9] 李全鹏. 温度和车辆荷载作用下CRTS Ⅲ型无砟轨道板损伤数值模拟分析[D]. 成都: 西南交通大学, 2018. [10] 高霞. 寒冷地区CRTS Ⅲ型板式无砟轨道力学特性研究[D]. 北京: 北京交通大学, 2014. [11] ZHAO P R, LIU X Y, LIU G. Experimental study of temperature gradient in track slab under outdoor conditions in Chengdu area[J]. Journal of Modern Transportation, 2014, 22(3): 148-155. doi: 10.1007/s40534-014-0050-2 [12] CAÑETE E, CHEN J, DÍAZ M, et al. Wireless sensor networks and structural health monitoring: experiences with slab track infrastructures[J]. International Journal of Distributed Sensor Networks, 2019, 15(3): 1-16. [13] WANG Q A, NI Y Q. Measurement and forecasting of high-speed rail track slab deformation under uncertain SHM data using variational heteroscedastic Gaussian process[J]. Sensors, 2019, 19(15): 3311.1-3311.18. doi: 10.3390/s19153311 [14] XU P, SUN Q X, LIU R K, et al. Key Equipment identification model for correcting milepost errors of track geometry data from track inspection cars[J]. Transportation Research Part C:Emerging Technologies, 2013, 35: 85-103. doi: 10.1016/j.trc.2013.06.006 [15] 汪鑫,王平,陈嵘,等. 基于多次波形匹配的高速铁路动检数据里程误差评估与修正[J]. 铁道学报,2020,42(2): 110-116.WANG Xin, WANG Ping, CHEN Rong, et al. Mileage error estimation and correction for high-speed railway track inspection data based on multiple data waveform[J]. Journal of the China Railway Society, 2020, 42(2): 110-116. [16] 李帅. 高速铁路轨道谱典型特征辨识及演化规律分析[D]. 成都: 西南交通大学, 2018. [17] TORRENCE C, COMPO G P. A practical guide to wavelet analysis[J]. Bulletin of the American Meteorological Society, 1998, 79(1): 61-78. doi: 10.1175/1520-0477(1998)079<0061:APGTWA>2.0.CO;2 [18] NAGARAJAIAH S, BASU B. Output only modal identification and structural damage detection using time frequency & wavelet techniques[J]. Earthquake Engineering and Engineering Vibration, 2009, 8(4): 583-605. doi: 10.1007/s11803-009-9120-6 [19] 赵林,刘学毅,毕澜潇,等. 高温荷载下CRTSⅡ型板式轨道上拱变形特性研究[J]. 铁道科学与工程学报,2019,16(2): 277-286.ZHAO Lin, LIU Xueyi, BI Lanxiao, et al. Study on upwarp deformation characteristics of CRTSⅡ prefrabricated track slab under high temperature load[J]. Journal of Railway Science and Engineering, 2019, 16(2): 277-286. [20] SHEATHER S J, JONES M C. A reliable data-based bandwidth selection method for kernel density estimation[J]. Journal of the Royal Statistical Society:Series B (Methodological), 1991, 53(3): 683-690. doi: 10.1111/j.2517-6161.1991.tb01857.x [21] HOCHREITER S, SCHMIDHUBER J. Long short-term memory[J]. Neural Computation, 1997, 9(8): 1735-1780. doi: 10.1162/neco.1997.9.8.1735 -
下载:
点击查看大图
计量
- 文章访问数: 239
- HTML全文浏览量: 144
- PDF下载量: 23
- 被引次数: 0