Temporal and Spatial Variation of Permeability Coefficient of Seasonal Frozen Soil in Western Sichuan
-
摘要: 冻融循环作用引起的边坡体内部水分迁移是川西地区季节冻土边坡失稳的主要原因，研究边坡土体渗透系数时间、空间变化特征是掌握水分迁移规律的重要手段. 针对冻融循环作用下季节性冻土坡面渗透系数时空变化问题，选取川西新都桥地区某边坡粗颗粒土为测试土样，设计冻土渗透系数试验装置，以30%乙二醇溶液为试验渗透溶液，分别制备不同初始含水率、细颗粒含量、干密度测试土柱；添加30%乙二醇放至低恒温箱中进行12 h以上冷冻处理，开展不同冻融循环次数作用下冻土渗透系数试验,并分析其渗透系数变化规律；在此基础上结合边坡冻融期含水率现场监测数据，分析渗透系数时空变化规律. 试验结果表明：初始含水量及干密度不断增加时，冻土非闭合孔隙度和渗透系数均呈减小趋势；冻土渗透系数随细颗粒含量的增加而减小，当细颗粒含量大于20%时，冻土渗透系数减小的幅度较小；冻融循环次数对冻土渗透性能起到抑制作用，当循环次数超过3次时，冻融作用对渗透性能影响不大；季节性冻土边坡1 m冻结深度以内，渗透系数随深度增加减小；11月—1月冻深范围内冻土渗透系数减小，1月—3月渗透系数开始增大.Abstract: The moisture migration caused by freeze-thaw cycle is the main reason for the instability of seasonal frozen soil slope in western Sichuan Province. It is an important means to master the rule of water migration by studying the spatiotemporal variation characteristics of permeability coefficient of slope soil. In view of the spatiotemporal variation of permeability coefficient of seasonal frozen soil slope under the action of freeze-thaw cycle, permafrost permeability coefficient tests were conducted on a self-developed device using the coarse-grained soil sample from a slope in Xinduqiao area of western Sichuan Province. The test soil columns with different initial moisture contents, fine particle contents and dry densities were prepared with the osmotic solution of 30% ethylene glycol, and then placed into the low constant temperature box for more than 12 h freezing treatment. The permafrost permeability coefficient tests under different freeze-thaw cycles were then carried out and variations of the permafrost permeability coefficient was analyzed. On this basis, combined with the on-site monitoring data of water content of slope in freeze-thaw period, the spatiotemporal variations of permeability coefficient were analyzed. Experimental results show as follows: with the increase of initial water content and dry density, the open porosity and permeability coefficient of frozen soil decrease. The permeability coefficient of frozen soil decreases with an increase in the fine particle content. When the content of fine particle content is more than 20%, the permeability coefficient of frozen soil decreases slightly. The number of freeze-thaw cycles has an inhibitory effect on the permafrost permeability; however, when the number of cycles is more than 3, the effect of freeze-thaw on the permeability of frozen soil is not significant. Within 1 m frozen depth of seasonal frozen soil slope, the permeability coefficient decreases with the increase of depth; in addition, the permafrost permeability coefficient decreases from November to January, and increases from January to March.
-
图 1 冻土坡面渗透系数模拟测试装置
Figure 1. Structure of permafrost slope permeability simulation test equipment
图 2 试样干密度与冻土非闭合孔隙度变化关系
Figure 2. Relationship between dry density and the non closure porosity of frozen soil
图 3 试样干密度与冻土渗透系数变化关系
Figure 3. Relationship between dry density and permafrost permeability coefficient
图 4 冻土初始含水量和非闭合孔隙度之间关系
Figure 4. Relationship between the initial ice content of frozen soil and the non closure porosity in different test groups
图 5 冻土初始含水量和渗透系数之间关系
Figure 5. Relationship between the initial ice content and permeability coefficient of frozen soil in different test groups
图 6 细颗粒含量与冻土非闭合孔隙度变化关系
Figure 6. Relationship between fine particle content and non closure porosity of frozen soil
图 7 细颗粒含量与冻土渗透系数变化关系
Figure 7. Relationship between fine particle content and permafrost permeability coefficient
图 8 冻融循环对冻土非闭合孔隙度影响
Figure 8. Effect of freeze-thaw cycles on non closure porosity of frozen soil
图 9 冻融循环对渗透系数影响
Figure 9. Effect of freeze-thaw cycles on permafrost permeability coefficient
图 10 不同土样非闭合孔隙度与渗透系数变化关系曲线
Figure 10. variation curve of open porosity and permeability coefficient of different soil samples
-
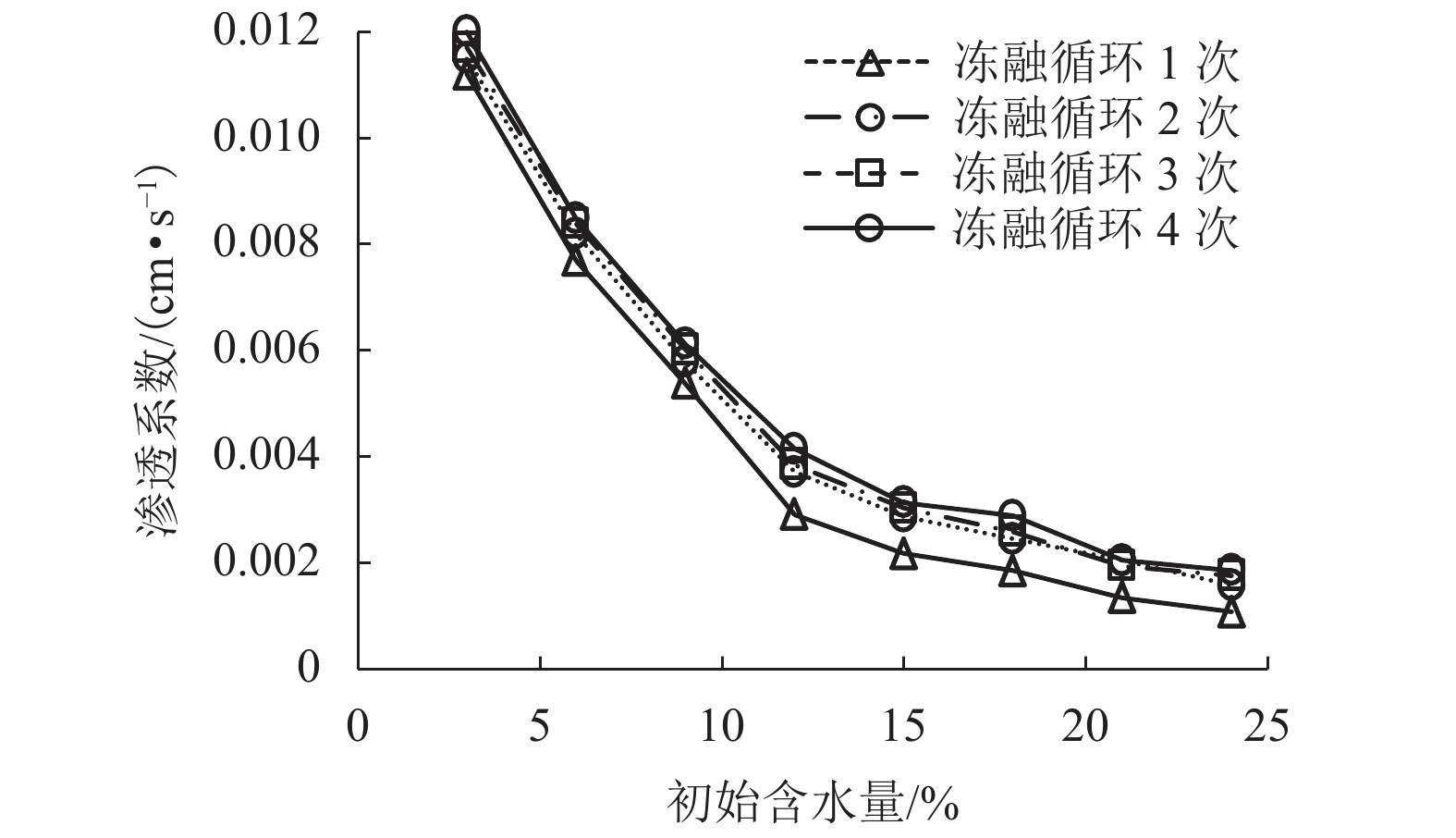
SRIKRISHNAN S S, TATSUYA ISHIKAWA, TETSUYA T. Stability assessment approach for soil slopes in seasonal cold regions[J]. Engineering Geology, 2017, 211: 154-169. 王丽黎. 冻融循环作用对土体边坡稳定性的影响研究[D]. 西安: 长安大学, 2016 杨白祥. 川藏铁路季节性粗颗粒冻土边坡破坏模式的模型试验研究[D]. 成都: 西南交通大学, 2017. 王立娜. 季节冻土区边坡冻融稳定性研究[D]. 哈尔滨: 哈尔滨工业大学, 2008 NIU Fujun, CHENG Guodong, NI Wankui, et al. Engineering-related slope failure in permafrost regions of the Qinghai-Tibet Plateau[J]. Cold Regions Science and Technology, 2005, 42(3): 215-225. doi: 10.1016/j.coldregions.2005.02.002 周志. 冻融循环作用下非饱和路基土水分迁移规律研究[D]. 哈尔滨: 哈尔滨工业大学, 2017. 曾桂军,张明义,李振萍,等. 饱和正冻土水分迁移及冻胀模型研究[J]. 岩土力学,2015,36(4): 1085-1092.ZENG Guijun, ZHANG Mingyi, LI Zhenping, et al. Study of moisture migration and frost heave model of freezing saturated soil[J]. Rock and Soil Mechanics, 2015, 36(4): 1085-1092. NAKAMURA D, SUZUKI T, GOTO T, et al. Changes in the permeability coefficient and the void ratio of compacted soil by the effect of freeze-thaw cycles[J]. Journal of Japan Society of Civil Engineers Ser C, 2011, 67(2): 264-275. MCROBERTS E C, MORGENSTERN N R. The stability of thawing slopes[J]. Canadian Geotechnical Journal, 1974, 11(4): 447-469. doi: 10.1139/t74-052 KONRAD J M. Physical process during freeze-thaw cycles in clayey silts[J]. Cold Regions Science and Technology, 1989, 16(3): 291-303. doi: 10.1016/0165-232X(89)90029-3 LI Ning, CHEN Bo, CHEN Feixong, et al. The coupled heat-moisture-mechanic model of the frozen soil[J]. Cold Regions Science and Technology, 2000, 31(3): 199-205. doi: 10.1016/S0165-232X(00)00013-6 刘飞. 渗流条件下多年冻土区斜坡路基稳定性研究[D].北京: 北京交通人学, 2009. 洪文江. 季节冻土区边坡冻融渗流稳定性研究[D]. 哈尔滨: 哈尔滨工业大学, 2015. SHOOP S A, BIGL S R. Moisture migration during freeze and thaw of unsaturated soils:Modeling and large scale experiments[J]. Cold Regions Science and Technology, 1997, 25(1): 33-45. doi: 10.1016/S0165-232X(96)00015-8 KANE D L. Snowmelt infiltration into seasonally frozen soils[J]. Cold Region Science and Technology, 1980, 3(2/3): 153-161. OTHMAN M A, BENSON C H. Effect of freeze-thaw on the hydraulic conductivity and morphology of compacted clay[J]. Canadian Geotechnical Journal, 1993, 30(2): 236-246. doi: 10.1139/t93-020 VIKLANDER P. Permeability and volume changes in till due to cyclic freeze/thaw[J]. Canadian Geotechnical Journal, 1998, 35(3): 471-477. doi: 10.1139/t98-015 CHAMBERLAIN E J, ISKANDER I, HUNSIKER S E. Effect of freeze-thaw cycles on the permeability and macrostructure of soils[C]//Proceedings of International Symposium on Frozen Soil Impacts on Agricultural. [S.l.]: Army Cold Regions Research and Engineering Laboratory, 1990: 145-155. CHAMBERLAIN E J. Physical changes in clays due to frost action and their effect on engineering structures[C]//Proceedings of the International Symposium on Frost in Geotechnical Engineering. Rotterdam: [s.n.], 1989: 863-893. 梁燕, 邢鲜丽, 李同录, 等. 晚更新世黄土渗透性的各向异性及其机制研究[J]. 岩土力学, 2012, 33(5): 1313-1318.LIANG Yan, XING Xianli, LI Tonglu, et al. Study of the anisotropic permeability and mechanism of Q3 loess[J]. Rock and Soil Mechanics, 2012, 33(5): 1313-1318. 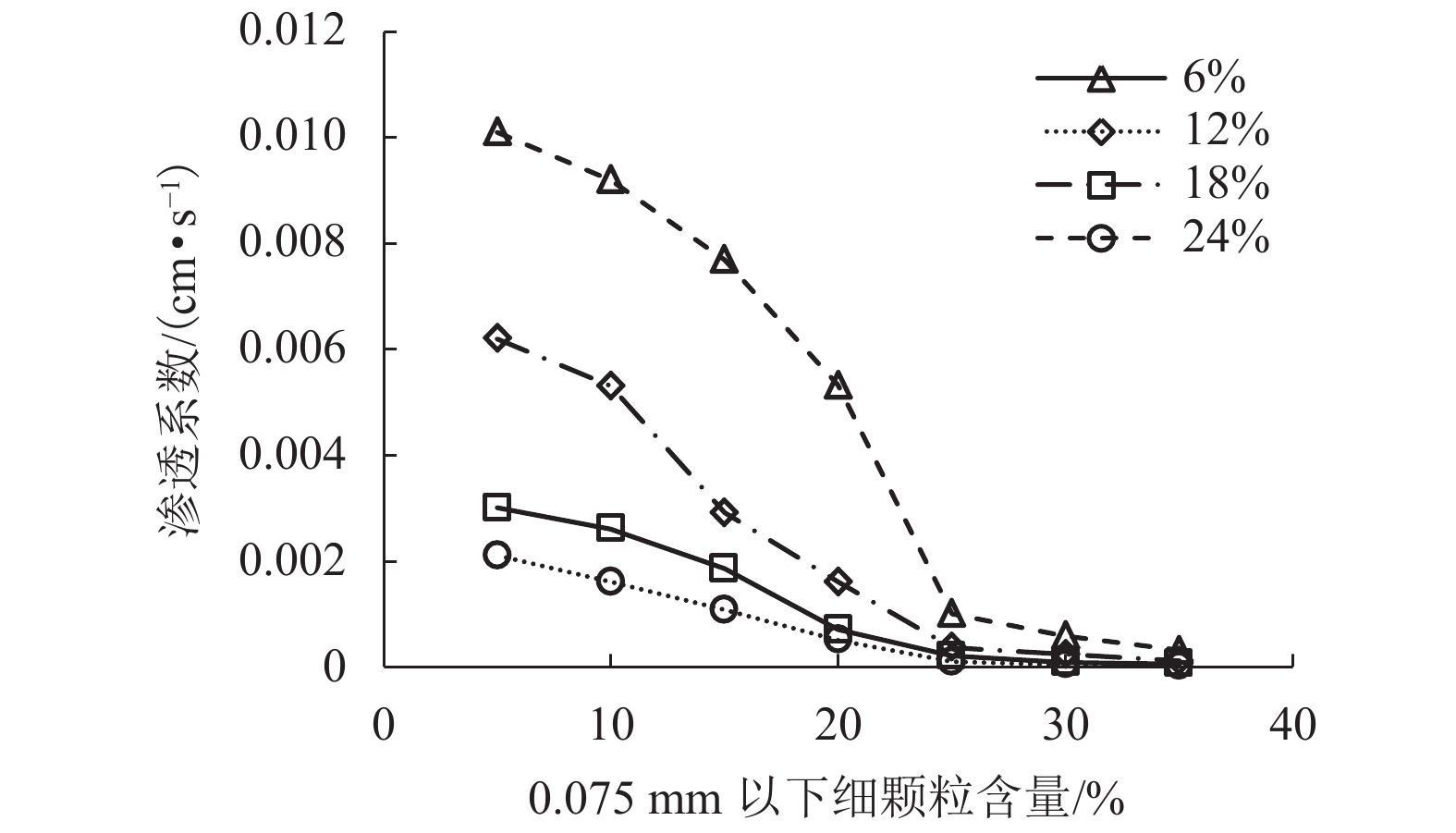肖东辉, 冯文杰, 张泽, 等. 冻融循环对兰州黄土渗透性变化的影响[J]. 冰川冻土, 2014, 36(5): 1192-1198.XIAO Donghui, FENG Wenjie, ZHANG Ze, et al. Research on the Lanzhou loess’s permeabilities changing with freezing-thawing cycles[J]. Journal of Glaciology and Geocryology, 2014, 36(5): 1192-1198 许健,王掌权,任建威,等. 原状与重塑黄土冻融过程渗透特性对比试验研究[J]. 工程地质学报,2017,25(2): 292-299.XU Jian, WANG Zhangquan, REN Jianwei, et al. Comparative experimental study on permeability of undisturbed and remolded loess under freezing-thawing condition[J]. Journal of Engineering Geology, 2017, 25(2): 292-299. 杨晴雯, 裴向军, 黄润秋. 改性钠羧甲基纤维素加固土冻融性能及损伤机制研究[J]. 岩石力学与工程学报, 2019, 38（增刊1）: 3102-3113.YANG Qingwen, PEI Xiangjun, HUANG Runqiu. Research on the effect of freeze and thaw cycles on the property and damage mechanism of M-CMC stabilized soil[J]. Chinese Journal of Rock Mechanics and Engineering, 2019, 38(S1): 3102-3113. 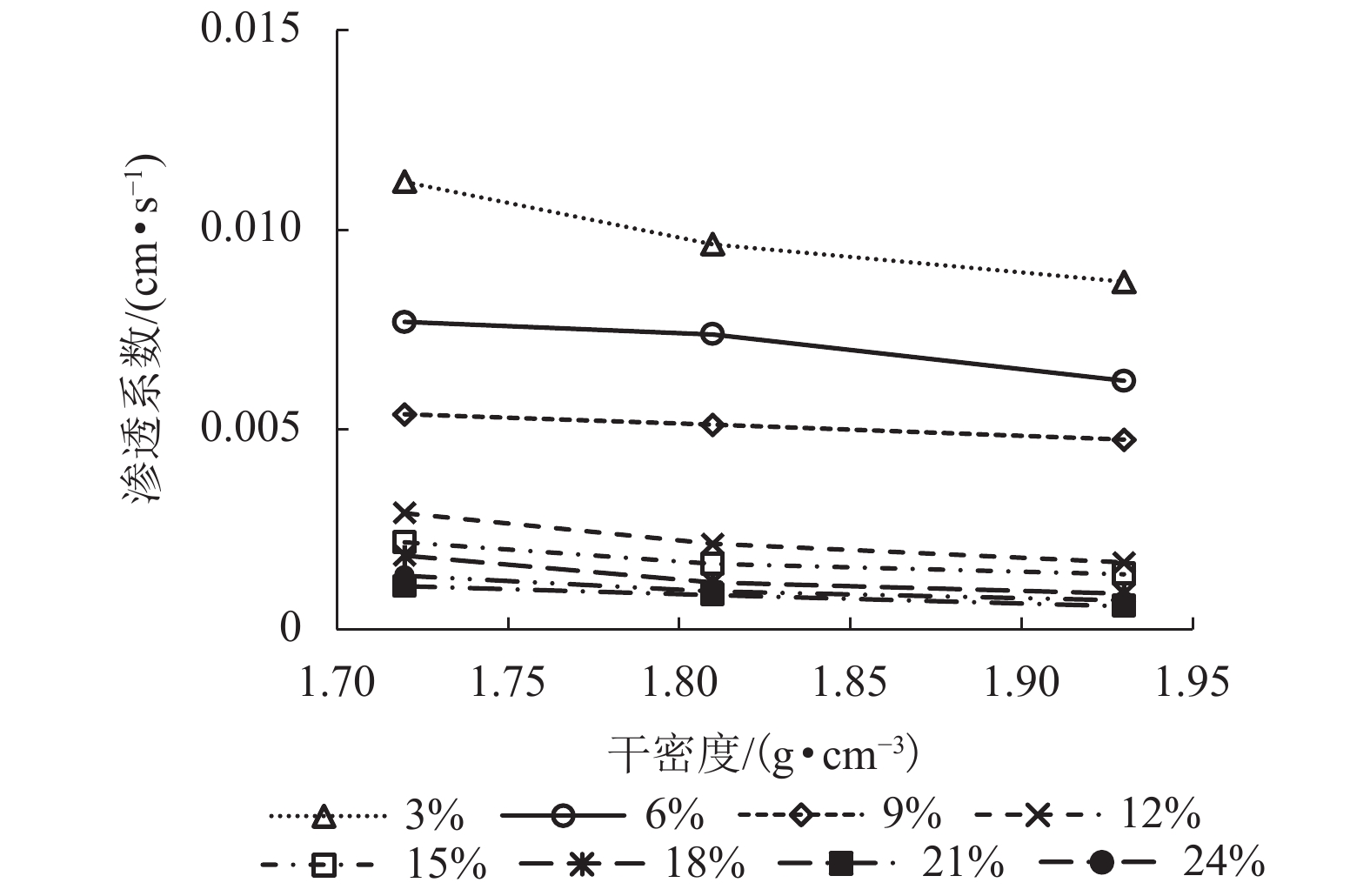王铁行,卢靖,张建锋. 考虑干密度影响的人工压实非饱和黄土渗透系数的试验研究[J]. 岩石力学与工程学报,2006,25(11): 2364-2368. doi: 10.3321/j.issn:1000-6915.2006.11.030WANG Tiehang, LU Jing, ZHANG Jianfeng. Experimental study on permeability coefficient of artificially compacted unsaturated loess considering influence of density[J]. Chinese Journal of Rock Mechanics and Engineering, 2006, 25(11): 2364-2368. doi: 10.3321/j.issn:1000-6915.2006.11.030 张虎,张建明,张致龙,等. 冻结状态青藏粉质黏土的渗透系数测量研究[J]. 岩土工程学报,2016,38(6): 1030-1035. doi: 10.11779/CJGE201606008ZHANG Hu, ZHANG Jianming, ZHANG Zhilong, et al. Measurement of hydraulic conductivity of Qinghai-Tibet Plateau silty clay under subfreezing temperatures[J]. Chinese Journal of Geotechnical Engineering, 2016, 38(6): 1030-1035. doi: 10.11779/CJGE201606008 胡学涛,梁冰,陈亿军,等. 冻融循环对固化污泥力学及微观结构特性影响[J]. 岩土力学,2016,37(5): 1317-1323.HU Xuetao, LIANG Bing, CHEN Yijun, et al. Mechanical and microstructural properties changes of solidified sewage sludge due to cyclic freezing and thawing[J]. Rock and Soil Mechanics, 2016, 37(5): 1317-1323. CHO S E, LEE S R. Instability of unsaturated soil slopes due to infiltration[J]. Computers and Geotechnics, 2001, 28(3): 185-208. doi: 10.1016/S0266-352X(00)00027-6 BENSON C H, DANIEL D E, BOUTWELL G P. Field performance of compacted clay liners[J]. Journal of Geotechnical and Geoenvironmental Engineering, 1999, 125(5): 390-403. doi: 10.1061/(ASCE)1090-0241(1999)125:5(390) DUNCAN J M. Factors of safety and reliability in geotechnical engineering[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2000, 126(4): 307-316. doi: 10.1061/(ASCE)1090-0241(2000)126:4(307) CERDA A. Seasonal and spatial variations in infiltration rates in badland surfaces under Mediterranean climatic conditions[J]. Water Resource, 1999, 35(1): 319-328. doi: 10.1029/98WR01659 OSAWA H, MATSUURA S, MATSUSHI Y, et al. Seasonal change in permeability of surface soils on a slow-moving landslide in a heavy snow region[J]. Engineering Geology, 2017, 221: 1-9. doi: 10.1016/j.enggeo.2017.02.019 BORMANN H, KLAASSEN K. Seasonal and land use dependent variability of soil hydraulic and soil hydrological properties of two Northern German soils[J]. Geoderma, 2008, 145(3/4): 295-302. NERIS J, JIMENEZ C, FUENTES J, et al. Vegetation and land-use effects on soil properties and water infiltration of Andisols in Tenerife (Canary Islands,Spain)[J]. Catena, 2012, 98: 55-62. doi: 10.1016/j.catena.2012.06.006 HINDS E, LU N, MIRUS B, et al. Effects of infiltration characteristics on spatial-temporal evolution of stability of an interstate highway embankment[J]. Journal of Geotechnical and Geoenvironment Engineering, 2019, 145(9): 1-11. LU N, WAYLLACE A, OH S. Infiltration-induced seasonally reactivated instability of a highway embankment near the Eisenhower Tunnel,Colorado,USA[J]. Engineering Geology, 2013, 162: 22-32. doi: 10.1016/j.enggeo.2013.05.002 赵彦旭,张虎元,吕擎峰,等. 压实黄土非饱和渗透系数试验研究[J]. 岩土力学,2010,31(6): 1809-1812. doi: 10.3969/j.issn.1000-7598.2010.06.022ZHAO Yanxu, ZHANG Huyuan, LÜ Qingfeng, et al. Experimental study of unsaturated permeability coefficient of compacted loess[J]. Rock and Soil Mechanics, 2010, 31(6): 1809-1812. 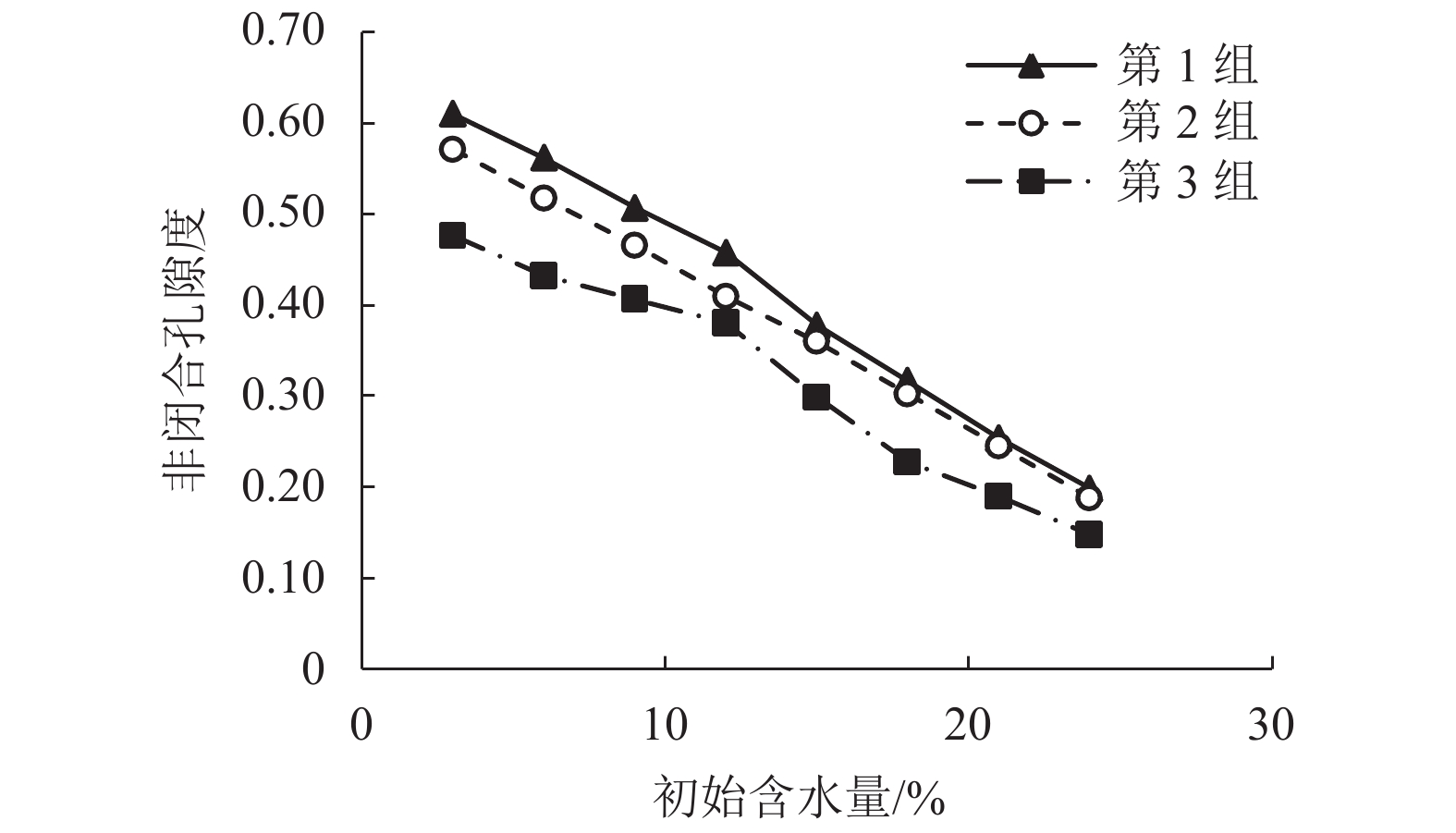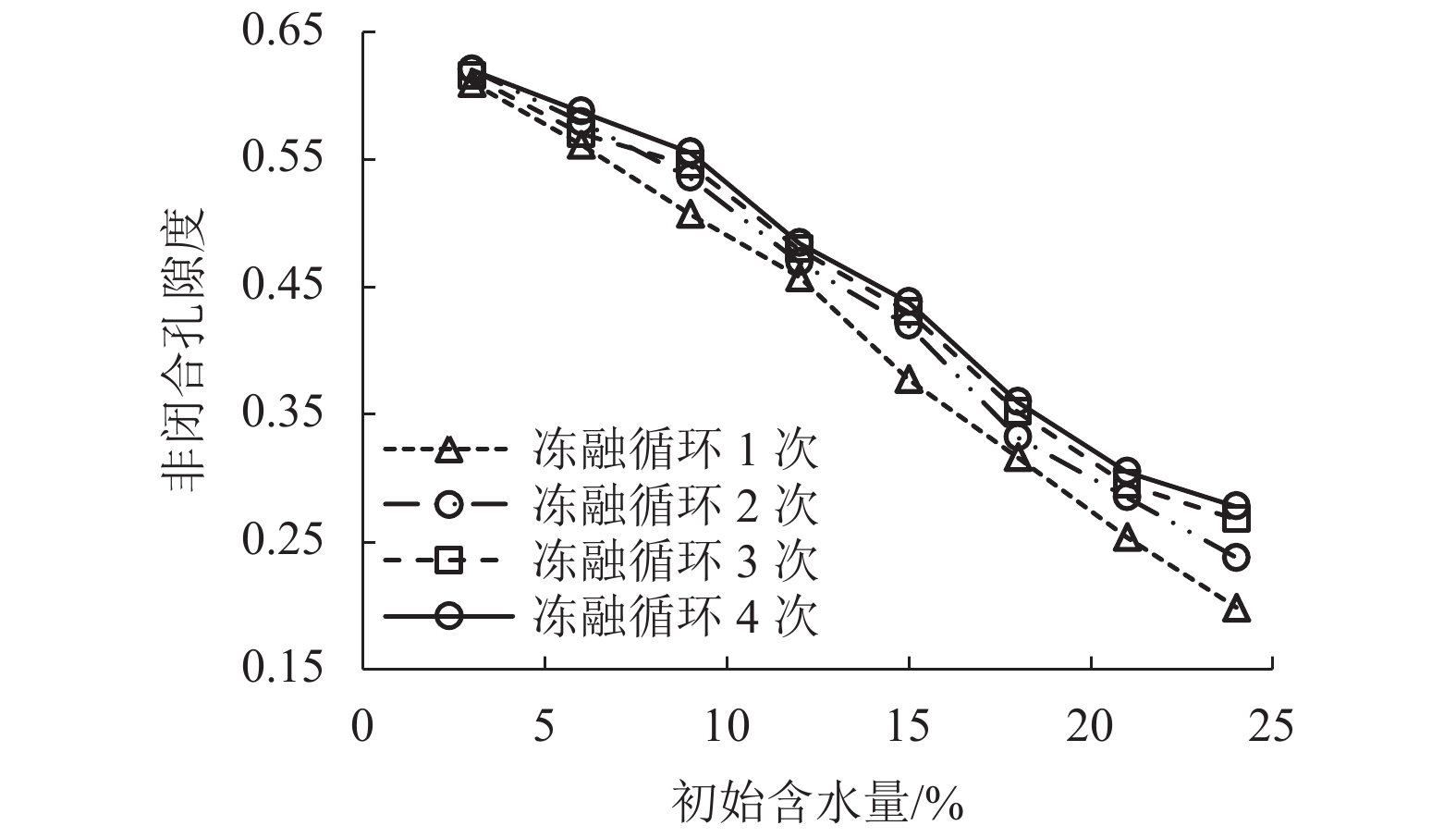doi: 10.3969/j.issn.1000-7598.2010.06.022 王铁行,杨涛,鲁洁. 干密度及冻融循环对黄土渗透性的各向异性影响[J]. 岩土力学,2016,37(增刊1): 72-78.WANG Tiehang, YANG Tao, LU Jie. Influence of dry density and freezing-thawing cycles on anisotropic permeability of loess[J]. Rock and Soil Mechanics, 2016, 37(S1): 72-78. 陈磊,李东庆,明锋. 分形渗透模型在饱和冻土中的应用[J]. 冰川冻土,2019,41(6): 1414-1421.CHEN Lei, LI Dongqing, MING Feng. Application of the fractal hydraulic conductivity model in the saturated frozen soil[J]. Journal of Glaciology and Geocryology, 2019, 41(6): 1414-1421. MCCAULEY C A, WHITE D M, LILLEY M R, et al. A comparison of hydraulic conductivities,permeabilities and infiltration rates in frozen and unfrozen soils[J]. Cold Regions Science and Technology, 2002, 34(2): 117-125. doi: 10.1016/S0165-232X(01)00064-7 HORIGUCHI K, MILLER R D. Experimental studies with frozen soil in an ice sandwich permeameter[J]. Cold Regions Science and Technology, 1980, 3(6): 177-183. 商允虎. 寒区冻土水理性质特征参数综合试验研究[D]. 哈尔滨: 黑龙江大学, 2015. -
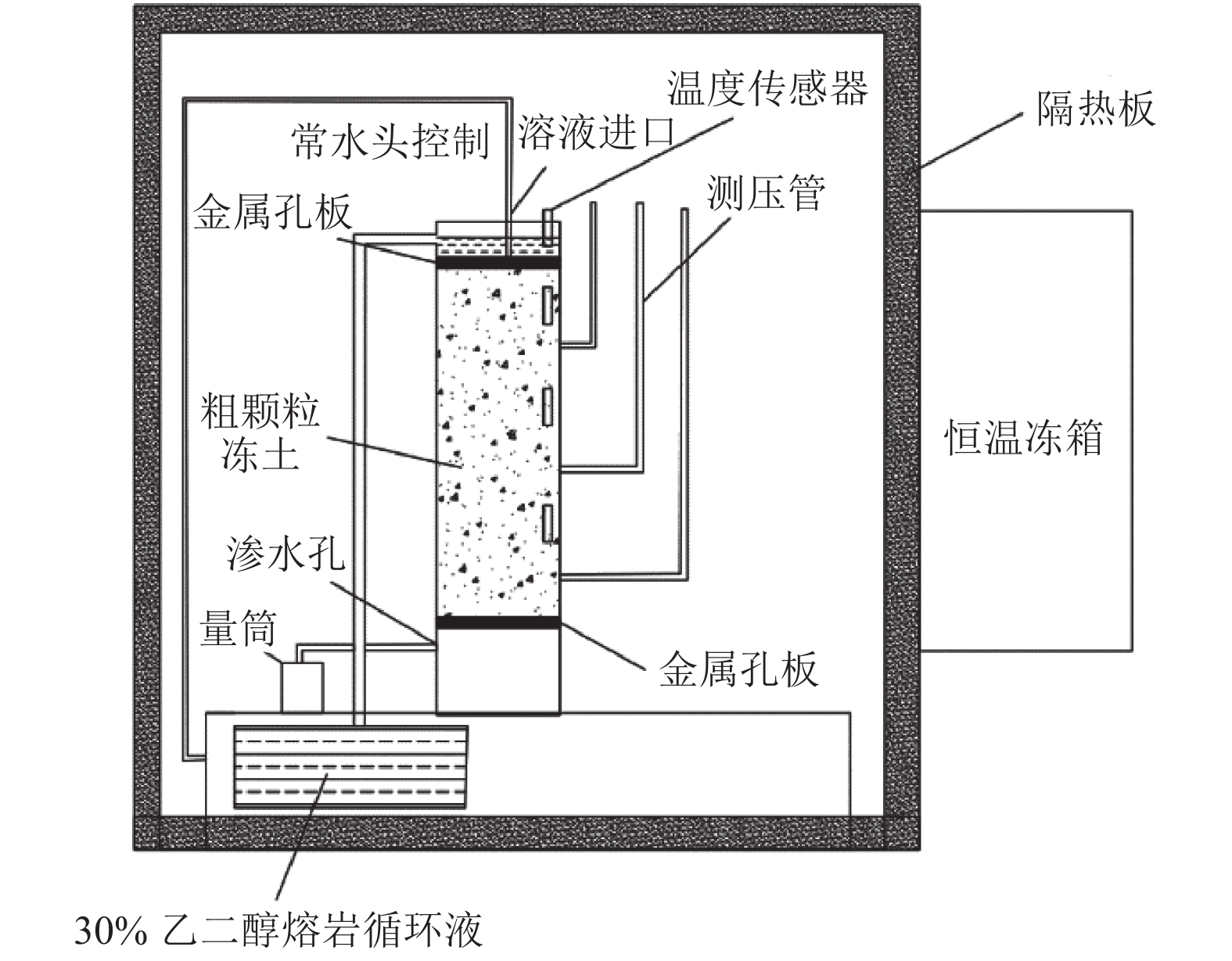
下载:
点击查看大图
图(11)
计量
- 文章访问数: 573
- HTML全文浏览量: 282
- PDF下载量: 22
- 被引次数: 0