Axial Load Distribution Law of High Temperature Thread Pair Considering Material Creep
-
摘要:
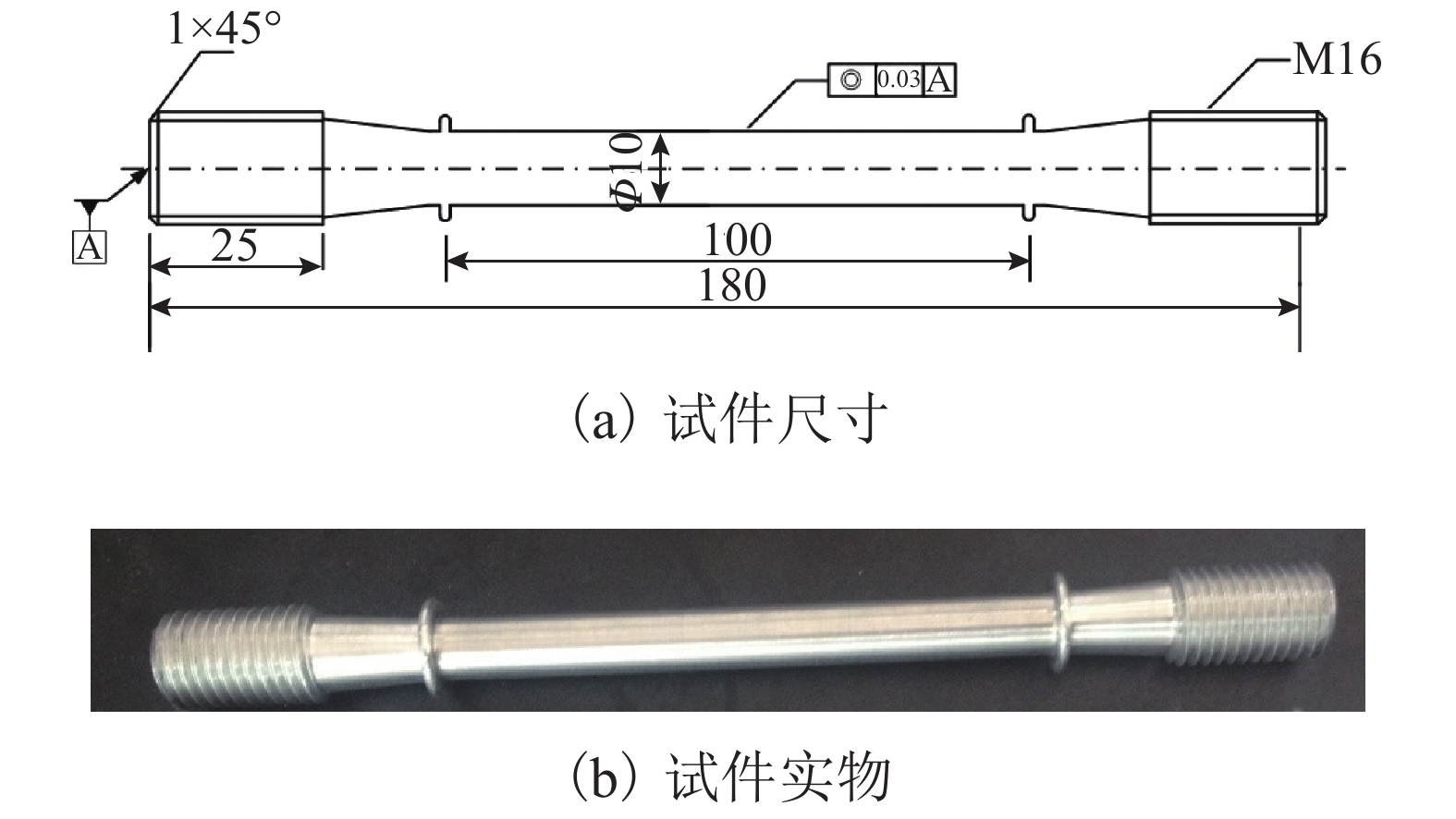
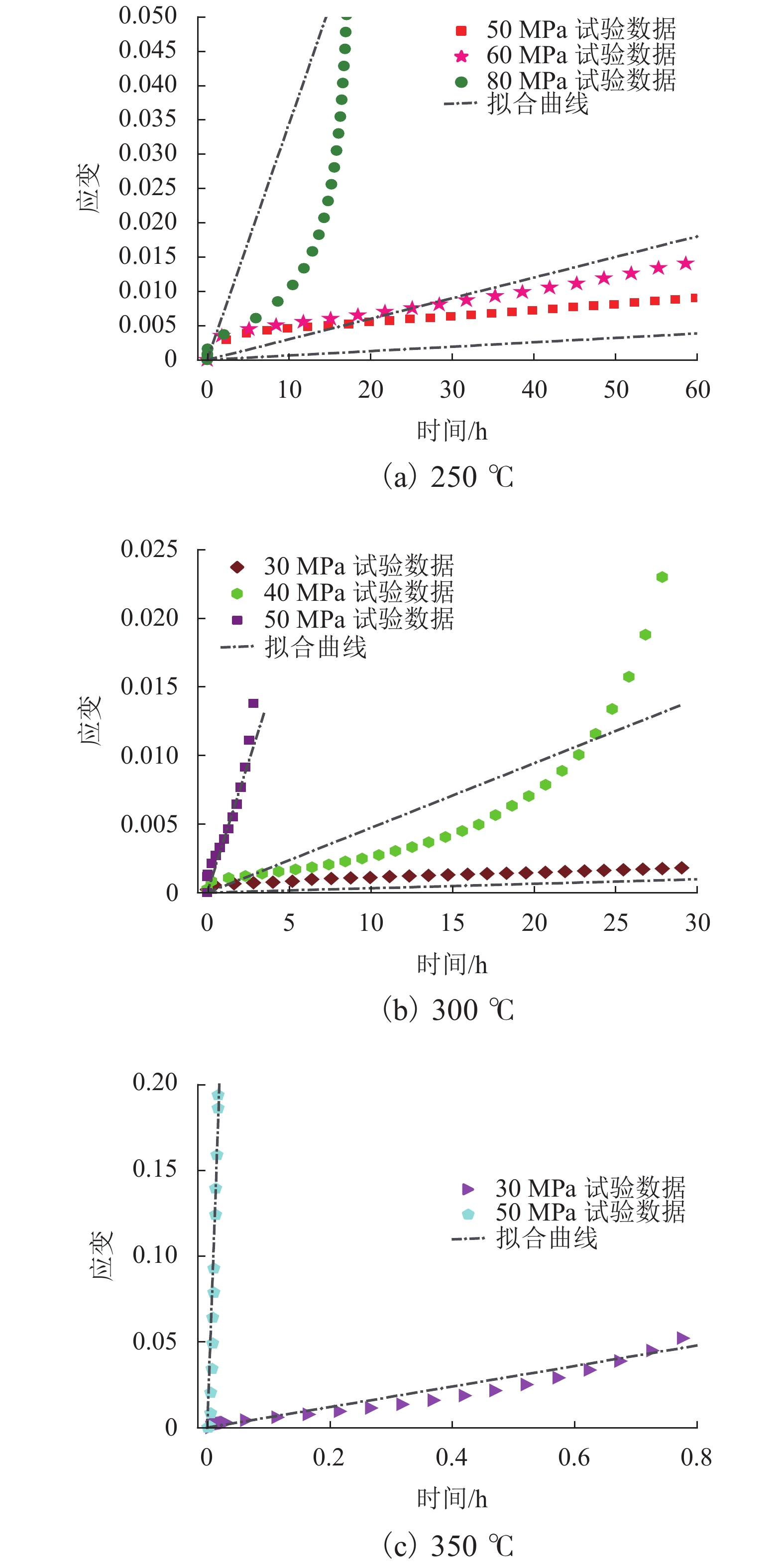
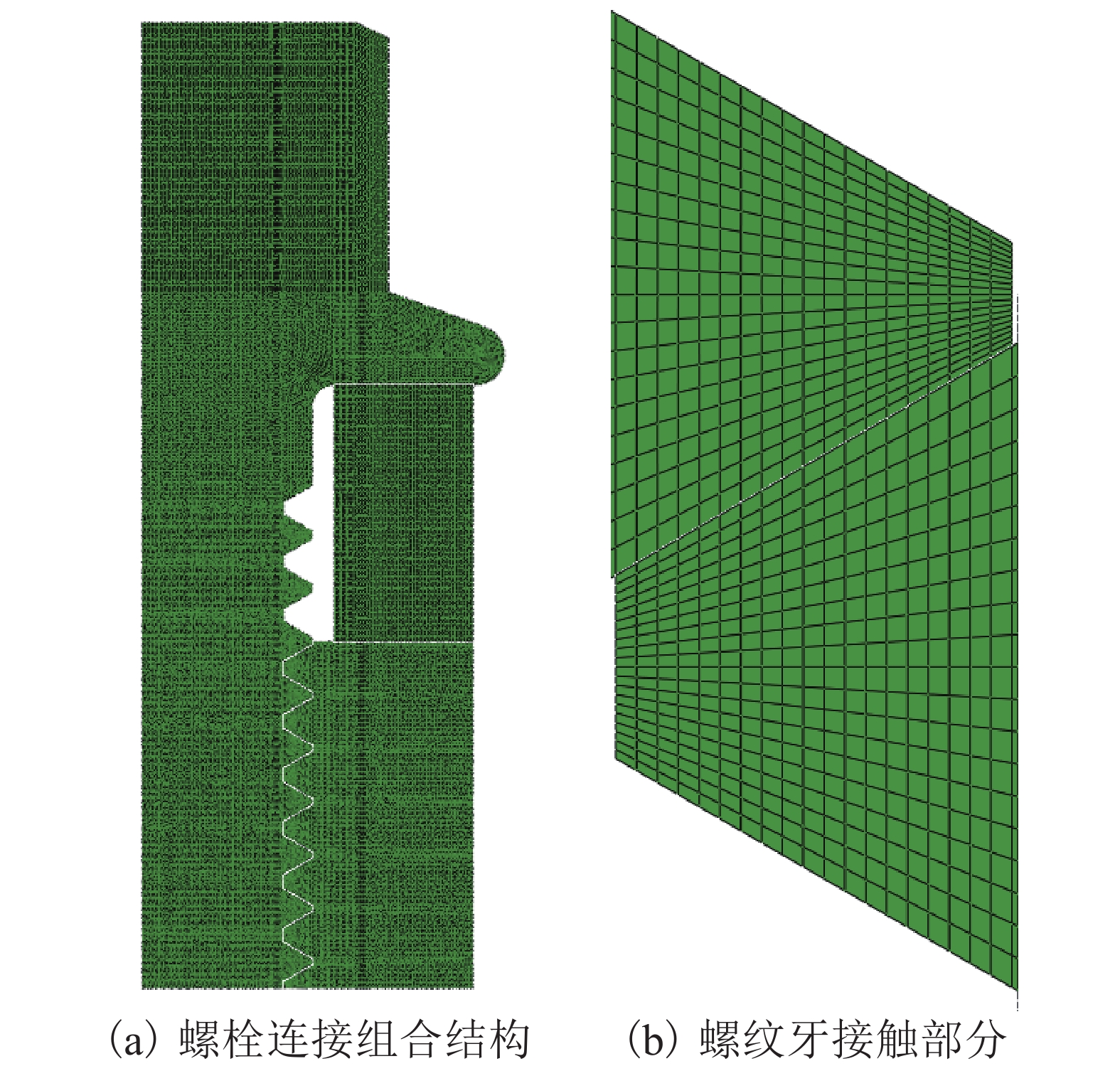
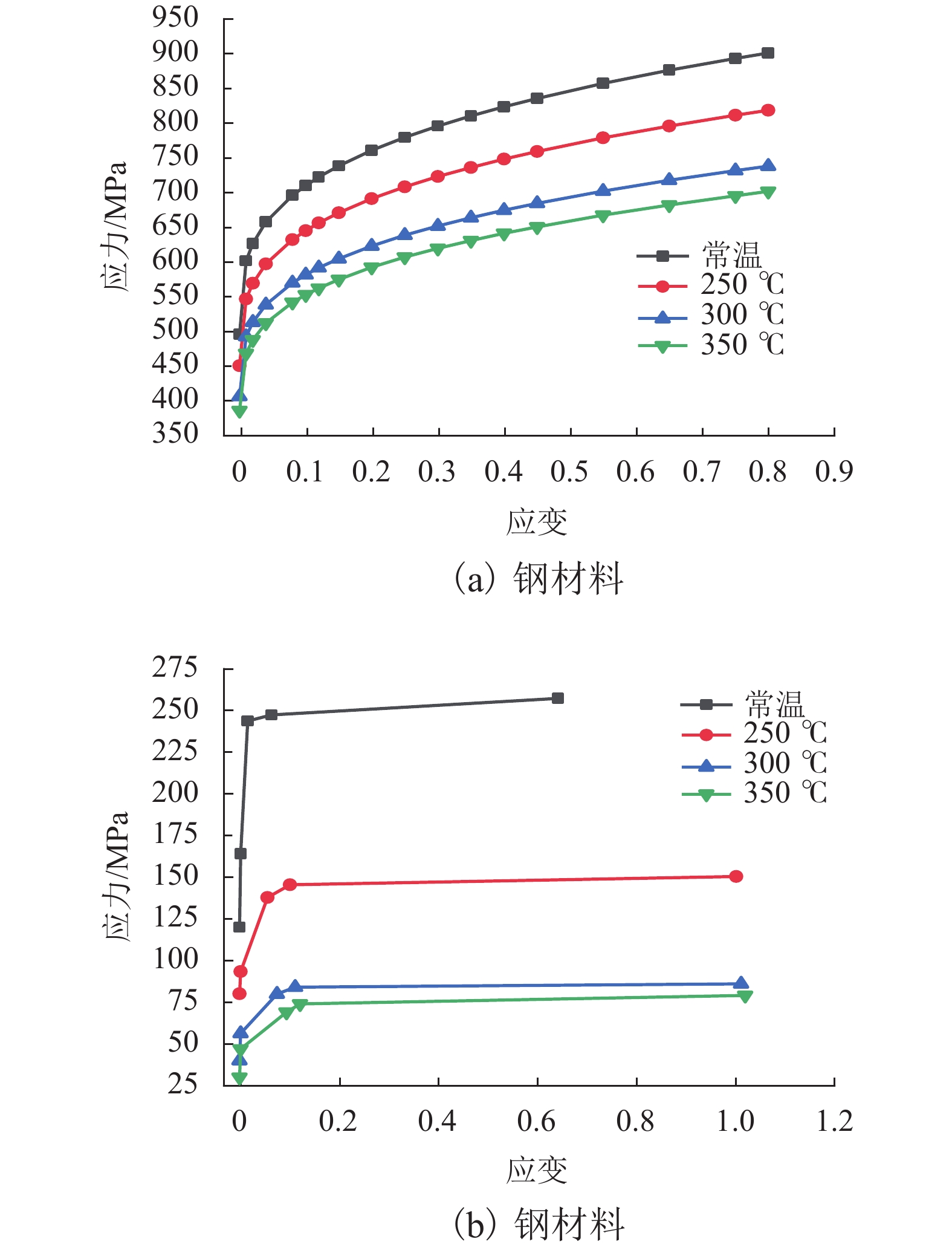
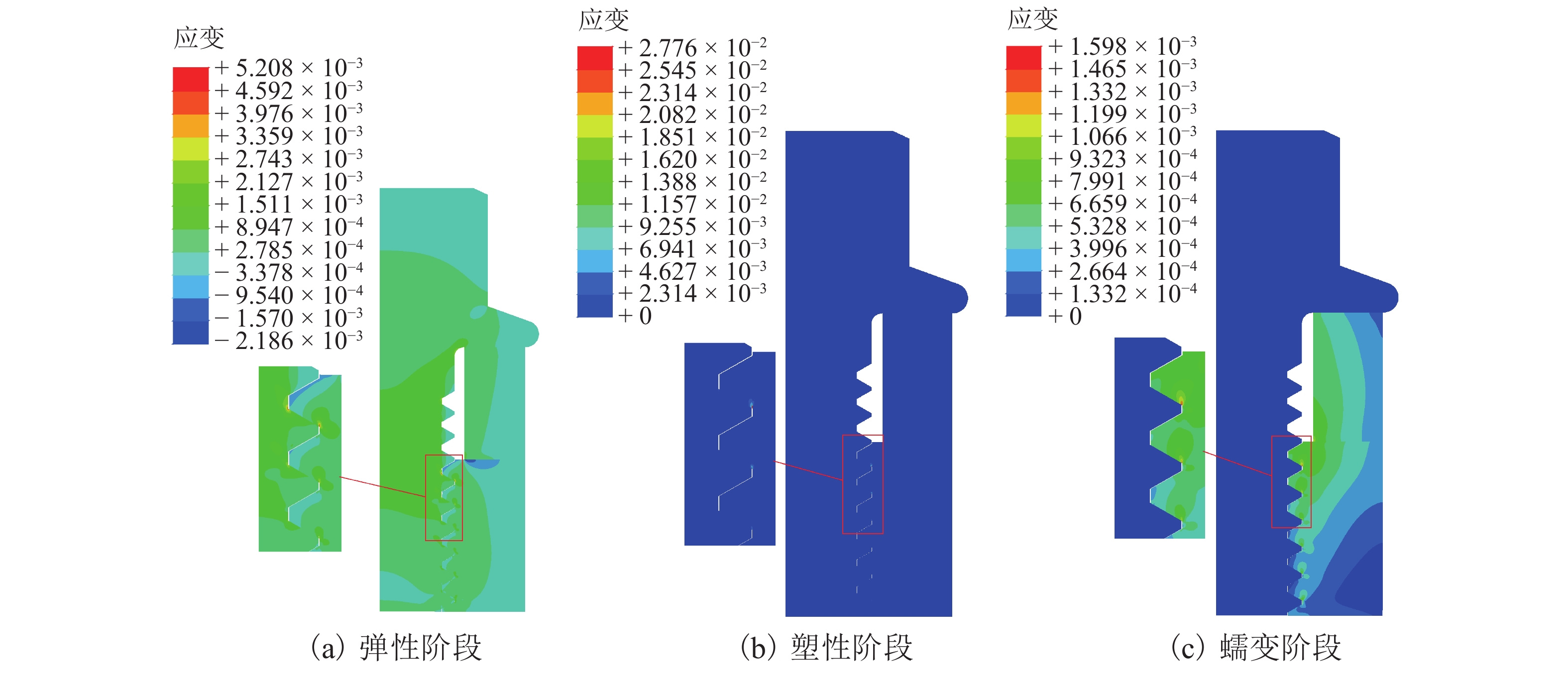
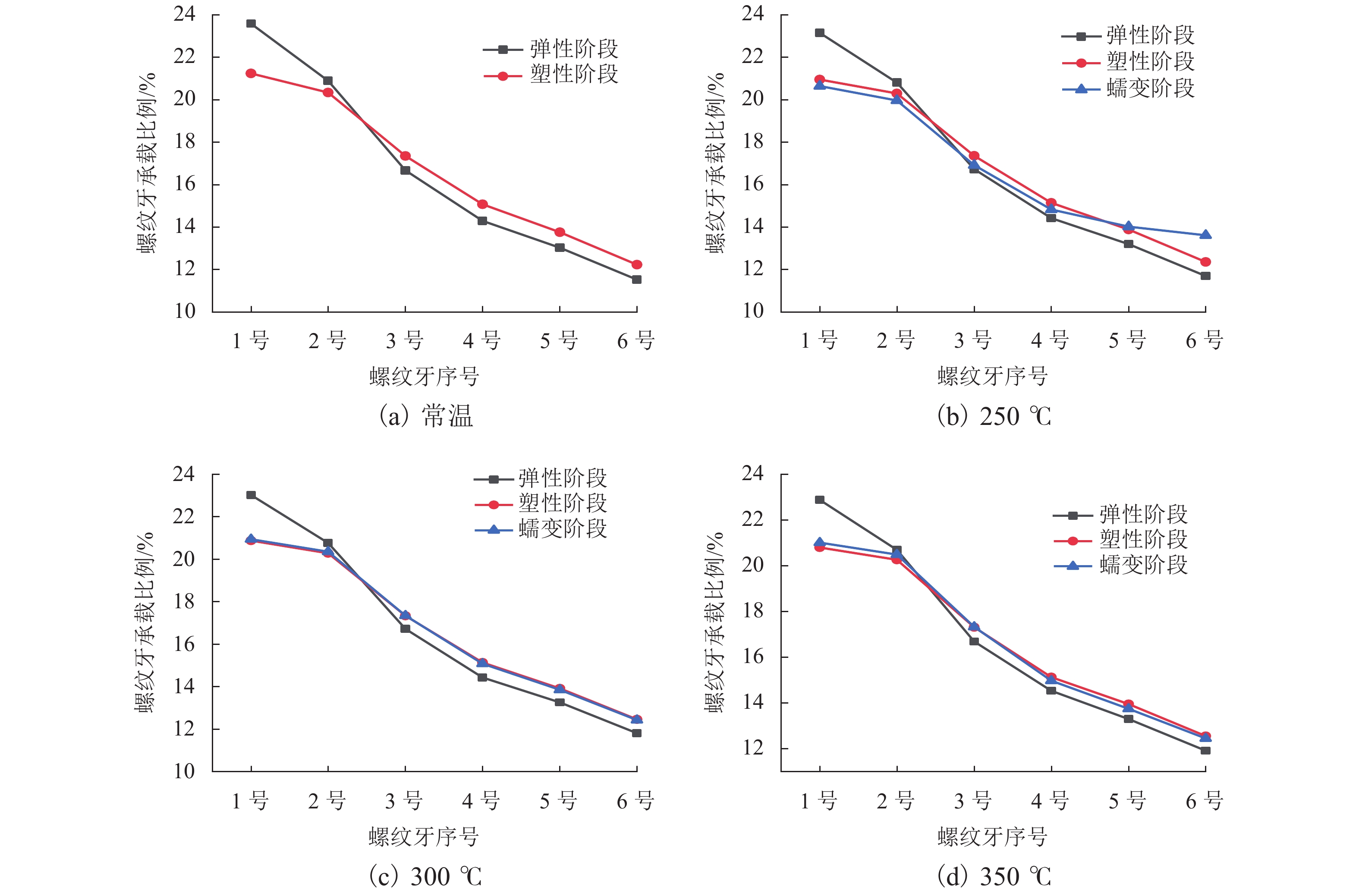
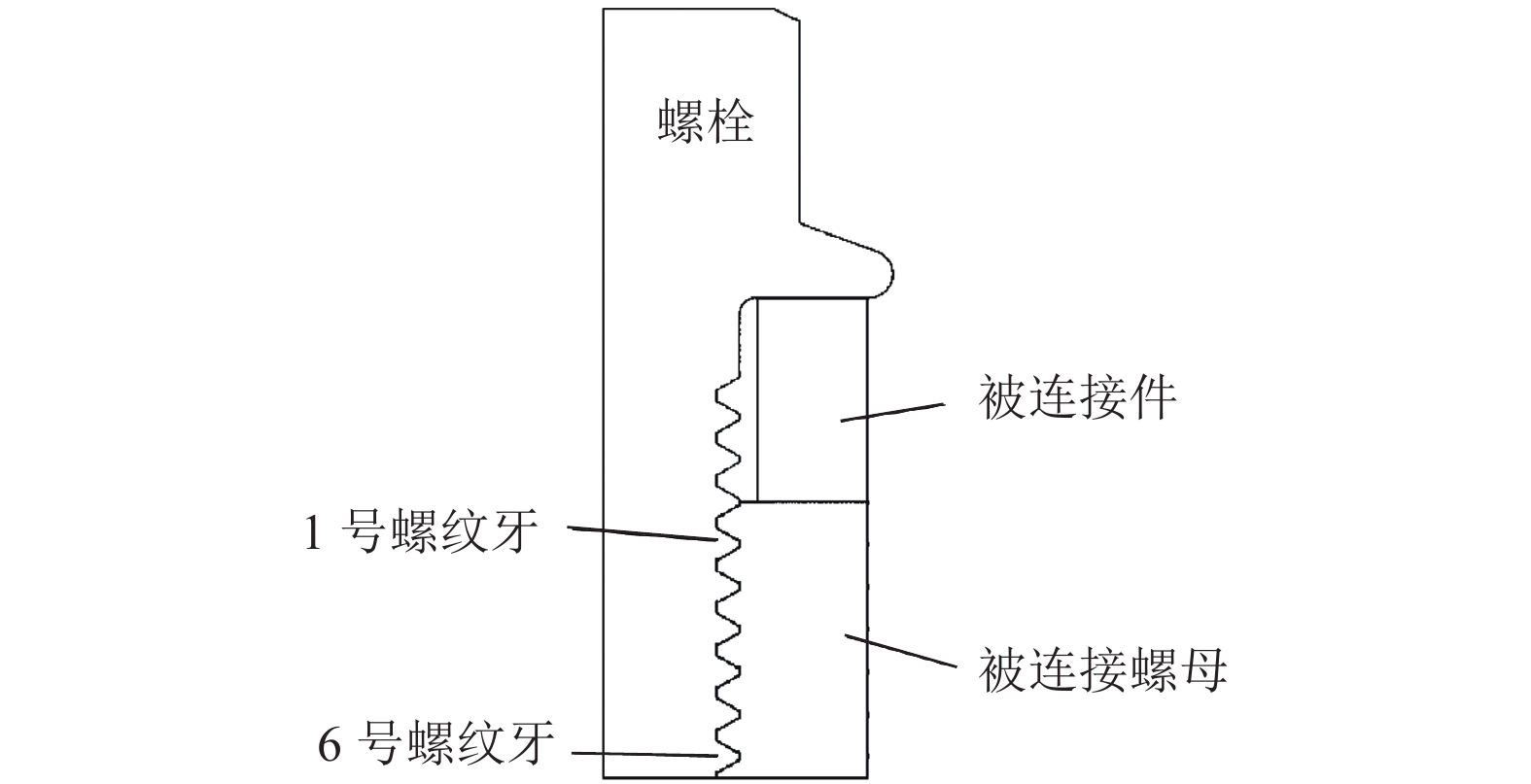
为了研究高温蠕变对螺纹副承载的影响，分别在常温、250、300、350 ℃下对铝合金试样进行单轴拉伸蠕变试验，通过试验数据拟合得到不同温度下铝合金的时间硬化蠕变模型参数；基于ABAQUS建立螺纹副承载分布有限元模型，描述螺栓连接组合结构在高温环境下的工作情况，研究螺纹副材料在线弹性、塑性、蠕变情况下的承载分布. 结果表明：螺栓连接组合结构在高温环境下工作时，被连接件铝合金材料发生蠕变，导致螺纹副1号螺纹牙受轴向载荷大幅减少；考虑材料线弹性后，1号螺纹牙承载比例为22.88%～23.15%；考虑材料塑性后，1号螺纹牙承载比例为20.80%～20.95%；考虑材料蠕变后，1号螺纹牙承载比例为20.65%～21.02%；考虑材料塑性和蠕变后，1号螺纹牙承载比例有所降低，所有螺纹牙所受轴向载荷趋于平均.
Abstract:In order to study the effect of high temperature creep on thread load, uniaxial tensile creep tests were conducted on aluminum alloy specimens at normal temperature, 250 ℃, 300 ℃, and 350 ℃. The time-hardening creep model parameters of the aluminum alloy at different temperatures were obtained by fitting the test data. To more accurately describe the working condition of a bolted connection structure in a high-temperature environment, a finite element model of the bolted connection structure was established using ABAQUS, and the effects of linear elasticity, plasticity, and creep on the load distribution were studied. The results show that when the bolted connection structure works in a high-temperature environment, the aluminum alloy material of the connected component creeps and the axial load of the No. 1 thread thus decreases greatly. Considering the material elasticity, the bearing ratio of the No. 1 thread is between 22.88% and 23.15%. Considering the material plasticity, the bearing ratio of the No. 1 thread is between 20.80% and 20.95%. Considering the material creep, the bearing ratio of the No. 1 thread is between 20.65% and 21.02%. Considering the plasticity and creep of the material, the bearing ratio of the No. 1 thread is reduced, and the axial load of all teeth tends to be average.
-
图 7 250 ℃下螺栓连接组合结构应变云图
Figure 7. Strain nephogram of bolted connection structure at 250 ℃
表 1 Time-hardening蠕变模型材料参数
Table 1. Material parameters of time-hardening creep model
温度/℃ A m n 250 1.935 × 10−9 −5.380 × 10−14 0.962 300 1.714 × 10−8 −2.617 × 10−15 0.034 350 3.884 × 10−6 −0.628 2.593 × 10−8 
下载: 导出CSV
表 2 铝合金材料属性
Table 2. Material properties of aluminum alloy
温度/℃ 弹性模量/GPa 泊松比 线膨胀系数/（× 10−5 ℃−1） 常温 73 0.31 2.05 250 65 0.29 2.25 300 62 0.29 2.55 350 59 0.29 2.85
下载: 导出CSV
表 3 方差和极差分析结果
Table 3. Results of variance and range analysis
温度/℃ 阶段 方差 极差 常温 弹性 0.001 847 0.120 5 塑性 0.001 092 0.090 1 弹性 0.001 682 0.114 5 250 塑性 0.001 011 0.085 9 蠕变 0.000 740 0.070 3 弹性 0.001 625 0.112 2 300 塑性 0.000 981 0.084 1 蠕变 0.001 017 0.085 1 弹性 0.001 557 0.109 7 350 塑性 0.000 952 0.082 5 蠕变 0.001 053 0.085 7
下载: 导出CSV
-
[1] ZHANG M, JIANG Y Y, LEE C H. Finite element modeling of self-loosening of bolted joints[J]. Journal of Mechanical Design, 2007, 129(2): 218-226. doi: 10.1115/1.2406092 [2] MANTELLI B M, MILANEZ F H, PEREIRA E N, et al. Statistical model for pressure distribution of bolted joints[J]. Journal of Thermophysics and Heat Transfer, 2010, 24(2): 432-437. [3] 晏启祥,李彬嘉,陈行,等. 撞击荷载作用下盾构隧道接头螺栓失效及参数分析[J]. 西南交通大学学报,2019,54(1): 23-31,38.YAN Qixiang, LI Binjia, CHEN Hang, et al. Failure and parametric analysis of shield tunnel bolts under impact load[J]. Journal of Southwest Jiaotong University, 2019, 54(1): 23-31,38. [4] FARRAHI G H, CHAMANI M, KASHYZADEH K R, et al. Failure analysis of bolt connections in fired heater of a petrochemical unit[J]. Engineering Failure Analysis, 2018, 92: 327-342. doi: 10.1016/j.engfailanal.2018.06.004 [5] 张明远,鲁连涛,张远彬,等. 振动条件下螺纹面磨损对紧固件抗松能力影响[J]. 西南交通大学学报,2018,53(3): 596-601. doi: 10.3969/j.issn.0258-2724.2018.03.022ZHANG Mingyuan, LU Liantao, ZHANG Yuanbin, et al. Effect of thread wear on anti-loosening ability of threaded fastener under vibration[J]. Journal of SouthWest JiaoTong University, 2018, 53(3): 596-601. doi: 10.3969/j.issn.0258-2724.2018.03.022 [6] 石秀勇,李国祥,胡玉平. 发动机飞轮螺栓的三维有限元计算分析[J]. 中国机械工程,2006,17(8): 845-848. doi: 10.3321/j.issn:1004-132X.2006.08.019SHI Xiuyong, LI Guoxiang, HU Yuping. 3D finite element analysis on flywheel bolt of engine[J]. China Mechanical Engineering, 2006, 17(8): 845-848. doi: 10.3321/j.issn:1004-132X.2006.08.019 [7] 闫桂玲,王弘,康国政,等. 缺口应力集中对5083-H111铝合金超高周疲劳性能的影响[J]. 西南交通大学学报,2016,51(5): 944-950. doi: 10.3969/j.issn.0258-2724.2016.05.018YAN Guiling, WANG Hong, KANG Guozheng, et al. Influence of notch stress concentration on fatigue properties of 5083-H111 aluminum alloy in very high cycle regime[J]. Journal of Southwest Jiaotong University, 2016, 51(5): 944-950. doi: 10.3969/j.issn.0258-2724.2016.05.018 [8] THOPPUL S D, FINEGAN J, GIBSON R F. Mechanics of mechanically fastened joints in polymer-matrix composite structures:a review[J]. Composite Sence and Technology, 2009, 69(3/4): 301-329. [9] HASHIMURA S, KAMIBEPPU K, NUTAHARA T, et al. Effects of clamp force on fatigue strength of aluminum alloy bolts[J]. Procedia Structural Integrity, 2019, 19: 204-213. doi: 10.1016/j.prostr.2019.12.022 [10] CHAABAN A, JUTRAS M. Static analysis of buttress threads using the finite element method[J]. Journal of Pressure Vessel Technology, 1992, 114(2): 209-212. [11] 张卫正,魏春源,苏志国,等. 内燃机铝合金活塞疲劳寿命预测研究[J]. 中国机械工程,2003,14(10): 865-867. doi: 10.3321/j.issn:1004-132X.2003.10.017ZHANG Weizheng, WEI Chunyuan, SU Zhiguo, et al. A study on forecasting of fatigue life for aluminium alloy piston of diesel engine[J]. China Mechanical Engineering, 2003, 14(10): 865-867. doi: 10.3321/j.issn:1004-132X.2003.10.017 [12] 郭宏超,毛宽宏,万金怀,等. 高强度钢材疲劳性能研究进展[J]. 建筑结构学报,2019,40(4): 17-28.GUO Hongchao, MAO kuanhong, WAN Jinhuai, et al. Research progress on fatigue properties of high strength steels[J]. Journal of Building Structures, 2019, 40(4): 17-28. [13] 王萌,湛利华,李文科,等. 2219铝合金蠕变时效研究及宏微观本构建模[J]. 热加工工艺,2017,46(6): 221-225.WANG Meng, ZHAN Lihua, LI Wenke, et al. Creep aging research and macro and micro constitutive modelling of 2219 aluminum alloy[J]. Hot Working Technology, 2017, 46(6): 221-225. [14] HANTOUCHE E G, AL KHATIB K K, MOROVAT M A. Modeling creep of steel under transient temperature conditions of fire[J]. Fire Safety Journal, 2018, 100: 67-75. doi: 10.1016/j.firesaf.2018.07.006 [15] WELCH M. Classical analysis of preloaded bolted joint load distributions[J]. International Journal of Structural Integrity, 2018, 9(4): 455-464. doi: 10.1108/IJSI-07-2017-0045 [16] NASRAOUI M T, CHAKHARI J, KHALFI B, et al. Modeling and analysis of a bolted joint under tension and shear loads[J]. Transactions of the Canadian Society for Mechanical Engineering, 2019, 43(3): 376-386. doi: 10.1139/tcsme-2018-0042 [17] BABU K N, NARESH H, GUPTA G. Design and analysis of bolted joint for rocket motor casing[J]. Materials Today:Proceedings, 2018, 5(2): 5165-5174. [18] ZHAO H. A numerical method for load distribution in threaded connections[J]. Journal of Mechanical Design, 1996, 118(2): 274-279. doi: 10.1115/1.2826880 [19] 陈海平,曾攀,方刚,等. 螺纹副承载的分布规律[J]. 机械工程学报,2010,46(9): 171-178. doi: 10.3901/JME.2010.09.171CHEN Haiping, ZENG Pan, FANG Gang, et al. Load distribution of bolted joint[J]. Journal of Mechanical Engineering, 2010, 46(9): 171-178. doi: 10.3901/JME.2010.09.171 [20] 胡昌明,贺红亮,胡时胜. 45号钢的动态力学性能研究[J]. 爆炸与冲击,2003,23(2): 188-192. doi: 10.3321/j.issn:1001-1455.2003.02.017HU Changming, HE Hongliang, HU Shisheng. A study on dynamic mechancial behaviors of 45 steel[J]. Explosion and Shock Waves, 2003, 23(2): 188-192. doi: 10.3321/j.issn:1001-1455.2003.02.017 [21] HOUSARI B A, NASSAR S A. Effect of thread and bearing friction coefficients on the vibration-induced loosening of threaded fasteners[J]. Journal of Vibration and Acoustics, 2007, 129(8): 484-494. -
下载:
点击查看大图
计量
- 文章访问数: 305
- HTML全文浏览量: 106
- PDF下载量: 12
- 被引次数: 0