矩形不锈钢管混凝土短柱轴压性能试验研究

唐红元; 李政周; 范璐瑶; 杨虹

doi:10.3969/j.issn.0258-2724.20200416

矩形不锈钢管混凝土短柱轴压性能试验研究

doi: 10.3969/j.issn.0258-2724.20200416

西华大学结构工程研究所，四川成都 610039

基金项目: 国家自然科学基金(51268044)；教育部春晖计划合作项目(192647)

详细信息

作者简介:
唐红元(1974—)，男，教授，博士，研究方向为钢结构及组合结构，E-mail： tanghyseu@163.com

中图分类号: TU398.9
计量
- 文章访问数: 229
- HTML全文浏览量: 94
- PDF下载量: 9
- 被引次数: 0
出版历程
- 收稿日期: 2020-06-28
- 修回日期: 2020-09-04
- 刊出日期: 2020-09-23

Experimental Investigation on Behavior of Rectangular Concrete-Filled Stainless Steel Tubular Stub Columns under Axial Loading

Institute of structural engineering，Xihua University，Chengdu 610039，China

摘要

摘要:
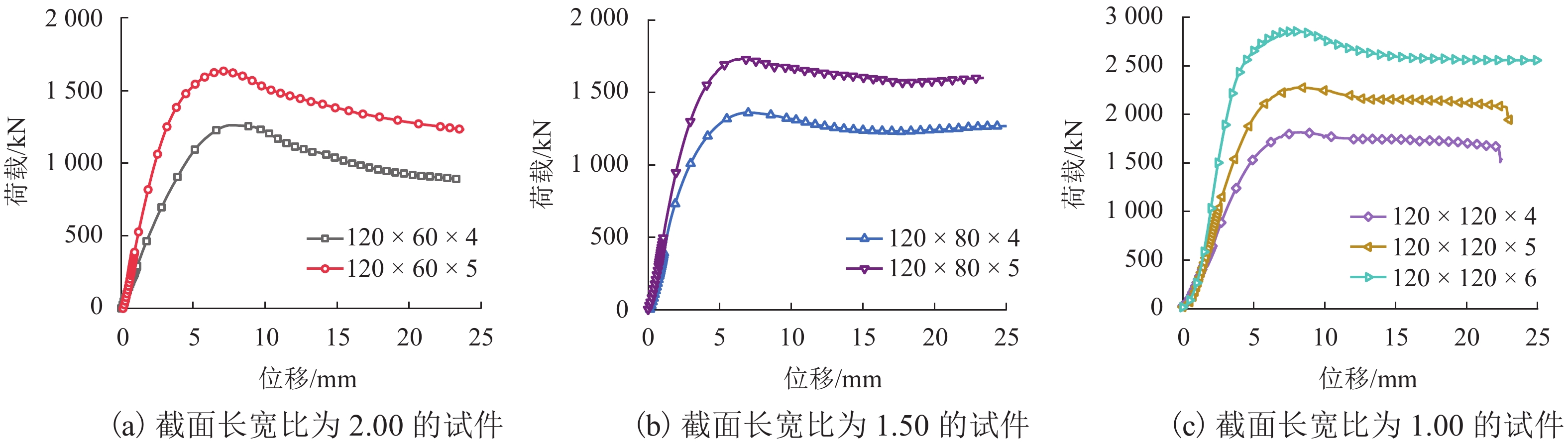
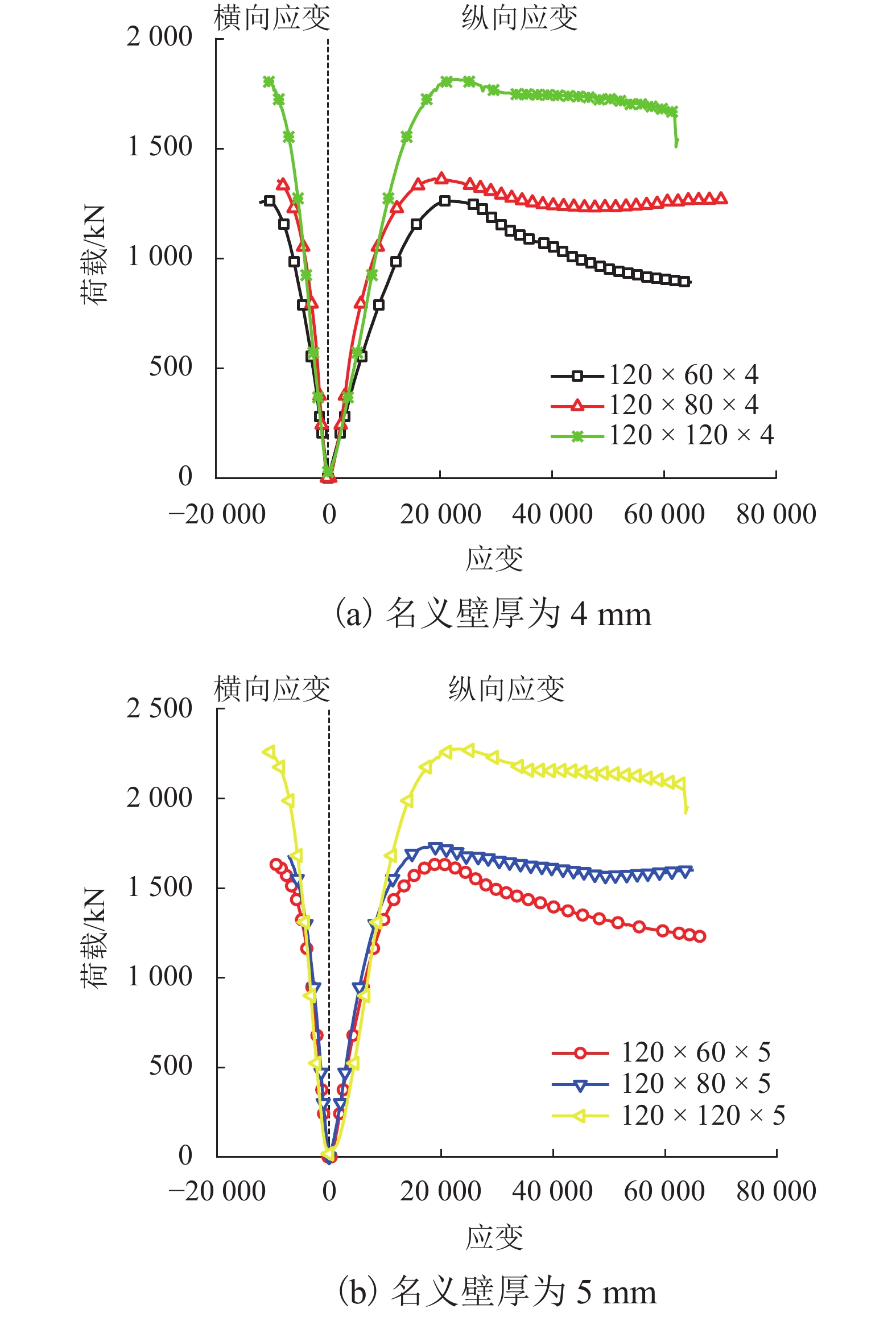
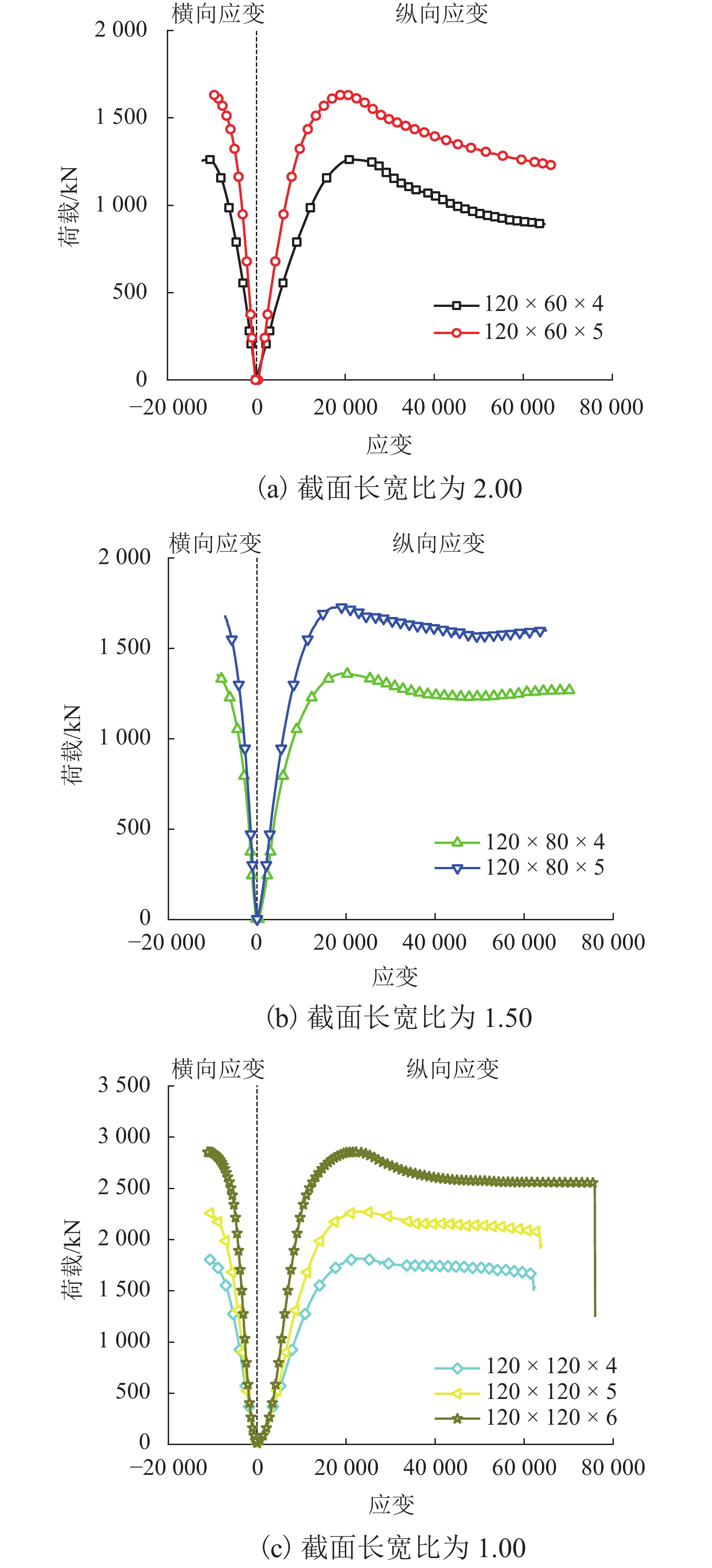
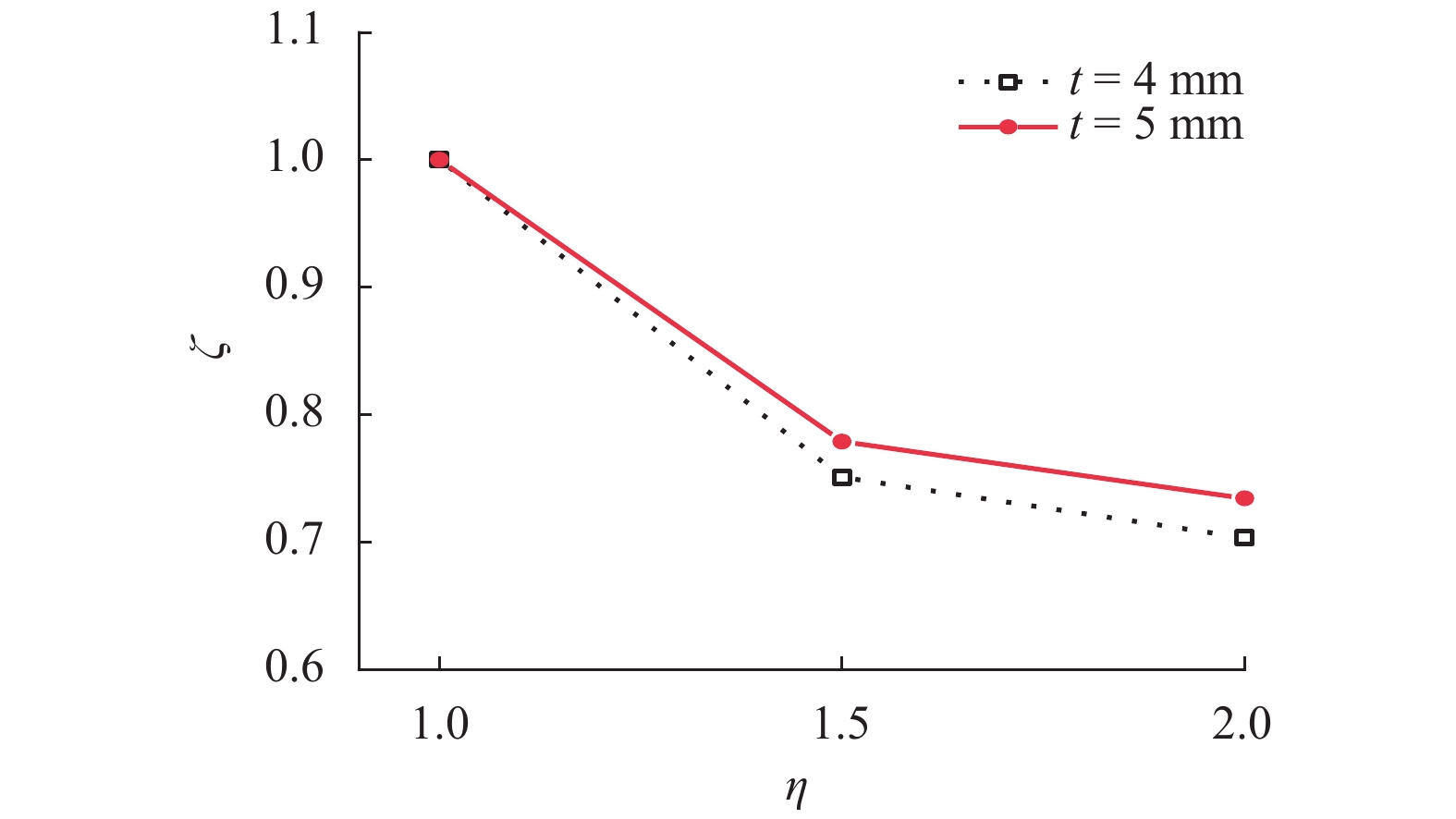
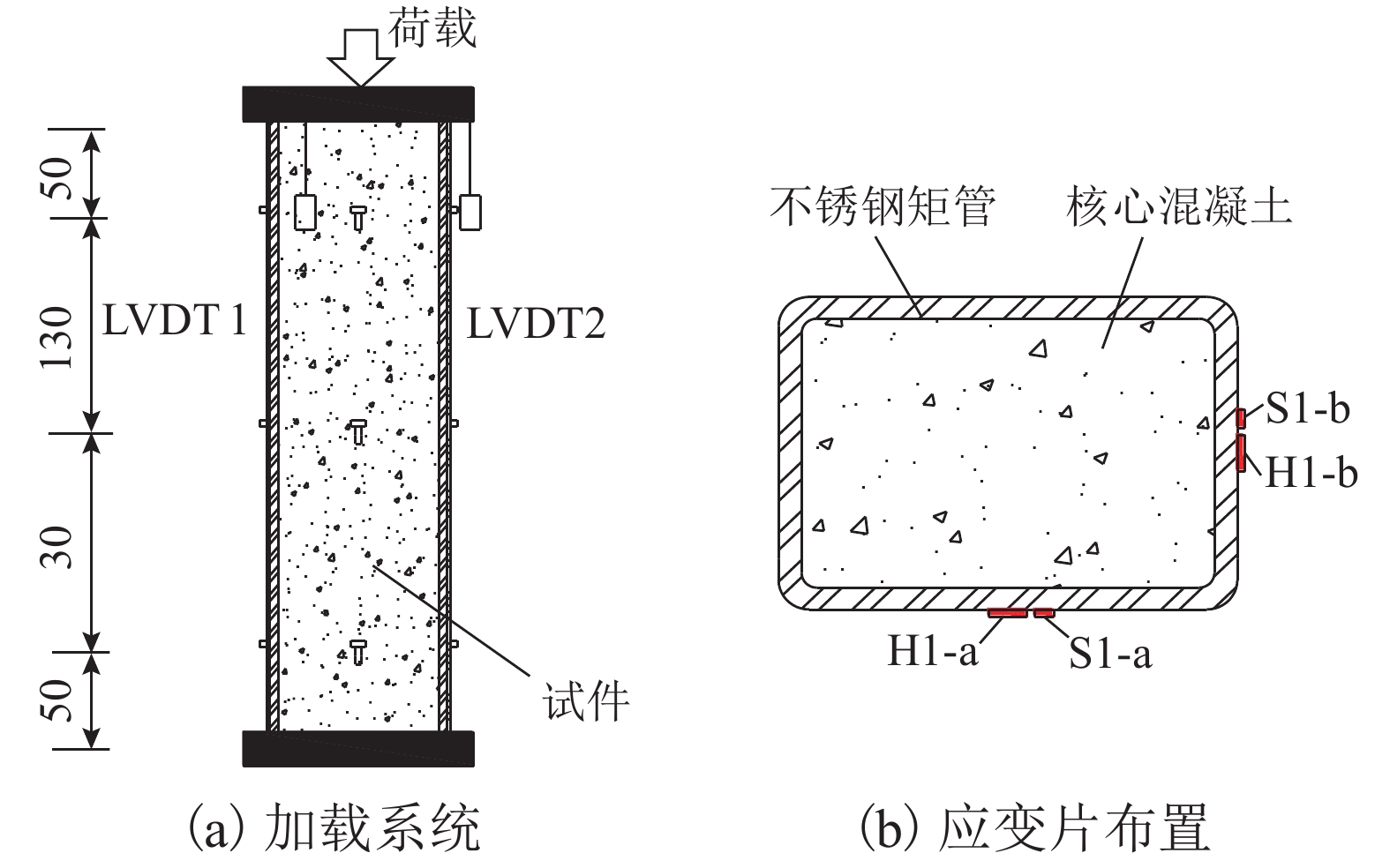
为了研究矩形不锈钢管混凝土短柱轴压承载力性能，对7组不同截面尺寸的矩形不锈钢管混凝土短柱进行轴压试验，得到了不同试件的破坏模式、荷载-位移曲线、荷载-横向应变曲线、荷载-纵向应变曲线、荷载-长宽比曲线，分析了矩形截面长宽比对试件承载力的影响. 研究结果表明：矩形不锈钢管混凝土短柱在轴向压力作用下，其典型破坏模式为试件局部向外屈曲破坏；在相同长宽比的情况下，壁厚由4 mm增加到6 mm时，试件承载力增加25%~57%；在相同壁厚的情况下，长宽比由1增加到2，试件承载力减小22%~30%；将本文试验数据与国内外普通碳钢钢管混凝土柱的相关规范和标准的计算结果进行对比分析，发现不锈钢管混凝土短柱轴压承载力较相同截面的普通碳钢钢管混凝土短柱承载力平均高出14%；通过数值拟合得到了轴压承载力计算公式，该计算公式能较好地预测矩形不锈钢管混凝土短柱轴压承载力.
- 不锈钢管混凝土 /
- 短柱 /
- 破坏模式 /
- 轴压承载力 /
- 长宽比
Abstract:
In order to study the axial compressive behavior of rectangular concrete-filled stainless steel tubular (CFSST) short columns, axial compression tests were conducted on seven groups of rectangular CFSST short columns with different cross-sectional sizes. The failure modes, load-displacement curves, load-circumferential strain curves, load-longitudinal strain curves, and load-cross-sectional aspect ratio curves of different specimens under axial compression were obtained. The influence of aspect ratio of the rectangular cross-section on the bearing capacity of the specimens was analyzed. The results show that the typical failure mode of rectangular CFSST short columns under axial compression was local outward buckling. Under the same aspect ratio, when the wall thickness of the specimens increases from 4 mm to 6 mm, the bearing capacity of the specimens increases by 25%–57%. With the fixed wall thickness, when the aspect ratio of specimens increases from 1 to 2, the bearing capacity decreases by 22%–30%. Comparison of the test results with the calculated results by relevant codes and standards indicates that the bearing capacity of CFSST stub columns is more than 14% higher than that of the concrete-filled conventional carbon steel tubular stub columns with the same section. Furthermore, a formula for calculating the axial compression bearing capacity is obtained by numerical fitting of the data obtained in this study and those from literature, which can well predict the bearing capacity of rectangular CFSST short columns.
- concrete-filled stainless steel tube /
- stub column /
- failure mode /
- axial compression bearing capacity /
- aspect ratio

HTML全文

图 1 加载系统和测点布置

Figure 1. Test setup and arrangement of strain gauges

下载: 全尺寸图片幻灯片

图 2 试件破坏模式

Figure 2. Failure modes of the specimens

下载: 全尺寸图片幻灯片

图 3 荷载-变形曲线

Figure 3. Load-displacement curves

下载: 全尺寸图片幻灯片

图 4 不同长宽比荷载-应变曲线

Figure 4. Load-strain curves with different aspect ratios

下载: 全尺寸图片幻灯片

图 5 不同壁厚荷载-应变曲线

Figure 5. Load-strain curves for different wall thicknesses

下载: 全尺寸图片幻灯片

图 6 长宽比对承载力比值的关系

Figure 6. Ralation of cross-sectional aspect ratio on bearing capacity

下载: 全尺寸图片幻灯片

图 7 基于本文和文献数据的线性拟合分析

Figure 7. Linear regression analysis of data obtained in this study and those from literature

下载: 全尺寸图片幻灯片

图 8 试验值与计算值的关系

Figure 8. Relationship between experimental value and calculated value

下载: 全尺寸图片幻灯片

表 1 试件参数

Table 1. Parameters of specimens

试件编号	a/mm	b/mm	t/mm	L/mm	f_cu/MPa	f_ck/MPa	σ_0.2/MPa
120 × 60 × 4	120.0	61.3	4.4	359.7	44.0	28.9	538
120 × 60 × 5	119.5	60.4	5.4	360.3	44.0	28.9	581
120 × 80 × 4	119.8	81.0	4.2	359.6	44.0	28.9	516
120 × 80 × 5	120.5	81.1	5.0	361.0	44.0	28.9	558
120 × 120 × 4	120.8	120.3	4.0	360.2	44.0	28.9	549
120 × 120 × 5	120.0	120.5	5.4	360.5	44.0	28.9	578
120 × 120 × 6	120.5	120.1	5.8	361.2	44.0	28.9	598

下载: 导出CSV

表 2 各试件的基本参数

Table 2. Basic parameters of all specimens

试件编号	A_s/mm²	A_c/mm²	σ_0.2/MPa	f_ck/MPa	η	数据来源
120 × 60 × 4	1523	5836	538	29.48	2.00	本文
120 × 60 × 5	1824	5390	581	29.48	2.00
120 × 80 × 4	1606	8094	516	29.48	1.50
120 × 80 × 5	1921	7847	558	29.48	1.50
120 × 120 × 4	1857	12745	578	29.48	1.00
120 × 120 × 5	2462	11939	598	29.48	1.00
120 × 120 × 6	2680	11829	549	29.48	1.00
200 × 110 × 4C40	2346	19088	503	31.22	1.80	文献[24]
160 × 80 × 3C40	1339	11637	536	31.22	2.00
160 × 80 × 3C60	1328	11568	536	41.47	2.00
140 × 80 × 3C40	1282	9861	486	31.22	1.75
140 × 80 × 3C60	1282	9861	486	41.47	1.75
150 × 150 × 6C40	3292	19250	497	31.22	1.00
150 × 150 × 6C60	3293	19281	497	41.47	1.00
150 × 150 × 3C40	1615	20988	448	31.22	1.00
150 × 150 × 3C60	1614	20989	448	41.47	1.00
100 × 100 × 2C30	856	9308	385	20.10	1.00	文献[17]
100 × 100 × 2C60	776	9269	385	35.51	1.00
100 × 100 × 5C30	1841	8123	458	20.10	1.00
100 × 100 × 5C60	1806	8151	458	35.51	1.00
50 × 50 × 2C20	384	2116	353	14.41	1.00	文献[18]
50 × 50 × 2C30	384	2116	353	23.38	1.00
50 × 50 × 3C20	564	1936	440	14.41	1.00
50 × 50 × 3C30	564	1936	440	23.38	1.00
100 × 100 × 3C20	1164	8836	358	14.41	1.00
100 × 100 × 3C30	1164	8836	358	23.38	1.00
100 × 100 × 5C20	1900	8100	435	14.41	1.00
100 × 100 × 5C30	1900	8100	435	23.38	1.00
150 × 150 × 3C20	1764	20736	268	14.41	1.00
150 × 150 × 3C30	1764	20736	268	23.38	1.00
150 × 150 × 5C20	2900	19600	340	14.41	1.00
150 × 150 × 5C30	2900	19600	340	23.38	1.00

下载: 导出CSV

表 3 承载力计算与试验值

Table 3. Calculated and tested values of bearing capacity

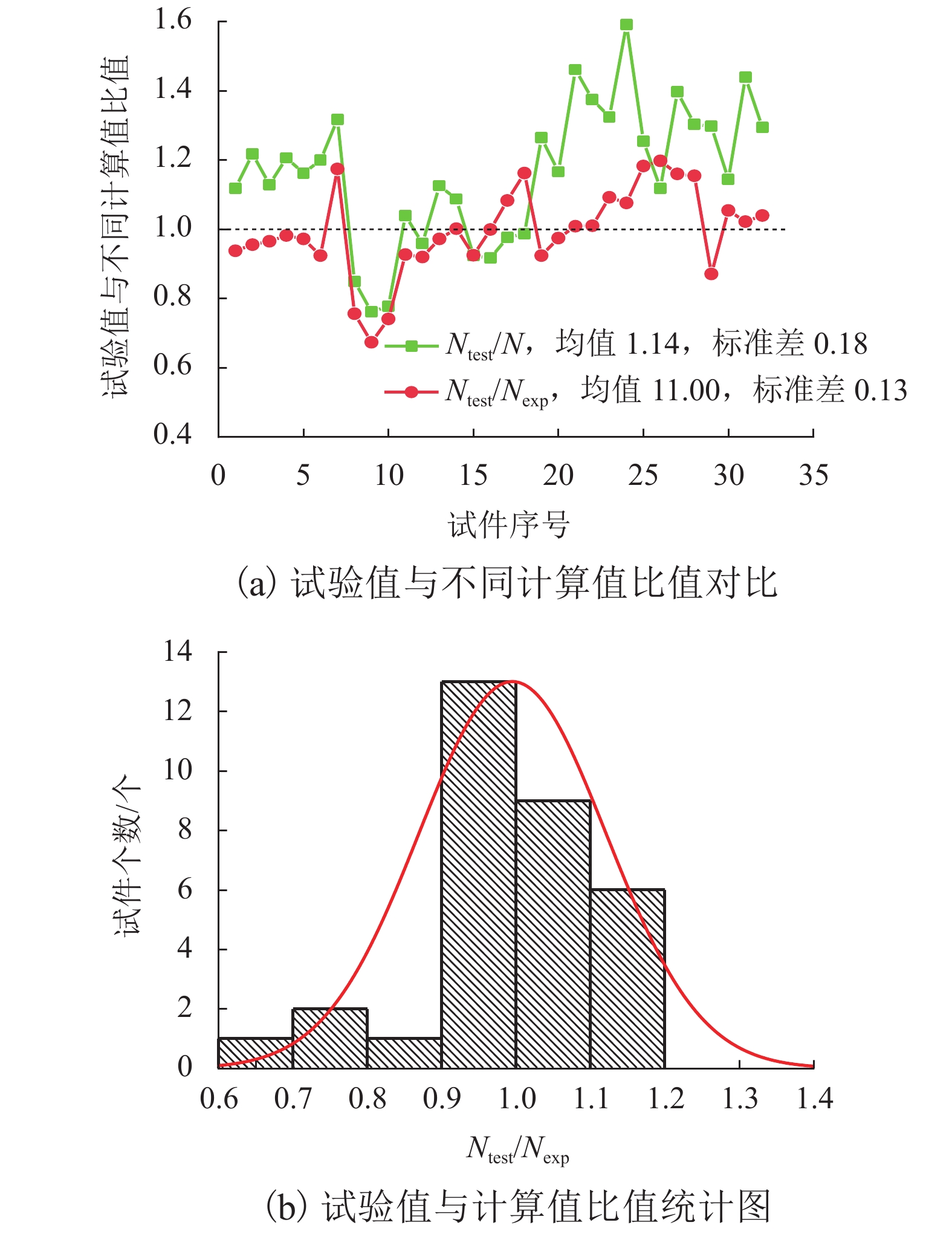
序号	试件编号	规范计算值 N /kN					N_test/kN	N_exp/kN
序号	试件编号	文献[28]	文献[29]	文献[30]	文献[31]	文献[32]	N_test/kN	N_exp/kN
1	120 × 60 × 4	985.75	970.45	954.93	1127.31	925.15	1261	1344
2	120 × 60 × 5	1115.91	1101.78	971.97	1340.03	1059.94	1632	1708
3	120 × 80 × 4	1090.13	1068.95	1132.21	1206.18	1006.19	1362	1410
4	120 × 80 × 5	1268.14	1247.58	1251.20	1435.89	1186.61	1732	1764
5	120 × 120 × 4	1455.26	1421.92	1584.14	1560.61	1323.19	1814	1866
6	120 × 120 × 5	1710.51	1679.26	1755.92	1895.83	1586.73	2274	2460
7	120 × 120 × 6	1946.23	1915.16	1938.93	2166.75	1823.13	2854	2430
8	200 × 110 × 4C40	1775.96	1692.74	1974.76	1915.92	2069.53	1627	2151
9	160 × 80 × 3C40	1081.01	1030.27	1209.70	1158.21	1259.98	882	1308
10	160 × 80 × 3C60	1191.53	1177.88	1352.79	1305.55	1427.86	1015	1369
11	140 × 80 × 3C40	930.91	887.91	1030.11	1008.94	1082.57	1049	1131
12	140 × 80 × 3C60	1031.98	1020.35	1160.93	1143.72	1233.44	1097	1192
13	150 × 150 × 6C40	2237.10	2153.17	2398.18	2458.97	2533.17	2768	2847
14	150 × 150 × 6C60	2436.20	2413.45	2652.82	2733.36	2830.11	2972	2967
15	150 × 150 × 3C40	1378.76	1287.25	1577.12	1495.00	1701.56	1381	1492
16	150 × 150 × 3C60	1593.48	1568.71	1852.90	1767.94	1701.15	1620	1621
17	100 × 100 × 2C30	516.65	517.06	571.55	546.95	608.80	534	613
18	100 × 100 × 2C60	627.90	672.20	721.54	696.10	790.01	687	651
19	100 × 100 × 5C30	1006.45	1006.81	1037.03	1115.46	1086.86	1410	1379
20	100 × 100 × 5C60	1116.59	1155.55	1162.70	1276.07	1259.15	1488	1431
21	50 × 50 × 2C20	166.04	174.22	177.42	178.63	155.86	261	224
22	50 × 50 × 2C30	185.02	198.32	198.70	205.09	165.81	282	235
23	50 × 50 × 3C20	276.05	283.54	283.80	314.89	266.74	417	393
24	50 × 50 × 3C30	293.42	305.59	287.35	341.35	275.84	543	404
25	100 × 100 × 3C20	544.03	578.18	586.94	570.90	501.53	716	709
26	100 × 100 × 3C30	623.29	678.83	682.87	676.75	543.06	757	757
27	100 × 100 × 5C20	943.22	974.52	993.26	1037.35	904.26	1449	1326
28	100 × 100 × 5C30	1015.87	1066.78	1042.10	1143.19	942.33	1490	1369
29	150 × 150 × 3C20	771.55	851.70	840.98	818.60	671.81	1062	897
30	150 × 150 × 3C30	957.55	1087.88	1078.87	1056.76	769.27	1209	1009
31	150 × 150 × 5C20	1268.43	1344.19	1362.93	1344.69	1174.16	1935	1668
32	150 × 150 × 5C30	1444.24	1567.43	1574.79	1582.84	1266.28	2048	1773

下载: 导出CSV

参考文献(32)

[1]	韩林海. 钢管混凝土结构-理论与实践[M]. 3版. 北京: 科学出版社, 2016.
[2]	韩林海,杨有福. 矩形钢管混凝土轴心受压构件强度承载力的试验研究[J]. 土木工程学报,2001,34(4): 22-31. doi: 10.3321/j.issn:1000-131X.2001.04.004 HAN Linhai, YANG Youfu. Study on axial bearing capacity of concrete-filled-steel-tube columns with rectangular section[J]. China Civil Engineering Journal, 2001, 34(4): 22-31. doi: 10.3321/j.issn:1000-131X.2001.04.004
[3]	郭红香,赵均海,魏雪英. 方钢管混凝土轴压短柱承载力分析[J]. 工业建筑,2008,38(3): 4,9-11. GUO Hongxiang, ZHAO Junhai, WEI Xueying. Analysis of bearing capacity of concrete-filled square steel tube column under axial load[J]. Industrial Construction, 2008, 38(3): 4,9-11.
[4]	龙跃凌,蔡健,黄炎生. 矩形钢管混凝土短柱轴压承载力[J]. 工业建筑,2010,40(7): 95-99. LONG Yueling, CAI Jian, HUANG Yansheng. Ultimate capacity of axially-loaded rectangular cft stub columns[J]. Industrial Construction, 2010, 40(7): 95-99.
[5]	LUO X Y, LIU W P. Mechanics behavior of concrete-filled square steel tube columns[J]. Applied Mechanics and Materials, 2012, 256/257/258/259: 662-665. doi: 10.4028/www.scientific.net/AMM.256-259.662
[6]	刘洁, 王正中. 方钢管混凝土短柱轴压极限承载力计算方法分析[J]. 建筑结构, 2015, 45（10）: 21-25, 42. LIU Jie, WANG Zhengzhong. Analysis on calculating method of ultimate bearing capacity of concrete-filled square steel tube short columns under axial load[J], Building Structure, 2015, 45（10）: 21-25, 42.
[7]	胡红松,林康,刘阳,等. 方钢管混凝土中钢管和混凝土抗压强度研究[J]. 建筑结构学报,2019,40(2): 161-168. HU Hongsong, LIN Kang, LIU Yang, et al. Study on compressive strength of steel tube and concrete in square CFT columns[J]. Journal of Building Structures, 2019, 40(2): 161-168.
[8]	王庆利,李瑞霖,李庆刚,等. 钢管高性能混凝土轴压短柱的静力性能(Ⅱ):机理分析及承载力[J]. 工业建筑,2013,43(3): 8-12. WANG Qingli, LI Ruilin, LI Qinggang, et al. Static performance of the high-performance concrete filled steel tubular stub column (Ⅱ):mechanism analysis and load bearing capacity[J]. Industrial Construction, 2013, 43(3): 8-12.
[9]	史庆轩,蔡文哲,王斌. 轴向往复荷载作用下钢管混凝土柱抗震性能试验研究[J]. 建筑结构学报,2020,40(9): 88-97. SHI Qingxuan, CAI Wenzhe, WANG Bin. Experimental research on seismic behavior of concrete-filled steel tube columns under cyclic axial loading[J]. Journal of Building Structures, 2020, 40(9): 88-97.
[10]	JUNG H S, CHOI C S. An experimental study on the behavior of square concrete-filled high strength steel tube columns[J]. Journal of Iron and Steel Research, 2011, 18(S1): 878-882.
[11]	IBAÑEZ C, HERNÁNDEZ-FIGUEIRIDO D, PIQUER A. Shape effect on axially loaded high strength CFST stub columns[J]. Journal of Constructional Steel Research, 2018, 147: 247-256. doi: 10.1016/j.jcsr.2018.04.005
[12]	ABHILASH M, JHANJHARI S, PARTHIBAN P, et al. Axial behaviour of semi-lightweight aggregate concrete-filled steel tube columns-A DOE approach[J]. Journal of Constructional Steel Research, 2019, 162(5): 105614.1-105614.16.
[13]	余敏,李书磊,王圣松. 钢管混凝土构件轴压承载力设计公式的可靠度分析[J]. 建筑钢结构进展,2017,19(2): 45-52,67. YU Min, LI Shulei, WANG Shengsong. Reliability analysis of the bearing capacity of concrete-filled steel tube under axial compression[J]. Progress in Steel Building Structures, 2017, 19(2): 45-52,67.
[14]	陈誉,李凤霞,王江. 热成型不锈钢圆管混凝土轴压短柱受力性能试验研究[J]. 建筑结构学报,2013,34(2): 106-112. CHEN Yu, LI Fengxia, WANG Jiang. Experimental study on axial compressive behavior of concrete-filled thermoforming stainless steel tubular stub columns[J]. Journal of Building Structures, 2013, 34(2): 106-112.
[15]	PATEL V I, LIANG Q Q, HADI M N S. Nonlinear analysis of axially loaded circular concrete-filled stainless steel tubular short columns[J]. Journal of Constructional Steel Research, 2014, 101: 9-18. doi: 10.1016/j.jcsr.2014.04.036
[16]	唐红元,范璐瑶,赵鑫,等. 圆不锈钢管混凝土短柱轴压承载力模型研究[J]. 工程科学与技术,2020,52(3): 10-20. TANG Hongyuan, FAN Luyao, ZHAO Xin, et al. Bearing capacity model of circular concrete-filled stainless steel stub columns under uniaxial compression[J]. Advanced Engineering Sciences, 2020, 52(3): 10-20.
[17]	代鹏,杨璐,卫璇,等. 不锈钢管混凝土短柱轴压承载力试验研究[J]. 工程力学,2019,36(增刊1): 298-305. DAI Peng, YANG Lu, WEI Xuan, et al. Experimental studies on the behavior and capacity of concrete filled stainless steel tube short columns[J]. Engineering Mechanics, 2019, 36(S1): 298-305.
[18]	LAM D, GARDNER L. Structural design of stainless steel concrete filled columns[J]. Journal of Constructional Steel Research, 2008, 64(11): 1275-1282. doi: 10.1016/j.jcsr.2008.04.012
[19]	BRIAN U, ZHONG T, HAN L H. Behaviour of short and slender concrete-filled stainless steel tubular columns[J]. Journal of Constructional Steel Research, 2011, 67(3): 360-378. doi: 10.1016/j.jcsr.2010.10.004
[20]	徐晨豪,赵俊亮,金国平. 圆不锈钢管混凝土轴压短柱三维有限元分析[J]. 混凝土,2017(7): 44-46,49. doi: 10.3969/j.issn.1002-3550.2017.07.011 XU Chenhao, ZHAO Junliang, JIN Guoping. Three-dimensional finite element analysis of concrete filled circular stainless steel tubular stubs[J]. Concrete, 2017(7): 44-46,49. doi: 10.3969/j.issn.1002-3550.2017.07.011
[21]	纪官运. 不锈钢管混凝土构件承载力计算方法及应用[D]. 大连: 大连理工大学, 2018.
[22]	DING F X, YIN Y X, MAO J F, et. al. Analytical behaviors of concrete-filled circular stainless steel tubular (CFCSST) stub columns under axial loading[J]. Structures, 2019, 19: 277-285. doi: 10.1016/j.istruc.2019.01.013
[23]	廖飞宇. 圆不锈钢管混凝土轴压力学性能的有限元分析[J]. 福建农林大学学报（自然科学版）, 2009, 38（6）: 659-662. LIAO Feiyu. Finite element analysis for circular concrete-filled stainless steel tubular column under axial compression[J]. Journal of Fujian Agriculture and Forestry University (Natural Science Edition), 2009, 38(6): 659-662.
[24]	YOUNG B, ELLOBODY E. Experimental investigation of concrete-filled cold-formed high strength stainless steel tube columns[J]. Journal of Constructional Steel Research, 2006, 62(5): 484-492. doi: 10.1016/j.jcsr.2005.08.004
[25]	DABAON M, EL-KHORIBY S, EL-BOGHDADI M, et al. Confinement effect of stiffened and unstiffened concrete-filled stainless steel tubular stub columns[J]. Journal of Constructional Steel Research, 2009, 65(8/9): 1846-1854.
[26]	国家质量监督检验检疫总局, 中国国家标准化管理委员会. 金属材料拉伸试验第1部分: 室温试验方法: GB/T 228.1—2010[S]. 北京: 中国标准出版社, 2011.
[27]	中华人民共和国建设部, 国家质量监督检验检疫总局. 普通混凝土力学性能试验方法标准: GB/T 50081—2002[S]. 北京: 中国建筑工业出版社, 2003
[28]	European Committee for Standardization. Design of composite steel and concrete structures, part 1.1: general rules and rules for buildings: EC4[S]. Brussels: European Committee for Standardization, 2004.
[29]	Architectural Institute of Japan. Recommendations for design and construction of concrete filled steel tubular structures: AIJ-CFT[S]. Tokyo: Architectural Institute of Japan, 1997.
[30]	国家能源局. 钢-混凝土组合结构设计规程: DL/T 5085—2021[S]. 北京: 中国计划出版社, 2021.
[31]	福建省住房和城乡建设厅. 钢管混凝土结构技术规程: DBJ/T 13-51—2010[S]. 福州: 福建省住房和城乡建设厅, 2010.
[32]	中国工程建设标准化协会. 矩形钢管混凝土结构技术规程: CECS 159—2004[S]. 北京: 中国计划出版社, 2004.

施引文献

附加材料(0)

访问统计

点击查看大图

图(8) / 表(3)

计量

文章访问数: 229
HTML全文浏览量: 94
PDF下载量: 9
被引次数: 0

矩形不锈钢管混凝土短柱轴压性能试验研究

doi: 10.3969/j.issn.0258-2724.20200416

作者简介: 唐红元(1974—)，男，教授，博士，研究方向为钢结构及组合结构，E-mail： tanghyseu@163.com

计量

出版历程

Experimental Investigation on Behavior of Rectangular Concrete-Filled Stainless Steel Tubular Stub Columns under Axial Loading

计量

出版历程

目录

作者简介:
唐红元(1974—)，男，教授，博士，研究方向为钢结构及组合结构，E-mail： tanghyseu@163.com