基于集成式神经网络的扁平箱梁颤振导数预测

梅瀚雨; 王骑; 廖海黎; 张岩

doi:10.3969/j.issn.0258-2724.20200408

基于集成式神经网络的扁平箱梁颤振导数预测

doi: 10.3969/j.issn.0258-2724.20200408

梅瀚雨^1,,
王骑^{1, 2, ,},
廖海黎^{1, 2},
张岩¹

1.
西南交通大学土木工程学院，四川成都 610031
2.
西南交通大学风工程四川省重点实验室，四川成都 610031

基金项目: 国家自然科学基金（51778547，51678508）

详细信息

作者简介:
梅瀚雨（1994—），男，博士研究生，研究方向为桥梁与隧道工程，E-mail：mhanyu8866@gmail.com

通讯作者:
王骑（1980—），男，教授，研究方向为大跨度桥梁抗风，E-mail：wangchee_wind@swjtu.edu.cn

中图分类号: TP183；U441.3
计量
- 文章访问数: 237
- HTML全文浏览量: 116
- PDF下载量: 15
- 被引次数: 0
出版历程
- 收稿日期: 2020-09-04
- 修回日期: 2020-11-10
- 刊出日期: 2020-11-11

Flutter Derivative Prediction of Flat Box Girder Based on Ensembled Neural Network

MEI Hanyu^1
,,
WANG Qi^{1, 2
, ,},
LIAO Haili^{1, 2},
ZHANG Yan¹

1.
School of Civil Engineering, Southwest Jiaotong University, Chengdu 610031, China
2.
Wind Engineering Key Laboratory of Sichuan Province, Southwest Jiaotong University, Chengdu 610031, China

摘要

摘要:
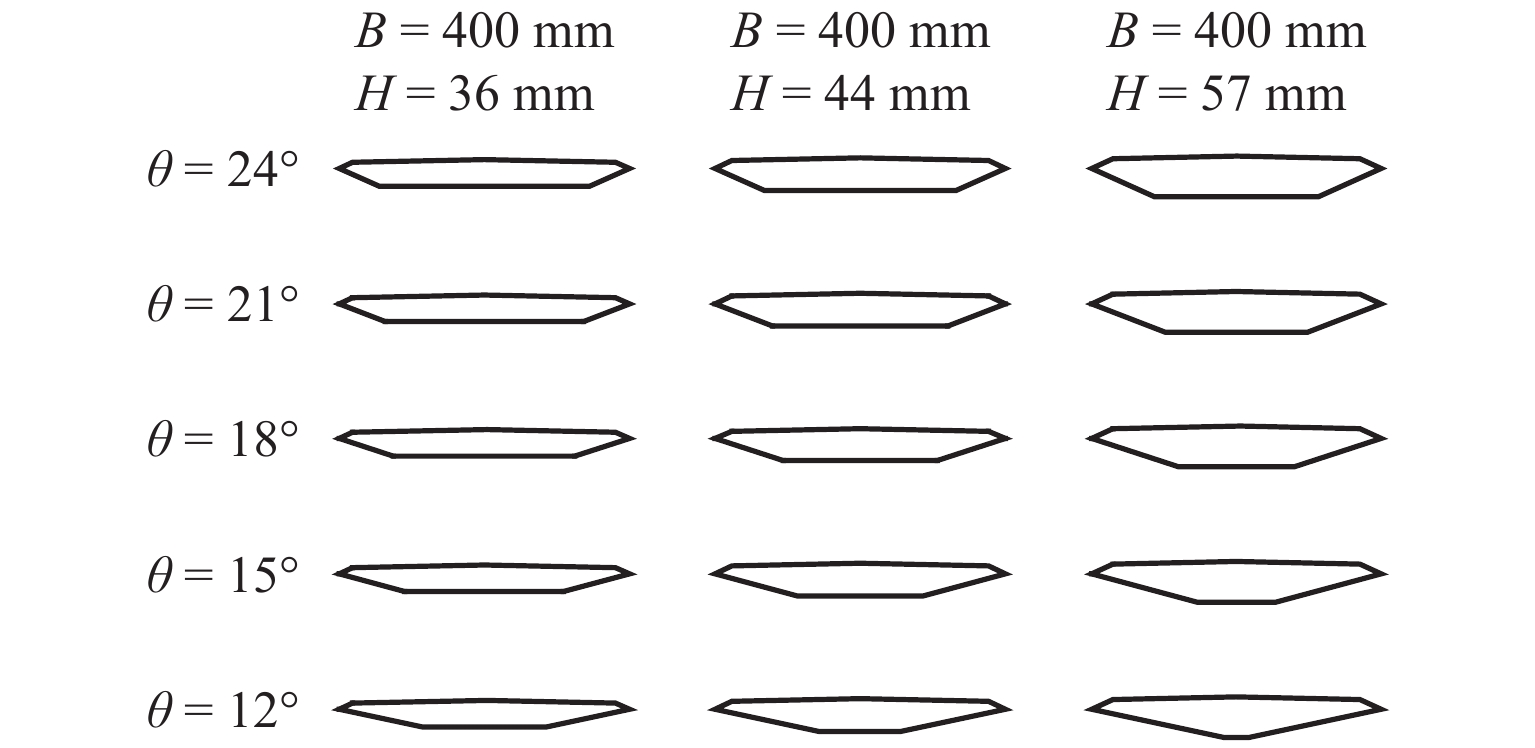
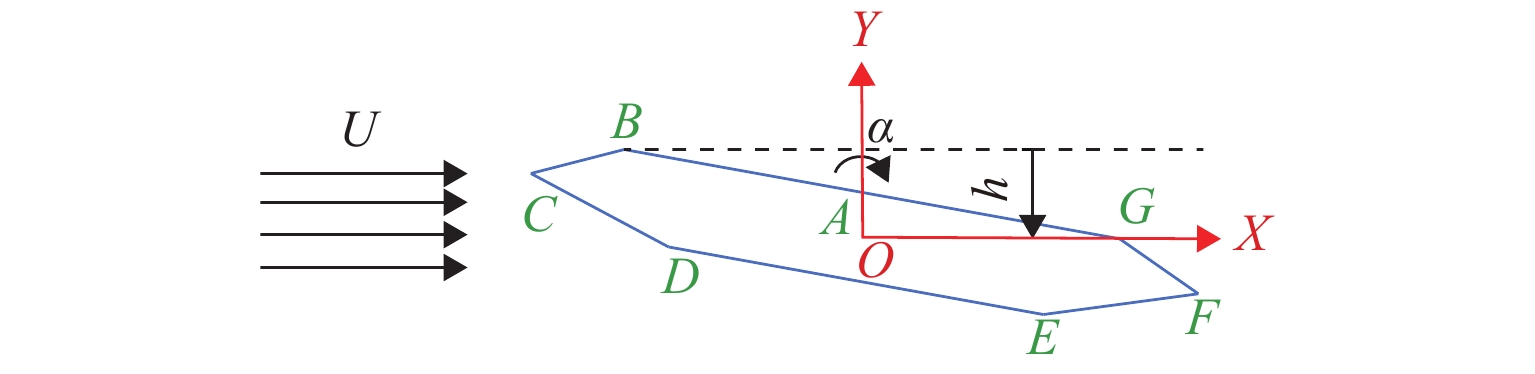
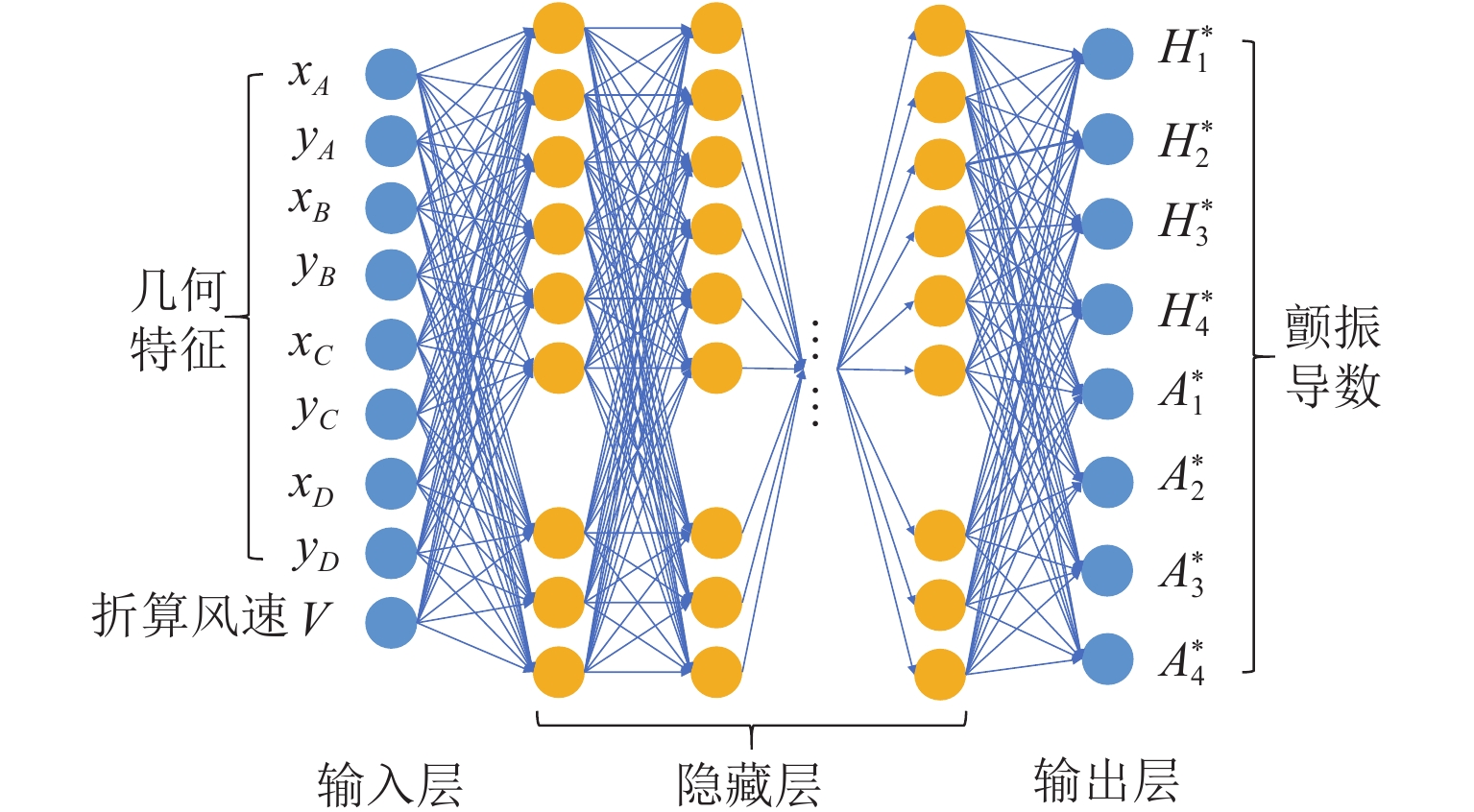
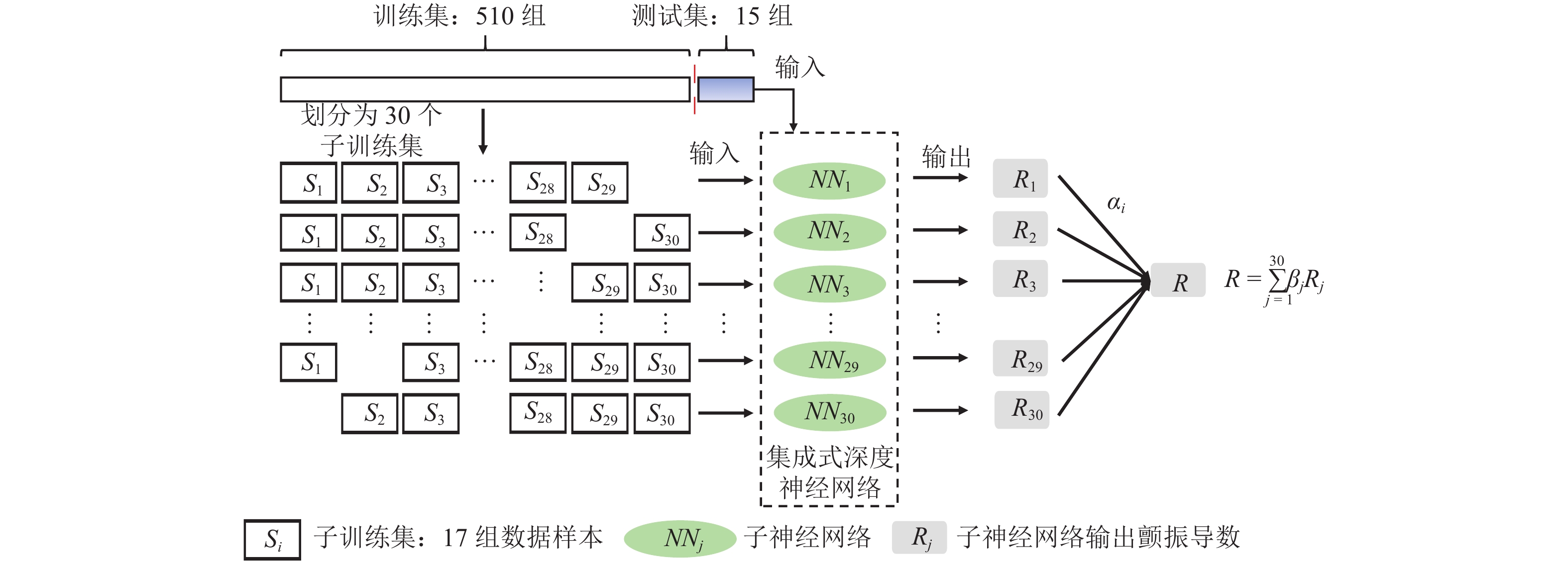
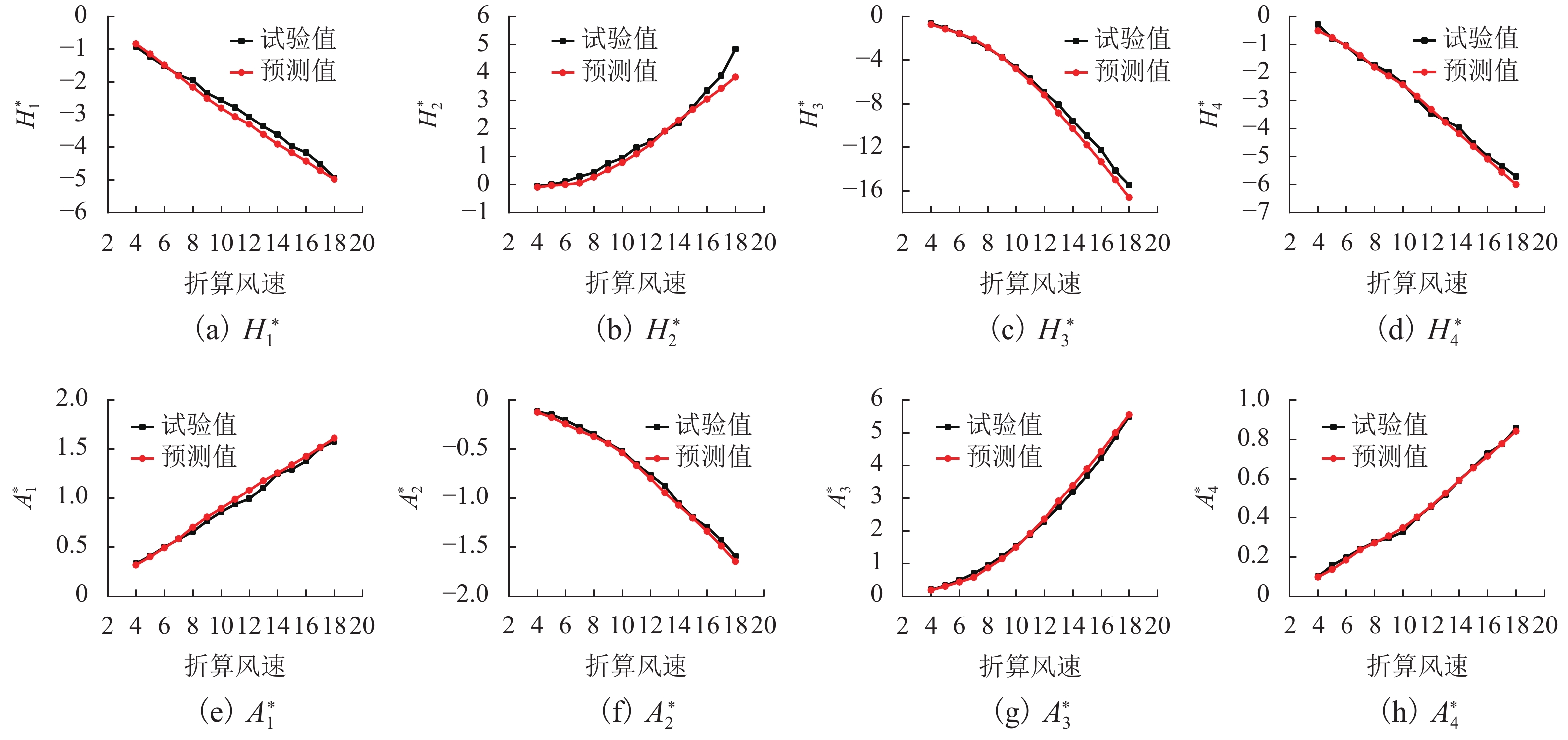
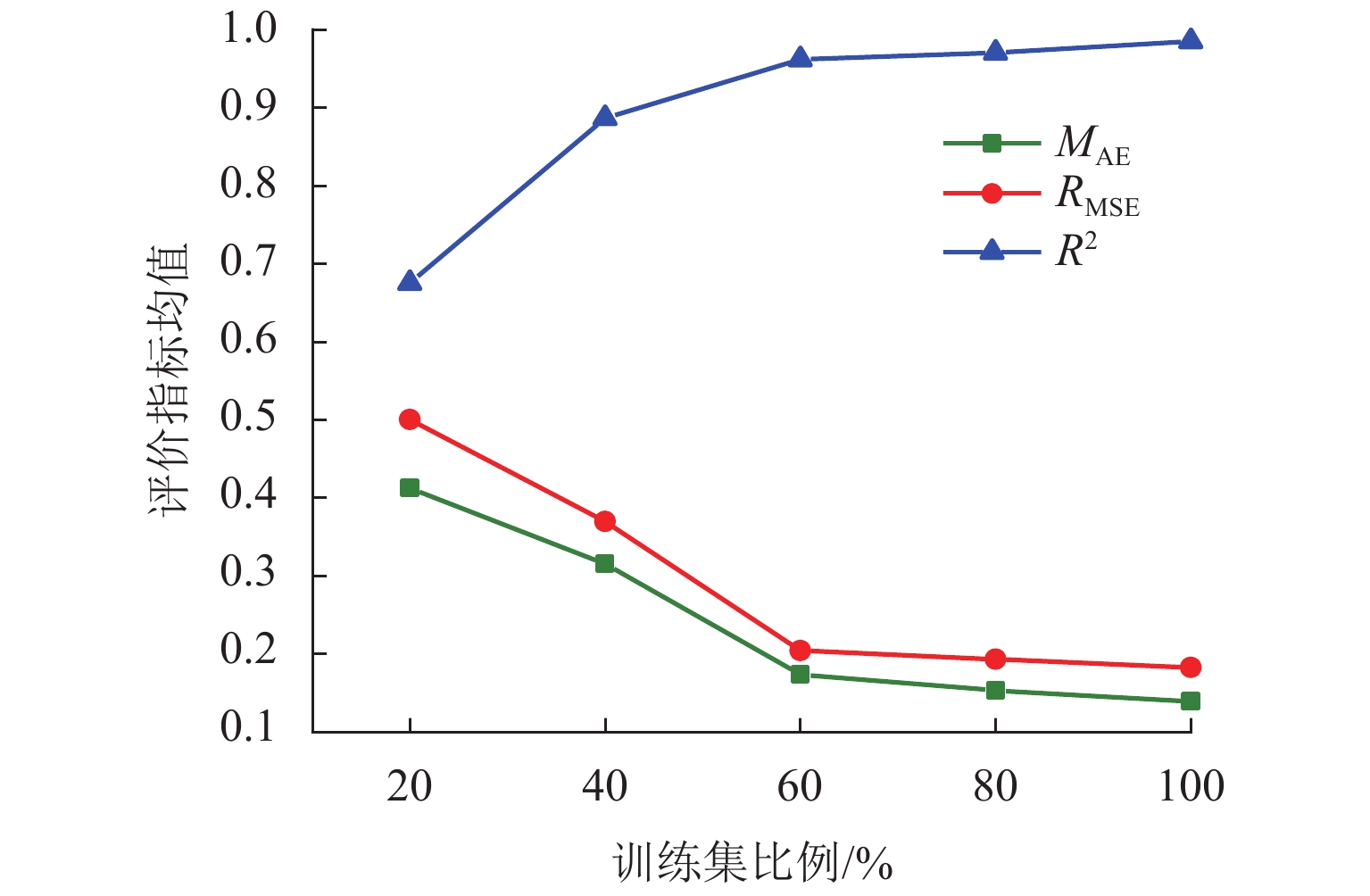
扁平箱梁因具有较优的颤振性能，已被应用于绝大多数大跨径桥梁. 为便于桥梁设计者在大跨度桥梁初步设计阶段快速评估扁平箱梁的颤振性能，提出了一种基于集成学习的深度神经网络模型，用于快速预测扁平箱梁颤振导数. 首先采用强迫振动风洞试验获取了15种典型扁平箱梁的颤振导数，结合自由振动风洞试验和二维颤振计算验证了颤振导数的准确性；基于风洞试验数据，构建了大小为525的颤振导数数据集，以此数据集为基础，对所提出的集成式深度神经网络开展了模型训练和性能测试. 计算结果表明：所提出的集成式深度神经网络模型仅依靠扁平箱梁的气动外形特征即可准确且快速地预测不同折算风速下的8个颤振导数，且仅利用本文60%的数据集进行训练即可获取较高精度的预测结果；对比传统的多项式回归模型和单一人工神经网络模型，本文所提出的集成式深度神经网络模型预测精度更高，可直接应用到桥梁初步设计阶段的气动选型和颤振计算中.
- 强迫振动 /
- 风洞试验 /
- 集成学习 /
- 神经网络 /
- 颤振导数
Abstract:
Flat box girder has been used in most long-span bridge because of its excellent flutter performance. To facilitate bridge designers to quickly evaluate the flutter performance of flat box girders in the preliminary design stage of long span bridges, a deep neural network model based on ensemble learning was proposed for quickly predicting flutter derivatives of flat box girders. Firstly, the flutter derivatives of 15 typical flat box girders were obtained by forced vibration wind tunnel tests, and the accuracy of flutter derivatives was verified by combining the free vibration wind tunnel test and two-dimensional flutter analysis. Then, a flutter derivative dataset with the size of 525 was constructed based on wind tunnel testing data. The proposed ensemble deep neural network model was trained and tested based on the dataset. The results show that the proposed ensemble deep neural network model can accurately and quickly predict the 8 flutter derivatives at different reduced wind speeds by relying only on the box geometry properties of the flat box girder, and only using 60% of the training dataset for training can obtain acceptable prediction results with enough precision. Compared with the traditional polynomial regression model and the single artificial neural network model, the ensemble deep neural network model proposed in this paper has higher prediction accuracy and can be directly applied to the geometry selection and flutter prediction procedure in the preliminary design stage of bridges.
- forced vibration /
- wind tunnel tests /
- ensemble learning /
- neural network /
- flutter derivatives

HTML全文

图 1 典型断面示意

Figure 1. Typical section schematic

下载: 全尺寸图片幻灯片

图 2 扁平箱梁模型断面

Figure 2. Sectional models of flat box girders

下载: 全尺寸图片幻灯片

图 3 安装在风洞中的强迫振动装置及模型

Figure 3. Sectional model assembled on forced vibration device in wind tunnel

下载: 全尺寸图片幻灯片

图 4 弹簧悬挂自由振动风洞试验

Figure 4. Free vibration wind tunnel tests

下载: 全尺寸图片幻灯片

图 5 带风攻角的断面顶点坐标示意

Figure 5. Coordinate of flat box girder with angle of attack

下载: 全尺寸图片幻灯片

图 6 子神经网络预测颤振导数

Figure 6. Sub-network for flutter derivative prediction

下载: 全尺寸图片幻灯片

图 7 集成式深度神经网络实现流程

Figure 7. Flow chart of building the integrated deep neural network

下载: 全尺寸图片幻灯片

图 8 测试断面详图

Figure 8. Detailed geometry of testing section

下载: 全尺寸图片幻灯片

图 9 测试断面颤振导数预测结果对比

Figure 9. Comparison between predicted and tested flutter derivatives of testing section

下载: 全尺寸图片幻灯片

图 10 测试断面颤振导数误差

Figure 10. Error results of flutter derivatives of testing section

下载: 全尺寸图片幻灯片

图 11 训练集大小对误差结果的影响

Figure 11. Effects of training set size on error results

下载: 全尺寸图片幻灯片

表 1 颤振临界风速结果对比

Table 1. Comparison of critical flutter wind speeds

风攻角/（°）	试验值/（m·s⁻¹）	计算值/（m·s⁻¹）	误差/%
0	11.56	11.92	3.11
+3	10.79	10.53	−2.41
+5	8.54	8.71	1.99

下载: 导出CSV

表 2 不同子神经网络结构设计参数

Table 2. Design parameters of different sub-neural networks

隐藏层层数	隐藏神经元个数	非线性激活函数	子神经网络个数/个
3, 4	12, 14, 16, 18, 20	tan h, sigmoid, ReLU	2 × 5 × 3= 30

下载: 导出CSV

表 3 误差结果对比

Table 3. Comparison of different errors

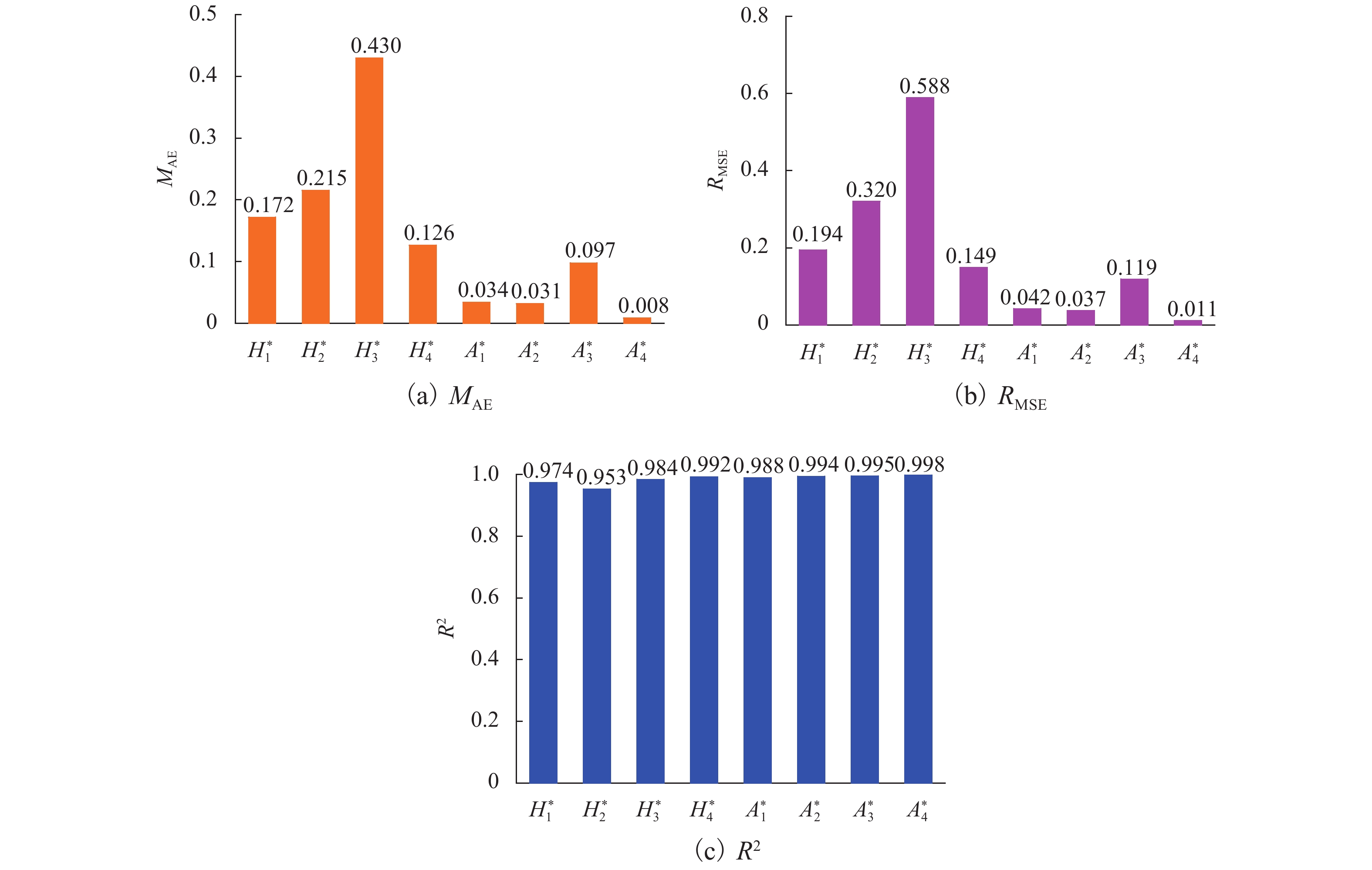
模型	${M}_{{\rm{AE}}}$	${R}_{{\rm{MSE}}}$	$ {R}^{2} $
多项式回归	0.437	0.538	0.781
神经网络模型	0.364	0.468	0.807
本文集成模型	0.139	0.183	0.985

下载: 导出CSV

参考文献(28)

[1]	SCANLAN R H, TOMKO J J. Airfoil and bridge deck flutter derivatives[J]. Journal of the Engineering Mechanics Division, 1971, 97(6): 1717-1737. doi: 10.1061/JMCEA3.0001526
[2]	陈政清,于向东. 大跨桥梁颤振自激力的强迫振动法研究[J]. 土木工程学报,2002,35(5): 34-41. doi: 10.3321/j.issn:1000-131X.2002.05.008 CHEN Zhengqing, YU Xiangdong. A new method for measuring flutter self-excited forces of long-span bridges[J]. China Civil Engineering Journal, 2002, 35(5): 34-41. doi: 10.3321/j.issn:1000-131X.2002.05.008
[3]	熊龙. 考虑静风效应及自激气动力跨向相关性的大跨度悬索桥精细化颤振分析方法[D]. 成都: 西南交通大学, 2017.
[4]	MEI H Y, WANG Q, LIAO H L, et al. Improvement of flutter performance of a streamlined box girder by using an upper central stabilizer[J]. Journal of Bridge Engineering, 2020, 25(8): 04020053.1-04020053.11. doi: 10.1061/(ASCE)BE.1943-5592.0001584
[5]	DIANA G, CHELI F, ZASSO A, et al. Suspension bridge parameter identification in full scale test[J]. Journal of Wind Engineering and Industrial Aerodynamics, 1992, 41(1/2/3): 165-176.
[6]	WU B, WANG Q, LIAO H L, et al. Hysteresis response of nonlinear flutter of a truss girder: experimental investigations and theoretical predictions[J]. Computers & Structures, 2020, 238: 106267.1-106267.17.
[7]	李永乐,廖海黎,强士中. 桥梁断面颤振导数识别的加权整体最小二乘法[J]. 土木工程学报,2004,37(3): 80-84. doi: 10.3321/j.issn:1000-131X.2004.03.012 LI Yongle, LIAO Haili, QIANG Shizhong. Identification for flutter derivatives of bridge deck cross section by weighting ensemble least-square method[J]. China Civil Engineering Journal, 2004, 37(3): 80-84. doi: 10.3321/j.issn:1000-131X.2004.03.012
[8]	HONORÉWALTHER J, LARSEN A. Two dimensional discrete vortex method for application to bluff body aerodynamics[J]. Journal of Wind Engineering and Industrial Aerodynamics, 1997, 67/68: 183-193. doi: 10.1016/S0167-6105(97)00072-X
[9]	HUANG L, LIAO H L, WANG B, et al. Numerical simulation for aerodynamic derivatives of bridge deck[J]. Simulation Modelling Practice and Theory, 2009, 17(4): 719-729. doi: 10.1016/j.simpat.2008.12.004
[10]	XU F Y, ZHANG Z B. Free vibration numerical simulation technique for extracting flutter derivatives of bridge decks[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2017, 170: 226-237. doi: 10.1016/j.jweia.2017.08.018
[11]	JUNG S, GHABOUSSI J, KWON S D. Estimation of aeroelastic parameters of bridge decks using neural networks[J]. Journal of Engineering Mechanics, 2004, 130(11): 1356-1364. doi: 10.1061/(ASCE)0733-9399(2004)130:11(1356)
[12]	LUTE V, UPADHYAY A, SINGH K K. Support vector machine based aerodynamic analysis of cable stayed bridges[J]. Advances in Engineering Software, 2009, 40(9): 830-835. doi: 10.1016/j.advengsoft.2009.01.008
[13]	MATSUMOTO M, KOBAYASHI Y, SHIRATO H. The influence of aerodynamic derivatives on flutter[J]. Journal of Wind Engineering and Industrial Aerodynamics, 1996, 60: 227-239. doi: 10.1016/0167-6105(96)00036-0
[14]	WU T, KAREEM A. Modeling hysteretic nonlinear behavior of bridge aerodynamics via cellular automata nested neural network[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2011, 99(4): 378-388. doi: 10.1016/j.jweia.2010.12.011
[15]	李乔,杨兴旺. 桥梁主梁断面空气力学特性分析的人工神经网络方法[J]. 中南公路工程,2000,25(3): 56-59. LI Qiao, YANG Xingwang. Artificial neural network method for analysis of aerodynamic characteristics of bridge girder section[J]. Central South Highway Engineering, 2000, 25(3): 56-59.
[16]	LI S W, LAIMA S J, LI H. Data-driven modeling of vortex-induced vibration of a long-span suspension bridge using decision tree learning and support vector regression[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2018, 172: 196-211. doi: 10.1016/j.jweia.2017.10.022
[17]	陈讷郁,葛耀君. 基于人工神经网络的典型桥梁断面气动参数识别[J]. 土木工程学报,2019,52(8): 91-97,128. CHEN Neyu, GE Yaojun. Aerodynamic parameter identification of typical bridge sections based on artificial neural network[J]. China Civil Engineering Journal, 2019, 52(8): 91-97,128.
[18]	RIZZO F, CARACOGLIA L. Artificial Neural Network model to predict the flutter velocity of suspension bridges[J]. Computers & Structures, 2020, 233: 106236.1-106236.20.
[19]	王骑,李郁林,李志国,等. 不同风攻角下薄平板的颤振导数[J]. 工程力学,2018,35(10): 10-16. doi: 10.6052/j.issn.1000-4750.2017.06.0487 WANG Qi, LI Yulin, LI Zhiguo, et al. Flutter derivatives of a thin plate model under different attack angles[J]. Engineering Mechanics, 2018, 35(10): 10-16. doi: 10.6052/j.issn.1000-4750.2017.06.0487
[20]	廖海黎,闫雨轩,王骑,等. 扁平箱梁颤振计算公式中联合折减系数的量化研究[J]. 中国公路学报,2019,32(1): 67-75,86. doi: 10.3969/j.issn.1001-7372.2019.01.008 LIAO Haili, YAN Yuxuan, WANG Qi, et al. Quantification of joint reduction coefficient of flutter closed-form solutions for flat box girders[J]. China Journal of Highway and Transport, 2019, 32(1): 67-75,86. doi: 10.3969/j.issn.1001-7372.2019.01.008
[21]	CHEN X Z, KAREEM A. Revisiting multimode coupled bridge flutter:some new insights[J]. Journal of Engineering Mechanics, 2006, 132(10): 1115-1123. doi: 10.1061/(ASCE)0733-9399(2006)132:10(1115)
[22]	ZHENG A, CASARI A. Feature engineering for machine learning: principles and techniques for data scientists[M]. Cambridge: O’Reilly Media, 2018.
[23]	MCCULLOCH W S, PITTS W. A logical calculus of the ideas immanent in nervous activity[J]. Bulletin of Mathematical Biology, 1990, 52(1/2): 99-115.
[24]	GOODFELLOW I, BENGIO Y, COURVILLE A, et al. Deep learning[M]. Cambridge: MIT press, 2016.
[25]	DASARATHY B V, SHEELA B V. A composite classifier system design: concepts and methodology[J]. Proceedings of the IEEE, 1979, 67(5): 708-713. doi: 10.1109/PROC.1979.11321
[26]	DIETTERICH T G. Ensemble learning[M]. Cambridge: MIT press, 2002, 2: 110-125.
[27]	KINGMA D P, BA J. Adam: A method for stochastic optimization[J/OL]. [2020-06-05]. https://arxiv.org/abs/1412.6980.
[28]	CHEN X Z. Improved understanding of bimodal coupled bridge flutter based on closed-form solutions[J]. Journal of Structural Engineering, 2007, 133(1): 22-31. doi: 10.1061/(ASCE)0733-9445(2007)133:1(22)