Optimal Siting and Sizing forInverter Feedback Devices Applied in Urban Rail Transit
-
摘要:
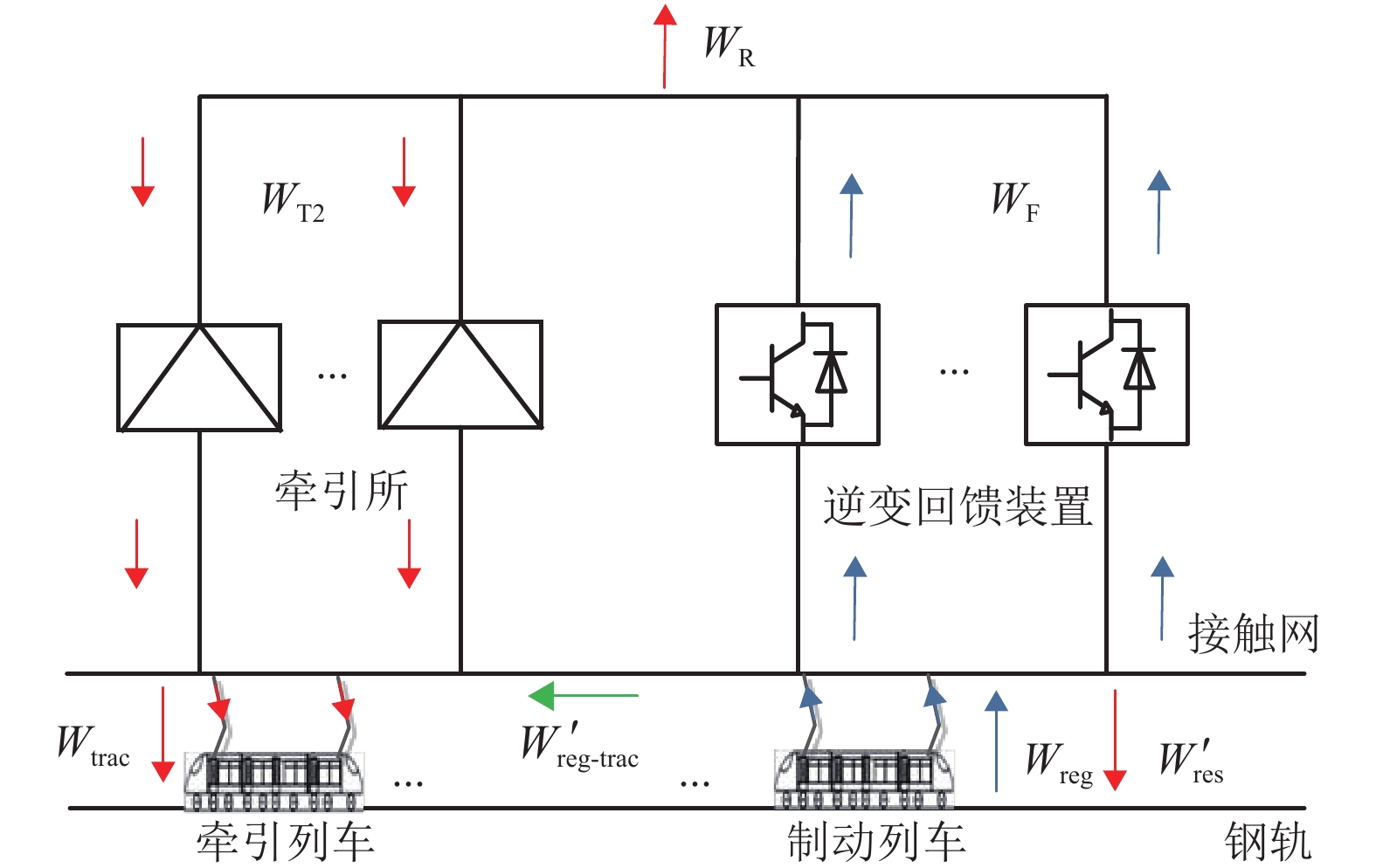
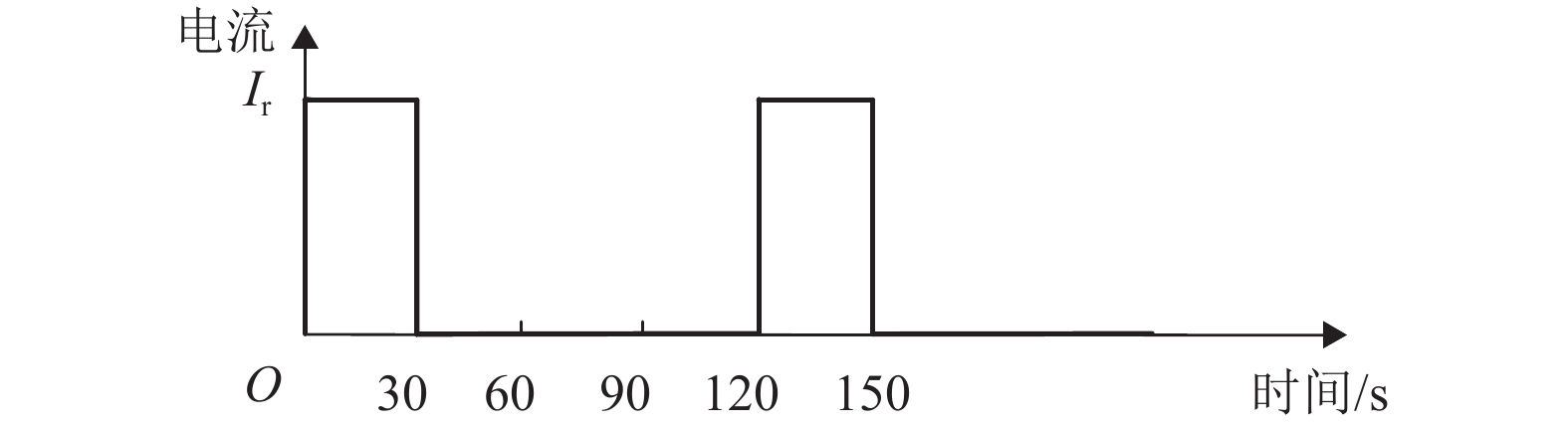
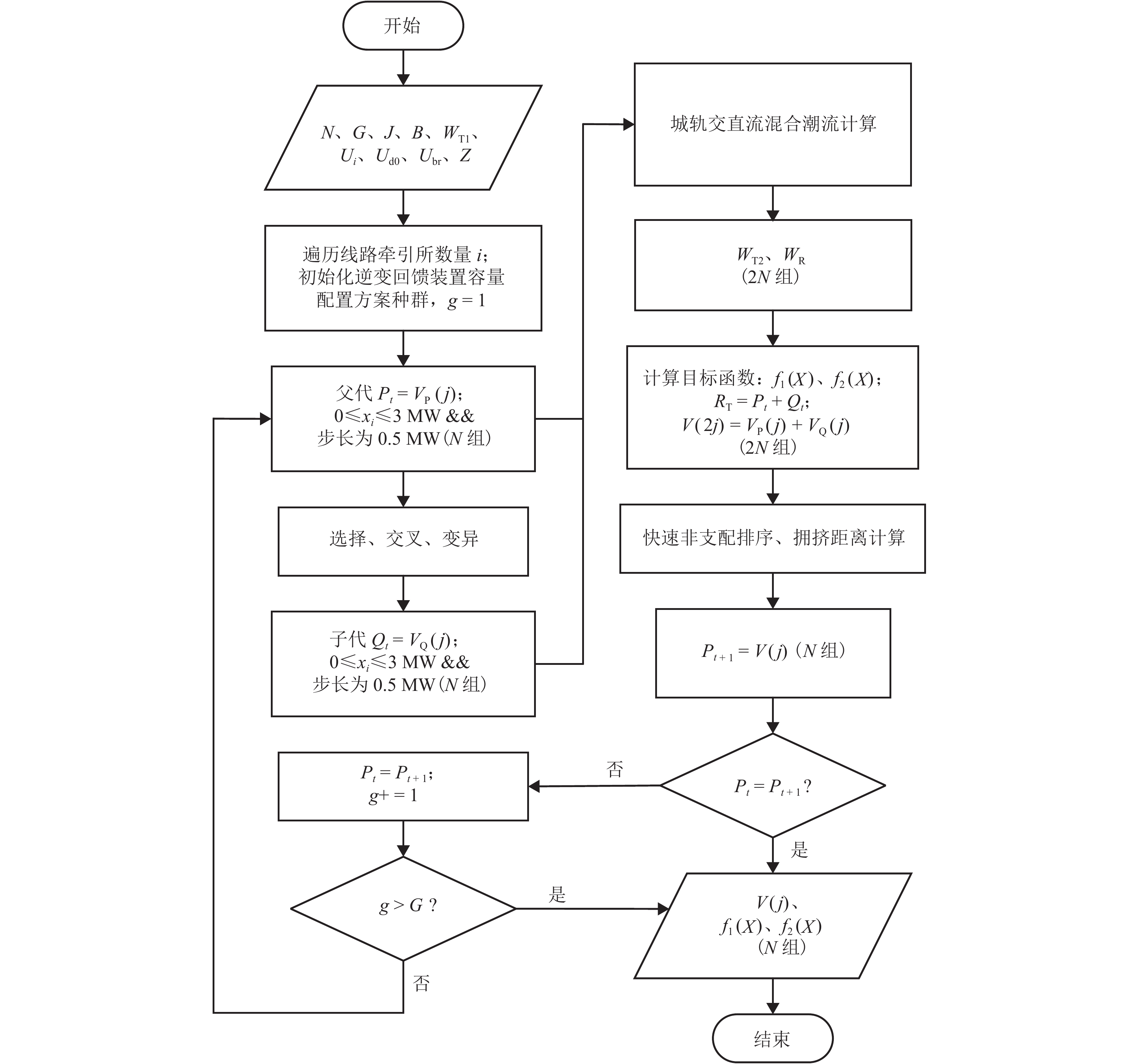
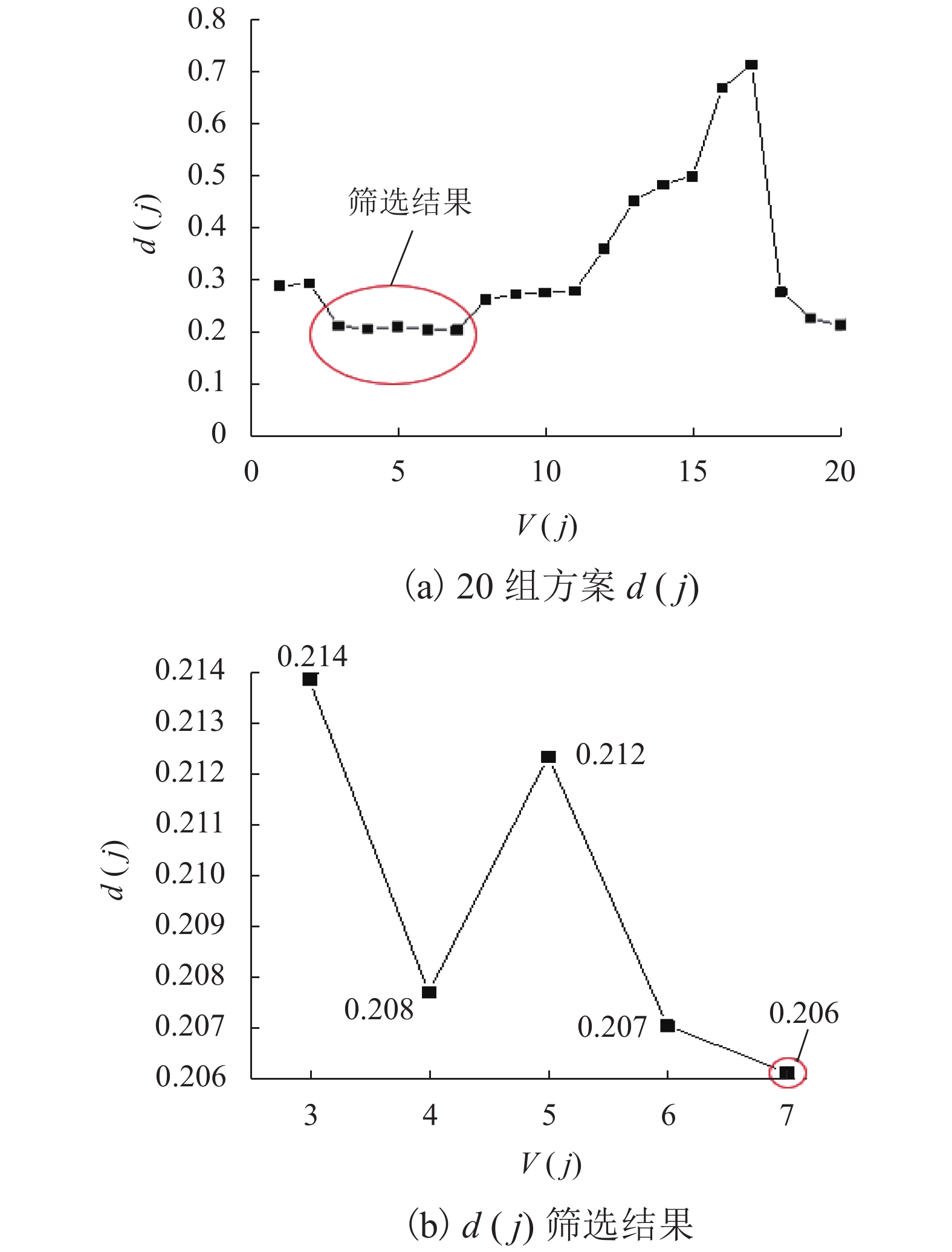
以节省逆变回馈装置投资成本和提高再生制动能量利用率为目标，建立了城轨牵引供电系统逆变回馈装置定容选址优化模型. 将考虑逆变回馈装置周期性间歇工作制的城轨牵引供电系统交直流混合潮流算法与带精英策略的快速非支配排序遗传算法（fast non-dominated sorting genetic algorithm Ⅱ，fast NSGA-Ⅱ）相结合，求解多目标函数的Pareto解集；并采用基于信息熵的序数偏好法（technique for order preference by similarity to ideal solution，TOPSIS）筛选逆变回馈装置定容选址的最优方案. 以广州地铁某线路为算例进行仿真验证，结果表明：优化方案相对该地铁工程实际逆变回馈装置配置方案，其装置投资成本节省70万元，系统级节能率提高3.25%，投资回报周期相应缩短.
Abstract:A multi-objective optimization model of siting and sizing of inverter feedback devices is established with an objective of saving the investment cost of inverter feedback devices and improving the utilization rate of regenerative braking energy. The AC-DC hybrid power flow algorithm that involves the intermittent work cycle of the inverter feedback device and the fast non-dominated sorting genetic algorithm Ⅱ (fast NSGA-Ⅱ) are combined to solve the Pareto solution set. The entropy-based technique for order preference by similarity to ideal solution (TOPSIS) is adopted to select the optimal site of the inverter feedback device. Cases with a metro line in Guangzhou were studied to compare the optimal solution with the actual configuration scheme of the inverter feedback device, showing that the optimal solution saved 700, 000 yuan of investment cost, increased the system level energy saving rate by 3.25%, and shortened the investment return period.
-
Key words:
- traction power supply system /
- inverter feedback device /
- optimal design /
- genetic algorithm /
- entropy
-
回头曲线是山区公路尤其是低标准公路越岭线的常用布线形式，线形参数值一般采用极限指标，甚至低于极限指标，其行驶安全性、舒适性和通过性一直备受关注. 轨迹曲率是描述汽车行驶特征的主要参数，道路设计人员是假定驾驶人跟随路中线行驶，行驶轨迹与路中线重合或是平行. 但在车流量较少的山区公路环境下，轨迹与路中线（或是行车道中心线）之间存在不同程度的横向偏离[1-3]，曲线路段的轨迹曲率半径与弯道设计半径并不相等，导致实际行驶状态背离设计预期. 所以，需要掌握回头曲线路段真实行车轨迹的形态和曲率特性，以深入了解山区道路驾驶行为特征.
现有研究主要聚焦于轨迹在曲线路段范围内的横向位置、偏移量和影响因素，譬如Fitzsimmons等[4-5]通过路面充气管来记录曲线路段的轨迹和速度，分析轨迹横向偏移以及切弯行为. Blana等[6-10]用路侧摄像法分析摄录到的S形曲线、交叉口车辆的轨迹偏移. 丁传鑫[11]开发了一款行驶轨迹观测仪器来获取车辆横向位置，分析了轨迹偏移与弯道半径之间的关系. Spacek[12]通过路侧传感器采集了车辆距离路边线的距离，绘制轨迹形态线并确定了6种轨迹模式. 徐进等[13-15]结合车载GPS数据和视频图像提取了轨迹线和轨迹线-路边线相对位置；王志聪[16]将无人机悬停在弯道上空拍摄交通运行图像，分析了试验路段的轨迹偏移量. Cerni等[17]用GPS设备记录车辆行驶轨迹，并计算轨迹曲率与弯道设计曲率之间的差值，结果发现弯道偏角越小、弯道越短，轨迹曲率与设计曲率之间的差值越大. Bella[18]使用驾驶模拟器分析了路侧环境比如行道树、护栏等对汽车轨迹和速度的影响，发现不管是左转弯和右转弯，驾驶人在过弯时均存在切弯行为.
综上可见，现有研究主要关注一般曲线路段的轨迹和速度特性，而回头曲线作为山区复杂线形公路独特运行环境的重要体现，其驾驶行为特性却罕有研究报道. 为此，本文通过实车路试采集了复杂线形公路的驾驶数据，通过对实际行驶轨迹曲率与道路曲率的计算与分析，得到了回头曲线路段的轨迹形态和轨迹曲率，计算了圆曲线范围内的轨迹等效半径，明确了回头曲线的过弯方式，并与山区大半径普通弯道进行了对比. 研究结果可为回头曲线路段的交通安全设施设计、交通管理、事故发生机制以及危险路段的安全改善提供实测数据支撑和理论依据.
1. 实车试验方案以及数据处理
1.1 试验道路以及被试
选取重庆市彭水县境内的国道G211线花地弯到宁家寨段作为试验对象，路线长度8.7 km，技术标准为山区四级公路，设计速度为20 km/h，路段范围内包含11处回头曲线，如图1所示，C1～C11为弯道编号. 该公路于2016年完成改建施工，包括路基拓宽和路面施工，因此路面平整，标线清晰，技术状况良好. 试验路段为沥青路面，横断面为双车道，直线路段行车道路宽度3.00 m，回头曲线范围内行车道加宽至4.20 m，缘线外侧有0.50 m宽的硬化土路肩. 11处回头曲线的几何参数见表1，曲线范围内的纵坡度主要集中在3%. 11处弯道在弯道入口的路侧地形条件和通视性如附加材料表S1所示.
表 1 回头曲线的几何参数Table 1. Geometric parameters of hairpin curves弯道编号 半径/m 转角/（°） 曲线长度/m 缓和
曲线长/m坡度/% 弯前（弯后）
坡度/%弯中内侧（外侧）
车道宽/mC1 20.156 192.73 92.975 25.000 3.0 3.0 (9.0) 4.25 (4.25) C2 20.233 186.19 90.797 25.000 3.0 7.0 (9.0) 4.25 (4.25) C3 20.079 180.09 88.138 25.000 3.0 9.0 (9.0) 4.25 (4.25) C4 20.029 169.51 84.381 25.000 3.0 9.0 (9.0) 4.25 (4.25) C5 22.425 159.43 87.519 25.000 2.7 9.0 (5.5) 4.25 (4.25) C6 20.861 190.62 94.561 25.000 2.8 2.8 (9.0） 4.25 (4.25) C7 22.315 150.60 83.815 25.000 3.0 9.0 (9.0) 4.75 (3.55) C8 20.26 172.64 86.202 25.000 3.0 9.0 (7.5) 4.25 (4.25) C9 20.304 186.58 91.257 25.000 3.0 6.5 (9.0) 4.25 (4.25) C10 20.327 180.54 89.188 25.000 3.0 7.2 (9.0) 4.25 (4.25) C11 20.347 194.61 94.259 25.000 3.0 6.9 (8.5) 4.25 (4.25) 注：表1中第7列弯前坡度是指缓和曲线之前的直线路段坡度；行驶方向C1至C11，路线总体趋势为上坡. 实车驾驶试验于2019年11月中旬开展，每日的试验均是在日间进行，无暴雨、狂风、雷电等极端气象条件. 试验路段车流量小，沿线偶有民居，但路侧干扰极少，行车时的驾驶自由度较大. 从社会上付费招募20名驾驶员作为被试，其中男性15人，女性5人，年龄分布在22～48岁，平均年龄为29.95岁. 由于试验道路的线形组合复杂，路侧危险度大，为确保试验的安全性，选择了驾龄较长的被试，驾龄分布在4～30 a，平均驾龄11.93 a，驾驶里程分布在1.8 × 104～2.0 × 105 km，平均里程8.4 × 104 km.
1.2 试验车辆与车载仪器
本文采用Race-Technology公司的第二代高精度GPS惯性测速系统Speed Box记录车辆连续行驶轨迹，输出频率为100 Hz，速度精度0.072 km/h，绝对位置精度2 m，相对位置精度3 cm （40 m范围内）；用带有网络时间校准功能的车载SV-MDOO9 HD行车记录仪记录前向和侧向的行驶环境；用前向碰撞预警系统Mobileye ME630采集左右轮迹线与同侧车道线的横向距离数据，该仪器还从CAN总线中连续读取汽车行驶速度数据. Mobileye的主要作用是根据轮迹线—路缘线横向距离计算出车辆形心与路缘线的侧向距离Ld，将轨迹线叠加在弯道内时需要使用Ld进行初始位置标定. 试验车辆为别克GL8商务车. 车载仪器和试验车辆如图2所示.
1.3 试验流程和异常数据筛除
试验采用自然驾驶，即让被试以平时的驾驶方式完成试验过程. 每位驾驶员在试验路线上往返一两个来回. 在正式驾驶试验开始前，确定出试验起点和终点位置，车辆起步后车载设备开始记录数据，车辆行驶至路线终点掉头返回起点，然后停止数据记录；前置行车记录仪一直处于开启状态. 试验结束后，观看行车记录仪的视频图像，对曲线路段范围内有超车和会车行为的轨迹线进行剔除，保留驾驶人能够使用整幅路面宽度时的轨迹线；同时对曲线路段范围内轨迹点GPS数据丢失、导致轨迹线异常的数据也进行剔除. 本文的试验车型是小客车，因此用车辆中心点的运动轨迹来指代车辆行驶轨迹.
1.4 轨迹曲率计算以及滤波
行驶试验结束后，导出Speed Box的GPS经纬度数据并进行大地坐标系转换，绘制轨迹线并计算轨迹曲率. 曲率的倒数就是曲率半径，即轨迹半径. 轨迹线是由相邻的轨迹点连接而成，因此利用三点定位法可以求得每个轨迹点处的曲率值，连接相邻点位的曲率K可得到整条行驶轨迹线的曲率曲线. 曲率见附加材料中曲率的计算和图S1.
计算出曲率后取相邻两轨迹点之间的距离，获得整个行驶轨迹的累积里程，可得到行驶里程变化的轨迹曲率曲线. 最后利用MATLAB软件滤波功能中的rlowes工具对轨迹曲率曲线进行滤波，将异常值赋予较小的权重，滤波程度通过span参数值的设定来改变滤波器的宽窗，保证曲线平滑且幅值不失真.
2. 轨迹束形态以及轨迹曲率
针对每处回头曲线，截取每位驾驶人落在曲线段以及前后直线段范围的行驶轨迹线，然后将全部驾驶人的有效轨迹线叠加显示在一起. 相应地，截取同一范围的轨迹曲率值，将不同被试的轨迹曲率曲线叠加到同一坐标系中进行分析.
2.1 轨迹以及曲率的一般性特征
在设计实操中，通常将转角β > 180° 的回头曲线称为“大头线”，将β ≈ 180° 的回头曲线称之为“平头线”，将β < 180° 的回头曲线称为“小头线”（β须大于150°）；在半径值相等时小头线的圆曲线长度最短、平头线居中、大头线最长.
图3给出了两处左转大头线（C1、C6）和两处左转平头线（C2、C10）的轨迹线分布和轨迹曲率. 图中：ZH为直线-缓和曲线连接点；HY为缓和曲线-圆曲线连接点；YH为圆曲线-缓和曲线连接点；HZ为缓和曲线-直线连接点；CR为道路设计曲率；CT为轨迹曲率. 4处左转小头线的结果见附加材料图S2所示. 根据试验车型参数，轨迹线与左右轮迹线之间的横向距离约为80 cm. 左转弯的“标准”驾驶行为是控制车辆在外侧车道行驶，轮迹线是分布在路缘线和路中线之间. 因此，当轨迹线贴近路中线或者路缘线时，表明轮胎已经越出了标线，即可以判定车辆暴露于风险之中.
图 3 左转曲线路段的轨迹线束和轨迹曲率（大头线和平头线）Figure 3. Tracks and curvatures on left-turn hairpin curves (deflection angle larger than 180o and equal to 180o)附加材料图S3、S4是右转回头曲线的车辆轨迹和轨迹曲率曲线，含4处大头线、两处平头线和两处小头线. 右转车辆的“标准”行为是全程在内侧车道行驶. 在图3、附加材料图S2～S4中还分别以C2、C5、C1和C4为例绘制了轨迹分布区域，根据轨迹分布区域与路中线之间的相对位置，可以直接判断出事故风险区域的分布以及严重程度.
山区双车道公路车流量较低，驾驶人绝大部分时候可以整幅路面规划行驶轨迹，驾驶习惯和驾驶风格的差异性在轨迹规划中得以充分体现. 根据轨迹形态、轨迹曲率幅值以及轨迹曲率-道路设计曲率对比关系可以得出以下结论：
1） 不管是左转轨迹还是右转轨迹，在入弯、弯中和出弯均可见严重的车道偏离，车辆暴露在对向行车道或者硬路肩上. 以左转为例，车辆在C2、C4、C10的出弯区段严重占用对向车道；C1在入弯阶段便开始占用对向车道.
2） 试验弯道使用缓和曲线（ZH～HY之间为第一缓和曲线，YH～HZ之间为第二缓和曲线）来过渡直线到圆曲线之间的曲率突变. 对比实测轨迹曲率发现，在点ZH之前汽车便已进入曲线行驶状态，表明驾驶人在直线段上提前开始转向操作，即提前入弯；同样，轨迹曲率是在点HZ之后降低至0，表明车辆驶出曲线路段之后曲线行驶状态仍继续维持一定的距离，即延迟出弯.
3） 从整体上看，车辆进入曲线时的轨迹曲率增长率要低于第一缓和曲线的曲率增长率；同样，驶离圆曲线之后的轨迹曲率下降率要低于第二缓和曲线的下降率.
2.2 左转轨迹和右转轨迹的曲率差异
观察轨迹曲率曲线的形态和幅值变化，能发现左转车辆和右转车辆的轨迹曲率在幅值、增长率、与路中线轨迹拓扑关系等方面存在比较显著的区别，为了便于分析以C6、C8和C10为例，绘制左转和右转轨迹曲率的分布区域，并将二者显示在同一坐标系内，如图4所示.
图 4 左转弯道和右转弯道轨迹曲率的一般性区别Figure 4. General distinction in track curvature between left-turn and right-turn hairpin curves由图4可知：
1） 在回头曲线中部，左转轨迹曲率的幅值低于或者接近道路设计曲率；右转轨迹曲率则显著高于道路设计曲率（除个别弯道外），即左转轨迹的曲率值在总体上低于右转轨迹，因此，在相同的速度下右转车辆的离心力更大.
2） 入弯阶段左转轨迹的曲率增长率要低于右转轨迹，出弯阶段左转轨迹曲率的下降率同样低于右转轨迹；右转轨迹曲率的分布区域在总体上位于道路设计曲率的内侧，左转轨迹的曲率分布则与道路设计曲率交叉.
上述分析表明，驾驶人在回头曲线范围内习惯于占用对向车道，尤其是左转驶入回头曲线. 基于此，为了避免对撞事故，可通过在弯道入口设置辅助标志进行文字提醒，或者是设置对向来车预警装置来提醒驾驶人规范驾驶.
3. 车辆轨迹的等效曲率半径
3.1 等效半径的定义和计算
在图3和附加材料图S2～S4中很多轨迹线的曲率峰值在回头曲线中部都超过了弯道设计曲率，尤其是右转车辆轨迹. 当轨迹曲率峰值Ctp大于设计曲率CR时，对应的峰值轨迹半径值Rtp必然小于弯道的设计半径Rd，如图5所示, 图中, Rte为等效半径. 驾驶人切弯的主要目的是舒缓轨迹曲率（增加轨迹半径），如果仅仅以曲率峰值点对应的轨迹半径来评判切弯效果，显然无法解释为什么有如此多驾驶人采用切弯方式来过弯. 为此，本文设计了等效半径的概念，如式（1）所示.
Rte=1Cte=11n∑ni=1Ct,i, (1) 式中：Cte为等效曲率，是圆曲线路段范围轨迹曲率的平均值；Ct,i为轨迹点i的曲率值；n为落在圆曲线路段范围内的轨迹坐标点个数，即图5中HY−YH范围内轨迹线的数据点.
若Rte > Rd，表明驾驶人通过切弯取得了舒缓轨迹的实际效果，在弯道圆曲线范围内平均轨迹半径得以提高；反之，表明切弯行为未起到实际的作用.
3.2 轨迹等效半径的特性与影响因素
针对每处回头曲线，计算出第j条轨迹线等效半径值Rte，j，j = 1，2 ，···，m，m为某一回头曲线上的有效轨迹线条数，然后提取出等效半径的最大值Rte,max、最小值Rte,min、平均值Rtem，如图6所示，分别用以表示最激进、最保守、中等驾驶水平的轨迹行为，再计算出等效半径的极差RR如式（2）所示.
RR=Rte,max−Rte,min. (2) 第j条轨迹线半径增量ΔRte，j以及轨迹半径最大值增量ΔRte,max分别为
ΔRte,j=Rte,j−Rd, (3) ΔRte,max=Rte,max−Rd. (4) 图7（a）、（b）是对各处回头曲线Rte,max进行升序排列的结果，同时给出了对应的Rte,min和Rd. 除了C11之外，左转弯的Rte,min与Rd非常接近，右转弯Rte,min则是低于Rd，这是由于右转时一些驾驶人紧贴弯道内沿行驶所致. 左、右转弯轨迹等效半径的最大值分别出现在C4和C5，即两处小头线. 图7（c）给出了轨迹等效半径平均值Rtem与Rd的对比，Rd实质上是路中线的半径值，除了C5和C11之外，右转轨迹在其余9处弯道的Rtem低于Rd，相比之下，左转轨迹Rtem要高于Rd.
图7（d）是ΔRte,max的升序排列结果，ΔRte,max值越大意味着切弯效果越明显，从图中能看到左转弯的ΔRte,max值总体上要高于右转弯，表明在回头曲线路段上左转驶入的车辆更容易取得切弯效用. 图7（e）是轨迹半径极差RR的升序排列折线，RR值越大表明轨迹半径的离散性越强，总体上看，右转弯轨迹半径的RR值显著高于左转轨迹，这是由于右转轨迹半径的Rte,min值更低所致.
本文11处回头曲线的平曲线半径值基本相同. 相比之下，各处回头曲线的转角值差异较大，图7（f）给出了ΔRte,max-曲线偏角的关系及趋势线，从图中能观察到平头线的ΔRte,max最低，而曲线转角增加或者减小时都会导致ΔRte,max增加，即在小头线和大头线上切弯更容易获得放大轨迹半径的实际效果.
本文11处弯道在平曲线范围内的坡度值几乎相同，因此坡度无法作为变量来分析. 由于双车道公路的双向交通是在同一路幅内混行，因此可分析坡向（上坡或者下坡）对轨迹半径的影响. 图8为按曲线偏转方向和坡向分类处理然后进行升序排列的结果，图中的数据点是某一弯道各条轨迹线等效半径增量的平均值. 图8（a）中，除C11以外，对于左转回头曲线，车辆下坡驶入曲线要比上坡驶入能够获得更大的轨迹半径增量. 根据图8（b），右转驶入时上坡和下坡各有3处弯道的轨迹半径增量非常接近，但从第4处弯道开始，下坡驶入弯道时的轨迹半径增量要显著高于上坡驶入. 基于此，可以认为下坡驶入能够获得更大的轨迹半径. 在3类回头曲线中，小头线呈现的规律最明显，如图8（c）所示.
速度也是影响轨迹特性的重要因素，本文选取了多项与速度相关的指标进行敏感性分析，发现Rte或ΔRte对入弯速度Ven和弯中速度Vmc的变化比较敏感，这里Ven是指第一缓和曲线之前40～50 m左右的速度值，对应的数据处理结果如图9所示. 对于左转弯而言，速度与轨迹半径之间存在一定的正相关性（拟合线的R2值分别为0.18、0.14和0.22，处于较低水平）. 这种影响是相互的：驾驶人期望快速通过弯道时，会通过切弯的方式来增加轨迹半径，而轨迹半径增加之后弯道通过速度自然会提高. 相比之下，右转弯轨迹半径对速度变化不敏感，因此可认为左转驶入回头曲线时，速度更容易对轨迹特性产生影响. 在车辆动力学层面，速度越高汽车惯性越大，驾驶人操控车辆的难度将增加，对于回头曲线而言，速度升高将增加汽车越出车道线甚至越出路面的几率.
图 9 行驶速度对回头曲线轨迹半径的影响Figure 9. Effect of driving speed on track radius for hairpin curves切弯行为会导致车辆偏离车道并可能导致交通事故. 由于切弯效果明显，驾驶人遇到左转弯时更倾向于采用切弯行为，尤其是下坡驶入左转弯道，因此应该对该类弯道应该加强管控，规范驾驶人的车道使用行为和行驶速度.
4. 增大轨迹半径的过弯方式
4.1 右转弯
驾驶人通过切弯来增加轨迹半径，在维持横向力不变的情况下能够操控汽车以更快的速度通过弯道. Cte越小, Rte越大，图10给出了5处回头曲线路段等效曲率最小值处对应的轨迹曲率曲线，图中：Lp为轨迹曲率峰值点位相较于圆曲线中点的偏移量. 除C1之外其余4处弯道的轨迹曲率峰值均出现在弯道平曲线中点（QZ）之前，见弯道C6中的标注. 图11是Cte最小值对应的轨迹线形态，从中能观察到一个共性特征：在入弯之前驾驶人将车辆位置向外侧调整，甚至占用外侧车道，进入弯道之后轨迹线逐渐向弯道内侧靠拢，然后以贴近弯道内侧的方式驶出弯道，即“外进内出”. 绘制出轨迹线与弯道内侧路缘线之间包络区域，如图12（a）所示，图12同时给出了另外4个弯道的包络区间，从中能观察到非常鲜明的特征，即包络区域的宽度在进入弯道之后逐渐变窄.
图 10 右转车辆轨迹等效半径最大值（Rte,max）对应的轨迹曲率Figure 10. Track curvature profiles corresponding to maximum equivalent radius of right-turn vehicle track
图 11 右转车辆轨迹等效半径最大值（Rte,max）对应的轨迹线Figure 11. Tracks corresponding to maximum equivalent radius of right-turn vehicle track
图 12 轨迹线-弯道内侧路缘线的包络区间Figure 12. Envelope interval formed by tracks and inner kerb of curves附加材料图S5是另外3处回头曲线路段Cte最小值对应的轨迹曲率曲线，其中C8给出了Cte最小值（驾驶员1）和倒数第二小值（驾驶员3）的轨迹曲率，从图中能看到轨迹曲率曲线在整体上是朝右侧偏移. 附加材料图S6是对应的轨迹线形态，从图中能看到C2、C4和C8（驾驶员3）的轨迹线在弯前直线和入弯时紧贴内侧路缘线，入弯后轨迹线逐渐向外侧车道偏移甚至占用了外侧车道，即“内进外出”，表明驾驶人有不同的过弯方式来增加轨迹半径. 以C8为例，驾驶员3是采用“内进外出”的方式，而驾驶员1是“外进内出”，而这两种方式都可以增加轨迹半径.
4.2 左转弯
附加材料图S7、S8分别是左转车辆在6处回头曲线路段上具有最大等效半径的轨迹线和轨迹曲率. 附加材料图S9是具有最大等效半径的“轨迹线-弯道内侧路缘线”包络区域，在图S9中，根据包络区域的形状可以将轨迹形态分成3类模式：第1类是“外进内出”，前3处弯道（C4、C8和C10）的轨迹线是这类形态；第2类是“外进中出”，汽车驶入弯道时轨迹靠近外侧，但汽车驶至弯道中部时轨迹调整至路幅中间位置，然后驶出弯道；第3类是“内进外出”，C5的轨迹线是这类形态. 这表明左弯与右转弯一样，驾驶人可以通过不同的方式来实现轨迹半径的增加.
根据附加材料图S8中的轨迹形态，驾驶人在切弯之后会继续占用对向车道，或者侵占路肩，因此事故风险主要集中在出弯阶段（即弯道下游），这需要引起设计者和管理者的注意，采取措施提醒驾驶人不要越出车道，并加强弯道下游外侧护栏的设置.
5. 结 论
1） 回头曲线的入弯、弯中和出弯均可见严重的车道偏离，车辆暴露在对向行车道或者硬路肩上.
2） 入弯时汽车在缓和曲线起点之前便已进入曲线行驶状态，表明驾驶人在直线段上提前开始转向操作；同样，出弯时车辆轨迹曲率在驶出缓和曲线之后的直线上降低至零，曲线行驶状态存在延后性.
3） 车辆入弯和出弯时的轨迹曲率变化率要低于缓和曲线的曲率变化率，同时，左转轨迹的曲率变化率要低于右转轨迹；在回头曲线中部，左转轨迹曲率的幅值低于或者接近道路设计曲率，右转轨迹曲率则高于道路设计曲率.
4） 提出了等效半径的概念，左转弯的轨迹等效半径要高于弯道设计半径，相比之下右转弯轨迹半径最小值和均值普遍低于设计半径.
5） 不管是左转弯还是右转弯，驾驶人可以通过不同的切弯方式来实现回头曲线路段轨迹半径的增加和最大化，但都需要侵占对向车道；切弯轨迹的曲率峰值点与圆曲线中心点错位：前移或者延后.
6） 驾驶人切弯时，左转弯的轨迹半径增量在总体上要高于右转弯，即在左转回头曲线上更容易取得切弯效用. 同时，在3类回头曲线中，小头线和大头线的切弯效果更明显.
7） 下坡驶入回头曲线时的轨迹半径要高于上坡驶入；对于左转回头曲线而言，轨迹半径与速度之间有一定的相关性.
致谢：中铁第四勘察设计院集团有限公司科学技术研究项目（2019K091-1）资助.
备注：附加材料在中国知网本文的详情页中获取.
-
图 2 安装逆变回馈装置的系统能量流向示意
Figure 2. Energy flow direction for installation of inverter feedback devices
图 4 基于NSGA-Ⅱ求解逆变回馈装置容量配置优化流程
Figure 4. Optimization process of siting and sizing for inverter feedback devices based on NSGA-Ⅱ algorithm
图 6 逆变回馈装置价格与容量关系
Figure 6. Relationship between price and capacity of inverter feedback devices
图 7 目标函数Pareto解集的最优方案变化过程
Figure 7. Change process of optimal scheme of Pareto solution set
图 10 区间所2逆变回馈装置工作占空比
Figure 10. Operating duty ratio of inverter feedback devices in section traction station 2
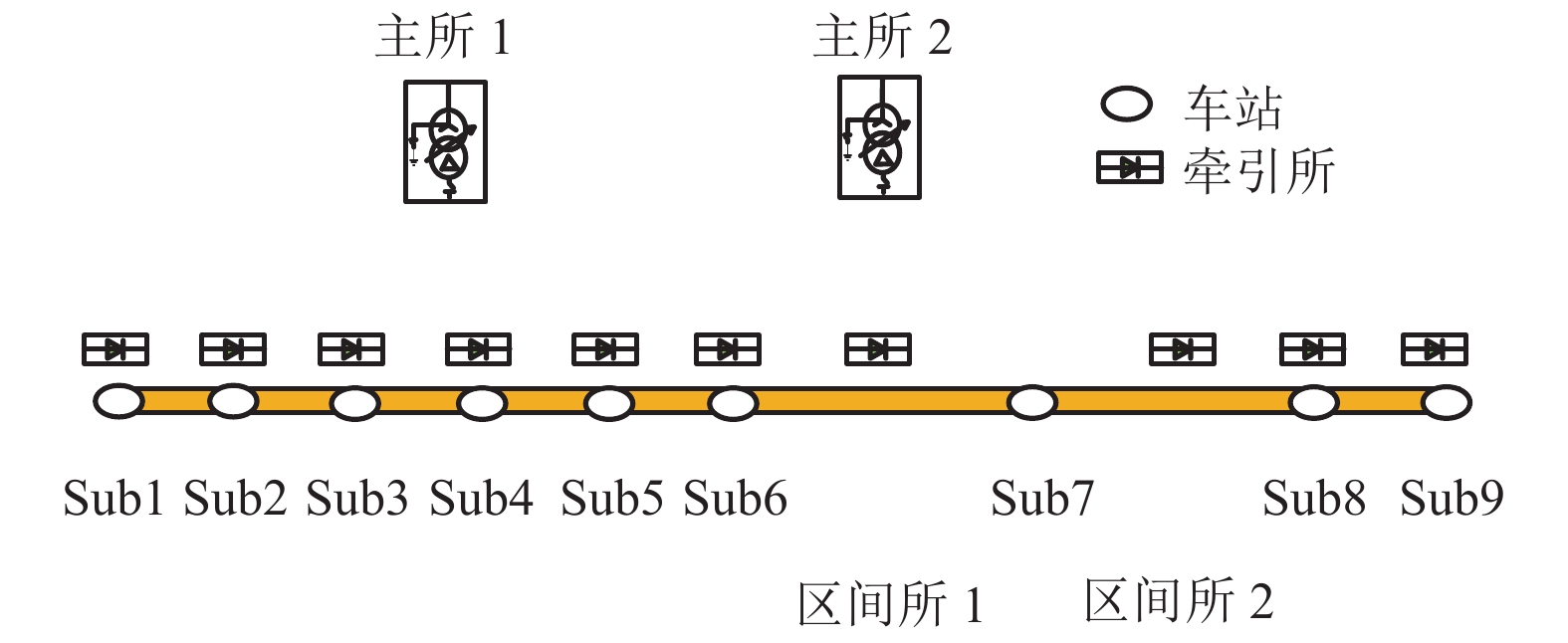
表 1 牵引所位置信息
Table 1. Traction station position information
牵引所 位置/km 牵引所 位置/km Sub1 0.243 Sub6 13.900 Sub2 2.456 区间所 1 16.287 Sub3 4.568 区间所 2 20.527 Sub4 7.804 Sub8 23.322 Sub5 10.670 Sub9 25.685 
下载: 导出CSV
表 2 仿真参数设置
Table 2. Simulation parameter setting
仿真参数 取值 仿真参数 取值 N 20 Z/MW 2×2.5 J 0.9 Ud0/V 1680 B 0.1 xmax/MW 3 G/次 100 Ui/V 1720 WT1/（kW•h） 3954.17 Ubr/V 1830
下载: 导出CSV
表 3 Pareto解集收敛结果
Table 3. Convergence results of Pareto solution set
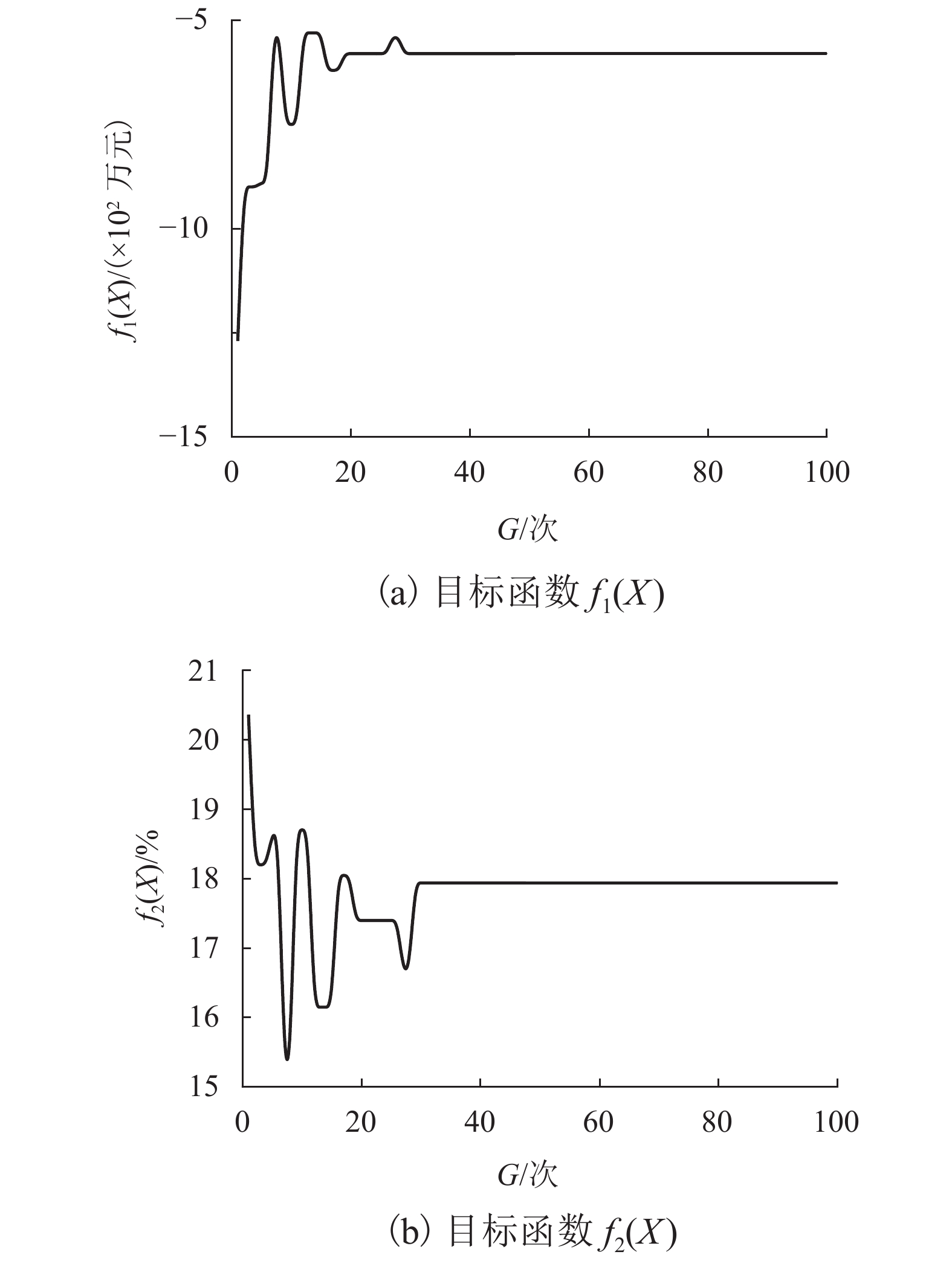
V(j) f1(X)/
（×102 万元）f2(X)/% V(j) f1(X)/
（×102 万元）f2(X)/% 1 −3.30 9.54 11 −7.30 19.81 2 −3.60 9.55 12 −8.60 20.28 3 −4.00 14.03 13 −10.10 20.46 4 −4.20 14.53 14 −10.70 20.86 5 −5.30 16.15 15 −11.10 21.48 6 −5.40 16.66 16 −14.90 21.68 7 −5.80 17.94 17 −16.80 21.7 8 −6.70 17.79 18 −6.90 17.61 9 −6.90 17.95 19 −6.20 18.05 10 −7.10 18.85 20 −5.80 17.39
下载: 导出CSV
表 5 逆变回馈装置方案对比
Table 5. Scheme comparison of inverter feedback devices
MW 牵引所 V(7)，Va 牵引所 V(7)，Va Sub1 0，2.0 Sub6 0，0 Sub2 2.0，0 区间所 1 0，0 Sub3 0，0 区间所 2 2.0，0 Sub4 1.5，0 Sub8 0，2.0 Sub5 0，0 Sub9 0，3.0
下载: 导出CSV
表 6 不同优化方案目标函数值对比
Table 6. Comparison of objective function values of different optimization schemes
优化方案 f1(X)/（×102万元） f2(X)/% V(7) 5.80 17.94 Va 6.50 14.69
下载: 导出CSV
表 4 最优方案V(7)每小时潮流计算结果
Table 4. Hourly power flow calculated by optimal scheme V(7)
kW•h 牵引所 WT2 WF WR Sub1 275.97 0 45.66 Sub2 459.14 270.84 Sub3 499.08 0 Sub4 501.06 238.75 Sub5 473.03 0 Sub6 292.77 0 区间所 1 321.41 0 区间所 2 462.30 273.07 Sub8 416.51 0 Sub9 280.59 0 合计 3981.86 782.66 45.66
下载: 导出CSV
-
[1] 许爱国,谢少军,姚远,等. 基于超级电容的城市轨道交通车辆再生制动能量吸收系统[J]. 电工技术学报,2010,25(3): 117-123.XU Aiguo, XIE Shaojun, YAO Yuan, et al. Regenerative braking energy absorption system for urban rail transit vehicles based on supercapacitor[J]. Transactions of China Electrotechnical Society, 2010, 25(3): 117-123. [2] ZHANG G, TIAN Z, TRICOLI P, et al. Inverter operating characteristics optimization for DC traction power supply systems[J]. IEEE Transactions on Vehicular Technology, 2019, 68(4): 3400-3410. doi: 10.1109/TVT.2019.2899165 [3] 步兵,滕昌敏,陈尔超,等. 城市轨道交通多车协作节能控制方法研究[J]. 铁道学报,2018,250(8): 47-55.BU Bing, TENG Changmin, CHEN Erchao, et al. Research on multi-vehicle cooperative energy saving control method in urban rail transit[J]. Journal of the China Railway Society, 2018, 250(8): 47-55. [4] TIAN Z, ZHANG G, ZHAO N, et al. Energy evaluation for DC railway systems with inverting substations[C]//IEEE International Conference on Electrical Systems for Aircraft. Nottingham: IEEE, 2018: 1-6. [5] 张驰,谭南林,刘敏杰,等. 地铁再生制动系统仿真及节能优化研究[J]. 中国铁道科学,2019,40(3): 112-118.ZHANG Chi, TAN Nanlin, LIU Minjie, et al. Simulation and energy-saving optimization of regenerative braking system in subway[J]. China Railway Science, 2019, 40(3): 112-118. [6] 陈怀鑫,杨中平,林飞,等. 基于遗传算法的城轨交通超级电容储能装置能量管理和容量配置优化研究[J]. 铁道学报,2019,41(9): 59-66.CHEN Huaixin, YANG Zhongping, LIN Fei, et al. Research on energy management and capacity allocation optimization of urban rail transit ultracapacitor energy storage device based on genetic algorithm[J]. Journal of the China Railway Society, 2019, 41(9): 59-66. [7] 诸斐琴,杨中平,林飞,等. 城轨交通牵引供电系统参数与储能系统容量配置综合优化[J]. 电工技术学报,2019,34(3): 579-588.ZHU Feiqin, YANG Zhongping, LIN Fei, et al. Comprehensive optimization of power supply system parameters and energy storage system capacity configuration in urban rail transit[J]. Transactions of China Electrotechnical Society, 2019, 34(3): 579-588. [8] 王一,程浩忠. 计及输电阻塞的帕累托最优多目标电网规划[J]. 中国电机工程学报,2008,28(13): 132-138.WANG Yi, CHENG Haozhong. Pareto optimal multi-objective power grid planning considering transmission congestion[J]. Chinese Journal of Electrical Engineering, 2008, 28(13): 132-138. [9] 吴广宁,付龙海,王颢,等. 基于改进遗传算法的接地网优化设计[J]. 西南交通大学学报,2007,42(2): 169-174.WU Guangning, FU Longhai, WANG Hao, et al. Optimal design of ground grid based on improved genetic algorithm[J]. Journal of Southwest Jiaotong University, 2007, 42(2): 169-174. [10] DEB K, PRATAP A, AGARWAL S, et al. A fast and elitist multiobjective genetic algorithm:NSGA-Ⅱ[J]. IEEE Transactions on Evolutionary Computation, 2002, 6(2): 190-197. [11] 冯士刚,艾芊. 带精英策略的快速非支配排序遗传算法在多目标无功优化中的应用[J]. 电工技术学报,2007,22(12): 146-151.FENG Shigang, AI Qian. Application of fast non-dominant sorting genetic algorithm with elite strategy in multi-objective reactive power optimization[J]. Transactions of China Electrotechnical Society, 2007, 22(12): 146-151. [12] SHI X, FANG H, PI G, et al. Time-Energy-Jerk dynamic optimal trajectory planning for manipulators based on quantic NURBS[C]//2018 3rd International Conference on Robotics and Automation Engineering (ICRAE). Guangzhou: IEEE, 2018: 44-49. [13] 国家市场监督管理总局, 中国国家标准化管理委员会. 城市轨道交通再生制动能量吸收逆变装置: GB/T 37423—2019[S]. 北京: 中国质检出版社, 2019. [14] 刘炜,许伶俐,廖钧,等. 含逆变回馈装置的城市轨道交直流混合潮流计[J]. 铁道学报,2019,41(11): 65-71.LIU Wei, XU Lingli, LIAO Jun, et al. Calculation of AC-DC hybrid power flow in urban rail with inverter feedback device[J]. Journal of the China Railway Society, 2019, 41(11): 65-71. [15] 刘炜,张扬鑫,张戬,等. 考虑牵引所多运行状态的城轨交直流供电计算[J]. 西南交通大学学报,2019,55(6): 1163-1170.LIU Wei, ZHANG Yangxin, ZHANG Jian, et al. Calculation of ac-dc power supply for urban rail considering multiple operating conditions of traction institute[J]. Journal of Southwest Jiaotong University, 2019, 55(6): 1163-1170. [16] 刘炜,娄颖,张戬,等. 计及城市轨道逆变回馈装置的交直流统一供电计算[J]. 电工技术学报,2019,34(20): 4381-4391.LIU Wei, LOU Ying, ZHANG Jian, et al. Calculation of AC and DC unified power supply considering urban rail inverter feedback device[J]. Journal of Electrical Technology, 2019, 34(20): 4381-4391. [17] 郭耀煌,郭春香,郭强. 基于偏序结构相似度的多准则决策[J]. 西南交通大学学报,2006,41(1): 1-6.GUO Yaohuang, GUO Chunxiang, GUO Qiang. Multi-criteria decision making based on similarity of partial order structure[J]. Journal of Southwest Jiaotong University, 2006, 41(1): 1-6. [18] 吴小刚,刘宗歧,田立亭,等. 基于改进多目标粒子群算法的配电网储能选址定容[J]. 电网技术,2014,38(12): 3405-3411.WU Xiaogang, LIU Zongqi, TIAN Liting, et al. Energy storage site selection and capacity determination of distribution network based on improved multi-objective particle swarm optimization[J]. Power System Technology, 2014, 38(12): 3405-3411. [19] CHEN Pengyu. Effects of normalization on the entropy-based TOPSIS method[J]. Expert Systems With Applications, 2019, 136(12): 33-41. -
下载:
下载:
点击查看大图
计量
- 文章访问数: 568
- HTML全文浏览量: 265
- PDF下载量: 20
- 被引次数: 0