Microscopic Model Analysis of Shield Tunnel Backfill Grouting Based on Displacement Effect
-
摘要:
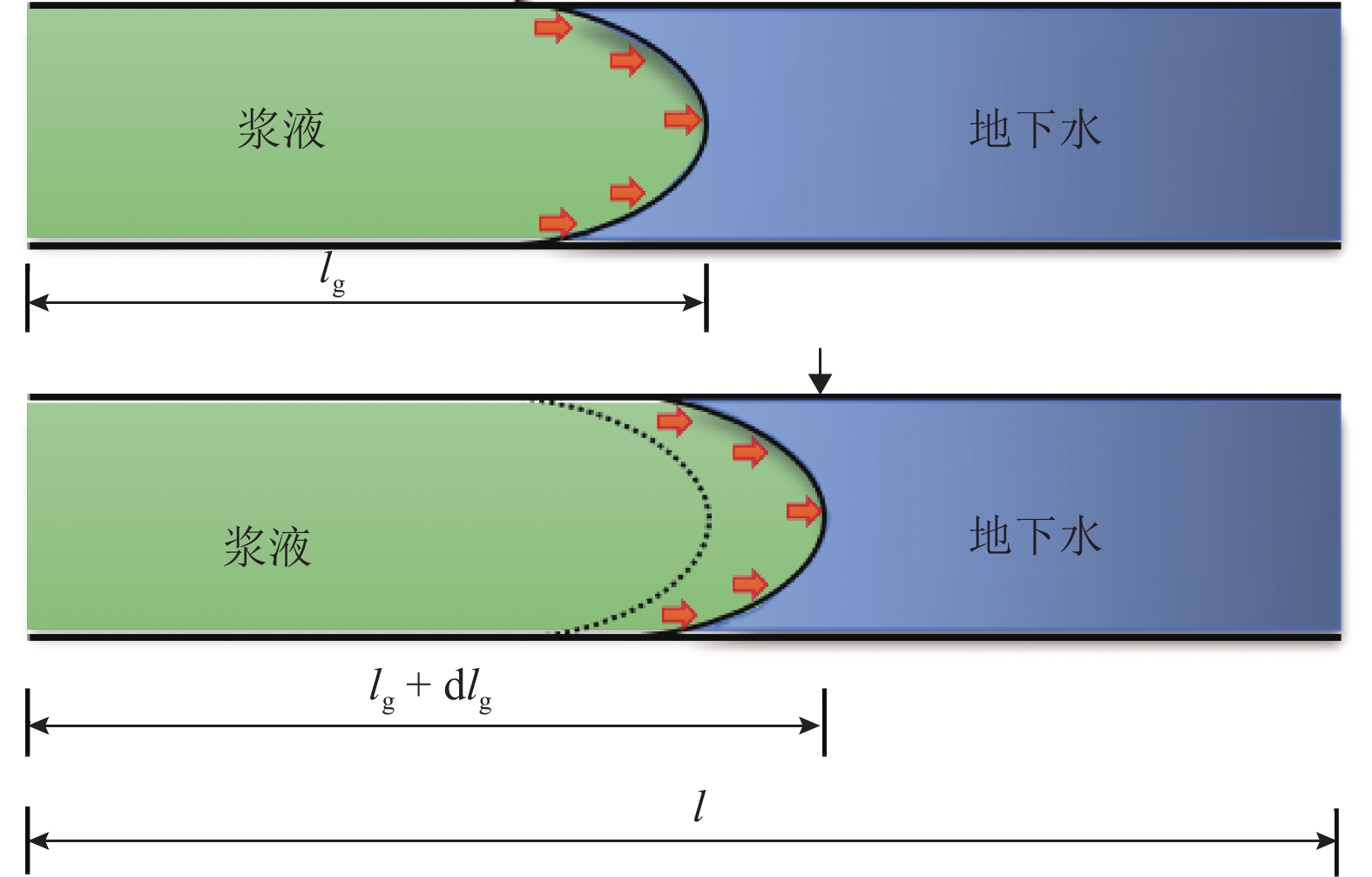
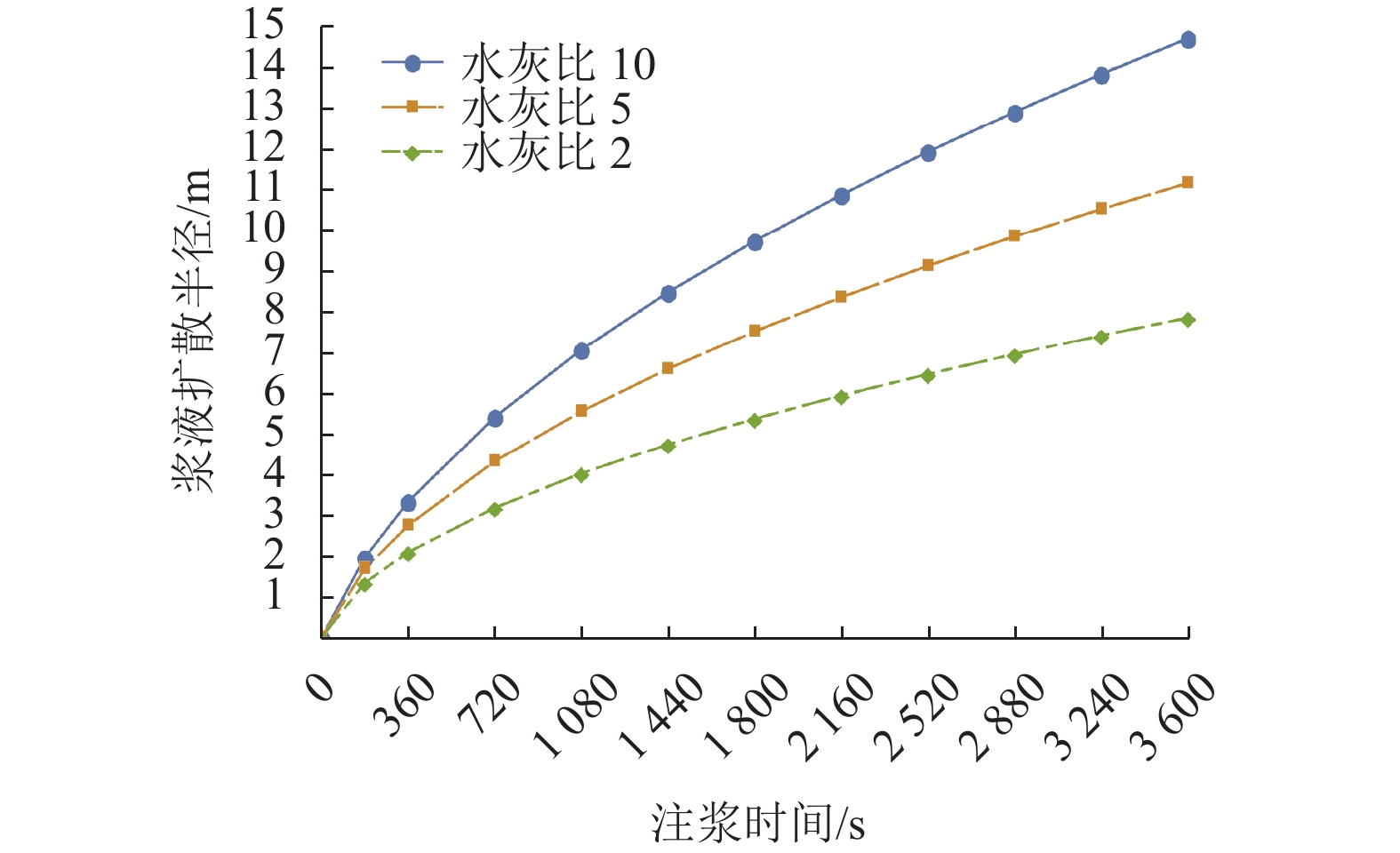
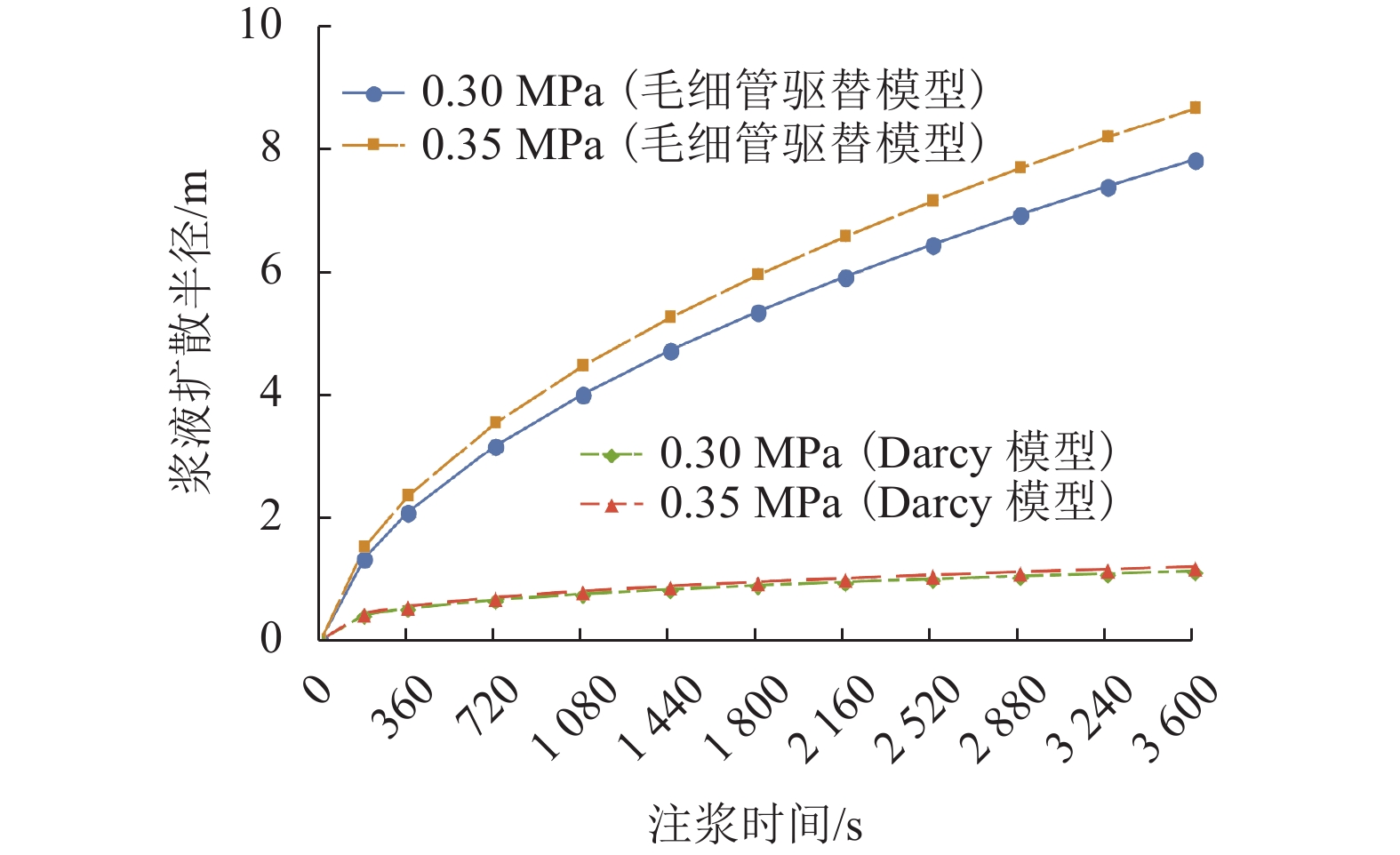
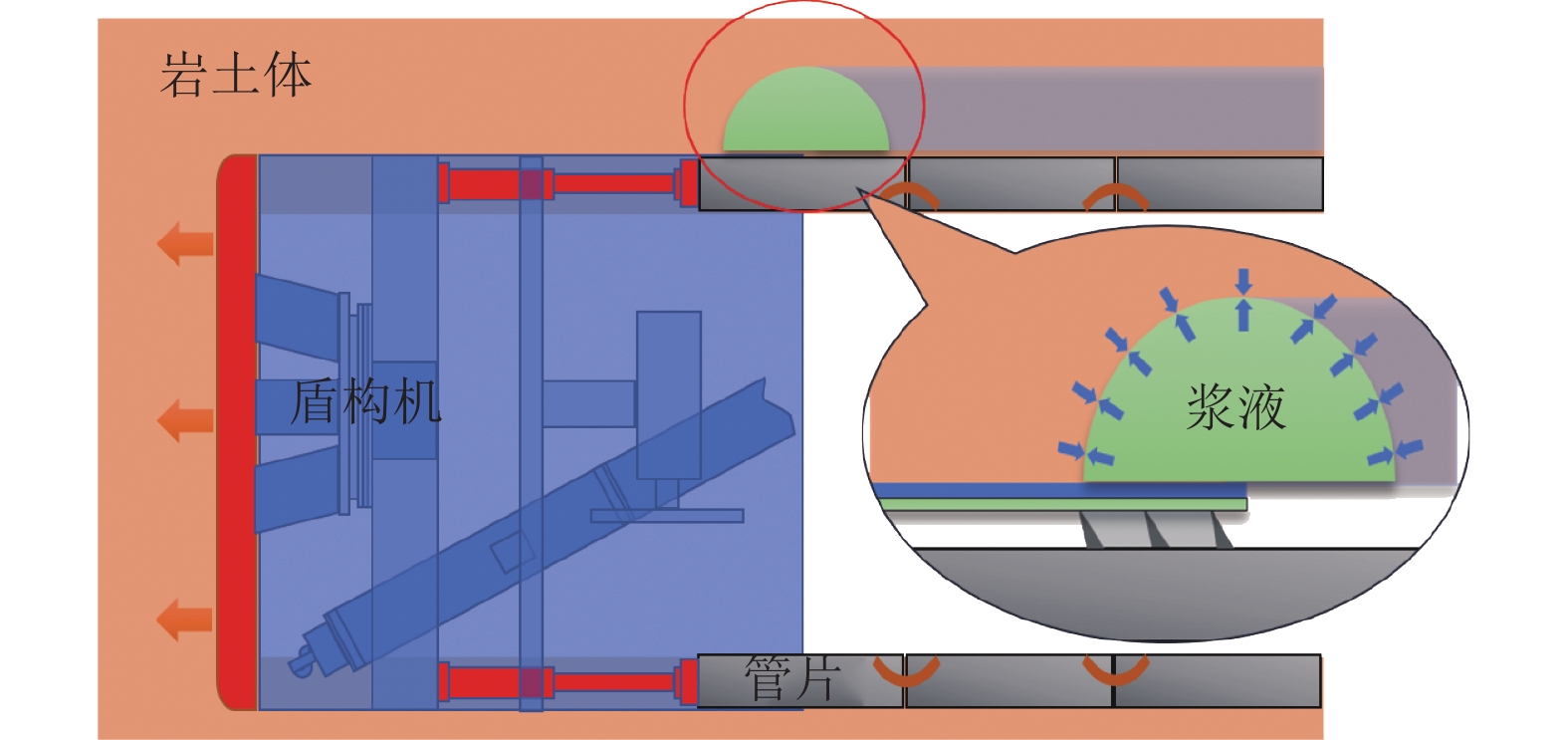
当盾构隧道位于水位线以下时，为了分析壁后注浆浆液驱动地下水体过程，基于毛细管组渗透理论，将浆液的渗流路径概化为毛细管，考虑牛顿流体浆液驱动地下水（牛顿流体）进行扩散，推导了半球形及柱形模型浆液渗流扩散半径计算式，并讨论了注浆压力、浆液水灰比、地层渗透系数的影响. 研究结果表明：浆液扩散半径主要与注浆压力、渗透率、注浆时间、孔隙率、浆液和地下水黏度等因素有关，浆液水灰比对于浆液扩散半径影响最为显著，浆液的黏度由0.004 7 Pa•s降至0.001 9 Pa•s时，浆液扩散半径在注浆时间为1 h时降低幅度为46.7%，相同注浆条件下可增大水灰比来增大浆液扩散半径；浆液扩散半径随渗透系数的增大而增大，地层的渗透系数大小一定程度上反映了浆液扩散的难易程度；在计算出浆液扩散半径（浆液加固范围）的基础上提出了注浆压力下限值计算方法，用以指导盾构隧道壁后注浆工程施工.
Abstract:When a shield tunnel under construction is below the water level, the shield backfill grouting slurry will drive the groundwater. In order to analyze this driving process, the seepage path of slurry in the soil is generalized to a capillary by capillary group penetration theory, the grout diffusion radius of hemispherical and cylindrical models are deduced considering the diffusion by Newtonian fluid slurry-driven water (Newtonian fluid), and the effects of grouting pressure, water-cement ratio, and formation permeability coefficient are discussed. Results show that the grout diffusion radius is mainly related to the grouting pressure, permeability, grouting time, porosity, and grout and groundwater viscosity. Especially, the grout water-cement ratio has the most significant effect on the grout diffusion radius. When the viscosity of the grout decreases from 0.004 7 to 0.001 9 Pa•s, the spreading radius of grout decreases by 46.7% at 1 h after grouting, indicating that the spreading radius of grout can be increased by adopting a higher water-cement ratio under the same grouting condition. Besides, the grout diffusion radius increases with an increase in the permeability coefficient, and the formation permeability coefficient reflects the difficulty of grout diffusion to a certain extent. Based on the calculation of grout diffusion radius (grout reinforcement range), a calculation method for the lower limit of the grouting pressure is proposed to guide the construction of backfill grouting of shield tunnel.
-
Key words:
- shield tunnel /
- backfill grouting /
- penetration grouting /
- displacement effect
-
图 3 不同水灰比下浆液扩散半径变化规律
Figure 3. Variation law of grout diffusion radius with different water cement ratios
图 4 不同注浆压力下浆液扩散半径变化规律
Figure 4. Variation law of radius with different grout pressures
图 5 不同渗透系数下浆液扩散半径变化扩散规律
Figure 5. Variation law of grout diffusion radius with different infiltration coefficients
水灰比 流变方程 浆液黏度/（Pa•s） 2 $\tau {\text{ = } }0.037\;2{\text{ + } }0.004\;7\gamma$ 0.00470 5 $\tau {\text{ = } }0.088\;0{\text{ + } }0.002\;7\gamma$ 0.00270 10 $\tau {\text{ = } }0.045\;4{\text{ + } }0.001\;9\gamma$ 0.00190 
下载: 导出CSV
表 2 注浆压力
Table 2. Values of grouting pressure
渗透系数/（cm•s−1） t/min P0/MPa 盾尾注浆 管片注浆 0.02 30 0.147 0.115 0.02 60 0.104 0.089 0.03 30 0.118 0.097 0.03 60 0.089 0.078 0.04 30 0.104 0.087 0.04 60 0.082 0.074
下载: 导出CSV
-
[1] 张凤祥, 朱合华, 傅德明. 盾构隧道[M]. 北京: 人民交通出版社, 2004. [2] GUGLIELMETTI V, GRASSO P, MAHTAB A, etal. Mechanized tunnelling in urban areas[M]. London: CRC Press, 2008 [3] 《岩土注浆理论与工程实例》协作组. 岩土注浆理论与工程实例[M]. 北京: 科学出版社, 2001. [4] 李志明,廖少明,戴志仁. 盾构同步注浆填充机理及压力分布研究[J]. 岩土工程学报,2010,32(11): 1752-1757.LI Zhiming, LIAO Shaoming, DAI Zhiren. Theoretical study on synchronous grouting filling patterns and pressure distribution of EPB shield tunnels[J]. Chinese Journal of Geotechnical Engineering, 2010, 32(11): 1752-1757. [5] 白云,戴志仁,张莎莎,等. 盾构隧道同步注浆浆液压力扩散模式研究[J]. 中国铁道科学,2011,32(4): 38-45.BAI Yun, DAI Zhiren, ZHANG Shasha, etal. Study on the grout pressure dissipation model in simultaneous backfill grouting during shield tunneling[J]. China Railway Science, 2011, 32(4): 38-45. [6] 张莎莎,戴志仁,白云. 盾构隧道同步注浆浆液压力消散规律研究[J]. 中国铁道科学,2012,33(3): 40-48. doi: 10.3969/j.issn.1001-4632.2012.03.07ZHANG Shasha, DAI Zhiren, BAI Yun. Research on the dissipation law of grout pressure during the simultaneous grouting of shield tunnel[J]. China Railway Science, 2012, 33(3): 40-48. doi: 10.3969/j.issn.1001-4632.2012.03.07 [7] 叶飞,朱合华,何川. 盾构隧道壁后注浆扩散模式及对管片的压力分析[J]. 岩土力学,2009,30(5): 1307-1312. doi: 10.3969/j.issn.1000-7598.2009.05.020YE Fei, ZHU Hehua, HE Chuan. Back-filled grouts diffusion model and its pressure to segments of shield tunnel[J]. Rock and Soil Mechanics, 2009, 30(5): 1307-1312. doi: 10.3969/j.issn.1000-7598.2009.05.020 [8] 叶飞,陈治,贾涛,等. 盾构隧道管片注浆幂律流型浆液渗透扩散模型[J]. 岩土工程学报,2016,38(5): 890-897. doi: 10.11779/CJGE201605014YE Fei, CHEN Zhi, JIA Tao, etal. Penetration diffusion model of exponential fluid for backfill grouting through segments of shield tunnel[J]. Chinese Journal of Geotechnical Engineering, 2016, 38(5): 890-897. doi: 10.11779/CJGE201605014 [9] 袁小会,韩月旺,钟小春. 盾构隧道壁后注浆压力分布模型[J]. 西南交通大学学报,2011,46(1): 18-23. doi: 10.3969/j.issn.0258-2724.2011.01.003YUAN Xiaohui, HAN Yuewang, ZHONG Xiaochun. Pressure distribution model of simultaneous backfill grouting of shield tunnel[J]. Journal of Southwest Jiaotong University, 2011, 46(1): 18-23. doi: 10.3969/j.issn.0258-2724.2011.01.003 [10] 王明年,黄海斌,汤渊,等. 盾构施工对盾尾浆液压力波动变化的影响[J]. 西南交通大学学报,2019,54(3): 461-467,586. doi: 10.3969/j.issn.0258-2724.20170199WANG Mingnian, HUANG Haibin, TANG Yuan, et al. Influence of shield construction on pressure fluctuation of segment grout[J]. Journal of Southwest Jiaotong University, 2019, 54(3): 461-467,586. doi: 10.3969/j.issn.0258-2724.20170199 [11] 宋天田,周顺华,徐润泽. 盾构隧道盾尾同步注浆机理与注浆参数的确定[J]. 地下空间与工程学报,2008,4(1): 130-133.SONG Tiantian, ZHOU Shunhua, XU Runze. Mechanism and determination of parameters of synchronous grouting in shield tunneling[J]. Chinese Journal of Underground Space and Engineering, 2008, 4(1): 130-133. [12] 张凤祥, 傅德明, 杨国祥, 等. 盾构隧道施工手册[M]. 北京: 人民交通出版社, 2005. [13] 陈湘生, 李兴高. 复杂环境下盾构下穿运营隧道综合技术[M]. 北京: 中国铁道出版社, 2011. [14] 王江涛, 陈建军, 吴庆红, 等. 南水北调中线穿黄工程泥水盾构施工技术[M]. 郑州: 黄河水利出版社, 2010. [15] YE F, QIN N, HAN X, etal. Displacement infiltration diffusion model of power-law grout as backfill grouting of a shield tunnel[J]. European Journal of Environmental and Civil Engineering, 2020, 24(1): 1-14. doi: 10.1080/19648189.2017.1363664 [16] 阮文军. 注浆扩散与浆液若干基本性能研究[J]. 岩土工程学报,2005,27(1): 69-73. doi: 10.3321/j.issn:1000-4548.2005.01.011RUAN Wenjun. Research on diffusion of grouting and basic properties of grouts[J]. Chinese Journal of Geotechnical Engineering, 2005, 27(1): 69-73. doi: 10.3321/j.issn:1000-4548.2005.01.011 -
下载:
点击查看大图
计量
- 文章访问数: 228
- HTML全文浏览量: 123
- PDF下载量: 6
- 被引次数: 0