基于二维耦合映像格子模型的图像加密

王永; 江功坤; 尹恩民

doi:10.3969/j.issn.0258-2724.20200331

基于二维耦合映像格子模型的图像加密

doi: 10.3969/j.issn.0258-2724.20200331

王永^{1, 2,},
江功坤¹,
尹恩民¹

1.
重庆邮电大学计算机科学与技术学院，重庆 400065
2.
桂林电子科技大学广西密码学与信息安全重点实验室，广西桂林 541004

基金项目: 国家自然科学基金（61472464）；贵州省科学技术基金计划（黔科合基础[2020]1Y422）

详细信息

作者简介:
王永（1977—），男，教授，博士，研究方向为信息安全，混沌密码学，E-mail：wangyong_cqupt@163.com

中图分类号: TP309.7
计量
- 文章访问数: 283
- HTML全文浏览量: 153
- PDF下载量: 17
- 被引次数: 0
出版历程
- 收稿日期: 2020-05-27
- 修回日期: 2020-10-16
- 网络出版日期: 2021-09-26
- 刊出日期: 2020-11-05

Image Encryption Based on 2D Coupled Map Lattices

1.
College of Computer Science and Technology，Chongqing University of Posts and Telecommunications，Chongqing 400065，China
2.
Guangxi Key Laboratory of Cryptography and Information Security，Guilin University of Electronic Technology，Guilin 541004，China

摘要

摘要:
为了平衡混沌系统的复杂性和效率之间的关系，将分段Logistic映射（piecewise Logistic map，PLM）引入到二维耦合映像格子（2D coupled map lattices，2DCML）模型中. 采用暂态转换以使模型的输出序列服从均匀分布，进而得到T2DCML模型，基于此模型提出了一类图像加密算法. 在加密算法中，利用模型输出的伪随机序列构造两个初等变换矩阵，对图像进行置乱操作；然后再从模型中提取状态值的比特构造整数序列，对置乱后的图像进行扩散操作；经过若干轮的置乱与扩散操作，产生最后的加密图像. 仿真实验及性能分析表明：该算法的相关系数的绝对平均值为0.001 3，信息熵为7.999 3，像素变化率（number of pixel change rate，NPCR）和统一平均变化强度（unified average change intensity，UACI）分别为99.63%和33.60%，能够有效满足图像在网络中安全传输的需求.
- 分段Logistic映射 /
- 二维耦合映像格子模型 /
- 混沌序列 /
- 图像加密
Abstract:
Piecewise Logistic map (PLM) is introduced into 2D coupled map lattices (2DCML) model to face a tradeoff between complexity and efficiency of chaotic systems, and a transformation method based on transient status values is used to make the output sequence of the model obey a uniform distribution. Then, the T2DCML model is built. According to the T2DCML model, an image encryption algorithm is proposed, in which encryption algorithm, the pseudo-random sequence output by the model is used to construct two elementary transformation matrices and the image is scrambled by the matrices. Then, the bits of the state value are extracted from the model to construct an integer sequence and the scrambled image is diffused by the integer sequence. Finally, the encrypted image is produced by multi-rounds of confusion and diffusion. Simulation experiments and performance analysis show that the absolute average correlation coefficient of the algorithm is 0.001 3, the information entropy is 7.999 3, and the number of pixel change rate (NPCR) and the unified average change intensity (UACI) is 99.63% and 33.60%, respectively, revealing that the algorithm can effectively meet the needs of the safe transmission of images in the network.
- piecewise Logistic map /
- 2D coupled map lattices /
- chaotic sequences /
- image encryption

HTML全文

图 1 局部混沌函数PLM的LE

Figure 1. LE of local chaotic function PLM

下载: 全尺寸图片幻灯片

图 2 2DCML模型中格子（4,4）的分叉图

Figure 2. Bifurcation diagram of lattice (4,4) in 2DCML

下载: 全尺寸图片幻灯片

图 3 2DCML模型中格子(4,4)的遍历图

Figure 3. Ergodic diagram of lattice (4,4) in 2DCML

下载: 全尺寸图片幻灯片

图 4 2DCML的概率密度分布

Figure 4. Probability density distribution of 2DCML

下载: 全尺寸图片幻灯片

图 5 T2DCML模型中格子(4,4)的分叉图

Figure 5. Bifurcation diagram of lattice (4,4) in T2DCML

下载: 全尺寸图片幻灯片

图 6 T2DCML的概率密度分布

Figure 6. Probability density distribution of T2DCML

下载: 全尺寸图片幻灯片

图 7 明文图像和密文图像

Figure 7. Plaintext images and ciphertext images

下载: 全尺寸图片幻灯片

图 8 图像加密前、后的直方图

Figure 8. Histograms before and after image encryption

下载: 全尺寸图片幻灯片

图 9 加密时间与加密像素点数量的关系

Figure 9. Relation between encryption time and number of pixels

下载: 全尺寸图片幻灯片

表 1 NIST套件的测试结果

Table 1. Test results of NIST suites

测试指标	P 值	通过率	结果
Frequency	0.719 747	0.993	通过
BlockFrequency	0.996 335	0.988	通过
CumulativeSums*	0.817 162	0.995	通过
Runs	0.765 632	0.988	通过
LongestRun	0.071 620	0.987	通过
Rank	0.179 584	0.990	通过
FFT	0.492 436	0.992	通过
NonOverlappingTemplate*	0.496 164	0.990	通过
OverlappingTemplate	0.209 948	0.983	通过
Universal	0.755 819	0.989	通过
ApproximateEntropy	0.075 719	0.986	通过
RandomExcursions*	0.627 887	0.989	通过
RandomExcursionsVariant*	0.540 402	0.992	通过
Serial*	0.676 598	0.986	通过
LinearComplexity	0.096 000	0.997	通过

下载: 导出CSV

表 2 加密前后相邻像素间的相关系数

Table 2. Correlation coefficients between adjacent pixels

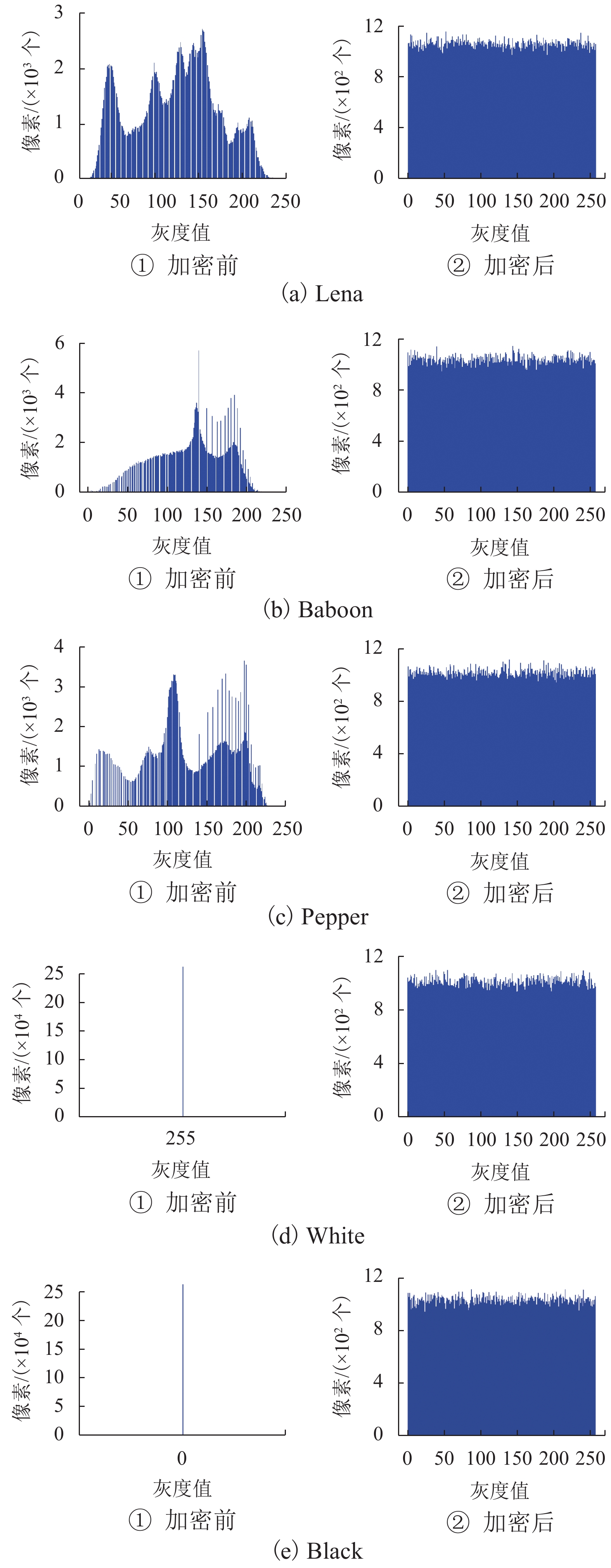
图像	水平方向	垂直方向	对角方向
Lena 明文	0.975 1	0.983 1	0.958 2
Lena 密文	0.001 2	0.000 6	0.001 6
Baboon 明文	0.888 0	0.746 8	0.716 0
Baboon 密文	0.001 1	0.000 4	0.003 3
Pepper 明文	0.977 4	0.975 8	0.962 7
Pepper 密文	0.000 8	0.002 6	0.001 2
White 明文	1.000 0	1.000 0	1.000 0
White 密文	−0.001 4	−0.000 1	0.002 9
Black 明文	1.000 0	1.000 0	1.000 0
Black 密文	0.003 0	−0.000 5	−0.002 2

下载: 导出CSV

表 3 加密前后图像的信息熵

Table 3. Information entropies of images

图像	明文信息熵	密文信息熵
Lena	7.445 5	7.999 3
Baboon	7.222 2	7.999 2
Pepper	7.364 4	7.999 3
White	0	7.999 3
Black	0	7.999 2

下载: 导出CSV

表 4 密文图像的差异

Table 4. Differences between ciphertext images %

图像	测试 1	测试 2	测试 3	测试 4
Lena	99.592	99.614	99.598	99.602
Baboon	99.619	99.599	99.592	99.598
Pepper	99.621	99.622	99.615	99.619
White	99.623	99.618	99.613	99.617
Black	99.607	99.611	99.617	99.579

下载: 导出CSV

表 5 密文图像的NPCR和UACI

Table 5. NPCR and UACI of ciphertext images %

图像	NPCR	UACI
Lena	99.59	33.44
Baboon	99.64	33.50
Pepper	99.60	33.50
White	99.59	33.53
Black	99.60	33.49

下载: 导出CSV

表 6 算法性能对比

Table 6. Comparison of algorithm performance

加密算法	相关系数				信息熵	NPCR/%	UACI/%
加密算法	水平	垂直	对角	绝对平均值	信息熵	NPCR/%	UACI/%
本文算法	−0.002 5	−0.000 2	0.001 1	0.001 3	7.999 3	99.63	33.60
文献[4]	−0.022 3	−0.008 4	−0.008 6	0.013 1	7.997 4	99.61	33.46
文献[5]	−0.038 1	−0.029 1	0.002 7	0.023 3	7.999 2	99.61	33.45
文献[6]	0.069 3	0.061 0	−0.024 2	0.051 5	7.999 1	99.57	33.41
文献[7]	0.001 4	0.003 8	0.001 1	0.002 1	7.999 3	99.59
文献[8]	−0.023 0	0.001 9	−0.003 4	0.009 4	7.969 6	99.62	33.51
文献[9]	−0.014 4	−0.003 4	0.010 7	0.009 5	7.997 0	99.60	32.91
文献[10]	0.016 3	−0.002 9	0.030 9	0.016 7	7.999 3	99.60	33.45

下载: 导出CSV

参考文献(21)

[1]	GARCIA-BOSQUE M, DÍEZ-SEÑORANS G, PÉREZ-RESA A, et al. A 1 gbps chaos-based stream cipher implemented in 0.18 μm CMOS technology[J]. Electronics, 2019, 8(6): 623. doi: 10.3390/electronics8060623
[2]	TEH J S, TAN K J, ALAWIDA M. A chaos-based keyed hash function based on fixed point representation[J]. Cluster Computing, 2019, 22(2): 649-660. doi: 10.1007/s10586-018-2870-z
[3]	ÖZKAYNAK F. Construction of robust substitution boxes based on chaotic systems[J]. Neural Computing and Applications, 2019, 31(8): 3317-3326. doi: 10.1007/s00521-017-3287-y
[4]	ZHANG Y. The fast image encryption algorithm based on lifting scheme and chaos[J]. Information Sciences, 2020, 520: 177-194. doi: 10.1016/j.ins.2020.02.012
[5]	ZHOU Minjun, WANG Chunhua. A novel image encryption scheme based on conservative hyperchaotic system and closed-loop diffusion between blocks[J]. Signal Processing, 2020, 171: 107484.1-107484.14.
[6]	FARAH M A B, GUESMI R, KACHOURI A, et al. A novel chaos based optical image encryption using fractional Fourier transform and DNA sequence operation[J]. Optics & Laser Technology, 2020, 121: 105777.1-105777.9.
[7]	张健,霍达. 基于混沌系统和DNA编码的量子图像加密算法[J]. 西南交通大学学报,2018,53(6): 1142-1149. doi: 10.3969/j.issn.0258-2724.2018.06.008 ZHANG Jian, HUO Da. Quantum image encryption algorithm based on chaotic system and DNA coding[J]. Journal of Southwest Jiaotong University, 2018, 53(6): 1142-1149. doi: 10.3969/j.issn.0258-2724.2018.06.008
[8]	XU Lu, ZHI Li, JIAN Li, et al. A novel bit-level image encryption algorithm based on chaotic maps[J]. Optics and Lasers in Engineering, 2016, 78: 17-25. doi: 10.1016/j.optlaseng.2015.09.007
[9]	YE Guodong. A block image encryption algorithm based on wave transmission and chaotic systems[J]. Nonlinear Dynamics, 2014, 75(3): 417-427. doi: 10.1007/s11071-013-1074-6
[10]	HUANG Xiaoling, YE Guodong. An image encryption algorithm based on hyper-chaos and DNA sequence[J]. Multimedia Tools and Applications, 2014, 72(1): 57-70. doi: 10.1007/s11042-012-1331-6
[11]	NEPOMUCENO E G, NARDO L G, ARIAS-GARCIA J, et al. Image encryption based on the pseudo-orbits from 1D chaotic map[J]. Chaos:an Interdisciplinary Journal of Nonlinear Science, 2019, 29(6): 061101.1-061101.8. doi: 10.1063/1.5099261
[12]	ALAWIDA M, TEH J S, SAMSUDIN A, et al. An image encryption scheme based on hybridizing digital chaos and finite state machine[J]. Signal Processing, 2019, 164: 249-266. doi: 10.1016/j.sigpro.2019.06.013
[13]	GOPALAKRISHNAN T, RAMAKRISHNAN S. Image encryption using hyper-chaotic map for permutation and diffusion by multiple hyper-chaotic maps[J]. Wireless Personal Communications, 2019, 109(1): 437-454. doi: 10.1007/s11277-019-06573-x
[14]	张健,霍达. 基于混沌系统的量子彩色图像加密算法[J]. 西南交通大学学报,2019,54(2): 421-427. ZHANG Jian, HUO Da. Quantum colour image encryption algorithm based on chaotic systems[J]. Journal of Southwest Jiaotong University, 2019, 54(2): 421-427.
[15]	WANG Xingyuan, ZHAO Hongyu, HOU Yutao, et al. Chaotic image encryption algorithm based on pseudo-random bit sequence and DNA plane[J]. Modern Physics Letters B, 2019, 33(22): 1950263.1-1950263.24. doi: 10.1142/S0217984919502634
[16]	GAYATHRI J, SUBASHINI S. A spatiotemporal chaotic image encryption scheme based on self adaptive model and dynamic keystream fetching technique[J]. Multimedia Tools and Applications, 2018, 77(19): 24751-24787. doi: 10.1007/s11042-018-5675-4
[17]	WEN Heping, YU Simin, LÜ Jinhu. Breaking an image encryption algorithm based on DAN encoding and spatiotemporal chaos[J]. Entropy, 2019, 21(3): 246. doi: 10.3390/e21030246
[18]	WANG Yong, LIU Zhaolong, MA Jianbin, et al. A pseudorandom number generator based on piecewise logistic map[J]. Nonlinear Dynamics, 2016, 83(4): 2373-2391. doi: 10.1007/s11071-015-2488-0
[19]	王永,赵毅,GAO J,等. 基于分段Logistic映射的二维耦合映像格子模型的密码学相关特性分析[J]. 电子学报,2019,47(3): 657-663. WANG Yong, ZHAO Yi, GAO J, et al. Cryptographic feature analysis on 2D coupled map lattices based on piecewise logistic map[J]. Acta Electronica Sinica, 2019, 47(3): 657-663.
[20]	李佩玥,石俊霞,郭嘉亮,等. 一种混沌伪随机序列均匀化普适算法的改进[J]. 电子学报,2015,43(4): 753-759. doi: 10.3969/j.issn.0372-2112.2015.04.018 LI Peiyue, SHI Junxia, GUO Jialiang, et al. Improvement of a universal algorithm for uniformization of chaotic pseudo-random sequences[J]. Acta Electronica Sinica, 2015, 43(4): 753-759. doi: 10.3969/j.issn.0372-2112.2015.04.018
[21]	WANG Xiaomin, ZHANG Jiashu. An image scrambling encryption using chaos-controlled Poker shuffle operation[C]//2008 International Symposium on Biometrics and Security Technologies. Isalambad: IEEE, 2008: 1-6.

施引文献

附加材料(0)

访问统计

点击查看大图

图(9) / 表(6)

计量

文章访问数: 283
HTML全文浏览量: 153
PDF下载量: 17
被引次数: 0

基于二维耦合映像格子模型的图像加密

doi: 10.3969/j.issn.0258-2724.20200331

作者简介: 王永（1977—），男，教授，博士，研究方向为信息安全，混沌密码学，E-mail：wangyong_cqupt@163.com

计量

出版历程

Image Encryption Based on 2D Coupled Map Lattices

计量

出版历程

目录

作者简介:
王永（1977—），男，教授，博士，研究方向为信息安全，混沌密码学，E-mail：wangyong_cqupt@163.com