Statistical Damage Model for Whole Deformation and Failure Process of Rock Considering Initial Void Closure
-
摘要:
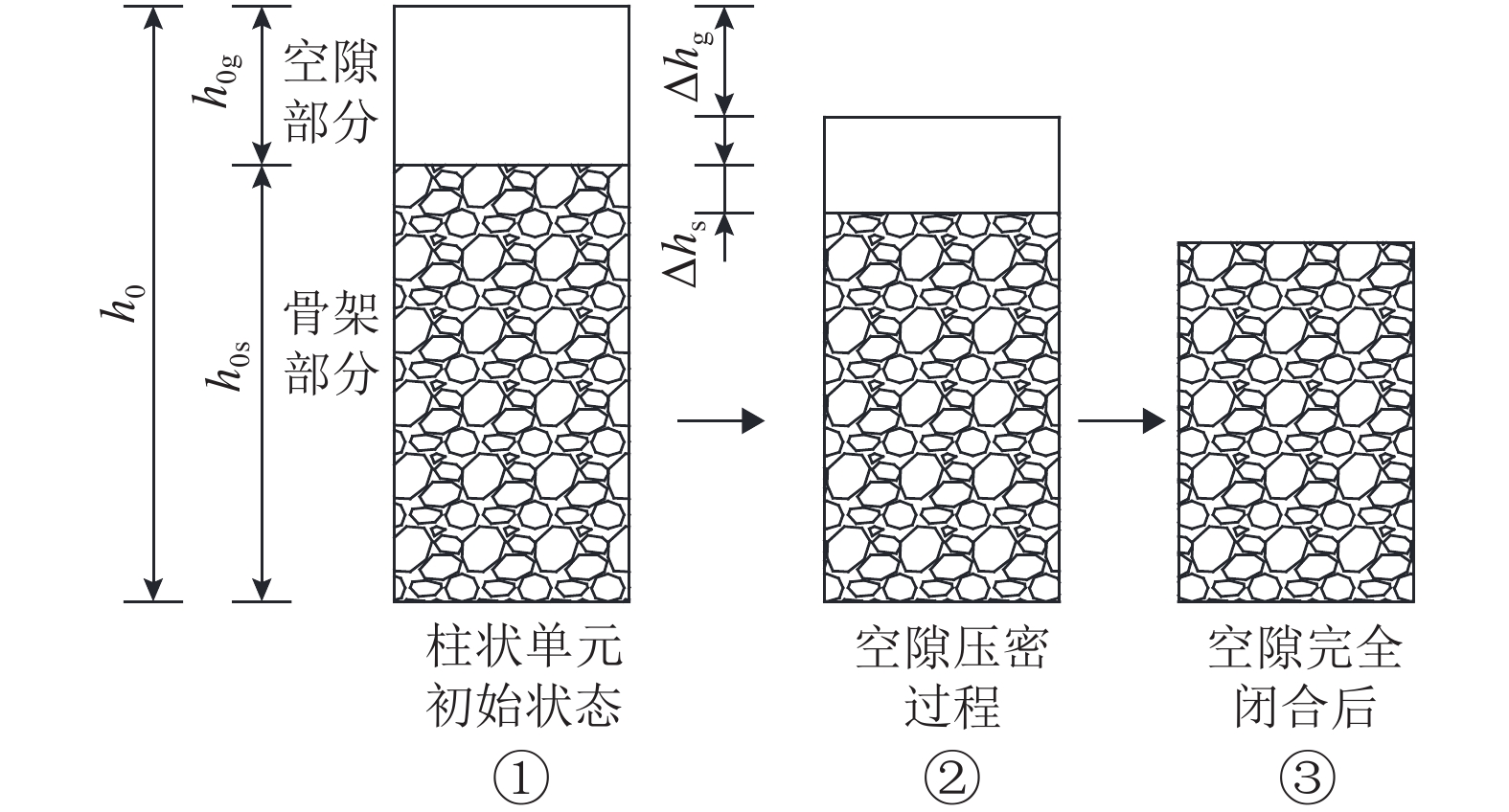
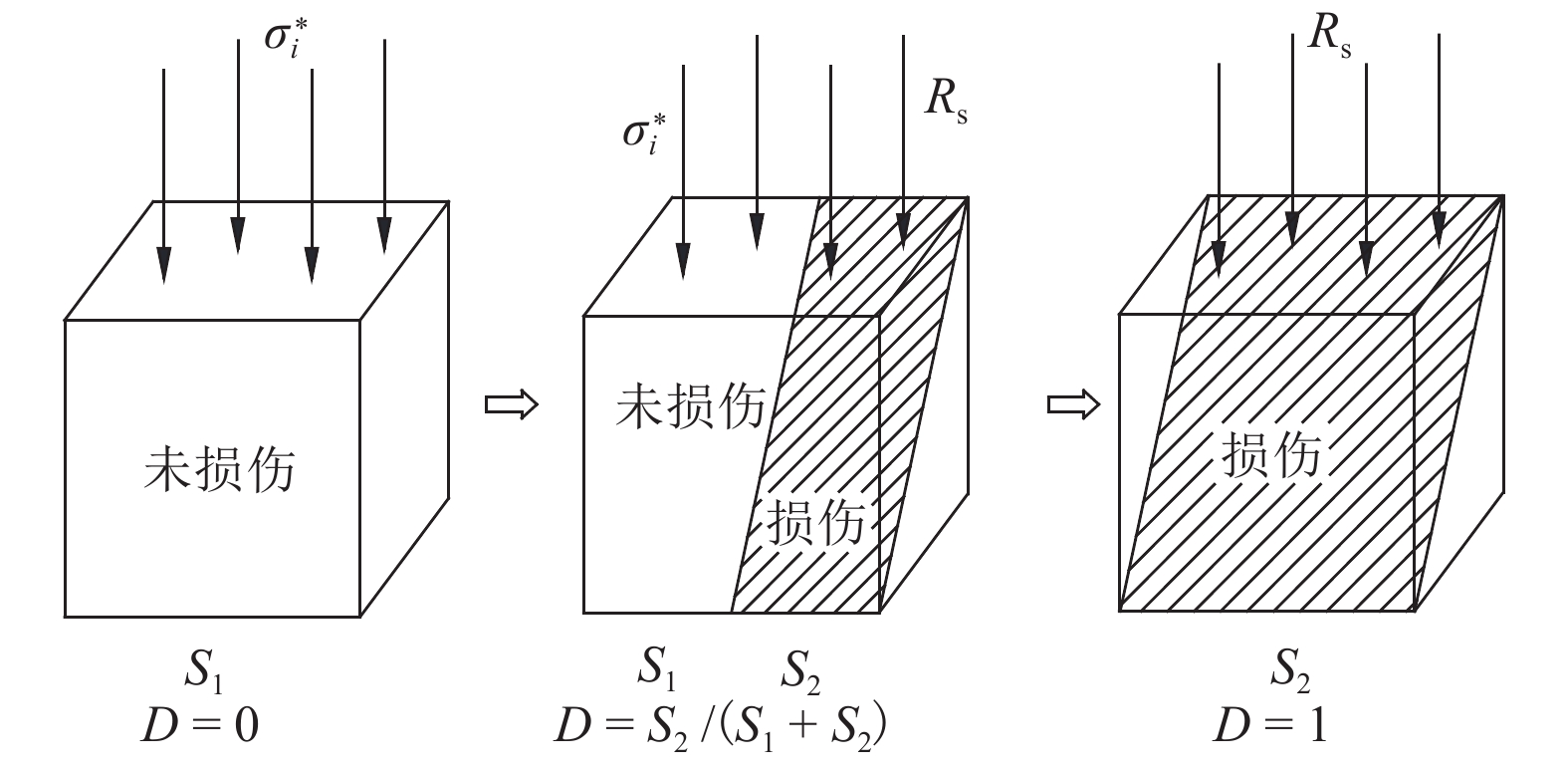
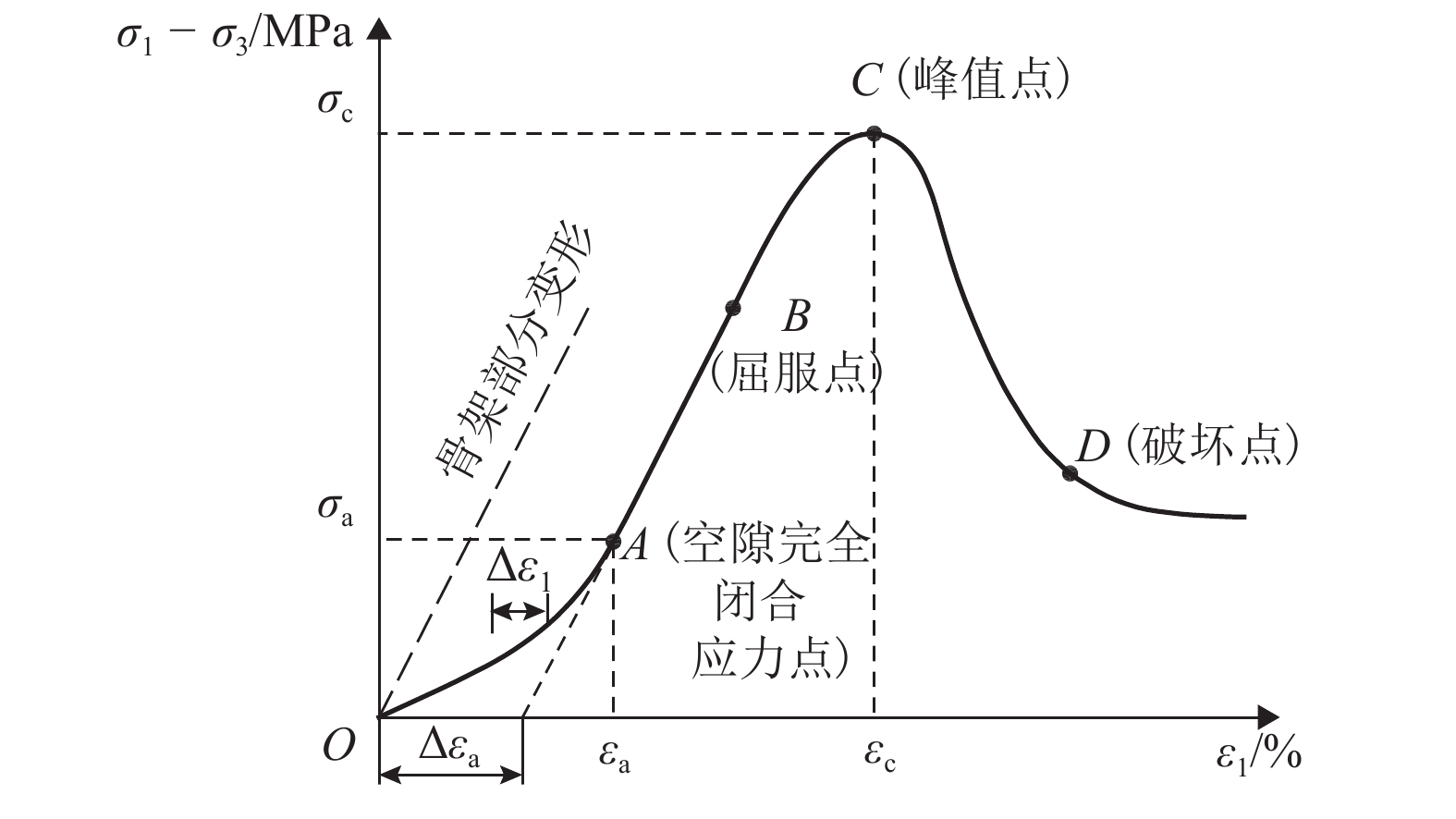
为了建立能够准确模拟岩石变形全过程的本构模型，深入分析了现有统计损伤模型难以描述岩石初始非线性变形阶段的局限性. 综合考虑岩石的变形机理，将岩石抽象为由空隙和骨架组成的材料，分析了岩石变形及空隙与骨架两部分变形之间的关系，提出了空隙应变比
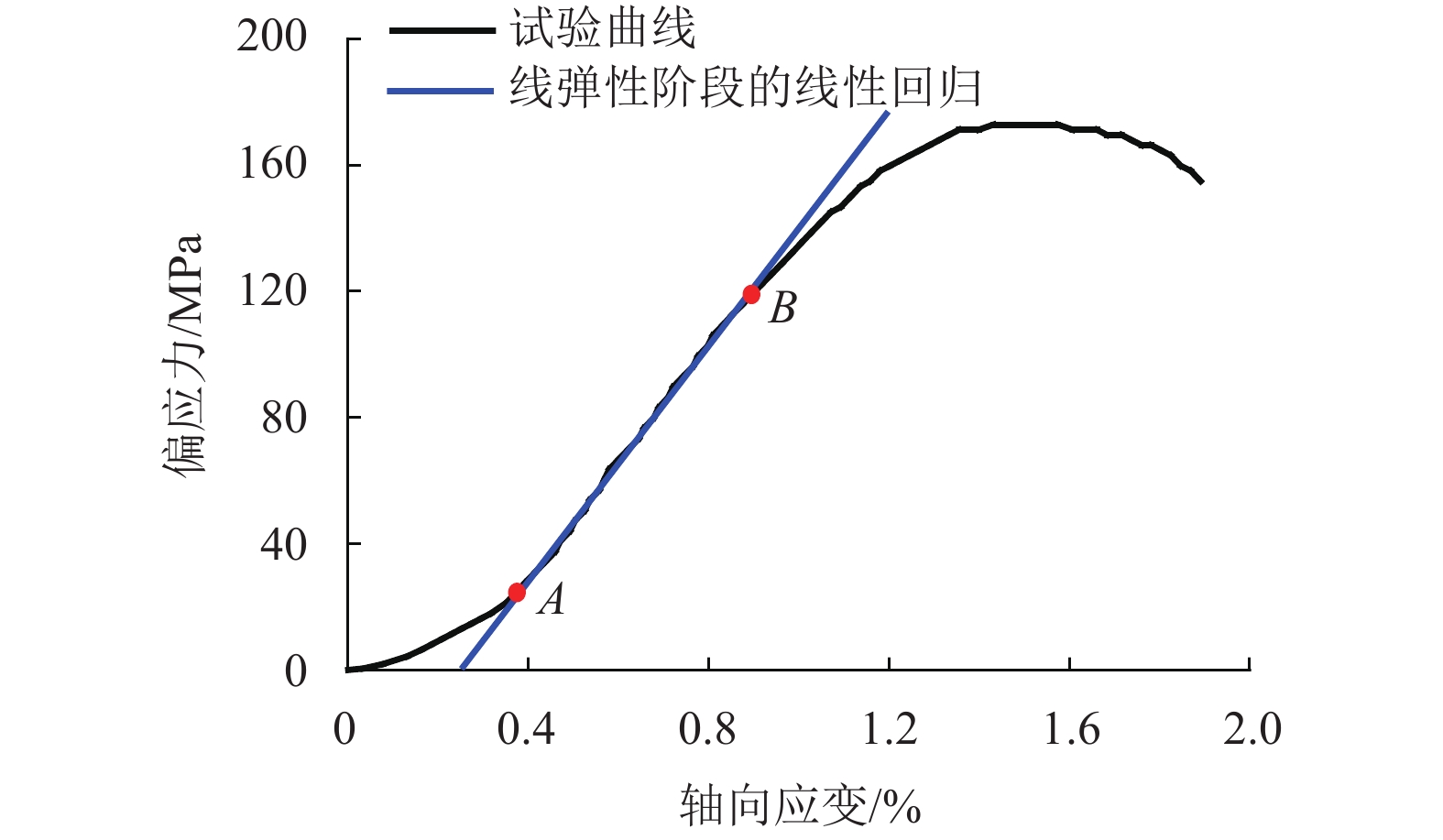
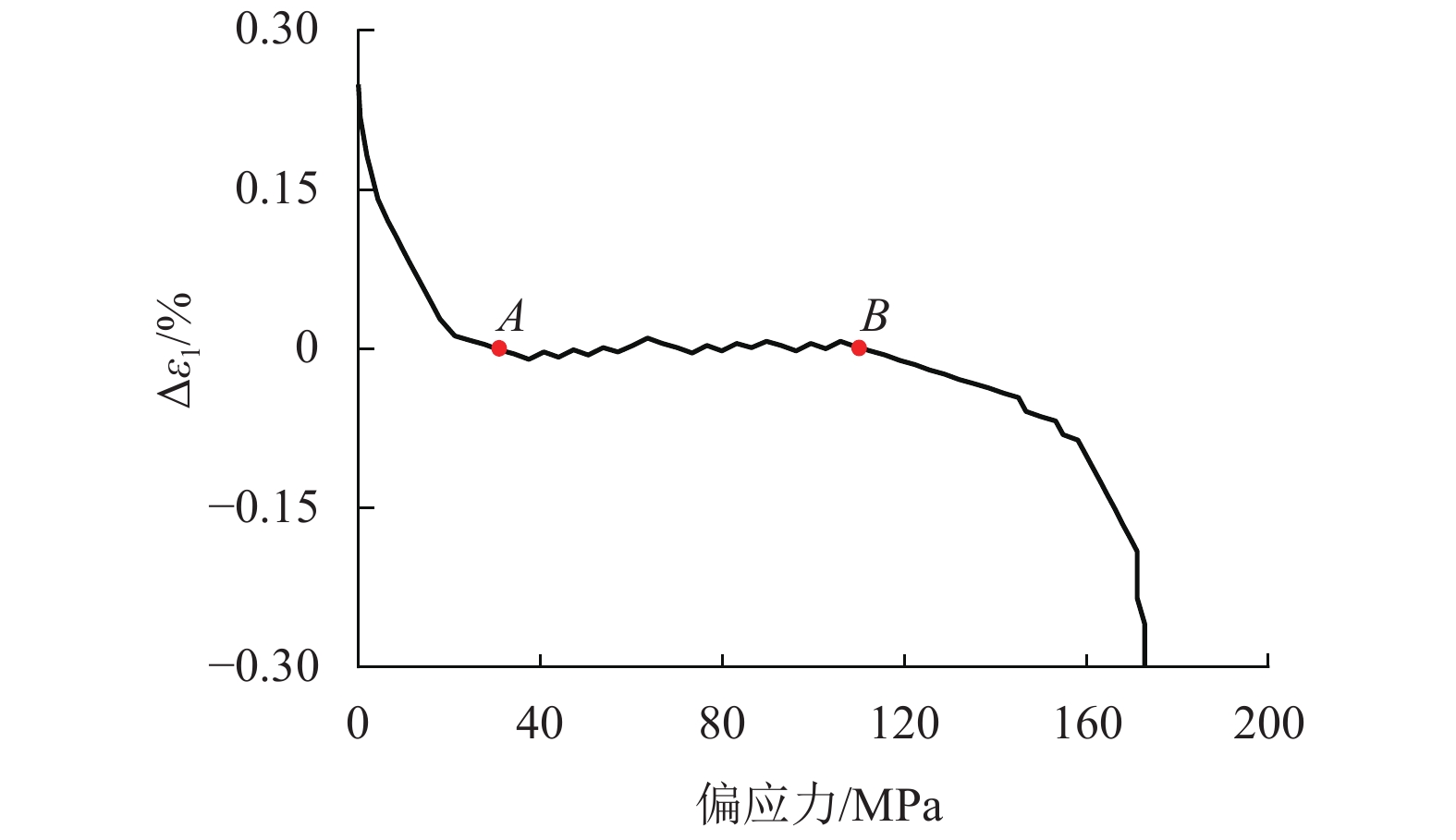
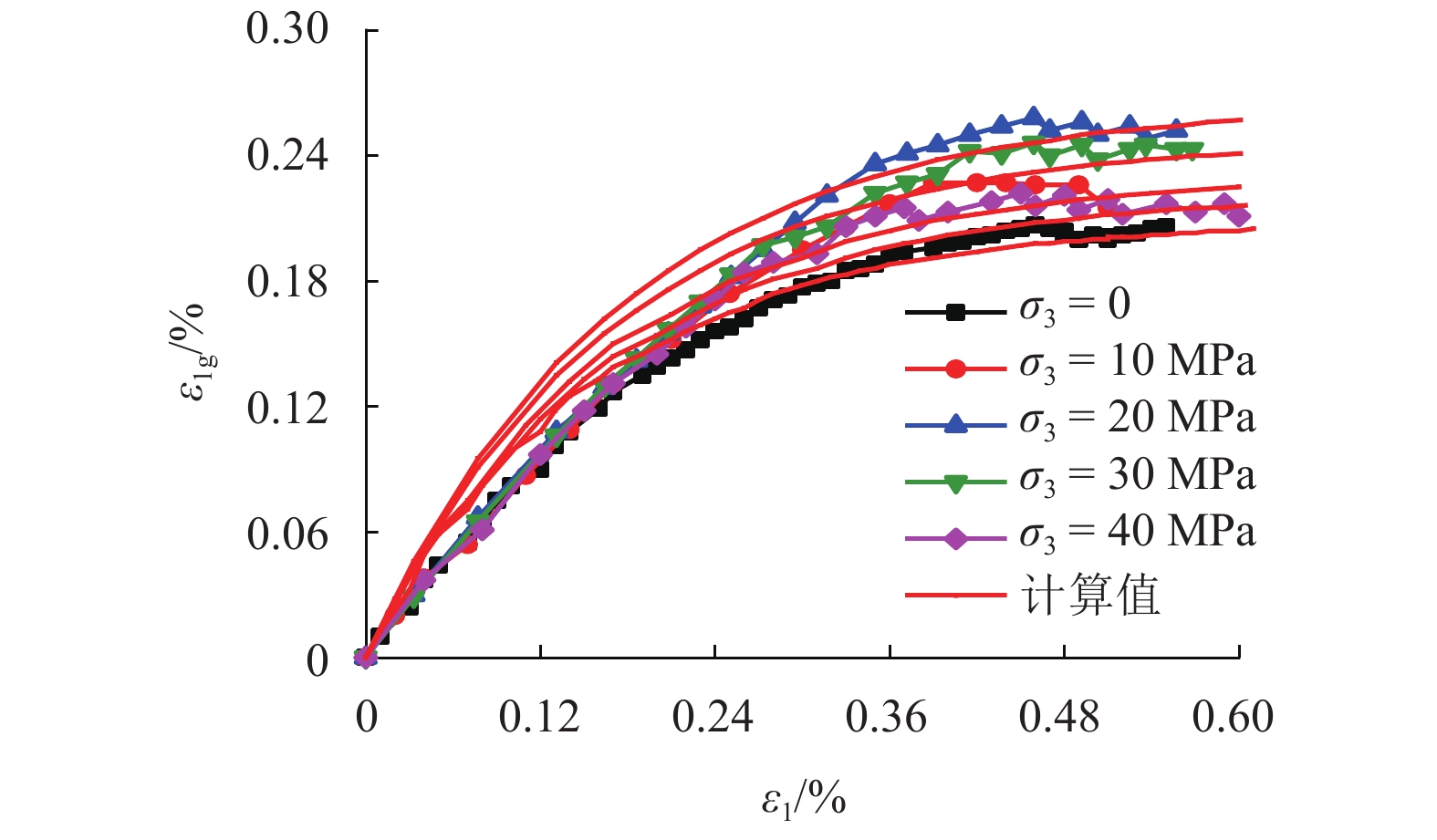
K 的概念；利用岩石三轴试验结果，提出了岩石骨架和空隙两部分应变的计算方法，推导了K 的演化方程；通过引入统计损伤理论，将岩石看作是由众多强度服从Weibull函数分布的微元组成，最终建立了能够反映岩石变形全过程的本构模型，并给出了模型相关参数的确定方法. 现有模型结果和试验结果比较分析表明：本文模型能够较好地模拟荷载作用下岩石变形破坏全过程的5个阶段，相关系数均在0.92以上，很好地解释了围压越大初始空隙压密阶段越短以及弹性模量、峰值强度和峰值应变均越大的力学行为特性.Abstract:In order to establish a constitutive model that can accurately simulate the whole deformation and failure process of rock, a deep analysis is made of the limitations of the existing statistical damage models incapable of well describing the initial nonlinear phase of rock deformation. Considering the deformation mechanism of rock comprehensively, the intact rock is abstracted as a material composed of rock skeleton and voids. Based on the analysis of the deformation relationships among the whole rock, rock skeleton and voids, the concept of rock void strain ratio
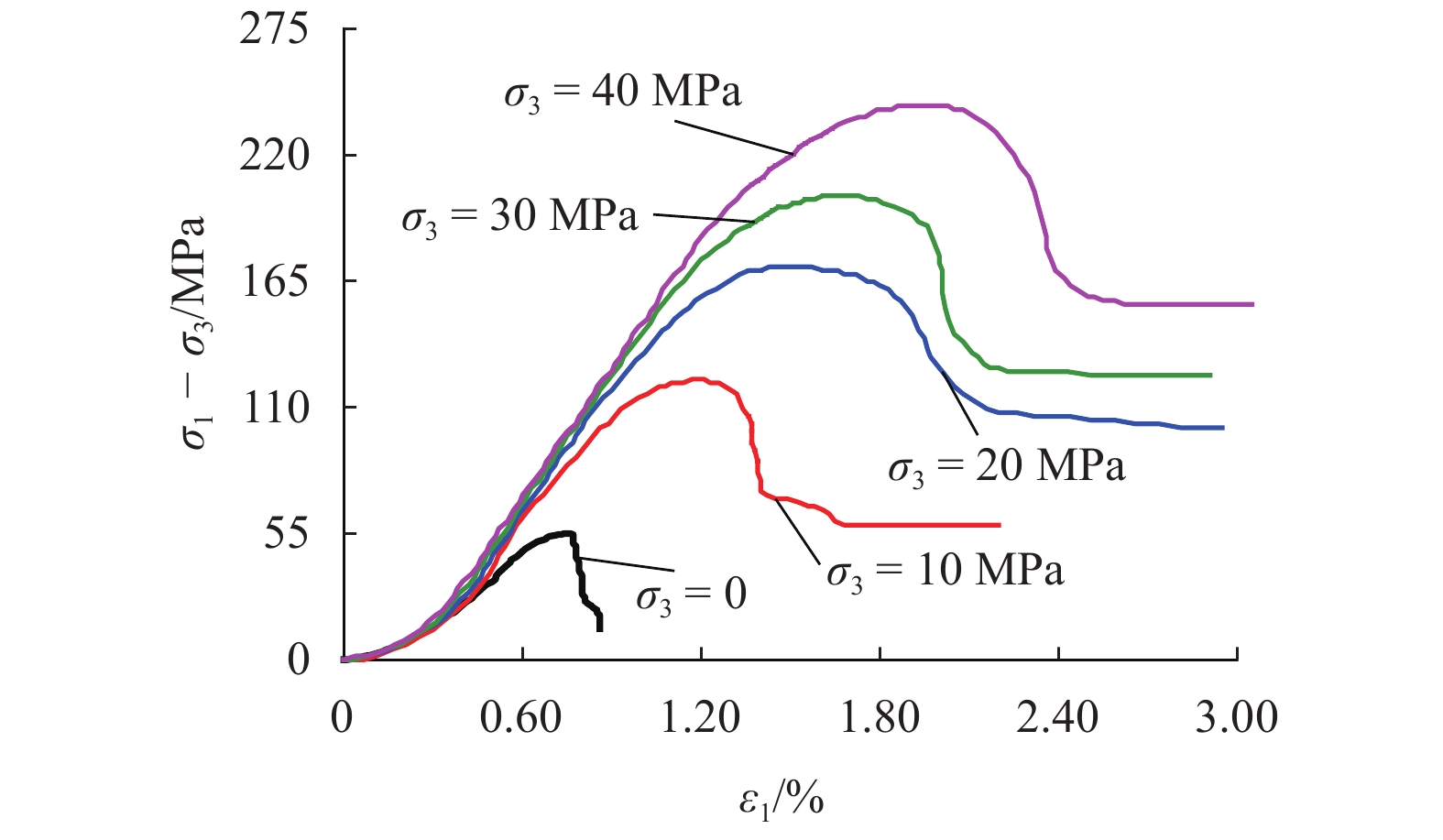
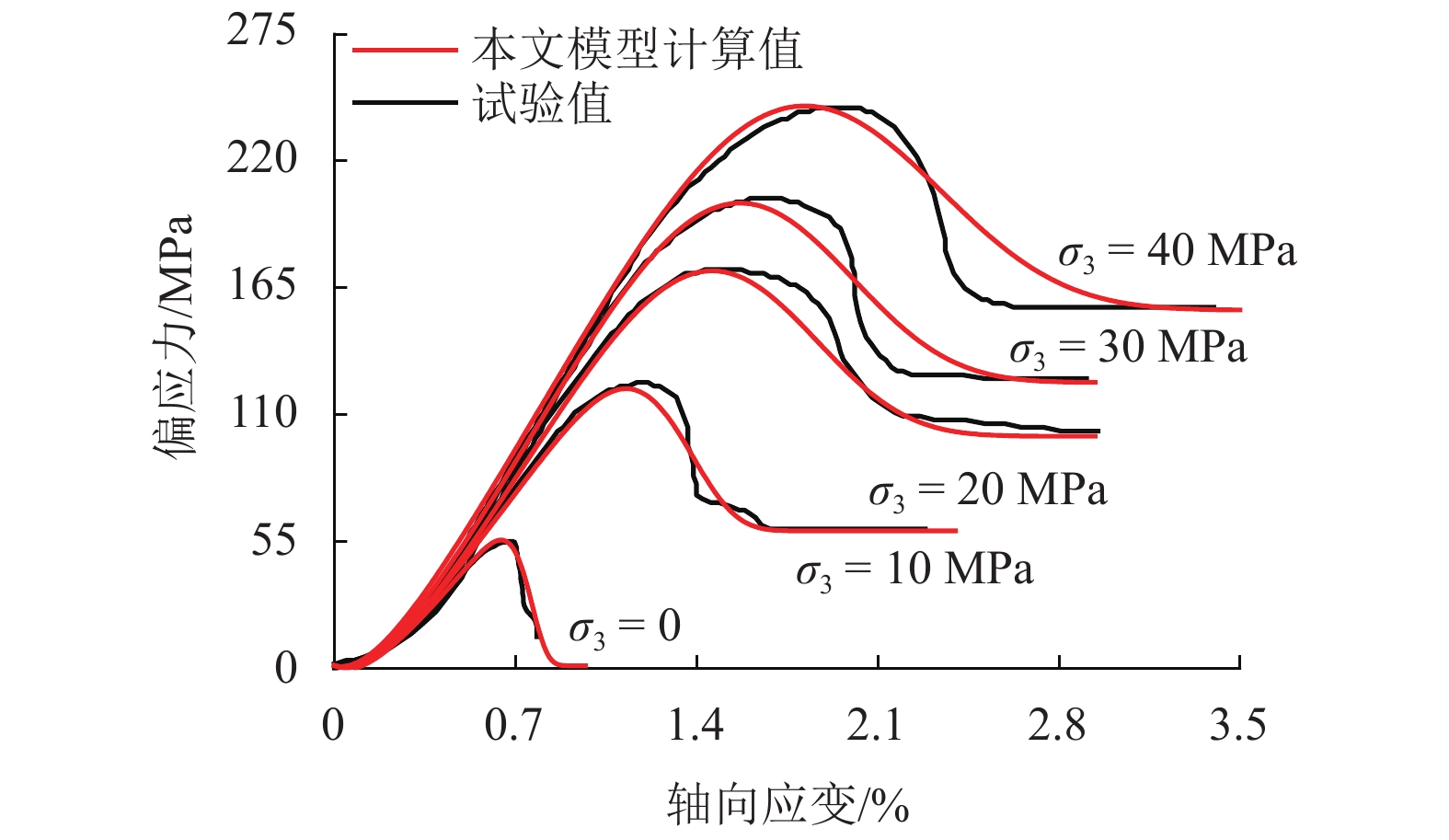
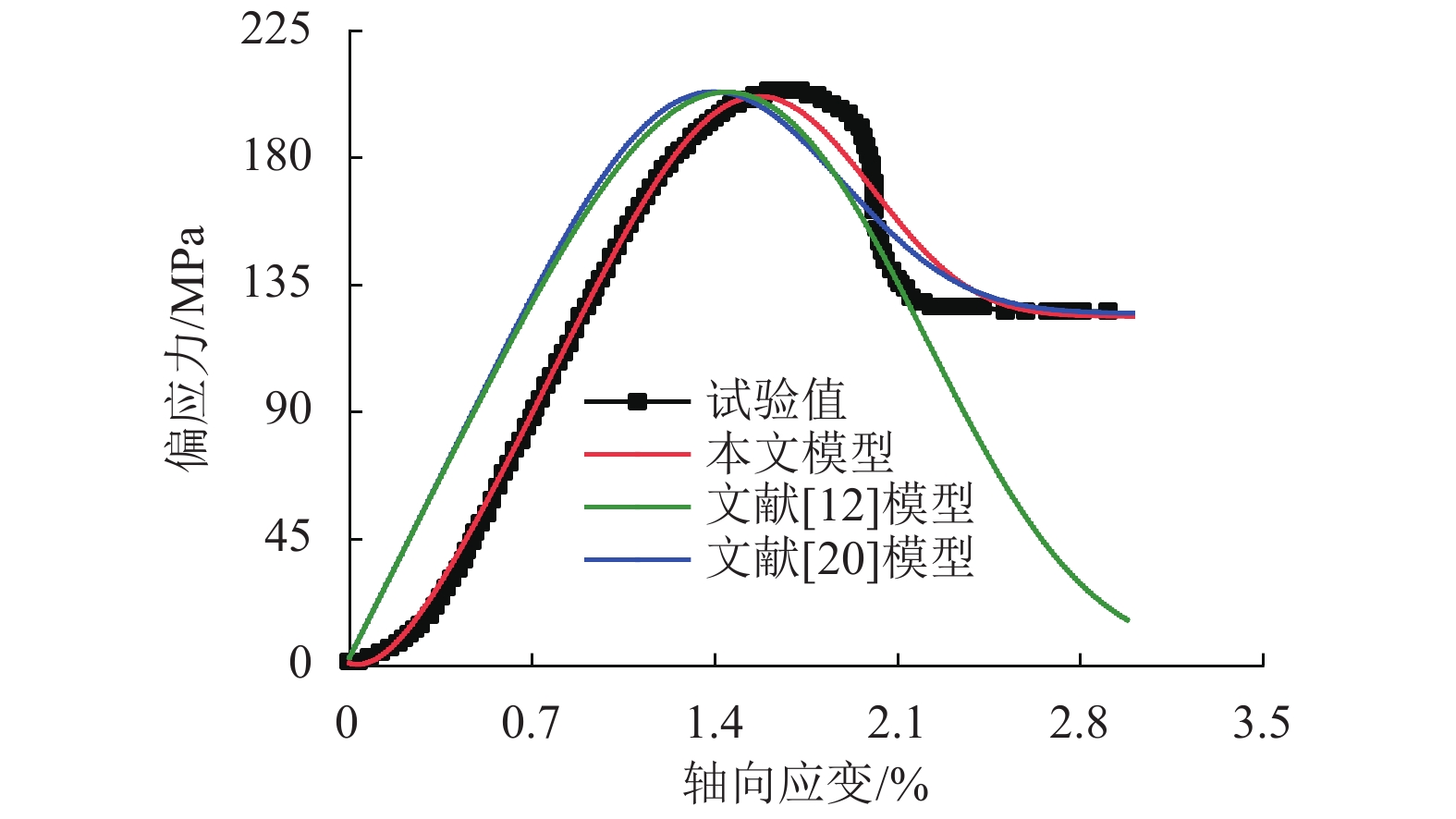
K is proposed; the calculation methods of rock skeleton strain and voids strain are presented using triaxial test results to derive the evolution equation ofK . By introducing the statistical damage theory, the rock is regarded as being composed of many micro elements whose strength obeys the distribution of Weibull function. Finally, a new constitutive model is established to describe the whole rock deformation process, and the determination methods of relevant model parameters are given. Compared with other model calculations and test results, this constitutive model can better simulate the five phases of the whole rock deformation and failure process under load, and the correlation coefficients are all larger than 0.92 for different confining test results. It also well explains the mechanical behavior characteristics that the larger the confining pressure, the shorter the initial void closure phase, and the larger the elastic modulus, peak strength and peak strain. -
车体作为地铁车辆关键承载零部件，在运行过程中承受来自转向架、车钩、车下设备以及乘客质量等一系列复杂载荷. 新造地铁车体由于轻量化需求，多采用铝合金型材整体焊接而成，一节车厢焊缝多达数千条. 以传统A型地铁为例，车体侧墙两边各开有5门4窗，且门窗尺寸远大于干线车体，大大增加了车身强度薄弱位置的数量.基于以上特点，地铁车体在承受复杂载荷时的疲劳问题越来越突出.
传统A型地铁铝合金车体长约为22 m、宽度约为3 m、高度约为3 m，整备质量约为25 t，超员载荷约为50 t. 整车的疲劳试验试验周期长、经费高、风险大. 在ANSYS软件中，子模型方法通过对局部关注区域的网格进行细化，并在区域边界处施加等效的边界条件，使得计算结果更精确，计算速度更快. 故可考虑截取车体受力最恶劣的部分，对该部分的边界施加等效边界条件后进行疲劳试验. 根据车体的受力状态以及运营维修经验，车体疲劳裂纹往往产生于牵枕缓部位[1]，因此可以截取车体底架端部包含牵枕缓部位的部分进行子模型疲劳试验.
胡杰鑫等[2]利用Monte Carlo方法，对铝合金地铁车体枕梁进行了虚拟疲劳试验，并与实际疲劳试验结果进行对比，验证了该方法的有效性；王玉伟[3]基于实测载荷编制CRH2型车枕梁关键部位的应力谱，研究了运营里程与损伤之间的关系；李珊珊[4]利用子模型方法，对CRH2型车枕梁结构网格进行了细分，提出了枕梁的补强方案；臧伟锋等[5]针对飞机机身壁板设计了一种新型工装，该工装使得机身壁板的应力分布与实际全尺寸机身的应力分布相一致，并进行了内压载荷疲劳试验；四方股份联合航空工业飞机强度研究所对CRH380中间车车体全长的1/3结构进行了气密强度疲劳试验[6]；Gutiérrez-Carvajal等[7]设置了多种载荷工况对铝合金车体枕梁进行了疲劳试验，利用累积损伤法评估了枕梁的疲劳寿命.
本文将设定边界条件下的静强度试验结果与有限元计算结果进行对比分析，验证了端部底架子模型（以下简称端部底架）有限元模型的正确性. 研究了端部底架边界条件模拟方法和试验加载方法，根据标准EN12663-1：2010 + A1：2014[8]（以下简称EN 12663标准）规定的载荷进行了疲劳损伤计算，得到了端部底架与全尺寸车体关键位置损伤分布的规律，验证了以端部底架子模型疲劳试验代替全尺寸车体疲劳试验的可行性. 通过端部底架疲劳试验结果对全尺寸车体的疲劳寿命进行了评估.
1. 端部底架边界条件及载荷
1.1 边界条件
在全尺寸车体模型中，车体的底架边梁与车体的侧墙连接，底架的端梁与车体的端墙连接，底架的尾部与车体地板及底架边梁连接. 截取下来的端部底架长5 m，与端墙、侧墙、地板以及边梁的连接均被截断. 所设置的边界条件需保证端部底架关键部位的应力分布与应力大小与全尺寸车体相一致.
在有限元计算时，容易获取端部底架边界节点的力和弯矩，该力和弯矩与施加于端部底架的外部载荷使得底架处于力平衡的状态. 在疲劳试验过程中，底架车钩、空簧和中心销处的集中力可以通过作动器施加，由于底架边界在全尺寸车体中变形较小，边界处的分布力则以约束产生的反力施加.
根据端部底架与全尺寸车体的连接方式，在端部底架的头部两侧与车体侧墙连接处、枕梁两侧与车体侧墙连接处约束端部底架的垂向自由度. 在尾部地板处约束底架的纵向和垂向自由度. 横向约束在运营过程中由车体的惯性产生，在台架试验中无法复现，因此选取与牵枕缓焊缝应力无关的边梁侧面进行约束，如图1所示，图中：X轴所示方向为纵向；Y轴所示方向为横向；Z轴所示方向为垂向.
1.2 试验载荷计算
根据EN 12663标准中关于车体疲劳载荷的规定：地铁车体应根据定员载荷（m1 + m3）和超员载荷（m1 + m4）分别设计疲劳载荷工况，其中：m1为车体整备质量；m3为定员乘客质量；m4为超员乘客质量，并按其在服役寿命期间所占的比例进行疲劳试验. 其他类型轨道交通车辆车体根据其载荷特点，选取恒幅定员或恒幅超员疲劳载荷进行疲劳试验.
由于地铁车体定员载荷和超员载荷在服役期间所占比重难以准确统计，为得到较为保守的结果，认为车体在服役过程中一直承受最大载荷，车体的疲劳寿命最短，即以恒幅超员载荷（m1 + m4）进行数值计算和疲劳试验，m1 = 28.279 t，m4 = 22.440 t.
EN 12663标准中规定整车纵向和横向疲劳载荷为 ± 0.15g，垂向载荷为g ± 0.15g，但均为单个载荷分别作用1000万次的疲劳载荷. 对于组合载荷，EN 12663标准第6.8节推荐引用VDV 152-2016[9]标准（以下简称VDV 152标准）.
VDV 152标准第5.3.2节中将X、Y、Z方向的载荷进行组合，建立了3个载荷工况，每个工况循环200万次，见表1.
表 1 标准之间疲劳载荷工况对比Table 1. Comparison of fatigue load cases between standards标准 工况 X Y Z VDV 152 1 ± 1.20 m/s2 g ± 1.90 m/s2 2 ± 1.60 m/s2 g ± 1.00 m/s2 3 ± 1.50 m/s2 ± 0.60 m/s2 g ± 1.00 m/s2 EN 12663 1 ± 0.15g 2 ± 0.15g 3 ± 0.15g VDV 152标准中载荷工况的组合与EN 12663标准中规定的3个方向载荷每个方向单独作用1000万次是等效的，即在疲劳试验中，可用VDV 152标准规定的疲劳载荷代替EN 12663标准中规定疲劳载荷[9].
对于X方向的载荷，VDV 152标准只在一个工况下循环了200万次，因此需根据等损伤原则，将X方向200万次载荷折算成EN 12663标准中与垂向、横向共同作用的1000万次载荷.
1.2.1 车钩载荷
车钩载荷主要源于列车牵引或制动时的不同步，对于A型地铁车辆，一般采用4动2拖编组，拖车为首尾车，最大车钩载荷发生在拖车和动车连接的车钩位置. 按启动加速度a = 1 m/s2计算，最大车钩载荷为
FXmax=4a(m1+m4)2=101.44kN. (1) 根据VDV 152标准第5.3.2.1节，最大车钩力仅在牵引（制动）不同步的瞬间产生，对于动力分散列车，车钩力的疲劳载荷为最大车钩力的25%. 因此，作用200万次车钩载荷的动态幅值为
FXmax/4=25KN .根据疲劳寿命-应力曲线幂函数表达式：
σmN=C. (2) 式中：σ为应力；m、C为材料常数，VDV 152标准第5.3.3.3节推荐m取4；N为循环次数.
按VDV 152标准，将0.15g作用200万次，根据式（2）折算成1000万次，则车钩载荷动态幅值
Fcoupler =16.96kN. 1.2.2 中心销牵引（制动）载荷
依据EN 12663标准按 ± 0.15g施加，中心销牵引（制动）载荷如式（3）.
FpivotX=0.15g(m1+m4)2=37.3kN. (3) 按式（3）将200万次载荷折算成1000万次，载荷
FpivotX=24.94kN. 中心销牵引（制动）载荷的加载高度根据实车确定，本文中加载高度距枕梁下表面为586.5 mm.
1.2.3 中心销横向载荷
列车在曲线运行时会承受来自于转向架横向止挡的横向力FY，依据EN 12663标准按± 0.15g施加，如式（4）.
FY=0.15g(m1+m4)2=37.3kN. (4) 该载荷由中心销和空气弹簧共同承担，在试验时仅施加中心销承受的横向载荷. 中心销横向载荷加载高度距枕梁下表面为297 mm. 根据空气弹簧参数，每一个转向架单个空气弹簧承担的横向载荷
FairsringY=3.78kN. 因此中心销承担的横向载荷为
FpivotY=FY−2FairsringY=29.74kN. (5) 1.2.4 空簧垂向载荷
根据表1超员载荷确定空簧承受的垂向载荷. 依据EN 12663标准，按g± 0.15g施加，由空气弹簧承担.
空簧载荷均值为
FZm=g(m1+m4)4=124.39kN. (6) 空簧载荷幅值为
FZa=0.15g(m1+m4)4=18.66kN. (7) 2. 端部底架及整车有限元建模分析
2.1 端部底架及整车有限元建模
采用Hypermesh对端部底架进行网格划分，网格类型为Shell181. 底架所用材料为铝合金，材料密度为2.7×10−9 t/mm3，弹性模量为69 GPa，泊松比为0.3. 中心销所用材料为钢，材料密度为7.85×10−9 t/mm3，弹性模量为210 GPa，泊松比为0.3. 中心销与枕梁下表面通过梁单元（Beam188）模拟的螺栓连接. 端部底架有限元模型共划分单元213586个，节点197352个. 底架的约束方式如图2所示，FZ为Z方向的载荷.通过刚性元在车钩座、中心销和空簧位置施加集中力载荷.
全尺寸车体建模方式与端部底架相同，共划分单元1956597个，节点1779596个，如图3所示.
车体在4个空簧位置约束垂向，在中心销横向止挡位置约束横向. 通过刚性元在车钩座、中心销空簧位置施加纵向集中力载荷，垂向载荷及横向载荷以重力场形式施加. 乘客质量通过柔性元均布在地板上，空调及车下设备等考虑其对整车刚度的加强，通过刚性元连接到设备安装座，车门及车窗通过刚性元连接到安装位置.
2.2 模型正确性验证
试验过程中，利用应变片对端部底架关键部位进行应力测量，测点布置见图4，S1～S9为应变片测点，R1～R4为应变花测点，应变花用相当应力进行评定.
当载荷加到最大时，读取各个位置的应力值如图5所示.
由图5可知：测点S1、S2、S3、S4、S5、S9、R1、R2、R3、R4的实测应力与计算应力相对误差较小，测点S3误差最小为0.64%；测点S6、S7、S8误差较大，其中测点S8误差最大为122.2%.
测点S8位于枕内加强筋的焊趾处，该处应力梯度较大，且打磨后的几何轮廓不平整，难以准确确定焊趾位置，因此应变片位置的细微差别会导致测量结果较大的变化；测点S6与测点S3为对称点、测点S7与测点S1为对称点，其仿真应力值误差分别为8.2%和12.2%，且测点S1和测点S3的实测应力值和仿真应力值相差较小，因此测点S6和测点S7误差较大的原因可能是试验中的约束条件没有仿真中的约束条件理想，约束工装本身与车体之间存在间隙导致.
本文中端部底架所需评估的部位主要位于枕梁内侧加强框与周边零部件的焊缝，无法直接粘贴应变片. 测点S6、S7、S8与所评估部位无直接联系，且测点部位在实际运营过程中状态良好. 除测点S6、S7、S8外，其余测点实测应力与计算应力误差较小，因此，认为端部底架有限元模型能够真实反映实际模型的应力状态.
3. 端部底架及整车疲劳寿命分析
3.1 疲劳理论
基于Miner线性累积损伤理论进行疲劳计算，如式（8）.
D=∑niNi, (8) 式中：D为损伤值，当D<1时，认为材料没有疲劳失效的风险.；ni为第i级应力谱下循环的次数；Ni为第i级应力谱下的疲劳寿命.
在ANSYS下计算单位静载荷下焊缝单元的名义应力，在nCode Designlife中施加恒幅疲劳载荷谱.
端部底架同时承受来自车钩座、中心销横向、中心销纵向和空簧垂向载荷，在试验过程中其单元的主应力方向不断发生变化，属于典型的多轴疲劳. 因此采用带绝对值的最大主应力进行疲劳分析.
在疲劳试验中，端部底架承受空簧载荷均值产生的应力，需进行平均应力修正，本文中选取FKM指导书[10]中规定的方法进行平均应力修正. 列车车体在实际服役过程中，结构承载的载荷循环次数远远超过材料疲劳极限处的循环次数，大量小幅值载荷仍能对车体造成损伤，因此将S-N曲线的第二段延伸至应力幅为0处，考虑小载荷循环的影响[11].
3.2 S-N曲线
本文根据Eurocode 9[12]标准建立端部底架铝合金材料不同焊缝类型的S-N曲线.
Δσ 代表循环应力范围. 根据端部底架焊缝类型选用Eurocode 9中7.2.3号焊缝、7.4.3号焊缝、9.4号焊缝和9.6号焊缝. 焊缝类型如图6所示.各焊缝对应的S-N曲线如图7所示. 由图7可知：各焊缝S-N曲线的拐点位于500万次循环处；S-N曲线的第一段斜率k1 = −1/3.4，第二段斜率k2 = −1/5.4.
3.3 疲劳计算结果
根据有限元模型与图6焊缝类型的对应关系，在nCode中将图7各焊缝的S-N曲线分别赋予给对应的焊缝单元，按1.2节计算的载荷进行疲劳计算. 得到端部底架和全尺寸车体的损伤云图如图8，对比如表2.
表 2 端部底架与全尺寸车体损伤对比Table 2. Damage comparison of the end underframe and the full-scale carbody端部底架损伤 整车损伤 损伤部位 0.5028 0.1910 地板下表面与枕内加强筋底板焊缝直角拐角处 0.1796 0.0962 地板下表面与枕内加强筋底板135°拐角附近区域 0.0857 0.0591 外侧枕内加强筋与枕梁下盖板焊缝 从表2可以看出：端部底架损伤最大的3个部位与全尺寸车体损伤最大的3个部位位置一致，且同一位置端部底架的损伤均大于全尺寸车体损伤. 因此通过端部底架疲劳试验验证整车的疲劳强度可以获得较为保守的结果.
3.4 端部底架疲劳试验
端部底架包括了车体运营过程中受力最恶劣的牵枕缓结构，采用接口工装和MTS液压作动器进行疲劳加载，如图9.
端部底架的垂向和横向运动由头部及枕梁两侧边梁的“C”字形工装提供约束，纵向运动通过固定尾部地板面提供约束，如图10所示. 按1.2节计算的载荷进行1000万次循环的疲劳试验，对图8（a）所示的区域进行渗透探伤，未发现裂纹，因此由端部底架的疲劳试验结果认为整车的疲劳寿命满足EN 12663标准的要求.
4. 结 论
1） 全尺寸车体的疲劳试验对试验设备、试验成本均有较高要求，用小尺寸子模型代替整车进行疲劳试验能够有效地缩短研发周期，降低试验成本. 本文采用端部底架子模型代替全尺寸车体的疲劳损伤评估结果偏于保守，从数值仿真和台架试验的角度验证了方法对车体疲劳寿命进行评估是可行的.
2） 使用子模型进行疲劳试验时，需保证子模型的边界远离可能的裂纹潜在部位，且保证子模型结构潜在危险点与全尺寸车体结构保持一致. 边界条件的设置可根据边界处刚度的方向特性，选取刚度最大的方向进行约束，释放他方向的约束. 通过有限元仿真设置的边界条件与试验进行对比，获得正确的有限元数值分析模型，为车体的寿命评估提供依据.
3） 结合名义应力法S-N曲线和线性损伤理论，分别计算了端部底架与全尺寸车体的疲劳损伤. 发现该方法依赖于网格质量和S-N曲线的选取，针对车体和其焊缝特点，在计算中均进行了考虑，因此采用的方法适合车体的寿命评估.
4） 采用端部底架子模型的疲劳试验与数值计算，并与全尺寸车体结构的对比分析，表明该车体能够满足EN 12663标准规定的疲劳寿命要求.
致谢：铝合金车体疲劳寿命评估及试验方法研究（2682019CX45）.
-
图 8 不同m值对应的损伤变量D随ε/ε0的变化
Figure 8. Variation of damage variables D with ε/ε0 for different m
图 9 Weibull分布参数ε0与εc的关系
Figure 9. Relationship between peak strain εc and the parameter ε0 of Weibull distribution
图 10 本文模型计算结果与试验曲线之间的比较
Figure 10. Comparison between the proposed constitutive model calculation values and experimental curves
图 11 不同模型计算结果与试验值的比较
Figure 11. Different model calculations versus experimental curve
表 1 岩石三轴试验参数
Table 1. Triaxial test parameters for rocks
σ3
/MPaE
/MPaεa
/%σc
/MPaεc
/%R
/MPa0 13.72 0.487 54.92 0.697 0 10 14.68 0.443 122.38 1.235 57.7 20 16.17 0.425 171.2 1.57 101.5 30 18.12 0.409 201.17 1.762 123.8 40 19.28 0.374 243.36 1.993 154.9 
下载: 导出CSV
表 2 本文岩石统计损伤模型参数
Table 2. Parameters of statistical damage model for rocks
σ3 /MPa a1 a2 ε0/% m ε0－εc/% 0 0.203 6.301 0.782 14.258 0.095 10 0.226 5.965 1.337 7.576 0.102 20 0.252 5.694 1.714 4.735 0.144 30 0.249 5.379 1.827 4.581 0.065 40 0.217 5.283 2.134 4.269 0.141
下载: 导出CSV
-
[1] YANG S Q. Experimental study on deformation,peak strength and crack damage behavior of hollow sandstone under conventional triaxial compression[J]. Engineering Geology, 2016, 213: 11-24. doi: 10.1016/j.enggeo.2016.08.012 [2] 张春会,赵全胜,王来贵,等. 三轴压缩岩石应变软化及渗透率演化的试验和数值模拟[J]. 煤炭学报,2015,40(8): 1774-1782.ZHANG Chunhui, ZHAO Quansheng, WANG Laigui, et al. Test and numerical modeling on strain softening behavior and permeability evolution of rock under triaxial compression[J]. Journal of China Coal Society, 2015, 40(8): 1774-1782. [3] 衡帅,杨春和,张保平,等. 页岩各向异性特征的试验研究[J]. 岩土力学,2015,36(3): 609-616.HENG Shuai, YANG Chunhe, ZHANG Baoping, et al. Experimental research on anisotropic properties of shale[J]. Rock and Soil Mechanics, 2015, 36(3): 609-616. [4] 卢允德,葛修润,蒋宇,等. 大理岩常规三轴压缩全过程试验和本构方程的研究[J]. 岩石力学与工程学报,2004,23(15): 2489-2493. doi: 10.3321/j.issn:1000-6915.2004.15.001LU Yunde, GE Xiurun, JIANG Yu, et al. Study on conventional triaxial compression test of complete process for marble and its constitutive equation[J]. Chinese Journal of Rock Mechanics and Engineering, 2004, 23(15): 2489-2493. doi: 10.3321/j.issn:1000-6915.2004.15.001 [5] KRAJCINOVIC D, SILVA M A D. Statistical aspects of the continuous damage theory[J]. International Journal of Solid and Structure, 1982, 18(7): 551-562. doi: 10.1016/0020-7683(82)90039-7 [6] CHEN S, QIAO C S, YE Q, et al. Comparative study on three-dimensional statistical damage constitutive modified model of rock based on power function and Weibull distribution[J]. Environmental Earth Science, 2018, 77(3): 108-116. doi: 10.1007/s12665-018-7297-6 [7] 张慧梅,雷利娜,杨更社. 等围压条件下岩石本构模型及损伤特性[J]. 中国矿业大学学报,2015,44(1): 59-63.ZHANG Huimei, LEI Lina, YANG Gengshe. Characteristic and representation model of rock damage process under constant confining stress[J]. Journal of China University of Mining and Technology, 2015, 44(1): 59-63. [8] 张明,王菲,杨强. 基于三轴压缩试验的岩石统计损伤本构模型[J]. 岩土工程学报,2013,35(11): 1965-1971.ZHANG Ming, WANG Fei, YANG Qiang. Statistical damage constitutive model for rocks based on triaxial compression tests[J]. Chinese Journal of Geotechnical Engineering, 2013, 35(11): 1965-1971. [9] WEN T, LIU Y R, YANG C G, et al. A rock damage constitutive model and damage energy dissipation rate analysis for characterising the crack closure effect[J]. Geomechanics and Geoengineering, 2018, 13(1): 54-63. doi: 10.1080/17486025.2017.1330969 [10] ZHOU S W, XIA C C, ZHAO H B, et al. Statistical damage constitutive model for rocks subjected to cyclic stress and cyclic temperature[J]. Acta Geophy, 2017, 65(5): 893-906. doi: 10.1007/s11600-017-0073-2 [11] LEMAITRE. How to use damage mechanics[J]. Nuclear Engineering and Dwsign, 1984, 80(2): 233-245. doi: 10.1016/0029-5493(84)90169-9 [12] 曹文贵,张升,赵明华. 软化与硬化特性转化的岩石损伤统计本构模型之研究[J]. 工程力学,2006,23(11): 110-115. doi: 10.3969/j.issn.1000-4750.2006.11.018CAO Wengui, ZHANG Sheng, ZHAO Minghua. Study on a statistical damage constitutive model with conversion between softening and hardening properties of rock[J]. Engineering Mechanics, 2006, 23(11): 110-115. doi: 10.3969/j.issn.1000-4750.2006.11.018 [13] 李海潮,张升. 基于修正Lemaitre应变等价性假设的岩石损伤模型[J]. 岩土力学,2017,38(5): 1321-1326.LI Haichao, ZHANG Sheng. A constitutive damage model of rock based on the assumption of modified Lemaitre strain equivalence hypothesis[J]. Rock and Soil Mechanics, 2017, 38(5): 1321-1326. [14] 刘冬桥,王焯,张晓云. 岩石应变软化变形特性及损伤本构模型研究[J]. 岩土力学,2017,38(10): 2901-2908.LIU Dongqiao, WANG Zhou, ZHANG Xiaoyun. Characteristics of strain softening of rocks and its damage constitutive model[J]. Rock and Soil Mechanics, 2017, 38(10): 2901-2908. [15] LI Y W, JIA D, RUI Z H, et al. Evaluation method of rock brittleness based on statistical constitutive relations for rock damage[J]. Journal of Petroleum Science and Engineering, 2017, 153: 123-132. doi: 10.1016/j.petrol.2017.03.041 [16] 曹文贵,张超,贺敏,等. 考虑孔隙压密阶段特征的岩石应变软化统计损伤模拟方法[J]. 岩土工程学报,2016,38(10): 1754-1761. doi: 10.11779/CJGE201610002CAO Wengui, ZHANG Chao, HE Min, et al. Statistical damage simulation method of strain softening deformation process for rock considering characteristics of void compaction stage[J]. Chinese Journal of Geotechnical Engineering, 2016, 38(10): 1754-1761. doi: 10.11779/CJGE201610002 [17] XU P, YANG S Q. A fracture damage constitutive model for fissured rock mass and its experimental verification[J]. Arabian Journal of Geosciences, 2017, 10(7): 2947-2954. [18] MENENDEZ B, ZHU W, WONG T F. Micromechanics of brittle faulting and cataclastic flow in Berea sandstone[J]. Journal of Structural Geology, 1996, 18(1): 1-16. doi: 10.1016/0191-8141(95)00076-P [19] HAJIAOBDOLMAJID V, KAISER P K, MARTIN C D. Modelling brittle failure of rock[J]. International Journal of Rock Mechanics and Mining Sciences, 2002, 39(6): 731-741. [20] ZHAO H, SHI C J, ZHAO M H, et al. Statistical damage constitutive model for rocks considering residual strength[J]. International Journal of Geomechanics, 2017, 17(1): 04016033.1-04016033.9. -
下载:
下载:
点击查看大图
计量
- 文章访问数: 368
- HTML全文浏览量: 220
- PDF下载量: 45
- 被引次数: 0