波形钢腹板PC组合箱梁纯扭全过程分析模型

周聪; 李立峰

doi:10.3969/j.issn.0258-2724.20200201

波形钢腹板PC组合箱梁纯扭全过程分析模型

doi: 10.3969/j.issn.0258-2724.20200201

周聪^{1, 2, 3,},
李立峰^1, ,

1.
湖南大学土木工程学院，湖南长沙 410082
2.
湖南科技大学土木工程学院，湖南湘潭 411201
3.
湖南科技大学结构抗风与振动控制湖南省重点实验室，湖南湘潭 411201

基金项目: 国家自然科学基金(52108140，51978257)；湖南省自然科学基金(2021JJ40213)；湖南省教育厅科学研究项目（21B0497）；湖南省交通厅科技项目(201914)

详细信息

作者简介:
周聪(1990—)，男，讲师，博士，研究方向为波形钢腹板组合箱梁、UHPC高性能结构，E-mail：congzhou1990@163.com

通讯作者:
李立峰(1971—)，男，教授，博士，博导，研究方向为UHPC预制装配结构、钢-混组合结构、桥梁抗震，E-mail：lilifeng@hnu.edu.cn

中图分类号: U448.21.3
计量
- 文章访问数: 215
- HTML全文浏览量: 144
- PDF下载量: 14
- 被引次数: 0
出版历程
- 收稿日期: 2020-04-15
- 修回日期: 2020-09-22
- 刊出日期: 2020-09-30

Full-Range Analytical Model for Prestressed Concrete Composite Box Girders with Corrugated Steel Webs Under Pure Torsion

ZHOU Cong^{1, 2, 3
,},
LI Lifeng^{1
, ,}

1.
College of Civil Engineering, Hunan University, Changsha 410082, China
2.
School of Civil Engineering, Hunan University of Science and Technology, Xiangtan 411201, China
3.
Hunan Provincial Key Laboratory of Structures for Wind Resistance and Vibration Control, Hunan University of Science and Technology, Xiangtan 411201, China

摘要

摘要:
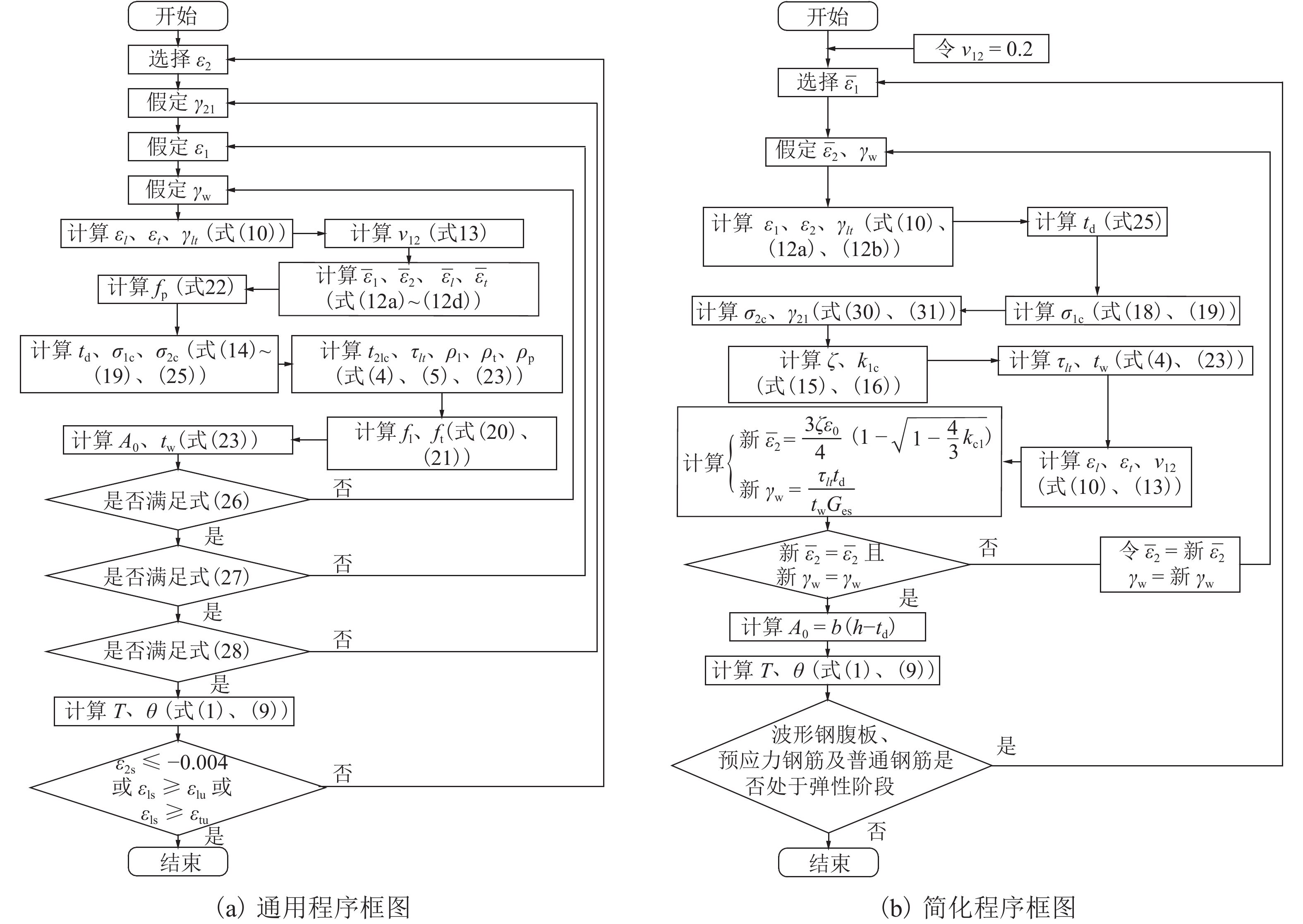
为准确预测波形钢腹板PC组合箱梁（PCCBGCSWs）在纯扭作用下的全过程受力行为，基于软化薄膜元理论提出了改进软化薄膜元模型（ISMMT）. 首先，对ISMMT的平衡、变形协调和材料本构方程以及通用求解程序进行了简要介绍；在此基础上，提出了当波形钢腹板、预应力及普通钢筋均处于弹性阶段时的简化求解程序框图，该简化程序仅有一层迭代循环；最后，完成了一根PCCBGCSWs试件的纯扭模型试验，通过试验得到了试件的扭矩-扭率曲线、波形钢腹板和混凝土翼缘板剪应变、预应力和普通钢筋应变等结果，将试验结果与ISMMT预测的理论结果进行了对比，同时将简化求解程序和通用求解程序的求解效率进行了比较. 结果表明： ISMMT不仅能准确预测PCCBGCSWs在纯扭作用下的全过程扭矩-扭率曲线，还能模拟各构件的应变发展历程，包括混凝土翼缘板、波形钢腹板、预应力和普通钢筋等；运用ISMMT预测本文模型梁的纯扭全过程受力行为时，若采用通用求解程序进行计算，所需的总迭代次数可高达7.9 × 10⁶次，采用简化求解程序最少为5次，最多也仅为193次，可极大提高求解效率；本文ISMMT为PCCBGCSWs的纯扭全过程分析提供了一种有效途径.
- 桥梁工程 /
- 波形钢腹板PC组合箱梁 /
- 纯扭 /
- 改进软化薄膜元模型 /
- 模型试验
Abstract:
To accurately predict the full-range mechanical behavior of prestressed concrete composite box girders with corrugated steel webs (PCCBGCSWs) subjected to pure torsion, a theoretical model called “the improved softened membrane model for torsion (ISMMT)” was proposed based on the softened membrane theory. First, the equilibrium equations, compatibility equations, constitutive laws of materials and general solution algorithm of the ISMMT were briefly introduced. On this basis, a simplified solution algorithm was additionally presented for the stage when both steel bars, the prestressing steel and the corrugated steel webs (CSWs) are in the elastic state, which contains only one iteration loop. To validate the feasibility and accuracy of the ISMMT, a PCCBGCSW specimen was tested under pure torsion. The results, including the overall torque-twist curve, shear strains in the CSWs and concrete flanges, and strains in the prestressing steels and steel bars, were obtained from the test. Then, the experimental results were compared with the theoretical results calculated by the ISMMT. The comparison of solving efficiency between the general computer program and the simplified one was also conducted. Results show that the ISMMT not only can provide accurate prediction for the full-range torque-twist curve of PCCBGCSWs under pure torsion, but also can make precise predictions for the entire stress evolution in components of the PCCBGCSWs during loading, including the concrete flanges, CSWs, prestressing steels, and steel bars. When using the ISMMT to predict the full-range behavior of the PCCBGCSW specimen under pure torsion in this study, the number of iterations could be as high as 7.9 × 10⁶ if the general computer program was used. However, if the simplified computer program was employed, the number of iterations could be significantly reduced (5 times at least and 193 times at most), which is a great improvement in solving efficiency in comparison with the general computer program. Therefore, the ISMMT provides an effective way to analyse the full torsional behaviour of PCCBGCSWs under pure torsion.
- bridge engineering /
- prestressed concrete composite box girders with corrugated steel webs /
- pure torsion /
- improved softened membrane model /
- model test

HTML全文

图 1 纯扭作用下波形钢腹板PC组合箱梁

Figure 1. Prestressed concrete composite box girder with corrugated steel webs subjected to pure torsion

下载: 全尺寸图片幻灯片

图 2 ISMMT的求解程序框图

Figure 2. Program block diagram for solution algorithm of the ISMMT

下载: 全尺寸图片幻灯片

图 3 试件尺寸

Figure 3. Size of the specimen

下载: 全尺寸图片幻灯片

图 4 纯扭加载装置

Figure 4. Loading equipment for pure torsion test

下载: 全尺寸图片幻灯片

图 5 扭转角计算示意

Figure 5. Calculation diagram of torsional angle

下载: 全尺寸图片幻灯片

图 6 应变测点布置

Figure 6. Arrangement of strain measuring points

下载: 全尺寸图片幻灯片

图 7 ISMMT预测结果与试验结果对比

Figure 7. Comparison of the results obtained from the ISMMT and experiment

下载: 全尺寸图片幻灯片

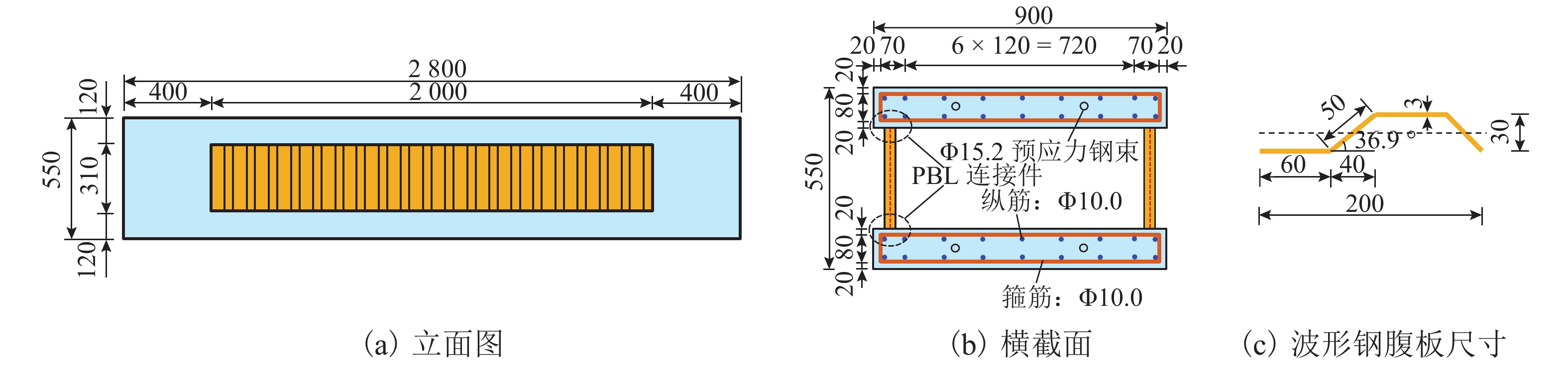
表 1 试件材料参数

Table 1. Material properties of the test beam

混凝土棱柱体抗压强度/MPa	波形钢腹板		预应力钢筋初应力/MPa	普通钢筋
混凝土棱柱体抗压强度/MPa	厚度/mm	屈服强度/MPa	预应力钢筋初应力/MPa	直径/mm	屈服强度/MPa
24.9	3.7	235	800	10	357

下载: 导出CSV

表 2 ISMMT预测结果与试验结果对比（开裂状态）

Table 2. Comparison of the predicted torques and twists from the ISMMT and the experiment (cracking state)

参数	$ {T_{11}}/$ (kN•m)	${T_{12} }/$ (kN•m)	$\dfrac{ { {T_{11} } } }{ { {T_{12} } } }$	${\theta _{ 11 } }/$ ((°)•m⁻¹)	${\theta _{ 12 } }/$ ((°)•m⁻¹)	$\dfrac{ { {\theta _{11} } } }{ { {\theta _{12 } } } }$
取值	160.6	174.5	0.92	0.073	0.161	0.45

下载: 导出CSV

表 3 ISMMT预测结果与试验结果对比（屈服状态）

Table 3. Comparison of the predicted torques and twists from the ISMMT and the experiment (yield state)

参数	${T_{ 21 } }/$ (kN•m)	${T_{22 } }/$ (kN•m)	$\dfrac{ { {T_{21} } } }{ { {T_{22 } } } }$	${\theta _{ 21 } }/$ ((°)•m⁻¹)	${\theta _{ 22} }/$ ((°)•m⁻¹)	$\dfrac{ { {\theta _{ 21 } } } }{ { {\theta _{ 22 } } } }$
取值	351.9	337.9	1.04	1.043	0.973	1.07

下载: 导出CSV

表 4 ISMMT预测结果与试验结果对比（极限状态）

Table 4. Comparison of the predicted torques and twists from the ISMMT and the experiment (limit state)

参数	${T_{ 31 } }/$ (kN•m)	$ {T_{32}} /$ (kN•m)	$\dfrac{ { {T_{ 31} } } }{ { {T_{ 32 } } } }$	$ {\theta _{31}} /$ ((°)•m⁻¹)	$ {\theta _{32 }} /$ ((°)•m⁻¹)	$\dfrac{ { {\theta _{31} } } }{ { {\theta _{32} } } }$
取值	354.9	339.5	1.04	1.547	1.590	0.97

下载: 导出CSV

参考文献(23)

[1]	JIANG R J, KWONG AU F T, XIAO Y F. Prestressed concrete girder bridges with corrugated steel webs:review[J]. Journal of Structural Engineering, 2015, 141(2): 04014108.1-04014108.9.
[2]	李立峰,周聪,王连华,等. 基于纽玛克法的变截面波形钢腹板组合箱梁畸变效应分析[J]. 中国公路学报,2018,31(6): 217-226. doi: 10.3969/j.issn.1001-7372.2018.06.008 LI Lifeng, ZHOU Cong, WANG Lianhua, et al. Analysis on distortion effect of non-prismatic composite box girders with corrugated steel webs based on newmark method[J]. China Journal of Highway and Transport, 2018, 31(6): 217-226. doi: 10.3969/j.issn.1001-7372.2018.06.008
[3]	LI L F, ZHOU C, WANG L H. Distortion analysis of non-prismatic composite box girders with corrugated steel webs[J]. Journal of Constructional Steel Research, 2018, 147: 74-86. doi: 10.1016/j.jcsr.2018.03.030
[4]	ZHANG B S, CHEN W Z, XU J. Mechanical behavior of prefabricated composite box girders with corrugated steel webs under static loads[J]. Journal of Bridge Engineering, 2018, 23(10): 04018077.1-04018077.11.
[5]	李宏江,叶见曙,万水,等. 波形钢腹板预应力混凝土箱梁的试验研究[J]. 中国公路学报,2004,17(4): 31-36. doi: 10.3321/j.issn:1001-7372.2004.04.007 LI Hongjiang, YE Jianshu, WAN Shui, et al. Experimental research on prestressed concrete box girder with corrugated steel webs[J]. China Journal of Highway and Transport, 2004, 17(4): 31-36. doi: 10.3321/j.issn:1001-7372.2004.04.007
[6]	聂建国,朱力,唐亮. 波形钢腹板的抗剪强度[J]. 土木工程学报,2013,46(6): 97-109. NIE Jianguo, ZHU Li, TANG Liang. Shear strength of trapezoidal corrugated steel webs[J]. China Civil Engineering Journal, 2013, 46(6): 97-109.
[7]	ZHANG B S, CHEN W Z, XU J. Shear behaviour of girders with trapezoidal corrugated steel webs-an experimental study[J]. Stahlbau, 2018, 87(8): 810-819. doi: 10.1002/stab.201810602
[8]	陈宜言. 波形钢腹板预应力混凝土桥设计与施工[M]. 北京: 人民交通出版社, 2009.
[9]	MO Y L, JENG C H, CHANG Y S. Torsional behavior of prestressed concrete box-girder bridges with corrugated steel webs[J]. ACI Structural Journal, 2000, 97(6): 849-859.
[10]	聂建国,唐亮. 波形钢腹板PC组合箱梁纯扭性能的非线性分析[J]. 中国公路学报,2007,20(5): 71-77. doi: 10.3321/j.issn:1001-7372.2007.05.013 NIE Jianguo, TANG Liang. Nonlinear analysis of pure torsion property for prestressed concrete composite box girders with corrugated steel webs[J]. China Journal of Highway and Transport, 2007, 20(5): 71-77. doi: 10.3321/j.issn:1001-7372.2007.05.013
[11]	丁勇,江克斌,周寅智,等. 波形钢腹板PC组合箱梁纯扭作用下抗扭承载力计算模型[J]. 计算力学学报,2013,30(1): 137-142. doi: 10.7511/jslx201301023 DING Yong, JIANG Kebin, ZHOU Yinzhi, et al. Analytical model for torsional strength of prestressed concrete box-girder with corrugated steel webs[J]. Chinese Journal of Computational Mechanics, 2013, 30(1): 137-142. doi: 10.7511/jslx201301023
[12]	KO H J, MOON J, SHIN Y W, et al. Non-linear analyses model for composite box-girders with corrugated steel webs under torsion[J]. Steel and Composite Structures, 2013, 14(5): 409-429. doi: 10.12989/scs.2013.14.5.409
[13]	HSU T T C, MO Y L. Unified theory of concrete structures[M]. Chichester: John Wiley & Sons, 2010.
[14]	沈孔健,万水,蒋正文,等. 波形钢腹板混凝土组合箱梁纯扭性能全过程分析[J]. 东南大学学报(自然科学版),2017,47(1): 112-117. doi: 10.3969/j.issn.1001-0505.2017.01.020 SHEN Kongjian, WAN Shui, JIANG Zhengwen, et al. Whole process analysis on pure torsional behavior of concrete composite box girders with corrugated steel webs[J]. Journal of Southeast University (Natural Science Edition), 2017, 47(1): 112-117. doi: 10.3969/j.issn.1001-0505.2017.01.020
[15]	SHEN K J, WAN S, MO Y L, et al. Behavior of single-box multi-cell box-girders with corrugated steel webs under pure torsion. part II: theoretical model and analysis[J]. Thin-Walled Structures, 2018, 129: 558-572.
[16]	SHEN K J, WAN S, MO Y L, et al. A softened membrane model for composite box-girders with corrugated steel webs under pure torsion[J]. Engineering Structures, 2018, 173: 357-371. doi: 10.1016/j.engstruct.2018.07.021
[17]	JENG C H, HSU T T C. A softened membrane model for torsion in reinforced concrete members[J]. Engineering Structures, 2009, 31(9): 1944-1954. doi: 10.1016/j.engstruct.2009.02.038
[18]	SHEN K J, WAN S, MO Y L, et al. A softened membrane model for prestressed concrete composite box girders with corrugated steel webs under pure torsion[J]. Advances in Structural Engineering, 2019, 22(2): 384-401. doi: 10.1177/1369433218788597
[19]	周聪,李立峰,王连华,等. 基于软化薄膜元理论的波形钢腹板PC组合箱梁纯扭全过程分析[J]. 土木工程学报,2018,51(10): 97-106. ZHOU Cong, LI Lifeng, WANG Lianhua, et al. Full-range analysis of prestressed composite box girders with corrugated steel webs subject to pure torsion based on softened membrane theory[J]. China Civil Engineering Journal, 2018, 51(10): 97-106.
[20]	ZHOU C, LI L F, WANG L H. Improved softened membrane model for prestressed composite box girders with corrugated steel webs under pure torsion[J]. Journal of Constructional Steel Research, 2019, 153: 372-384. doi: 10.1016/j.jcsr.2018.10.023
[21]	周聪. 波形钢腹板组合箱梁扭转性能研究[D]. 长沙: 湖南大学, 2019.
[22]	JENG C H, CHAO M. Unified rational formula for pre-cracking torsional stiffness of solid and hollow reinforced concrete members[J]. Engineering Structures, 2015, 99(15): 92-107.
[23]	SHEN K J, WAN S, MO Y L, et al. Behavior of single-box multi-cell box-girders with corrugated steel webs under pure torsion. Part Ⅱ: experimental and numerical studies[J]. Thin-Walled Structures, 2018, 129: 542-557.