考虑费用支付模式的公路网养护调度模型

毛新华; 王建伟; 袁长伟

doi:10.3969/j.issn.0258-2724.20200192

考虑费用支付模式的公路网养护调度模型

doi: 10.3969/j.issn.0258-2724.20200192

毛新华^1,2,3,4,,
王建伟^1,2,3,4,
袁长伟^1,2,3,4, ,

基金项目: 国家自然科学基金（71701022），教育部人文社会科学研究项目（18YJAZH120），陕西省自然科学研究计划项目（2020JQ-360），中央高校基本科研业务费专项资金（300102341513），

详细信息

作者简介:
毛新华（1986—），男，副教授，博士，研究方向为公路养护管理，E-mail：maoxinhua@chd.edu.cn

通讯作者:
袁长伟（1981—），男，教授，博士，研究方向为基础设施系统建模，E-mail：changwei@chd.edu.cn

中图分类号: U418.2
计量
- 文章访问数: 349
- HTML全文浏览量: 193
- PDF下载量: 13
- 被引次数: 0
出版历程
- 收稿日期: 2020-04-15
- 修回日期: 2020-07-16
- 网络出版日期: 2020-08-14
- 刊出日期: 2021-08-15

Maintenance Scheduling Model for Road Networks Considering Payment Modes

MAO Xinhua^{1,2,3,4
,},
WANG Jianwei^1,2,3,4,
YUAN Changwei^{1,2,3,4
, ,}

摘要

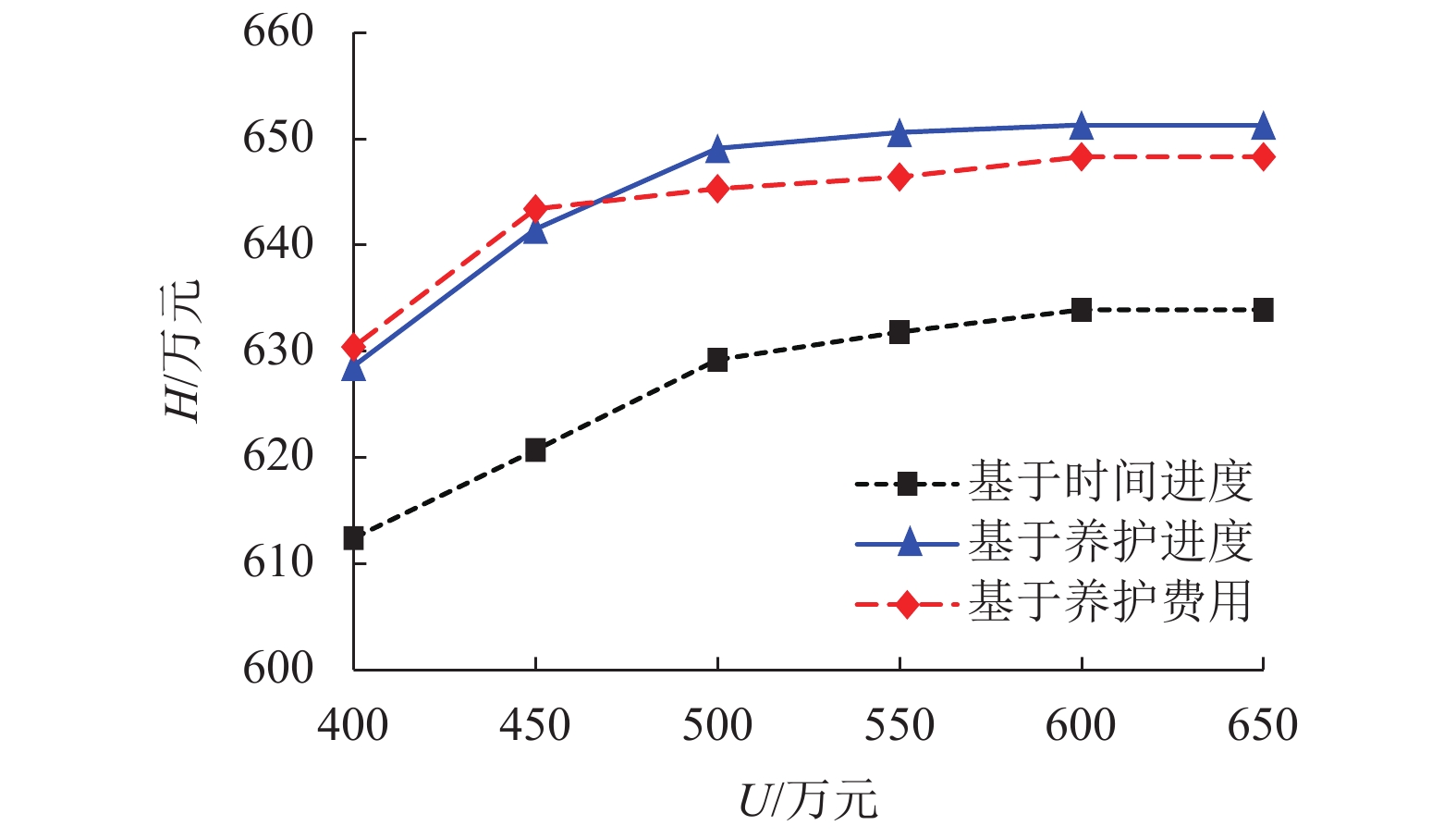
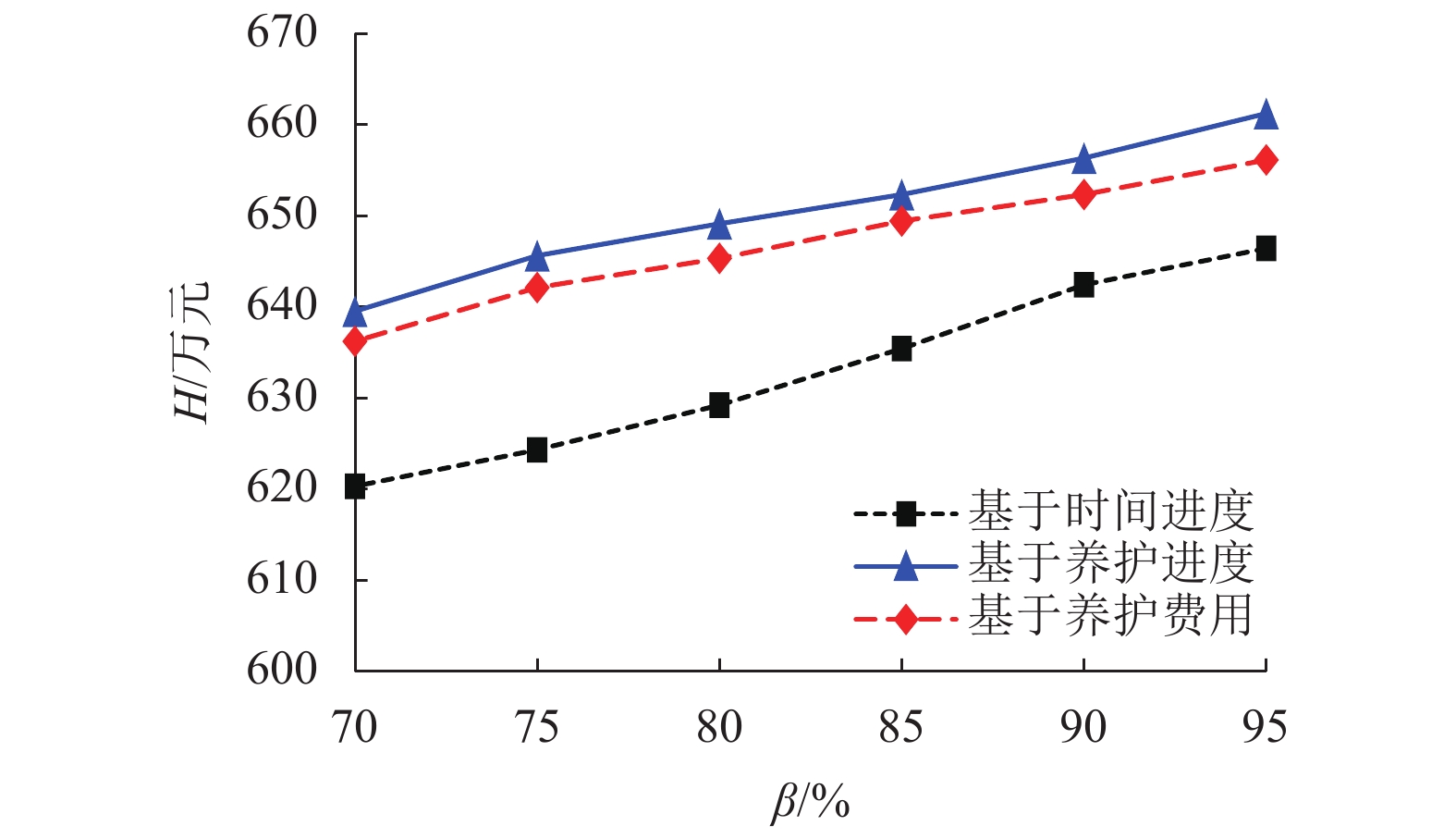
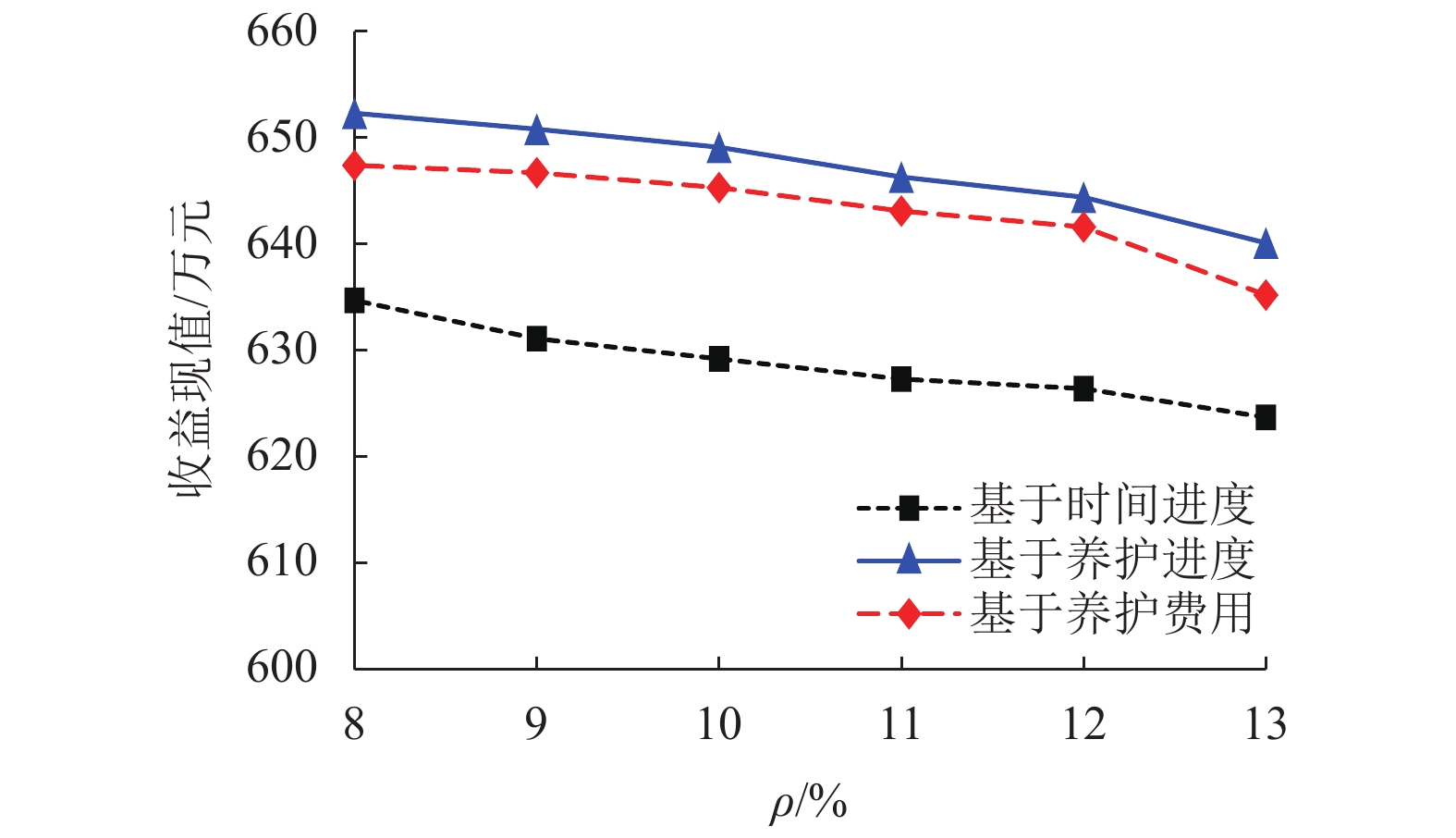
摘要: 为使公路养护承包方获取最大的收益现值，研究了业主不同费用支付模式下的路网养护调度问题. 首先，定义了基于时间进度、基于养护进度以及基于养护费用的3种支付模式；其次，构建了以承包方收益现值最大化为目标的养护调度混合整数非线性规划模型，并采用禁忌搜索算法进行求解；最后，通过案例分析验证模型和算法的有效性. 研究结果表明：在3种不同的支付模式下，指派给各养护队的路段以及各路段的养护顺序均有较大的差异；当承包方垫资能力达到一定的水平后，继续提升垫资能力不一定能获得更优的养护调度方案，且无法产生更多的收益现值；业主的支付比例与收益现值之间具有近似单调递增的关系，而折现率与收益现值之间具有负指数关系；增加养护队数量可获取更多的收益现值，但其边际收益逐步降低，只有当承包方的垫资能力和养护队数量同步增长时，才能获取更多的收益现值.
- 公路养护 /
- 混合整数规划模型 /
- 支付模式 /
- 禁忌搜索算法
Abstract: To ensure that the maintenance contractor obtains the maximum present value of revenue, the road network maintenance scheduling problem was explored under different payment modes of the client. First, three payment modes, i.e., time-based payment mode, progress-based payment mode and maintenance-cost-based payment mode were defined. Second, a mixed integer nonlinear programming model for maintenance scheduling was built with the goal of maximizing the present value of the contractor ’s revenue, and a tabu search algorithm was used to solve the model. Finally, the proposed model and algorithm were validated by a case study. Research results show that three different payment modes have large differences in terms of the road segments assigned to each maintenance crew and the maintenance sequence of each road segment. When the contractor’s advanced capital reaches a certain level, the continual rise of advance-fund capability may not be able to result in a better maintenance scheduling solution and cannot produce more present value of revenue. The relationship between the client’s payment ratio and the present value of revenue is close to monotonically increasingwhereas there is a negative exponential relationship between the discount rate and the present value of revenue. Increasing the number of maintenance crews can have more present value of revenue, but its marginal benefits are gradually reduced. Only when the contractor’s advance-fund capability and the number of maintenance crews increase synchronously, can more present value of revenue be obtained.
- road maintenance /
- mixed integer programming model /
- payment mode /
- tabu search algorithm

HTML全文

图 1 养护施工队指派列表示意

Figure 1. Maintenance crew assignment list

下载: 全尺寸图片幻灯片

图 2 养护先后顺序列表示意

Figure 2. Maintenance sequence list

下载: 全尺寸图片幻灯片

图 3 养护施工队指派变换示意

Figure 3. Maintenance crew assignment mutation

下载: 全尺寸图片幻灯片

图 4 养护先后顺序交换示意

Figure 4. Maintenance sequence swap

下载: 全尺寸图片幻灯片

图 5 承包方累计净现金流量变化

Figure 5. Variation of contractor’s cumulative net cash flow

下载: 全尺寸图片幻灯片

图 6 垫资能力敏感性分析

Figure 6. Sensitivity analysis of contractor’s advance-fund capacity

下载: 全尺寸图片幻灯片

图 7 支付比例敏感性分析

Figure 7. Sensitivity analysis ofpayment ratio

下载: 全尺寸图片幻灯片

图 8 折现率敏感性分析

Figure 8. Sensitivity analysis ofdiscount rate

下载: 全尺寸图片幻灯片

图 9 养护队数量敏感性分析

Figure 9. Sensitivity analysis of maintenance crews

下载: 全尺寸图片幻灯片

表 1 各路段的养护工期、成本及定额

Table 1. Duration, maintenance cost and quota of each link

n	线路编号	d_n/d	c_n/万元	w_n/万元	n	线路编号	d_n/d	c_n/万元	w_n/万元	n	线路编号	d_n/d	c_n/万元	w_n/万元
1	A	13	69	96	9	I	12	63	88	17	Q	15	80	112
2	B	10	51	72	10	J	14	74	104	18	R	11	57	80
3	C	12	63	88	11	K	10	51	72	19	S	16	86	120
4	D	14	74	104	12	L	8	40	56	20	T	17	91	128
5	E	17	91	128	13	M	10	51	72	21	U	17	91	128
6	F	15	80	112	14	N	11	57	80	22	V	15	80	112
7	G	13	69	96	15	O	11	57	80	23	W	17	91	128
8	H	14	74	104	16	P	13	69	96	24	X	11	57	80

下载: 导出CSV

表 2 最优养护调度方案

Table 2. Optimal maintenance scheduling schemes

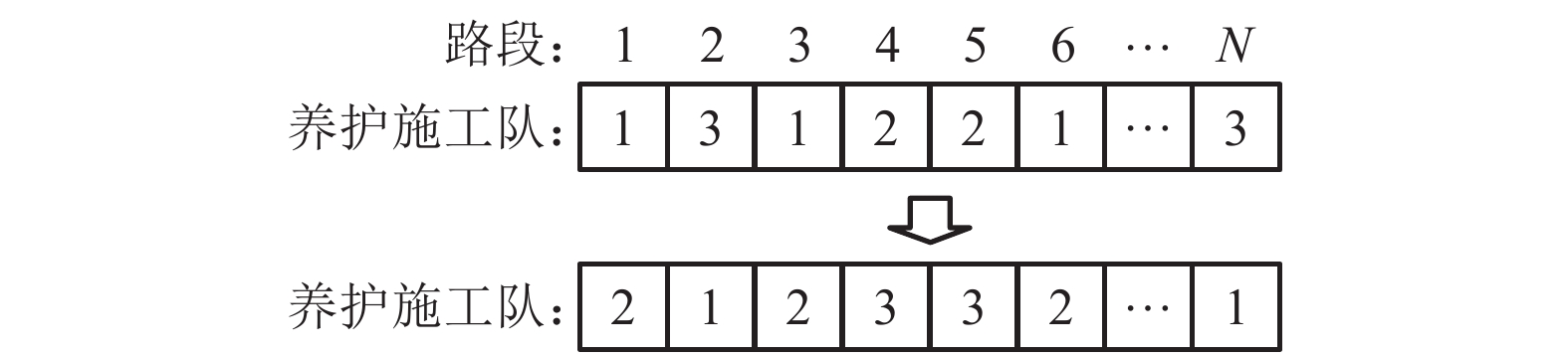
支付模式	最优养护调度方案	支付方案	H/万元
基于时间进度	养护队1：N—L—K—P—E—D—W—J 养护队2：V—C—Q—F—G—O—T—H 养护队3：M—X—A—B—R—S—I—U	支付时间：第29、55、87、105天，支付额（万元）：431.0，456.0，444.0，1014.0	629.2
基于养护进度	养护队1：W—V—J—P—H—R—M—L 养护队2：F—T—U—D—C—G—I 养护队3：S—E—Q—A—N—O—X—K—B	支付时间、：第30、58、88、105 ，支付额（万元）：659.0，498.0，553.0，635.0	649.1
基于养护费用	养护队1：U—W—F—G—A—C—R—M 养护队2：E—Q—H—J—P—X—B—L 养护队3：T—S—V—D—I—O—N—K	支付时间：第33、57、84、105天，支付额（万元）：526.0，476.0，551.0，792.0	645.3

下载: 导出CSV

参考文献(21)

HACKL J, ADEY B T, LETHANH N. Determination of near-optimal restoration programs for transportation networks following natural hazard events using simulated annealing[J]. Computer-Aided Civil and Infrastructure Engineering, 2018, 33: 618-637.

CERAVOLO R, MIRAGLIA G, SURACE C. Strategy for the maintenance and monitoring of electric road infrastructures based on recursive lifetime prediction[J]. Journal of Civil Structural Health Monitoring, 2017, 7: 303-314. doi: 10.1007/s13349-017-0227-6

YU B, GUO Z, PENG Z, et al. Agent-based simulation optimization model for road surface maintenance scheme[J]. Journal of Transportation Engineering,Part B:Pavements, 2019, 145(1): 1-9.

FONTAINE P, MINNER S. A dynamic discrete network design problem for maintenance planning in traffic networks[J]. Annals of Operations Research, 2017, 253(2): 757-772. doi: 10.1007/s10479-016-2171-y

SANTOS J, FERREIRA A, FLINTSCH G, et al. A multi-objective optimisation approach for sustainable pavement management[J]. Structure and Infrastructure Engineering, 2018, 14(7): 854-868. doi: 10.1080/15732479.2018.1436571

ZHANG L, FU L, GU W, et al. A general iterative approach for the system-level joint optimization of pavement maintenance,rehabilitation,and reconstruction planning[J]. Transportation Research Part B:Methodological, 2017, 105: 378-400.

CHU J C, HUANG K H. Mathematical programming framework for modeling and comparing network-level pavement maintenance strategies[J]. Transportation Research Part B:Methodological, 2018, 109: 1-25.

TORRES-MACHI C, PELLICER E, YEPES V, et al. Towards a sustainable optimization of pavement maintenance programs under budgetary restrictions[J]. Journal of Cleaner Production, 2017, 148: 90-102.

DENYSIUK R, MOREIRA A V, MATOS J C, et al. Two-stage multiobjective optimization of maintenance scheduling for pavements[J]. Journal of Infrastructure Systems, 2017, 23(3): 04017001.1-04017001.12.

ZHANG W, WANG N, NICHOLSON C. Resilience-based post-disaster recovery strategies for road-bridge networks[J]. Structure and Infrastructure Engineering, 2017, 13(11): 1404-1413. doi: 10.1080/15732479.2016.1271813

LI Y, DONG Y, FRANGOPOL D M, et al. Long-term resilience and loss assessment of highway bridges under multiple natural hazards[J]. Structure and Infrastructure Engineering, 2020, 16(4): 626-641. doi: 10.1080/15732479.2019.1699936

LI Z, JIN C, HU P, et al. Resilience-based transportation network recovery strategy during emergency recovery phase under uncertainty[J]. Reliability Engineering & System Safety, 2019, 188: 503-514.

YEPES V, TORRES-MACHI C, CHAMORRO A, et al. Optimal pavement maintenance programs based on a hybrid greedy randomized adaptive search procedure algorithm[J]. Journal of Civil Engineering and Management, 2016, 22(4): 540-550. doi: 10.3846/13923730.2015.1120770

SCHOBI R, CHATZI E N. Maintenance planning using continuous-state partially observable Markov decision processes and non-linear action models[J]. Structure and Infrastructure Engineering, 2016, 12(8): 977-994.

KUHN K D. Network-level infrastructure management using approximate dynamic programming[J]. Journal of Infrastructure Systems, 2010, 16(2): 103-111. doi: 10.1061/(ASCE)IS.1943-555X.0000019

MEDURY A, MADANAT S. Incorporating network considerations into pavement management systems:a case for approximate dynamic programming[J]. Transportation Research Part C:Emerging Technologies, 2013, 33: 134-150.

DURANGO-COHEN P L, SARUTIPAND P. Maintenance optimization for transportation systems with demand responsiveness[J]. Transportation Research Part C:Emerging Technologies, 2009, 17(4): 337-348.

OZER H, YANG R, AL-QADI I L. Quantifying sustainable strategies for the construction of highway pavements in Illinois[J]. Transportation Research Part D:Transport and Environment, 2017, 51: 1-13.

何正文,郑维博,刘人境. 不同支付条件银行授信约束折现流项目调度[J]. 系统工程理论与实践,2016,36(8): 2013-2023. doi: 10.12011/1000-6788(2016)08-2013-11

HE Zhengwen, ZHENG Weibo, LIU Renjing. Creditconstrained project scheduling with discounted cash flow under different payment terms[J]. System Engineering−Theory and Practice, 2016, 36(8): 2013-2023. doi: 10.12011/1000-6788(2016)08-2013-11

NABER A. Resource-constrained project scheduling with flexible resource profiles in continuous time[J]. Computers & Operations Research, 2017, 84: 33-45.

SHAO S, XU S X, HUANG G Q. Variable neighborhood search and tabu search for auction-based waste collection synchronization[J]. Transportation Research Part B:Methodological, 2020, 133(3): 1-20.

施引文献

附加材料(0)

访问统计