极限分析法求解含软弱夹层边坡稳定性

徐鹏; 尚念林; 鲍晶晶; 李婷

doi:10.3969/j.issn.0258-2724.20200156

极限分析法求解含软弱夹层边坡稳定性

doi: 10.3969/j.issn.0258-2724.20200156

徐鹏^1,,
尚念林²,
鲍晶晶³,
李婷^{1, 4, ,}

1.
石家庄铁道大学省部共建交通工程结构力学行为与系统安全国家重点实验室，河北石家庄 050043
2.
山东宝泰置业有限公司，山东济南 271100
3.
西南交通大学土木工程学院，四川成都 610031
4.
石家庄铁道大学土木工程学院，河北石家庄 050043

基金项目: 国家自然科学基金(52108331)；河北省自然科学基金(E2021210010)；河北省高等学校科学技术研究项目(ZD2021096，QN2021127)；河北省引进留学人员资助项目（C20210305）

详细信息

作者简介:
徐鹏（1988—），男，讲师，研究方向为道路与铁道工程，E-mail：bk20090201@my.swjtu.edu.cn

通讯作者:
李婷（1992—），女，讲师，研究方向为地基变形控制与路基工程等，E-mail：liting9225@126.com

中图分类号: TU41
计量
- 文章访问数: 369
- HTML全文浏览量: 174
- PDF下载量: 39
- 被引次数: 27
出版历程
- 收稿日期: 2020-04-02
- 修回日期: 2020-09-04
- 刊出日期: 2020-09-16

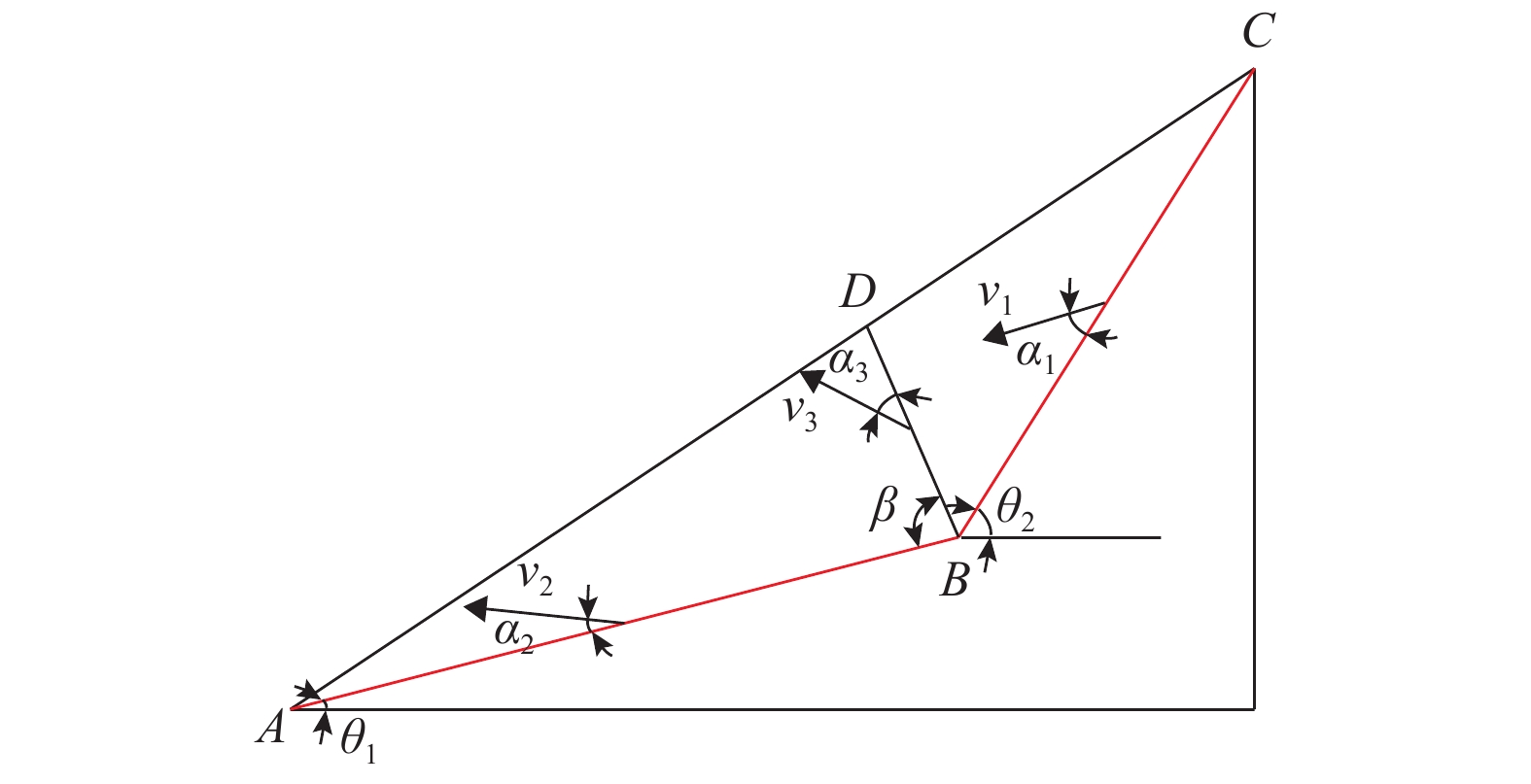
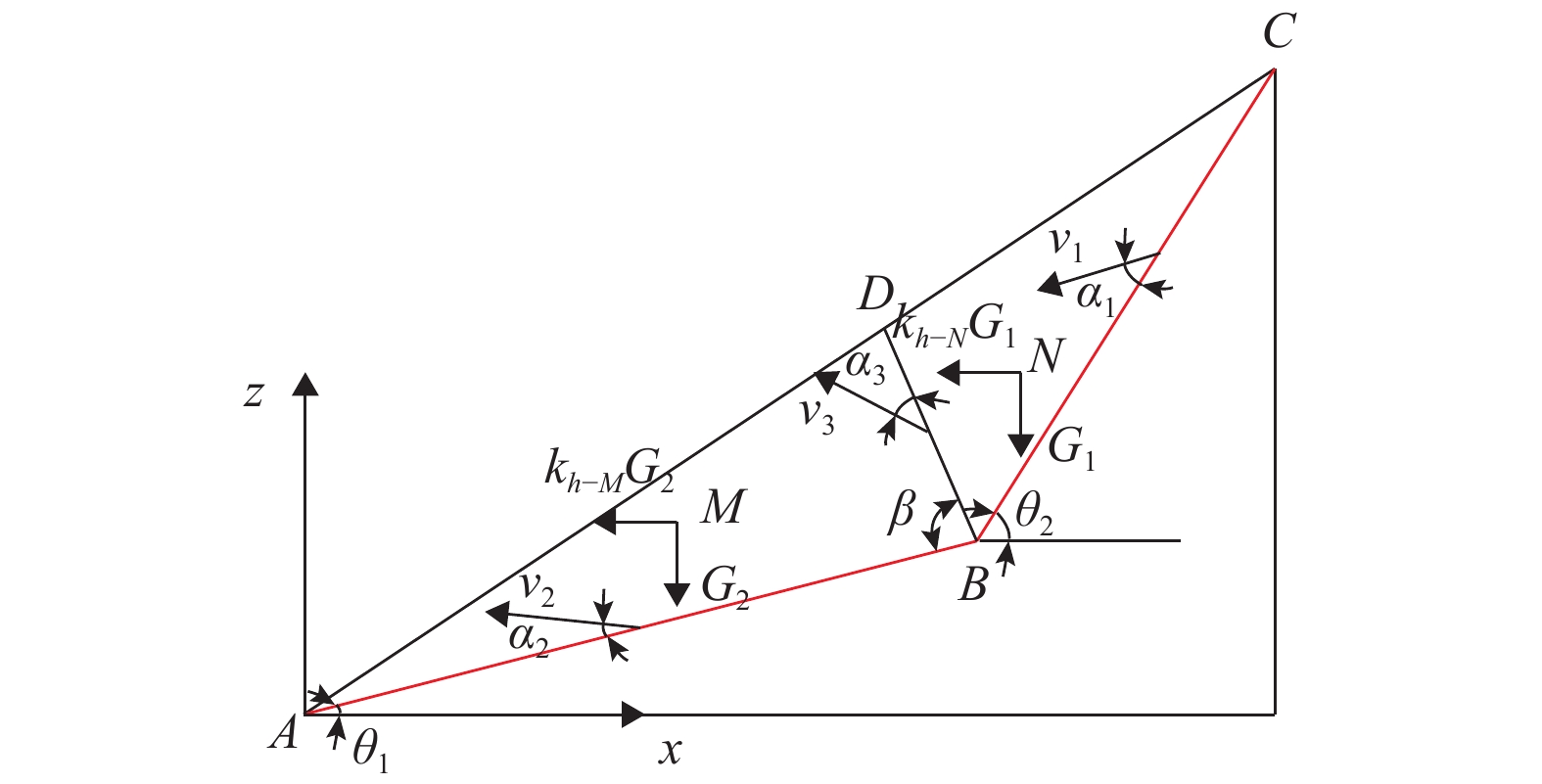
Stability Analysis of Slopes with Weak Layers Using Limit Analysis Method

XU Peng^1
,,
SHANG Nianlin²,
BAO Jingjing³,
LI Ting^{1, 4
, ,}

1.
State Key Laboratory of Mechanical Behavior and System Safety of Traffic Engineering Structures, Shijiazhuang Tiedao University, Shijiazhuang 050043, China
2.
Shandong Baotai Real Estate Co., Ltd., Jinan 271100, China
3.
School of Civil engineering, Southwest Jiaotong University, Chengdu 610031, China
4.
School of Civil engineering, Shijiazhuang Tiedao University, Shijiazhuang 050043, China

摘要

摘要:
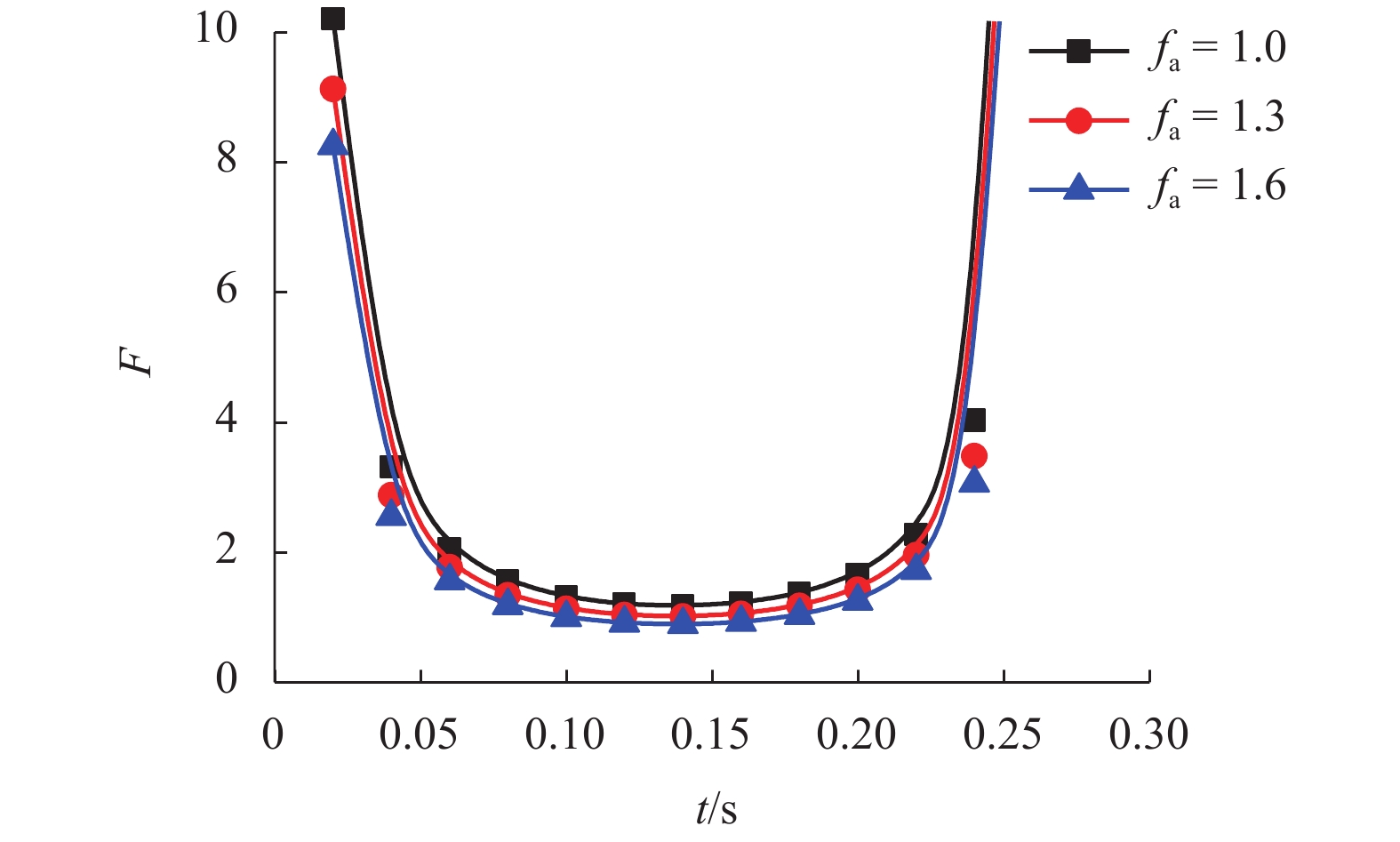
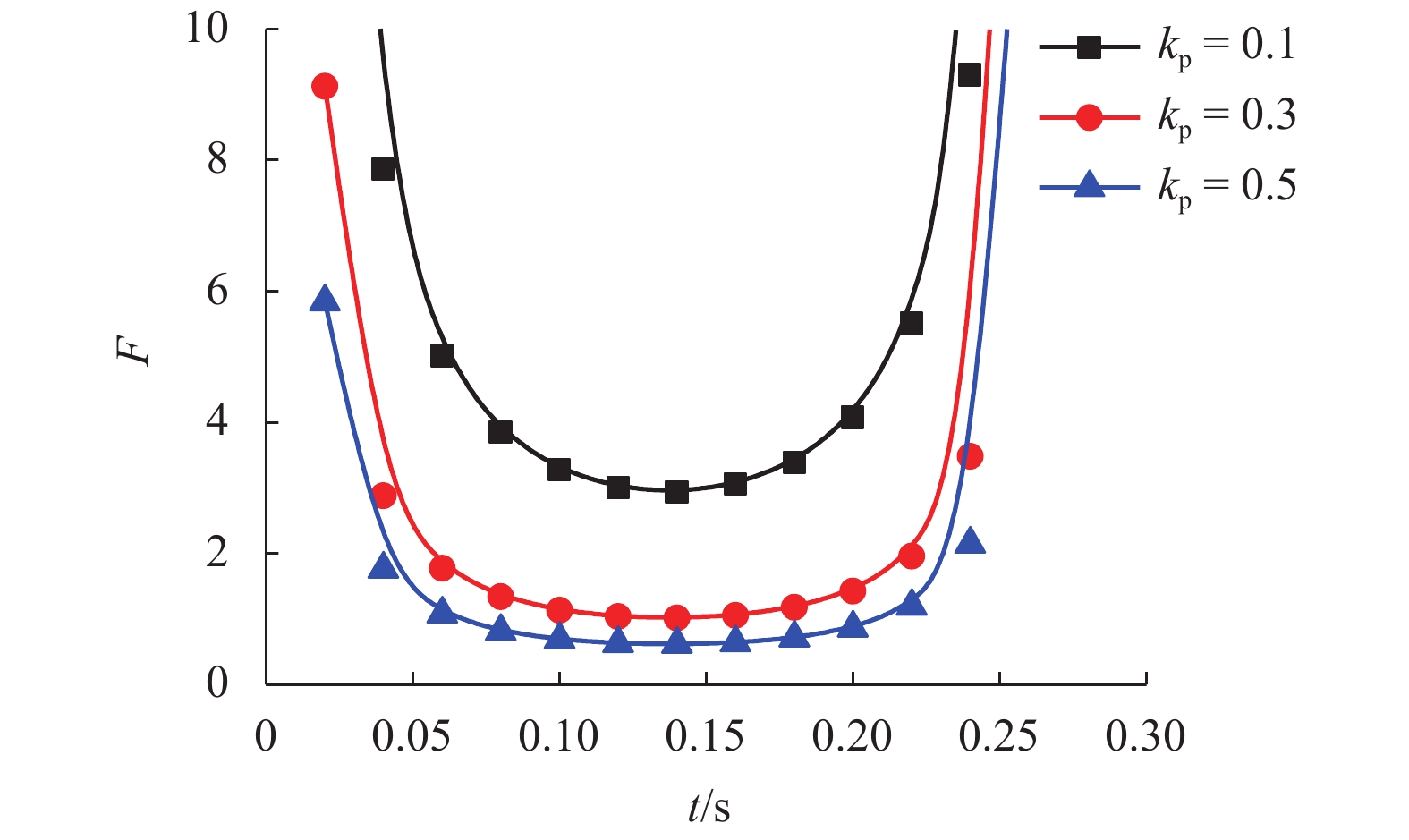
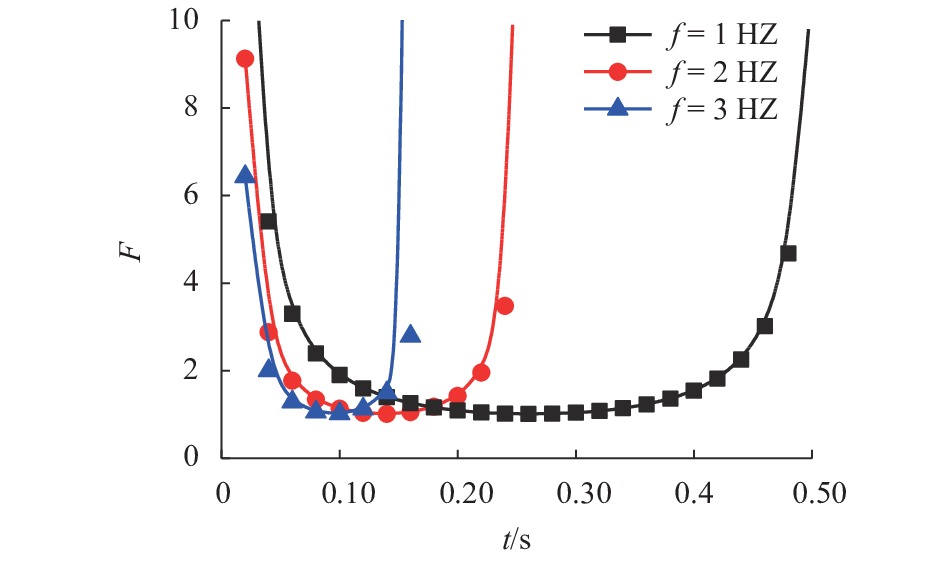
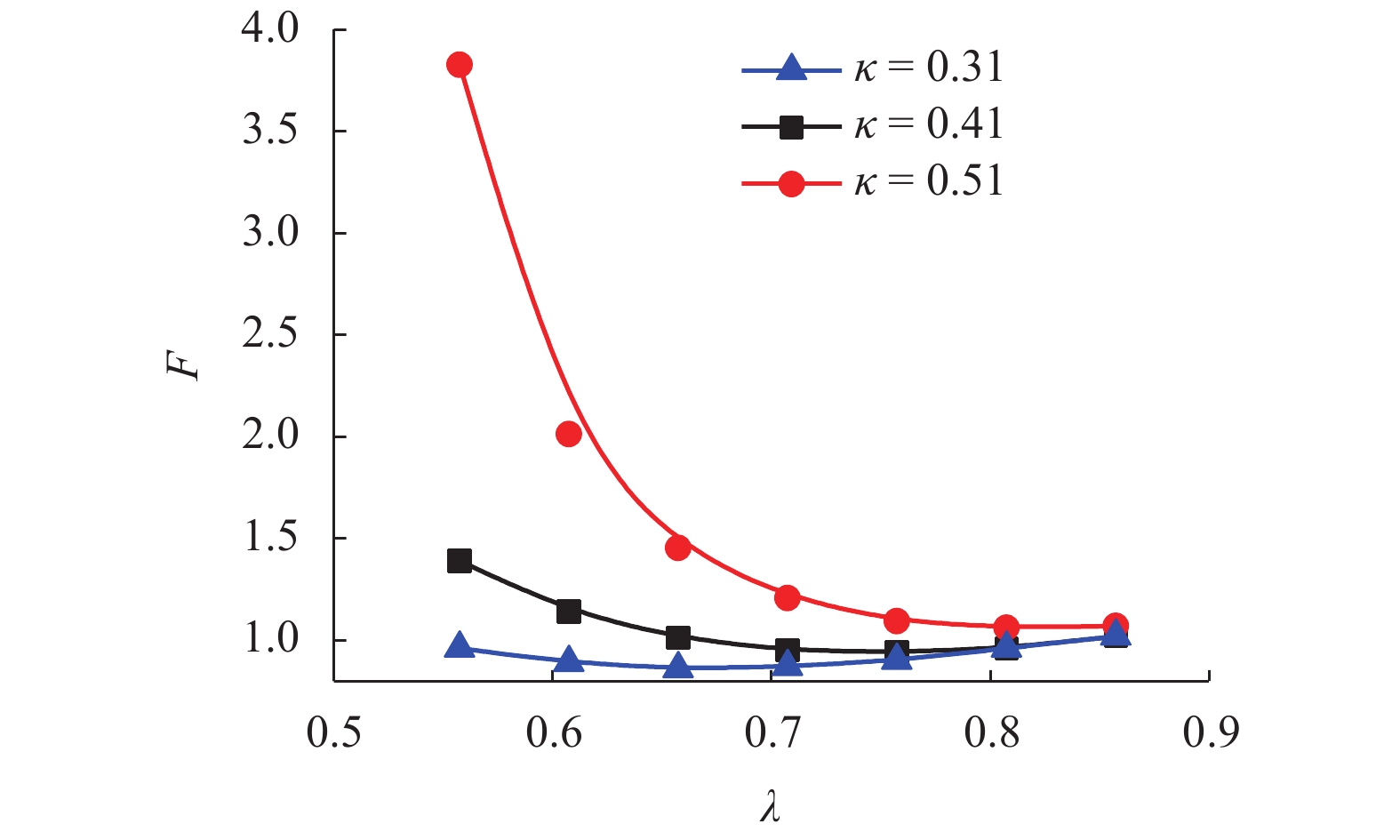
软弱夹层对边坡的稳定性影响显著，目前设计中通常采用极限平衡法计算边坡的稳定性，其在求解中需要建立多个平衡方程. 为了分析含软弱夹层边坡的稳定性，首先，采用极限分析法建立了计算模型；其次，通过极限平衡法验证了求解的准确性；最后，分析了荷载、夹层形状、夹层强度等对稳定性的影响. 研究结果表明：边坡安全系数随着外荷载强度的增大而减小，其中，当加速度放大系数由1.0增大为1.6时，安全系数由1.20降为0.89；当外荷载频率越大时，边坡越易提前产生破坏；软弱夹层形状对边坡安全系数影响显著，特别是当其靠近坡顶与坡面时；安全系数随着软弱夹层摩擦角与黏聚力的减小而近似线性降低，其中，当黏聚力由9 kPa降为5 kPa时，安全系数降低约30%.
- 软弱夹层 /
- 边坡 /
- 极限平衡法 /
- 极限分析法 /
- 安全系数
Abstract:
Weak layers have a significant effect on the stability of slopes. The stability of slopes is usually calculated by the limit equilibrium method in current designs, in which multiple equilibrium equations need to be established and solved. Compared with the limit equilibrium method, the limit analysis method is more rigorous, and requires only one energy equation to be solved. In order to analyze the stability of slopes with weak interlayers, a stability calculation model was established by the limit analysis method, and then the accuracy of the solution was verified by the limit equilibrium method. Finally, the effects of load, weak layer shape, and weak layer strength on stability were analyzed. The results show that the slope safety factor decreases with an increase in the load intensity. When the acceleration amplification factor increases from 1.0 to 1.6 the safety factor decreases from 1.20 to 0.89. With a higher frequency of the external load, the slope is easier to be damaged in advance. Besides, the shape of the weak layer has a significant effect on the slope safety factor, especially when it is close to the top and surface of the slope. The safety factor decreases approximately linearly with the decrease of the friction angle and cohesion of weak layers. When the cohesion strength decreases from 9 kPa to 5 kPa, the safety factor decreases by about 30%.
- weak layer /
- slope /
- limit equilibrium method /
- limit analysis method /
- safety factor

HTML全文

图 1 边坡模型

Figure 1. Slope model

下载: 全尺寸图片幻灯片

图 2 速度矢量图

Figure 2. Diagram of velocity vectors

下载: 全尺寸图片幻灯片

图 3 力学模型

Figure 3. Mechanical model

下载: 全尺寸图片幻灯片

图 4 f_a对F的影响

Figure 4. Effect of f_a on F

下载: 全尺寸图片幻灯片

图 5 k_p对F的影响

Figure 5. Effect of k_p on F

下载: 全尺寸图片幻灯片

图 6 f对F的影响

Figure 6. Effect of f on F

下载: 全尺寸图片幻灯片

图 7 软弱夹层形状对F的影响

Figure 7. Effect of slip zone shapes on F

下载: 全尺寸图片幻灯片

图 8 c和F的关系曲线

Figure 8. Ralation curves of c and F

下载: 全尺寸图片幻灯片

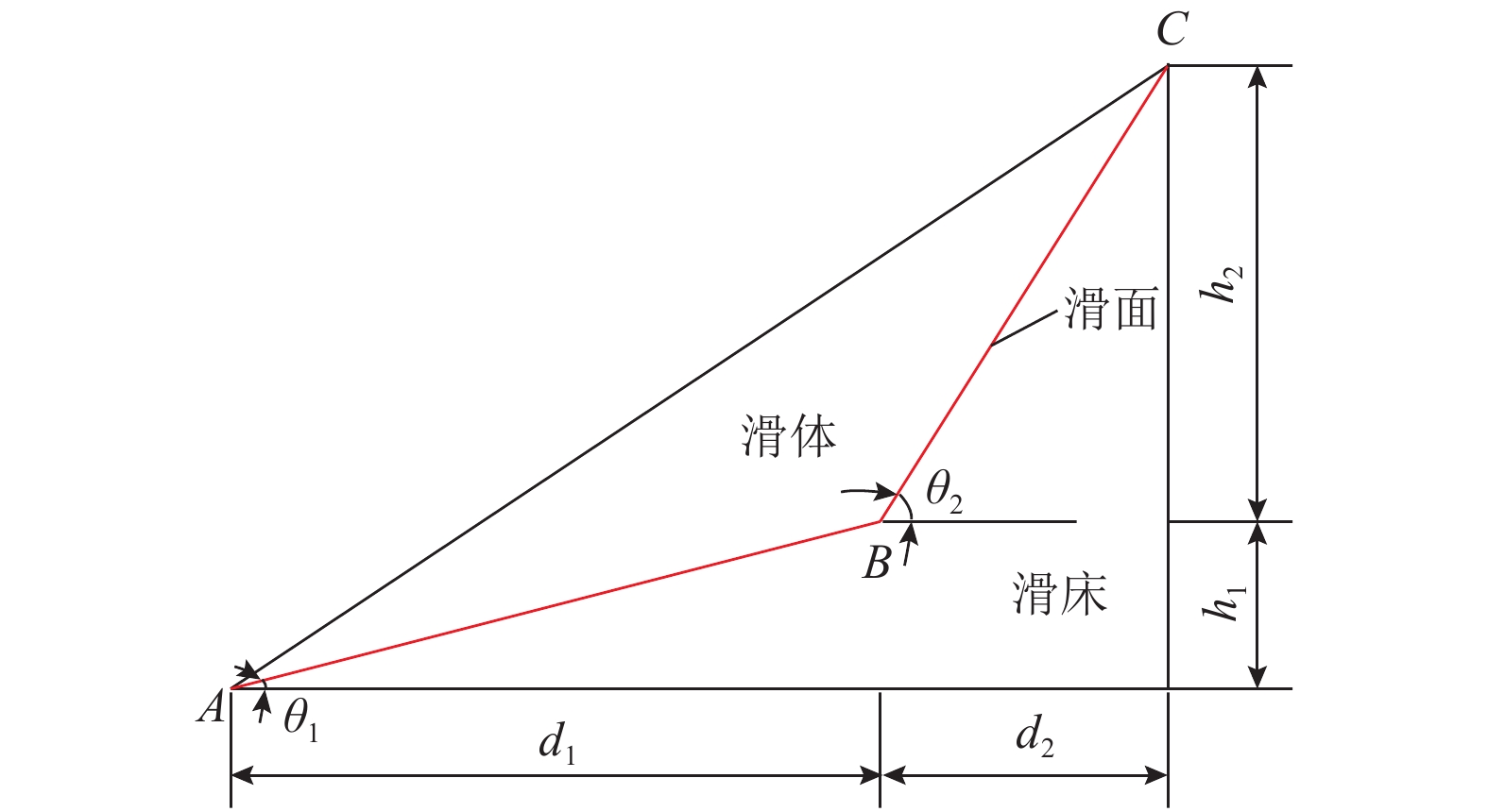
表 1 计算结果

Table 1. Calculation results

工况	k_P	d₁ /m	d₂ /m	h₁ /m	h₂ /m	γ /（kN•m⁻³）	c /kPa	φ /（^o）	安全系数
工况	k_P	d₁ /m	d₂ /m	h₁ /m	h₂ /m	γ /（kN•m⁻³）	c /kPa	φ /（^o）	本文方法	摩根斯坦-普莱斯法
1	0	11.59	4.95	3.11	4.95	20	6	30	2.02	2.00
2	0.2	11.59	4.95	3.11	4.95	20	6	30	1.35	1.32
3	0.4	11.59	4.95	3.11	4.95	20	6	30	0.99	0.97
4	0.2	11.59	4.95	3.11	4.95	20	6	20	1.05	1.03
5	0.2	9.78	3.54	2.08	3.54	20	6	20	1.22	1.19
注：表中本文方法计算结果为时间 t 内的最小值.

下载: 导出CSV

表 2 计算结果

Table 2. Calculation results

k_P	d₁ /m	d₂ /m	h₁ /m	h₂ /m	γ /（kN•m⁻³）	c /kPa	φ /（^o）	安全系数
k_P	d₁ /m	d₂ /m	h₁ /m	h₂ /m	γ /（kN•m⁻³）	c /kPa	φ /（^o）	本文方法	二楔块法^[16]	有限元
0	53.56	90.18	1.03	30.00	10.2	0	17	1.36	1.35	1.39

下载: 导出CSV

参考文献(17)

[1]	刘汉香,许强,周飞,等. 含软弱夹层斜坡地震动力响应特性的振动台试验研究[J]. 岩石力学与工程学报,2015,34(5): 994-1005. LIU Hanxiang, XU Qiang, ZHOU Fei, et al. Shaking table test for seismic responses of slopes with a weak interlayer[J]. Chinese Journal of Rock Mechanics and Engineering, 2015, 34(5): 994-1005.
[2]	闫孔明,刘飞成,朱崇浩,等. 地震作用下含倾斜软弱夹层斜坡场地的动力响应特性研究[J]. 岩石力学与工程学报,2017,36(11): 2686-2698. YAN Kongming, LIU Feicheng, ZHU Chonghao, et al. Dynamic responses of slopes with intercalated soft layers under seismic excitations[J]. Chinese Journal of Rock Mechanics and Engineering, 2017, 36(11): 2686-2698.
[3]	唐云波,刘炎,相晨琳. 汶川地区含软弱层岩质边坡地震响应研究[J]. 路基工程,2018(6): 114-118. TANG Yunbo, LIU Yan, XIANG Chenlin. Research on seismic response of rock slope with weak layer in Wenchuan region[J]. Subgrade Engineering, 2018(6): 114-118.
[4]	刘晋南, 蒋鑫, 邱延峻, 等. 水平地震荷载作用下斜坡路基动力稳定性分析. 中外公路, 2010, 30（5）: 42-45. LIU Jinnan, JIANG Xin, QIU Yanjun. Analysis of dynamic stability of subgrade slope under horizontal earthquake load [J]. Journal of China & Foreign Highway, 2010, 30(5): 42-45.
[5]	CHEN W F. Limit analysis and soil plasticity[M]. Amsterdam: Elsevier Scientific Company, 1975.
[6]	XU P, HATAMI K, JIANG G. Seismic rotational stability analysis of reinforced soil retaining walls[J]. Computers and Geotechnics, 2020, 118(4): 103297.1-103297.10.
[7]	MICHALOWSKI R L. Limit analysis and stability charts for 3D slope failures[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2010, 136(4): 583-593. doi: 10.1061/(ASCE)GT.1943-5606.0000251
[8]	何思明,张晓曦,吴永. 基于上限定理的边坡潜在破裂面确定方法与稳定性判识研究[J]. 岩土力学,2012,33(1): 162-166. doi: 10.3969/j.issn.1000-7598.2012.01.025 HE Siming, ZHANG Xiaoxi, WU Yong. Study of stability discriminant of slope and position determination of potential sliding surface based on upper bound theorem[J]. Rock and Soil Mechanics, 2012, 33(1): 162-166. doi: 10.3969/j.issn.1000-7598.2012.01.025
[9]	UTILI S. Investigation by limit analysis on the stability of slopes with cracks[J]. Géotechnique, 2013, 63(2): 140-154.
[10]	XU P, HATAMI K, JIANG G. Seismic sliding stability analysis of reinforced soil retaining walls. Geosynthetics International, 2019, 26(5), 485-496.
[11]	CHOUDHURY D, NIMBALKAR S. Seismic passive resistance by pseudo-dynamic method[J]. Geotechnique, 2006, 55(7): 517-520.
[12]	BASHA B M, BABU G L S. Seismic reliability assessment of external stability of reinforced soil walls using pseudo-dynamic method[J]. Geosynthetics International, 2009, 16(3): 197-215. doi: 10.1680/gein.2009.16.3.197
[13]	GHOSH P G. Seismic active earth pressure behind a nonvertical retaining wall using pseudo-dynamic analysis[J]. Canadian Geotechnical Journal, 2008, 45(1): 117-123. doi: 10.1139/T07-071
[14]	钱家欢. 土工原理与计算[M]. 北京: 中国水利水电出版社, 1996.
[15]	中华人民共和国住房和城乡建设部. 建筑边坡工程技术规范: GB 50330—2013[S]. 北京: 中国建筑工业出版社, 2014.
[16]	QIAN X D, KOERNER R M, GRAY D H. Translational failure analysis of landfills[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2003, 129(6): 506-519. doi: 10.1061/(ASCE)1090-0241(2003)129:6(506)
[17]	周炜,李海波,刘亚群,等. 地震作用下顺层岩质边坡锚固特性的拟动力分析[J]. 岩石力学与工程学报,2016,35(增刊2): 3570-3576. ZHOU Wei, LI Haibo, LIU Yaqun, et al. Pseudo-dynamic analysis of anchored characteristics of layered rock slopes subjected to seismic loads[J]. Chinese Journal of Rock Mechanics and Engineering, 2016, 35(S2): 3570-3576.

施引文献

期刊类型引用(15)

1.	陆粤，王铭，陈嵘，李小珍，王平. 基于行车平稳性的大跨度铁路桥梁成桥线形评价方法研究. 铁道标准设计. 2024(06): 44-51 . 百度学术
2.	张明金，周远洲，沈孔健，苑仁安，郑清刚. 常泰长江大桥主航道桥桥塔横向偏位及其控制方案研究. 桥梁建设. 2023(01): 1-8 . 百度学术
3.	黄春阳. 基于监测数据的独塔斜拉桥施工过程受力性能分析. 安徽建筑. 2023(04): 137-138+185 . 百度学术
4.	苑仁安，张明金，郑清刚，傅战工，喻济昇. 超大跨斜拉桥横桥向恒载非对称力学行为. 西南交通大学学报. 2023(03): 527-534 . 本站查看
5.	黄学漾. 双塔双索面异形塔柱斜拉桥施工控制关键技术探讨. 福建交通科技. 2023(06): 51-57 . 百度学术
6.	汪劲丰，杨松伟，亢阳阳，向华伟. 分阶段施工中钢箱梁制造参数的通用计算方法. 浙江大学学报(工学版). 2022(03): 550-557 . 百度学术
7.	李江刚，石建华，张巨生. 鳊鱼洲长江大桥南汊航道桥施工控制关键技术. 桥梁建设. 2022(04): 8-15 . 百度学术
8.	李鹏飞，王石磊，魏思聪，李毅，罗吉庆. 大型空间异形钢塔斜拉桥拉索张拉控制. 公路交通科技. 2022(10): 49-58 . 百度学术
9.	周仁忠，黄灿，郑建新. 福厦高铁泉州湾跨海大桥主桥施工控制关键技术. 桥梁建设. 2022(06): 131-139 . 百度学术
10.	黄继荣，马牛静，王荣辉，陈广韬. 叠合梁斜拉桥快速施工过程中主梁线形及索力调控精细化分析. 交通世界. 2022(36): 145-148 . 百度学术
11.	张飞，黄福云，王燕. V型墩刚构桥悬浇施工中应变修正与应力监测. 山东建筑大学学报. 2020(03): 36-41 . 百度学术
12.	廖贵星，严汝辉，胡辉跃，张燕飞，徐恭义. 武汉青山长江公路大桥中跨钢箱梁施工控制关键技术. 桥梁建设. 2020(S1): 126-132 . 百度学术
13.	高玉峰，杨永清，蒲黔辉，李晓斌. 桥梁施工监测控制理论及工程应用2019年度研究进展. 土木与环境工程学报(中英文). 2020(05): 98-105 . 百度学术
14.	董晓兵，余友江. 青海哇加滩黄河特大桥施工控制. 桥梁建设. 2019(04): 96-101 . 百度学术
15.	梅秀道，卢亦焱. 基于索长的大跨径斜拉桥施工控制计算方法及应用. 桥梁建设. 2019(06): 42-47 . 百度学术