约束下考虑坐标分量误差相关性的直线拟合

宋占峰; 郭捷佳; 李军

doi:10.3969/j.issn.0258-2724.20200120

约束下考虑坐标分量误差相关性的直线拟合

doi: 10.3969/j.issn.0258-2724.20200120

中南大学土木工程学院，湖南长沙 410075

基金项目: 国家自然科学基金（51678574）

详细信息

作者简介:
宋占峰（1973—），男，副教授，博士，研究方向为道路与铁道线路优化设计方法，E-mail：songzhanfeng@csu.edu.cn

通讯作者:
李军（1973—），男，副教授，博士，研究方向为道路与铁道工程信息化及优化，E-mail：lijun_csu@csu.edu.cn

中图分类号: U212.3
计量
- 文章访问数: 432
- HTML全文浏览量: 242
- PDF下载量: 20
- 被引次数: 0
出版历程
- 收稿日期: 2020-03-24
- 修回日期: 2020-08-03
- 网络出版日期: 2020-08-24
- 刊出日期: 2020-08-24

Fitting a Straight-Line to Data Points with Correlated Noise Between Coordinate Components under Constraints

School of Civil Engineering，Central South University，Changsha 410075，China

摘要

摘要:
直线拟合在曲线拟合研究及工程实践中受到广泛关注，常用的普通最小二乘和正交最小二乘忽略了坐标分量误差相关性的存在. 基于此，首先论证了在铁路线路整正中全站仪测量坐标点的纵横坐标间存在误差相关性，同时线路中直线的拟合受到相邻线元的约束；然后，基于极大似然估计及拉格朗日条件极值原理，推导出了顾及约束和坐标分量误差相关性的直线拟合通用模型，并给出了高斯-牛顿迭代算法搜索最优解；最后，采用了实测的数据进行了验证及测试. 试验结果表明：该方法能在任何误差分布情况下考虑约束估计直线参数及其精度；考虑坐标相关误差时，参数估计精度在约束及无约束下分别提高了9.2%和2.7%；高斯-牛顿算法在约束及无约束情况下分别仅6次及3次迭代就搜索出最优直线.
- 直线 /
- 曲线拟合 /
- 参数估计 /
- 误差相关 /
- 条件极值 /
- 算法
Abstract:
Straight-line fitting has received extensive attention both in curve fitting research and engineering practice. The methods of ordinary least squares and orthogonal least squares fitting ignore the existence of the observation error correlation. The coordinate pairs of surveying points, obtained by a total station in railway realignment, not only have different levels of precision but also have correlated noise. Meanwhile, straight-line fitting is usually under constraints in the realignment. Thus, a straight-line fitting model was derived based on the maximum likelihood estimation and Lagrange conditional extremum theory, considering constraints and correlated noise between coordinate components, and a Gauss-Newton algorithm was presented to search for the optimum. The method was tested with the field surveying data. Experimental results show that the proposed fitting method is capable of estimating straight-line parameters and their precisions in all circumstances by specifying stochastic models. When considering correlated noise, the precision of estimated parameters improve 9.2% with a constraint and improve 2.7% without constraints, respectively. The Gauss-Newton algorithm takes only 6 and 3 iteration times with a constraint and without constraints respectively, for locating the optimum straight-line.
- straight-line /
- curve fitting /
- parameter estimation /
- correlated noise /
- conditional extremum /
- algorithm

HTML全文

图 1 全站仪测量原理

Figure 1. Measuring principle

下载: 全尺寸图片幻灯片

图 2 拟合原理

Figure 2. Fitting principle

下载: 全尺寸图片幻灯片

图 3 高斯-牛顿迭代算法

Figure 3. Gauss-Newton iteration algorithm

下载: 全尺寸图片幻灯片

图 4 约束及无约束的直线拟合

Figure 4. Straight-line fitting with a constraint and without constraint

下载: 全尺寸图片幻灯片

表 1 实地观测点坐标及采用的3种随机模型

Table 1. Coordinate pairs of field surveying data and three stochastic models for fitting

点号	x/m	y/m	C 中非零元素			P₁中非零元素			P₂中非零元素	P₃中非零元素
点号	x/m	y/m	$\sigma _x^2$/mm²	$\sigma _y^2$/mm²	${\sigma _{xy}}$/mm²	p_x	p_y	p_xy	${p_x}/{p_y}$	${p_x}/{p_y}$
1	688.639	1398.869	7.3371	9.7881	−0.8902	0.1378	0.1033	0.0125	1	10000
2	701.467	1383.525	7.3289	9.3014	−0.9080	0.1381	0.1088	0.0135	1	10000
3	714.294	1368.180	7.3340	8.8888	−0.9115	0.1381	0.1140	0.0142	1	10000
4	727.121	1352.835	7.3547	8.5485	−0.9080	0.1378	0.1185	0.0146	1	10000
5	739.953	1337.495	7.3948	8.2767	−0.9044	0.1371	0.1225	0.0150	1	10000
6	752.783	1322.152	7.4602	8.0684	−0.9071	0.1359	0.1257	0.0153	1	10000
7	765.609	1306.806	7.5584	7.9166	−0.9210	0.1342	0.1281	0.0156	1	10000
8	778.434	1291.460	7.6977	7.8126	−0.9487	0.1319	0.1299	0.0160	1	10000
9	791.262	1276.115	7.8867	7.7477	−0.9909	0.1289	0.1312	0.0165	1	10000
10	804.088	1260.770	8.1340	7.7132	−1.0462	0.1251	0.1320	0.0170	1	10000
11	816.915	1245.425	8.4471	7.7012	−1.1111	0.1207	0.1324	0.0174	1	10000
12	829.740	1230.078	8.8323	7.7054	−1.1805	0.1156	0.1325	0.0177	1	10000
13	842.564	1214.731	9.2939	7.7206	−1.2485	0.1100	0.1324	0.0178	1	10000
14	855.389	1199.384	9.8346	7.7437	−1.3087	0.1040	0.1321	0.0176	1	10000
15	868.213	1184.036	10.4556	7.7729	−1.3546	0.0979	0.1316	0.0171	1	10000
16	881.043	1168.694	11.1562	7.8077	−1.3803	0.0916	0.1309	0.0162	1	10000
17	893.875	1153.353	11.9355	7.8489	−1.3806	0.0855	0.1301	0.0150	1	10000
18	906.703	1138.009	12.7917	7.8981	−1.3511	0.0796	0.1289	0.0136	1	10000
19	919.537	1122.670	13.7218	7.9569	−1.2880	0.0740	0.1276	0.0120	1	10000
20	932.371	1107.331	14.7236	8.0277	−1.1886	0.0687	0.1261	0.0102	1	10000

下载: 导出CSV

表 2 顾及约束和相关误差的直线拟合过程

Table 2. Process of straight-line fitting with both a constraint and correlated noise

迭代数/次	$\hat a$	$\hat b$/m	${\hat \sigma _0}$/mm	${\sigma _a}$	${\sigma _b}$/mm	w/mm
0	−0.681654264	2210.153480	59093.318880	6.14777 × 10⁻²	93044.287650	−479524.603400
1	−0.935165106	2013.498778	5844.096808	6.07990 × 10⁻³	9201.714082	−59428.755230
2	−1.146887043	2183.687057	448.743795	9.66425 × 10⁻⁴	1148.244207	−9789.990571
3	−1.195130784	2221.779805	10.362946	3.19907 × 10⁻⁵	35.137584	−394.045005
4	−1.197201392	2223.403509	16.492003	5.52543 × 10⁻⁵	59.714483	−0.691388
5	−1.197204886	2223.406205	16.525002	5.55595 × 10⁻⁵	60.003229	−0.000002
6	−1.197204886	2223.406205	16.525002	5.55598 × 10⁻⁵	60.003515	0

下载: 导出CSV

表 3 约束下3种随机模型拟合直线的参数估值及其精度

Table 3. Parameter estimation of fitting line and their precisions of three stochastic models with constraints

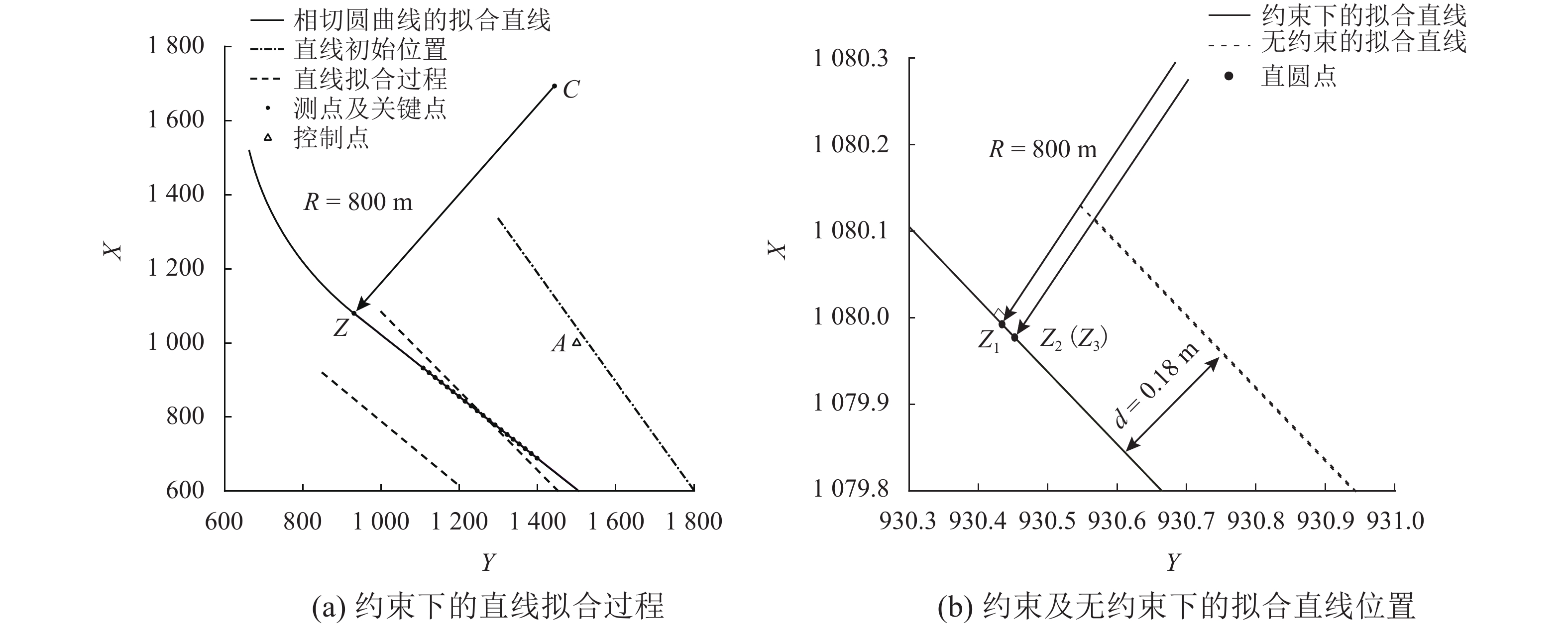
随机模型	$\hat a$	$\hat b$/m	${\hat \sigma _0}$/mm	${\sigma _a}$	${\sigma _b}$/mm	x_Z/m	y_Z/m	迭代数/次	耗时/s
P₁	−1.19720489	2223.4062	16.525	5.55598 × 10⁻⁵	60.0	1079.9809	930.4478	6	0.494
P₂	−1.19722236	2223.4251	49.031	6.12012 × 10⁻⁵	66.1	1079.9772	930.4522	6	0.503
P₃	−1.19722233	2223.4250	76.478	6.12012 × 10⁻⁵	66.1	1079.9772	930.4522	6	0.496

下载: 导出CSV

表 4 无约束下3种随机模型拟合直线的参数估值及其精度

Table 4. Parameter estimation of line fitting and their precisions of three stochastic models without constraint

随机模型	$\hat a$	$\hat b$/m	${\hat \sigma _0}$/mm	${\sigma _a}$	${\sigma _b}$/mm	迭代数/次	耗时/s
P₁	−1.196269322	2222.672000	2.293655	3.10233 × 10⁻⁵	25.008852	3	0.461
P₂	−1.196259074	2222.663879	6.710739	3.16316 × 10⁻⁵	25.743943	3	0.414
P₃	−1.196259065	2222.663872	0.462488	3.16316 × 10⁻⁵	25.743942	3	0.438

下载: 导出CSV

参考文献(12)

[1]	KRYSTEK M, ANTON M. A least-squares algorithm for fitting data points with mutually correlated coordinates to a straight line[J]. Measurement Science and Technology, 2011, 22(3): 035101.1-035101.9.
[2]	PETROLINI A. Linear least squares fit when both variables are affected by equal uncorrelated errors[J]. American Journal of Physics, 2014, 82(12): 1178-1185.
[3]	丁克良,沈云中,欧吉坤. 整体最小二乘法直线拟合[J]. 辽宁工程技术大学学报(自然科学版),2010,29(1): 44-47. DING Keliang, SHEN Yunzhong, OU Jikun. Methods of line-fitting based on total least-squares[J]. Journal of Liaoning Technical University (Natural Science), 2010, 29(1): 44-47.
[4]	宋占峰,彭欣,吴清华. 基于中线坐标的地铁调线优化算法[J]. 西南交通大学学报,2014,49(4): 656-661. doi: 10.3969/j.issn.0258-2724.2014.04.015 SONG Zhanfeng, PENG Xin, WU Qinghua. Optimization algorithm for horizontal realignment based on coordinate of metro centerline[J]. Journal of Southwest Jiaotong University, 2014, 49(4): 656-661. doi: 10.3969/j.issn.0258-2724.2014.04.015
[5]	宋占峰,王健,李军. 缓和曲线正交拟合的Levenberg-Marquardt算法[J]. 西南交通大学学报,2020,55(1): 144-149. doi: 10.3969/j.issn.0258-2724.20190130 SONG Zhanfeng, WANG Jian, LI Jun. Levenberg-Marquardt algorithm for orthogonal fitting of transition curves[J]. Journal of Southwest Jiaotong University, 2020, 55(1): 144-149. doi: 10.3969/j.issn.0258-2724.20190130
[6]	KARL P. On lines and planes of closest fit to systems of points in space[J]. Philosophical Magazine, 1901, 2(11): 559-572.
[7]	刘经南,曾文宪,徐培亮. 整体最小二乘估计的研究进展[J]. 武汉大学学报(信息科学版),2013,38(5): 505-512. LIU Jingnan, ZENG Wenxian, XU Peiliang. Overview of total least squares methods[J]. Geomatics and Information Science of Wuhan University, 2013, 38(5): 505-512.
[8]	KRYSTEK M, ANTON M. A weighted total least-squares algorithm for fitting a straight line[J]. Measurement Science and Technology, 2007, 18(11): 3438-3442. doi: 10.1088/0957-0233/18/11/025
[9]	SONG Z F, DING H, LI J, et al. Circular curve-fitting method for field surveying data with correlated noise[J]. Journal of Surveying Engineering, 2018, 144(4): 04018010.1-04018010.9.
[10]	AMIRI-SIMKOOEI A R, ZANGENEH-NEJAD F, ASGARI J, et al. Estimation of straight line parameters with fully correlated coordinates[J]. Measurement, 2014, 48: 378-386. doi: 10.1016/j.measurement.2013.11.005
[11]	SHEN Y F, LI B F, CHEN Y. An iterative solution of weighted total least-squares adjustment[J]. Journal of Geodesy, 2011, 85(4): 229-238. doi: 10.1007/s00190-010-0431-1
[12]	鲁铁定,陶本藻,周世健. 基于整体最小二乘法的线性回归建模和解法[J]. 武汉大学学报(信息科学版),2008,33(5): 504-507. LU Tieding, TAO Benzao, ZHOU Shijian. Modeling and algorithm of linear regression based on total least squares[J]. Geomatics and Information Science of Wuhan University, 2008, 33(5): 504-507.