Reliability Analysis of Coupled Train-Bridge Systems Based on ARMAX Surrogate Model
-
摘要:
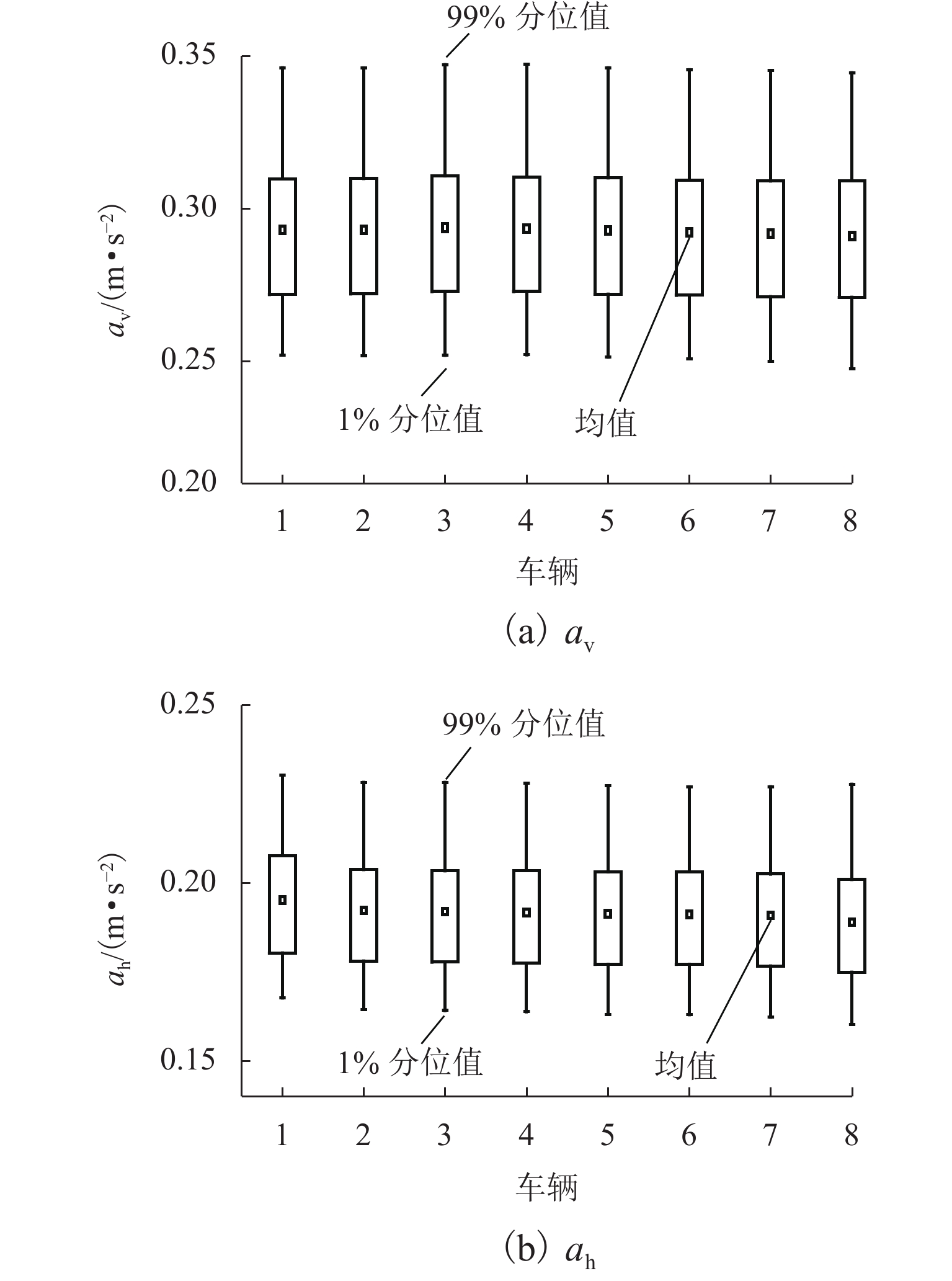
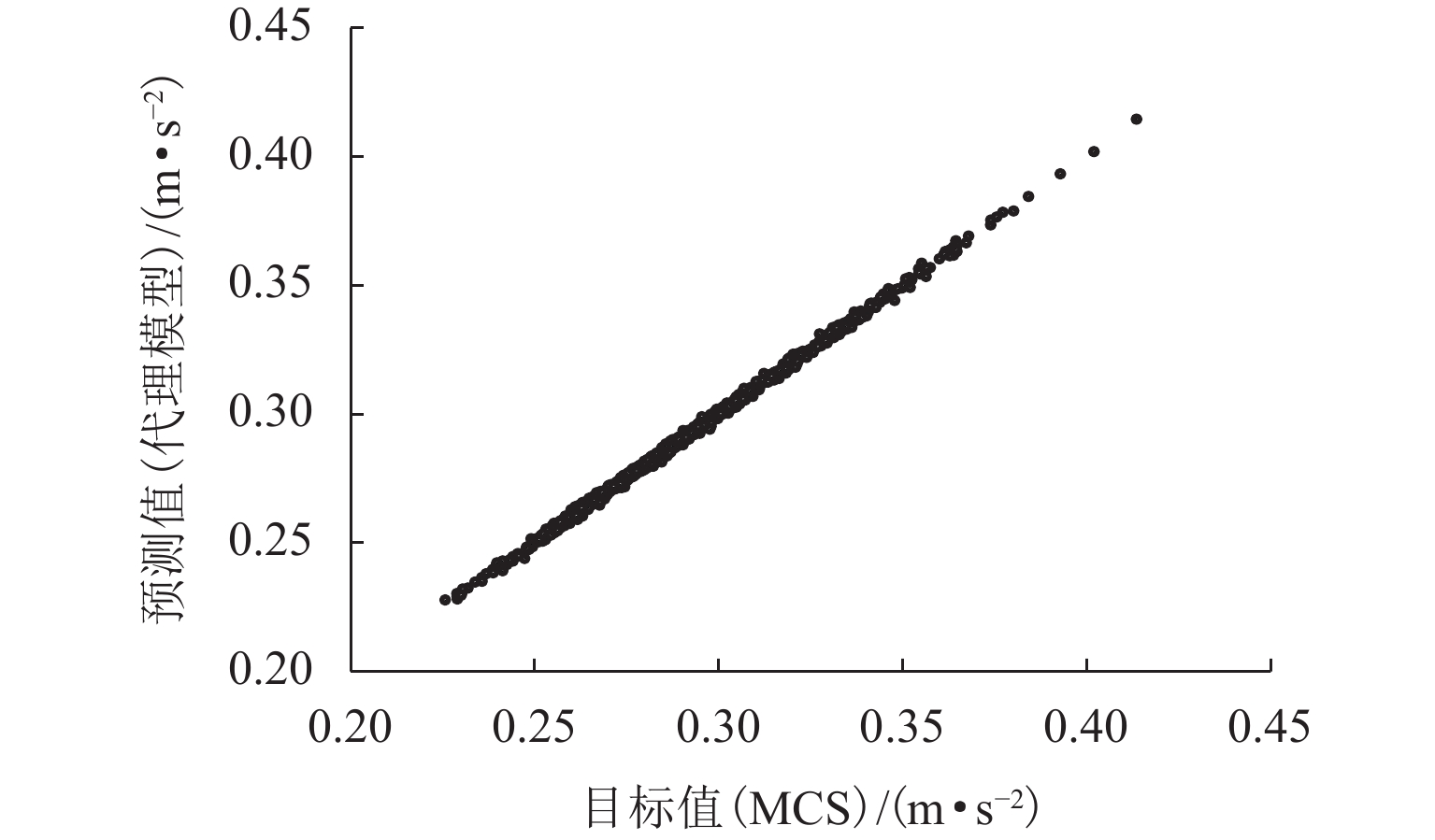
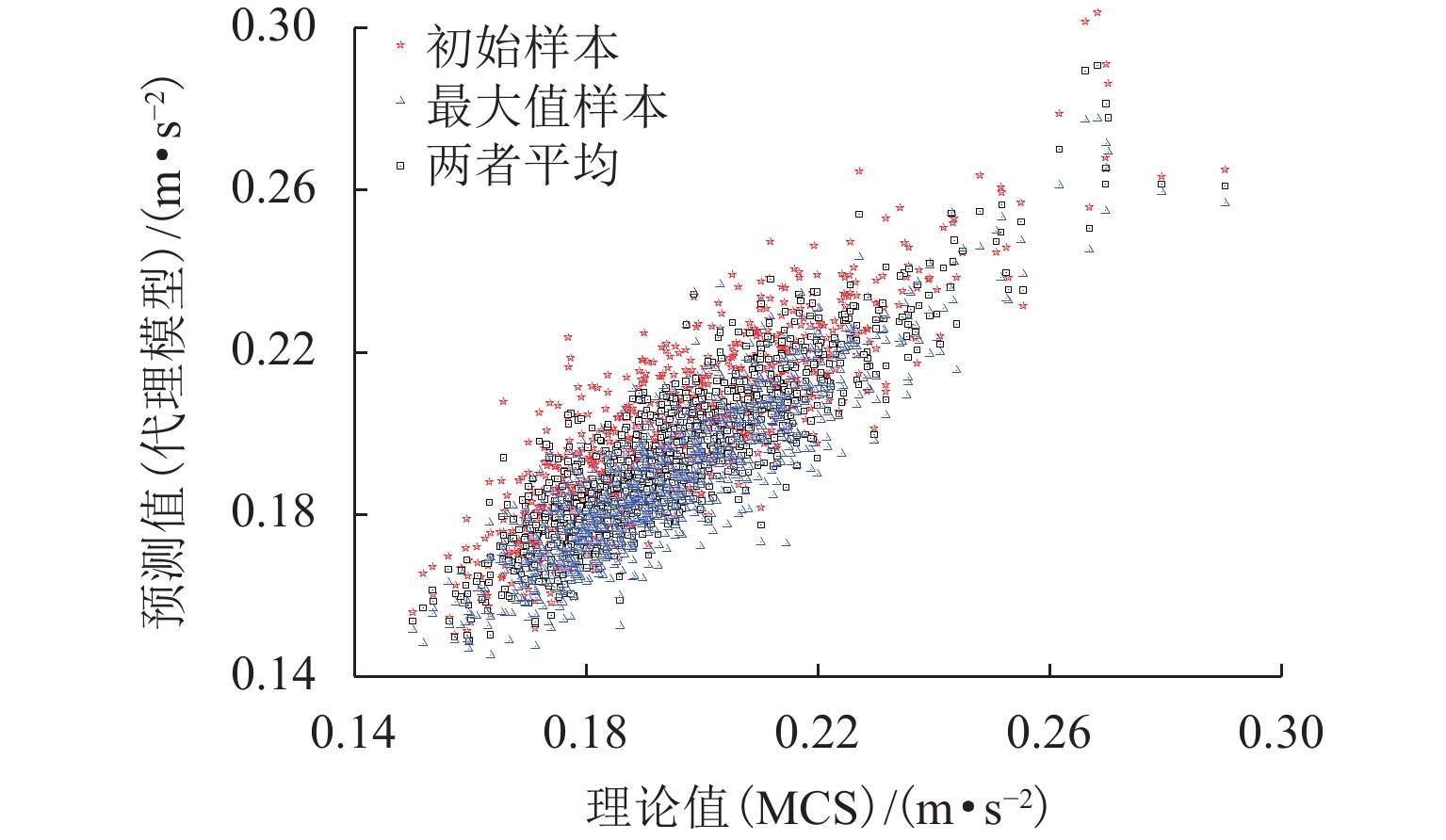
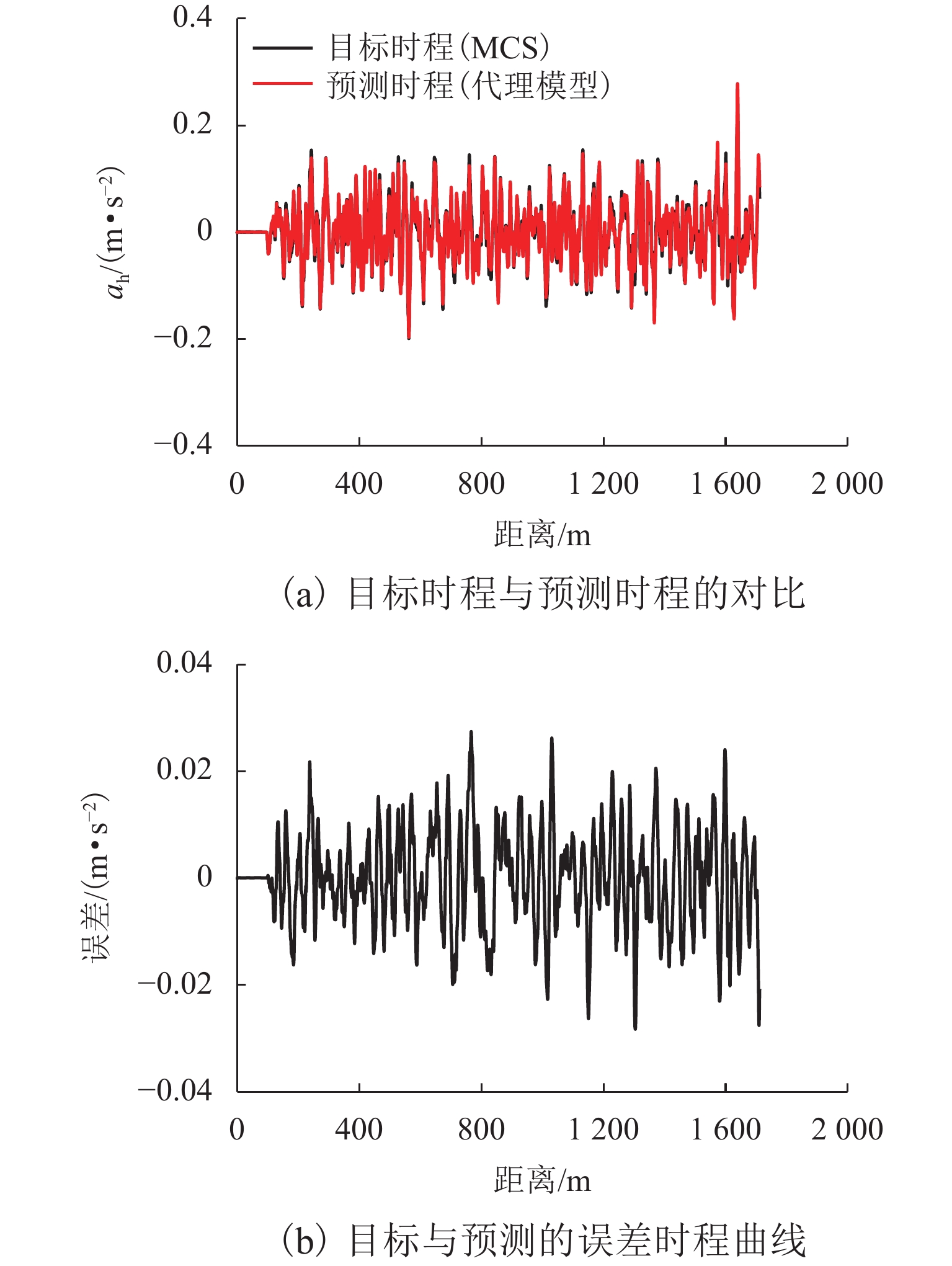
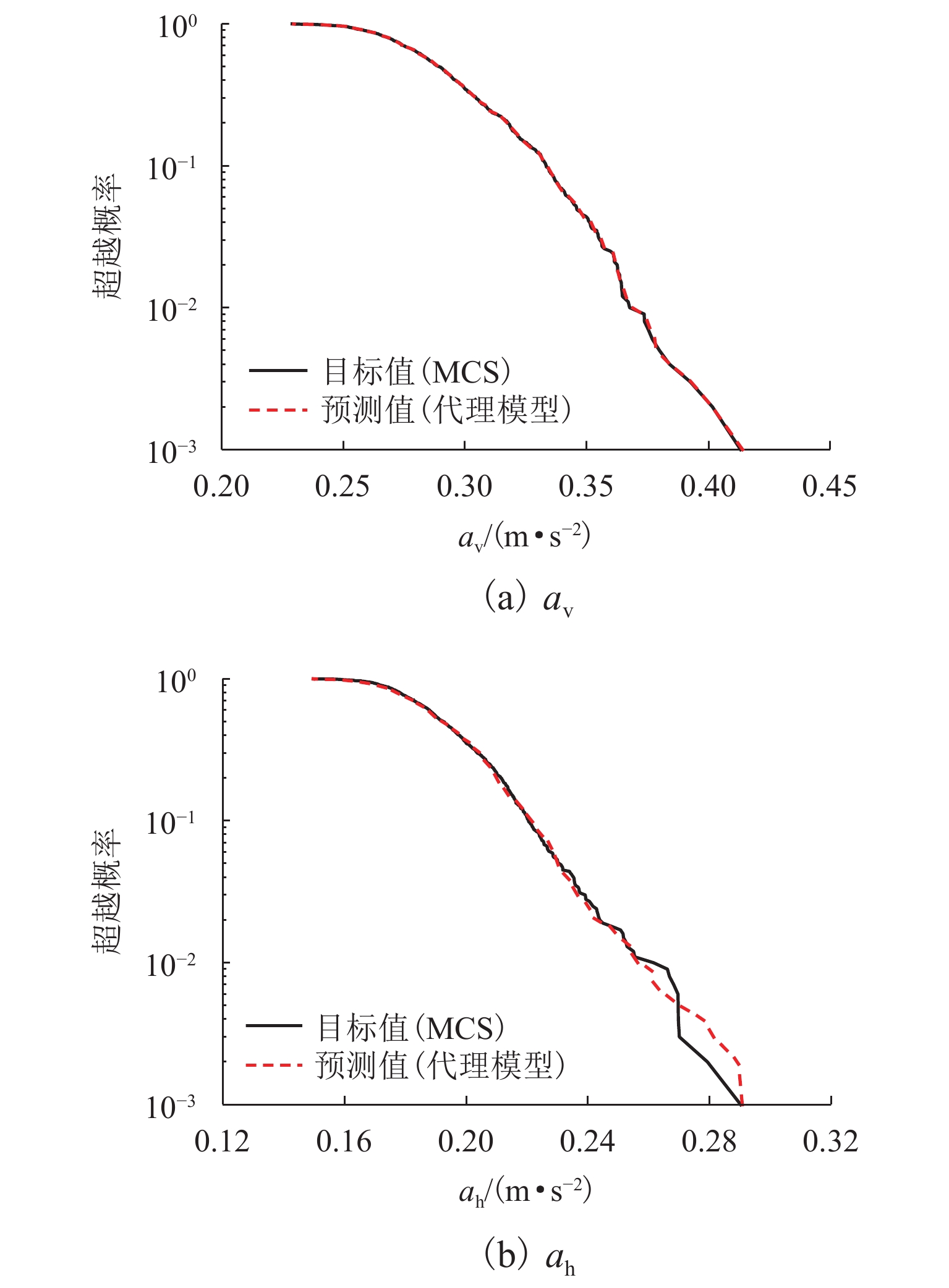
为探究车-桥耦合系统可靠性的效率和精度,建立列车-桥梁的耦合振动模型,并采用自回归方法模拟轨道不平顺. 回顾ARMAX (auto-regressive moving average exogenous)模型的基本原理,提出了基于ARMAX代理模型的车-桥耦合系统可靠性分析框架;利用代理模型获得列车响应预测值,并与直接蒙特卡罗模拟(monte carlo simulation,MCS)法结果进行对比,探讨了代理模型在分析行车安全时的计算精度和可靠性分析效率. 结果表明:代理模型预测列车竖向和横向加速度响应的效率显著高于MCS法,约为3个数量级;预测竖向、横向车体加速度的精度分别为98.66%、86.55%,求解精度较好,可显著提高车-桥耦合系统可靠性分析的效率.
Abstract:In order to improve the efficiency of the coupled train-bridge system reliability analysis, a train-bridge coupling vibration model is established, and the track irregularity is simulated by auto-regressive (AR) method. After basic principles of the (auto-regressive moving average exogenous (ARMAX) model are reviewed, the reliability analysis framework of the train-bridge coupling system based on the ARMAX surrogate model is proposed. The acceleration responses predicted by the surrogate model are then compared with those by the direct Monte Carlo method to examine the calculation accuracy and reliability analysis efficiency of the surrogate model in analyzing driving safety. The results show that the efficiency of the surrogate model in predicting the vertical and lateral acceleration responses of trains is significantly higher than that of the MCS method, by about 3 orders of magnitude; besides, acceptable solution accuracy of 98.66% and 86.55% can be achieved for vertical and horizontal car body acceleration prediction, respectively. Therefore, the surrogate model can significantly improve the reliability analysis efficiency of coupled train-bridge systems.
-
Key words:
- ARMAX model /
- train-bridge system /
- surrogate model /
- reliability /
- dynamic system
-
[1] 冯星梅. 中小跨度铁路桥梁横向振动模拟及适应快速行车结构型式的研究[D]. 北京: 铁道部科学研究院, 2000. [2] 晋智斌. 车-线-桥耦合系统及车-桥随机振动[D]. 成都: 西南交通大学, 2007. [3] 张志超,张亚辉,林家浩. 车桥耦合系统非平稳随机振动分析的虚拟激励-精细积分法[J]. 工程力学,2008,25(11): 197-204.ZHANG Zhichao, ZHANG Yahui, LIN Jiahao. Pem-pim scheme for non-stationary random vibration analysis of vehicle-bridge systems[J]. Engineering Mechanics, 2008, 25(11): 197-204. [4] 朱艳,李小珍,强士中. 高速铁路简支梁桥车桥系统随机响应[J]. 西南交通大学学报,2011,46(4): 535-540. doi: 10.3969/j.issn.0258-2724.2011.04.002ZHU Yan, LI Xiaozhen, QIANG Shizhong. Stochastic responses of train-bridge coupling system for simply-supported high-speed railway bridge[J]. Journal of Southwest Jiaotong University, 2011, 46(4): 535-540. doi: 10.3969/j.issn.0258-2724.2011.04.002 [5] 朱思宇. 车-桥耦合系统振动的随机特性及极值分析[D]. 成都: 西南交通大学, 2017. [6] 彭勇波,李杰. 非线性随机振动分析的概率密度演化方法[J]. 西南交通大学学报,2014,49(2): 220-226. doi: 10.3969/j.issn.0258-2724.2014.02.006PENG Yongbo, LI Jie. Probability density evolution method of nonlinear random vibration analysis[J]. Journal of Southwest Jiaotong University, 2014, 49(2): 220-226. doi: 10.3969/j.issn.0258-2724.2014.02.006 [7] 余志武,毛建锋,谈遂,等. 车桥竖向随机振动的概率密度演化分析[J]. 中南大学学报(自然科学版),2015,46(4): 1420-1427. doi: 10.11817/j.issn.1672-7207.2015.04.032YU Zhiwu, MAO Jianfeng, TAN Sui, et al. Probability density evolution analysis of track-bridge vertical coupled vibration with irregularity random excitation[J]. Journal of Central South University (Science and Technology), 2015, 46(4): 1420-1427. doi: 10.11817/j.issn.1672-7207.2015.04.032 [8] XIA H, ZHANG N, DE ROECK G. Dynamic analysis of high speed railway bridge under articulated trains[J]. Computers & Structures, 2003, 81(26/27): 2467-2478. [9] AU F T K, WANG J J, CHEUNG Y K. Impact study of cable-stayed railway bridges with random rail irregularities[J]. Engineering Structures, 2002, 24(5): 529-541. doi: 10.1016/S0141-0296(01)00119-5 [10] LEI X Y, NODA N A. Analyses of dynamic response of vehicle and track coupling system with random irregularity of track vertical profile[J]. Journal of Sound and Vibration, 2002, 258(1): 147-165. doi: 10.1006/jsvi.2002.5107 [11] 苏成,钟春意,周立成. 车桥耦合系统随机振动的时域显式解法[J]. 应用数学和力学,2017,38(1): 99-108. doi: 10.1007/s10483-017-2158-6SU Cheng, ZHONG Chunyi, ZHOU Licheng. Random vibration analysis of coupled vehicle-bridge systems with the explicit time-domain method[J]. Applied Mathematics and Mechanics, 2017, 38(1): 99-108. doi: 10.1007/s10483-017-2158-6 [12] 陈皓,程晓卿,俞秀莲,等. 列车脱轨系数的精确预测方法研究[J]. 计算机仿真,2013,30(7): 142-146. doi: 10.3969/j.issn.1006-9348.2013.07.032CHEN Hao, CHENG Xiaoqing, YU Xiulian, et al. Research on accurate prediction method of train derailment coefficient[J]. Computer Simulation, 2013, 30(7): 142-146. doi: 10.3969/j.issn.1006-9348.2013.07.032 [13] 庞学苗. 基于人工神经网络的轮轨力预测[D]. 南京: 南京理工大学, 2012. [14] HAN X, XIANG H Y, LI Y L, et al. Predictions of vertical train-bridge response using artificial neural network-based surrogate model[J]. Advances in Structural Engineering, 2019, 22(12): 2712-2723. doi: 10.1177/1369433219849809 [15] XIANG H Y, TANG P, ZHANG Y, et al. Random dynamic analysis of vertical train-bridge systems under small probability by surrogate model and subset simulation with splitting[J]. Railway Engineering Science, 2020, 28(3): 305-315. doi: 10.1007/s40534-020-00219-6 [16] 魏延宝,林红权,马增良,等. 基于ARMAX模型的集中供热系统负荷预测研究[J]. 自动化与仪表,2014,29(7): 1-4,21. doi: 10.3969/j.issn.1001-9944.2014.07.001WEI Yanbao, LIN Hongquan, MA Zengliang, et al. Central heating system load prediction based on ARMAX model[J]. Automation & Instrumentation, 2014, 29(7): 1-4,21. doi: 10.3969/j.issn.1001-9944.2014.07.001 [17] 李永乐. 风-车-桥系统非线性空间耦合振动研究[D]. 成都: 西南交通大学, 2003. [18] 朱艳. 车桥系统随机振动理论与应用研究[D]. 成都: 西南交通大学, 2010. [19] 李小珍. 高速铁路列车-桥梁系统耦合振动理论及应用研究[D]. 成都: 西南交通大学, 2000. [20] 贾进峰,张进秋,张建,等. 基于路面谱随机激励的履带车辆舒适性仿真研究[J]. 系统仿真学报,2012,24(6): 1350-1354. doi: 10.16182/j.cnki.joss.2012.06.024JIA Jinfeng, ZHANG Jinqiu, ZHANG Jian, et al. Ride comfort simulation of tracked vehicles from stochastic excitation based on road surface spectrum[J]. Journal of System Simulation, 2012, 24(6): 1350-1354. doi: 10.16182/j.cnki.joss.2012.06.024 [21] 陈果. 车辆-轨道耦合系统随机振动分析[D]. 成都: 西南交通大学, 2000. [22] 刘德军. 风-列车-线路-桥梁系统耦合振动研究[D]. 成都: 西南交通大学, 2010. [23] 向活跃,唐平,王涛,等. 基于子集分裂模拟的车-桥系统极值响应统计[J]. 振动与冲击,2020,39(5): 105-111,136.XIANG Huoyue, TANG Ping, WANG Tao, et al. Extreme value response statistics of a vehicle-bridge system based on SS/S method[J]. Journal of Vibration and Shock, 2020, 39(5): 105-111,136. [24] 罗德河,郑东健,甘声玄,等. 基于ARMAX模型的混凝土坝损伤诊断[J]. 武汉大学学报(工学版),2018,51(4): 294-298. doi: 10.14188/j.1671-8844.2018-04-003LUO Dehe, ZHENG Dongjian, GAN Shengxuan, et al. Damage diagnosis of concrete dams based on ARMAX model[J]. Engineering Journal of Wuhan University, 2018, 51(4): 294-298. doi: 10.14188/j.1671-8844.2018-04-003 [25] ZHANG N, TIAN Y, XIA H. A train-bridge dynamic interaction analysis method and its experimental validation[J]. Engineering, 2016, 2(4): 528-536. doi: 10.1016/J.ENG.2016.04.012 [26] 李小珍,朱艳,晋智斌. 车辆-桥梁耦合系统垂向振动的随机分析[J]. 钢结构,2010,25(12): 5,13-16.LI Xiaozhen, ZHU Yan, JIN Zhibin. Stochastic analysis of train-bridge time-varying vertical system[J]. Steel Construction, 2010, 25(12): 5,13-16. -




 下载:
下载: