三维岩体滑坡诱发冲击波近场波的特性试验研究

韩林峰; 王平义; 牟萍; 王梅力; 吴国茂

doi:10.3969/j.issn.0258-2724.20200078

三维岩体滑坡诱发冲击波近场波的特性试验研究

doi: 10.3969/j.issn.0258-2724.20200078

韩林峰^{1, 2,},
王平义^2, ,,
牟萍²,
王梅力^{2, 3},
吴国茂⁴

1.
重庆交通大学土木工程学院, 重庆 400074
2.
重庆交通大学国家内河航道整治工程技术研究中心, 重庆 400074
3.
重庆交通大学建筑与城市规划学院, 重庆 400074
4.
遵义水利水电勘测设计研究院, 贵州遵义563002

基金项目: 国家自然科学基金（51479015）；重庆市基础科学与前沿技术研究专项（cstc2017jcyjBX0070）；重庆市自然科学基金（cstc2020jcyj-bshX0101）

详细信息

作者简介:
韩林峰（1988—），男，副教授，博士，研究方向为滑坡涌浪灾害及防灾减灾，E-mail：linf_han@163.com

通讯作者:
王平义（1964—），男，教授，博士，研究方向为水力学及河流动力学，E-mail：py-wang@163.com

中图分类号: P642
计量
- 文章访问数: 285
- HTML全文浏览量: 153
- PDF下载量: 18
- 被引次数: 0
出版历程
- 收稿日期: 2020-03-09
- 录用日期: 2021-11-23
- 修回日期: 2020-06-30
- 网络出版日期: 2021-12-15
- 刊出日期: 2021-06-11

Experimental Study on Near-Field Characteristics of Impulse Waves Generated by Three-Dimensional Rock Slide

HAN Linfeng^{1, 2
,},
WANG Pingyi^{2
, ,},
MU Ping²,
WANG Meili^{2, 3},
WU Guomao⁴

1.
School of Civil Engineering, Chongqing Jiaotong University, Chongqing 400074, China
2.
National Engineering Technology Research Center for Inland Waterway Regulation, Chongqing Jiaotong University, Chongqing 400074, China
3.
School of Architecture and Urban Planning, Chongqing Jiaotong University, Chongqing 400074, China
4.
Zunyi Survey and Design Institute of Water Conservancy and Hydropower, Zunyi 563002, China

摘要

摘要:
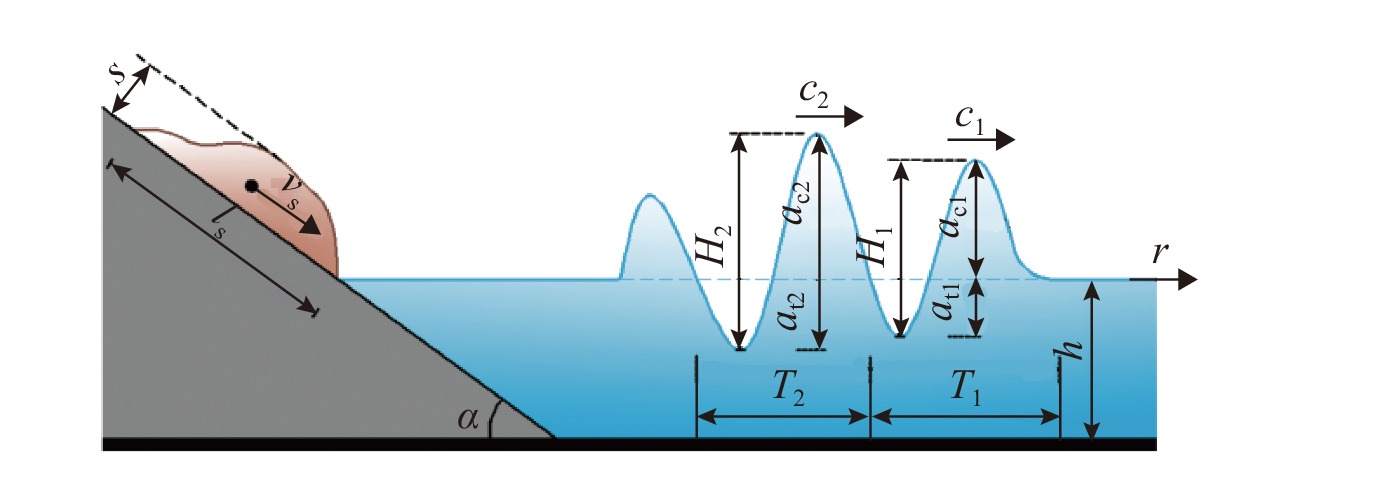
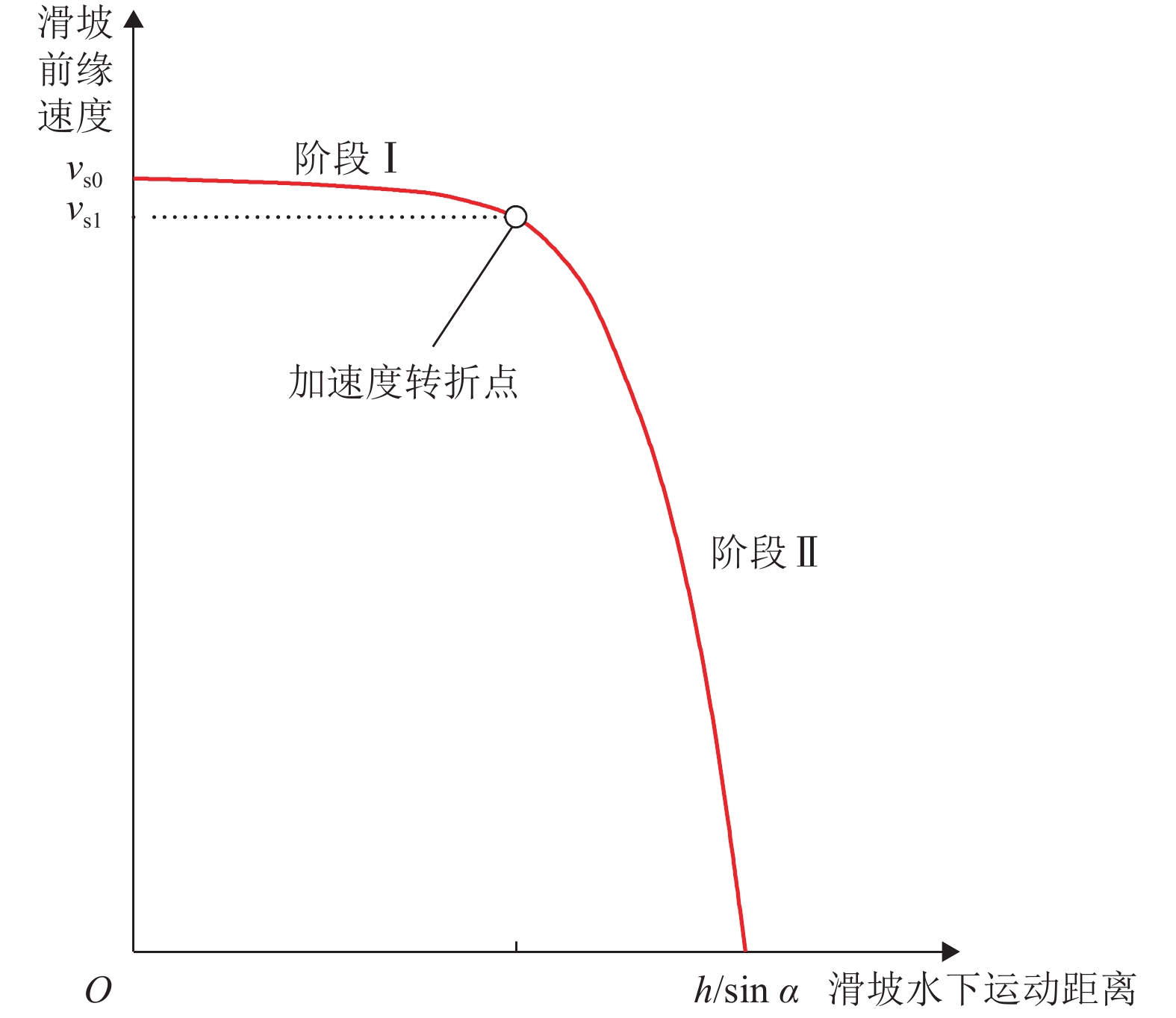
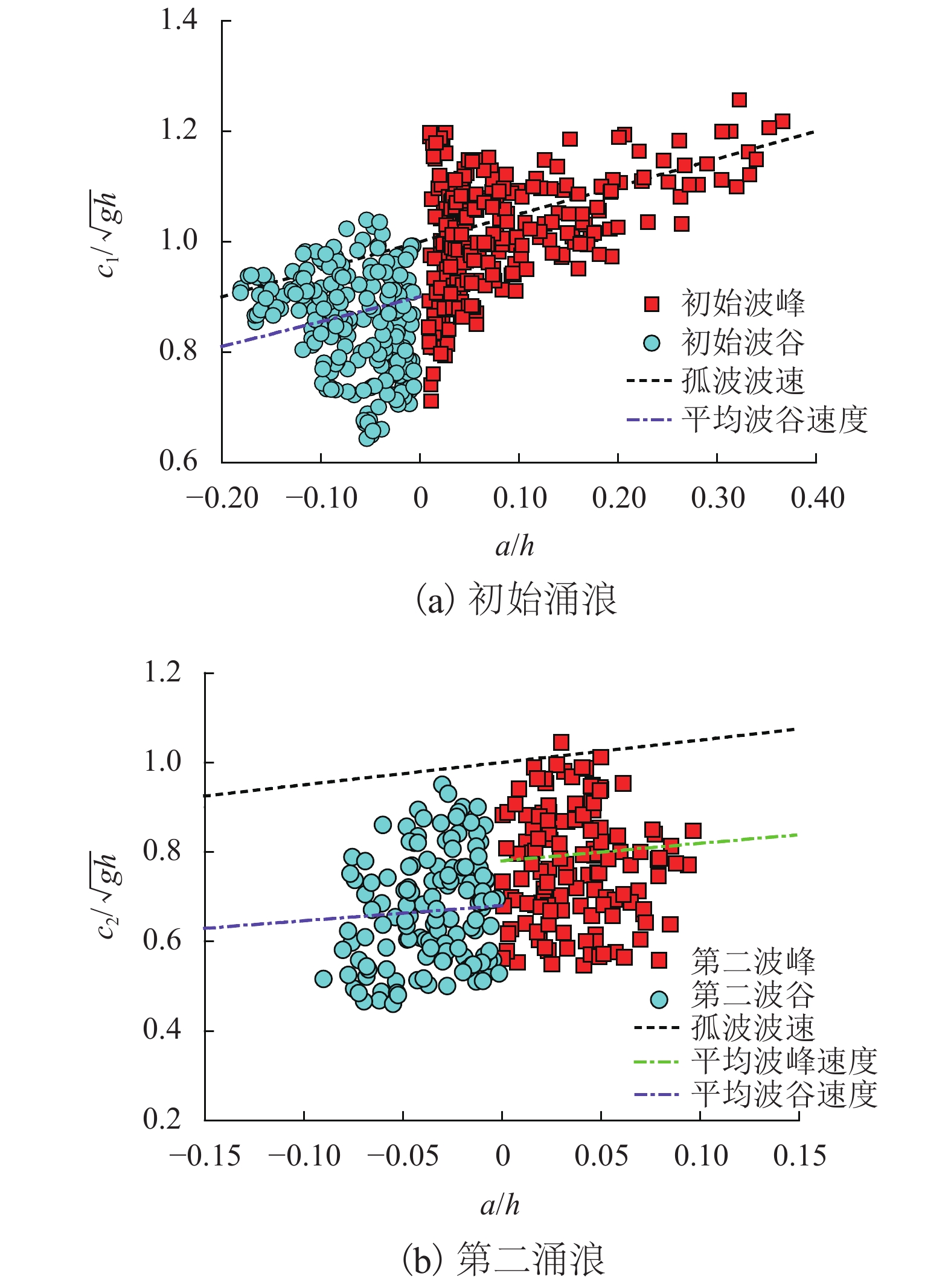
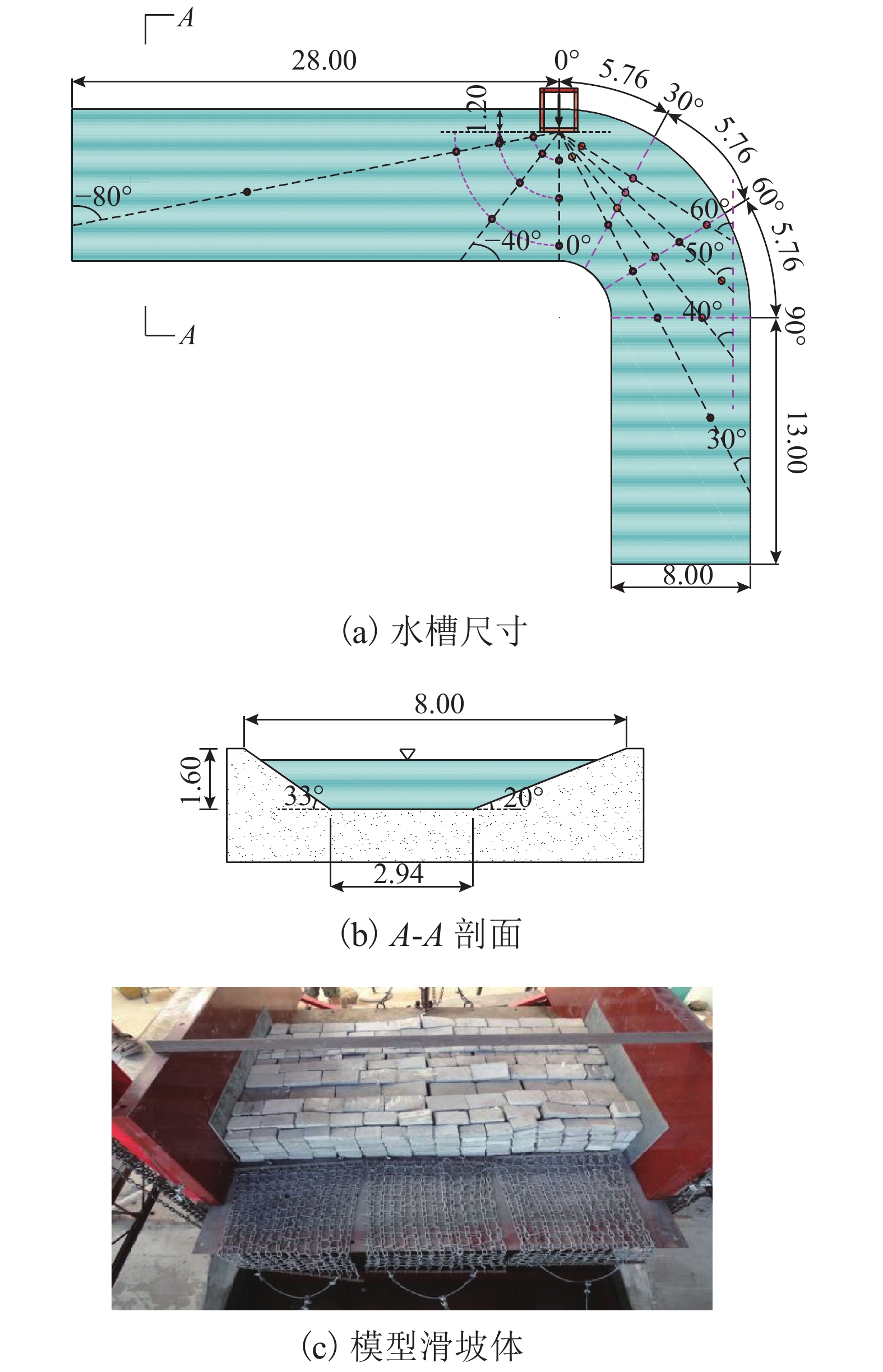
为了预测水库库岸滑坡入水后产生的冲击波（涌浪）到达承灾体的时间及立波高度，以水库岩体滑坡所诱发的冲击波为研究对象，对近场区涌浪的波场特征进行研究. 首先，根据弗劳德相似准则，并结合三峡库区典型岩体滑坡参数及其裂隙发育情况，建立碎裂岩体滑坡涌浪三维物理模型；其次，通过模型试验揭示了近场涌浪的产生机理及传播规律；最后，通过多元回归分析建立了近场涌浪预测模型. 研究结果表明：初始涌浪产生的主要驱动力是滑坡体对水体的置换和拖拽所致，其中初始波谷振幅大小主要取决于水面塌陷的持续时间；根据滑坡水下运动过程，引入两种临界水深，提出初始波谷产生时间的计算方法；初始波峰的传播速度与孤立波波速非常接近，而初始波谷、第二波波峰与波谷的传播速度则要小于孤立波波速，其无量纲相位波速分别为孤波波速的0.90倍、0.78倍、0.68倍.
- 岩体滑坡 /
- 滑坡冲击波 /
- 波场特征 /
- 模型试验
Abstract:
In order to predict the arrival time and wave height of the shock wave (surge) from a landslide source to the hazard-affected body, the near-field wave characteristics of the surge induced by the reservoir rock mass landslide were experimentally studied. Firstly, according to the typical rockslide parameters and rock fracture characteristics in the Three Gorges reservoir area, a three-dimensional physical laboratory model for cracked rockslide generated impulse waves was built based on the generalized Froude similarity. Then, the near-field wave generation mechanism and propagation law were revealed though model tests. Finally, a prediction model of near-field waves was established by multiple regression analysis. The results showed that the main driving force of the first wave is the displacement and drag of the landslide to the water body; the size of the leading wave trough amplitude depends on the duration of the water collapse. According to the underwater movement process of the landslide, two critical water depths are introduced in this paper, and the calculation method of the first wave trough generation time is proposed. Furthermore, the first wave crest propagates at velocities up to the approximate solitary wave celerity. The celerity of the first wave trough and the second wave is lower than that of the solitary wave, and their measureless phase wave speeds are 0.9, 0.78 and 0.68 times the solitary wave celerity, respectively.
- rockslide /
- impulse waves generated by landslide /
- wave field characteristics /
- model test

HTML全文

图 1 三维岩体滑坡涌浪模型实验设置（单位：m）

Figure 1. Experimental setup for impulse waves generated by three-dimensional rock landslide（unit：m）

下载: 全尺寸图片幻灯片

图 2 三维岩体滑坡涌浪产生过程

Figure 2. Tsunami generation by three-dimensional rock slide

下载: 全尺寸图片幻灯片

图 3 近场涌浪定义草图

Figure 3. Definition sketch for near-field waves

下载: 全尺寸图片幻灯片

图 4 散体滑坡水下运动过程

Figure 4. Underwater movement process of granular landslides

下载: 全尺寸图片幻灯片

图 5 涌浪波速与相对波幅的关系

Figure 5. Relationship between wave propagation celerity and relative wave amplitude

下载: 全尺寸图片幻灯片

参考文献(22)

[1]	HELLER V, HAGER W H, MINOR H E. Landslide generated impulse waves in reservoirs[R]. Zurich: ETH Zurich, 2009.
[2]	许春青. 滑坡预测预报模型比较分析[D]. 哈尔滨: 哈尔滨工程大学, 2011.
[3]	WATTS P. Tsunami features of solid block underwater landslides[J]. Journal of Waterway Port Coastal and Ocean Engineering, 2000, 126(3): 144-152. doi: 10.1061/(ASCE)0733-950X(2000)126:3(144)
[4]	SAELEVIK G, JENSEN A, PEDERSEN G. Experimental investigation of impact generated tsunami; related to a potential rock slide,Western Norway[J]. Coastal Engineering, 2009, 56(9): 897-906. doi: 10.1016/j.coastaleng.2009.04.007
[5]	HELLER V, SPINNEKEN J. Improved landslide tsunami prediction:effects of block model parameters and slide model[J]. Journal of Geophysical Research, 2013, 118(3): 1489-1507.
[6]	PANIZZO A, DEGIROLAMO P, PETACCIA A. Forecasting impulse waves generated by subaerial landslides[J]. Journal of Geophysical Research, 2005, 110(C12): C12025.1-C12025.23. doi: 10.1029/2004JC002778
[7]	LINDSTRØM E K, PEDERSEN G K, JENSEN A, et al. Experiments on slide generated waves in a 1∶500 scale fjord model[J]. Coastal Engineering, 2014, 92(4): 12-23.
[8]	岳书波,刁明军,王磊. 滑坡涌浪的初始形态及其衰减规律的研究[J]. 水利学报,2016,47(6): 816-825. YUE Shubo, DIAO Mingjun, WANG Lei. Research on initial formation and attenuation of landslide-generated waves[J]. Journal of Hydraulic Engineering, 2016, 47(6): 816-825.
[9]	肖莉丽,殷坤龙,王佳佳,等. 基于物理模拟试验的库岸滑坡冲击涌浪[J]. 中南大学学报(自然科学版),2014,45(5): 1618-1626. XIAO Lili, YIN Kunlong, WANG Jiajia, et al. Impulse wave generated by reservoir landslides based on physical model experiments[J]. Journal of Central South University (Science and Technology), 2014, 45(5): 1618-1626.
[10]	FRITZ H M, HAGER W H, MINOR H E. Near field characteristics of landslide generated impulse waves[J]. Journal of Waterway Port Coastal and Ocean Engineering, 2004, 130(6): 287-302. doi: 10.1061/(ASCE)0733-950X(2004)130:6(287)
[11]	ZWEIFEL A, HAGER W H, MINOR H E. Plane impulse waves in reservoirs[J]. Journal of Waterway Port Coastal and Ocean Engineering, 2006, 132(5): 358-368. doi: 10.1061/(ASCE)0733-950X(2006)132:5(358)
[12]	HELLER V. Landslide generated impulse waves: prediction of near field characteristics[D]. Zurich: ETH Zurich, 2007.
[13]	HUANG B L, YIN Y P, WWANG S C, et al. A physical similarity model of an impulsive wave generated by Gongjiafang landslide in Three Gorges Reservoir,China[J]. Landslides, 2014, 11(3): 513-525. doi: 10.1007/s10346-013-0453-x
[14]	MCFALL B C, FRITZ H M. Physical modelling of tsunamis generated by three-dimensional deformable granular landslides on planar and conical island slopes[J]. Proceedings Mathematical, Physical, and Engineering Sciences, 2016, 472(2188): 20160052.1-20160052.24. doi: 10.1098/rspa.2016.0052
[15]	DI RISIO M, SAMMARCO P. Analytical modeling of landslide-generated waves[J]. Journal of Waterway Port Coastal and Ocean Engineering, 2008, 134(1): 53-60. doi: 10.1061/(ASCE)0733-950X(2008)134:1(53)
[16]	MOHAMMED F, FRITZ H M. Physical modeling of tsunamis generated by three-dimensional deformable granular landslides[J]. Journal of Geophysical Research:Oceans, 2013, 118(6): 3221.
[17]	韩林峰,王平义,王梅力,等. 碎裂岩体滑坡运动特征及近场涌浪变化规律[J]. 浙江大学学报(工学版),2019,53(12): 2325-2334. HAN Linfeng, WANG Pingyi, WANG Meili, et al. Motion characteristics of cataclastic rockslides and change rules of impulse waves in near-field zone[J]. Journal of Zhejiang University (Engineering Science), 2019, 53(12): 2325-2334.
[18]	DEAN R G, DALRYMPLE R A. Advanced series on ocean engineering 2: water wave mechanics for engineers and scientists[M]. Singapore: World Scientific Publishing, 1991.
[19]	韩林峰,王平义. 基于动量平衡的三维滑坡涌浪最大近场波幅预测[J]. 岩石力学与工程学报,2018,37(11): 165-173. HAN Linfeng, WANG Pingyi. Prediction of maximum near-field wave amplitude of impulse wave generated by three-dimensional landslide based on momentum balance[J]. Chinese Journal of Rock Mechanics and Engineering, 2018, 37(11): 165-173.
[20]	VIROULET S, CEBRON D, KIMMOUN O, et al. Shallow water waves generated by subaerial solid landslides[J]. Geophysical Journal International, 2013, 193(2): 747-762. doi: 10.1093/gji/ggs133
[21]	MOHAMMED F. Physical modeling of tsunamis generated by three-dimensional deformable granular landslides[D]. Atlanta: Georgia Institute of Technology, 2010.
[22]	GRILLI S T, SVENDSEN I A, SUBRAMANYA R. Breaking criterion and characteristics for solitary waves on slopes[J]. Journal of Waterway Port Coastal and Ocean Engineering, 1997, 123(3): 102. doi: 10.1061/(ASCE)0733-950X(1997)123:3(102)