钢芯铝绞线的拉扭耦合力学性能

张龙; 黄珏; 钟永力; 晏致涛

doi:10.3969/j.issn.0258-2724.20200076

钢芯铝绞线的拉扭耦合力学性能

doi: 10.3969/j.issn.0258-2724.20200076

张龙^1,,
黄珏²,
钟永力³,
晏致涛^3, ,

基金项目: 国家自然科学基金（51778097）

详细信息

作者简介:
张龙（1977—），男，高级工程师，硕士，研究方向为输电线路工程，E-mail：11984726@qq.com

通讯作者:
晏致涛（1978—），男，教授，博士，研究方向为输电线路工程，E-mail：yzt@cqust.edu.cn

中图分类号: TB121
计量
- 文章访问数: 608
- HTML全文浏览量: 310
- PDF下载量: 13
- 被引次数: 0
出版历程
- 收稿日期: 2020-03-07
- 修回日期: 2020-07-23
- 网络出版日期: 2021-03-29
- 刊出日期: 2021-08-15

Mechanical Properties of Tension-Torsion Coupling in Aluminum Conductor Steel Reinforced

摘要

摘要: 导线扭转参数属于导线基本力学性能之一，尤其是拉扭耦合效应会极大地影响覆冰输电线舞动分析的准确性. 为此，对典型7股钢芯铝绞线LGJ/JL/G1A-70/10进行了扭转试验，并结合有限元仿真软件ANSYS对相应构件进行建模与数值分析，与基于钢丝绳拉扭耦合理论的4种理论进行了对比. 数值分析结果与扭转试验结果吻合较好，且对比分析表明：拧绕系数的取值浮动较大，会导致不容忽视的误差；在正常运行应力状态下，导线拉伸会产生较大的扭转效应，导线的截面扭转也会产生轻微张力变化；导线的拉扭耦合和扭拉耦合系数不相等；基于钢丝绳的理论均未考虑子股导线的滑移变形及坐标更新，会在一定程度上高估轴向刚度以及拉扭耦合效应.
- 钢芯铝绞线 /
- 导线 /
- 扭转 /
- 拉扭耦合 /
- 有限元
Abstract: The torsion parameter of the conductor is one of its basic mechanical properties. Moreover, the tension-torsioncoupling effect of iced transmission lines will greatly affect the accuracy of galloping analysis. To analyze this effect, the torsional test was carried out for the typical 7-strand aluminum conductor steel reinforced (ACSR) LGJ/JL/G1A-70/10, and the modeling and numerical analysis of the corresponding components are carried out by using the finite element simulation software ANSYS, the results ofwhich is compared with those calculated by the 4 theories based on the tension-torsioncoupling theory of wire rope. The results of numerical analysis are in good agreement with those of the torsion test. Thetwist factor values fluctuate greatly, which will lead to significant errors. Under the normal stress state, the conductor tension will produce a large torsion effect, and the section torsion of the conductor will also lead to a slight tension change. The tension-torsion coupling coefficient is not equal to the torsion-tension one. The theories based on steel wire rope do not consider the slip deformation and coordinate update of sub strand conductors, which overestimates the axial stiffness and the coupling effect of tension and torsion to a certain extent.
- aluminum conductor steel reinforced (ACSR) /
- conductor /
- torsion /
- tension-torsion coupling /
- finite element

HTML全文

钢筋锈蚀损伤是引起钢筋混凝土结构劣化的主要因素，严重影响建筑结构的安全性和耐久性^[1]. 特别是在冻融循环作用下混凝土会产生较大的膨胀压力，促使混凝土产生开裂或原有裂纹的扩展，加快钢筋的锈蚀，降低钢筋混凝土结构的耐久性. 普通混凝土材料具有取材容易、造价低、抗压性能高等优点，广泛应用于建筑工程. 但混凝土抗拉强度与韧性较低，无法有效控制结构的裂缝宽度，进而降低了结构本身抵御外界侵蚀介质的能力，造成不可逆转的耐久性损伤. 因此，寻求一种抗拉性能较好，韧性较高，并且可有效控制裂缝发展的材料尤其重要.

超高韧性水泥基复合材料（ECC）是20世纪90年代基于微观力学与断裂力学提出的一种具有超高韧性的新型纤维增强材料^[2-3]. 研究表明，ECC材料能提高混凝土结构的抗弯性能，具有较好的变形能力，可有效控制裂缝的发展，特别是在屈服前^[4-6]. 纤维在混凝土内部均匀分布，能对基体起到很好的约束作用，抵抗冻融循环作用产生的膨胀压力，同时可以有效控制裂缝的发展，从而提高混凝土的抗冻性^[7].

近年来，大量研究集中于冻融循环作用对钢筋混凝土梁性能的影响^[8-10]，部分学者研究了冻融损伤作用下ECC梁的性能^[11-16]. 在冻融循环作用下，使用ECC材料替代普通混凝土，可增强混凝土的承载力、刚度和抗裂性能^[11-13]，ECC材料具有良好的抗冻性^[14]. 聚丙烯纤维水泥基复合材料（PP-ECC）的极限拉应变可达普通混凝土的 120倍～400倍，有显著的拉伸韧性，抗冻性能远优于普通混凝土^[15]. 目前，研究大多为单一冻融循环作用对钢筋混凝土梁性能的影响，而现实中的结构是在荷载作用下服役的. Duan等^[16]通过对冻融-弯曲荷载耦合作用下钢筋混凝土梁进行弯曲试验，分析梁的极限承载力、延性和中性轴深度等的演化发现，冻融循环和持续荷载对钢筋混凝土梁的抗弯性能有显著影响，并提出冻融-弯曲荷载耦合作用下钢筋混凝土梁承载力计算模型.

冻融-弯曲荷载耦合作用下ECC梁的劣化更能反映寒区结构物的劣化损伤. 故本文制作7根PP-ECC梁，研究其在冻融作用和荷载-冻融耦合作用下的裂缝发展形态、变形及抗弯承载力变化规律；然后，基于李福海等^[17]的正常环境下PP-ECC梁抗弯承载力计算模型对冻融环境下PP-ECC梁的抗弯承载力进行分析，建立适用于PP-ECC梁冻融荷载耦合作用下抗弯承载力计算模型，并通过试验结果对其进行验证，为冻融荷载耦合作用下PP-ECC梁性能研究提供一定的理论依据和参考.

1. 试验概括

1.1 原材料与试件制作

本试验制作了7根PP-ECC梁，试件尺寸为100 mm × 120 mm × 1100 mm，保护层厚度为25 mm，试件参数见表1. 具体构造如图1所示，钢筋性能参数为实测值，具体见表2. 试验中PP-ECC材料的主要成分为水泥、粉煤灰、水和PP纤维，具体配比如表3.

表 1 PP-ECC梁具体试验参数

Table 1. Specific test parameters of PP-ECC beam

试验梁分组	试件编号	冻融循环次数/次	弯曲荷载/%	抗弯性能试验
第Ⅰ组	E0-0	0		是
第Ⅱ组	E0-300	300
第Ⅱ组	E0-500	500
第Ⅲ组	E0.25-300	300	25
第Ⅲ组	E0.25-500	500	25
第Ⅳ组	E0.50-300	300	50
第Ⅳ组	E0.50-500	500	50

下载: 导出CSV

| 显示表格

图 1 试件构造

Figure 1. Structure of the specimen

下载: 全尺寸图片幻灯片

表 2 钢筋性能指标

Table 2. Rebar performance indexes

型号	直径/ mm	截面面积/mm²	屈服强度/MPa	极限强度/MPa	弹性模量/GPa
Q235	6	28.26	236	390	196
HRB400	6	28.26	406	576	197
HRB400	10	78.50	411	535	203

下载: 导出CSV

| 显示表格

表 3 PP-ECC梁的配合比

Table 3. Mix proportion of PP-ECC beam kg/m³

水泥	粉煤灰	PP纤维	水
820.0	442.0	18.2	504.8

下载: 导出CSV

| 显示表格

1.2 试验方法

1.2.1 冻融循环试验

根据我国寒冷地区冬季最低温和最高温，设置最高温度为15 ℃，最低温度为−20 ℃. 一个循环周期历时8 h （恒温及冰冻各2 h，恒温至冰冻（冰冻至恒温）经历2 h），一天循环3次，相对湿度设置为85%，但当温度下降至−20 ℃时，环境箱内的水分会结冰，使箱内相对湿度下降；在温度达到0 ℃后，试件的温度低于箱内空气温度，试件表面的热空气会发生液化，相对湿度会暂时达到100%，当温度保持在15 ℃时，箱内相对湿度稳定在85%，具体温湿度循环变化见图2.

图 2 温湿度循环示意

Figure 2. Temperature and humidity cycle

下载: 全尺寸图片幻灯片

1.2.2 持荷设计

当混凝土受到的外部荷载不超过自身抗弯强度（极限荷载对应强度）的30% （即持荷比为0.30）时，构件内部无明显裂缝，处于稳定的阶段；当外部荷载达到极限荷载的50% （即持荷比为0.50）时，构件内部会因应力集中导致界面间的裂缝有一定程度的发展，但发展的程度相对稳定^[18]. 因此，试验选取持荷比为0.25和0.50对ECC梁进行冻融循环与弯曲荷载耦合试验. 在冻融过程中采用4点加载，装置如图3所示.

图 3 持荷冻融试件加载装置

Figure 3. Loading device for load-bearing freeze-thaw specimens

下载: 全尺寸图片幻灯片

1.2.3 试验加载及测量方式

试验采用三分点加载，装置如图4所示. 试验梁受力长度为900 mm，纯弯段为300 mm. 试验采用逐级加载，具体加载如下：

图 4 三分点加载试验

Figure 4. Three-point loading test

下载: 全尺寸图片幻灯片

1）预加载：为使试验过程中梁与加载设备更加贴合，同时检测加载装置及仪表等是否正常工作，需进行预加载，预加载值不超过理论开裂荷载的70%.

2）正式加载：在试验正式开始时先采用力控制方式以100 N/s的速度加载至1 kN并保持3 min，考虑分配梁的自重，此后采用位移控制的方式分级加载，每级加载速率为2 mm/min，每加载1 mm位移保持6 min，使裂缝充分发展.

变形测量：在跨中和2个支座处各安放1个百分表，跨中变形数值减去支座沉降平均值即为试验梁的跨中挠度.

混凝土表面应变：在试验梁两侧纯弯段沿高度方向（120 mm）等距布置3个应变片，在顶面和底面沿宽度方向（100 mm）等距布置2个应变片，如图5.

图 5 应变片布置

1—荷载传感器；2—分配工装；3—PP—ECC梁侧面；4—铰支座；5—应变片；6—百分表；7—PP-ECC梁顶面.

Figure 5. Strain gauge layout

下载: 全尺寸图片幻灯片

裂缝观测：在试件两侧喷上白漆，并在梁的侧面绘制40 mm × 40 mm的网格，用记号笔标出加载过程中裂缝的发展位置及形态，同时使用裂缝观测仪测量每级加载下裂缝的宽度.

2. 试验结果与分析

2.1 变形分析

PP-ECC梁跨中荷载-位移曲线可分为未裂阶段、带裂缝工作阶段、破坏阶段，如图6所示. 在加载初期，试验梁受拉区未出现裂缝，曲线呈线性发展. 在带裂缝工作阶段，试验梁表面裂缝数量随荷载的增加而不断增加，截面的抗弯刚度逐渐下降，随着荷载继续增加，钢筋开始屈服. 受拉钢筋去屈服后，裂缝数量基本保持不变，但主裂缝宽度迅速变大，试验梁逐渐发生破坏，荷载保持基本不变，但挠度变形一直在增加，表现出一定的延性.

图 6 跨中荷载-位移曲线

Figure 6. Mid-span load displacement curve

下载: 全尺寸图片幻灯片

2.2 极限抗弯承载力

本文采用文献[19]中的等效能量法确定PP-ECC梁的屈服荷载. 此外，PP-ECC梁变形能力强，达到峰值荷载后不会突然破坏，承载能力会逐渐降低. 因此，将承载力降低到峰值荷载的85.00%时对应的荷载与位移视为PP-ECC梁的极限荷载与极限位移.

表4为PP-ECC梁冻融-弯曲荷载耦合作用下4点弯曲试验结果. 从表中可以看到：1）在单一冻融循环下，PP-ECC梁的屈服载荷、极限载荷随着冻融循环次数的增加而减小，经过300次冻融循环后，屈服载荷和极限载荷分别下降13.58%和15.10%，平均每100次循环分别下降4.53%和5.33%；经过500次冻融循环后，屈服载荷和极限载荷分别下降26.89%和28.70%，且300～500次循环区间内平均每100次循环屈服载荷和极限载荷分别下降了6.66%和6.80%. 前期下降幅度小后期下降幅度大，故在500次冻融循环内冻融循环对试件的损伤是一个先慢后快的趋势.

表 4 PP-ECC梁四点弯曲试验结果

Table 4. Four-point bending test results of PP-ECC beam

试件编号	屈服荷载/kN	极限荷载/kN	极限抗弯承载力/（kN·m）	裂缝最大宽度/mm	最终裂缝数量/条
E0-0	33.95	33.97	5.10	0.90	36
E0-300	29.34	28.84	4.33	1.10	30
E0-500	24.82	24.22	3.63	1.34	25
E0.25-300	30.88	30.72	4.61	1.25	32
E0.25-500	24.64	25.02	3.75	1.42	29
E0.50-300	26.67	26.01	3.90	1.55	23
E0.50-500	21.21	21.87	3.28	1.80	18

下载: 导出CSV

| 显示表格

2）经历相同冻融循环次数的PP-ECC梁，持荷比为0.25的梁极限抗弯承载力最高，这是由于持荷比为0.25的试验梁受压区基体材料在弯曲荷载的作用下被压实，内部孔隙和微裂缝闭合，减小了冻融过程中对基体的损伤，使基体材料被压实，受压区域内部更加密实，从而提高了试验梁的极限抗弯承载力^[20]；持荷比为0.50的PP-ECC梁极限抗弯承载力最低，这表明在本试验中此工况下的试验梁冻融损伤最为严重. 故适当的弯曲荷载对试件梁受压区起到保护作用，减小冻融环境下受压区的损伤，从而提高试件梁的抗弯承载，但过大的弯曲荷载会对梁受拉区、受压区造成较为严重的损伤，加快了试验梁在冻融环境中的劣化，从而对梁抗弯承载力产生不利影响.

2.3 裂缝形态及分布

试验梁裂缝分布如图7所示. PP-ECC梁开裂过程如下：当荷载达到开裂荷载后，受拉区开始出现弯曲裂缝，由于PP纤维在基体中呈现均匀乱向分布，具备较好的桥联作用，使得受拉区基体材料在试件开裂后并不退出工作，而是协同钢筋继续参与全截面受力；由于受拉区主要为竖向裂缝，随着荷载的逐渐增加，裂缝向受压区延伸，并在剪切区内扩展，开始出现斜裂缝；受拉钢筋屈服后，裂缝迅速扩展且梁挠度增幅逐渐增大. 可以看到不同损伤程度的PP-ECC梁均呈现多条裂缝稳态发展模式，但裂缝分布具有一定差异，对比图7可以看到，横向裂缝主要出现在经历500次冻融的梁体上，未冻融以及300次冻融循环的梁没有横向裂缝.

图 7 裂缝分布

Figure 7. Crack distribution

下载: 全尺寸图片幻灯片

PP-ECC梁最大裂缝宽度以及裂缝数量见表4. 随着冻融循环次数的增加，裂缝最大宽度有所增大，但主裂缝数量逐渐减少；相同冻融循环次数下E0.50-300、E0.50-500比未持荷的梁的最终裂缝数量分别降低23.3%、28.0%，最大宽度分别增加72.2%、100.0%. 这表明受荷载和冻融的PP-ECC性能发生劣化，PP纤维与基体的桥联作用减弱，控制裂缝的效果降低，不利于基体实现多裂缝开展，产生的裂缝数量减少，而增大了PP-ECC梁的最大裂缝宽度.

2.4 PP-ECC梁截面应变分布

不同工况下PP-ECC梁基体表面的平均应变曲线如图8所示. 各PP-ECC梁基本符合平截面假定，在荷载作用下，跨中截面的混凝土应变曲线沿梁高近似线性变化；随着荷载级别的增加，PP-ECC梁表面沿截面高度的应变均有所增加. 在单一冻融循环作用下，试验梁中性轴随冻融次数的增加不断上移，这是因为基体内部在冻胀压力作用下产生许多微裂缝，同时纤维与基体的桥联作用也随之下降，导致试验梁抗弯承载力降低、性能劣化；在荷载-冻融耦合作用下，梁侧面的应变均低于自然环境下梁的应变，且随持荷比的增加，梁侧面应变值逐渐减小.

图 8 梁截面混凝土应变分布

Figure 8. Concrete strain distribution of beam section

下载: 全尺寸图片幻灯片

3. 冻融循环和冻融循环-弯曲荷载耦合作用下PP-ECC梁抗弯承载力

3.1 冻融循环作用下PP-ECC梁抗弯承载力计算

3.1.1 基本假定

1）冻融环境下梁体截面仍满足平截面假定.

2）加载全过程中钢筋与基体无相对滑移，黏结性能良好. 文献[21]研究表明，冻融循环作用下钢筋与混凝土之间黏结性能的退化对梁承载力的影响并不显著，故可忽略其对冻融后PP-ECC梁极限承载力的影响，假定两者黏结性能没有劣化.

3）冻融循环作用后，由于纤维的桥联作用，PP-ECC梁受拉区开裂后仍与钢筋共同承担受拉区拉力.

4）冻融循环作用后PP-ECC材料初裂应力与应变、极限应力与应变均发生不同程度的变化，但抗拉和抗压应力-应变曲线形状相似，故采用与正常环境下PP-ECC梁相同的简化本构模型.

3.1.2 抗弯承载力计算分析

经历冻融循环作用的PP-ECC梁加载全过程仍经历弹性阶段、带裂缝工作阶段、破坏阶段. 在破坏阶段，试验梁抗弯承载力下降的主要原因是梁上混凝土强度的降低^[21]，故基于正常环境下PP-ECC梁抗弯承载力的计算模型，考虑PP-ECC梁受拉区及受压区混凝土性能的退化，结合PP-ECC材料经受N次冻融循环的应力及应变劣化规律，推导PP-ECC梁在冻融环境下的抗弯承载力计算模型.

3.1.3 材料劣化规律

为得到经历冻融循环作用下PP-ECC材料N次冻融循环混凝土压缩和拉伸应力及应变劣化规律，本次试验以100个冻融循环为一个周期（共500个冻融循环）对PP-ECC材料进行轴心抗压试验以及单轴拉伸试验.

图9为轴心抗压试验结果. 随着冻融循环次数的增加，试件轴心抗压强度不断降低，极限压缩应变不断增加，且二者与冻融循环次数均近似呈线性相关. 原因在于冻融环境中试件会产生冻胀压力，加快试件内部微裂缝的发展，加剧混凝土内部的损伤，造成轴心抗压强度的下降，破坏愈加明显.

图 9 冻融过程中PP-ECC的极限压缩性能变化

Figure 9. Variations in ultimate compression performance of PP-ECC during freeze-thaw process

下载: 全尺寸图片幻灯片

对图9中不同冻融循环次数下试件的抗压强度和极限压缩应变试验数据进行拟合，得到冻融循环作用下PP-ECC材料抗压强度和极限压缩应变的演化规律，如式（1）、（2）.

${\sigma }_{{\rm{cu}}N}={\sigma }_{{\rm{cu}}}（-0.000\;80N + 1.03），$

(1)

${\varepsilon }_{{\rm{cu}}N}^{}={\varepsilon }_{{\rm{cu}}}^{}（0.000\;53N + 0.98） ,$

(2)

式中：σ_cuN、ε_cuN分别为经历N次冻融循环后PP-ECC极限抗压强度（MPa）、极限压缩应变（%）；σ_cu为冻融循环前PP-ECC轴心抗压强度，MPa；ε_cu为未冻融循环PP-ECC极限压缩应变（%）.

图10为单轴拉伸试验结果. 在冻融环境中，PP-ECC试件的开裂抗拉强度和极限抗拉强度随冻融循环次数增加而降低，且降低速率随着随冻融循环次数增加而增加. 与普通混凝土相比，在基体内部掺入PP纤维，能够减缓抗拉强度损失速率，提高其抗冻性^[22]，随着冻融次数的增加，PP纤维和基体之间的桥联作用会遭到破坏，由于冻融循环次数的累积，试件内部出现许多微裂缝，裂缝间的纤维桥联作用逐渐减弱，裂缝控制能力降低，PP纤维在基体中的有利作用逐步被削弱.

图 10 冻融过程中PP-ECC的拉伸性能变化

Figure 10. Variations in tensile properties of PP-ECC during freeze-thaw process

下载: 全尺寸图片幻灯片

对不同冻融循环下试件的极限抗拉强度和极限拉伸应变试验数据进行拟合，得到N 次冻融循环作用下PP-ECC材料开裂抗拉强度σ_tcN 、开裂拉伸应变ε_tcN、极限抗拉强度σ_tuN和极限拉伸应变ε_tuN的退化规律，如式（3）～（6）.

${\sigma }_{{\rm{tc}}N}={\sigma }_{{\rm{tc}}}(-7.27\times {10}^{-7}{N}^{2}-5.86\times {10}^{-5}N + 0.98) ，$

(3)

$\varepsilon _{{\rm{tc}}N}^{} = \varepsilon _{{\rm{tc}}}^{}( - 1.97 \times {10^{ - 6}}{N^2} + 5.43 \times {10^{ - 4}}N + 1.01) ，$

(4)

${\sigma }_{{\rm{tu}}N}={\sigma }_{{\rm{tu}}}(-4.06\times {10}^{-7}{N}^{2}-3.79\times {10}^{-4}N + 1.01) ，$

(5)

${\varepsilon }_{{\rm{tu}}N}={\varepsilon }_{{\rm{tu}}}(-1.67\times {10}^{-6}{N}^{2} + 2.75\times {10}^{-4}N + 1.01) ，$

(6)

式中：σ_tc、σ_tu分别为未冻融下PP-ECC材料开裂抗拉强度、极限抗拉强度；ε_tc、ε_tu 分别为未冻融下PP-ECC开裂拉伸应变、极限拉伸应变.

3.1.4 单一冻融循环作用下抗弯承载力计算模型

将3.1.3节公式代入正常环境下PP-ECC梁抗弯承载力计算模型（推导公式见参考文献[]）中，得到冻融环境下PP-ECC梁抗弯承载力 ${M}_{{\rm{u}}N}$ 为

$\begin{split} &{M_{{\rm{u}}N}} = {T_{\rm{s}}}(h - a_{\rm{s}} - {x_{{\rm{n}}N}}) + \frac{2}{3}f_1^{}\left(h - \frac{1}{2}{x_{{\rm{c}}N}}\right) + \\ &\quad {f_2}\left(h - \frac{1}{2}{x_{{\rm{c}}N}} - \frac{1}{3}{x_{{\rm{n}}N}}\right) + {f_3}\left(h - \frac{1}{3}{x_{{\rm{c}}N}} - \frac{1}{3}{x_{{\rm{n}}N}}\right) , \end{split}$

(7)

$\left\{ \begin{array}{l} {f}_{1}=\dfrac{b}{2}{\sigma }_{{\rm{tc}}N}^{}(h-{x}_{{\rm{c}}N}^{}-{x}_{{\rm{n}}N}),\\ {f}_{2}=b{\sigma }_{{\rm{tc}}N}^{}{x}_{{\rm{c}}N}^{},\\ {f}_{3}=\dfrac{b}{2}({\sigma }_{{\rm{tu}}N}^{}-{\sigma }_{{\rm{tc}}N}^{}){x}_{{\rm{c}}N}^{},\end{array} \right.$

(8)

${x_{{\rm{c}}N}} = h - {x_{{\rm{n}}N}} - \frac{{{\varepsilon _{{\rm{tc}}N}}}}{{{\varepsilon _{{\rm{tu}}N}}}}(h - {x_{{\rm{n}}N}}),$

(9)

${x_{{\rm{n}}N}} = \frac{{{\sigma _{{\rm{tc}}N}}h + {\sigma _{{\rm{tu}}N}}{x_{{\rm{c}}N}}}}{{{\sigma _{{\rm{tc}}N}} + {\sigma _{{\rm{cu}}N}}}} + \frac{{2{\alpha _4}{\varepsilon _{\rm{y}}}{A_{\rm{s}}}}}{{b({\sigma _{{\rm{tc}}N}} + {\sigma _{{\rm{cu}}N}})}} ,$

(10)

式中：h为ECC梁高，b为ECC梁宽，T_s为PP-ECC梁受拉区钢筋合力， ${x}_{{\rm{n}}N}$ 为冻融环境下受压区高度， ${x}_{{\rm{c}}N}$ 为冻融环境下受拉区开裂高度，a_s为保护层厚度，ε_y为钢筋屈服应变，σ_y 为钢筋的屈服应力，α₄=σ_y/ε_y，A_s为受拉钢筋面积.

3.1.5 试验结果验证

通过试验得到PP-ECC材料的单轴拉伸本构参数和单轴受压本构参数，如表5所示，将其中参数代入到本文推导的计算模型中，得到冻融环境下PP-ECC梁抗弯承载力计算值，并与试验值进行对比，结果见表6.

表 5 PP-ECC材料本构参数

Table 5. Constitutive parameters of PP-ECC materials

PP-ECC 单轴拉伸本构参数				单轴受压本构参数
σ_tc/MPa	ε_tc/%	σ_tu/MPa	ε_tu/%	σ_cu/MPa	ε_cu/%
0.86	0.088	2.33	3.789	31.65	0.38

下载: 导出CSV

| 显示表格

表 6 抗弯承载力对比

Table 6. Comparison of flexural bearing capacity

冻融循环次数/次	抗弯承载力		计算值/ 试验值
冻融循环次数/次	计算值/ （kN·m）	试验值/ （kN·m）	计算值/ 试验值
0	4.50	5.10	0.88
300	4.18	4.33	0.97
500	3.88	3.63	1.06

下载: 导出CSV

| 显示表格

将试验的计算值与试验值的比值进行方差分析，如式（11）.

$s = \frac{{{{({s_1} - M)}^2} + {{({s_2} - M)}^2} + \cdots + {{({s_n} - M)}^2}}}{n} ，$

(11)

式中：s为方差；M为所有数据平均值；s₁，s₂， $\cdots$ ，s_n为原始数据；n为原始数据的个数.

对表5中数据进行计算得到方差s = 0.0054，结合方差和计算值与试验值的比值可知，计算值接近试验值，两者拟合良好、吻合度高，故该计算模型适用于本次试验冻融环境下PP-ECC梁抗弯承载力的设计计算.

3.2 冻融-弯曲荷载耦合作用下PP-ECC梁抗弯承载力计算

对于承受持荷和冻融循环共同作用的PP-ECC 梁，持荷和冻融循环均会对梁体混凝土造成不同程度的损伤，同时，2种因素会相互作用，从而对试件梁抗弯承载力造成影响，故计算荷载和冻融循环耦合作用下PP-ECC梁的抗弯承载力时应综合考虑持荷和冻融的劣化作用.

3.2.1 冻融-弯曲荷载耦合作用下抗弯承载力计算模型

持荷冻融耦合作用下的PP-ECC梁抗弯承载力受持荷比和冻融循环次数2种因素的影响，为了分析2种因素共同耦合作用对试验梁的承载力影响，在冻融环境下PP-ECC梁抗弯承载力模型基础上，引入持荷比损伤系数γ.

对冻融循环次数相同持荷比不同的PP-ECC梁抗弯承载力进行对比，如图11，承载力随着持荷比的增大呈现先增大后减小的趋势，分析显示二者的关系符合二次函数关系，故将持荷比损伤系数γ表达式设为

图 11 抗弯承载力

Figure 11. Flexural bearing capacity

下载: 全尺寸图片幻灯片

$\gamma = a{\omega ^2} + b\omega + c ，$

(12)

式中：a、b、c为常数，ω为持荷比.

将已知参数代入荷载冻融耦合作用下PP-ECC梁抗弯承载力预测模型 $(M_{{\rm{FL,u}}N}=\gamma M_{{\rm{u}}N})$ 中，根据冻融300次不同持荷比的试件梁抗弯承载力数据进行拟合，得到常数a = −1.89，b = 0.74， c = 1，故荷载冻融耦合作用下PP-ECC梁抗弯承载力的计算模型为

$\begin{split} &M_{{\rm{FL,u}}N}=\gamma {M}_{{\rm{u}}N}^{}=\gamma {T}_{{\rm{s}}}(h-{a}_{{\rm{s}}}-{x}_{{\rm{n}}N}) + \dfrac{2}{3}\gamma {f}_{1}(h-{x}_{{\rm{c}}N})+\\ &\quad \gamma {f}_{2}\left(h-\dfrac{1}{2}{x}_{{\rm{c}}N}-\dfrac{1}{3}{x}_{{\rm{n}}N}\right) + \gamma {f}_{3}\left(h-\dfrac{1}{3}{x}_{{\rm{c}}N}-\dfrac{1}{3}{x}_{{\rm{n}}N}\right), \end{split}$

(13)

$\gamma = - 1.89{\omega ^2} + 0.74\omega + 1 .$

(14)

3.2.2 试验结果验证

利用得到的荷载冻融耦合作用下PP-ECC梁抗弯承载力计算公式，计算各梁的抗弯承载力，并与实测抗弯承载力进行对比，结果见表7.

表 7 抗弯承载力对比

Table 7. Comparison of flexural bearing capacity

冻融循环次数/次	持荷比	抗弯承载力		计算值/ 试验值
冻融循环次数/次	持荷比	计算值/ （kN·m）	试验值/ （kN·m）	计算值/ 试验值
300	0	4.18	4.33	0.97
	0.25	4.46	4.61	0.97
	0.50	3.75	3.90	0.96
500	0	3.88	3.63	1.07
	0.25	4.14	3.75	1.10
	0.50	3.48	3.28	1.06

下载: 导出CSV

| 显示表格

对表7数据进行方差分析得到，方差为0.0032，由此可知计算值与实测值吻合度高，能够作为本实验荷载冻融耦合作用下PP-ECC梁抗弯承载力的计算模型，并为其他研究冻融-弯曲荷载耦合下PP-ECC混凝土抗弯承载力预测模型的科研人员提供参考.

4. 结　论

1） PP-ECC梁的屈服载荷和极限载荷随冻融次数增加逐渐下降，500次冻融循环后，屈服载荷和极限载荷分别下降26.89%和28.70%.

2）对PP-ECC梁施加适当的弯曲荷载可以降低受压区混凝土的冻融损伤，但过大的弯曲荷载会加剧冻融损伤.

3）不同损伤工况下各PP-ECC梁均呈现多条裂缝稳态发展的模式，但裂缝发展分布具有差异化，横向裂缝仅出现在500次冻融循环的梁体上. 随冻融损伤加剧，梁体最大裂缝宽度增大，裂缝的产生与发展贯穿了PP-ECC梁的试验过程.

4）单一冻融及持荷冻融耦合作用下PP-ECC梁均符合平截面假定. 在冻融作用下，试件中性轴随冻融次数的增加而不断上移；在荷载-冻融耦合作用下，试件侧面的应变均低于自然环境下梁的应变，且随持荷比的增加，试件侧面应变值逐渐减小.

5）试验得到的冻融以及冻融荷载耦合作用下得到的承载力预测模型吻合度分别达到0.88～1.06和0.96～1.10，模型拥有较高的吻合度，可以为冻融以及冻融荷载耦合作用下PP-ECC梁性能研究提供一定帮助.

图 1 扭转试验机及试件

Figure 1. Torsion testing machine and test specimens

下载: 全尺寸图片幻灯片

图 2 铝绞线试件扭矩转角曲线

Figure 2. Torque-rotation angle of aluminum conductor specimen

下载: 全尺寸图片幻灯片

图 3 LGJ/JL/G1A-70/10有限元模型

Figure 3. Finite element model of LGJ/JL/G1A-70/10

下载: 全尺寸图片幻灯片

图 4 ANSYS数值模拟与试验对比

Figure 4. Comparison between numerical simulation by ANSYS and test results

下载: 全尺寸图片幻灯片

图 5 扭矩-轴力关系

Figure 5. Relationship between torque and axial force

下载: 全尺寸图片幻灯片

图 6 扭转作用下导线von Mises应力

Figure 6. von Mises stress of conductor under torsion

下载: 全尺寸图片幻灯片

图 7 两端固定下轴力诱发扭矩

Figure 7. Axial force induced torque with two end fixed

下载: 全尺寸图片幻灯片

图 8 一端自由下轴力诱发扭矩

Figure 8. Axial force induced torque with one end free

下载: 全尺寸图片幻灯片

图 9 自由端扭矩诱发拉伸

Figure 9. Torsion induced tension with one end free

下载: 全尺寸图片幻灯片

表 1 钢芯铝绞线LGJ/JL/G1A-70/10的物理参数

Table 1. Physical parameters of wires

参数		值
根 × 直径/mm	钢	1 × 3.80
根 × 直径/mm	铝	6 × 3.80
截面积/mm²	钢/铝	11.3/68.0
截面积/mm²	总截面	79.3
铝、钢截面比		6.02
直径/mm		11.4
单位质量/（t•km⁻¹）		0.275
计算拉断力/kN		23.36
综合弹性模量/MPa		74300
节距/mm		13
线膨胀系数/（℃⁻¹）		18.8 × 10⁻⁶

下载: 导出CSV

表 2 试件剪切模量

Table 2. Shear modulus of test specimens

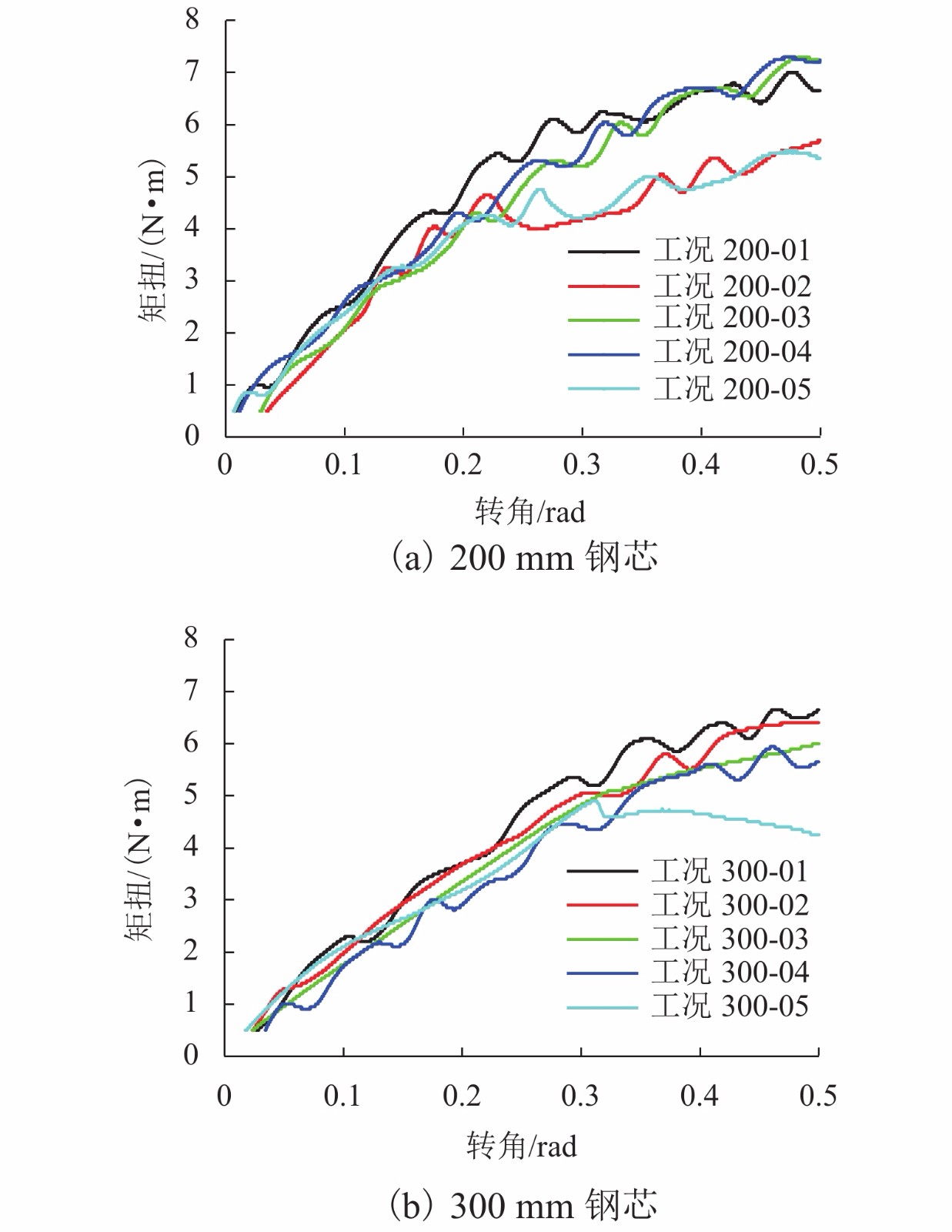
工况	$\overline J$ /mm⁴	$\overline G$ /GPa
200-01	1125.893	4.378
200-02	1125.893	4.745
200-03	1125.893	3.882
200-04	1125.893	3.761
200-05	1125.893	4.684
300-01	1125.893	4.659
300-02	1125.893	4.565
300-03	1125.893	4.268
300-04	1125.893	4.058
300-05	1125.893	3.734
平均值	1125.893	4.405

下载: 导出CSV

表 3 纯扭下的轴力与扭矩

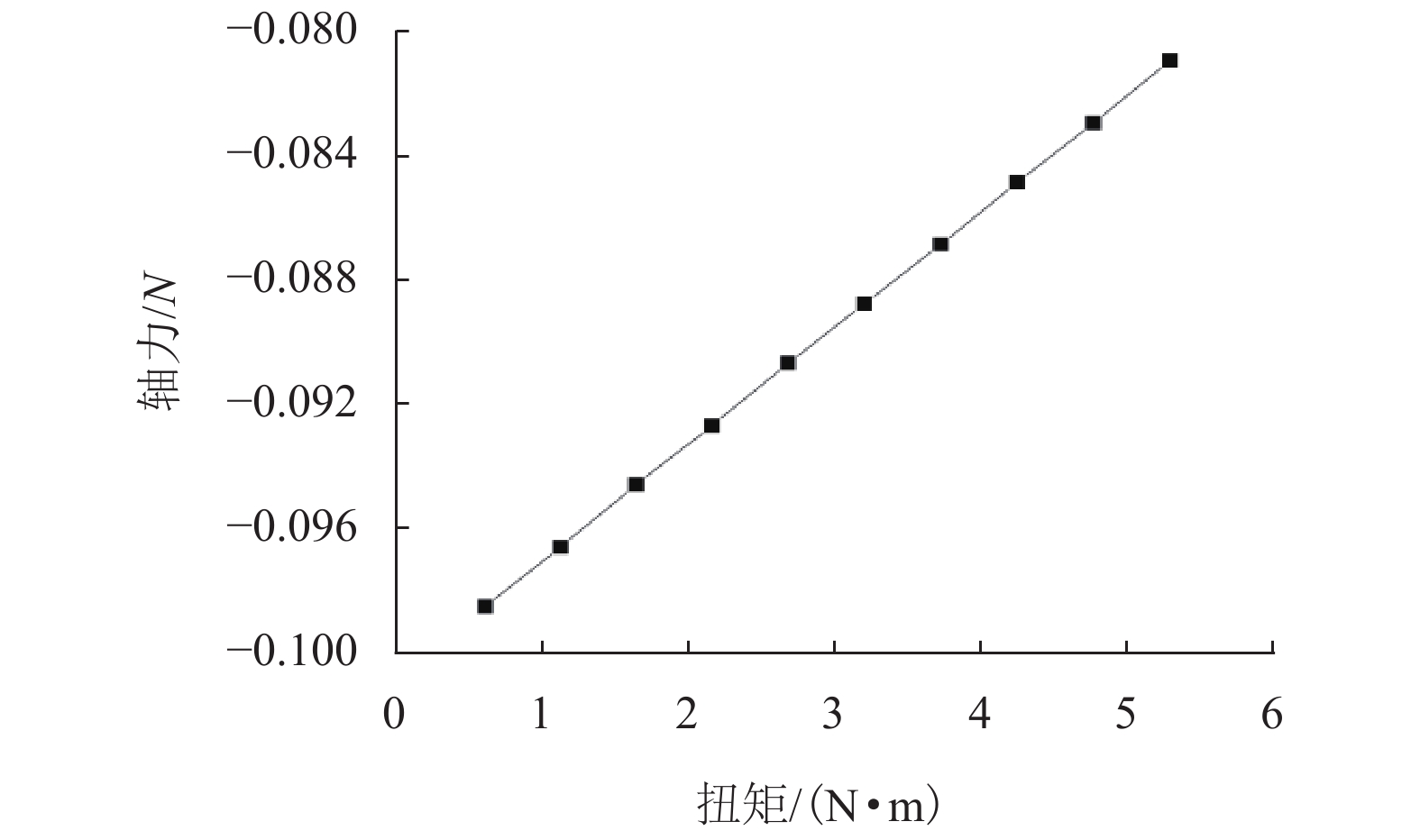
Table 3. Axis force and torque under pure torsion

转角/ rad	S-轴力/N	S-扭矩/ （N•m）	L-轴力/N	L-扭矩/ （N•m）	平均扭矩/ （N•m）
0.02	0.099	0.628	0.099	0.630	0.607
0.04	0.097	1.138	0.097	1.141	1.099
0.06	0.096	1.648	0.095	1.654	1.593
0.08	0.094	2.160	0.093	2.167	2.088
0.10	0.092	2.672	0.091	2.682	2.584
0.12	0.090	3.185	0.089	3.198	3.081
0.14	0.088	3.699	0.087	3.715	3.579
0.16	0.086	4.213	0.085	4.232	4.078
0.18	0.084	4.728	0.083	4.751	4.578
0.20	0.082	5.243	0.081	5.270	5.078

下载: 导出CSV

表 4 刚度方程对比

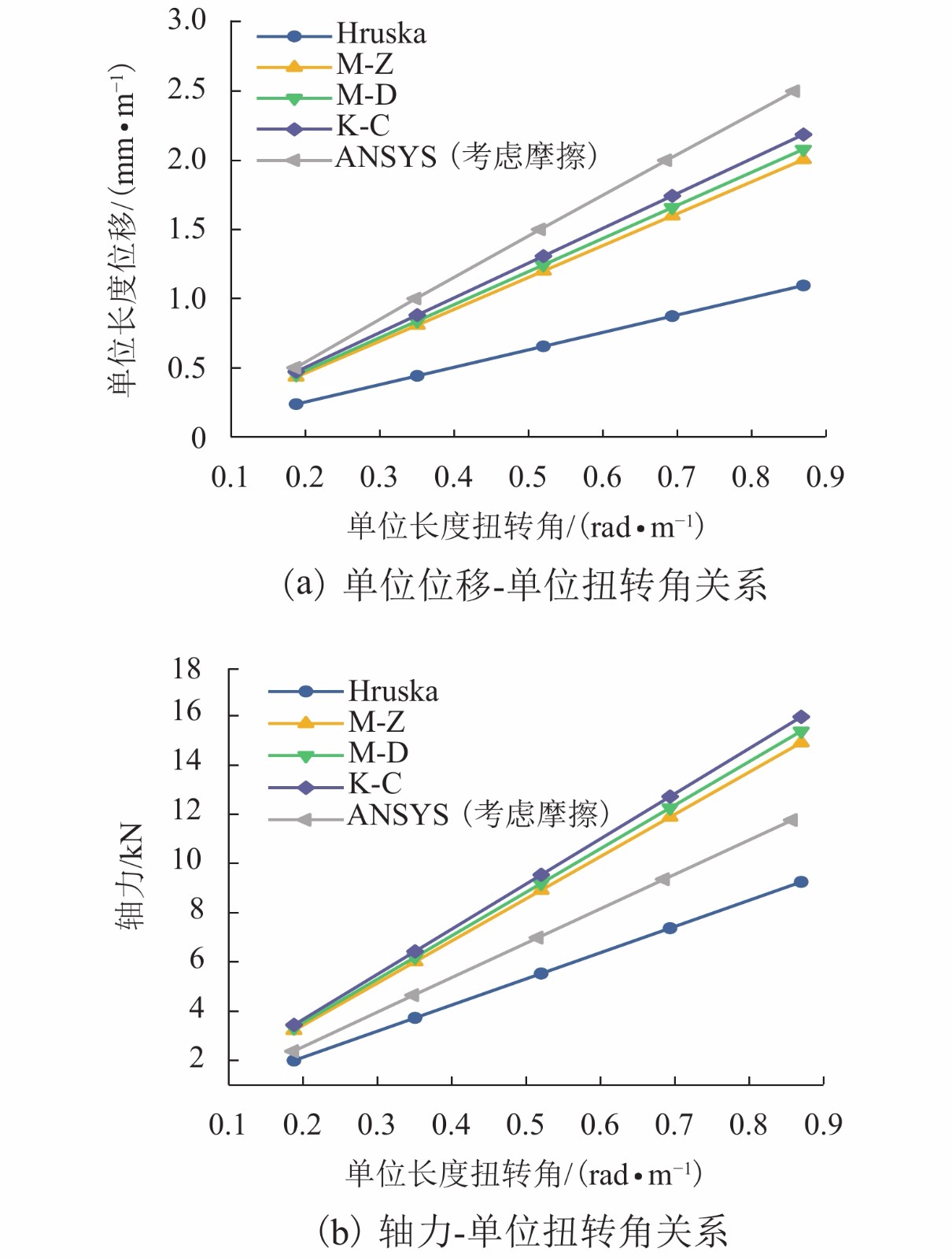
Table 4. Comparison of stiffness equation

方法	${F_\varepsilon }$ /kN	${M_\phi }$ / （N•m²•rad⁻¹）	${F_\phi }$ / （N•m）	${M_\varepsilon }$ / （N•m）
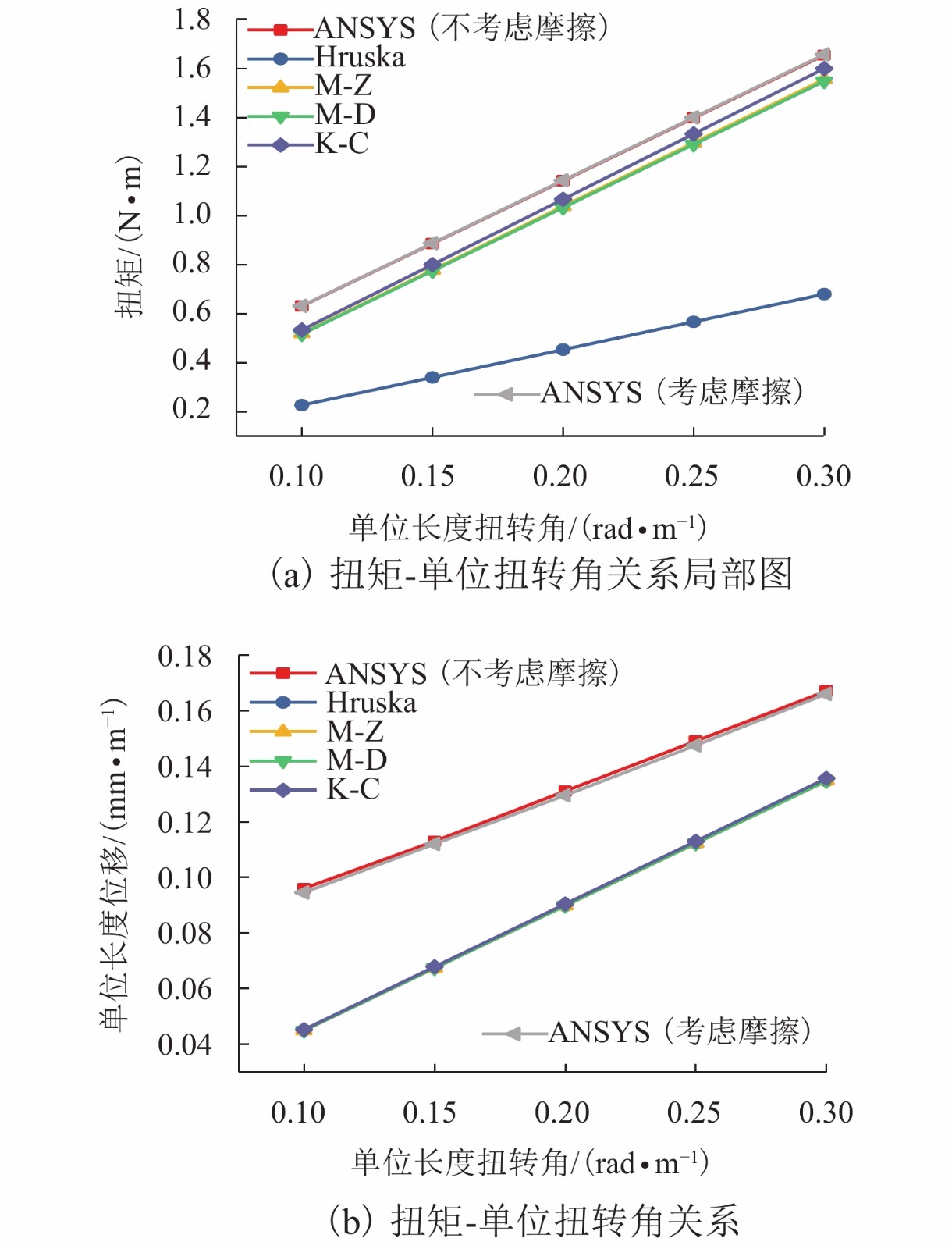
ANSYS 仿真	5 429.92	6.138	2 101.98	2 255.77
Hruska	6 224.01	3.517	2 792.47	2 792.47
M-Z	6 224.01	6.436	2 792.47	2 792.47
M-D	6 224.01	6.349	2 792.47	2 655.59
K-C	6 183.53	6.496	2 792.47	2 583.80

下载: 导出CSV

表 5 各方法精度对比

Table 5. Accuracy comparison of methods

方法	剪切模量/GPa	与试验误差/%
ANSYS仿真	4.572	3.79
郭应龙等^[4]	2.934	33.39
Hruska	2.012	54.33
M-Z	4.606	4.56
M-D	4.583	4.04
K-C	4.736	7.51
扭转试验	4.405

下载: 导出CSV

参考文献(21)

晏致涛,黄静文,李正良. 基于结点6自由度的分裂导线有限元模型[J]. 工程力学,2012,29(8): 325-332. doi: 10.6052/j.issn.1000-4750.2010.08.0626

YAN Zhitao, HUANG Jingwen, LI Zhengliang. Finite element model of split conductor based on 6-DOF node[J]. Engineering mechanics, 2012, 29(8): 325-332. doi: 10.6052/j.issn.1000-4750.2010.08.0626

谢增,刘吉轩,刘超群,等. 架空输电线路分裂导线扭转刚度计算新方法[J]. 西安交通大学学报,2012,46(2): 100-105.

XIE Zeng, LIU Jixuan, LIU Chaoqun, et al. A new method for calculating torsional stiffness of split conductor of overhead transmission line[J]. Journal of Xi’an Jiaotong University, 2012, 46(2): 100-105.

中华人民共和国国家质量监督检验检疫总局, 中国国家标准化管理委员会. 圆线同心绞架空导线: GB/T 1179—2017 [S]. 北京: 中国标准出版社, 2017.

郭应龙, 李国兴, 尤传永. 输电线路舞动[M]. 北京: 中国电力出版社, 2003: 131-140.

SUSLOV B M. On the modulus of wire ropes[J]. Wire and Wire Products, 1936, 111: 176-182.

HRUSKA F H. Calculations of stresses in wire rope[J]. Wire and Wire Products, 1951, 26: 766-767,799-801.

LANTEIGNE J. Theoretical estimation of the response of helically armored cables to tension,torsion,and bending[J]. Journal of Applied Mechanics, 1985, 52(2): 423-432. doi: 10.1115/1.3169064

MACHIDA S, DURELLI A J. Response of a strand to axial and torsional displacements[J]. Journal of Mechanical Engineering Science, 1973, 15(4): 241-251. doi: 10.1243/JMES_JOUR_1973_015_045_02

MC CONNELL K G, ZEMKE W P. A model to predict the coupled axial torsion properties of ACSR electrical conductors[J]. Experimental Mechanics, 1982, 22(7): 237-244. doi: 10.1007/BF02326388

KNAPP R H. Derivation of a new stiffness matrix for helically armoured cables considering tension and torsion[J]. International Journal for Numerical Methods in Engineering, 1979, 14(4): 515-529. doi: 10.1002/nme.1620140405

COSTELLO G A, PHILLIPS J W. Effective modulus of twisted wire cables[J]. Journal of the Engineering Mechanics Division, 1976, 102(1): 171-181. doi: 10.1061/JMCEA3.0002092

LOVE B A E H. A treatise on the mathematical theory of elasticity[M]. [S.l.]: Dover Publications, 1944.

KUMAR K. S, Cochran J E. Closed-form analysis for elastic deformations of multilayered strands[J]. Journal of Applied Mechanics, 1987, 54(4): 898. doi: 10.1115/1.3173136

XIANG L, WANG H Y, CHEN Y, et al. Elastic-plastic modeling of metallic strands and wire ropes under axial tension and torsion loads[J]. International Journal of Solids and Structures, 2017, 129: 103-118. doi: 10.1016/j.ijsolstr.2017.09.008

JOLICOEUR C, CARDOU A. A numerical comparison of current mathematical models of twisted wire cables under axisymmetric loads[J]. Journal of Energy Resources Technology, 1991, 113(4): 241-249. doi: 10.1115/1.2905907

RAOOF M, KRAINCANIC I. Critical examination of various approaches used for analyzing helical cables[J]. The Journal of Strain Analysis for Engineering Design, 1994, 29(1): 43-55. doi: 10.1243/03093247V291043

CHEN Y, MENG F, GONG X. Full contact analysis of wire rope strand subjected to varying loads based on semi-analytical method[J]. International Journal of Solids and Structures, 2017, 117: 51-66. doi: 10.1016/j.ijsolstr.2017.04.004

张秋桦. 张拉导线应力及刚度的研究[D]. 北京: 华北电力大学, 2017.

杨光甫. 钢芯铝绞线等效弯曲刚度研究[D]. 北京: 华北电力大学, 2015.

卢银均,刘闯,孟遂民. 钢芯铝绞线弯曲状态受力分析[J]. 三峡大学学报(自然科学版),2018,40(3): 66-69.

LU Yinjun, LIU Chuang, MENG Suimin. Stress analysis of steel cored aluminum strand in bending state[J]. Journal of Three Gorges University (Natural Science), 2018, 40(3): 66-69.

UTTING W S, JONES N. The response of wire rope strands to axial tensile loads—part I:experimental results and theoretical predictions[J]. International Journal of Mechanical Sciences, 1987, 29(9): 605-619. doi: 10.1016/0020-7403(87)90033-6

施引文献

附加材料(0)

访问统计

点击查看大图

图(9) / 表(5)

计量

文章访问数: 608
HTML全文浏览量: 310
PDF下载量: 13
被引次数: 0

1. 试验概括
1.1 原材料与试件制作
1.2 试验方法
2. 试验结果与分析
2.1 变形分析
2.2 极限抗弯承载力
2.3 裂缝形态及分布
2.4 PP-ECC梁截面应变分布
3. 冻融循环和冻融循环-弯曲荷载耦合作用下PP-ECC梁抗弯承载力
3.1 冻融循环作用下PP-ECC梁抗弯承载力计算
3.2 冻融-弯曲荷载耦合作用下PP-ECC梁抗弯承载力计算
4. 结　论

1. 试验概括
1.1 原材料与试件制作
1.2 试验方法
2. 试验结果与分析
2.1 变形分析
2.2 极限抗弯承载力
2.3 裂缝形态及分布
2.4 PP-ECC梁截面应变分布
3. 冻融循环和冻融循环-弯曲荷载耦合作用下PP-ECC梁抗弯承载力
3.1 冻融循环作用下PP-ECC梁抗弯承载力计算
3.2 冻融-弯曲荷载耦合作用下PP-ECC梁抗弯承载力计算
4. 结　论

参考文献(21)

施引文献

附加材料(0)

访问统计

钢芯铝绞线的拉扭耦合力学性能

doi: 10.3969/j.issn.0258-2724.20200076

作者简介: 张龙（1977—），男，高级工程师，硕士，研究方向为输电线路工程，E-mail：11984726@qq.com

通讯作者: 晏致涛（1978—），男，教授，博士，研究方向为输电线路工程，E-mail：yzt@cqust.edu.cn

计量

出版历程

Mechanical Properties of Tension-Torsion Coupling in Aluminum Conductor Steel Reinforced

1. 试验概括

1.1 原材料与试件制作

1.2 试验方法

1.2.1 冻融循环试验

1.2.2 持荷设计

1.2.3 试验加载及测量方式

2. 试验结果与分析

2.1 变形分析

2.2 极限抗弯承载力

2.3 裂缝形态及分布

2.4 PP-ECC梁截面应变分布

3. 冻融循环和冻融循环-弯曲荷载耦合作用下PP-ECC梁抗弯承载力

3.1 冻融循环作用下PP-ECC梁抗弯承载力计算

3.1.1 基本假定

3.1.2 抗弯承载力计算分析

3.1.3 材料劣化规律

3.1.4 单一冻融循环作用下抗弯承载力计算模型

3.1.5 试验结果验证

3.2 冻融-弯曲荷载耦合作用下PP-ECC梁抗弯承载力计算

3.2.1 冻融-弯曲荷载耦合作用下抗弯承载力计算模型

3.2.2 试验结果验证

4. 结 论

计量

出版历程

目录

1. 试验概括

1.1 原材料与试件制作

1.2 试验方法

2. 试验结果与分析

2.1 变形分析

2.2 极限抗弯承载力

2.3 裂缝形态及分布

2.4 PP-ECC梁截面应变分布

3. 冻融循环和冻融循环-弯曲荷载耦合作用下PP-ECC梁抗弯承载力

3.1 冻融循环作用下PP-ECC梁抗弯承载力计算

3.2 冻融-弯曲荷载耦合作用下PP-ECC梁抗弯承载力计算

4. 结 论

作者简介:
张龙（1977—），男，高级工程师，硕士，研究方向为输电线路工程，E-mail：11984726@qq.com

通讯作者:
晏致涛（1978—），男，教授，博士，研究方向为输电线路工程，E-mail：yzt@cqust.edu.cn

4. 结　论

4. 结　论