Stress Characteristics of Tunnel Lining Structures Under Landslides with Different Angles of Sliding Zone
-
摘要:
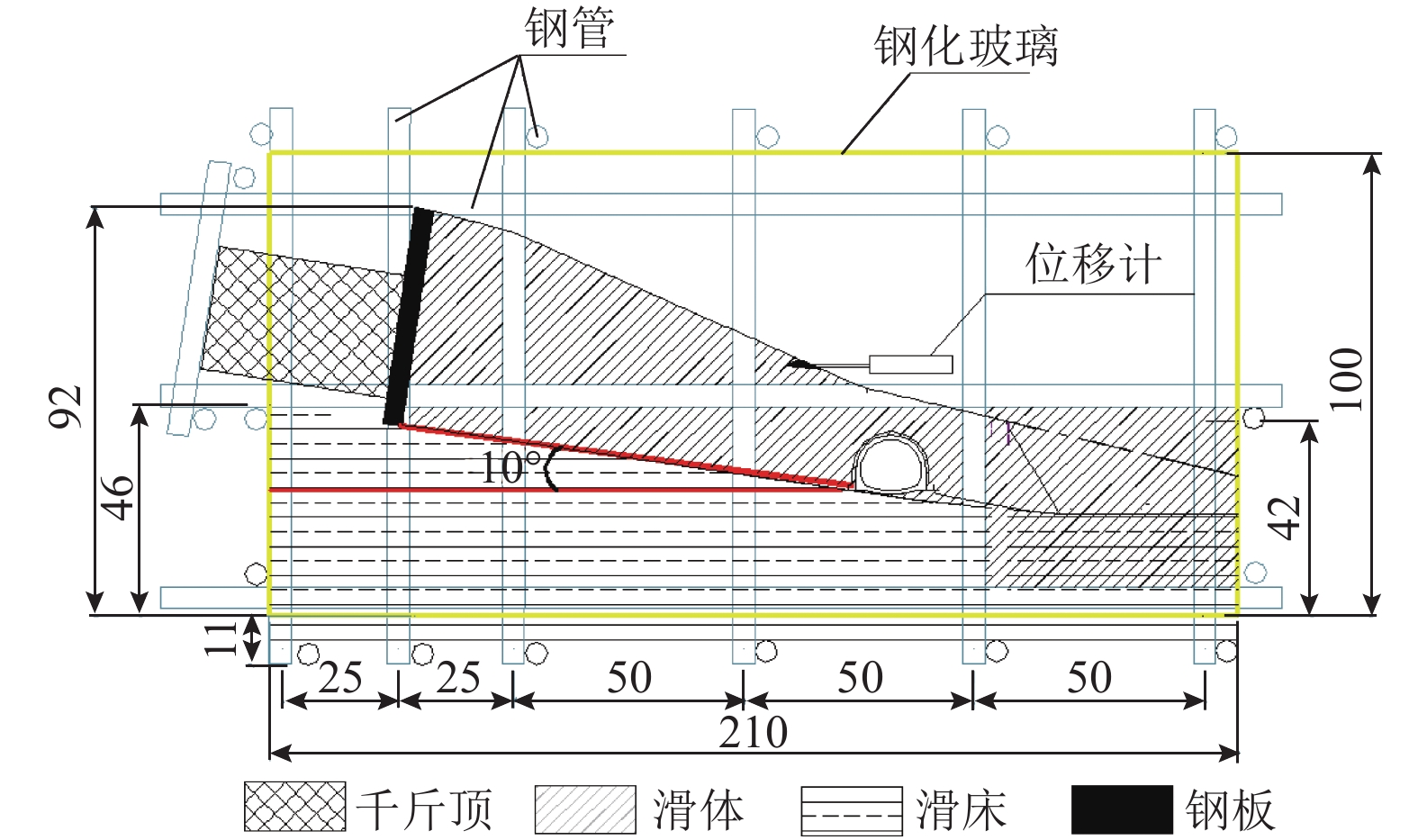
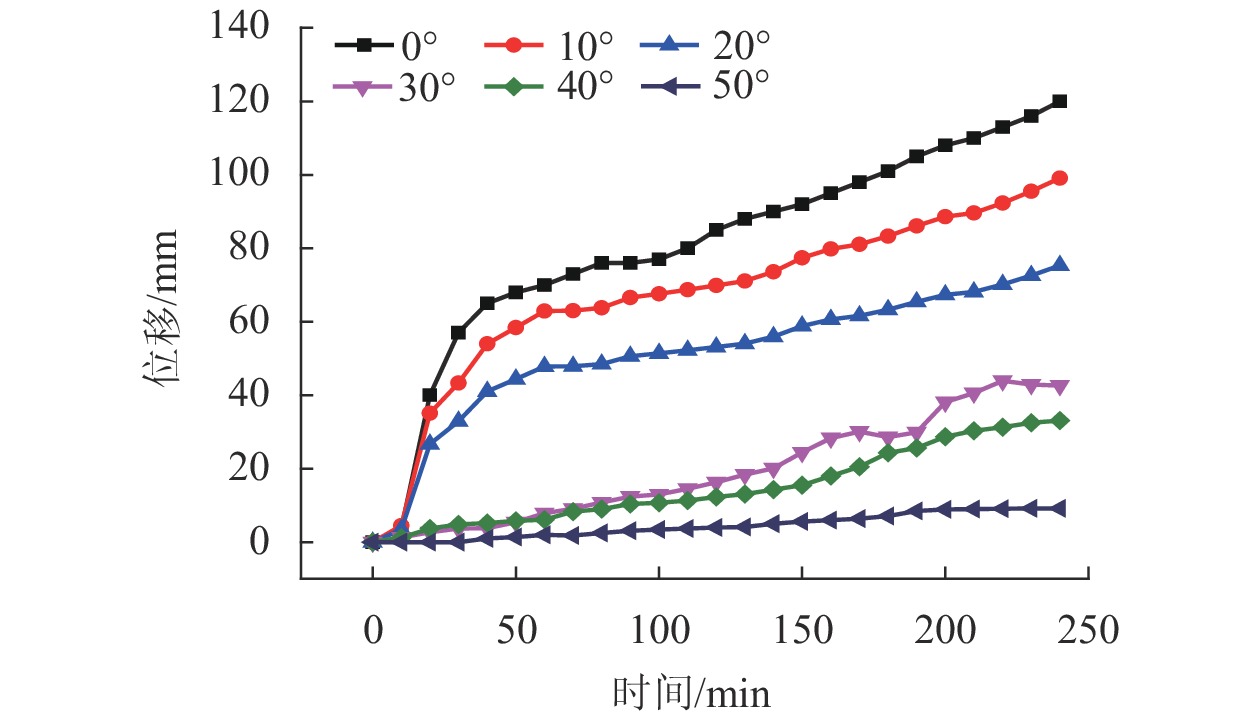
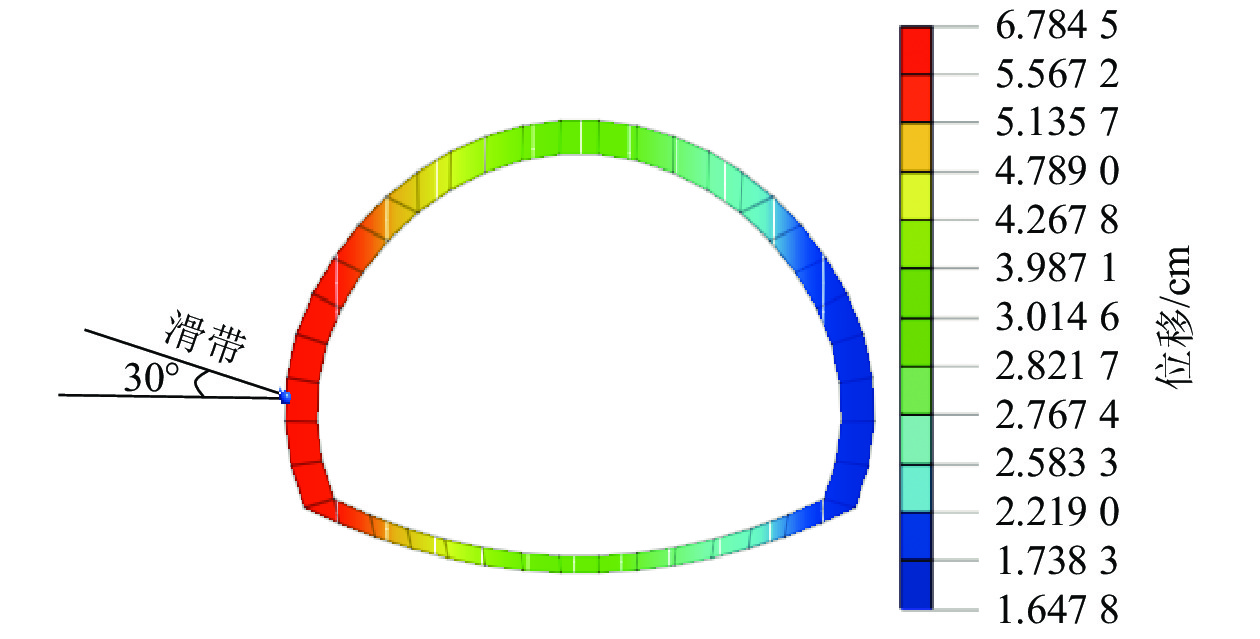
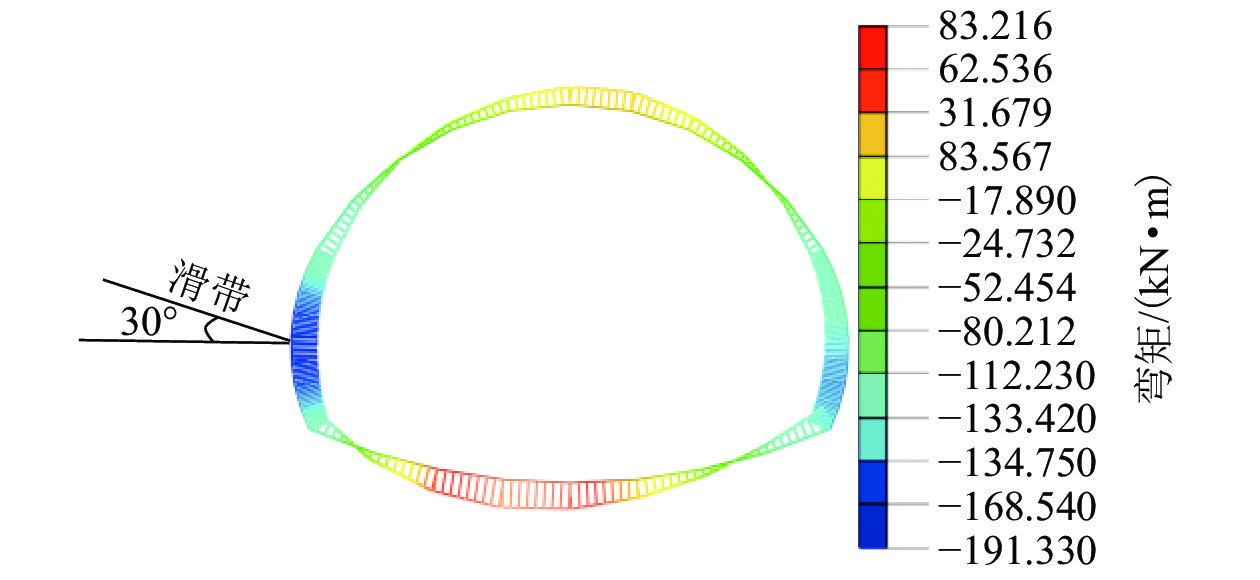
随着越来越多的隧道工程穿越滑坡区，滑坡与隧道相互作用过程的研究尤为重要. 为研究不同滑带角度滑坡对隧道衬砌结构受力的影响，以大（同）准（格尔）铁路南坪隧道为例，采用室内模型试验、数值模拟的方法，对0°、10°、20°、30°、40°、50°不同滑带角度条件下滑坡推力作用下隧道衬砌结构受力的影响特征及变化规律进行研究. 研究结果表明：滑带角度越小，隧道变形越大，作用在隧道衬砌结构上的弯矩、剪力及土压力越大，并在拱脚处出现最大值，形成隧道拱结构左右受力不对称特征，呈现偏压现象；通过计算隧道拱结构左右两侧的竖向偏压应力比显示，在拱肩位置且滑带为0时，偏压应力比为1.17，随着滑带角度的增大，隧道衬砌拱结构左右应力差越来越小，趋于平衡拱；在拱脚位置，偏压应力比随滑带角度的增大而逐渐增大，隧道衬砌拱结构左右两侧所受应力差越来越大，趋向于偏压隧道，最小偏压比和最大偏压比分别为1.08、1.87.
Abstract:With more and more tunnel projects passing through landslide areas, research on the interaction between landslide and tunnel is particularly important. To better understand the influence of landslide with different angles of sliding zone on the stress of tunnel lining structure, taking the Nanping tunnel of Datong–Zhungeer railway as an example, laboratory model tests and numerical simulations were conducted to study the influence characteristics and variation rules of tunnel lining structure stress under different angles of sliding zone (namely 0°, 10°, 20°, 30°, 40° and 50°). The results show that the smaller the angle of sliding zone, the greater the tunnel deformation, and the greater the bending moment, shear force and earth pressure acting on the tunnel lining structure. Moreover, the maximum stress appears at the arch foot, and the forces on the left and right tunnel arch structure are asymmetric, showing a phenomenon of bias pressure. The calculation of the vertical bias stress ratio of the left and right sides of the tunnel arch structure shows that at the arch shoulder position, when the angle of sliding zone is 0, the bias stress ratio is 1.17. As the angle of sliding zone increases, the difference between the left and right stresses of the tunnel lining arch structure is getting smaller and smaller, tending to balance around the arch; but at the arch foot position, the bias stress ratio gradually increases with the increase of the angle of sliding zone. The stress difference between the left and right sides of the tunnel lining linebreak left="0.7" right="1.3"/> arch structure becomes larger and larger. For the bias tunnel, the minimum bias ratio is 1.08 and the maximum bias ratio is 1.87.
-
Key words:
- landslide /
- tunnel /
- sliding zone angle /
- lining structure /
- mechanical characteristics /
- bias stress ratio
-
图 4 不同滑带角度条件下坡体位移
Figure 4. Displacements of slope with various angles of sliding zone
表 1 模型试验材料力学参数
Table 1. Mechanical parameters of model materials
名称 密度 ρ/
（kg•m−3）E/MPa c/kPa φ/（°） 滑坡体 1 900 18.65 27.79 25.35 滑带 1 800 9.36 15.82 15.63 滑床 2 200 23.72 54.24 54.32 隧道衬砌 2 100 289.61 236.65 61.71 
下载: 导出CSV
表 2 模型试验加载方案
Table 2. Loading scheme in model test
滑带角度/（°） 荷载/kN 加载时
间/min维持时
间/min0、10、20、30、40、50 0.5 10 20 1.0 10 20 5.0 20 40 10.0 20 40 15.0 20 40 20.0 30 40 25.0 30 40
下载: 导出CSV
表 3 不同滑带角度下隧道弯矩与剪应力值
Table 3. Bending and shear stress values of tunnel under different angles of sliding zone
滑带角度/（°） 弯矩/（kN•m） 剪力/kN 0 
10 
20 
30 
40 
50 
下载: 导出CSV
表 4 不同滑带角度下隧道土压力值
Table 4. Distribution of earth pressure on tunnel under different angles of sliding zone
滑带角度/（°） 土压力分布/kPa 0 
10 
20 
30 
40 
50 
下载: 导出CSV
表 5 模型试验下不同滑带角度隧道衬砌偏压应力比
Table 5. Bias stress ratio at different sliding angles in model test
滑带角度/（°） Δ1 Δ2 0 1.17 1.08 10 1.09 1.25 20 1.04 1.27 30 1.07 1.29 40 1.02 1.54 50 1.01 1.87
下载: 导出CSV
表 6 数值模拟下不同滑带角度隧道衬砌偏压应力比
Table 6. Bias stress ratios in numerical simulation
滑带角度/（°） Δ1 Δ2 0 1.21 0.98 10 1.20 1.22 20 1.14 1.25 30 1.11 1.48 40 1.09 1.83 50 1.06 2.34
下载: 导出CSV
-
[1] 马惠民,吴红刚. 隧道-滑坡体系的研究进展和展望[J]. 地下空间与工程学报,2016,12(2): 522-530.MA Huimin, WU Honggang. Progress and expectation of research on tunnel-landslide system[J]. Chinese Journal of Underground Space and Engineering, 2016, 12(2): 522-530. [2] 吴红刚, 吴道勇, 马惠民, 等. 隧道–滑坡体系类型和隧道变形模式研究[J]. 岩石力学与工程学报, 2012, 31(增刊2): 3632-3642.WU Honggang, WU Daoyong, MA Huimin, et al. Tunnel-landslide system type and tunnel deformation pattern research[J]. Journal of Rock Mechanics and Engineering, 2012, 31 (S2): 3632-3642. [3] 张鲁新,周德培. 蠕动滑坡成因及隧道变形机理的分析[J]. 岩石力学与工程学报,1999,18(2): 217-221. doi: 10.3321/j.issn:1000-6915.1999.02.023ZHANG Luxin, ZHOU Depei. Analysis of the causes of the peristaltic landslide and the mechanism of tunnel deformation[J]. Journal of Rock Mechanics and Engineering, 1999, 18(2): 217-221. doi: 10.3321/j.issn:1000-6915.1999.02.023 [4] 陈小云,吴红刚,艾挥. 正交体系下隧道与滑带相交力学模型与加固研究[J]. 科学技术与工程,2017,17(9): 73-78. doi: 10.3969/j.issn.1671-1815.2017.09.012CHEN Xiaoyun, WU Honggang, AI Hui. Study on the mechanical model and reinforcement of the intersection of tunnels and slides under the orthogonal system[J]. Science and Technology and Engineering, 2017, 17(9): 73-78. doi: 10.3969/j.issn.1671-1815.2017.09.012 [5] 陶志平. 滑坡地段隧道变形机理及灾害预测和治理研究[D]. 成都: 西南交通大学, 2003. [6] 毛坚强,周德培. 滑坡-隧道相互作用受力变形规律的研究[J]. 西南交通大学学报,2002,37(4): 371-376. doi: 10.3969/j.issn.0258-2724.2002.04.005MAO Jianqiang , ZHOU Depei. Deformation analysis for landslide-tunnel interaction[J]. Journal of Southwest Jiaotong University, 2002, 37(4): 371-376. doi: 10.3969/j.issn.0258-2724.2002.04.005 [7] 陈刚. 武罐路阳坡里滑坡与隧道的相互作用分析[D]. 成都: 西南交通大学, 2009. [8] 王旭. 滑坡隧道与抗滑桩相互作用机理研究及数值模拟[D]. 北京: 北京交通大学, 2014. [9] BOSSI G, SCHENATO L, MARCATO G. Structural health monitoring of a road tunnel intersecting a large and active landslide[J]. Applied Sciences, 2017, 7(12): 1271. doi: 10.3390/app7121271 [10] POISEL R, TINKHOF K M, PREH A. Landslide caused damages in a gallery[J]. Rock Mechanics and Rock Engineering, 2016, 49(6): 2301-2315. doi: 10.1007/s00603-015-0765-3 [11] NOFERINI L, PIERACCINI M, MECATTI D, et al. Using GB-SAR technique to monitor slow moving landslide[J]. Engineering Geology, 2007, 95(3): 88-98. [12] BOSSI G, ZABUSKI L, PASUTO A, et al. Capabilities of continuous and discontinuous modelling of a complex,structurally controlled landslide[J]. Geotechnical and Geological Engineering, 2016, 34(5): 1677-1686. doi: 10.1007/s10706-016-0057-z [13] LACASSE S, NADIM F. Landslide risk assessment and mitigation strategy[C]//First World Landslide Forum, Global Landslide Risk Reduction, International Consortium of Landslides. Tokyo: [s.n.], 2009: 31-61. [14] BENNETT P J, KOBAYASHI Y, SOGA K, et al. Wireless sensor network for monitoring transport tunnels[J]. Proceeings of the Institution of Civil Engineers:Geotechnical Engineering, 2010, 163(3): 147-156. [15] BARLA G, DEBERNARDI D, PERINO A. Lessons learned from deep-seated landslides activated by tunnel excavation[J]. Geomechanics and Tunnelling, 2015, 8(5): 394-401. doi: 10.1002/geot.201500028 [16] CRUDEN D, LAN H. Using the working classification of landslides to assess the danger from a natural slope[J]. Engineering Geology for Society and Territory, 2015, 2: 3-12. [17] LUNARDI P, BARLA G. Full-face excavation in difficult ground[J]. Geomechanics and Tunneling, 2014, 7(5): 461-468. doi: 10.1002/geot.201400037 [18] MARINOS P, HOEK E. Estimating the geotechnical properties of heterogeneous rock masses such as flysch[J]. Bulletin of Engineering Geology and the Environment, 2001, 60(2): 85-92. [19] TANTIANUPARP P, SHI X, ZHANG L, et al. Characterization of landslide deformations in Three Gorges area using multiple InSAR data stacks[J]. Remote Sensor, 2013, 5(6): 2704-2719. doi: 10.3390/rs5062704 [20] CHIU Y C, LEE C H, WANG T T. Lining crack evolution of an operational tunnel influenced by slope instability[J]. Tunnelling and Underground Space Technology, 2017, 65: 167-178. doi: 10.1016/j.tust.2017.03.004 [21] 杜升涛. 抗滑桩在隧道-滑坡正交体系下的加固技术研究[D]. 北京: 中国铁道科学研究院, 2014. [22] 陶志平,周德培. 用抗滑桩整治滑坡地段隧道变形的模型试验研究[J]. 岩石力学与工程学报,2004,23(3): 457-460. doi: 10.3321/j.issn:1000-6915.2004.03.018TAO Zhiping, ZHOU Depei. Model testing research on controlling tunnel deformation in landslide field with antislide piles[J]. Journal of Rock Mechanics and Engineering, 2004, 23(3): 457-460. doi: 10.3321/j.issn:1000-6915.2004.03.018 [23] 郑颖人,赵尚毅. 有限元强度折减法在土坡与岩坡中的应用[J]. 岩石力学与工程学报,2004,23(19): 3381-3388. doi: 10.3321/j.issn:1000-6915.2004.19.029ZHENG Yingren, ZHAO Shangyi. Application of strength reduction FEM in soil and rock slope[J]. Journal of Rock Mechanics and Engineering, 2004, 23(19): 3381-3388. doi: 10.3321/j.issn:1000-6915.2004.19.029 [24] 谭红. 赣龙铁路马蹄径隧道滑坡分析与整治[J]. 岩土工程界,2003,6(11): 63-65.TAN Hong. Analyses of landslides of Matijing tunnel,Gan-Long railway and their control[J]. Geotechnical Engineering World, 2003, 6(11): 63-65. [25] 喻渝. 相田二号隧道山体滑坡及隧道衬砌病害整治[J]. 铁道标准设计,1996(1): 20-22. [26] 于清杨,刘伟,佴磊,等. 偏压隧道偏压应力比特征分析[J]. 吉林大学学报(地球科学版),2018,48(6): 1797-1803.YU Qingyang, LIU Wei, WEI Lei, et al. Analysis of bias stress ratio in bias tunnels[J]. Jilin University Journal (Earth Science Edition), 2018, 48(6): 1797-1803. [27] 罗兴华,兰晓峰,舒中文,等. 大准铁路南坪隧道-滑坡体系变形特征及处治技术[J]. 铁道建筑,2018,58(10): 55-59. doi: 10.3969/j.issn.1003-1995.2018.10.14LUO Xinghua, LAN Xiaofeng, SHU Zhongwen, et al. Deformation characteristics and treatment techniques of Nanping tunnel-landslide system in Datong-Zhungeer railway[J]. Railway Construction, 2018, 58(10): 55-59. doi: 10.3969/j.issn.1003-1995.2018.10.14 [28] 林承华,胡志平,吴银亮. 骡坪隧道洞口山体滑坡稳定性分析及治理措施研究[J]. 路基工程,2019(2): 225-229.LIN Chenghua, HU Zhiping, WU Yinliang. Analysis of landslide stability and governance measures at the mouth of the Luping tunnel[J]. Subgrade Engineering, 2019(2): 225-229. [29] 北京迈达斯技术有限公司. Midas GTS NX用户手册[M/OL]. (2018-06-09)[2019-06-18]. https://www.doc88.com/p-2847819962113.html. [30] 熊浩. 圆形地下连续墙力学特性及其围护效果研究[D]. 武汉: 湖北工业大学, 2014. [31] 齐良锋,简浩,唐丽云. 引入接触单元模拟桩土共同作用[J]. 岩土力学,2005,26(1): 127-130. doi: 10.3969/j.issn.1000-7598.2005.01.027QI Liangfeng, JIAN Hao, TANG Liyun. The computiong model of adopting contact element to simulate the pile-soil’s reciprocity[J]. Rock and Soil Mechanics, 2005, 26(1): 127-130. doi: 10.3969/j.issn.1000-7598.2005.01.027 -
下载:
点击查看大图
计量
- 文章访问数: 457
- HTML全文浏览量: 222
- PDF下载量: 26
- 被引次数: 0