Comprehensive Evaluation Model for One-Dimensional Crash Energy Management of Trains
-
摘要:
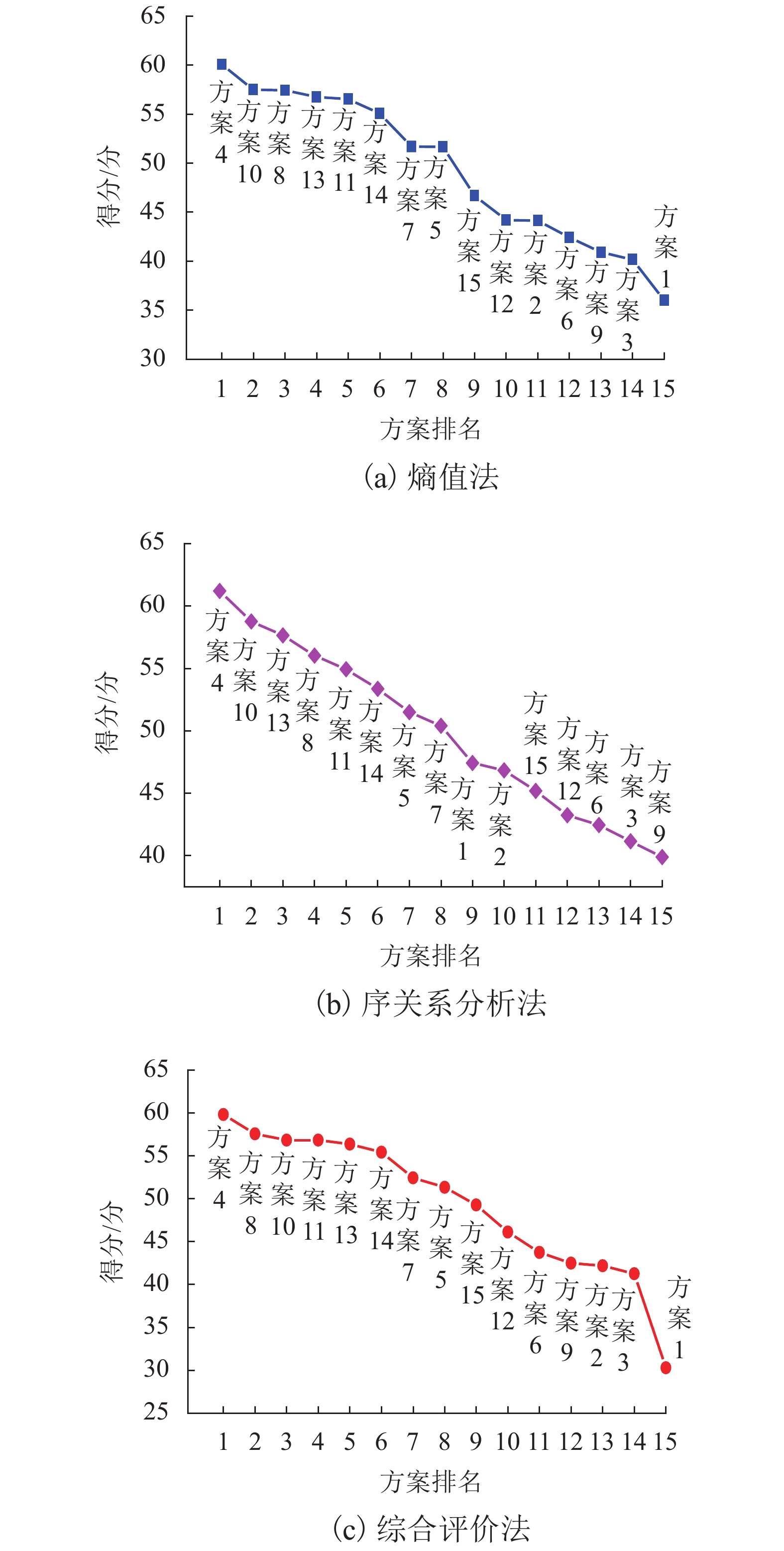
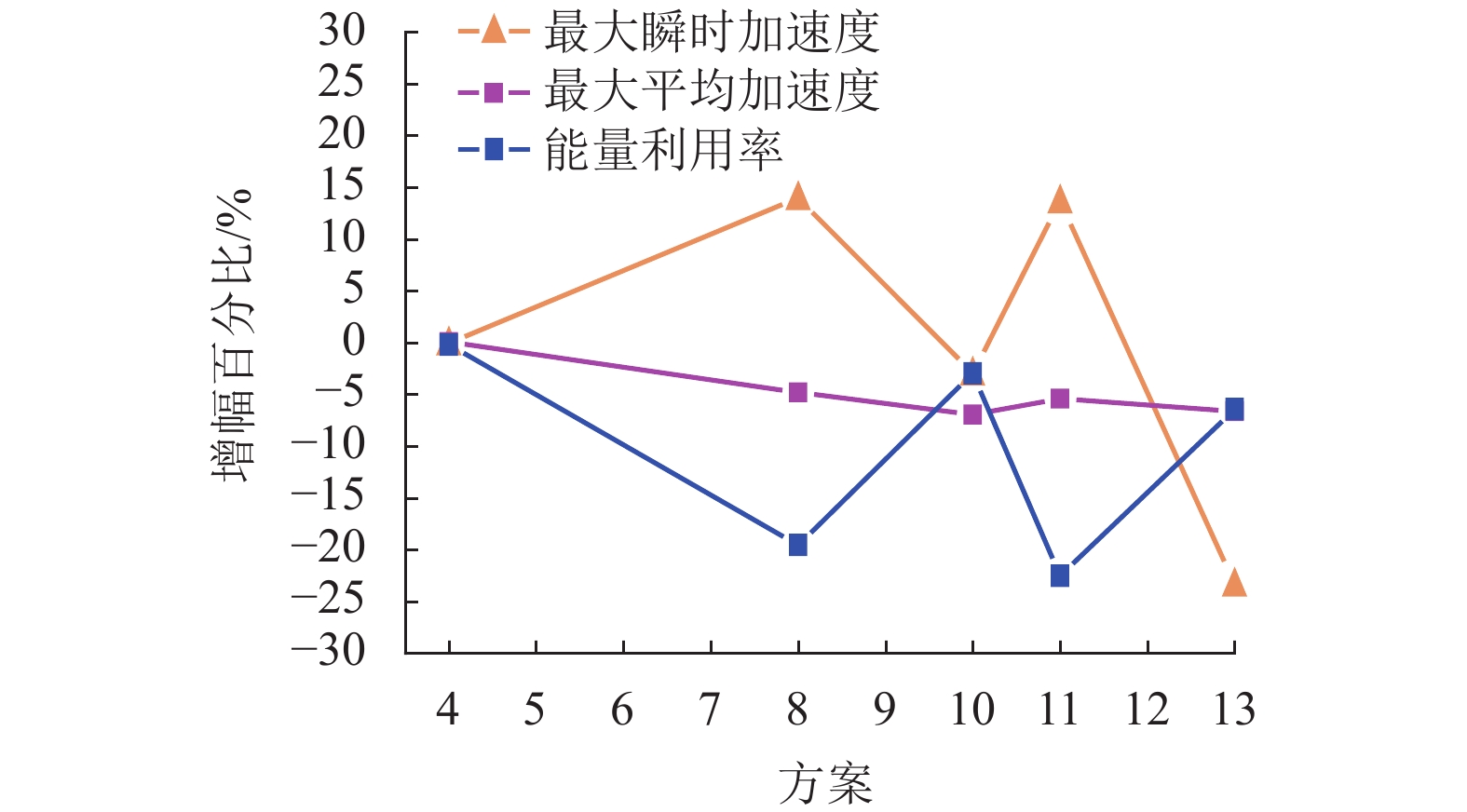
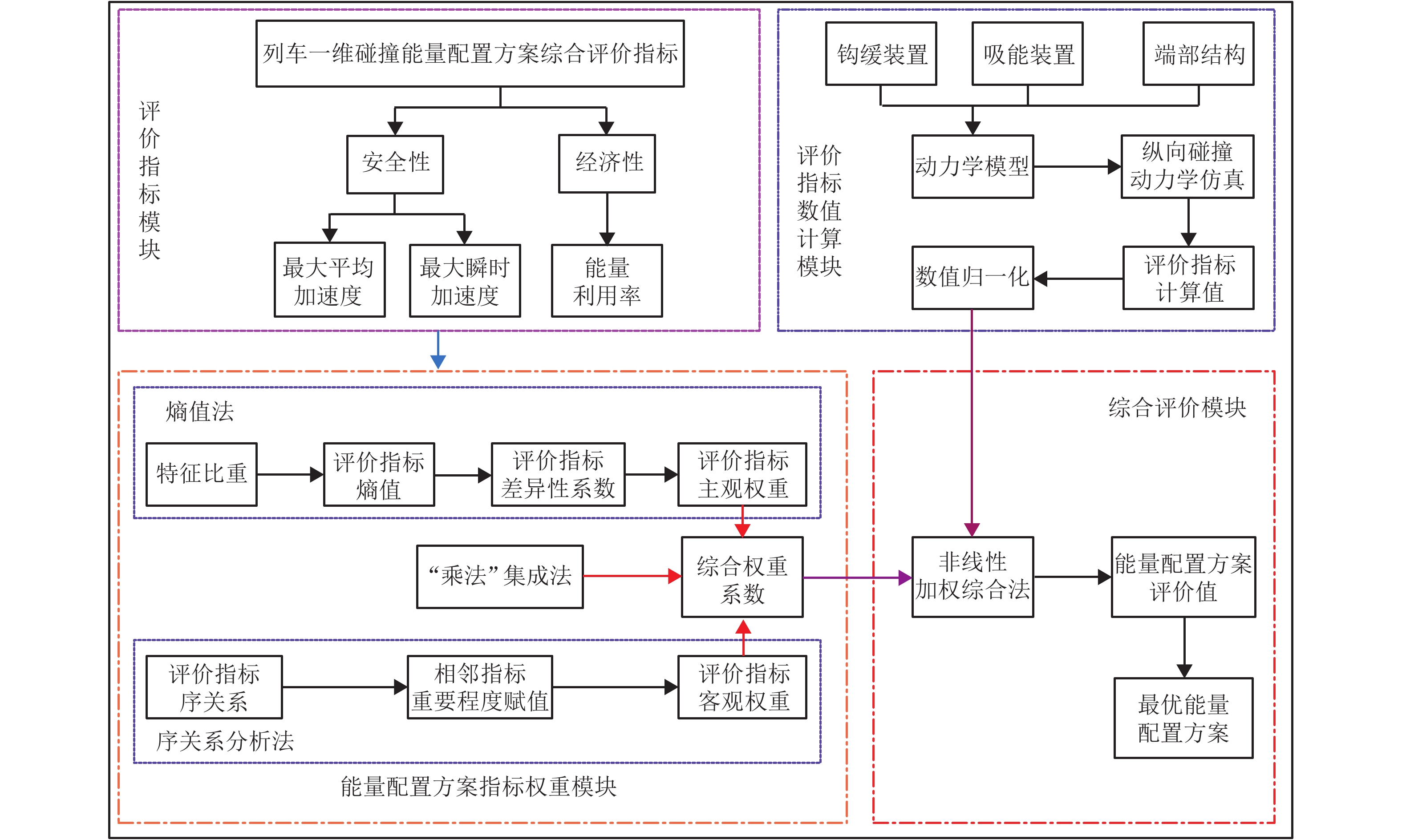
为了更科学全面地对列车碰撞能量方案进行配置和评价，以列车最大平均加速度、最大瞬时加速度和能量利用率为评价指标，利用序关系分析法和熵值法得到的主、客观指标权重推导出更加合理的综合权重系数；采用非线性加权综合法融合权重信息和评价指标信息，获得了列车一维碰撞能量管理综合评价模型；采用此模型对某型列车的15种能量配置方案进行综合评价. 研究结果表明：此模型综合评价结果与各指标性能变化幅度分析结果一致，具有较好的适用性和可靠性；方案4为最优方案，其最大瞬时加速度指标性能比方案8下降14.03%，但最大平均加速度指标性能和能量利用率指标性能分别比方案8提升了4.92%和19.44%；该结果既体现了对安全性影响最大的最大平均加速度指标的重要性，又综合考虑了与经济性相关的能量利用率指标.
Abstract:In order to configure and evaluate the train collision energy scheme more scientifically and comprehensively, the maximum average acceleration, maximum instantaneous acceleration and energy utilization rate of trains were taken as evaluation indexes, and a more reasonable comprehensive weight coefficient was derived by using the subjective and objective index weights obtained by the order relation analysis and entropy method. A comprehensive evaluation model of train one-dimensional collision energy management was obtained by fusing weight information and evaluation index information with nonlinear weighted synthesis method, then 15 energy allocation schemes of a certain type of train were comprehensively evaluated by using this model. The results indicate that the comprehensive evaluation results are consistent with that of the change range of all indexes, and it has better applicability and reliability. Scheme 4 is the optimal scheme, in which the maximum instantaneous acceleration index decreases by 14.03%, but the maximum average acceleration index and energy utilization rate index increase by 4.92% and 19.44% compared with scheme 8 respectively. These results both reflect the importance of the maximum average acceleration index, which has the greatest impact on safety, and comprehensively considers the energy utilization rate index related to economy.
-
图 1 列车一维碰撞能量管理综合评价流程
Figure 1. Flow chart for comprehensive evaluation of train one-dimensional collision energy management
图 2 15种能量配置方案的各指标计算结果
Figure 2. Calculation results of each index for 15 energy allocation schemes
图 3 各能量配置方案综合评价结果排序
Figure 3. Ranking of comprehensive evaluation results of each energy allocation scheme
图 4 方案4、8、10、11、13各指标数值变化幅度百分比
Figure 4. Percentage changes of each indicator value of schemes 4，8，10，11 and 13
表 1 ${r_k}$ 赋值
Table 1. Assignment reference table of ${r_k}$
${r_k}$ 说明 1.0 指标${x_{k - 1}}$与指标${x_k}$具有同样重要性 1.2 指标${x_{k - 1}}$与指标${x_k}$稍微重要 1.4 指标${x_{k - 1}}$与指标${x_k}$明显重要 1.6 指标${x_{k - 1}}$与指标${x_k}$强烈重要 1.8 指标${x_{k - 1}}$与指标${x_k}$极端重要 
下载: 导出CSV
表 2 列车碰撞能量配置方案[10]
Table 2. Train collision energy allocation schemes
方案 头车钩缓装置 中间车钩缓装置 吸能装置 阻抗
力/kN额定容
量/kJ阻抗
力/kN额定容
量/kJ阻抗
力/kN额定容
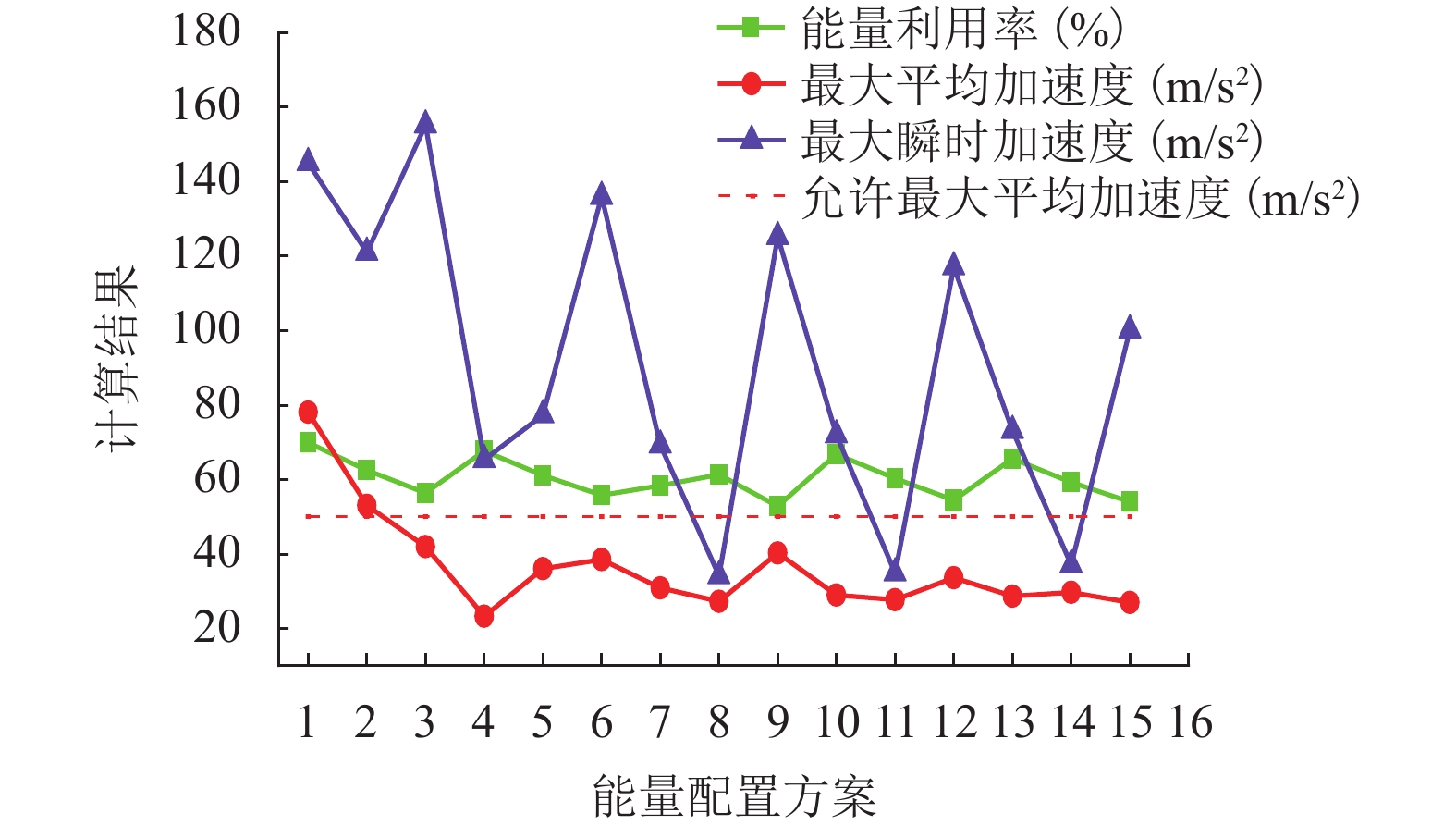
量/kJ1 1000 387.5 1000 743 1400 970 2 387.5 1200 883 3 387.5 1400 1023 4 1200 457.5 1000 743 1400 970 5 1200 883 6 1400 1023 7 1000 387.5 1000 743 1600 1110 8 1200 883 9 1400 1023 10 1200 457.5 1000 743 1600 1110 11 1200 883 12 1400 1023 13 1400 527.5 1000 743 1600 1110 14 1200 883 15 1400 1023
下载: 导出CSV
表 3 15种能量配置方案的各指标数据一致化和无量纲化处理结果
Table 3. Data consistency and dimensionless processing results of 15 energy allocation schemes
方案 能量利
用率/%最大平均加
速度/（m•s−2）最大瞬时加
速度/（m•s−2）1 68.5178 18.7772 36.2090 2 54.1003 37.5183 42.3262 3 42.0498 45.7863 33.6498 4 64.1945 59.7502 56.4960 5 51.3224 50.1960 53.4373 6 40.9935 48.3586 38.5186 7 46.0210 54.0545 55.4972 8 51.7137 56.8104 64.4235 9 35.2421 47.0725 41.2653 10 62.3947 55.5243 54.8106 11 49.7770 56.4430 64.2363 12 38.2938 52.0334 43.3251 13 60.1842 55.7080 54.4985 14 47.7034 54.9731 63.6745 15 37.4918 56.9942 47.6321
下载: 导出CSV
表 4 指标序关系及${r_k}$赋值表
Table 4. Index order relation and assignment table of ${r_k}$
类别 取值 指标序关系 ${x_2} \succ {x_3} \succ {x_1} (x_1^* \succ x_2^* \succ x_3^*)$ ${r_2}$ 1.8 ${r_3}$ 1.2
下载: 导出CSV
表 5 G1-法计算的各评价指标权重
Table 5. Weight of each evaluation index by G1 method
指标类型 权重 最大平均加速度 0.4954 最大瞬时加速度 0.2752 能量利用率 0.2294
下载: 导出CSV
表 6 熵值法计算的各评价指标权重
Table 6. Weight of each evaluation index by entropy method
指标类型 权重 最大平均加速度 0.3328 最大瞬时加速度 0.3336 能量利用率 0.3336
下载: 导出CSV
表 7 各评价指标综合权重
Table 7. Comprehensive weight of each evaluation index
指标类型 权重 最大平均加速度 0.4948 最大瞬时加速度 0.2755 能量利用率 0.2297
下载: 导出CSV
-
[1] JACOBSEN K, TYRELL D. Impact test of a crash-energy management passenger rail car[C]//2004 ASME/IEEE Joint Rail Conference. Baltimore: ASME, 2004: 19-26. [2] TYRELL D, JACOBSEN K, PARENT D. Preparations for a train-to-train impact test of crash-energy management passenger rail equipment[C]//2005 Joint Rail Conference. Pueblo: ASME, 2005: 107- 116. [3] CAROLAN M, MUHLANGER M, PERLMAN B, et al. Occupied volume integrity testing: elastic test results and analyses[C]//ASME 2011 Rail Transportation Division Fall Technical Conference. Minneapolis: ASME, 2011: 47-57. [4] CAROLAN M, PERLMAN B, TYRELL D. Crippling test of a budd pioneer passenger car[C]//ASME 2012 Joint Rail Conference. Philadelphia: ASME, 2012: 225-235. [5] WALDECK H. ICE动力车碰撞仿真[J]. 电力牵引快报,1996(4): 26-32.WALDECK H. ICE power car crash simulation[J]. Electric Traction Report, 1996(4): 26-32. [6] TYRELL D,张钟浩. 机车抗碰撞能力改进研究[J]. 国外内燃机车,2002(3): 23-31.TYRELL D, ZHANG Zhonghao. Research on improvement of anti-collision ability of locomotive[J]. Foreign Diesel Locomotive, 2002(3): 23-31. [7] Rail Track PLC. Structural requirements for railway vehicle: GM/RT—2100[S]. London: Safety and Standards Directo Rate, 1994. [8] LU G. Energy absorption requirement for crashworthy vehicles[J]. Proceedings of the Institution of Mechanical Engineers,Part F:Journal of Rail and Rapid Transit, 2002, 216(1): 31-39. [9] 杨宝柱,肖守讷,杨超. 能量吸收方案对列车碰撞响应的影响[J]. 城市轨道交通研究,2018(3): 54-57.YANG Baozhu, XIAO Shoune, YANG Chao. The effect of energy absorbing schemes on train crash responses[J]. Urban Mass Transit, 2018(3): 54-57. [10] 袁成标. 基于列车碰撞动力学的纵向碰撞建模及能量管理研究[D]. 成都: 西南交通大学, 2018. [11] 郭亚军. 综合评价理论、方法及应用[M]. 北京: 科学出版社, 2007: 16-17, 45-47, 73. [12] 王文华,黄仁乐,皱保平,等. 基于序关系分析法的配电网风险评估方法[J]. 计算机与数字工程,2018,46(8): 1516-1519,1552. doi: 10.3969/j.issn.1672-9722.2018.08.007WANG Wenhua, HUANG Renle, ZHOU Baoping, et al. Based on-sequence relation analysis risk assessment method of distribution network[J]. Computer and Digital Engineering, 2018, 46(8): 1516-1519,1552. doi: 10.3969/j.issn.1672-9722.2018.08.007 [13] 李航,李根,张帅阳,等. 基于序关系分析法的车辆主动悬架控制器仿真研究[J]. 中国工程机械学报,2018,16(3): 231-236.LI Hang, LI Gen, ZHANG Shuaiyang, et al. Simulation research on vehicle active suspension controller based on the order relation analysis method[J]. Chinese Journal of Construction Machinery, 2018, 16(3): 231-236. [14] 梁东,李远富,樊敏. 基于区间数距离的铁路线路方案决策模型与方法[J]. 西南交通大学学报,2019,54(4): 823-830.LIANG Dong , LI Yuanfu , FAN Min. Decision making model and method based on distance measure between interval numbers in railway location[J]. Journal of Southwest Jiaotong University, 2019, 54(4): 823-830. [15] 徐健,杜贞栋,林洪孝,等. 基于序关系分析法的节水型社会评价指标权重的确定[J]. 水电能源科学,2014,32(10): 132-134.XU Jian, DU Zhendong, LIN Hongxiao, et al. Confirmation of index weight of water-saving social construction based on order relation analysis method[J]. Water Resources and Power, 2014, 32(10): 132-134. [16] 高瑾瑾,郑源,李涧鸣. 基于改进序关系分析法的抽水蓄能电站经济效益综合评价[J]. 长江科学院院报,2018,35(4): 137-142. doi: 10.11988/ckyyb.20161372GAO Jinjin, ZHENG Yuan, LI Jianming. Comprehensive evaluation of economic benefits of pumped storage power plants by improved order relation analysis method[J]. Journal of Yangtze River Scientific Research Institute, 2018, 35(4): 137-142. doi: 10.11988/ckyyb.20161372 [17] 梁晨. 子午线轮胎综合接地性能评价体系与方法研究[D]. 南京: 江苏大学, 2013. [18] 余建英, 何旭宏. 数据统计分析与SPSS应用[M]. 北京: 人民邮电出版社, 2003: 87. [19] 王学军,郭亚军,兰天. 构造一致性判断矩阵的序关系分析法[J]. 东北大学学报,2006,27(1): 115-118.WANG Xuejun, GUO Yajun, LAN Tian. Rank correlation analysis of formation of consistent judgment matrix[J]. Journal of Northeastern University, 2006, 27(1): 115-118. [20] 刘祎. 多功能包装机设计质量综合评价系统研究[D]. 太原: 中北大学, 2016. -
下载:
点击查看大图
计量
- 文章访问数: 523
- HTML全文浏览量: 211
- PDF下载量: 7
- 被引次数: 0