Comparison of AOA Localization in Ultrashort Wave under Various Azimuth Calculation Methods
-
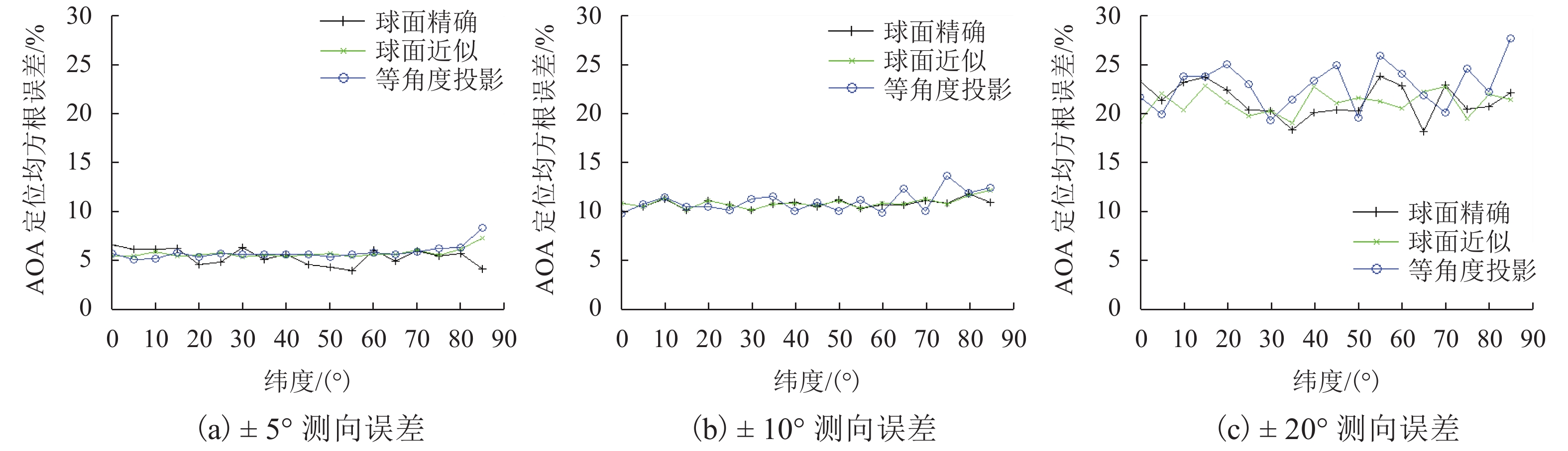
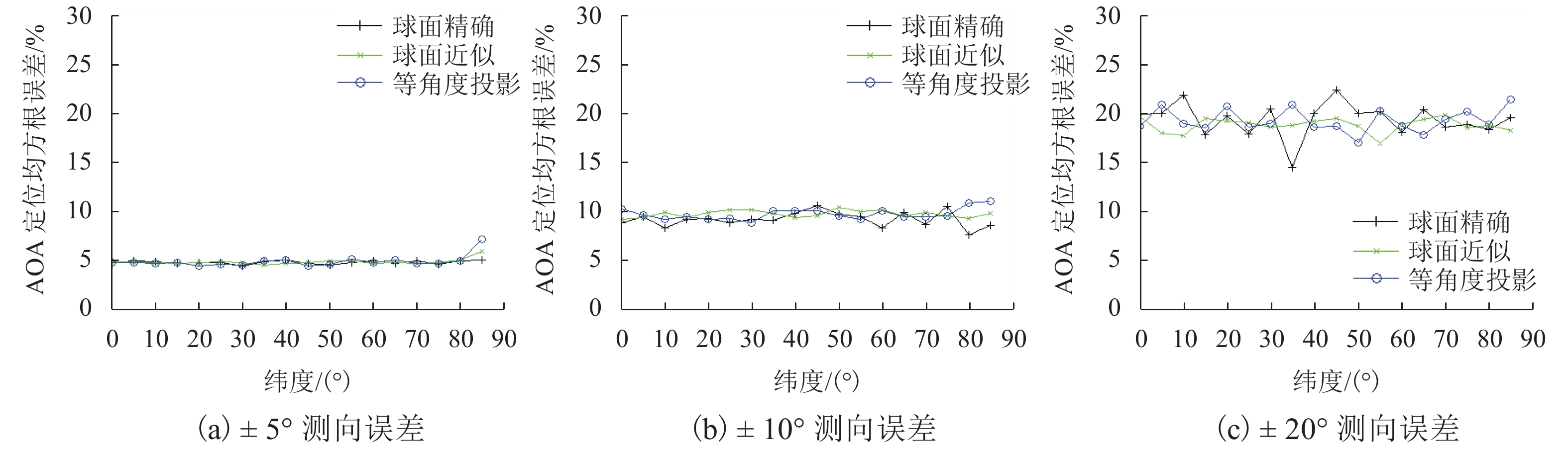
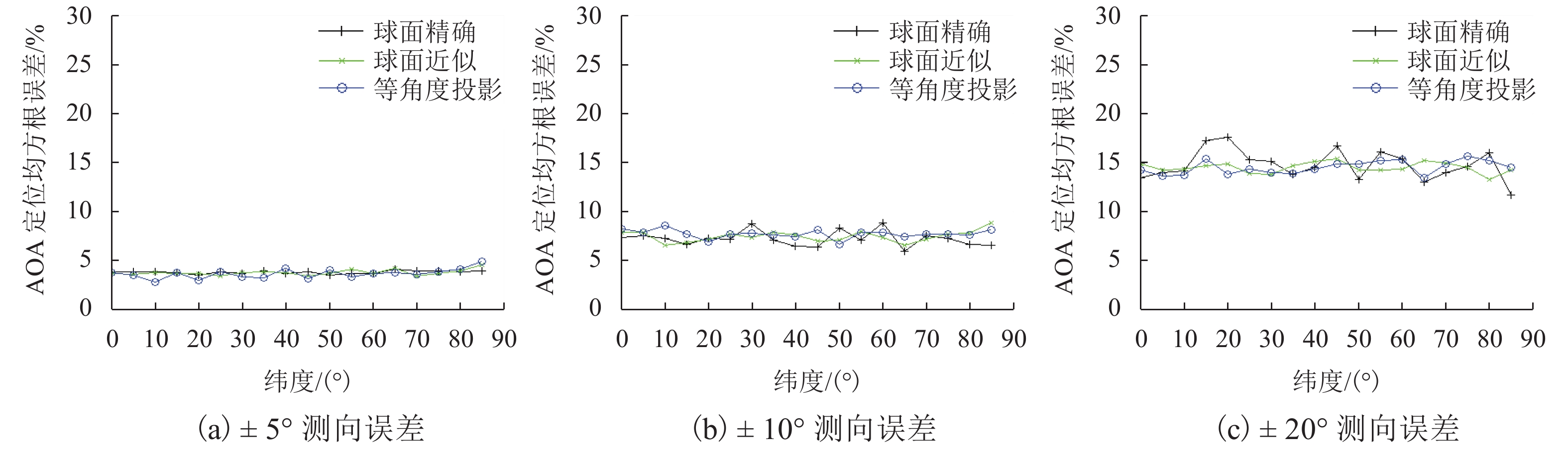
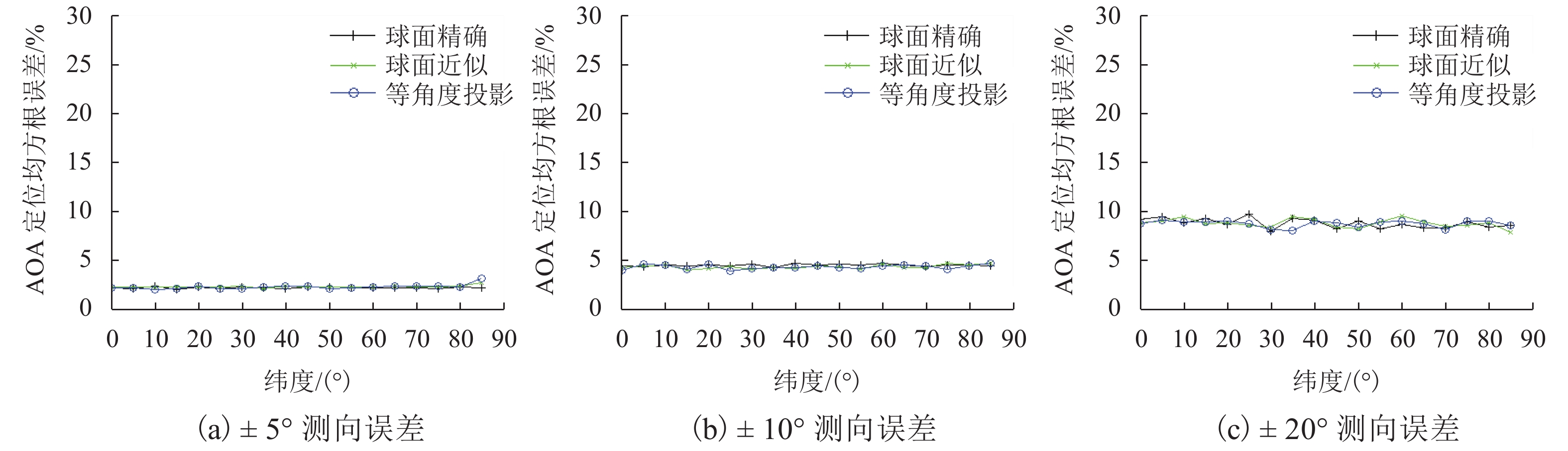
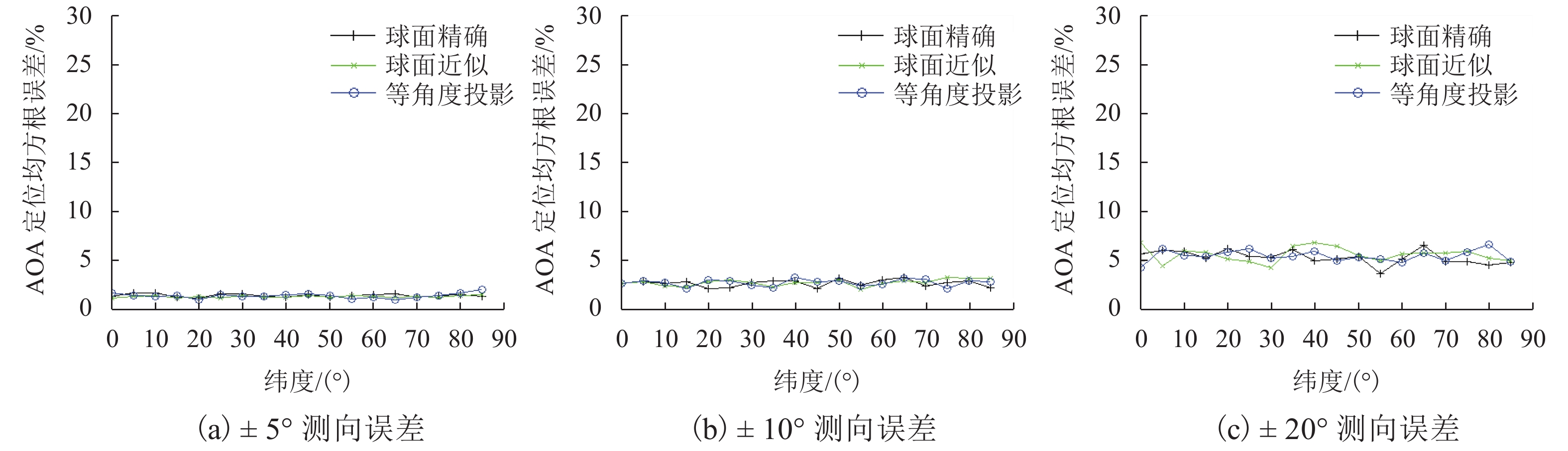
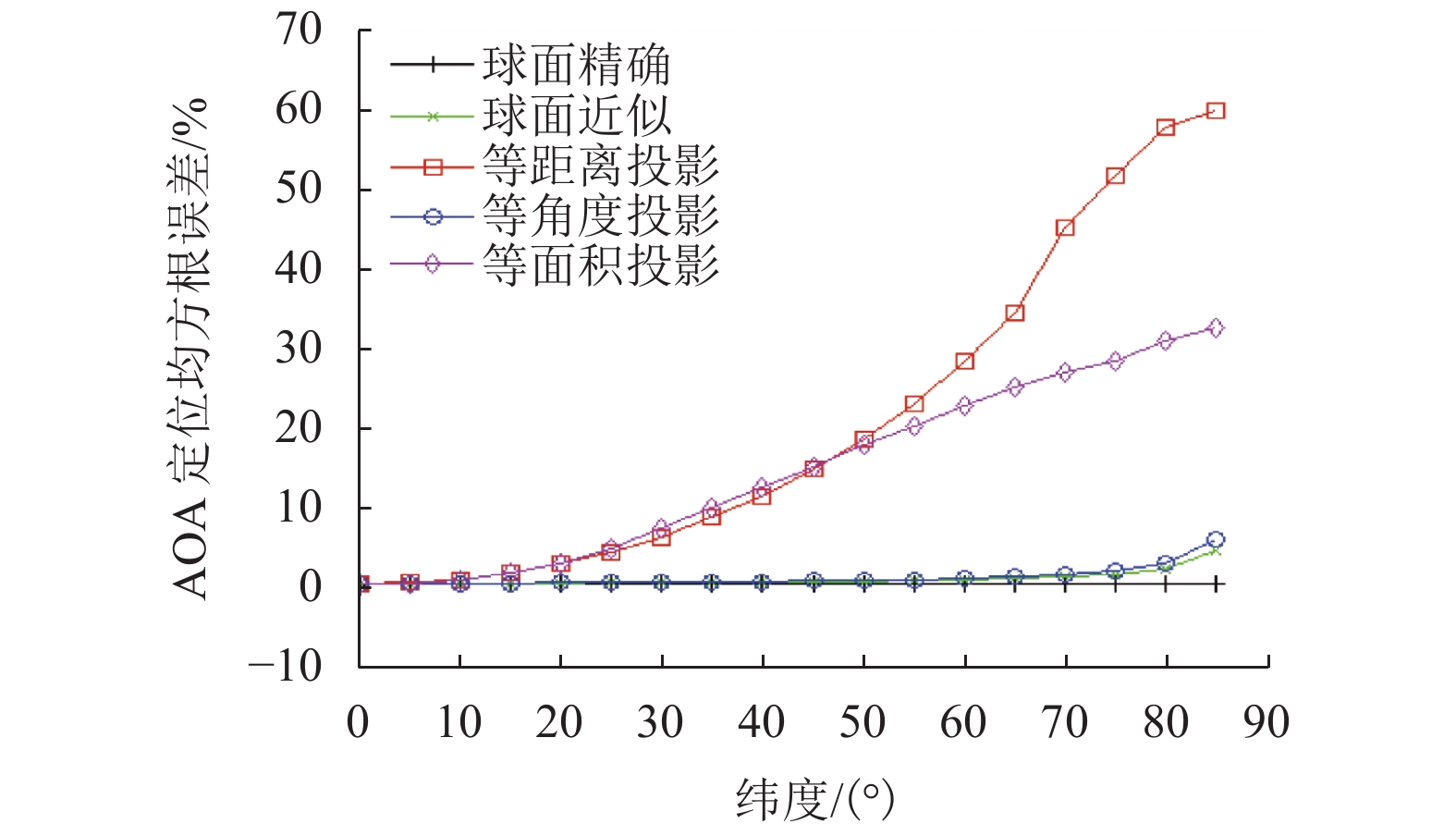
摘要: 考虑到方位角计算是AOA (angle of arrival)定位的基础之一,首先,提出了以大地坐标计算方位角的球面近似法和正轴圆柱投影-平面法;进而,建立了球面精确AOA定位方程、球面近似AOA定位方程和正轴圆柱投影-平面AOA定位方程;最后,采用无约束非线性规划方法建立了基于大地坐标的分别与上述方程相对应的3个最优化AOA定位模型,并以网格逐点搜索求解法进行了模型验证. 验证结果的分析表明:在不考虑测向误差时,球面精确AOA定位模型的精度最高,且与纬度无关,但其定位运算时间最长;球面近似AOA定位模型和正轴圆柱投影-平面AOA定位模型的精度均较高,后者的定位误差略大于前者,定位运算时间也长于前者;要提高AOA定位网的定位精度,既可提高各站点的测向精度,也可增加测向站点数,并应综合考虑定位时效性要求和精度要求选择合适的AOA定位模型.Abstract: Given that azimuth calculation is fundamental to angle-of-arrival (AOA) localization, the spherical approximation method and normal cylindrical projection-plane method for azimuth calculation on geodetic coordinates are proposed firstly. Furthermore, the AOA localization equations based on spherical accuracy calculation, spherical approximation calculation, and normal cylindrical projection-rectangle are established respectively. Finally, the unconstrained nonlinear programming method is used to establish the three optimization AOA localization models on geodetic coordinates, which correspond to the above equations respectively, and the models are verified by the point-by-point grid search method. The numerical results show without considering the direction-finding error, the spherical accuracy AOA localization model has the highest precision, which is independent of latitude, but its positioning operation time is the longest. As for the spherical approximation AOA localization model and the normal cylindrical projection-rectangle AOA localization model, both have a high precision, the positioning error of the latter is slightly higher than that of the former, and its positioning operation time is also longer than that of the former. The positioning accuracy of AOA localization network can be improved by increasing either the direction finding accuracy of each site or the number of direction finding sites. The appropriate AOA localization model is selected according to the overall positioning requirements of the timeliness and precision.
-
Key words:
- passive location /
- AOA localization /
- azimuth calculation /
- optimal modeling /
- geodetic coordinates
-
表 1 AOA定位仿真参数设置
Table 1. Setting of simulation parameters in AOA localization
参数 说明 定位网络构成 在东西长、南北长均约 20 km 的范围内,均匀布设 3、4、5、9、16 个站点构成的定位网络,其中有 4 个站点的网络无中心站点. 待定位信号源的位置 在定位网络之内,在经线上等间隔取 10 个点,在纬线上等间隔取 10 个点,共取 100 个不同的点. 测向误差 1) 不考虑误差 2) −5°~5° 随机均匀分布 3) −10°~10° 随机均匀分布 4) −20°~20° 随机均匀分布 AOA 定位误差 求 100 个定位误差的均方根 -
范平志, 邓平, 刘林. 蜂窝网无线定位[M]. 北京: 电子工业出版社, 2002: 61-74. XU Jun, MA Maode, LAW C L. Cooperative angle-of-arrival position localization[J]. Measurement, 2015, 59: 302-313. HE Y, BEHNAD A. Accuracy analysis of the two-reference-node angle-of-arrival localization system[J]. IEEE Wireless Communications Letters, 2015, 4(3): 329-332. doi: 10.1109/LWC.2015.2415788 田晗. 多站测向交叉定位中的非线性改进最小二乘法[J]. 科技通报,2018,34(5): 112-116.TIAN Han. The improved nonlinear least squares for cross location of multi station direction[J]. Bulletin of Science and Technology, 2018, 34(5): 112-116. 白晶,马燕飞,刘晓丽. 考虑地球曲率情况下测向定位系统中的最优交会角[J]. 无线电通信技术,2019,45(1): 78-83. doi: 10.3969/j.issn.1003-3114.2019.01.15BAI Jing, MA Yanfei, LIU Xiaoli. Optimum cut angle in bearing-only location system with consideration of earth curvature[J]. Radio Communications Technology, 2019, 45(1): 78-83. doi: 10.3969/j.issn.1003-3114.2019.01.15 王存良,朱喜明. 无源测向定位的地球椭球面算法[J]. 电光系统,2018(3): 31-35.WANG Cunliang, ZHU Ximing. Earth ellipsoid algorithm for passive bearing-only location[J]. Electronic and Electro-Optical Systems, 2018(3): 31-35. 马方立,徐扬,徐鹏. 基于大地经纬度的二维TDOA无源定位[J]. 通信学报,2019(5): 136-143.MA Fangli, XU Yang, XU Peng. 2D-TDOA passive location based on geodetic longitude and latitude[J]. Journal on Communications, 2019(5): 136-143. ITU-R. Spectrum monitoring handbook[M]. Geneva: ITU, 2011: 145. 国家无线电办公室. 省级无线电监测设施建设规范和技术要求(试行): 国无办[2019]3号[S]. 2019, 北京: [出版者不详]. 罗来恩. 坐标方位角计算新方法[J]. 测绘通报,2004(5): 63-64. doi: 10.3969/j.issn.0494-0911.2004.05.023LUO Lai’en. A new method for calculating coordinate azimuth[J]. Bulletin of Surveying and Mapping, 2004(5): 63-64. doi: 10.3969/j.issn.0494-0911.2004.05.023 柳茂春. 无线电干扰计算[M]. 北京: 国防工业出版社, 1988: 132-133. 国家地震局地球物理研究所. 近震分析[M]. 北京: 地震出版社, 1978: 31-32. 季凯敏,王解先. 利用大地坐标计算真方位角的两种方法[J]. 工程勘察,2009,37(4): 84-86.JI Kaimin, WANG Jeixian. Two ways of calculating true azimuth by geodetic coordinates[J]. Geotechnical Investigation & Surveying, 2009, 37(4): 84-86. 孔祥元, 郭际明, 刘宗泉. 大地测量学基础[M]. 2版. 武汉: 武汉大学出版社, 2010: 25-58. 吕晓华, 李少梅. 地图投影原理与方法[M]. 北京: 测绘出版社, 2016: 166-176. MA Fangli, XU Yang, XU Peng. A nonlinear programming based universal optimization model of TDOA passive location[C]//Proceedings of 12th International Conference on Intelligent Systems and Knowledge Engineering (ISKE2017). Nanjing: IEEE Press, 2017: 399-402. -




 下载:
下载: