Finite Element Model Updating of Box Girder Bridges with Corrugated Steel Webs
-
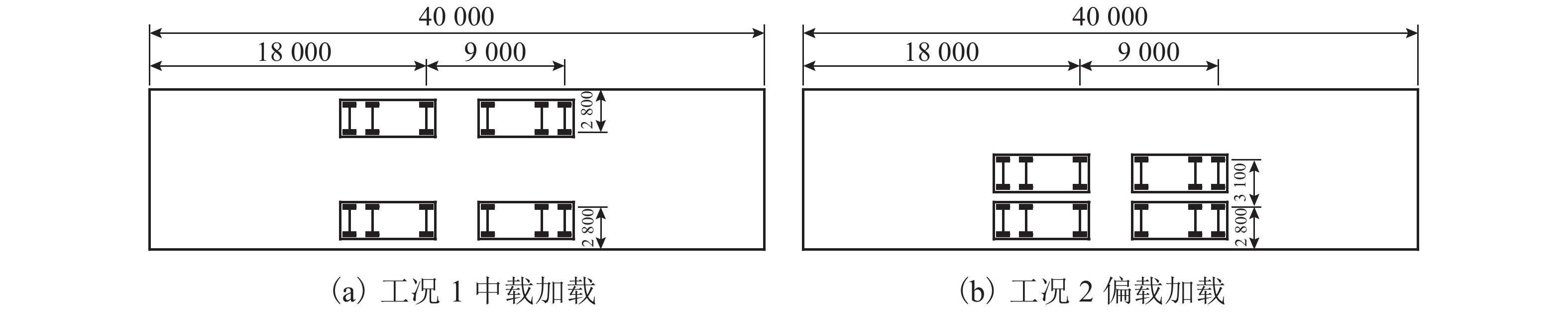
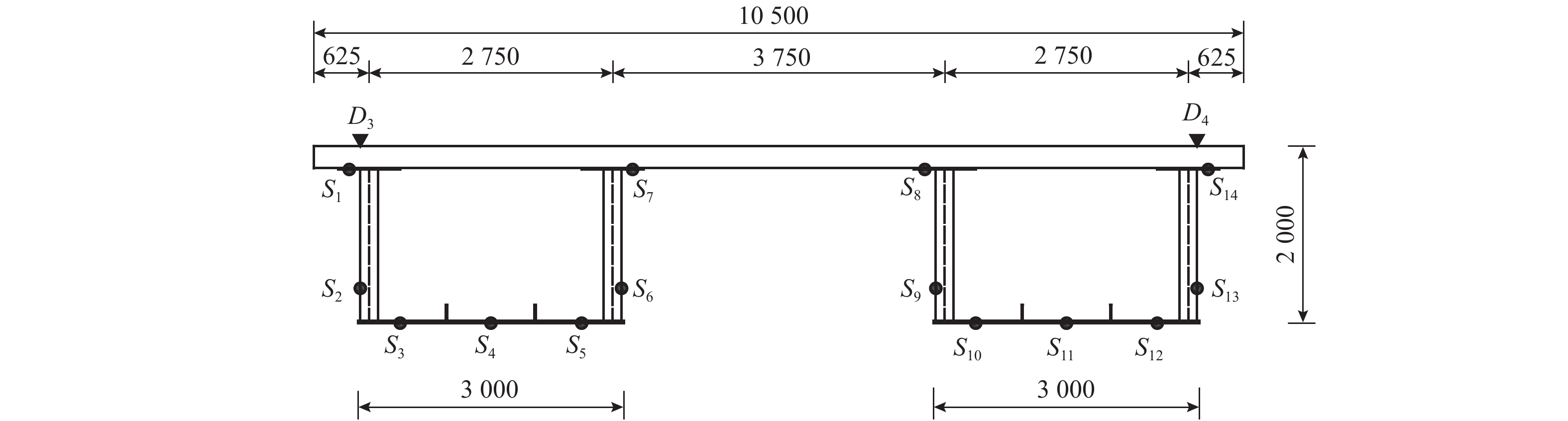
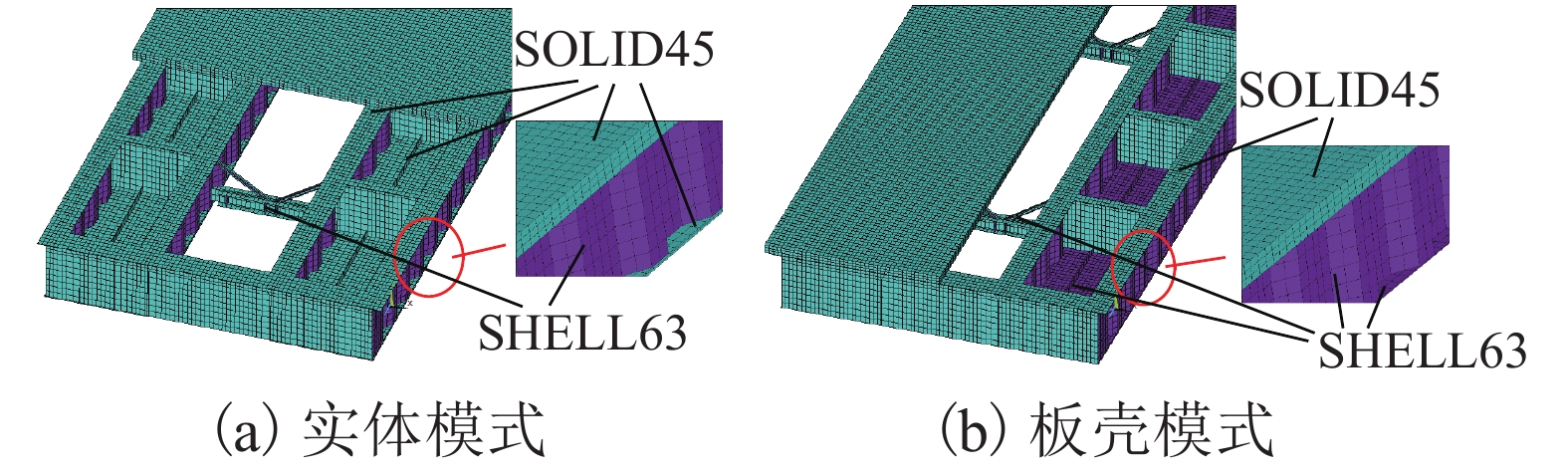
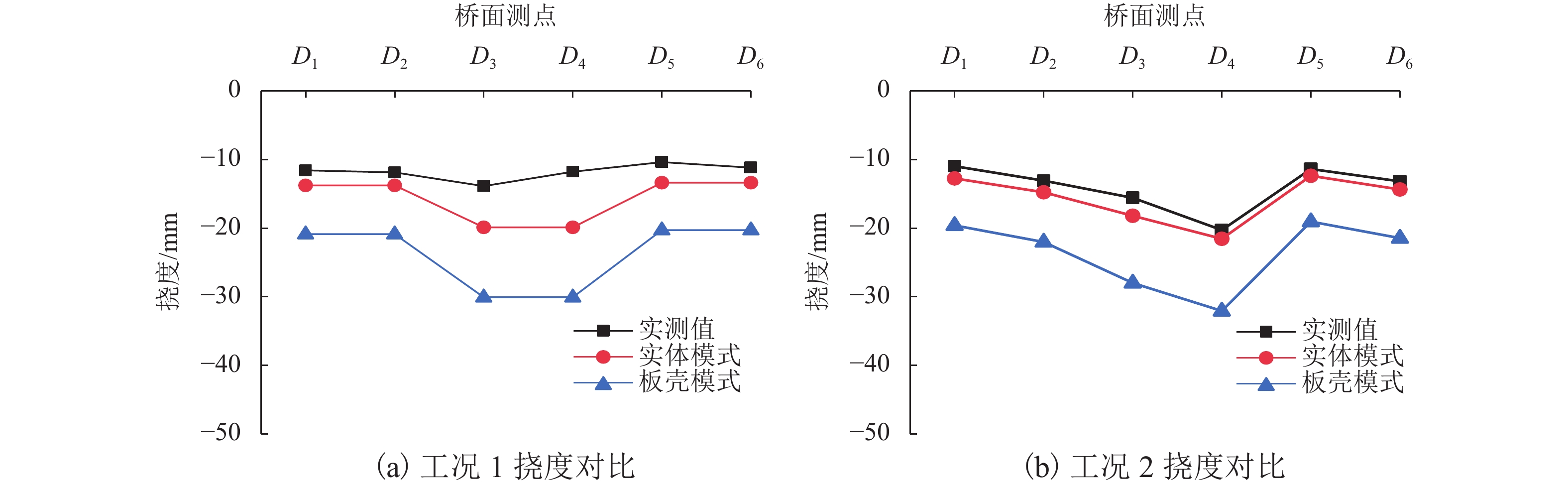
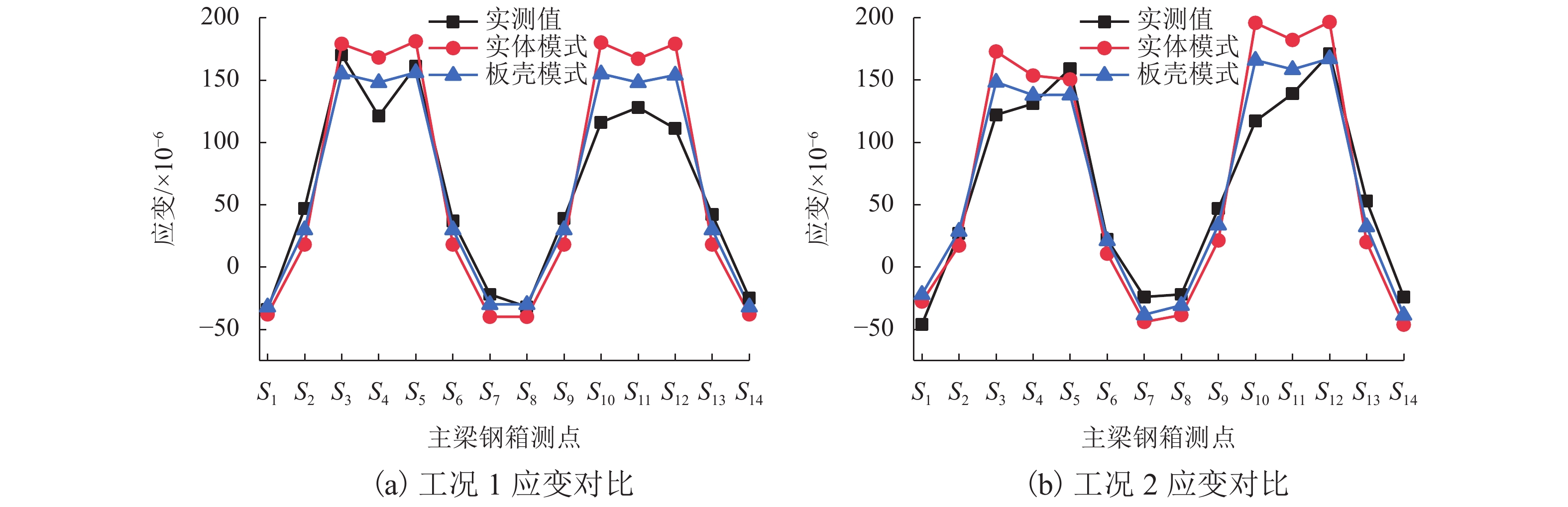
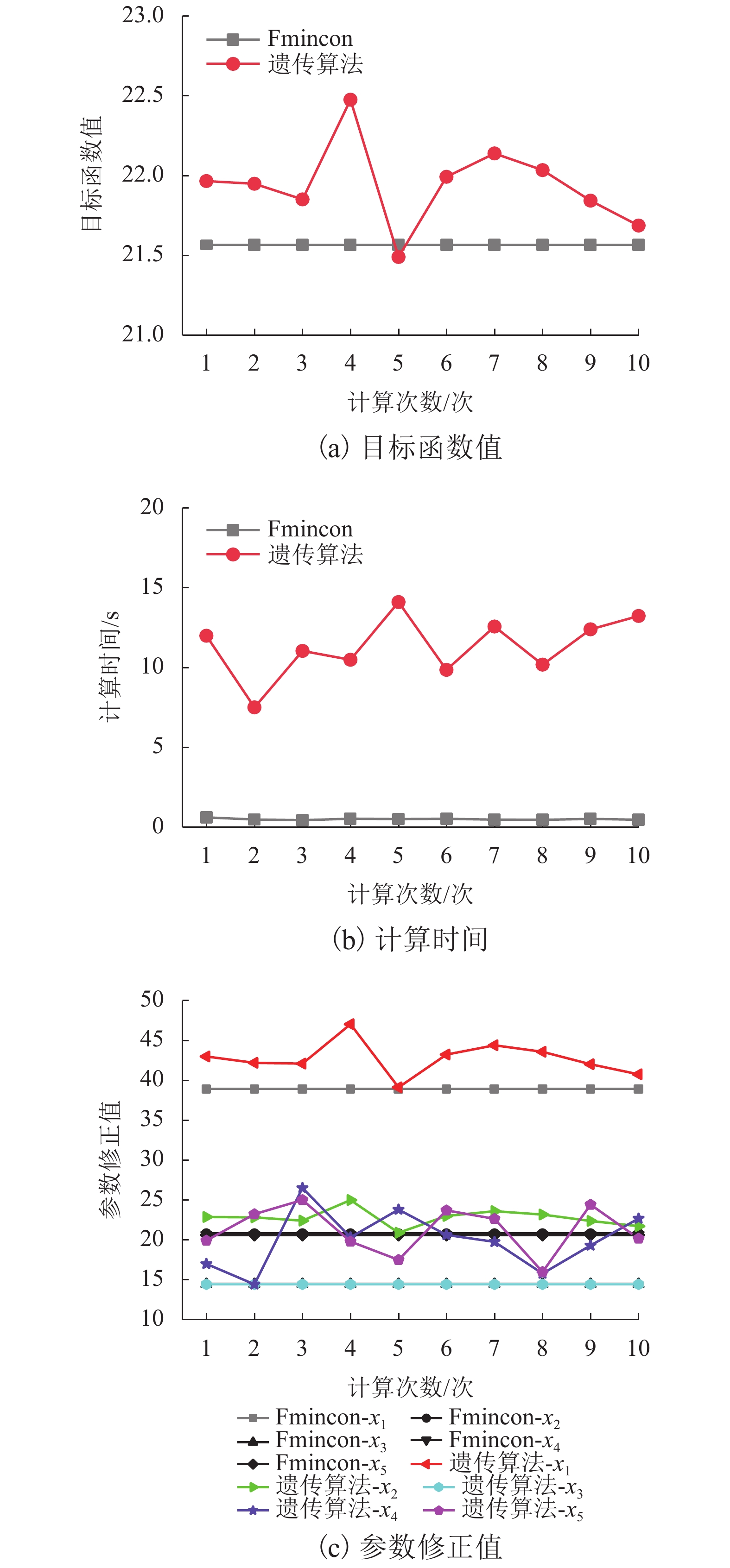
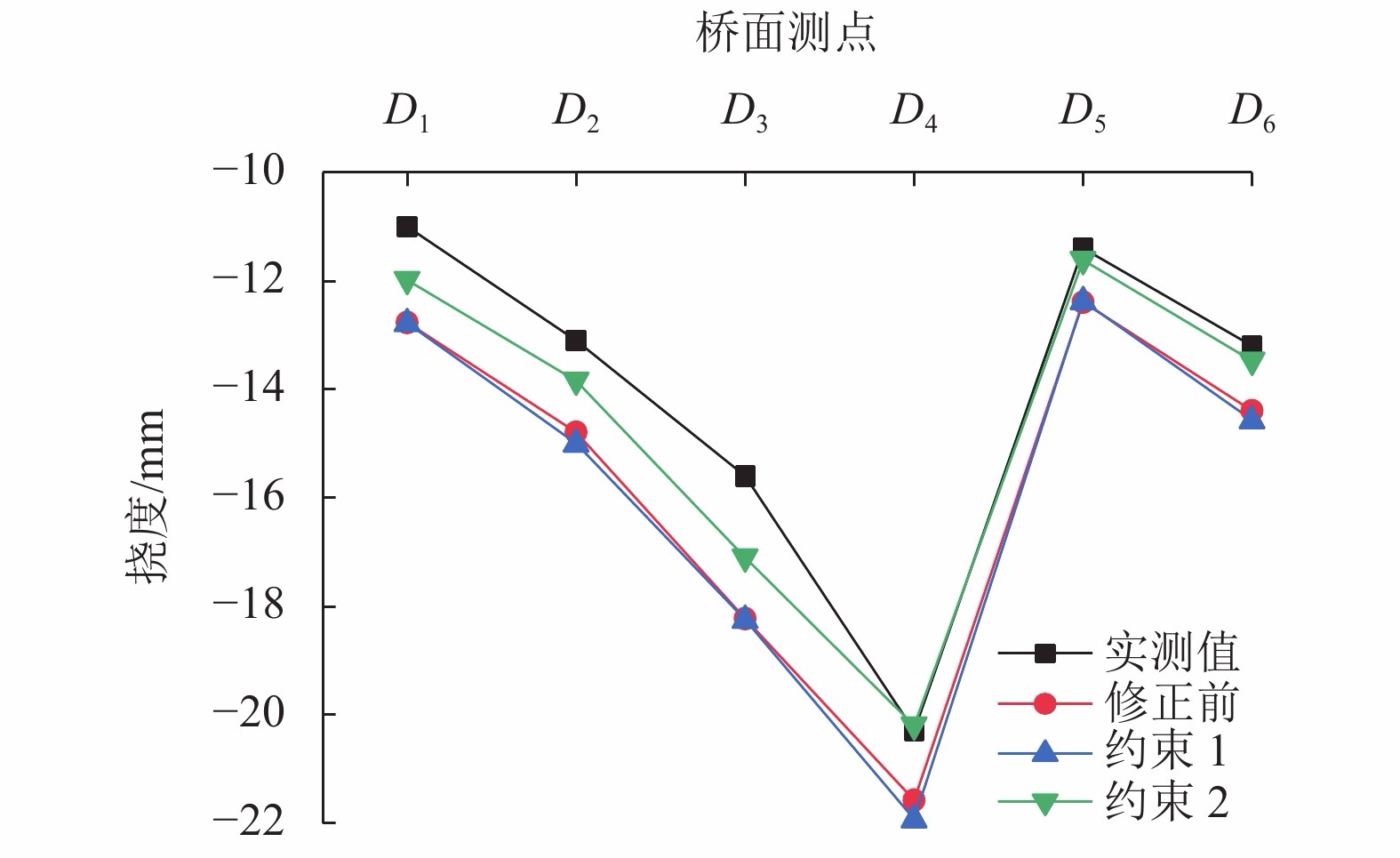
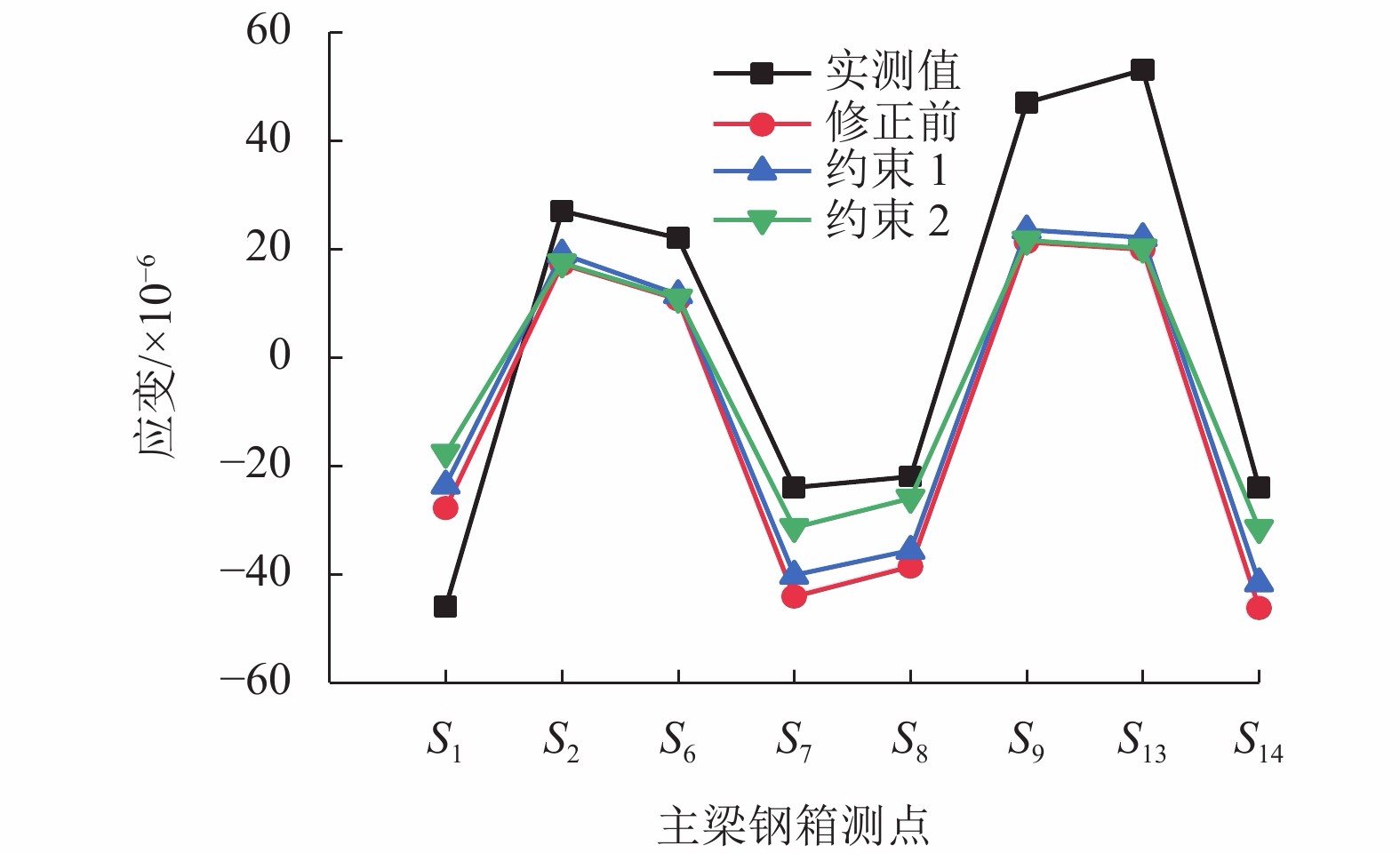
摘要: 为了缩小波形钢腹钢箱-混凝土组合箱梁桥有限元值与实测值之间的偏差，提出了采用响应面法和Fmincon算法相结合的桥梁有限元模型修正方法. 以甘肃景中机场连接线的一座波形钢腹钢箱-混凝土组合箱梁桥为研究对象，首先对其进行静、动载试验，获得其弯曲振动频率、挠度及应变的实测值；其次分别采用实体和板壳模式的有限元建模获得该桥相应的弯曲振动频率、挠度及应变的计算值，通过与实测值对比分析后，选取较为精确的实体模式有限元模型作为修正的初始有限元模型；随后在合理选择设计参数的基础上，通过中心复合试验设计得到相应的结构响应，采用最小二乘法拟合得到结构响应和设计参数之间的二次多项式回归方程，并构造目标响应与相应响应实测值差值的目标函数；最后运用Fmincon算法对目标函数进行迭代计算，获得参数修正值及该桥的基准有限元模型. 研究结果表明：采用响应面法和Fmincon算法相结合的方法对波形钢腹钢箱-混凝土组合箱梁桥的有限元模型进行修正切实可行，具有修正过程简单、计算收敛速度快等特点，计算时间在0.25～0.75 s内，一阶弯曲振动频率相对误差由4.85%依据不同响应组合修正到1.62%～2.91%不等；通过对遗传算法和Fmincon算法的比较发现，Fmincon算法显著提高了模型修正效率，可为实际工程中该类桥梁的有限元建模分析及力学性能分析提供参考.Abstract: In order to reduce the error between the finite element values and measured values of the box girder bridge with corrugated steel webs, a bridge finite element model updating method using response surface method and Fmincon algorithm was presented, taking a box girder bridge with corrugated steel webs in the connecting line of Jingzhong airport in Gansu province, China as the research object. Firstly, static and dynamic load tests were carried out to obtain the measured values of bending vibration frequency, deflection and strain. Secondly, the calculated values of these parameters were obtained by the finite element modeling using solid and plate-shell elements, respectively. After comparison of the calculated values with the measured values, a more accurate solid finite element model was selected as the updated initial finite element model. Then, on the basis of reasonable selection of design parameters, the corresponding structural response was obtained through the central composite test design, the quadratic polynomial regression equation between the structural response and design parameters was obtained by least square method fitting, and the objective function of the difference between the measured value of the target response and the corresponding response was constructed. Finally, Fmincon algorithm was used to calculate the objective function iteratively, and the updated value of parameters and the baseline finite element model of the bridge were obtained. The results show that it is feasible to modify the finite element model of the composite box girder bridge with corrugated steel webs by combining the response surface method and the Fmincon algorithm, which has the characteristics of simple modification process and fast convergence speed. The calculation time was within 0.25–0.75 s, and the relative error of the first-order bending vibration frequency was updated from 4.85% to 1.62%–2.91% according to different response combinations. Through the comparison between Genetic algorithm and Fmincon algorithm, it was found that Fmincon algorithm improves the model updating efficiency significantly, which can provide reference for the finite element modeling analysis and mechanical performance analysis of this kind of bridges in engineering practices.
-
图 7 不同初始值对优化结果的影响
Figure 7. Influence of different initial values on optimization results
图 9 工况2挠度修正前后比对
Figure 9. Deflection comparison before and after updating in condition 2
图 10 工况2应变修正前后比对
Figure 10. Strain comparison before and after updating in condition 2
图 11 工况1挠度修正前后比对
Figure 11. Deflection comparison before and after updating in condition 1
图 12 工况1应变修正前后比对
Figure 12. Strain comparison before and after updating in condition 1
图 13 工况2不同目标响应组合挠度比对
Figure 13. Comparison of deflections for different response combinations in condition 2
图 14 工况2不同目标响应组合应变比对
Figure 14. Comparison of strains fordifferent response combinations in condition 2
表 1 材料属性
Table 1. Material properties
材料种类 密度/（kg•m−3） 弹性模量/GPa 泊松比 C55混凝土 2 549 35.5 0.20 钢材 7 850 206.0 0.30 
下载: 导出CSV
表 2 一阶弯曲振动频率对比
Table 2. Comparison of the first-order bending vibration frequency
名称 一阶弯曲振动频率/Hz 相对误差/% 实测值 3.09 实体模式 2.94 4.85 板壳模式 2.45 20.71
下载: 导出CSV
表 3 设计参数
Table 3. Design parameters
因素名称 参数 初值 单位变化
程度/%x1 桥面板弹性模量/GPa 35.5 40 x2 桥面板密度/（kg•m−3） 2549 20 x3 波形钢腹板弹性模量/GPa 206 30 x4 钢底板弹性模量/GPa 206 30 x5 箱间横联弹性模量/GPa 206 30
下载: 导出CSV
表 4 5因素参数设计试验
Table 4. Five-factors parameter design test
试验组合 参数值 x1/GPa x2/（kg•m−3） x3/GPa x4/GPa x5/GPa 1 21.3 2039.2 144.2 144.2 267.8 2 49.7 3058.8 144.2 144.2 144.2 3 21.3 2039.2 144.2 144.2 144.2 4 49.7 3058.8 144.2 144.2 267.8 5 21.3 2039.2 267.8 144.2 144.2 6 49.7 3058.8 267.8 144.2 267.8 7 21.3 2039.2 267.8 144.2 267.8 8 49.7 3058.8 267.8 144.2 144.2 9 21.3 2039.2 144.2 267.8 144.2 10 49.7 3058.8 144.2 267.8 267.8 11 21.3 2039.2 144.2 267.8 267.8 12 49.7 3058.8 144.2 267.8 144.2 13 21.3 2039.2 267.8 267.8 267.8 14 49.7 3058.8 267.8 267.8 144.2 15 21.3 2039.2 267.8 267.8 144.2 16 49.7 3058.8 267.8 267.8 267.8 17 7.1 2549.0 206.0 206.0 206.0 18 63.9 2549.0 206.0 206.0 206.0 19 35.5 1529.4 206.0 206.0 206.0 20 35.5 3568.6 206.0 206.0 206.0 21 35.5 2549.0 82.4 206.0 206.0 22 35.5 2549.0 329.6 206.0 206.0 23 35.5 2549.0 206.0 82.4 206.0 24 35.5 2549.0 206.0 329.6 206.0 25 35.5 2549.0 206.0 206.0 82.4 26 35.5 2549.0 206.0 206.0 329.6 27 35.5 2549.0 206.0 206.0 206.0 28 35.5 2549.0 206.0 206.0 206.0 29 35.5 2549.0 206.0 206.0 206.0 30 35.5 2549.0 206.0 206.0 206.0
下载: 导出CSV
表 5 频率-挠度响应组合修正结果
Table 5. Updated results of the frequency-deflection response combination
因素名称 上边界 下边界 设计值 修正后 x1 49.700 21.300 35.500 38.903 x2 30.588 20.392 25.490 20.786 x3 26.780 14.420 20.600 14.475 x4 26.780 14.420 20.600 20.600 x5 26.780 14.420 20.600 20.600
下载: 导出CSV
表 6 两种算法约束条件下的修正结果
Table 6. Updated results under the constraint of two algorithms
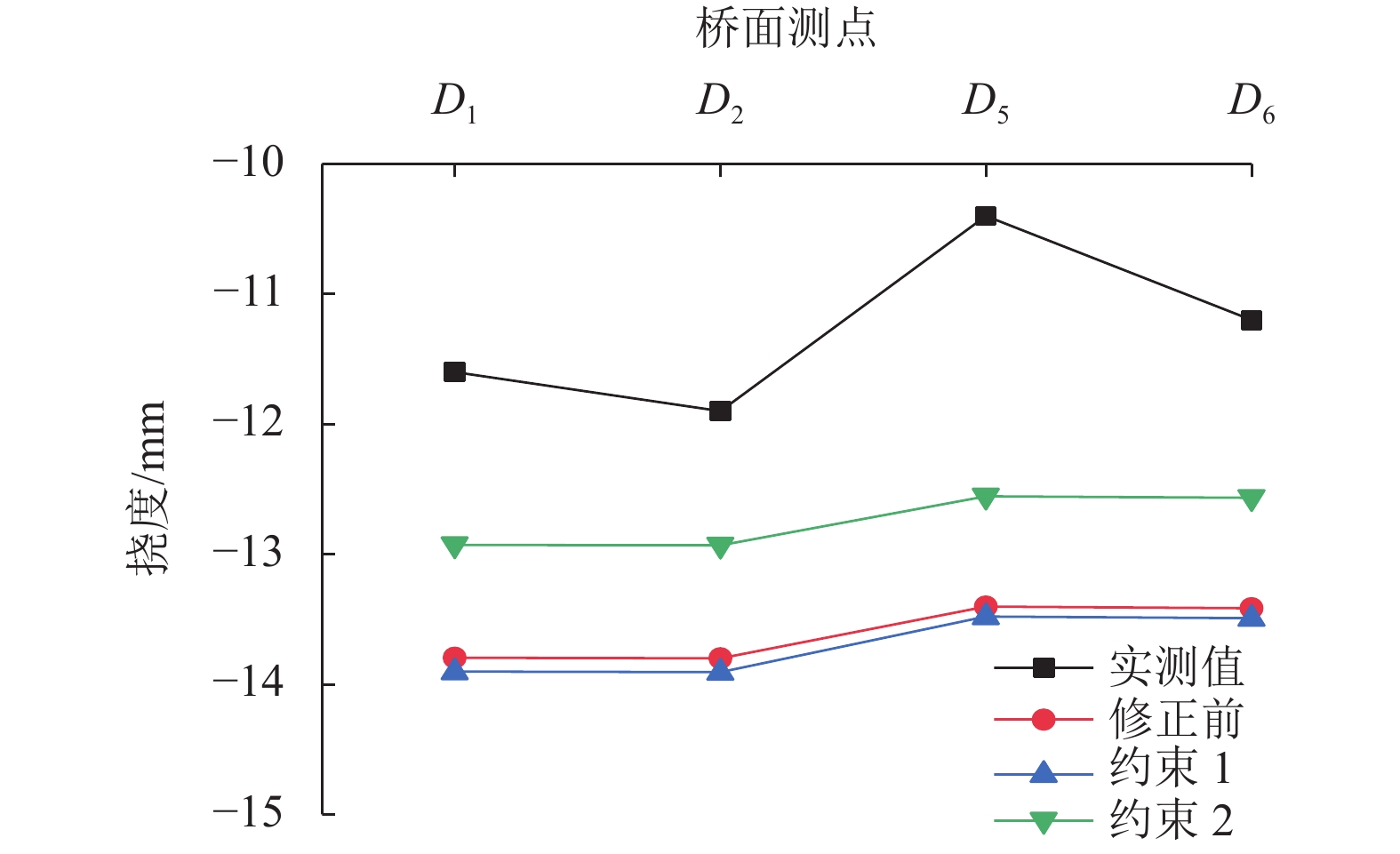
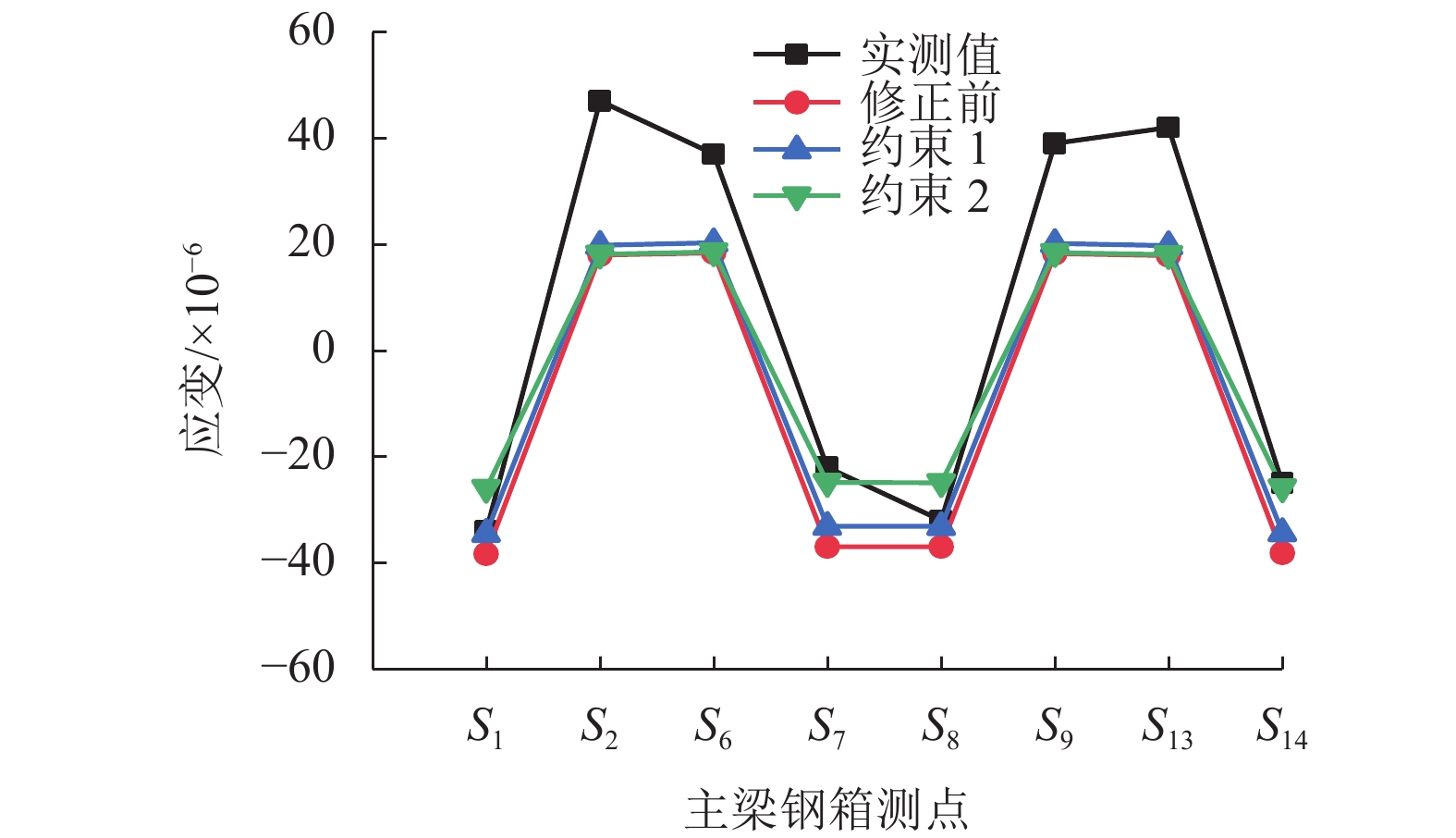
因素名称 约束1 约束2 x1 38.903 48.470 x2 20.786 25.733 x3 14.475 20.654 x4 20.600 20.600 x5 20.600 20.600
下载: 导出CSV
表 7 修正前后频率比对
Table 7. Frequency comparison before and after updating
项目 一阶弯曲振动频率/Hz 相对误差/% 实测值 3.09 修正前 2.94 4.85 约束 1 3.14 1.62 约束 2 3.02 2.27
下载: 导出CSV
表 8 不同目标响应组合频率比对
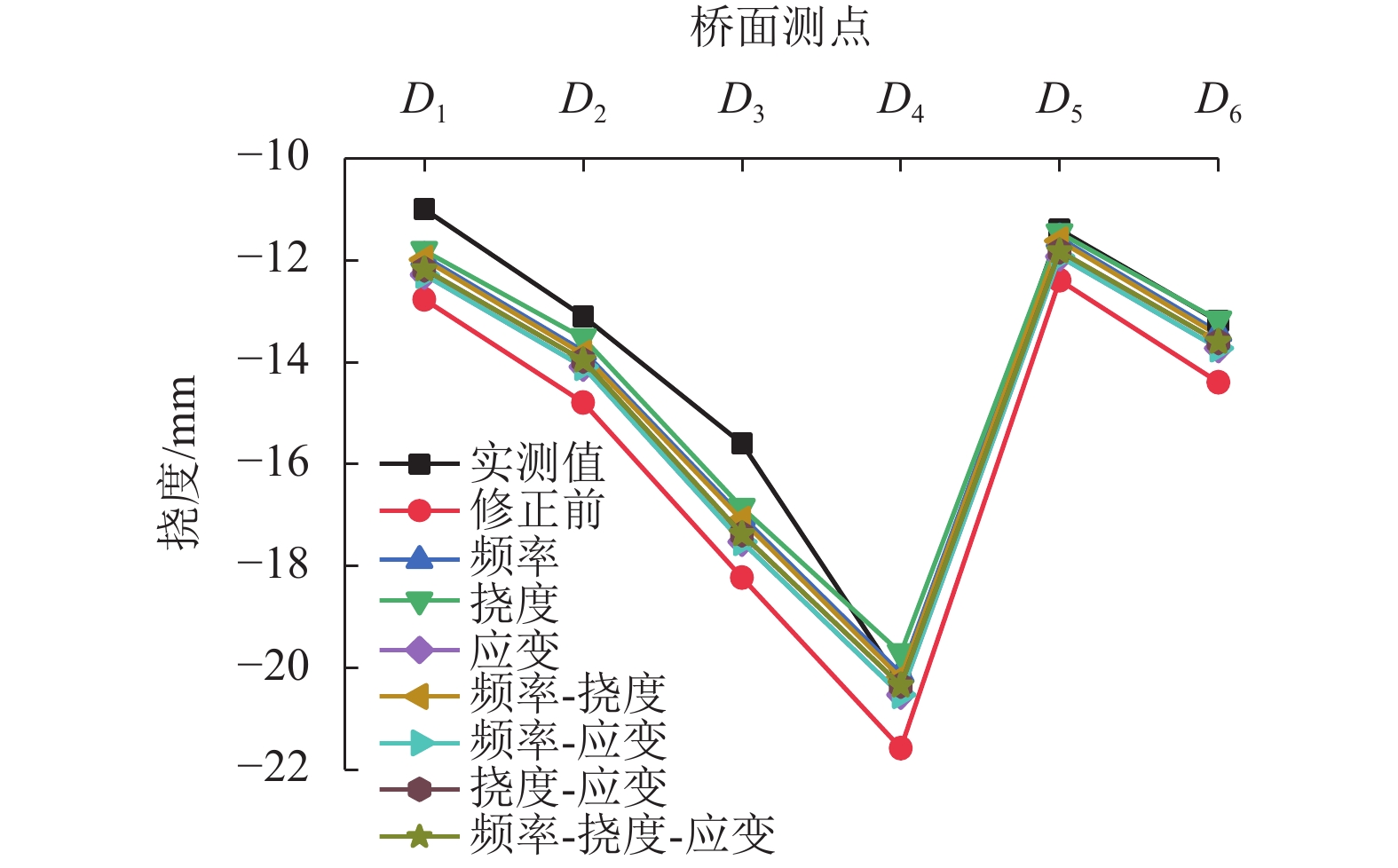
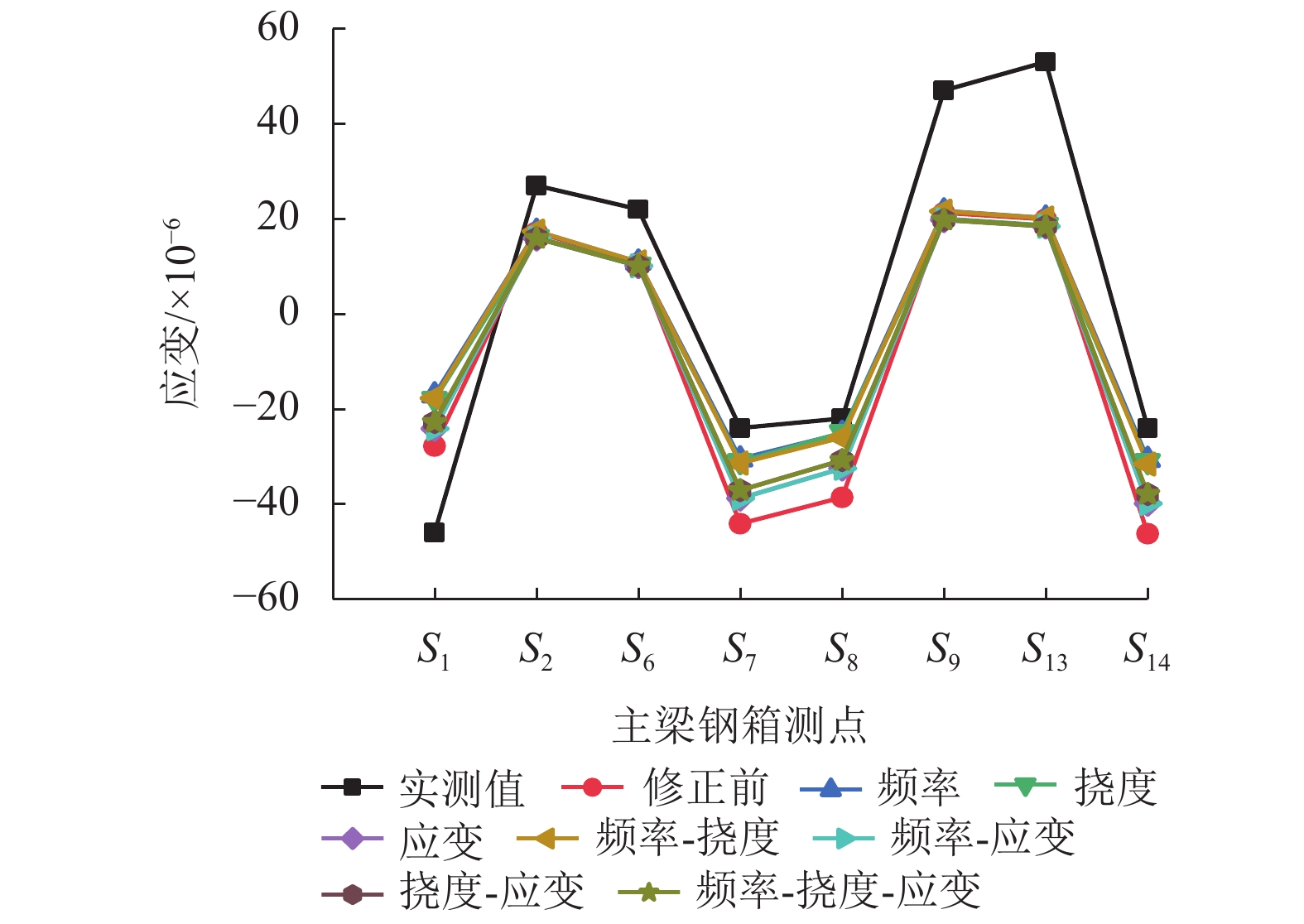
Table 8. Comparison of frequencies of different response combinations
响应组合 一阶弯曲振动频率/Hz 相对误差/% 实测值 3.09 修正前 2.94 4.85 频率 3.04 1.62 挠度 3.04 1.62 应变 3.00 2.91 频率-挠度 3.02 2.27 频率-应变 3.00 2.91 挠度-应变 3.02 2.27 频率-挠度-应变 3.02 2.27
下载: 导出CSV
-
NIE Jianguo, ZHU Yingjie, TAO Muxuan, et al. Optimized prestressed continuous composite girder bridges with corrugated steel webs[J]. Journal of Bridge Engineering, 2017, 22(2): 04016121.1-04016121.15. doi: 10.1061/(ASCE)BE.1943-5592.0000995 万利军,单炜,姜华. 基于响应面法的桥梁动力学有限元模型修正[J]. 公路交通科技,2014,31(8): 96-101. doi: 10.3969/j.issn.1002-0268.2014.08.017WAN Lijun, SHAN Wei, JIANG Hua. Modification of finite element model of bridge dynamics based on response surface method[J]. Journal of Highway and Transportation Research and Development, 2014, 31(8): 96-101. doi: 10.3969/j.issn.1002-0268.2014.08.017 DENG Lu, CAI Chunsheng. Bridge model updating using response surface method and genetic algorithm[J]. Journal of Engineering Mechanics ASCE, 2010, 15: 553-564. REN Weixin, CHEN Huabin. Finite element model updating in structural dynamics by using the response surface method[J]. Engineering Structures, 2010(32): 2455-2465. 朱彤,殷广庆. 基于响应面的预应力混凝土桥动力有限元模型研究[J]. 防灾减灾工程学报,2013,33(6): 644-650.ZHU Tong, YIN Guangqing. Research on dynamic finite element model of prestressed concrete bridge based on response-surface[J]. Journal of Disaster Prevention and Mitigation Engineering, 2013, 33(6): 644-650. 韩建平,骆勇鹏,郑沛娟,等. 基于响应面的刚构-连续组合梁桥有限元模型修正[J]. 工程力学,2013,30(12): 85-90,106.HAN Jianping, LUO Yongpeng, ZHENG Peijuan, et al. Finite element model updating for a rigid Frame-continuous girders bridge based on response surface method[J]. Engineering Mechanics, 2013, 30(12): 85-90,106. 魏锦辉,任伟新. 基于响应面方法的桥梁静动力有限元模型修正[J]. 公路交通科技,2015,32(2): 68-73. doi: 10.3969/j.issn.1002-0268.2015.02.011WEI Jinhui, REN Weixin. Static and dynamic bridge finite element model updating based on response surface method[J]. Journal of Highway and Transportation Research and Development, 2015, 32(2): 68-73. doi: 10.3969/j.issn.1002-0268.2015.02.011 HUANG Haidong, HUANG Shanshan, KYPROS P. Modeling for assessment of long-term behavior of prestressed concrete box-girder bridges[J]. Journal of Bridge Engineering, 2018, 23(3): 04018002.1-04018002.15. doi: 10.1061/(ASCE)BE.1943-5592.0001210 单德山,顾晓宇,李中辉,等. 桥梁结构有限元模型的仿射-区间不确定修正[J]. 中国公路学报,2019,32(2): 67-76. doi: 10.3969/j.issn.1001-7372.2019.02.007SHAN Deshan, GU Xiaoyu, LI Zhonghui, et al. Affine-interval uncertainty updating of finite element model for cable-stayed bridge[J]. China Journal of Highway and Transport, 2019, 32(2): 67-76. doi: 10.3969/j.issn.1001-7372.2019.02.007 单宝英,郭萍,张帆,等. 基于遗传算法与方案优选的多目标优化模型求解方法[J]. 中国农业大学学报,2019,24(6): 157-165.SHAN Baoying, GUO Ping, ZHANG Fan, et al. A multi-objective optimization model solving method based on genetic algorithm and scheme evaluation[J]. Journal of China Agricultural University, 2019, 24(6): 157-165. 王艳艳,窦明,李桂秋,等. 基于和谐目标优化的流域初始排污权分配方法[J]. 水利水电科技进展,2015,35(2): 12-16,51. doi: 10.3880/j.issn.1006-7647.2015.02.003WANG Yanyan, DOU Ming, LI Guiqiu, et al. The allocation methods of watershed initial emissions permits based on harmonious objectives optimiz[J]. Advances in Science and Technology of Water Resources, 2015, 35(2): 12-16,51. doi: 10.3880/j.issn.1006-7647.2015.02.003 李立峰,李辉辉,徐开铎,等. 基于均匀设计响应面法的桥梁地震易损性分析[J]. 公路交通科技,2017,34(11): 100-109.LI Lifeng, LI Huihui, XU Kaiduo, et al. Analysis on bridge seismic fragility based on uniform design response surface method[J]. Journal of Highway and Transportation Research and Development, 2017, 34(11): 100-109. 蒋国庆,陈万华,王元兴. 修正的响应面方法优化螺栓法兰连接结构几何参数[J]. 国防科技大学学报,2019,41(5): 38-42. doi: 10.11887/j.cn.201905006JIANG Guoqing, CHEN Wanhua, WANG Yuanxing. Optimization of geometrical parameters of bolted flange by modified response surface method[J]. Journal of National University of Defense Technology, 2019, 41(5): 38-42. doi: 10.11887/j.cn.201905006 宗周红, 任伟新. 桥梁有限元模型修正和模型确认[M]. 北京: 人民交通出版社, 2012: 109-110. 何嘉华,周宏甫,刘二辉,等. 基于神经网络和遗传算法的温差发电器优化设计[J]. 机械设计,2018,35(9): 31-36.HE Jiahua, ZHOU Hongfu, LIU Erhui, et al. Optimization design of thermoelectric generator based on neural network and genetic algorithm[J]. Journal of Machine Design, 2018, 35(9): 31-36. -
下载:
点击查看大图
计量
- 文章访问数: 704
- HTML全文浏览量: 360
- PDF下载量: 41
- 被引次数: 0