圆拱结构平面外稳定分析方法

丁敏; 王佳佳; 蒋秀根; 曹琼琼; 王宏志

doi:10.3969/j.issn.0258-2724.20191158

圆拱结构平面外稳定分析方法

doi: 10.3969/j.issn.0258-2724.20191158

丁敏^1,,
王佳佳^1,2,
蒋秀根^1, ,,
曹琼琼^1,3,
王宏志¹

基金项目: 国家自然科学基金（11672362）

详细信息

作者简介:
丁敏（1980—），女，副教授，博士，硕士生导师，研究方向为工程结构安全性能，E-mail：dingmin@cau.edu.cn

通讯作者:
蒋秀根（1966—），男，教授，硕士生导师，研究方向为工程结构安全性能，E-mail：jiangxg@cau.edu.cn

中图分类号: TU311.1
计量
- 文章访问数: 644
- HTML全文浏览量: 301
- PDF下载量: 30
- 被引次数: 0
出版历程
- 收稿日期: 2019-12-04
- 修回日期: 2020-04-20
- 网络出版日期: 2020-12-14
- 刊出日期: 2021-02-01

Out-of-Plane Stability Analysis Method for Circular Arch Structures

摘要

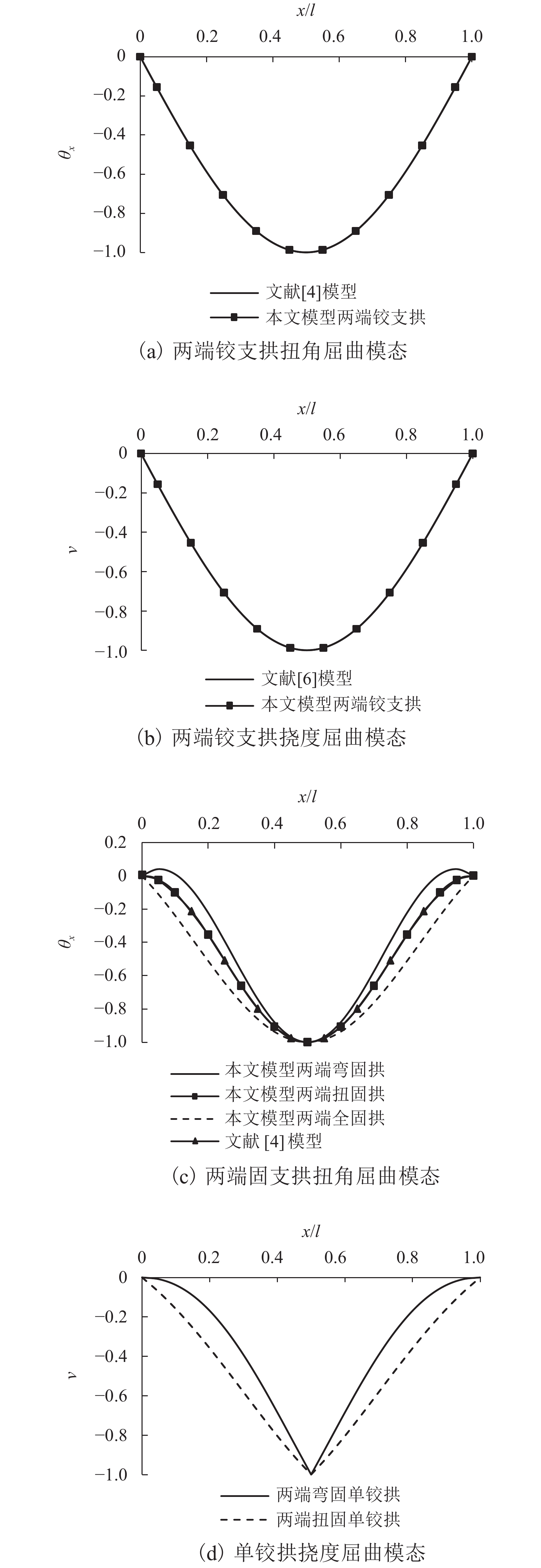
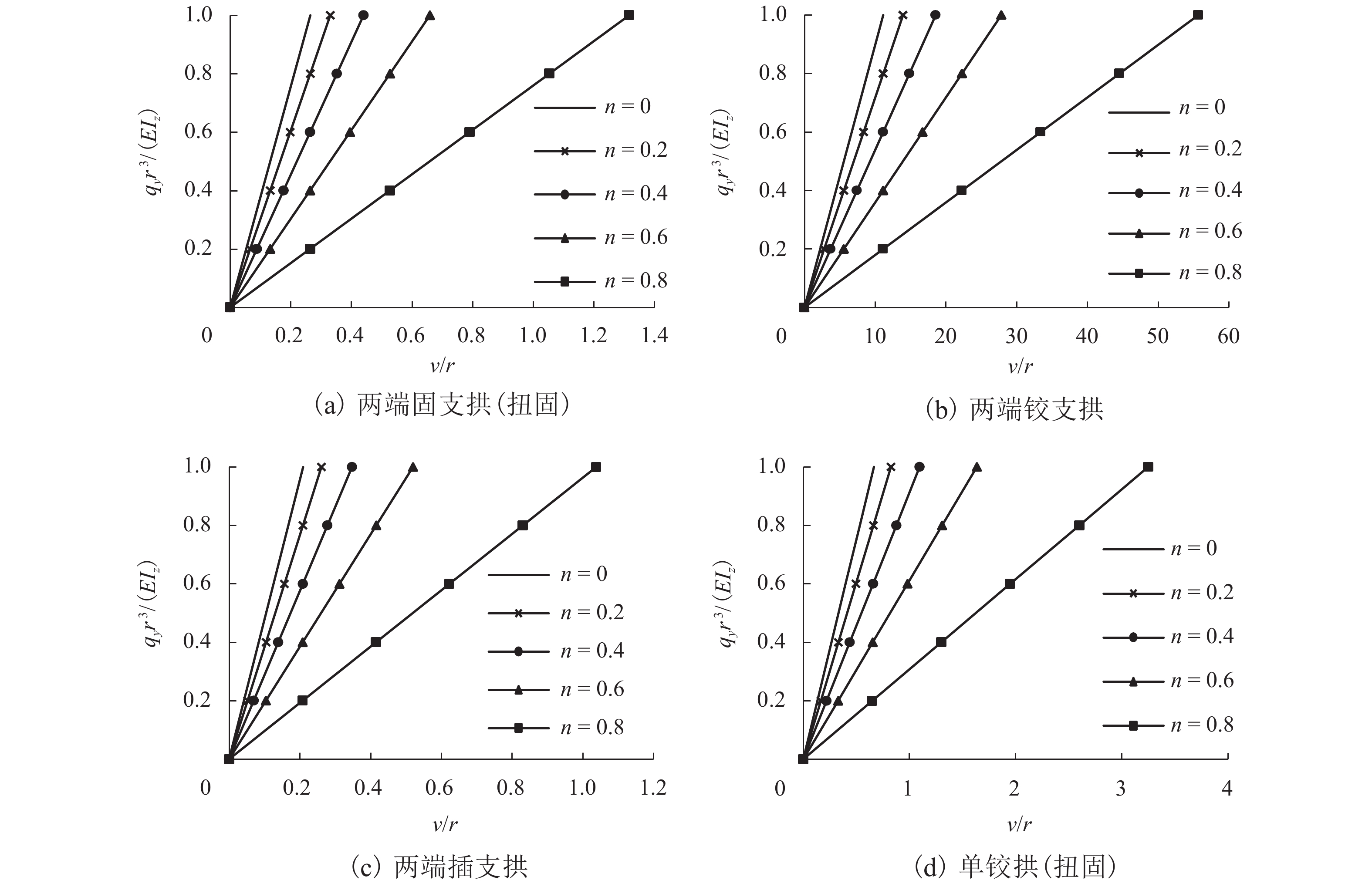
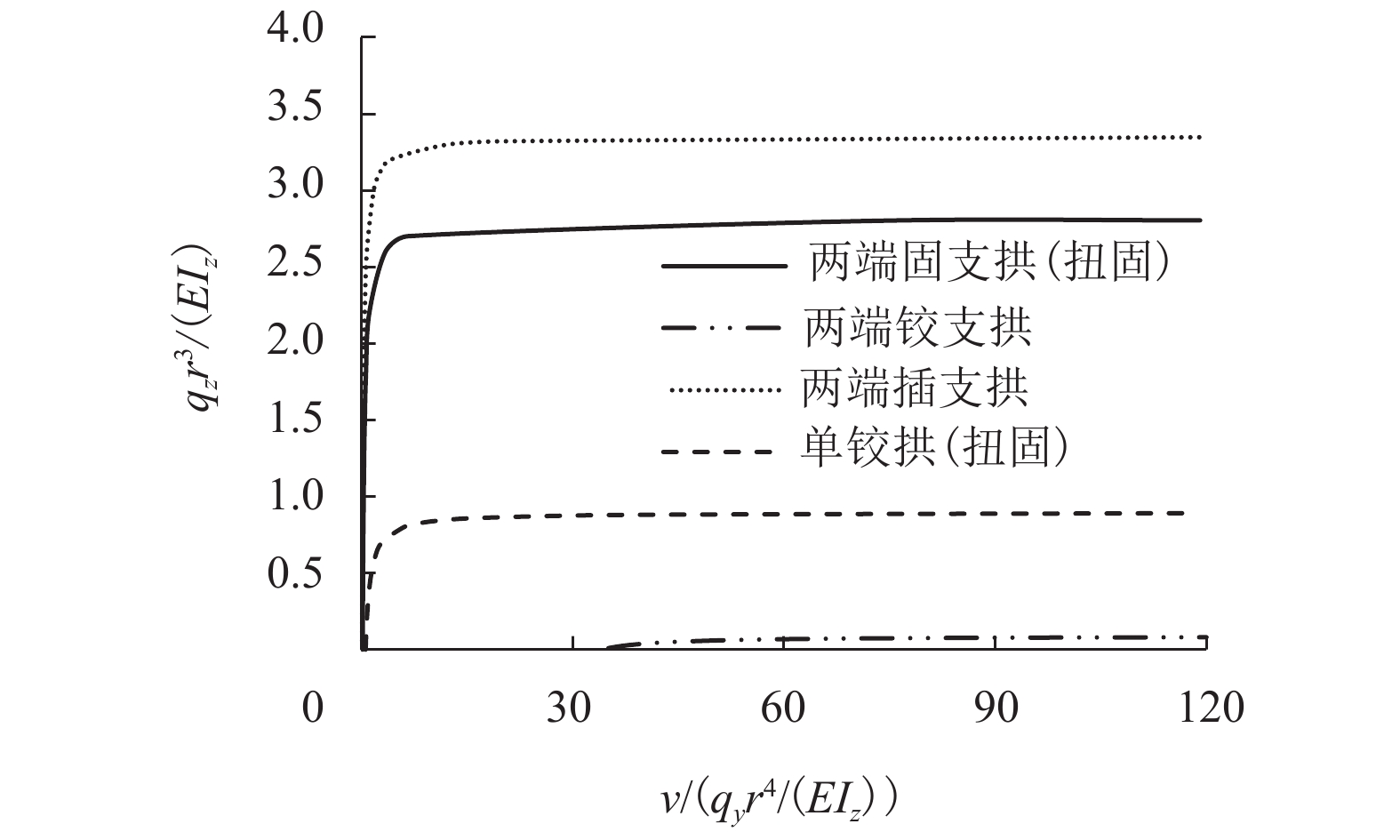
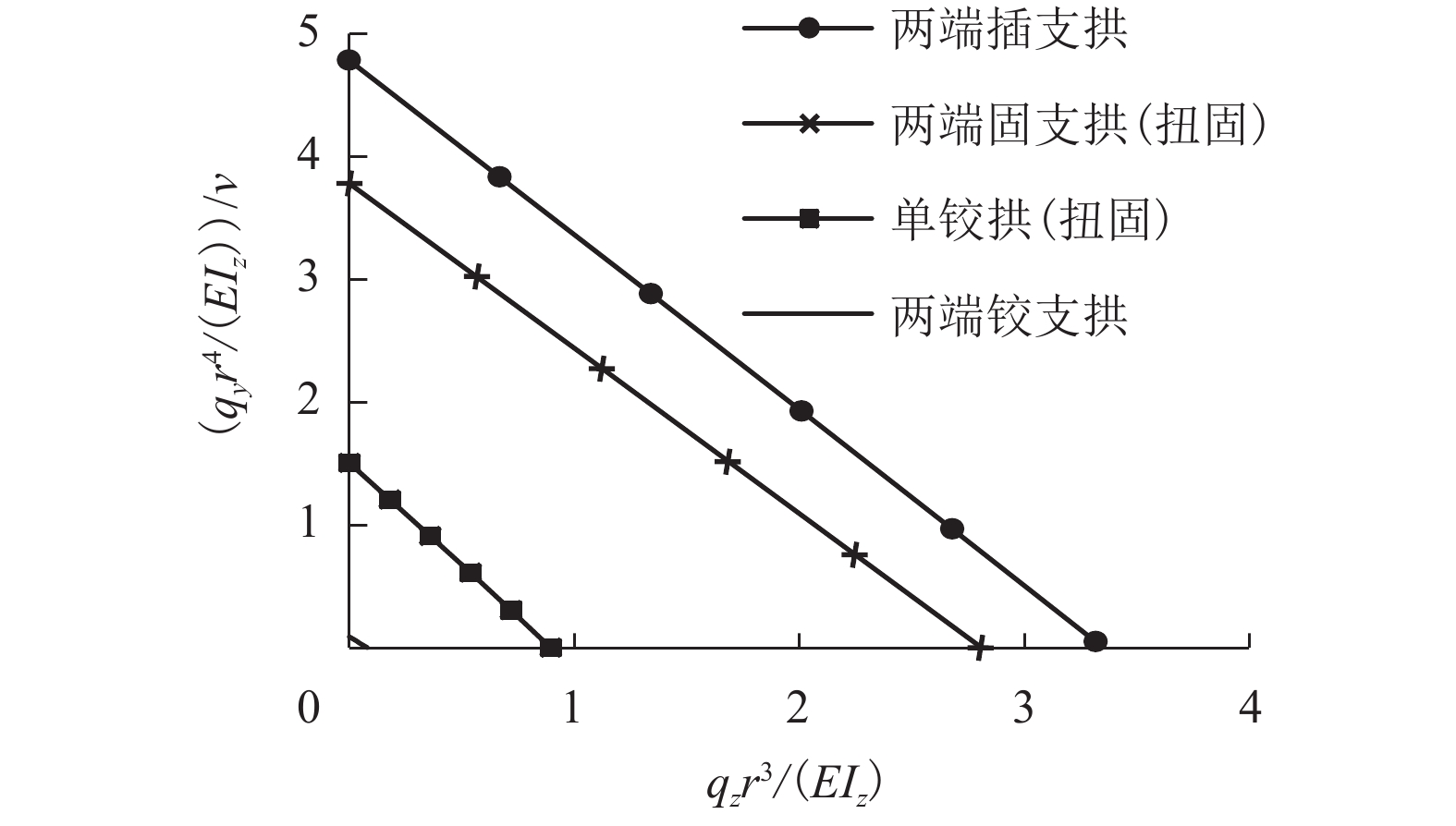
摘要: 为研究圆拱结构的平面外稳定问题，根据其与圆曲梁变形的相关性，首先考虑二阶弯矩效应建立了圆曲梁平衡方程，结合圆曲梁几何方程和物理方程，推导了考虑大位移的自由扭转圆曲梁的挠度控制方程和扭转角控制方程，分别给出了圆曲梁的挠度和扭转角的解析解一般格式及相应简化格式，同时获得了圆曲梁变形和内力表达式；在此基础上，提出了圆拱结构平面外分岔失稳和极值点失稳的分析方法；计算了4种圆拱结构的平面外分岔失稳临界荷载系数及失稳模态，并与文献模型作对比分析；根据4种圆拱结构的荷载-位移曲线进行了极值点失稳分析. 研究结果表明：采用本文模型计算的两端铰支圆拱平面外分岔失稳临界荷载系数与文献模型结果相差为0，而且可以得到工程中常用但鲜有人研究的跨中单铰拱及两端插支拱的平面外分岔失稳临界荷载；各类圆拱在面内均布径向荷载作用下的平面外分岔失稳模态均为单波对称；圆拱径向荷载的存在不改变圆拱面外荷载位移曲线的线性特征，却降低了面外抗弯刚度，当径向荷载达到某一值时，面外抗弯刚度为0，则发生面外失稳.
- 圆拱 /
- 圆曲梁 /
- 平面外稳定 /
- 大位移 /
- 几何非线性
Abstract: In order to analyze the out-of-plane stability behavior of circular arch structures, according to the deformation correlation of circular arch with circular curved beam, the equilibrium equations of circular curved beam were firstly established by taking secondary moment effect into account. Combined with the geometric equation and physical equation of circular curved beam, the deflection control equation and torsion angle control equation of circular curved beam with free torsion were derived by considering large displacement. Both the general formats and corresponding simplified formats of analytical solution for circular curved beam deflection and torsion angle were obtained. Meanwhile, the expressions for deformation and internal force of circular curved beam were also derived. On this basis, the methods to analyze the out-of-plane bifurcation instability and extreme point instability of circular arch structure were presented. Critical load coefficients and their instability modes of four kinds of circular arch structure were calculated when out-of-plane bifurcation instability occurs, and the calculation results between the proposed model and the models from the literature were discussed; their load-displacement curves were calculated, and the extreme point instability of circular arch structures was analyzed. The results show that the critical load coefficient of the circular arch with two ends simply supported can be calculated by this model and has no difference with other models. In addition, this model is also useful to calculate the critical load coefficient of that with single hinge at mid-span or that with two ends inserted supported which are rarely seen in research. The out-of-plane bifurcation instability modes of all kinds of circular arch under in-plane uniformly distributed radial load are in the form of single symmetric wave. The radial load does not change the linear character of the out-of-plane load vs. displacement curve, but reduces the out-of-plane flexural rigidity. When the radial load reaches a certain value, the out-of-plane flexural rigidity becomes 0, and then the out-of-plane instability occurs.
- circular arch /
- circular curved beam /
- out-of-plane stability /
- large displacement /
- geometric nonlinearity

HTML全文

图 1 圆曲梁坐标系

Figure 1. Coordinate system of circular curved beam

下载: 全尺寸图片幻灯片

图 2 圆拱失稳模态对比

Figure 2. Instability mode comparison of circular arch

下载: 全尺寸图片幻灯片

图 3 圆拱面外荷载与面外跨中挠度关系

Figure 3. Relationship between out-of-plane load and mid-span deflection for circular arch

下载: 全尺寸图片幻灯片

图 4 圆拱径向荷载与面外跨中挠度关系

Figure 4. Relationship between radial load and out-of-plane deflection at mid-span for circular arch

下载: 全尺寸图片幻灯片

图 5 圆拱相对径向荷载与面外弯曲刚度影响曲线

Figure 5. Influence curve of relative radial load and out-of-plane bending stiffness for circular arch

下载: 全尺寸图片幻灯片

表 1 不同工况下圆曲梁位移简化表达式

Table 1. Simplified expressions for displacement of circular curved beam under different load conditions

λ	位移	挠度基函数	特解	位移参数
$ - \dfrac{1}{\eta } <\lambda <0$	挠度	$\begin{array}{l}{ {{f} }_v} = \left( {\begin{array}{{20}{c}}{1},{x},{\sin \left( {\dfrac{\alpha }{r}x} \right)},{\cos \left( {\dfrac{\alpha }{r}x} \right)},\end{array}} \right.\\\left. {\begin{array}{{20}{c}}{\sin \left( {\dfrac{\beta }{r}x} \right)},{\cos \left( {\dfrac{\beta }{r}x} \right)}\end{array}} \right)\end{array}$	${v_{{\rm{p1}}}}$	$\alpha = \sqrt { - \dfrac{{\sqrt {{\lambda ^2} - 4\lambda - 4\lambda \eta } + \lambda - 2}}{2}} $, ${\zeta _1} = \dfrac{{\left( {1 + \lambda \eta } \right) + {\alpha ^2}\eta }}{{\eta + 1}}$
$ - \dfrac{1}{\eta } <\lambda <0$	扭角	$\begin{array}{l}{{f}_{\theta {{x}}}} = \left( {\begin{array}{{20}{c}}{0,}0,{\dfrac{{{\zeta _1}}}{r}\sin \left( {\dfrac{\alpha }{r}x} \right),}{\dfrac{{{\zeta _1}}}{r}\cos \left( {\dfrac{\alpha }{r}x} \right),}\end{array}} \right.\\\left. {\begin{array}{{20}{c}}{\dfrac{{{\zeta _2}}}{r}\sin \left( {\dfrac{\beta }{r}x} \right),}{\dfrac{{{\zeta _2}}}{r}\cos \left( {\dfrac{\beta }{r}x} \right)}\end{array}} \right)\end{array}$	${\theta _{x{\rm{p1}}}}$	$\beta = \sqrt {\dfrac{{\sqrt {{\lambda ^2} - 4\lambda - 4\lambda \eta } - \lambda + 2}}{2}} $, ${\zeta _2} = \dfrac{ {\left( {1 + \lambda \eta } \right) + {\beta ^2}\eta } }{ { {\eta + 1} } }$

$\lambda = - \dfrac{1}{\eta }$	挠度	${ {{f} }_v} = \left( {\begin{array}{*{20}{c} }1,x,{ {x^2} },{ {x^3} },{\sin \left( {\dfrac{\beta }{r}x} \right)},{\cos \left( {\dfrac{\beta }{r}x} \right)}\end{array} } \right)$	${v_{{\rm{p2}}}}$	$\alpha = 0$, ${\zeta _1} = \dfrac{{\eta + 1}}{\eta }$
$\lambda = - \dfrac{1}{\eta }$	扭角	$\begin{array}{l}{{f}_{\theta {{x}}}} = \left( {\begin{array}{{20}{c}}{0,}{0,}{ - 2{\zeta _1}r,}{ - 6{\zeta _1}rx,}\end{array}} \right.\\\left. {\begin{array}{{20}{c}}{\dfrac{{{\zeta _2}}}{r}\sin \left( {\dfrac{\beta }{r}x} \right),}{\dfrac{{{\zeta _2}}}{r}\cos \left( {\dfrac{\beta }{r}x} \right)}\end{array}} \right)\end{array}$	${\theta _{x{\rm{p2}}}}$	$\beta = \sqrt {\dfrac{{1 + 2\eta }}{\eta }} $, ${\zeta _2} = \dfrac{{1 + 2\eta }}{{\eta + 1}}$

$\lambda < - \dfrac{1}{\eta }$	挠度	$\begin{array}{l}{{ f}_v} = \left( {\begin{array}{{20}{c}}{1,}{x,}{\sinh \left( {\dfrac{\alpha }{r}x} \right),}{\cosh \left( {\dfrac{\alpha }{r}x} \right),}\end{array}} \right.\\\left. {\begin{array}{{20}{c}}{\sin \left( {\dfrac{\beta }{r}x} \right),}{\cos \left( {\dfrac{\beta }{r}x} \right)}\end{array}} \right)\end{array}$	${v_{{\rm{p1}}}}$	$\alpha = \sqrt {\dfrac{{\sqrt {{\lambda ^2} - 4\lambda - 4\lambda \eta } + \lambda - 2}}{2}} $, ${\zeta _1} = \dfrac{ {\left( {1 + \lambda \eta } \right) - {\alpha ^2}\eta } }{ { {\eta + 1} } }$
$\lambda < - \dfrac{1}{\eta }$	扭角	$\begin{array}{l}{{f}_{\theta { {x} } } } = \left( {\begin{array}{{20}{c} }{0,}{0,}{\dfrac{ { {\zeta _1} } }{r}\sinh \left( {\dfrac{\alpha }{r}x} \right),}{\dfrac{ { {\zeta _1} } }{r}\cosh \left( {\dfrac{\alpha }{r}x} \right),}\end{array} } \right.\\\left. {\begin{array}{{20}{c} }{\dfrac{ { {\zeta _2} } }{r}\sin \left( {\dfrac{\beta }{r}x} \right),}{\dfrac{ { {\zeta _2} } }{r}\cos \left( {\dfrac{\beta }{r}x} \right)}\end{array} } \right)\end{array}$	${\theta _{x{\rm{p1}}}}$	$\beta = \sqrt {\dfrac{{\sqrt {{\lambda ^2} - 4\lambda - 4\lambda \eta } - \lambda + 2}}{2}} $, ${\zeta _2} = \dfrac{ {\left( {1 + \lambda \eta } \right) + {\beta ^2}\eta } } {{\eta + 1} }$
注：${v_{{\rm{p1}}}} \!=\! - \dfrac{\eta }{{1 \!+\! \lambda \eta }}\dfrac{{{q_y}{r^2}}}{{2E{I_{\textit{z}}}}}{x^2} \!+\! \dfrac{1}{{1 \!+\! \lambda \eta }}\dfrac{{{r^4}}}{{E{I_{\textit{z}}}}}{q_y}$；${\theta _{x{\rm{p1}}}} \!=\! \dfrac{{1 \!+\! \eta }}{{1 \!+\! \lambda \eta }}\dfrac{{{q_y}{r^3}}}{{E{I_{\textit{z}}}}}$；${v_{{\rm{p2}}}} \!=\! - \dfrac{{{\eta ^2}}}{{2\eta + 1}}\dfrac{1}{{E{I_{\textit{z}}}}}\dfrac{{{q_y}{x^4}}}{{24}} \!+\! \dfrac{\eta }{{2\eta + 1}}\dfrac{{{r^2}}}{{E{I_{\textit{z}}}}}\dfrac{{{q_y}{x^2}}}{2}$；${\theta _{x{\rm{p2}}}} \!=\! \dfrac{{\left( {\eta \!+\! 1} \right)\eta }}{{2\eta \!+\! 1}}\dfrac{r}{{E{I_{\textit{z}}}}}\dfrac{{{q_y}{x^2}}}{2}$.

下载: 导出CSV

表 2 圆曲梁支座边界条件

Table 2. Support boundary conditions of circular curved beam

边界条件	分类	物理量	固支			铰支	插支	自由端
边界条件	分类	物理量	弯固	扭固^①	全固	铰支	插支	自由端
几何边界条件	弯曲	挠度	$v = 0$	$v = 0$	$v = 0$	$v = 0$	$v = 0$
	弯曲	弯曲转角	${\theta _{\textit{z}}} = 0$				${\theta _{\textit{z}}} = 0$
	扭转	扭角	${\theta _x} = 0$	${\theta _x} = 0$	${\theta _x} = 0$	${\theta _x} = 0$
		扭角一阶导数		${\theta '_x} = 0$
		扭率			${\kappa _x} = 0$^②		（${\kappa _x} = 0$）^③	（${\kappa _x} = 0$）^③
自然边界条件	弯曲	弯矩				${M_{\textit{z}}} = 0$		${M_{\textit{z}}} = 0$
	弯曲	剪力						${V_y} = 0$
	扭转	扭矩					$T_x = 0$	$T_x = 0$
	扭转	双力矩					$B = 0$	$B = 0$
注：① 此条件为文献[4-5]采用的嵌固边界条件；② 此条件为文献[1，27]所给，需要注意的是：该条件在形式上综合了${\theta _{\textit{z}}} = 0$及 ${\theta '_x} = 0$ 这两个条件，然而对于自由扭转曲梁，此条件对应于零扭矩条件，显然此条件只适用于约束扭转曲梁、不适用于自由扭转曲梁；③ 此条件仅适用于等截面自由扭转圆曲梁.

下载: 导出CSV

表 3 各类圆拱临界荷载系数

Table 3. Critical load coefficients of all circular arches

拱类型	模型		圆心角/（°）
拱类型	模型		10	20	30	40	50	60	70	80	90
两端固支拱	本模型	弯固	1 293.009	321.037	141.081	78.141	49.055	33.301	23.845	17.748	13.604
		扭固	1 291.014	319.054	139.120	76.210	47.162	31.454	22.051	16.014	11.937
		全固	1 289.013	317.053	137.118	74.208	45.162	29.459	20.064	14.040	9.981
	文献模型	文献[3]（扭固）	1 293.003	321.012	141.028	78.049	48.916	33.108	23.595	17.438	13.235
		文献[4]（扭固）	1 291.014	319.054	139.120	76.210	47.162	31.454	22.051	16.014	11.937
		文献[4]简化（扭固）	1 293.003	321.012	141.028	78.049	48.916	33.108	23.595	17.438	13.235
		文献[6]（全固）	1 294.704	322.711	142.723	79.740	50.600	34.784	25.260	19.091	14.873
两端铰支拱	本模型		321.012	78.049	33.108	17.438	10.247	6.400	4.138	2.722	1.800
两端铰支拱	文献[3-4,6]		321.012	78.049	33.108	17.438	10.247	6.400	4.138	2.722	1.800
两端插支拱	本模型		1 293.003	321.012	141.028	78.049	48.916	33.108	23.595	17.438	13.235
本模型跨中单铰拱	弯固		324.093	81.093	36.093	20.343	13.053	9.093	6.705	5.156	4.093
本模型跨中单铰拱	扭固		144.221	36.221	16.222	9.223	5.984	4.226	3.167	2.480	2.010

拱类型	模型		圆心角/（°）
拱类型	模型		100	110	120	130	140	150	160	170	180
两端固支拱	本模型	弯固	10.673	8.534	6.933	5.709	4.757	4.007	3.406	2.921	2.525
		扭固	9.078	7.014	5.492	4.349	3.479	2.810	2.292	1.887	1.570
		全固	7.145	5.111	3.623	2.520	1.695	1.075	0.609	0.260	0
	文献模型	文献[3]（扭固）	10.247	8.052	6.400	5.130	4.138	3.352	2.722	2.214	1.800
		文献[4]（扭固）	9.078	7.014	5.492	4.349	3.479	2.810	2.292	1.887	1.570
		文献[4]简化（扭固）	10.247	8.052	6.400	5.130	4.138	3.352	2.722	2.214	1.800
		文献[6]（全固）	11.867	9.653	7.979	6.684	5.664	4.848	4.186	3.644	3.194
两端铰支拱	本模型		1.183	0.765	0.481	0.288	0.161	0.079	0.031	0.007	0
两端铰支拱	文献[3-4,6]		1.183	0.765	0.481	0.288	0.161	0.079	0.031	0.007	0
两端插支拱	本模型		10.247	8.052	6.400	5.130	4.138	3.352	2.722	2.214	1.800
本模型跨中单铰拱	弯固		3.333	2.771	2.343	2.011	1.747	1.534	1.359	1.215	1.094
本模型跨中单铰拱	扭固		1.676	1.429	1.242	1.098	0.985	0.895	0.823	0.764	0.717
注：文献[3]中由于方程过于复杂，放弃了对原位移微分方程的分析，引入小扭转位移的假设对方程进行简化求解. 经过计算可知，文献[4]简化后的模型计算结果与文献[3]模型计算结果完全一致.

下载: 导出CSV

表 4 坐标变量无量纲化

Table 4. Dimensionless of coordinate variables

变量	${q_{\textit{z}}}$	${q_y}$	v
无量纲化	${ { {q_{\textit{z} } }{r^3} }/ {(E{I_{\textit{z}}}) } }$	${ { {q_y}{r^3} } / {(E{I_{\textit{z}}}) } }$	${v / r},\; {v / { { {( { { { {q_y}{r^4} } / {(E{I_{\textit{z} } } } } } ))} } } }$

下载: 导出CSV

参考文献(27)

姚玲森. 曲线梁[M]. 北京: 人民交通出版社, 1989: 1-2.

王佳佳,丁敏,蒋秀根,等. 考虑二阶弯矩效应的自由扭转圆曲梁静力分析[J]. 中国农业大学学报,2019,24(3): 109-116. doi: 10.11841/j.issn.1007-4333.2019.03.14

WANG Jiajia, DING Min, JIANG Xiugen, et al. Static analysis of circular curved beam with free torsion considering second-order moment effect[J]. Journal of China Agricultural University, 2019, 24(3): 109-116. doi: 10.11841/j.issn.1007-4333.2019.03.14

铁摩辛柯 S P, 盖莱 J M. 弹性稳定理论[M]. 2版. 北京: 科学出版社, 1965: 274-281.

项海帆, 刘光栋. 拱结构的稳定与振动[M]. 北京: 人民交通出版社, 1991: 75-87.

窦超. 钢拱平面外稳定性能及设计方法[D]. 北京: 清华大学, 2012.

郭彦林, 窦超. 现代拱形钢结构设计原理与应用[M]. 北京: 科学出版社, 2013: 61-86.

窦超,郭彦林. 压弯圆弧拱平面外稳定承载力设计方法[J]. 建筑结构学报,2012,33(7): 27-36.

DOU Chao, GUO Yanlin. Out-of-plane inelastic stability design of circular arches under combination of compression and bending[J]. Journal of Building Structures, 2012, 33(7): 27-36.

窦超,郭彦林. 圆弧拱平面外弹性弯扭屈曲临界荷载分析[J]. 工程力学,2012,29(3): 83-89,94.

DOU Chao, GUO Yanlin. Study on flexural-torsional buckling load of circular arches[J]. Engineering Mechanics, 2012, 29(3): 83-89,94.

郭彦林,赵思远,窦超. 面外支撑非均匀布置的箱型与圆管截面拱平面外弹性屈曲[J]. 工程力学,2014,31(7): 29-35.

GUO Yanlin, ZHAO Siyuan, DOU Chao. Out-of-plane elastic buckling of close-section steel arches with non-uniform distributed lateral bracings[J]. Engineering Mechanics, 2014, 31(7): 29-35.

窦超,郭彦林. 均匀受压圆弧拱平面外弹塑性稳定设计方法[J]. 建筑结构学报,2012,33(1): 104-110.

DOU Chao, GUO Yanlin. Out-of-plane inelastic stability and strength design of circular arches in uniform compression[J]. Journal of Building Structures, 2012, 33(1): 104-110.

窦超,郭彦林. 受弯圆弧拱平面外稳定承载力分析[J]. 建筑结构学报,2012,33(7): 18-26.

DOU Chao, GUO Yanlin. Out-of-plane inelastic stability of circular arches under bending moment[J]. Journal of Building Structures, 2012, 33(7): 18-26.

邓婷. 基于大位移模型的圆拱几何非线性分析及其应用[D]. 北京: 中国农业大学, 2018.

CHAI H Y. Flexural-torsional stability of curved beams[J]. Journal of Engineering Mechanics Division, 1982, 108(6): 1351-1369.

CHAI H Y, PFEIFFER P A. Elastic stability of curved members[J]. Journal of Structural Engineering, 1983, 109(12): 2922-2940.

CHAI H Y, PFEIFFER P A. Buckling of curved beams with in-plane deformation[J]. Journal of Structural Engineering, 1984, 106(2): 291-300.

YANG Y B, KUO S R. Effect of curvature on stability of curved beams[J]. Journal of Structural Engineering, 1987, 113(6): 1185-1202. doi: 10.1061/(ASCE)0733-9445(1987)113:6(1185)

YANG Y B, KUO S R. Curved beam elements for nonlinear analysis[J]. Journal of Engineering Mechanics, 1989, 115(4): 840-855. doi: 10.1061/(ASCE)0733-9399(1989)115:4(840)

YANG Y B, KUO S R. Static stability of curved thin-walled beams[J]. Journal of Engineering Mechanics, 1986, 112(8): 821-841. doi: 10.1061/(ASCE)0733-9399(1986)112:8(821)

段炼. 曲梁弯扭屈曲分析[J]. 工程力学,1989,6(3): 41-54.

DUAN Lian. Analysis of bending and torsional buckling of curved beam[J]. Engineering Mechanics, 1989, 6(3): 41-54.

KANG Y J, YOO C H. Thin-walled curved beams I formulation of nonlinear equations[J]. Journal of Engineering Mechanics,ASCE, 1994, 120(10): 2072-2101. doi: 10.1061/(ASCE)0733-9399(1994)120:10(2072)

KANG Y J, YOO C H. Thin-walled curved beams II analytical solution for bucking of arches[J]. Journal of Engineering Mechanics, 1994, 120(10): 2102-2125. doi: 10.1061/(ASCE)0733-9399(1994)120:10(2102)

许强,童根树. 任意开口薄壁截面圆弧曲梁的通用线性理论[J]. 工程力学,2002,19(6): 141-147. doi: 10.3969/j.issn.1000-4750.2002.06.028

XU Qiang, TONG Genshu. General linear theory of curved beam with arbitrary thin-wall section[J]. Engineering Mechanics, 2002, 19(6): 141-147. doi: 10.3969/j.issn.1000-4750.2002.06.028

杨永华. 弹性开口薄壁截面圆弧钢拱的稳定承载力研究[D]. 上海: 同济大学, 2006.

刘磊,许克宾. 曲杆结构非线性分析中的直梁单元和曲梁单元[J]. 铁道学报,2001,23(6): 72-76. doi: 10.3321/j.issn:1001-8360.2001.06.016

LIU Lei, XU Kebin. Curved-beam element and straight-beam element used in the nonlinear analysis of curved frame structures[J]. Journal of the China Railway Society, 2001, 23(6): 72-76. doi: 10.3321/j.issn:1001-8360.2001.06.016

刘磊. 大跨度混凝土桥梁的双非线性分析[D]. 北京: 北京交通大学, 2000.

程鹏. 两铰圆弧拱非线性弯曲理论和弹塑性稳定[D]. 杭州: 浙江大学, 2005.

HEINS C P. Bending and torsional design in structural members[M]. [S.l.]: Heath and Company, 1975: 124-125.

施引文献

附加材料(0)

访问统计